A DFT Study on the O2 Adsorption Properties of Supported PtNi Clusters
Abstract
:1. Introduction
2. Methodology
3. Energetic Analysis
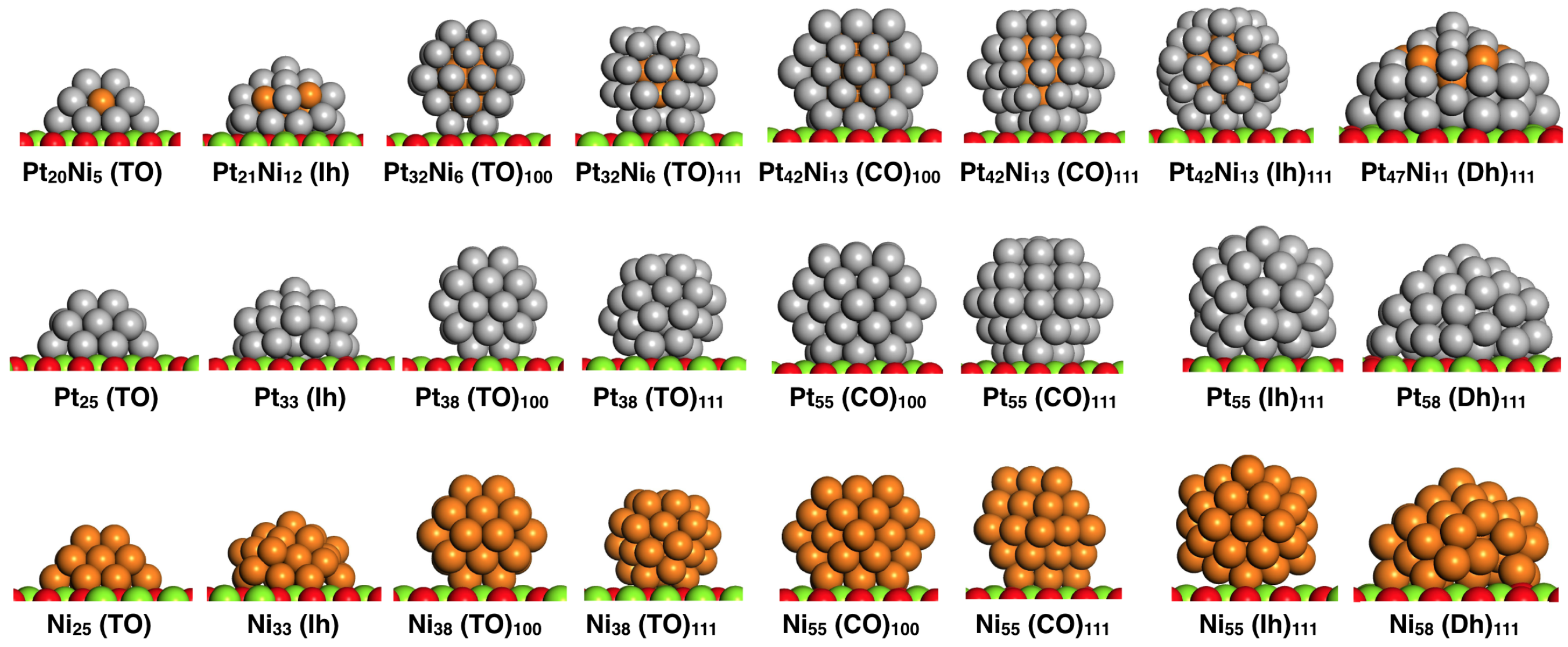
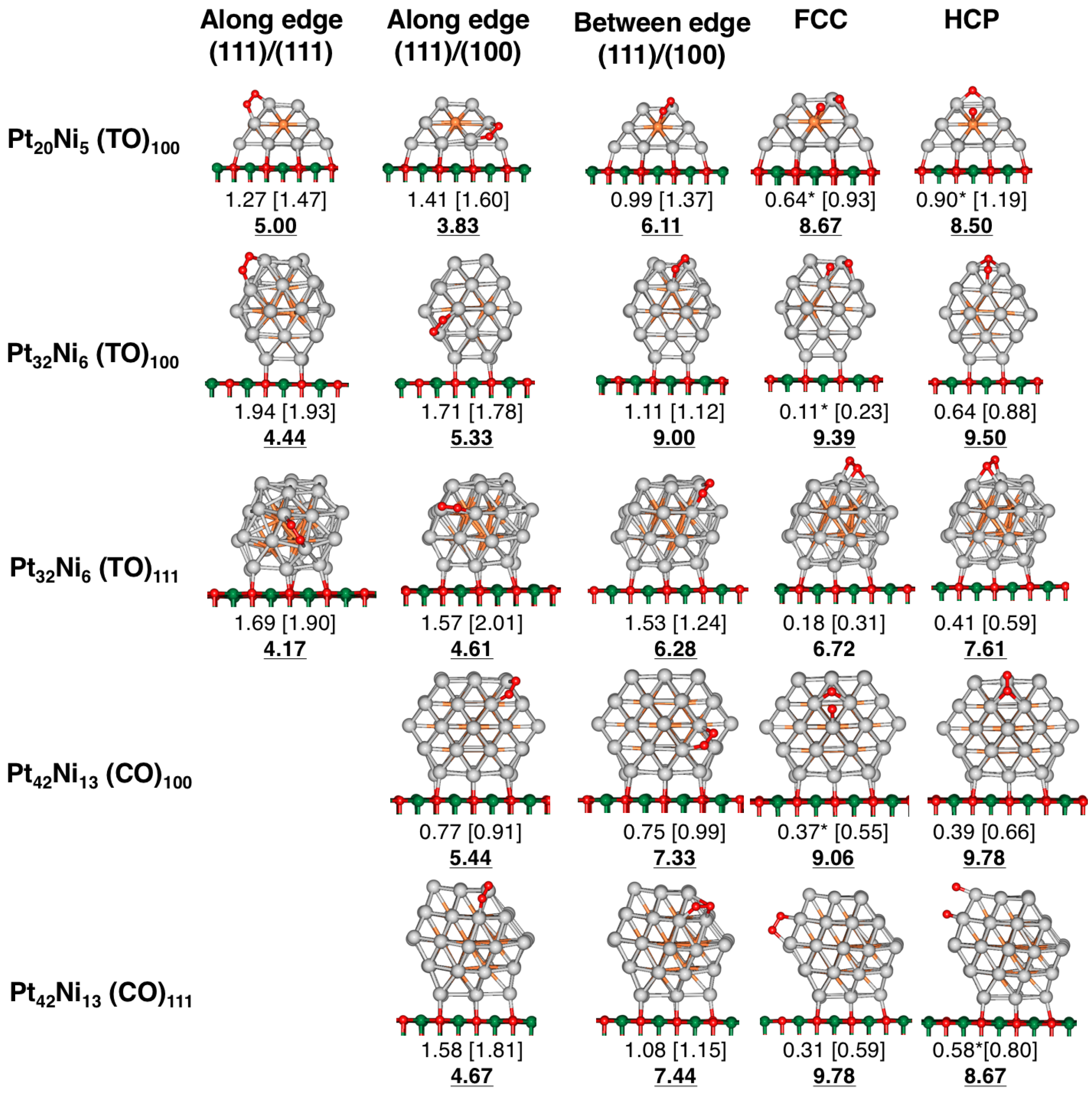
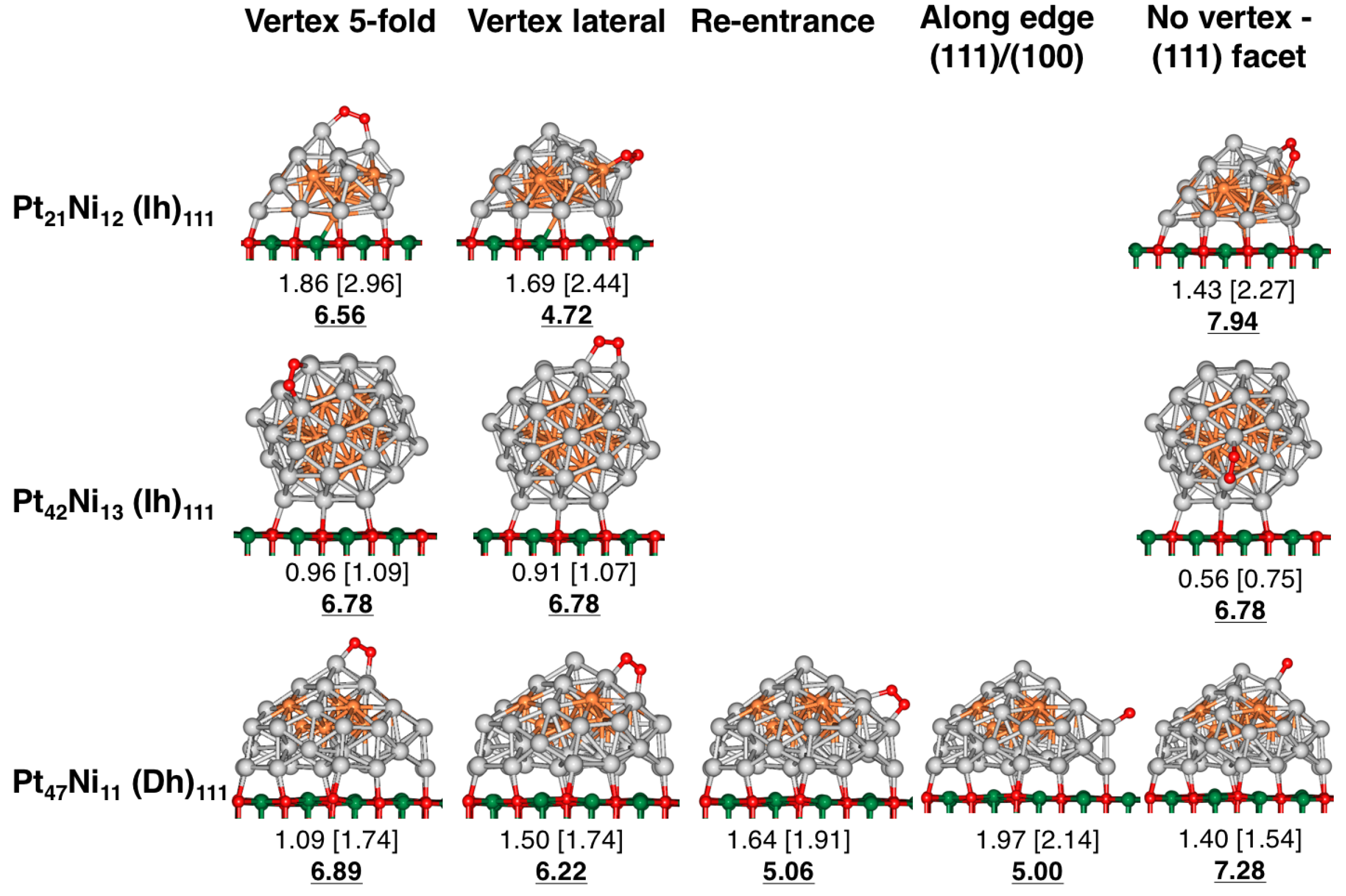
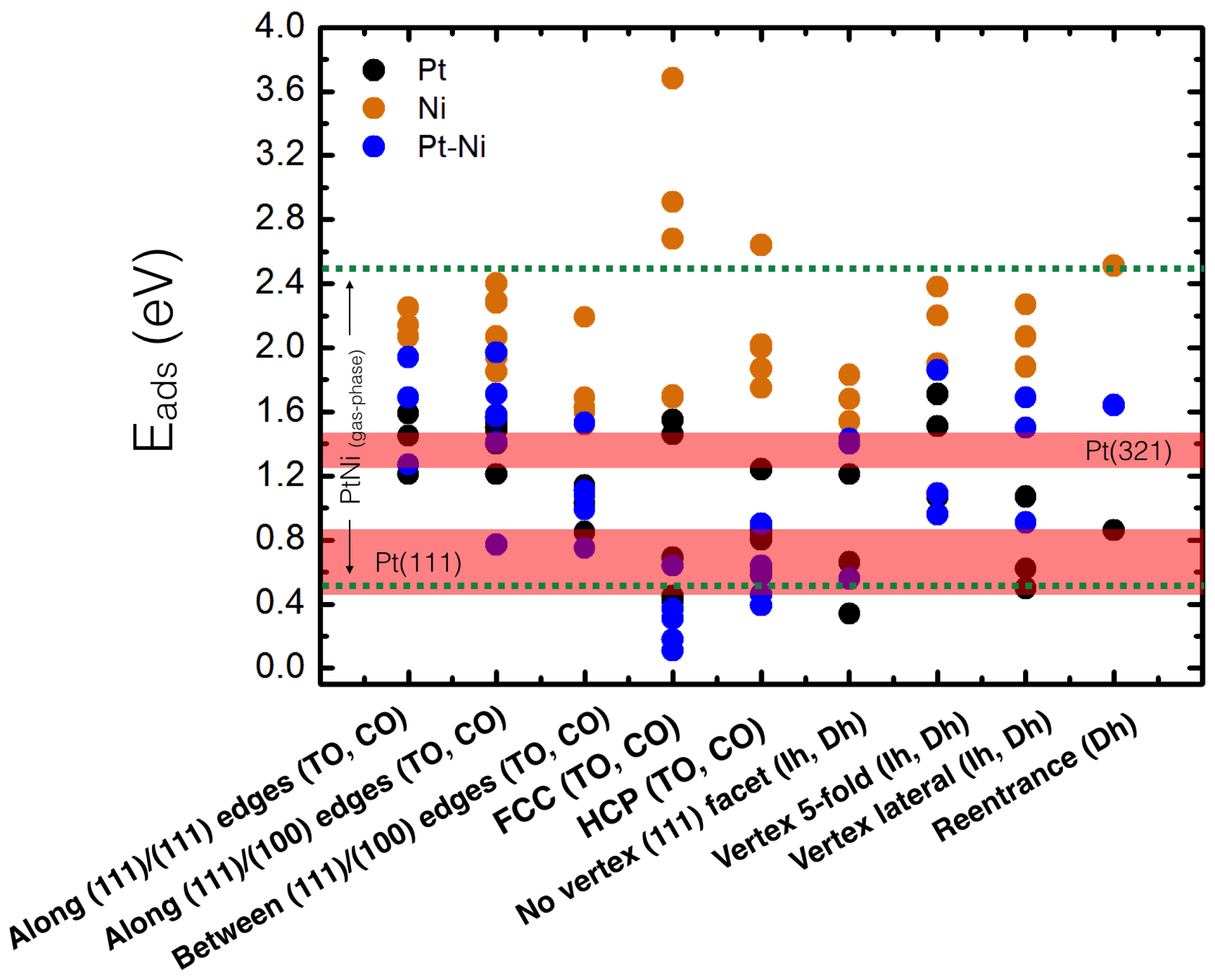
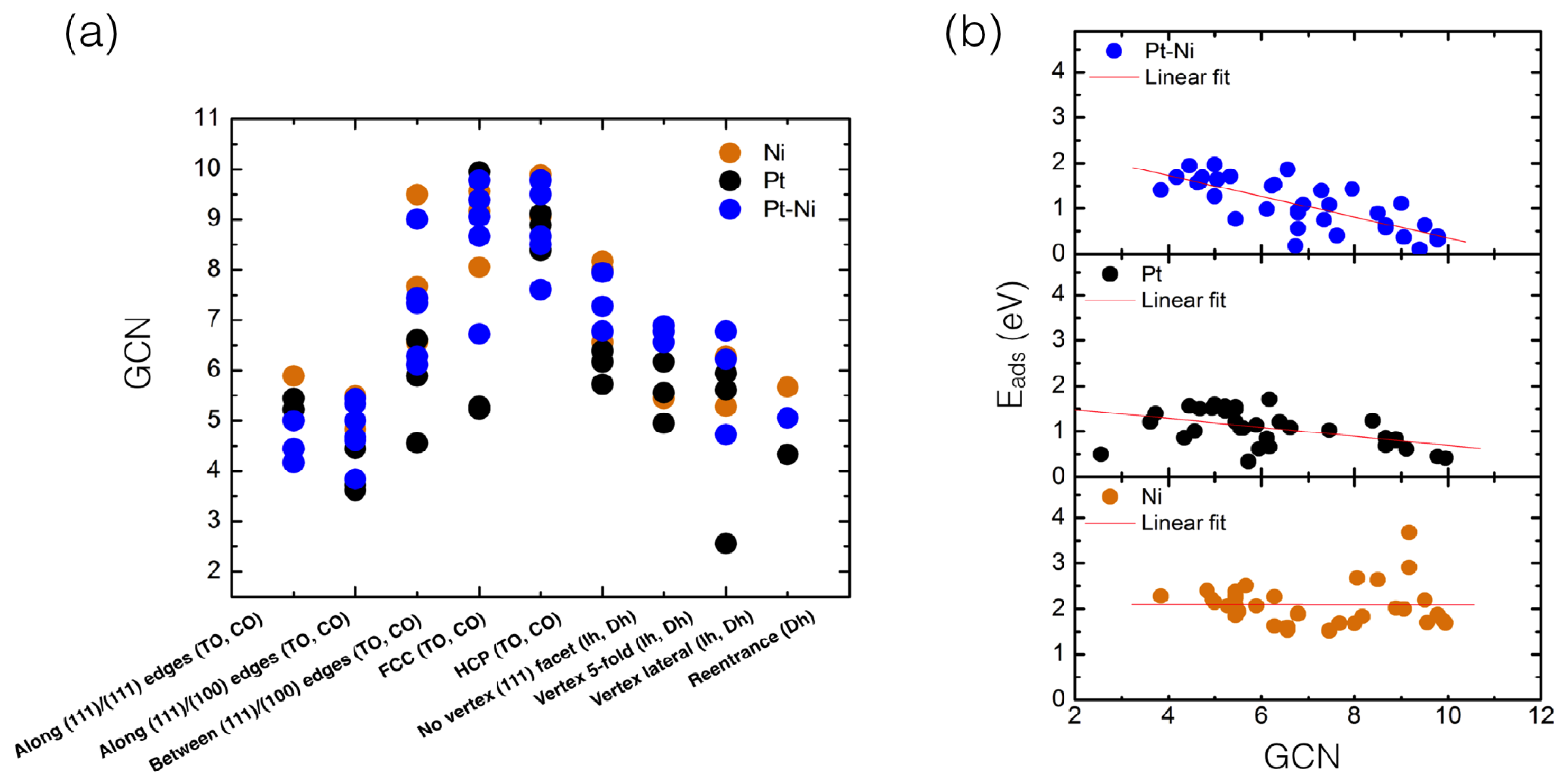
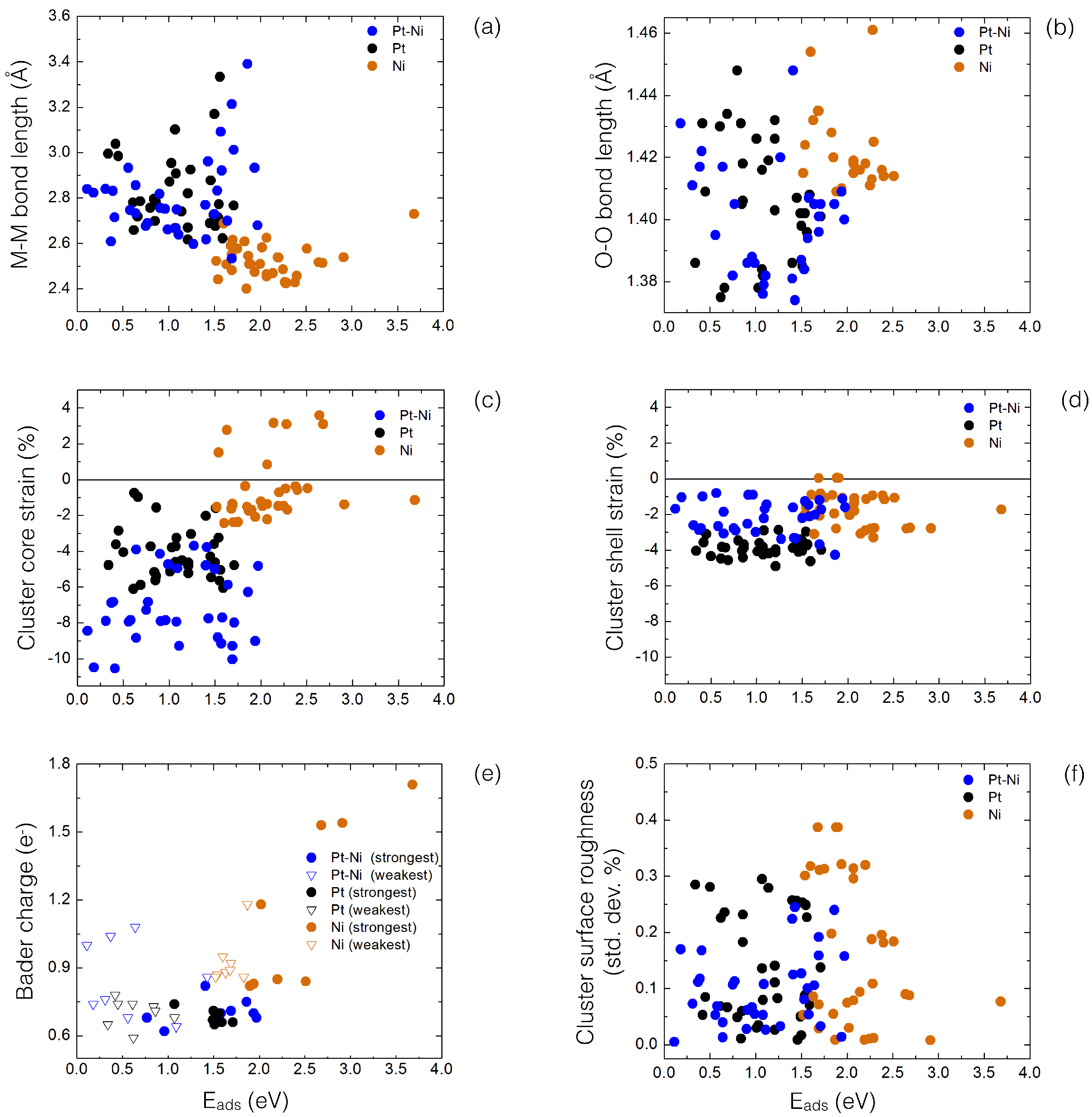
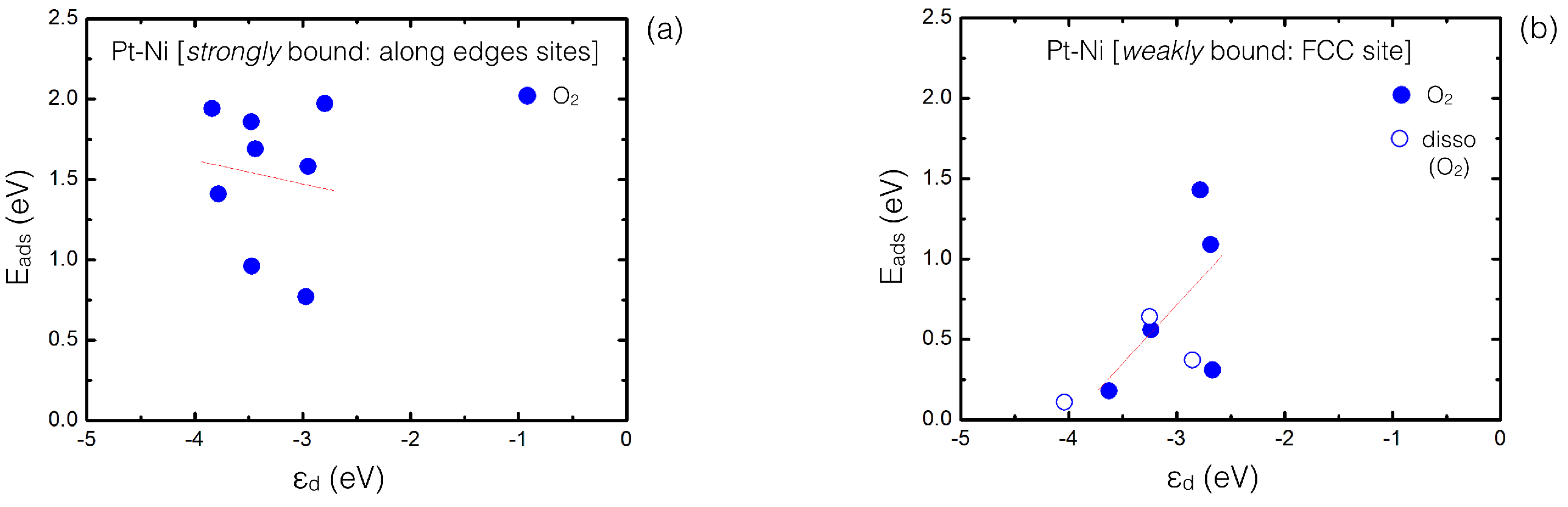
4. Results and Discussion
4.1. O Adsorption Trends on Supported PtNi Nanoparticles
4.2. Inclusion of van der Waals Corrections
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Steele, B.C.H.; Heinzel, A. Materials for Fuel-Cell Technologies. Nature 2001, 414, 345–352. [Google Scholar] [CrossRef] [PubMed]
- Yamada, T.; Sadakiyo, M.; Shigematsu, A.; Kitagawa, H. Proton-Conductive Metal–Organic Frameworks. Bull. Chem. Soc. Jpn. 2016, 89, 1–10. [Google Scholar] [CrossRef]
- Meng, X.; Wang, H.-N.; Song, S.-Y.; Zhang, H.-J. Proton-Conducting Crystalline Porous Materials. Chem. Soc. Rev. 2017, 46, 464–480. [Google Scholar] [CrossRef] [PubMed]
- Sakaushi, K.; Antonietti, M. Carbon- and Nitrogen-Based Porous Solids: A Recently Emerging Class of Materials. Bull. Chem. Soc. Jpn. 2015, 88, 386–398. [Google Scholar] [CrossRef]
- Shao, M.; Chang, Q.; Dodelet, J.-P.; Chenitz, R. Recent Advances in Electrocatalysts for Oxygen Reduction Reaction. Chem. Rev. 2016, 116, 3594–3657. [Google Scholar] [CrossRef] [PubMed]
- Debe, M.K. Electrocatalyst Approaches and Challenges for Automotive Fuel Cells. Nature 2012, 486, 43–51. [Google Scholar] [CrossRef] [PubMed]
- Greeley, J.; Stephens, I.E.L.; Bondarenko, A.S.; Johansson, T.P.; Hansen, H.A.; Jaramillo, T.F.; Rossmeisl, J.; Chorkendorff, I.; Norskov, J.K. Alloys of Platinum and Early Transition Metals as Oxygen Reduction Electrocatalysts. Nat. Chem. 2009, 1, 552–556. [Google Scholar] [CrossRef] [PubMed]
- Strasser, P.; Koh, S.; Anniyev, T.; Greeley, J.; More, K.; Yu, C.; Liu, Z.; Kaya, S.; Nordlund, D.; Ogasawara, H.; et al. Lattice-Strain Control of the Activity in Dealloyed Core–Shell Fuel Cell Catalysts. Nat. Chem. 2010, 2, 454–460. [Google Scholar] [CrossRef] [PubMed]
- Stamenkovic, V.R.; Mun, B.S.; Arenz, M.; Mayrhofer, K.J.J.; Lucas, C.A.; Wang, G.; Ross, P.N.; Marković, N.M. Trends in Electrocatalysis on Extended and Nanoscale Pt-Bimetallic Alloy Surfaces. Nat. Mater. 2007, 6, 241–247. [Google Scholar] [CrossRef] [PubMed]
- Gasteiger, H.A.; Kocha, S.S.; Sompalli, B.; Wagner, F.T. Activity Benchmarks and Requirements for Pt, Pt-alloy, and non-Pt Oxygen Reduction Catalysts for PEMFCs. Appl. Catal. B Environ. 2005, 56, 9–35. [Google Scholar] [CrossRef]
- Stamenkovic, V.R.; Fowler, B.; Mun, B.S.; Wang, G.; Ross, P.N.; Lucas, C.A.; Marković, N.M. Improved Oxygen Reduction Activity on Pt3Ni(111) via Increased Surface Site Availability. Science 2007, 315, 493–497. [Google Scholar] [CrossRef] [PubMed]
- Strasser, P. Catalysts by Platonic Design. Science 2015, 349, 379–380. [Google Scholar] [CrossRef] [PubMed]
- Carpenter, M.K.; Moylan, T.E.; Kukreja, R.S.; Atwan, M.H.; Tessema, M.M. Solvothermal Synthesis of Platinum Alloy Nanoparticles for Oxygen Reduction Electrocatalysis. J. Am. Chem. Soc. 2012, 134, 8535–8542. [Google Scholar] [CrossRef] [PubMed]
- Cui, C.; Gan, L.; Heggen, M.; Rudi, S.; Strasser, P. Compositional Segregation in Shaped Pt Alloy Nanoparticles and Their Structural Behaviour During Electrocatalysis. Nat. Mater. 2013, 12, 765–771. [Google Scholar] [CrossRef] [PubMed]
- Choi, S.-I.; Shao, M.; Lu, N.; Ruditskiy, A.; Peng, H.-C.; Park, J.; Guerrero, S.; Wang, J.; Kim, M.J.; Xia, Y. Synthesis and Characterization of Pd@Pt–Ni Core–Shell Octahedra with High Activity toward Oxygen Reduction. ACS Nano 2014, 8, 10363–10371. [Google Scholar] [CrossRef] [PubMed]
- Choi, S.-I.; Xie, S.; Shao, M.; Odell, J.H.; Lu, N.; Peng, H.-C.; Protsailo, L.; Guerrero, S.; Park, J.; Xia, X.; et al. Synthesis and Characterization of 9 nm Pt–Ni Octahedra with a Record High Activity of 3.3 A/mgPt for the Oxygen Reduction Reaction. Nano Lett. 2013, 13, 3420–3425. [Google Scholar] [CrossRef] [PubMed]
- Cui, C.; Gan, L.; Li, H.-H.; Yu, S.-H.; Heggen, M.; Strasser, P. Octahedral PtNi Nanoparticle Catalysts: Exceptional Oxygen Reduction Activity by Tuning the Alloy Particle Surface Composition. Nano Lett. 2012, 12, 5885–5889. [Google Scholar] [CrossRef] [PubMed]
- Huang, X.; Zhao, Z.; Chen, Y.; Zhu, E.; Li, M.; Duan, X.; Huang, Y. A Rational Design of Carbon-Supported Dispersive Pt-based Octahedra as Efficient Oxygen Reduction Reaction Catalysts. Energy Environ. Sci. 2014, 7, 2957–2962. [Google Scholar] [CrossRef]
- Zhang, C.; Hwang, S.Y.; Peng, Z. Size-dependent Oxygen Reduction Property of Octahedral Pt–Ni Nanoparticle Electrocatalysts. J. Mater. Chem. A 2014, 2, 19778–19787. [Google Scholar] [CrossRef]
- Zhang, C.; Hwang, S.Y.; Trout, A.; Peng, Z. Solid-State Chemistry-Enabled Scalable Production of Octahedral Pt–Ni Alloy Electrocatalyst for Oxygen Reduction Reaction. J. Am. Chem. Soc. 2014, 136, 7805–7808. [Google Scholar] [CrossRef] [PubMed]
- Bao, H.; Li, J.; Jiang, L.; Shang, M.; Zhang, S.; Jiang, Z.; Wei, X.; Huang, Y.; Sun, G.; Wang, J.-Q. Structure of PtnNi Nanoparticles Electrocatalysts Investigated by X-ray Absorption Spectroscopy. J. Phys. Chem. C 2013, 117, 20584–20591. [Google Scholar] [CrossRef]
- Wang, G.; van Hove, M.A.; Ross, P.N.; Baskes, M.I. Monte Carlo Simulations of Segregation in Pt–Ni Catalyst Nanoparticles. J. Chem. Phys. 2005, 122, 024706. [Google Scholar] [CrossRef] [PubMed]
- Radillo-Díaz, A.; Coronado, Y.; Pérez, L.; Garzón, I.L. Structural and Electronic Properties of PtPd and PtNi Nanoalloys. Eur. Phys. J. D 2009, 52, 127–130. [Google Scholar] [CrossRef]
- Di Paola, C.; Baletto, F. Oxygen Adsorption on Small PtNi Nanoalloys. Phys. Chem. Chem. Phys. 2011, 13, 7701–7707. [Google Scholar] [CrossRef] [PubMed]
- Fortunelli, A.; Goddard, W.A., III; Sementa, L.; Barcaro, G.; Negreiros, F.R.; Jaramillo-Botero, A. The Atomistic Origin of the Extraordinary Oxygen Reduction Activity of Pt3Ni7 Fuel Cell Catalysts. Chem. Sci. 2015, 6, 3915–3925. [Google Scholar] [CrossRef]
- Calle-Vallejo, F.; Sautet, P.; Loffreda, D. Understanding Adsorption-Induced Effects on Platinum Nanoparticles: An Energy-Decomposition Analysis. J. Phys. Chem. Lett. 2014, 5, 3120–3124. [Google Scholar] [CrossRef] [PubMed]
- Calle-Vallejo, F.; Martínez, J.I.; García-Lastra, J.M.; Sautet, P.; Loffreda, D. Fast Prediction of Adsorption Properties for Platinum Nanocatalysts with Generalized Coordination Numbers. Angew. Chem. Int. Ed. 2014, 53, 8316–8319. [Google Scholar] [CrossRef] [PubMed]
- Calle-Vallejo, F.; Loffreda, D.; Koper, M.T.M.; Sautet, P. Introducing Structural Sensitivity into Adsorption–Energy Scaling Relations by Means of Coordination Numbers. Nat. Chem. 2015, 7, 403–410. [Google Scholar] [CrossRef] [PubMed]
- Calle-Vallejo, F.; Tymoczko, J.; Colic, V.; Vu, Q.H.; Pohl, M.D.; Morgenstern, K.; Loffreda, D.; Sautet, P.; Schuhmann, W.; Bandarenka, A.S. Finding Optimal Surface Sites on Heterogeneous Catalysts by Counting Nearest Neighbors. Science 2015, 350, 185–189. [Google Scholar] [CrossRef] [PubMed]
- Asara, G.G.; Paz-Borbón, L.O.; Baletto, F. “Get in Touch and Keep in Contact”: Interface Effect on the Oxygen Reduction Reaction (ORR) Activity for Supported PtNi Nanoparticles. ACS Catal. 2016, 6, 4388–4393. [Google Scholar] [CrossRef]
- Litster, S.; McLean, G. PEM Fuel Cell Electrodes. J. Power Sources 2004, 130, 61–76. [Google Scholar] [CrossRef]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, M.; et al. QUANTUM ESPRESSO: A Modular and Open-Source Software Project for Quantum Simulations of Materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Rappe, A.M.; Rabe, K.M.; Kaxiras, E.; Joannopoulos, J.D. Optimized pseudopotentials. Phys. Rev. B 1990, 41, 1227–1230. [Google Scholar] [CrossRef]
- Garrity, K.F.; Bennett, J.W.; Rabe, K.M.; Vanderbilt, D. Pseudopotentials for High-Throughput DFT Calculations. Comput. Mater. Sci. 2014, 81, 446–452. [Google Scholar] [CrossRef]
- Broqvist, P.; Grönbeck, H.; Panas, I. Surface Properties of Alkaline Earth Metal Oxides. Surf. Sci. 2004, 554, 262–271. [Google Scholar] [CrossRef]
- Paier, J.; Marsman, M.; Hummer, K.; Kresse, G.; Gerber, I.C.; Àngyàn, J. Screened Hybrid Density Functionals Applied to Solids. J. Chem. Phys. 2006, 124, 154709. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S. Accurate Description of van der Waals Complexes by Density Functional Theory Including Empirical Corrections. J. Comput. Chem. 2004, 25, 1463–1473. [Google Scholar] [CrossRef] [PubMed]
- Rossi, K.; Ellaby, T.; Paz-Borbón, L.O.; Atanasov, I.; Pavan, L.; Baletto, F. Melting of Large Pt@MgO(100) Icosahedra. J. Phys. Condens. Matter 2017, 29, 145402. [Google Scholar] [CrossRef] [PubMed]
- Engelke, M.J. Local Atomic Arrangements in Ni–Pt: The Bulk and Near-Surface Regimes. Ph.D. Thesis, ETH Zürich, Swiss Federal Institute of Technology, Zurich, Switzerland, 2010. [Google Scholar]
- Darlington, M.J.D. Stability of Single Crystal Pt and Pt3Ni Surfaces During Electro-Oxidation. Ph.D. Thesis, The University of Liverpool, Liverpool, UK, 2014. [Google Scholar]
- Li, T.; Balbuena, P.B. Computational Studies of the Interactions of Oxygen with Platinum Clusters. J. Phys. Chem. B 2001, 105, 9943–9952. [Google Scholar] [CrossRef]
- Jennings, P.C.; Aleksandrov, H.A.; Neyman, K.M.; Johnston, R.L. A DFT Study of Oxygen Dissociation on Platinum Based Nanoparticles. Nanoscale 2014, 6, 1153–1165. [Google Scholar] [CrossRef] [PubMed]
- Shao, M.; Peles, A.; Shoemaker, K. Electrocatalysis on Platinum Nanoparticles: Particle Size Effect on Oxygen Reduction Reaction Activity. Nano Lett. 2011, 11, 3714–3719. [Google Scholar] [CrossRef] [PubMed]
- Bocquet, M.-L.; Cerdà, J.; Sautet, P. Transformation of Molecular Oxygen on a Platinum Surface: A theoretical Calculation of STM images. Phys. Rev. B 1999, 59, 15437–15445. [Google Scholar] [CrossRef]
- Eichler, A.; Hafner, J. Molecular Precursors in the Dissociative Adsorption of O2 on Pt(111). Phys. Rev. Lett. 1997, 79, 4481–4484. [Google Scholar] [CrossRef]
- McEwen, J.S.; Bray, J.M.; Wucb, C.; Schneider, W.F. How Low Can You Go? Minimum Energy Pathways for O2 Dissociation on Pt(111). Phys. Chem. Chem. Phys. 2012, 14, 16677–16685. [Google Scholar] [CrossRef] [PubMed]
- Gland, J.L.; Sexton, B.A.; Fisher, G.B. Oxygen Interactions with the Pt(111) Surface. Surf. Sci. 1980, 95, 587–602. [Google Scholar] [CrossRef]
- Steininger, H.; Lehwald, S.; Ibach, H. Adsorption of Oxygen on Pt(111). Surf. Sci. 1982, 123, 1–17. [Google Scholar] [CrossRef]
- Bray, J.M.; Schneider, W.F. Potential Energy Surfaces for Oxygen Adsorption, Dissociation, and Diffusion at the Pt(321) Surface. Langmuir 2011, 27, 8177. [Google Scholar] [CrossRef] [PubMed]
- Jennings, P.C.; Aleksandrov, H.A.; Neyman, K.M.; Johnston, R.L. DFT Studies of Oxygen Dissociation on the 116-Atom Platinum Truncated Octahedron Particle. Phys. Chem. Chem. Phys. 2014, 16, 26539–26545. [Google Scholar] [CrossRef] [PubMed]
- Jennings, P.C.; Aleksandrow, H.A.; Neyman, K.M.; Johnston, R.L. O2 Dissociation on M@Pt Core–Shell Particles for 3d, 4d, and 5d Transition Metals. J. Phys. Chem. C 2015, 119, 11031. [Google Scholar] [CrossRef]
- Huang, X.; Zhao, Z.; Cao, L.; Chen, Y.; Zhu, E.; Lin, Z.; Li, M.; Yan, A.; Zettl, A.; Morris Wang, Y.; et al. High-Performance Transition Metal-Doped Pt3Ni Octahedra for Oxygen Reduction Reaction. Science 2015, 348, 1230–1234. [Google Scholar] [CrossRef] [PubMed]
- Hernandez-Fernandez, P.; Masini, F.; McCarthy, D.N.; Strebel, C.E.; Friebel, D.; Deiana, D.; Malacrida, P.; Nierhoff, A.; Bodin, A.; Wise, A.M.; et al. Mass-selected Nanoparticles of PtxY as Model Catalysts for Oxygen Electroreduction. Nat. Chem. 2014, 6, 732–738. [Google Scholar] [CrossRef] [PubMed]
- Norskov, J.K.; Bligaard, T.; Hvolbaek, B.; Abild-Pedersen, F.; Chorkendorff, I.; Christensen, C.H. The Nature of the Active Site in Heterogeneous Metal Catalysis. Chem. Soc. Rev. 2008, 37, 2163–2171. [Google Scholar] [CrossRef] [PubMed]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Paz-Borbón, L.O.; Baletto, F. A DFT Study on the O2 Adsorption Properties of Supported PtNi Clusters. Inorganics 2017, 5, 43. https://doi.org/10.3390/inorganics5030043
Paz-Borbón LO, Baletto F. A DFT Study on the O2 Adsorption Properties of Supported PtNi Clusters. Inorganics. 2017; 5(3):43. https://doi.org/10.3390/inorganics5030043
Chicago/Turabian StylePaz-Borbón, Lauro Oliver, and Francesca Baletto. 2017. "A DFT Study on the O2 Adsorption Properties of Supported PtNi Clusters" Inorganics 5, no. 3: 43. https://doi.org/10.3390/inorganics5030043





