Transient and Fast Generation of Bose-Einstein-Condensate Macroscopic Quantum Superposition States via Impurity Catalysing
Abstract
:1. Introduction
2. The Impurities-Doped BEC Model
3. Deterministic Creation of MQS States
3.1. Creating Multi-Component MQS States
3.2. Creating a Pair of Approximately Orthogonal Cat States
4. Engineering MQS States in Phase Space
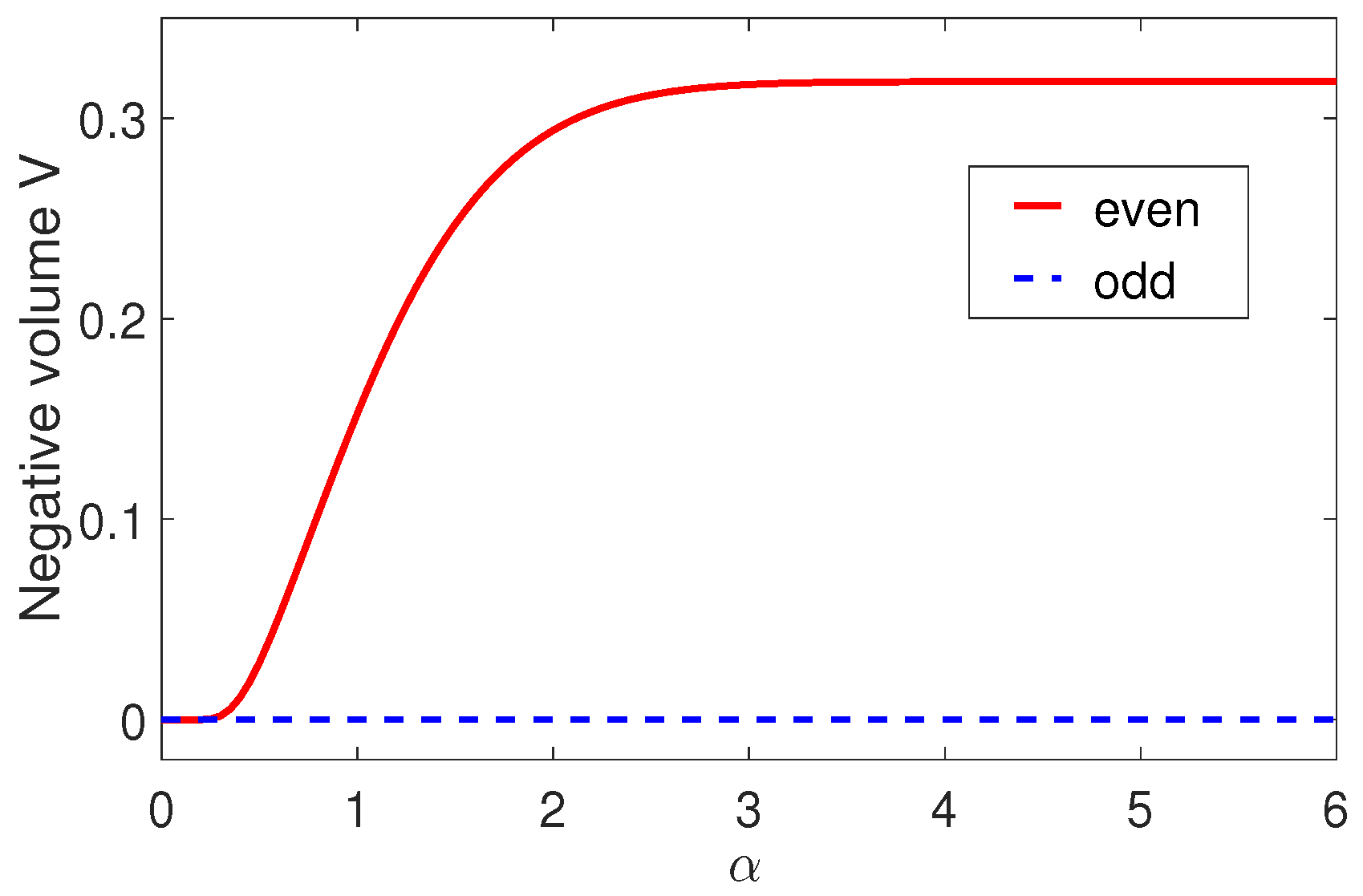
4.1. Wigner Function of MQS States
4.2. The Transition between Classic Mixed and Quantum Superposition
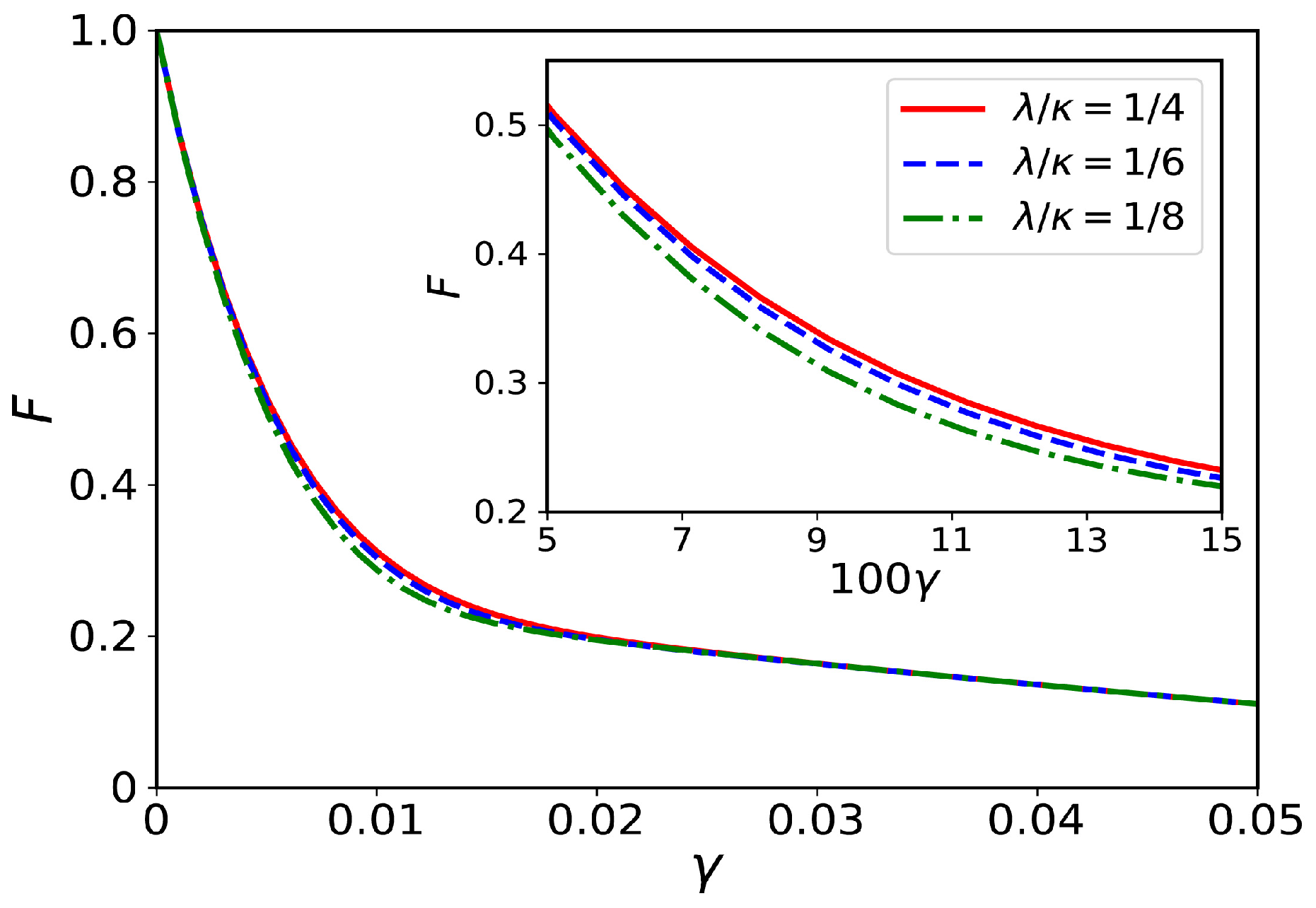
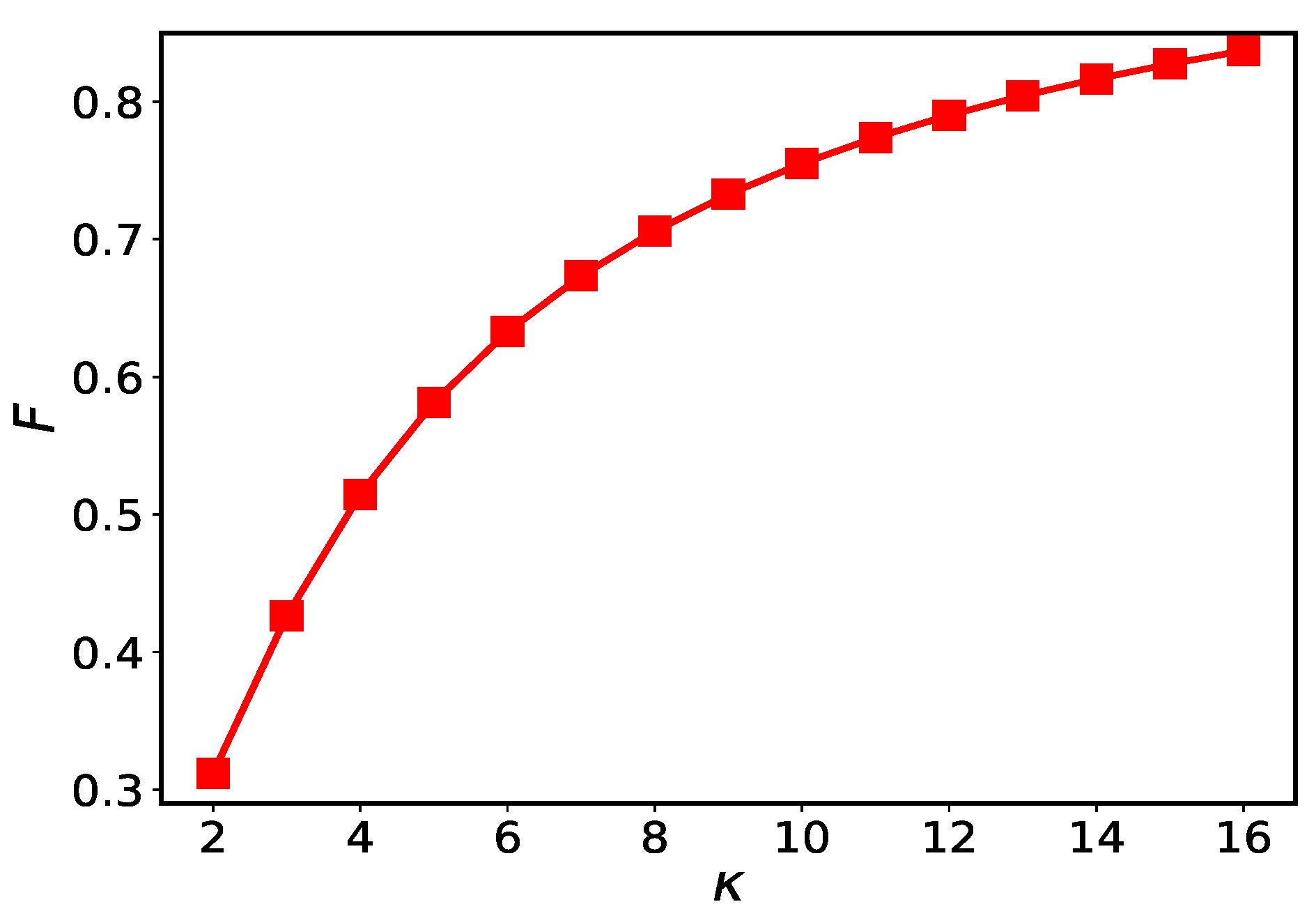
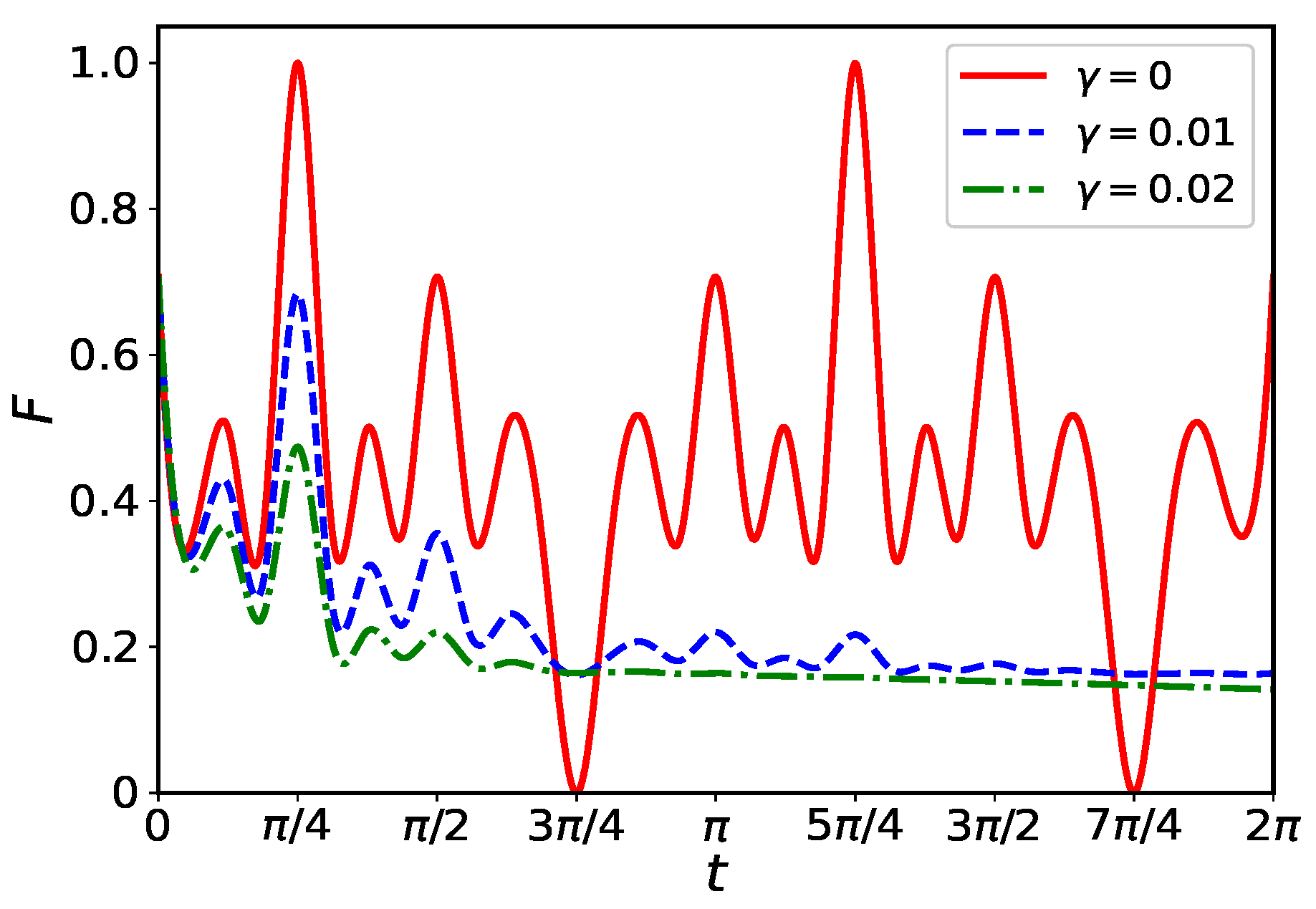
5. Fast Generation of High-Fidelity MQS States in Open Systems
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dirac, P.A.M. The Principles of Quantum Mechanics; Oxford University Press: Oxford, UK, 1958. [Google Scholar]
- Zurek, W.H. Decoherence and the Transition from Quantum to Classical. Phys. Today 1991, 44, 36. [Google Scholar] [CrossRef]
- Schrödinger, E. Die gegenwärtige Situation in der Quantenmechanik. Naturwissenschaften 1935, 23, 807. [Google Scholar] [CrossRef]
- Ghobadi, R.; Kumar, S.; Pepper, B.; Bouwmeester, D.; Lvovsky, A.I.; Simon, C. Optomechanical Micro-Macro Entanglement. Phys. Rev. Lett. 2014, 112, 080503. [Google Scholar] [CrossRef]
- Stobińska, M.; Jeong, H.; Ralph, T.C. Violation of Bell’s inequality using classical measurements and nonlinear local operations. Phys. Rev. A 2007, 75, 052105. [Google Scholar] [CrossRef]
- Jeong, H.; Son, W.; Kim, M.S.; Ahn, D.; Brukner, Č. Quantum nonlocality test for continuous-variable states with dichotomic observables. Phys. Rev. A 2003, 67, 012106. [Google Scholar] [CrossRef]
- Vlastakis, B.; Kirchmair, G.; Leghtas, Z.; Nigg, S.E.; Frunzio, L.; Girvin, S.M.; Mirrahimi, M.; Devoret, M.H.; Schoelkopf, R.J. Deterministically Encoding Quantum Information Using 100-Photon Schrödinger Cat States. Science 2013, 342, 607. [Google Scholar] [CrossRef]
- Leghtas, Z.; Kirchmair, G.; Vlastakis, B.; Schoelkopf, R.J.; Devoret, M.H.; Mirrahimi, M. Hardware-Efficient Autonomous Quantum Memory Protection. Phys. Rev. Lett. 2013, 111, 120501. [Google Scholar] [CrossRef]
- Albert, V.V.; Shu, C.; Krastanov, S.; Shen, C.; Liu, R.-B.; Yang, Z.-B.; Schoelkopf, R.J.; Mirrahimi, M.; Devoret, M.H.; Jiang, L. Holonomic Quantum Control with Continuous Variable Systems. Phys. Rev. Lett. 2016, 116, 140502. [Google Scholar] [CrossRef]
- Cai, W.; Ma, Y.; Wang, W.; Zou, C.-L.; Sun, L. Bosonic quantum error correction codes in superconducting quantum circuits. Fund. Res. 2021, 1, 50–67. [Google Scholar] [CrossRef]
- Albert, V.V.; Mundhada, S.O.; Grimm, A.; Touzard, S.; Devoret, M.H.; Jiang, L. Pair-cat codes: Autonomous error-correction with low-order nonlinearity. Quantum Sci. Technol. 2019, 4, 035007. [Google Scholar] [CrossRef] [Green Version]
- Pezzè, L.; Smerzi, A.; Oberthaler, M.K.; Schmied, R.; Treutlein, P. Quantum metrology with nonclassical states of atomic ensembles. Rev. Mod. Phys. 2018, 90, 035005. [Google Scholar] [CrossRef]
- Facon, A.; Dietsche, E.-K.; Grosso, D.; Haroche, S.; Raimond, J.-M.; Brune, M.; Gleyzes, S. A sensitive electrometer based on a Rydberg atom in a Schrödinger-cat state. Nature 2016, 535, 262. [Google Scholar] [CrossRef]
- McConnell, R.; Zhang, H.; Ćuk, S.; Hu, J.; Schleier-Smith, M.H.; Vuletić, V. Generating entangled spin states for quantum metrology by single-photon detection. Phys. Rev. A 2013, 88, 063802. [Google Scholar] [CrossRef]
- Duan, L.M.; Lukin, M.D.; Cirac, J.I.; Zoller, P. Long-distance quantum communication with atomic ensembles and linear optics. Nature 2001, 414, 413. [Google Scholar] [CrossRef]
- van Enk, S.J.; Hirota, O. Entangled coherent states: Teleportation and decoherence. Phys. Rev. A 2001, 64, 022313. [Google Scholar] [CrossRef]
- Wineland, D.J. Nobel Lecture: Superposition, entanglement, and raising Schrödinger’s cat. Rev. Mod. Phys. 2013, 85, 1103. [Google Scholar] [CrossRef]
- Fröwis, F.; Sekatski, P.; Dür, W.; Gisin, N.; Sangouard, N. Macroscopic quantum states: Measures, fragility, and implementations. Rev. Mod. Phys. 2018, 90, 025004. [Google Scholar] [CrossRef]
- Xie, H.; Shang, X.; Liao, C.G.; Chen, Z.H.; Lin, X.M. Macroscopic superposition states of a mechanical oscillator in an optomechanical system with quadratic coupling. Phys. Rev. A 2019, 100, 033803. [Google Scholar] [CrossRef]
- Omran, A.; Levine, H.; Keesling, A.; Semeghini, G.; Wang, T.T.; Ebadi, S.; Bernien, H.; Zibrov, A.S.; Pichler, H.; Choi, S.; et al. Generation and manipulation of Schrödinger cat states in Rydberg atom arrays. Science 2019, 365, 570. [Google Scholar] [CrossRef]
- Chen, Y.H.; Qin, W.; Wang, X.; Miranowicz, A.; Nori, F. Shortcuts to Adiabaticity for the Quantum Rabi Model: Efficient Generation of Giant Entangled Cat States via Parametric Amplification. Phys. Rev. Lett. 2021, 126, 023602. [Google Scholar] [CrossRef]
- Qin, W.; Miranowicz, A.; Jing, H.; Nori, F. Generating long-lived macroscopically distinct superposition states in atomic ensembles. Phys. Rev. Lett. 2021, 127, 093602. [Google Scholar] [CrossRef] [PubMed]
- Parkins, A.S.; Walls, D.F. The physics of trapped dilute-gas BoseDEinstein condensates. Phys. Rep. 1998, 303, 1–80. [Google Scholar] [CrossRef]
- Dalfovo, F.; Giorgini, S.; Pitaevskii, L.P.; Stringari, S. Theory of Bose-Einstein condensation in trapped gases. Rev. Mod. Phys. 1999, 71, 463. [Google Scholar] [CrossRef]
- Leggett, A.J. Bose-Einstein condensation in the alkali gases: Some fundamental concepts. Rev. Mod. Phys. 2001, 73, 307. [Google Scholar] [CrossRef]
- Cirac, J.I.; Lewenstein, M.; Mølmer, K.; Zoller, P. Quantum superposition states of Bose-Einstein condensates. Phys. Rev. A 1998, 57, 1208. [Google Scholar] [CrossRef]
- Gordon, D.; Savage, C.M. Creating macroscopic quantum superpositions with Bose-Einstein condensates. Phys. Rev. A 1999, 59, 4623. [Google Scholar] [CrossRef]
- Dalvit, D.A.R.; Dziarmaga, J.; Zurek, W.H. Decoherence in Bose-Einstein condensates: Towards bigger and better Schrödinger cats. Phys. Rev. A 2000, 62, 013607. [Google Scholar] [CrossRef]
- Louis, P.J.Y.; Brydon, P.M.R.; Savage, C.M. Macroscopic quantum superposition states in Bose-Einstein condensates: Decoherence and many modes. Phys. Rev. A 2001, 64, 053613. [Google Scholar] [CrossRef]
- Huang, Y.P.; Moore, M.G. Creation, detection, and decoherence of macroscopic quantum superposition states in double-well Bose-Einstein condensates. Phys. Rev. A 2006, 73, 023606. [Google Scholar] [CrossRef]
- Dunningham, J.; Hallwood, D. Creation of macroscopic superpositions of flow states with Bose-Einstein condensates. Phys. Rev. A 2006, 74, 023601. [Google Scholar] [CrossRef] [Green Version]
- Piazza, F.; Pezzé, L.; Smerzi, A. Macroscopic superpositions of phase states with Bose-Einstein condensates. Phys. Rev. A 2008, 78, 051601. [Google Scholar] [CrossRef]
- Csire, G.; Apagyi, B. Macroscopic quantum superpositon states of two-component Bose-Einstein condensates. Phys. Rev. A 2012, 85, 033613. [Google Scholar] [CrossRef]
- Nolan, S.P.; Haine, S.A. Generating macroscopic superpositions with interacting Bose-Einstein condensates: Multimode speedups and speed limits. Phys. Rev. A 2018, 98, 063606. [Google Scholar] [CrossRef]
- Calsamiglia, J.; Mackie, M.; Suominen, K. Superposition of Macroscopic Numbers of Atoms and Molecules. Phys. Rev. Lett. 2001, 87, 160403. [Google Scholar] [CrossRef]
- Bar-Gill, N.; Rao, D.D.B.; Kurizki, G. Single-atom-aided probe of the decoherence of a Bose-Einstein condensate. Phys. Rev. Lett. 2011, 107, 010404. [Google Scholar] [CrossRef] [PubMed]
- Lau, H.W.; Dutton, Z.; Wang, T.; Simon, C. Proposal for the Creation and Optical Detection of Spin Cat States in Bose-Einstein Condensates. Phys. Rev. Lett. 2014, 113, 090401. [Google Scholar] [CrossRef] [PubMed]
- Pezzè, L.; Gessner, M.; Feldmann, P.; Klempt, C.; Santos, L.; Smerzi, A. Heralded Generation of Macroscopic Superposition States in a Spinor Bose-Einstein Condensate. Phys. Rev. Lett. 2019, 123, 260403. [Google Scholar] [CrossRef]
- Balewski, J.B.; Krupp, A.T.; Gaj, A.; Peter, D.; Buchler, H.P.; Low, R.; Hofferberth, S.; Pfau, T. Coupling a single electron to a Bose-Einstein condensate. Nature 2013, 502, 664. [Google Scholar] [CrossRef]
- Spethmann, N.; Kindermann, F.; John, S.; Weber, C.; Meschede, D.; Widera, A. Dynamics of Single Neutral Impurity Atoms Immersed in an Ultracold Gas. Phys. Rev. Lett. 2012, 109, 235301. [Google Scholar] [CrossRef]
- Will, S.; Best, T.; Braun, S.; Schneider, U.; Bloch, I. Coherent Interaction of a Single Fermion with a Small Bosonic Field. Phys. Rev. Lett. 2011, 106, 115305. [Google Scholar] [CrossRef] [Green Version]
- Zipkes, C.; Palzer, S.; Sias, C.; Köhl, M. A trapped single ion inside a Bose-Einstein condensate. Nature 2010, 464, 388. [Google Scholar] [CrossRef] [PubMed]
- Chikkatur, A.P.; Gölitz, A.; Stamper-Kurn, D.M.; Inouye, S.; Gupta, S.; Ketterle, W. Suppression and Enhancement of Impurity Scattering in a Bose-Einstein Condensate. Phys. Rev. Lett. 2000, 85, 483. [Google Scholar] [CrossRef] [PubMed]
- Yuan, J.B.; Lu, W.J.; Song, Y.J.; Kuang, L.M. Single-impurity-induced Dicke quantum phase transition in a cavity-Bose-Einstein condensate. Sci. Rep. 2017, 7, 7404. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Kuang, L.M. Controlling quantum coherence of a two-component Bose-Einstein condensate via an impurity atom. Quantum Inf. Process. 2020, 19, 188. [Google Scholar] [CrossRef]
- Li, Z.; Han, Y.; Kuang, L.M. Complementarity between micro-micro and micro-macro entanglement in a Bose-Einstein condensate with two Rydberg impurities. Commun. Theor. Phys. 2020, 72, 025101. [Google Scholar] [CrossRef]
- Han, Y.; Li, Z.; Kuang, L.M. Quantum dynamics of an impurity-doped Bose-Einstein condensate system. Commun. Theor. Phys. 2020, 72, 095102. [Google Scholar] [CrossRef]
- Ng, H.T.; Bose, S. Single-atom-aided probe of the decoherence of a Bose-Einstein condensate. Phys. Rev. A 2008, 78, 023610. [Google Scholar] [CrossRef]
- Bruderer, M.; Jaksch, D. Probing BEC phase fluctuations with atomic quantum dots. New J. Phys. 2006, 8, 87. [Google Scholar] [CrossRef]
- Song, Y.J.; Kuang, L.M. Controlling decoherence speed limit of a single impurity atom in a Bose-Einstein-condensate reservoir. Ann. Phys. 2019, 531, 1800423. [Google Scholar] [CrossRef]
- Vogt, T.; Viteau, M.; Chotia, A.; Zhao, J.; Comparat, D.; Pillet, P. Electric-Field Induced Dipole Blockade with Rydberg Atoms. Phys. Rev. Lett. 2007, 99, 073002. [Google Scholar] [CrossRef] [Green Version]
- Büchler, H.P.; Micheli, A.; Zoller, P. Three-body interactions with cold polar molecules. Nat. Phys. 2007, 3, 726. [Google Scholar] [CrossRef]
- Yukawa, E.; Milburn, G.J.; Nemoto, K. Fast macroscopic-superposition-state generation by coherent driving. Phys. Rev. A 2018, 97, 013820. [Google Scholar] [CrossRef]
- Titulaer, U.M.; Glauber, R.J. Density Operators for Coherent Fields. Phys. Rev. 1966, 145, 1041. [Google Scholar] [CrossRef]
- Bialynicka-Birula, Z. Properties of the Generalized Coherent State. Phys. Rev. 1968, 173, 1207. [Google Scholar] [CrossRef]
- Stoler, D. Generalized Coherent States. Phys. Rev. D 1971, 4, 2309. [Google Scholar] [CrossRef]
- Kuang, L.M.; Zhou, L. Generation of atom-photon entangled states in atomic Bose-Einstein condensate via electromagnetically induced transparency. Phys. Rev. A 2003, 68, 043606. [Google Scholar] [CrossRef]
- Kuang, L.M.; Chen, Z.B.; Pan, J.W. Generation of entangled coherent states for distant Bose-Einstein condensates via electromagnetically induced transparency. Phys. Rev. A 2007, 76, 052324. [Google Scholar] [CrossRef]
- Yurke, B.; Stoler, D. Generating quantum mechanical superpositions of macroscopically distinguishable states via amplitude dispersion. Phys. Rev. Lett. 1986, 57, 13. [Google Scholar] [CrossRef]
- Liao, J.Q.; Tian, L. Macroscopic quantum superposition in cavity optomechanics. Phys. Rev. Lett. 2016, 116, 163602. [Google Scholar] [CrossRef]
- Lee, K.S.; Kim, M.S.; Bǔzek, V. Amplification of multicomponent superpositions of coherent states of light with quantum amplifiers. J. Opt. Soc. Am. B 1994, 11, 6. [Google Scholar] [CrossRef]
- Bu, K.; Singh, U.; Wu, J. Catalytic coherence transformations. Phys. Rev. A 2016, 93, 042326. [Google Scholar] [CrossRef]
- Braunstein, S.L.; van Loock, P. Quantum information with continuous variables. Rev. Mod. Phys. 2005, 77, 513. [Google Scholar] [CrossRef]
- Weedbrook, C.; Pirandola, S.; García-Patrón, R.; Cerf, N.J.; Ralph, T.C.; Shapiro, J.H.; Lloyd, S. Gaussian quantum information. Rev. Mod. Phys. 2012, 84, 62. [Google Scholar] [CrossRef]
- Louisell, W.H. Quantum Statistical Properties of Radiation; Wiley: New York, NY, USA, 1973. [Google Scholar]
- Hillery, M.; O’Connell, R.F.; Scully, M.O.; Wigner, E.P. Distribution functions in physics: Fundamentals. Phys. Rep. 1984, 106, 121. [Google Scholar] [CrossRef]
- Buzěk, V.; Knight, P.L. The origin of squeezing in a superposition of coherent states. Opt. Commun. 1991, 81, 5. [Google Scholar] [CrossRef]
- Buzěk, V.; Vidiella-Barranco, A.; Knight, P.L. Superpositions of coherent states: Squeezing and dissipation. Phys. Rev. A 1992, 45, 9. [Google Scholar] [CrossRef]
- Kenfack, A.; Życzkowski, K. Negativity of the Wigner function as an indicator of non-classicality. J. Opt. B Quantum Semiclass. Opt. 2004, 6, 396. [Google Scholar] [CrossRef]
- Meng, X.G.; Li, K.C.; Wang, J.S.; Zhang, X.Y.; Zhang, Z.T.; Yang, Z.S.; Liang, B.L. Continuous-Variable Entanglement and Wigner-Function Negativity via Adding or Subtracting Photons. Ann. Phys. 2020, 532, 1900585. [Google Scholar] [CrossRef]
- Jack, M.W. Effect of atom loss on collapse and revivals of phase coherence in small atomic samples. Phys. Rev. A 2003, 67, 043612. [Google Scholar] [CrossRef]
- Jack, M.W. Decoherence due toThree-Body Loss and its Effect on the State of a Bose-Einstein Condensate. Phys. Rev. Lett. 2002, 89, 140402. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.; Fu, L.B.; Yi, X.X. Effect of decoherence on the dynamics of Bose-Einstein condensates in a double-well potential. Phys. Rev. A 2007, 75, 045601. [Google Scholar] [CrossRef]
- Johansson, J.R.; Nation, P.D.; Nori, F. QuTiP: An open-source Python framework for the dynamics of open quantum systems. Comput. Phys. Commun. 2012, 183, 1760. [Google Scholar] [CrossRef]
- Johansson, J.R.; Nation, P.D.; Nori, F. QuTiP 2: A Python framework for the dynamics of open quantum systems. Comput. Phys. Commun. 2013, 184, 1234. [Google Scholar] [CrossRef]
- Gao, Y.P.; Liu, X.F.; Wang, T.J.; Cao, C.; Wang, C. Photon excitation and photon-blockade effects in optomagnonic microcavities. Phys. Rev. A 2019, 100, 043831. [Google Scholar] [CrossRef]
- Aldana, S.; Bruder, C.; Nunnenkamp, A. Equivalence between an optomechanical system and a Kerr medium. Phys. Rev. A 2013, 88, 043826. [Google Scholar] [CrossRef] [Green Version]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Lu, W. Transient and Fast Generation of Bose-Einstein-Condensate Macroscopic Quantum Superposition States via Impurity Catalysing. Photonics 2022, 9, 622. https://doi.org/10.3390/photonics9090622
Li Z, Lu W. Transient and Fast Generation of Bose-Einstein-Condensate Macroscopic Quantum Superposition States via Impurity Catalysing. Photonics. 2022; 9(9):622. https://doi.org/10.3390/photonics9090622
Chicago/Turabian StyleLi, Zhen, and Wangjun Lu. 2022. "Transient and Fast Generation of Bose-Einstein-Condensate Macroscopic Quantum Superposition States via Impurity Catalysing" Photonics 9, no. 9: 622. https://doi.org/10.3390/photonics9090622




