Generation and Applications of Extreme-Ultraviolet Vortices
Abstract
:1. Introduction
2. Generation of XUV Vortices with Laser-Based Sources
2.1. High Harmonic Vortex Generation
2.1.1. First Experiments and Theory
2.1.2. XUV Attosecond Helical Pulses
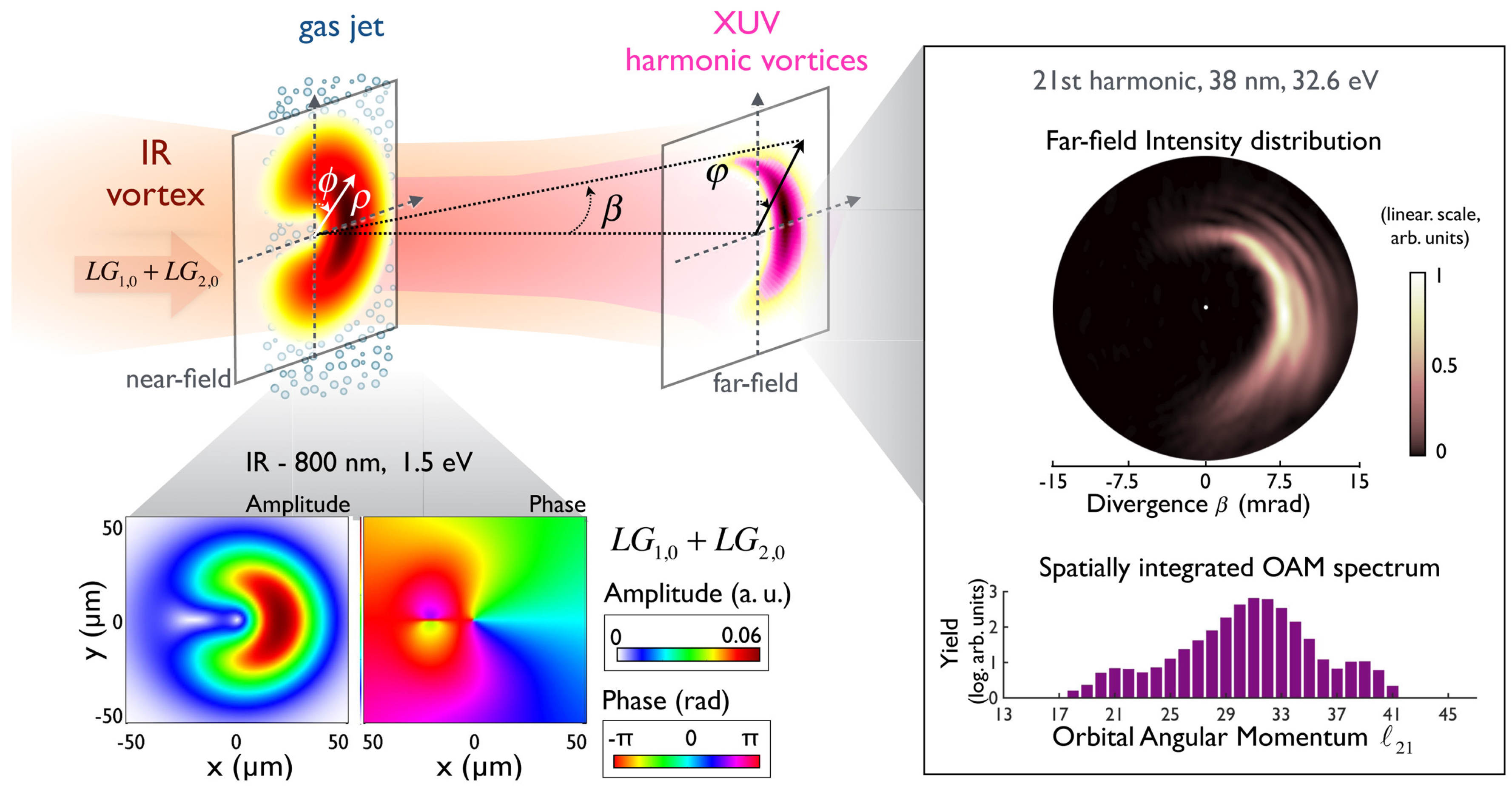
2.1.3. OAM Mode Mixing
2.1.4. OAM Two-Color Mixing
2.2. Plasma-Based Vortex Generation
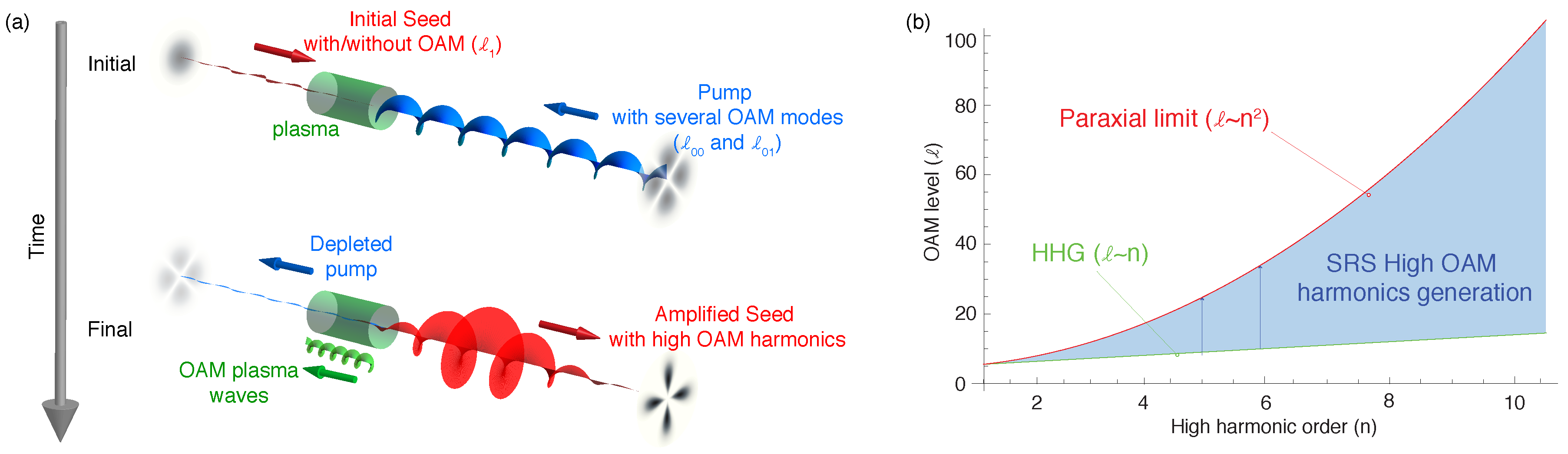
2.2.1. Generation and Amplification of Ultra-Intense Vortex Beams
2.2.2. High Orbital Angular Momentum Harmonics in Plasmas
2.2.3. Plasma Holograms and Phase Plates for Ultra-Intense Lasers
2.3. Compton-Based Vortex Generation
3. Generation of XUV Vortices with Accelerator-Based Sources
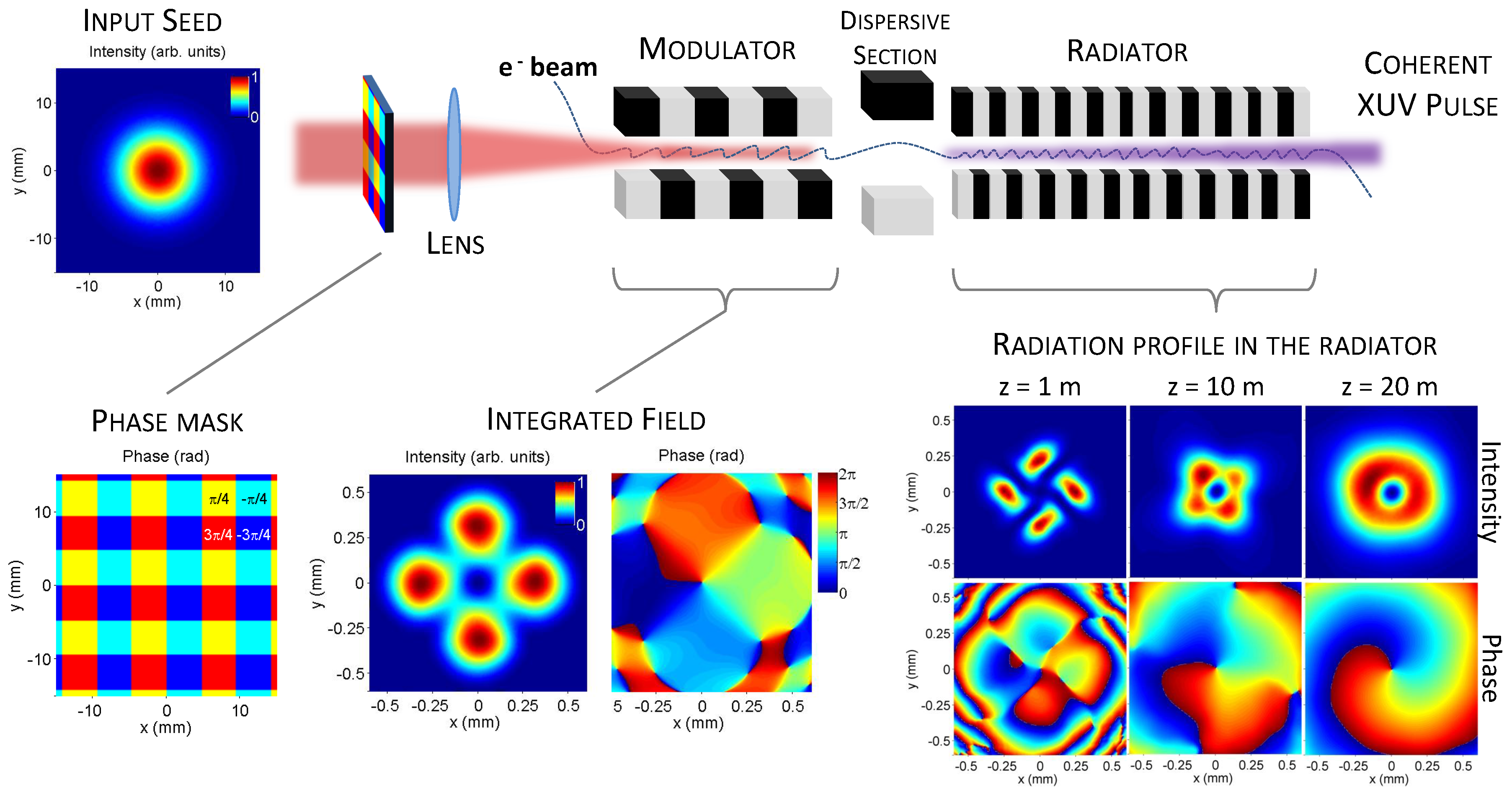
3.1. Undulator Based OAM Radiation
3.2. High-Intensity X-ray Pulses: FELs
4. Perspectives and Applications
Acknowledgments
Conflicts of Interest
References
- Poynting, J.H. The Wave Motion of a Revolving Shaft, and a Suggestion as to the Angular Momentum in a Beam of Circularly Polarised Light. Proc. R. Soc. Lond. A 1909, 82, 560. [Google Scholar] [CrossRef]
- Allen, L.; Beijersbergen, M.W.; Spreeuw, R.J.C.; Woerdman, J.P. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys. Rev. A 1992, 45, 8185. [Google Scholar] [CrossRef] [PubMed]
- Beth, B. Mechanical Detection and Measurement of the Angular Momentum of Light. Phys. Rev. 1936, 50, 115. [Google Scholar] [CrossRef]
- Allen, L.; Barnett, S.M.; Padgett, M.J. (Eds.) Optical Angular Momentum; Institute of Physics Publishing: Bristol, UK, 2003. [Google Scholar]
- Andrews, D.L.; Babiker, M. (Eds.) The Angular Momentum of Light; Cambridge University Press: New York, NY, USA, 2012. [Google Scholar]
- Torres, J.P.; Torner, L. (Eds.) Twisted Photons; Wiley-VCH: Weinheim, Germany, 2011. [Google Scholar]
- Strickland, D.; Mourou, G. Compression of amplified chirped optical pulses. Opt. Commun. 1985, 56, 219. [Google Scholar] [CrossRef]
- Agostini, P.; DiMauro, L.F. The physics of attosecond light pulses. Rep. Prog. Phys. 2004, 67, 813–855. [Google Scholar] [CrossRef]
- Krausz, F.; Ivanov, M. Attosecond physics. Rev. Mod. Phys. 2009, 81, 163–234. [Google Scholar] [CrossRef]
- Schafer, K.J.; Yang, B.; DiMauro, L.F.; Kulander, K.C. Above threshold ionization beyond the high harmonic cutoff. Phys. Rev. Lett. 1993, 70, 1599–1602. [Google Scholar] [CrossRef] [PubMed]
- Corkum, P.B. Plasma perspective on strong field multiphoton ionization. Phys. Rev. Lett. 1993, 71, 1994–1997. [Google Scholar] [CrossRef] [PubMed]
- Gaarde, M.B.; Tate, J.L.; Schafer, K.J. Macroscopic aspects of attosecond pulse generation. J. Phys. B At. Mol. Opt. Phys. 2008, 41, 132001. [Google Scholar] [CrossRef]
- Popmintchev, T.; Chen, M.-C.; Popmintchev, D.; Arpin, P.; Brown, S.; Alisauskas, S.; Andriukaitas, G.; Balciunas, T.; Mücke, O.; Pugzlys, A.; et al. Bright coherent ultrahigh harmonics in the keV X-ray regime from mid-infrared femtosecond lasers. Science 2012, 336, 1287. [Google Scholar] [CrossRef] [PubMed]
- Silva, F.; Teichmann, S.M.; Cousin, S.L.; Biegert, J. Spatiotemporal isolation of attosecond soft X-ray pulses in the water window. Nat. Commun. 2015, 6, 6611. [Google Scholar] [CrossRef] [PubMed]
- Popmintchev, D.; Hernández-García, C.; Dollar, F.; Mancuso, C.; Pérez-Hernández, J.A.; Chen, M.-C.; Hankla, A.; Gao, X.; Shim, B.; Gaeta, A.L.; et al. Ultraviolet surprise: Efficient soft X-ray high-harmonic generation in multiply ionized plasmas. Science 2015, 350, 1225. [Google Scholar] [CrossRef] [PubMed]
- Zürch, M.; Kern, C.; Hansinger, P.; Dreischuh, A.; Spielmann, C. Strong-field physics with singular light beams. Nat. Phys. 2012, 8, 743–746. [Google Scholar] [CrossRef]
- Patchkovskii, S.; Spanner, M. Nonlinear optics: high harmonics with a twist. Nat. Phys. 2012, 8, 707–708. [Google Scholar] [CrossRef]
- Hernández-García, C.; Picón, A.; San Román, J.; Plaja, L. Attosecond Extreme Ultraviolet Vortices from High-Order Harmonic Generation. Phys. Rev. Lett. 2013, 111, 083602. [Google Scholar] [CrossRef] [PubMed]
- Gariepy, G.; Leach, J.; Kim, K.T.; Hammond, T.J.; Frumker, E.; Boyd, R.W.; Corkum, P.B. Creating High-Harmonic Beams with Controlled Orbital Angular Momentum. Phys. Rev. Lett. 2014, 113, 153901. [Google Scholar] [CrossRef] [PubMed]
- Hernández-García, C. A twist in coherent X-rays. Nat. Phys. 2017, 13, 327. [Google Scholar] [CrossRef]
- Rego, L.; San Román, J.; Picón, A.; Plaja, L.; Hernández-García, C. Non-perturbative twist in the generation of extreme ultraviolet vortices. Phys. Rev. Lett. 2016, 117, 163202. [Google Scholar] [CrossRef] [PubMed]
- Gauthier, D.; Ribic, P.R.; Adhikary, G.; Camper, A.; Chappuis, C.; Cucini, R.; DiMauro, L.F.; Dovillaire, G.; Frassetto, F.; Géneaux, R.; et al. Tunable orbital angular momentum in high-harmonic generation. Nat. Commun. 2017, 8, 14971. [Google Scholar] [CrossRef] [PubMed]
- Kong, F.; Zhang, C.; Bouchard, F.; Li, Z.; Brown, G.G.; Ko, D.H.; Hammond, T.J.; Arissian, L.; Boyd, R.W.; Karimi, E.; et al. Controlling the orbital angular momentum of high harmonic vortices. Nat. Commun. 2017, 8, 14970. [Google Scholar] [CrossRef] [PubMed]
- Hernández-García, C.; San Román, J.; Plaja, L.; Picón, A. Quantum-path signatures in attosecond helical beams driven by optical vortices. New J. Phys. 2015, 17, 093029. [Google Scholar] [CrossRef]
- Hernández-García, C.; Pérez-Hernández, J.A.; Ramos, J.; Jarque, E.C.; Roso, L.; Plaja, L. High order harmonic propagation in gases within the Discrete Dipole Approximation. Phys. Rev. A 2010, 82, 033432. [Google Scholar] [CrossRef]
- Keldysh, L.V. Ionization in the Field of a Strong Electromagnetic Wave. Zh. Eksp. Teor. Fiz. 1964, 47, 1945. [Google Scholar]
- Faisal, F.H.M. Multiple absorption of laser photons by atoms. J. Phys. B 1973, 6, L89. [Google Scholar] [CrossRef]
- Reiss, H.R. Effect of an intense electromagnetic field on a weakly bound system. Phys. Rev. A 1980, 22, 1786. [Google Scholar] [CrossRef]
- Lewenstein, M.; Balcou, P.; Ivanov, M.Y.; L’Huillier, A.; Corkum, P.B. Theory of high-harmonic generation by low frequency laser fields. Phys. Rev. A 1994, 49, 2117. [Google Scholar] [CrossRef] [PubMed]
- Pérez-Hernández, J.A.; Roso, L.; Plaja, L. Harmonic generation beyond the Strong-Field Approximation: the physics behind the short-wave-infrared scaling laws. Opt. Express 2009, 17, 9891. [Google Scholar] [CrossRef] [PubMed]
- Pérez-Hernández, J.A.; Hernández-García, C.; Ramos, J.; Plaja, L.; Roso, L. Book Chapter: Progress in Ultrafast Intense Laser Science VII; Springer: Berlin/Heidelberg, Germany, 2011; pp. 145–162. [Google Scholar]
- Hernández-García, C.; Popmintchev, T.; Murnane, M.M.; Kapteyn, H.C.; Plaja, L.; Becker, A.; Jaron-Becker, A. Group velocity matching in high-order harmonic generation driven by mid-infrared lasers. New J. Phys. 2016, 18, 073031. [Google Scholar] [CrossRef]
- L’Huillier, A.; Balcou, P.; Candel, S.; Schafer, K.J.; Kulander, K.C. Calculations of high-order harmonic-generation processes in xenon at 1064 nm. Phys. Rev. A 1992, 46, 2778. [Google Scholar] [CrossRef] [PubMed]
- Rego, L.; San Román, J.; Plaja, L.; Picón, A.; Hernández-García, C. Ultrashort extreme-ultraviolet vortices. In Vortex Dynamics; Perez-De-Tejada, H., Ed.; InTech: Rijeka, Croatia, 2017. [Google Scholar]
- Bellini, M.; Lynga, C.; Tozzi, A.; Gaarde, M.B.; Hänsch, T.W.; L’Huillier, A.; Wahlström, C.-G. Temporal Coherence of Ultrashort High-Order Harmonic Pulses. Phys. Rev. Lett. 1998, 81, 297. [Google Scholar] [CrossRef]
- Hernández-García, C.; Sola, I.J.; Plaja, L. Signature of the transversal coherence length in high-order harmonic generation. Phys. Rev. A 2013, 88, 043848. [Google Scholar] [CrossRef]
- Lompré, L.; L’Huillier, A.; Ferray, M.; Monot, P.; Mainfray, G.; Manus, C. High-order harmonic generation in xenon: intensity and propagation effects. J. Opt. Soc. Am. B 1990, 7, 754–761. [Google Scholar] [CrossRef]
- Farkas, G.; Toth, C. Proposal for attosecond light pulse generation using laser induced multiple-harmonic conversion processes in rare gases. Phys. Lett. A 1992, 168, 447. [Google Scholar] [CrossRef]
- Paul, P.M.; Toma, E.S.; Breger, P.; Mullot, G.; Augé, F.; Balcou, P.; Muller, H.G.; Agostini, P. Observation of a train of attosecond pulses from high harmonic generation. Science 2001, 292, 1689. [Google Scholar] [CrossRef] [PubMed]
- Géneaux, R.; Camper, A.; Auguste, T.; Gobert, O.; Caillat, J.; Taïeb, R.; Ruchon, T. Synthesis and characterization of attosecond light vortices in the extreme ultraviolet. Nat. Commun. 2016, 7, 12583. [Google Scholar] [CrossRef] [PubMed]
- Pariente, G.; Quéré, F. Spatio-temporal light springs: extended encoding of orbital angular momentum in ultrashort pulses. Opt. Lett. 2015, 40, 2037. [Google Scholar] [CrossRef] [PubMed]
- Hernández-García, C.; Rego, L.; San Román, J.; Picón, A.; Plaja, L. Attosecond twisted beams from high-order harmonic generation driven by optical vortices. High Power Laser Sci. Eng. 2017, 5, e3. [Google Scholar] [CrossRef]
- Mairesse, Y.; de Bohan, A.; Frasinski, L.J.; Merdji, H.; Dinu, L.C.; Monchicourt, P.; Breger, P.; Kovacev, M.; Taieb, R.; Carré, B.; et al. Attosecond Synchronization of High-Harmonic Soft X-rays. Science 2003, 302, 1540. [Google Scholar] [CrossRef] [PubMed]
- Fleischer, A.; Kfir, O.; Diskin, T.; Sidorenko, P.; Cohen, O. Spin angular momentum and tunable polarization in high-harmonic generation. Nat. Photonics 2014, 8, 543. [Google Scholar] [CrossRef]
- Lambert, G.; Vodungbo, B.; Gautier, J.; Mahieu, B.; Malka, V.; Sebban, S.; Zeitoun, P.; Luning, J.; Perron, J.; Andreev, A.; et al. Towards enabling femtosecond helicity-dependent spectroscopy with high-harmonic sources. Nat. Commun. 2015, 6, 6167. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Brown, G.; Ko, D.H.; Kong, F.; Arissian, L.; Corkum, P.B. Perturbative High Harmonic Wave Front Control. Phys. Rev. Lett. 2017, 118, 033905. [Google Scholar] [CrossRef] [PubMed]
- Vieira, J.; Mendonça, J.T. Nonlinear Laser Driven Donut Wakefields for Positron and Electron Acceleration. Phys. Rev. Lett. 2014, 112, 215001. [Google Scholar] [CrossRef]
- Tajima, T.; Dawson, J.M. Laser electron accelerator. Phys. Rev. Lett. 1979, 43, 267. [Google Scholar] [CrossRef]
- Oz, E.; Muggli, P. An accurate Rb density measurement method for a plasma wakefield accelerator experiment using a novel Rb reservoir. Nucl. Instrum. Methods Phys. Res. A 2016, 829, 321–325. [Google Scholar] [CrossRef]
- Vieira, J.; Trines, R.M.G.M.; Alves, E.P.; Fonseca, R.A.; Mendonça, J.T.; Bingham, R.; Norreys, P.; Silva, L.O. Amplification and generation of ultra-intense twisted laser pulses via stimulated Raman scattering. Nat. Commun. 2016, 7, 10371. [Google Scholar] [CrossRef] [PubMed]
- Vieira, J.; Trines, R.M.G.M.; Alves, E.P.; Fonseca, R.A.; Mendonça, J.T.; Bingham, R.; Norreys, P.; Silva, L.O. High orbital angular momentum harmonic generation. Phys. Rev. Lett. 2016, 117, 265001. [Google Scholar] [CrossRef] [PubMed]
- Gordon, D.F.; Hafizi, B.; Ting, A. Nonlinear conversion of photon spin to photon orbital angular momentum. Opt. Lett. 2009, 34, 3280. [Google Scholar] [CrossRef] [PubMed]
- Mendonça, J.T.; Vieira, J. High harmonic generation in underdense plasmas by intense laser pulses with orbital angular momentum. Phys. Plasmas 2015, 22, 123106. [Google Scholar] [CrossRef]
- Bulanov, S.V.; Naumova, N.M.; Pegoraro, F. Interaction of an ultrashort, relativistically strong laser pulse with an overdense plasma. Phys. Plasmas 1994, 1, 745. [Google Scholar] [CrossRef]
- Zhang, X.; Shen, B.; Shi, Y.; Wang, X.; Zhang, L.; Wang, W.; Xu, J.; Yi, L.; Xu, Z. Generation of Intense High-Order Vortex Harmonics. Phys. Rev. Lett. 2015, 114, 173901. [Google Scholar] [CrossRef] [PubMed]
- Quéré, F.; Thaury, C.; Monot, P.; Dobosz, S.; Martin, P.; Geindre, J.-P.; Audebert, P. Coherent Wake Emission of High-Order Harmonics from Overdense Plasmas. Phys. Rev. Lett. 2006, 96, 125004. [Google Scholar] [CrossRef] [PubMed]
- Denoeud, A.; Chopineau, L.; Leblanc, A.; Quéré, F. Interaction of Ultraintense Laser Vortices with Plasma Mirrors. Phys. Rev. Lett. 2017, 118, 033902. [Google Scholar] [CrossRef] [PubMed]
- Monchocé, S.; Kahaly, S.; Leblanc, A.; Videau, L.; Combis, P.; Réau, F.; Garzella, D.; Oliveira, P.D.; Martin, P.; Quéré, F. Optically controlled solid-density transient plasma gratings. Phys. Rev. Lett. 2014, 112, 145008. [Google Scholar] [CrossRef] [PubMed]
- Leblanc, A.; Denoeud, A.; Chopineau, L.; Mennerat, G.; Martin, P.; Quéré, F. Plasma holograms for ultrahigh-intensity optics. Nat. Phys. 2017. [Google Scholar] [CrossRef]
- Shi, Y.; Shen, B.; Zhang, L.; Zhang, X.; Wang, W.; Xu, Z. Light Fan Driven by a Relativistic Laser Pulse. Phys. Rev. Lett. 2014, 112, 235001. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Shen, B.; Shi, Y.; Zhang, L.; Ji, L.; Wang, X.; Xu, Z.; Tajima, T. Intense harmonics generation with customized photon frequency and optical vortex. New J. Phys. 2016, 18, 083046. [Google Scholar] [CrossRef]
- Forslund, D.W.; Kindel, J.M.; Lindman, E.L. Theory of stimulated scattering processes in laser-irradiated plasmas. Phys. Fluis 1975, 18, 1002. [Google Scholar] [CrossRef]
- Shvets, G.; Fisch, N.J.; Pukhov, A.; Meyer-ter-Vehn, J. Superradiant Amplification of an Ultrashort Laser Pulse in a Plasma by a Counterpropagating Pump. Phys. Rev. Lett. 1998, 81, 4879. [Google Scholar] [CrossRef]
- Trines, R.M.G.M.; Fiúza, F.; Bingham, R.; Fonseca, R.A.; Silva, L.O.; Cairns, R.A.; Norreys, P.A. Simulations of efficient Raman amplification into the multipetawatt regime. Nat. Phys. 2011, 7, 87. [Google Scholar] [CrossRef]
- Mendonça, J.T.; Thidé, B.; Then, H. Stimulated Raman and Brillouin Backscattering of Collimated Beams Carrying Orbital Angular Momentum. Phys. Rev. Lett. 2009, 102, 185005. [Google Scholar] [CrossRef] [PubMed]
- Courtial, J.; Dholakia, K.; Allen, L.; Padgett, M.J. Second-harmonic generation and the conservation of orbital angular momentum with high-order Laguerre-Gaussian modes. Phys. Rev. A 1997, 56, 4193. [Google Scholar] [CrossRef]
- Jentschura, U.D.; Serbo, V.G. Generation of High-Energy Photons with Large Orbital Angular Momentum by Compton Backscattering. Phys. Rev. Lett. 2011, 106, 013001. [Google Scholar] [CrossRef] [PubMed]
- Petrillo, V.; Dattoli, G.; Drebot, I.; Nguyen, F. Compton Scattered X-Gamma Rays with Orbital Momentum. Phys. Rev. Lett. 2016, 117, 123903. [Google Scholar] [CrossRef] [PubMed]
- Terhalle, B.; Langner, A.; Päivänranta, B.; Guzenko, V.A.; David, C.; Ekinci, Y. Generation of extreme ultraviolet vortex beams using computer generated holograms. Opt. Lett. 2011, 36, 4143. [Google Scholar] [CrossRef] [PubMed]
- Peele, A.G.; McMahon, P.J.; Paterson, D.; Tran, C.Q.; Mancuso, A.P.; Nugent, K.A.; Hayes, J.P.; Harvey, E.; Lai, B.; McNulty, I. Observation of an X-ray vortex. Opt. Lett. 2002, 27, 1752. [Google Scholar] [CrossRef] [PubMed]
- Sasaki, S.; McNulty, I. Proposal for Generating Brilliant X-ray Beams Carrying Orbital Angular Momentum. Phys. Rev. Lett. 2008, 100, 124801. [Google Scholar] [CrossRef] [PubMed]
- Bahrdt, J.; Holldack, K.; Kuske, P.; Müller, R.; Scheer, M.; Schmid, P. First Observation of Photons Carrying Orbital Angular Momentum in Undulator Radiation. Phys. Rev. Lett. 2013, 111, 034801. [Google Scholar] [CrossRef] [PubMed]
- Hemsing, E.; Dunning, M.; Hast, C.; Raubenheimer, T.; Xiang, D. First Characterization of Coherent Optical Vortices from Harmonic Undulator Radiation. Phys. Rev. Lett. 2014, 113, 134803. [Google Scholar] [CrossRef] [PubMed]
- Allaria, E.; Appio, R.; Badano, L.; Barletta, W.A.; Bassanese, S.; Biedron, S.G.; Borga, A.; Busetto, E.; Castronovo, D.; Cinquegrana, P.; et al. Highly coherent and stable pulses from the FERMI seeded free-electron laser in the extreme ultraviolet. Nat. Photonics 2012, 6, 669. [Google Scholar] [CrossRef]
- Hemsing, E.; Knyazik, A.; Dunning, M.; Xiang, D.; Marinelli, A.; Hast, C.; Rosenzweig, J.B. Coherent optical vortices from relativistic electron beams. Nat. Phys. 2013, 9, 549. [Google Scholar] [CrossRef]
- Allaria, E.; Castronovo, D.; Cinquegrana, P.; Craievich, P.; Dal Forno, M.; Danailov, M.B.; D’Auria, G.; Demidovich, A.; De Ninno, G.; Di Mitri, S.; et al. Two-stage seeded soft-X-ray free-electron laser. Nat. Photonics 2013, 7, 913. [Google Scholar] [CrossRef]
- Hemsing, E.; Marinelli, A. Echo-Enabled X-ray Vortex Generation. Phys. Rev. Lett. 2012, 109, 224801. [Google Scholar] [CrossRef] [PubMed]
- Ribic, P.R.; Gauthier, D.; de Ninno, G. Generation of Coherent Extreme-Ultraviolet Radiation Carrying Orbital Angular Momentum. Phys. Rev. Lett. 2014, 112, 203602. [Google Scholar] [CrossRef]
- Picón, A.; Mompart, J.; de Aldana, J.R.V.; Plaja, L.; Calvo, G.F.; Roso, L. Photoionization with orbital angular momentum beams. Opt. Express 2010, 18, 3660. [Google Scholar] [CrossRef] [PubMed]
- Picón, A.; Benseny, A.; Mompart, J.; de Aldana, J.R.V.; Plaja, L.; Calvo, G.F.; Roso, L. Transferring orbital and spin angular momenta of light to atoms. New J. Phys. 2010, 12, 083053. [Google Scholar] [CrossRef]
- Jauregui, R. Rotational effects of twisted light on atoms beyond the paraxial approximation. Phys. Rev. A 2004, 70, 033415. [Google Scholar] [CrossRef]
- Babiker, M.; Power, W.L.; Allen, L. Light-induced Torque on Moving Atoms. Phys. Rev. Lett. 1994, 73, 1239. [Google Scholar] [CrossRef] [PubMed]
- Müller, R.A.; Seipt, D.; Beerwerth, R.; Ornigotti, M.; Szameit, A.; Fritzsche, S.; Surzhykov, A. Photoionization of neutral atoms by X waves carrying orbital angular momentum. Phys. Rev. A 2016, 94, 041402. [Google Scholar] [CrossRef]
- Peshkov, A.A.; Serbo, V.G.; Fritzsche, S.; Surzhykov, A. Absorption of twisted light by a mesoscopic atomic target. Phys. Scr. 2016, 91, 064001. [Google Scholar] [CrossRef]
- Alexandrescu, A.; Cojoc, D.; DiFabrizio, E.I. Mechanism of Angular Momentum Exchange between Molecules and Laguerre-Gaussian Beams. Phys. Rev. Lett. 2006, 96, 243001. [Google Scholar] [CrossRef] [PubMed]
- Babiker, M.; Bennett, C.R.; Andrews, D.L.; Romero, L.D. Orbital Angular Momentum Exchange in the Interaction of Twisted Light with Molecules. Phys. Rev. Lett. 2002, 89, 143601. [Google Scholar] [CrossRef] [PubMed]
- Toyoda, K.; Takahashi, F.; Takizawa, S.; Tokizane, Y.; Miyamoto, K.; Morita, R.; Omatsu, T. Transfer of Light Helicity to Nanostructures. Phys. Rev. Lett. 2013, 110, 143603. [Google Scholar] [CrossRef] [PubMed]
- Schmiegelow, C.T.; Schulz, J.; Kaufmann, H.; Ruster, T.; Poschinger, U.G.; Schmidt-Kaler, F. Transfer of optical orbital angular momentum to a bound electron. Nat. Commun. 2016, 7, 12998. [Google Scholar] [CrossRef] [PubMed]
- Giammanco, F.; Perona, A.; Marsili, P.; Conti, F.; Fidecaro, F.; Gozzini, S.; Lucchesini, A. Influence of the photon orbital angular momentum on electric dipole transitions: negative experimental evidence. Opt. Lett. 2017, 42, 219. [Google Scholar] [CrossRef] [PubMed]
- Quinteiro, G.F.; Tamborenea, P.I. Electronic transitions in disk-shaped quantum dots induced by twisted light. Phys. Rev. B 2009, 79, 155450. [Google Scholar] [CrossRef]
- Wätzel, J.; Berakdar, J. Discerning on a sub-optical-wavelength the attosecond time delays in electron emission from magnetic sublevels by optical vortices. Phys. Rev. A 2016, 94, 033414. [Google Scholar] [CrossRef]
- Wätzel, J.; Pavlyukh, Y.; Schäffer, A.; Berakdar, J. Optical vortex driven charge current loop and optomagnetism in fullerenes. Carbon 2016, 99, 439. [Google Scholar] [CrossRef]
- Van Veenendaal, M.; McNulty, I. Prediction of strong dichroism induced by x rays carrying orbital momentum. Phys. Rev. Lett. 2007, 98, 157401. [Google Scholar] [CrossRef] [PubMed]
- Zambrana-Puyalto, X.; Vidal, X.; Molina-Terriza, G. Angular momentum-induced circular dichroism in non-chiral nanostructures. Nat. Commun. 2014, 5, 4922. [Google Scholar] [CrossRef] [PubMed]
- Seipt, D.; Müller, R.A.; Surzhykov, A.; Fritzsche, S. Two-color above-threshold ionization of atoms and ions in XUV Bessel beams and intense laser light. Phys. Rev. A 2016, 94, 053420. [Google Scholar] [CrossRef]
- Fujita, H.; Sato, M. Ultrafast generation of skyrmionic defects with vortex beams: Printing laser profiles on magnets. Phys. Rev. B 2017, 95, 054421. [Google Scholar] [CrossRef]
- Seki, S.; Yu, X.Z.; Ishiwata, S.; Tokura, Y. Observation of skyrmions in a multiferroic material. Science 2012, 336, 198. [Google Scholar] [CrossRef] [PubMed]
- Grillo, V.; Gazzadi, G.C.; Karimi, E.; Mafakheri, E.; Boyd, R.W.; Frabboni, S. Highly efficient electron vortex beams generated by nanofabricated phase holograms. Appl. Phys. Lett. 2014, 104, 043109. [Google Scholar] [CrossRef]
- Asenjo-Garcia, A.; de Abajo, F.J.G. Dichroism in the interaction between vortex electron beams, plasmons, and molecules. Phys. Rev. Lett. 2014, 113, 066102. [Google Scholar] [CrossRef] [PubMed]
- Djiokap, J.M.N.; Hu, S.X.; Madsen, L.B.; Manakov, N.L.; Meremianin, A.V.; Starace, A.F. Electron vortices in photoionization by circularly polarized attosecond pulses. Phys. Rev. Lett. 2015, 115, 113004. [Google Scholar] [CrossRef] [PubMed]
- Pengel, D.; Kerbstadt, S.; Johannmeyer, D.; Englert, L.; Bayer, T.; Wollenhaupt, M. Electron Vortices in Femtosecond Multiphoton Ionization. Phys. Rev. Lett. 2017, 118, 053003. [Google Scholar] [CrossRef] [PubMed]
- Rury, A.S. Examining resonant inelastic spontaneous scattering of classical Laguerre-Gauss beams from molecules. Phys. Rev. A 2013, 87, 043408. [Google Scholar] [CrossRef]
- Van Veenendaal, M. Interaction between X-ray and magnetic vortices. Phys. Rev. B 2015, 92, 245116. [Google Scholar] [CrossRef]
- Paganin, D. Coherent X-ray Optics; Oxford University Press: New York, NY, USA, 2006. [Google Scholar]
- Nugent, K.A. Coherent methods in the X-ray sciences. Adv. Phys. 2010, 59, 1. [Google Scholar] [CrossRef]
- Zadernovsky, A.A. Excitation of Nuclei by Photon Beams Carrying Orbital Angular Momentum. Laser Phys. 2006, 16, 571. [Google Scholar] [CrossRef]
- Calvo, G.F.; Picón, A. Spin-induced angular momentum switching. Opt. Lett. 2007, 32, 838. [Google Scholar] [CrossRef] [PubMed]
- Picón, A.; Benseny, A.; Mompart, J.; Calvo, G.F. Spin and orbital angular momentum propagation in anisotropic media: theory. J. Opt. 2011, 13, 064019. [Google Scholar] [CrossRef]
- Bliokh, K.Y.; Rodríguez-Fortuño, F.J.; Nori, F.; Zayats, A.V. Spin-orbit interactions of light. Nat. Photonics 2015, 9, 796–803. [Google Scholar] [CrossRef]
- Cardano, F.; Marrucci, L. Spin-orbit photonics. Nat. Photonics 2015, 9, 776–778. [Google Scholar] [CrossRef]
- Turpin, A.; Rego, L.; Picón, A.; San Román, J.; Hernández-García, C. Extreme Ultraviolet Fractional Orbital Angular Momentum Beams from High Harmonic Generation. Sci. Rep. 2017, 7, 43888. [Google Scholar] [CrossRef] [PubMed]
- Zhan, Q. Cylindrical vector beams: from mathematical concepts to applications. Adv. Opt. Photonics 2009, 1, 1–57. [Google Scholar] [CrossRef]
- Hernández-García, C.; Turpin, A.; San Román, J.; Picón, A.; Drevinskas, R.; Cerkauskaite, A.; Kazansky, P.G.; Durfee, C.G.; Sola, I.J. Extreme ultraviolet vector beams driven by infrared lasers. Optica 2017. submitted. [Google Scholar]

© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hernández-García, C.; Vieira, J.; Mendonça, J.T.; Rego, L.; San Román, J.; Plaja, L.; Ribic, P.R.; Gauthier, D.; Picón, A. Generation and Applications of Extreme-Ultraviolet Vortices. Photonics 2017, 4, 28. https://doi.org/10.3390/photonics4020028
Hernández-García C, Vieira J, Mendonça JT, Rego L, San Román J, Plaja L, Ribic PR, Gauthier D, Picón A. Generation and Applications of Extreme-Ultraviolet Vortices. Photonics. 2017; 4(2):28. https://doi.org/10.3390/photonics4020028
Chicago/Turabian StyleHernández-García, Carlos, Jorge Vieira, Jose T. Mendonça, Laura Rego, Julio San Román, Luis Plaja, Primoz R. Ribic, David Gauthier, and Antonio Picón. 2017. "Generation and Applications of Extreme-Ultraviolet Vortices" Photonics 4, no. 2: 28. https://doi.org/10.3390/photonics4020028




