Assessment of Gate Width Size on Lifetime-Based Förster Resonance Energy Transfer Parameter Estimation
Abstract
:1. Introduction
2. Materials and Methods
2.1. Time-Resolved Optical Tomography System
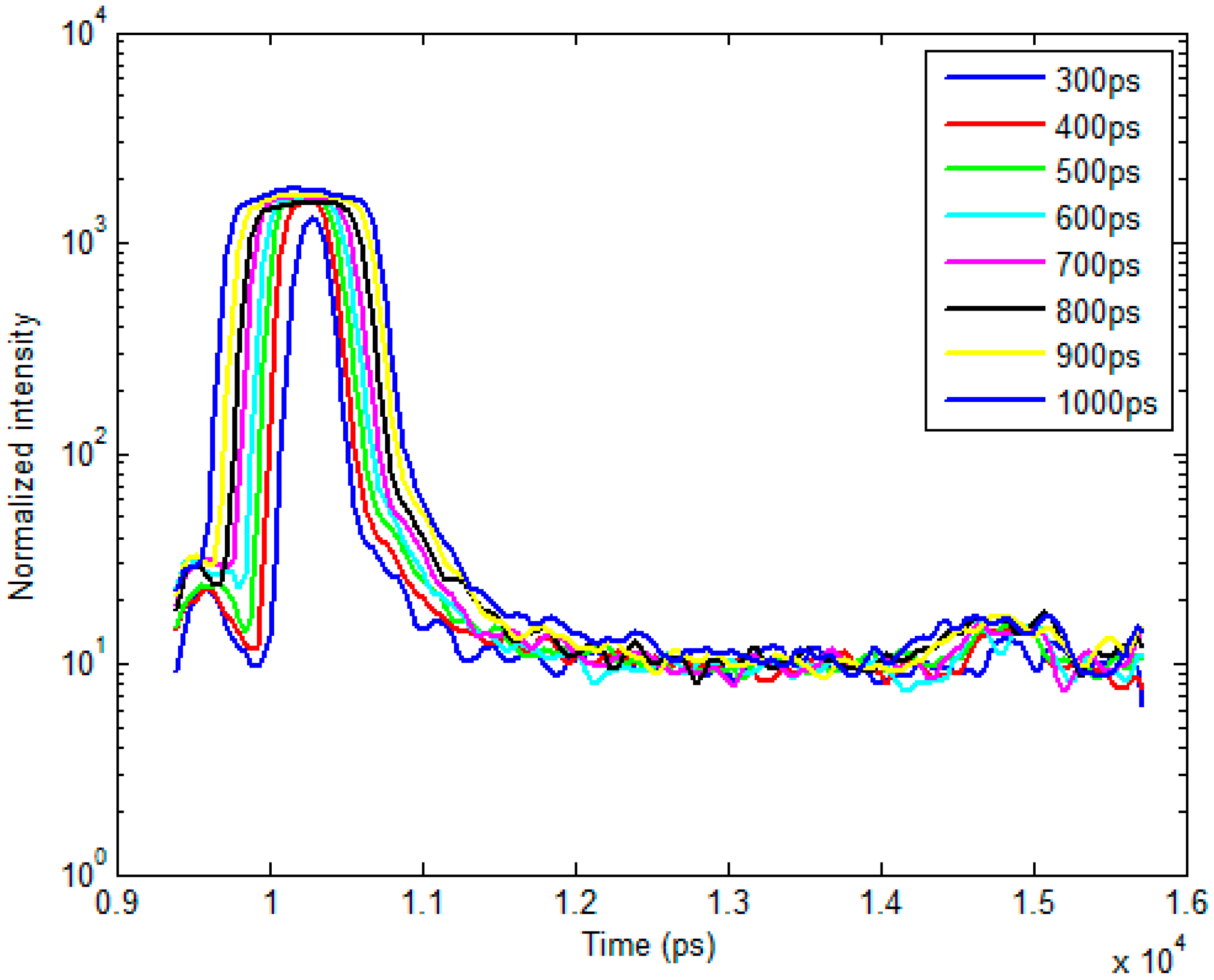
2.2. Bi-Exponential Model
2.3. In Silico Analysis of Varying A:D Ratios and Lifetimes
2.4. In Vitro Experiments Using an NIR FRET Pair Conjugated with Mouse Antibodies
2.5. In Vivo Experiments with Murine Models
2.6. Fitting Methods Using Bi-Exponential Model
3. Results and Discussion
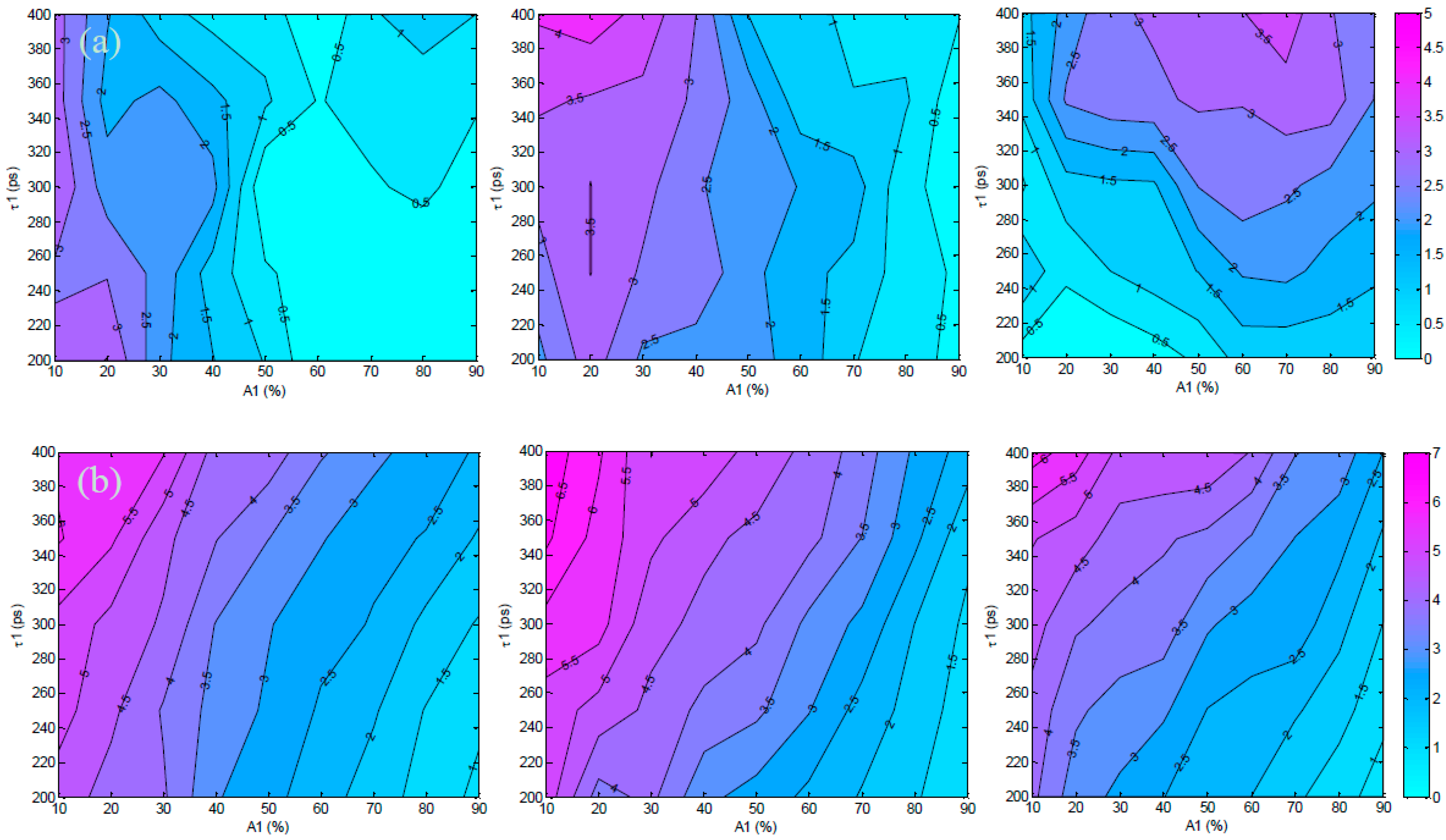
3.1. In Silico Investigation


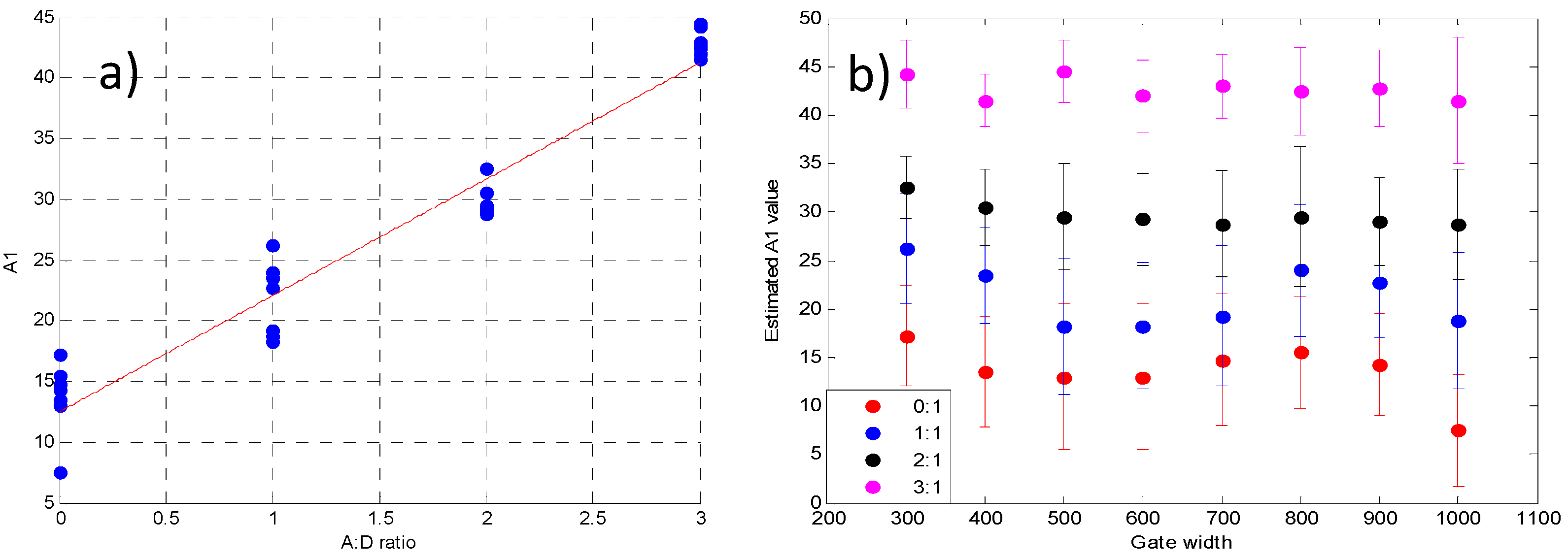
3.2. Validation Using Mouse IgG in Vitro Using Varying A:D Ratios
3.3. Analysis of the Selected A:D Ratio (2:1) in Vivo
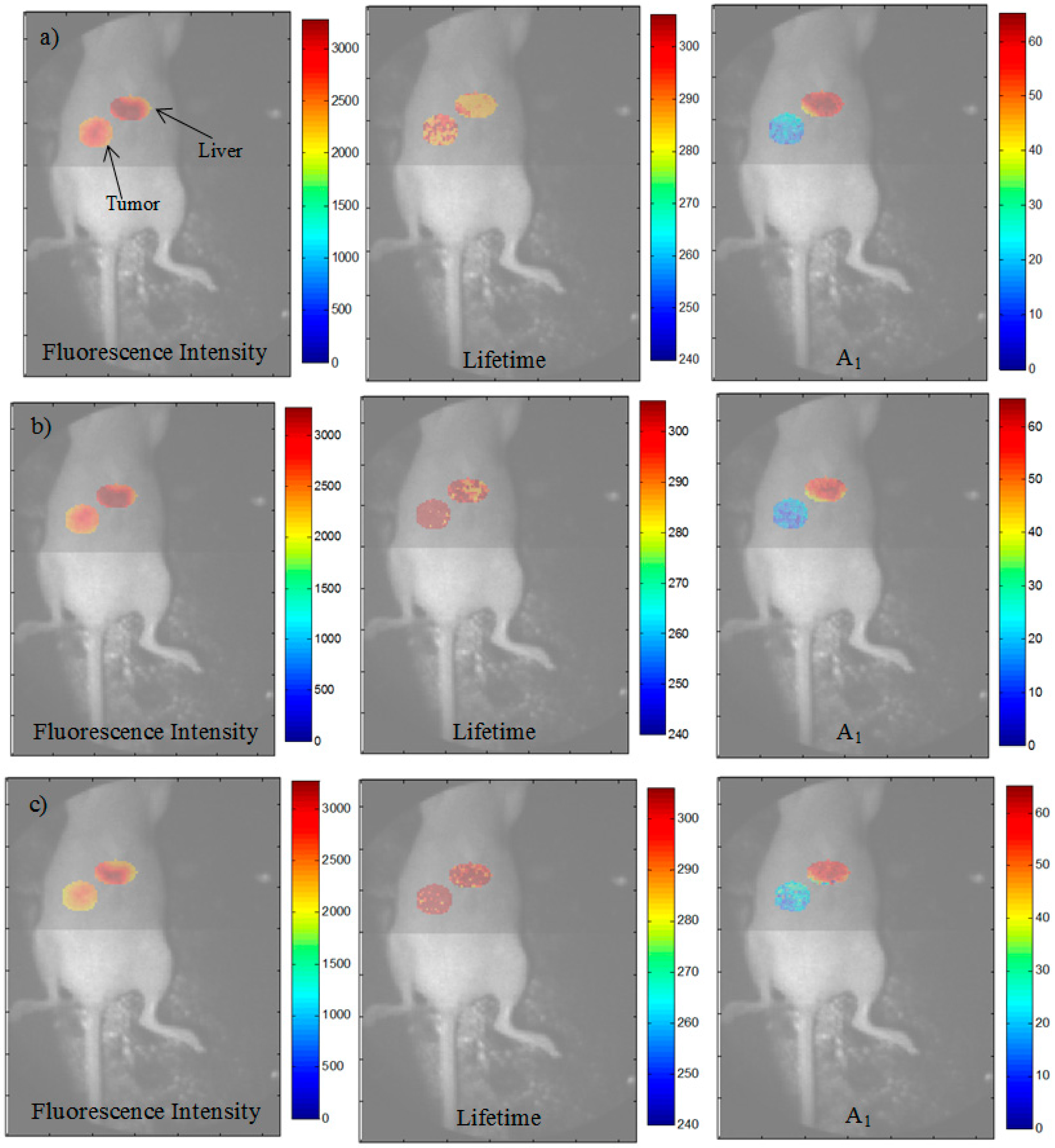
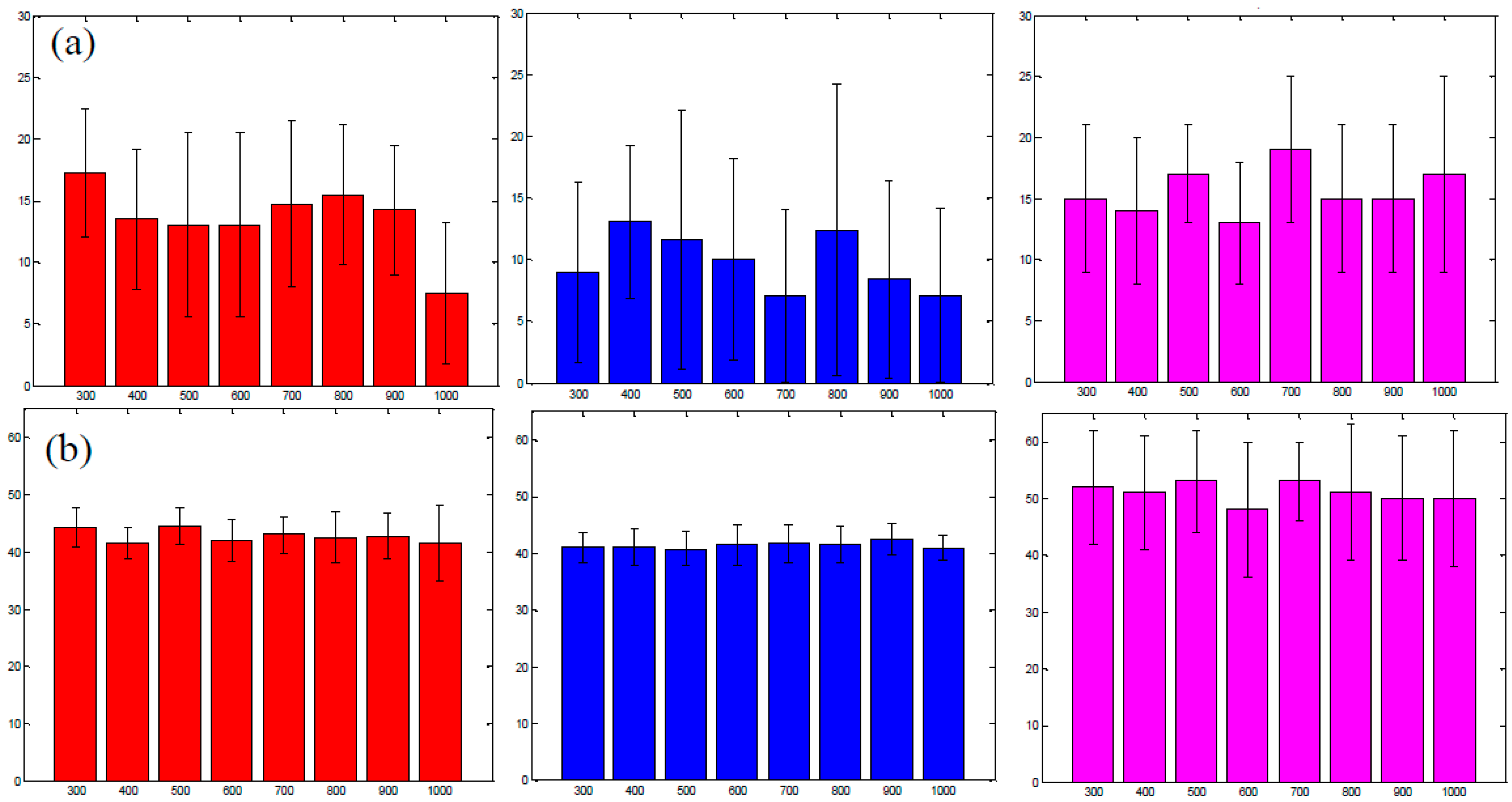
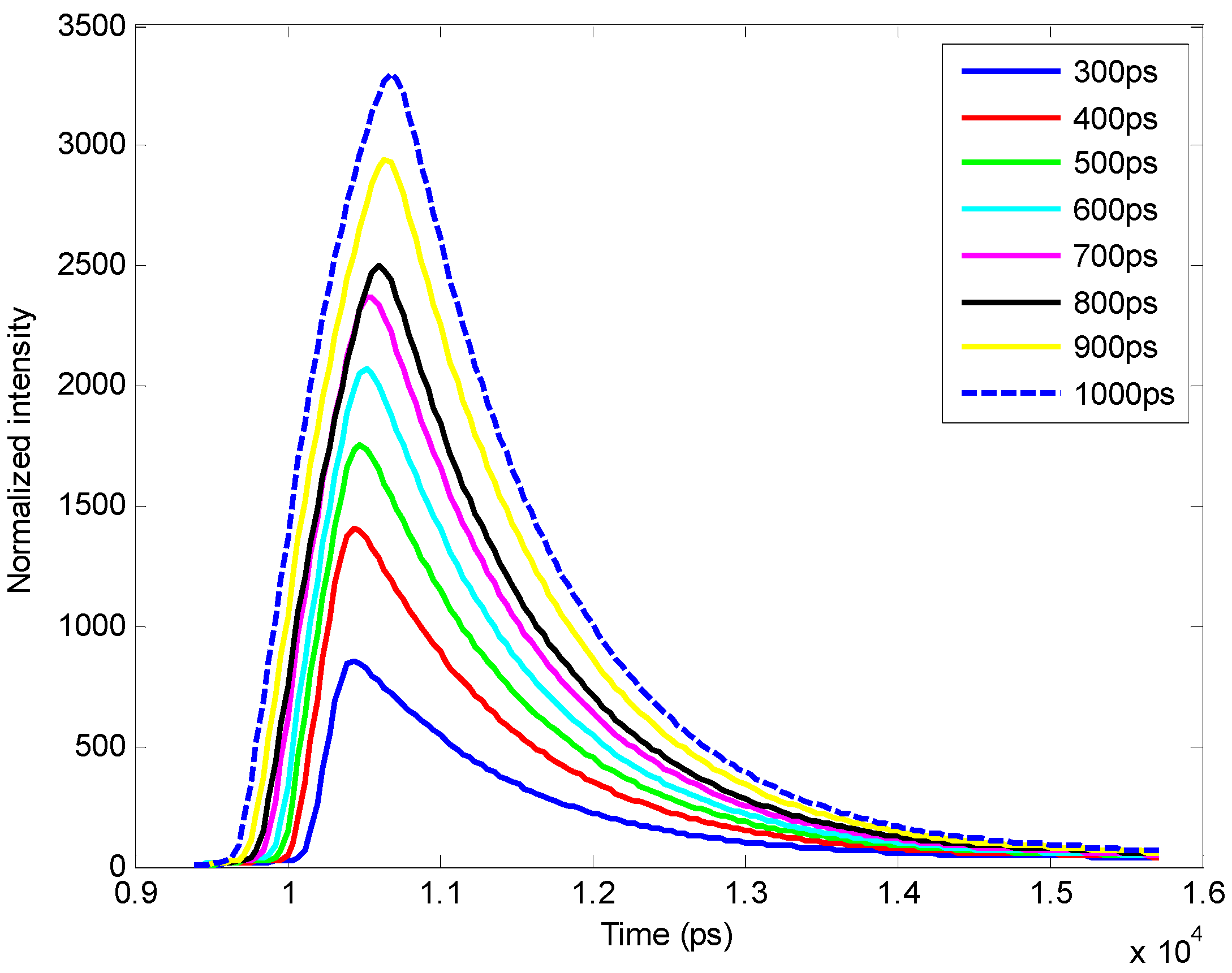
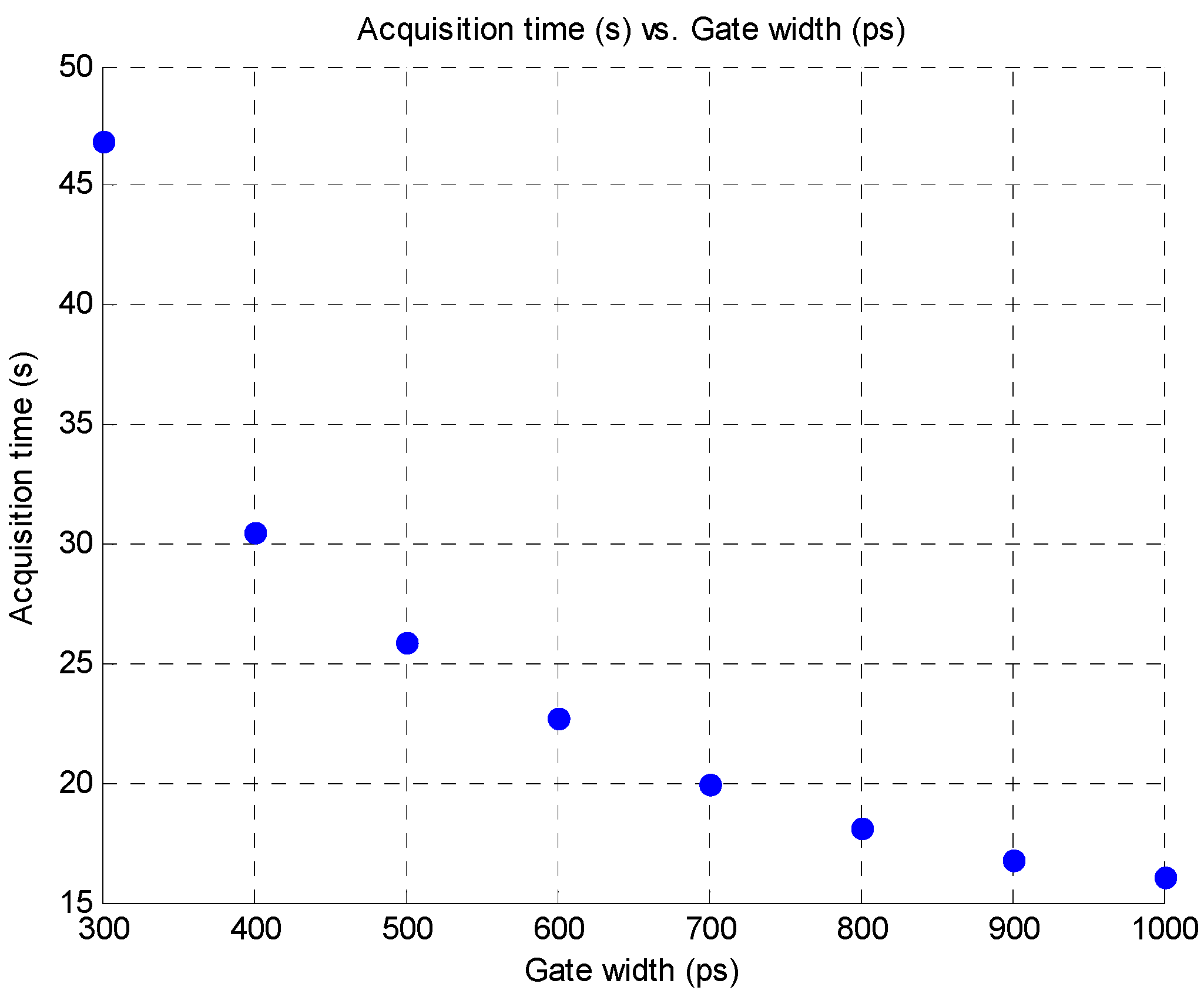
3.4. Improvement in Imaging Protocols
4. Conclusion
Acknowledgements
Author Contributions
Conflicts of Interest
References
- Sun, Y.; Wallrabe, H.; Seo, S.A.; Periasamy, A. FRET microscopy in 2010: The legacy of Theodor Förster on the 100th anniversary of his birth. Chem. Phys. Chem. 2011, 12, 462–474. [Google Scholar] [CrossRef] [PubMed]
- Jares-Erijman, E.A.; Jovin, T.M. FRET imaging. Nat. Biotechnol. 2003, 21, 1387–1395. [Google Scholar] [CrossRef] [PubMed]
- Warren, S.; Kimberley, C.; Margineanu, A.; Laine, R.; Dunsby, C.; Katan, M.; French, P. FLIM-FRET of Cell Signalling in Chemotaxis. Opt. Mol. Probes Imaging Drug Deliv. 2013, 9. [Google Scholar] [CrossRef]
- Wallrabe, H.; Periasamy, A. Imaging protein molecules using FRET and FLIM microscopy. Curr. Opin. Biotechnol. 2005, 16, 19–27. [Google Scholar] [CrossRef] [PubMed]
- Biskup, C.; Zimmer, T.; Kelbauskas, L.; Hoffmann, B.; Klöcker, N.; Becker, W.; Bergmann, A.; Benndorf, K. Multi-dimensional fluorescence lifetime and FRET measurements. Microsc. Res. Tech. 2007, 70, 442–451. [Google Scholar] [CrossRef] [PubMed]
- Pelet, S.; Previte, M.J.R.; So, P.T.C. Comparing the quantification of Förster resonance energy transfer measurement accuracies based on intensity, spectral, and lifetime imaging. J. Biomed. Opt. 2006, 11. [Google Scholar] [CrossRef]
- Kelly, D.J.; Warren, S.C.; Alibhai, D.; Kumar, S.; Alexandrov, Y.; Munro, I.; Margineanu, A.; McCormack, J.; Welsh, N.J.; Serwa, R.A.; et al. Automated multiwell fluorescence lifetime imaging for Förster resonance energy transfer assays and high content analysis. Anal. Methods 2015, 7, 4071–4089. [Google Scholar] [CrossRef]
- Kumar, S.; Alibhai, D.; Margineanu, A.; Laine, R.; Kennedy, G.; McGinty, J.; Warren, S.; Kelly, D.; Alexandrov, Y.; Munro, I.; et al. FLIM FRET technology for drug discovery: Automated multiwell-plate high-content analysis, multiplexed readouts and application in situ. Chem. Phys. Chem. 2011, 12, 609–626. [Google Scholar] [CrossRef] [PubMed]
- Venugopal, V.; Chen, J.; Barroso, M.; Intes, X. Quantitative tomographic imaging of intermolecular FRET in small animals. Biomed. Opt. Express 2012, 3, 3161–3175. [Google Scholar] [CrossRef] [PubMed]
- Zhao, L.; Abe, K.; Rajoria, S.; Pian, Q.; Barroso, M.; Intes, X. Spatial light modulator based active wide-field illumination for ex vivo and in vivo quantitative NIR FRET imaging. Biomed. Opt. Express 2014, 5, 944–960. [Google Scholar] [CrossRef] [PubMed]
- McGinty, J.; Stuckey, D.W.; Soloviev, V.Y.; Laine, R.; Wylezinska-Arridge, M.; Wells, D.J.; Arridge, S.R.; French, P.M.W.; Hajnal, J.V; Sardini, A. In vivo fluorescence lifetime tomography of a FRET probe expressed in mouse. Biomed. Opt. Express 2011, 2, 1907–1917. [Google Scholar] [PubMed]
- Abe, K.; Zhao, L.; Periasamy, A.; Intes, X.; Barroso, M. Non-invasive in vivo imaging of near infrared-labeled transferrin in breast cancer cells and tumors using fluorescence lifetime FRET. PLoS ONE 2013, 8. [Google Scholar] [CrossRef] [PubMed]
- Jacques, S.L. Optical Properties of Biological Tissues: A Review. Phys. Med. Biol. 2013, 58, 37–61. [Google Scholar] [CrossRef] [PubMed]
- Pansare, V.J.; Hejazi, S.; Faenza, W.J.; Prud’Homme, R.K. Review of long-wavelength optical and NIR imaging materials: Contrast agents, fluorophores, and multifunctional nano carriers. Chem. Mater. 2012, 24, 812–827. [Google Scholar] [CrossRef] [PubMed]
- Sarder, P.; Maji, D.; Achilefu, S. Molecular Probes for Fluorescence Lifetime Imaging. Bioconjug. Chem. 2015, 26, 963–974. [Google Scholar] [CrossRef] [PubMed]
- Isherwood, B.; Timpson, P.; Mcghee, E.J.; Anderson, K.I.; Canel, M.; Serrels, A.; Brunton, V.G.; Carragher, N.O. Live cell in vitro and in vivo imaging applications: Accelerating drug discovery. Pharmaceutics 2011, 3, 141–170. [Google Scholar] [CrossRef] [PubMed]
- Nolting, D.D.; Gore, C.J.; Pham, W. Near-Infrared Dyes: Probe Development and Applications in Optical Mole-cular Imaging. Curr. Org. Synth. 2011, 8, 521–534. [Google Scholar] [CrossRef] [PubMed]
- Zheng, G.; Chen, Y.; Intes, X.; Chance, B.; Glickson, J.D. Contrast-enhanced near-infrared (NIR) optical imaging for subsurface cancer detection. J. Porphyr. Phthalocya. 2004, 8, 1106–1117. [Google Scholar] [CrossRef]
- Stockholm, D.; Bartoli, M.; Sillon, G.; Bourg, N.; Davoust, J.; Richard, I. Imaging calpain protease activity by multiphoton FRET in living mice. J. Mol. Biol. 2005, 346, 215–222. [Google Scholar] [CrossRef] [PubMed]
- Nobis, M.; McGhee, E.J.; Morton, J.P.; Schwarz, J.P.; Karim, S.A.; Quinn, J.; Edward, M.; Campbell, A.D.; McGarry, L.C.; Evans, T.R.J.; et al. Intravital FLIM-FRET imaging reveals dasatinib-induced spatial control of Src in pancreatic cancer. Cancer Res. 2013, 73, 4674–4686. [Google Scholar] [CrossRef] [PubMed]
- Berezin, M.Y.; Achilefu, S. Fluorescence lifetime measurements and biological imaging. Chem. Rev. 2010, 110, 2641–2684. [Google Scholar] [CrossRef] [PubMed]
- Chang, C.-W.; Sud, D.; Mycek, M.-A. Fluorescence lifetime imaging microscopy. Methods Cell Biol. 2007, 81, 495–524. [Google Scholar] [PubMed]
- Padilla-Parra, S.; Tramier, M. FRET microscopy in the living cell: Different approaches, strengths and weaknesses. Bioessays 2012, 34, 369–376. [Google Scholar] [CrossRef] [PubMed]
- Pian, Q.; Yao, R.; Zhao, L.; Intes, X. Hyperspectral time-resolved wide-field fluorescence molecular tomography based on structured light and single-pixel detection. Opt. Lett. 2015, 40, 431–434. [Google Scholar] [CrossRef] [PubMed]
- Sharman, K.K.; Periasamy, A.; Ashworth, H.; Demas, J.N. Error analysis of the rapid lifetime determination method for double-exponential decays and new windowing schemes. Anal. Chem. 1999, 71, 947–952. [Google Scholar] [CrossRef] [PubMed]
- Venugopal, V. A Small Animal Time-Resolved Optical Tomography Platform Using Wide-Field Excitation. Ph.D. Thesis, Rensselaer Polytechnic Institute, Troy, NY, USA, 2011. [Google Scholar]
- Ma, G.; Mincu, N.; Lesage, F.; Gallant, P.; McIntosh, L. System IRF impact on fluorescence lifetime fitting in turbid medium. Proc. SPIE 2005, 5699, 263–273. [Google Scholar]
- Zhong, W.; Wu, M.; Chang, C.-W.; Merrick, K.A.; Merajver, S.D.; Mycek, M.-A. Picosecond-resolution fluorescence lifetime imaging microscopy: A useful tool for sensing molecular interactions in vivo via FRET. Opt. Express 2007, 15, 18220–18235. [Google Scholar] [CrossRef] [PubMed]
- Venugopal, V.; Chen, J.; Intes, X. Development of an optical imaging platform for functional imaging of small animals using wide-field excitation. Biomed. Opt. Express 2010, 1, 143–156. [Google Scholar] [CrossRef] [PubMed]
- Omer, T.; Zhao, L.; Intes, X.; Hahn, J. Reduced temporal sampling effect on accuracy of time-domain fluorescence lifetime Förster resonance energy transfer. J. Biomed. Opt. 2014, 19. [Google Scholar] [CrossRef] [PubMed]
- Gerritsen, H.C.; Asselbergs, M.A.H.; Agronskaia, A.V.; Van Sark, W.G.J.H.M. Fluorescence lifetime imaging in scanning microscopes: Acquisition speed, photon economy and lifetime resolution. J. Microsc. 2002, 206, 218–224. [Google Scholar] [CrossRef] [PubMed]
- Zhao, L.; Abe, K.; Barroso, M.; Intes, X. Active wide-field illumination for high-throughput fluorescence lifetime imaging. Opt. Lett. 2013, 38, 3976–3979. [Google Scholar] [CrossRef] [PubMed]
- Venugopal, V.; Intes, X. Adaptive wide-field optical tomography. J. Biomed. Opt. 2013, 18. [Google Scholar] [CrossRef] [PubMed]
- Köllner, M.; Wolfrum, J. How many photons are necessary for fluorescence-lifetime measurements? Chem. Phys. Lett. 1992, 200, 199–204. [Google Scholar] [CrossRef]
- Keller, S.B.; Dudley, J.A.; Binzel, K.; Jasensky, J.; De Pedro, H.M.; Frey, E.W.; Urayama, P. Calibration approach for fluorescence lifetime determination for applications using time-gated detection and finite pulse width excitation. Anal. Chem. 2008, 80, 7876–7881. [Google Scholar] [CrossRef] [PubMed]
- Sinsuebphon, N.; Bevington, T.; Zhao, L.; Ken, A.; Barroso, M.; Intes, X. Comparison of NIR FRET pairs for quantitative transferrin-based assay. In Multimodal Biomedical Imaging IX; Azar, F. S., Intes, X., Eds.; Proc. SPIE: San Francisco, CA, USA, 2014. [Google Scholar]
- Wallrabe, H.; Chen, Y.; Periasamy, A.; Barroso, M. Issues in confocal microscopy for quantitative FRET analysis. Microsc. Res. Tech. 2006, 69, 196–206. [Google Scholar] [CrossRef] [PubMed]
- Qian, Z.M.; Li, H.; Sun, H.; Ho, K. Targeted drug delivery via the transferrin receptor-mediated endocytosis pathway. Pharmacol. Rev. 2002, 54, 561–587. [Google Scholar] [CrossRef] [PubMed]
- Danhier, F.; Feron, O.; Préat, V. To exploit the tumor microenvironment: Passive and active tumor targeting of nanocarriers for anti-cancer drug delivery. J. Control. Release 2010, 148, 135–146. [Google Scholar] [CrossRef] [PubMed]
- Chen, J. Mesh-based Monte Carlo method in time-domain widefield fluorescence molecular tomography. J. Biomed. Opt. 2012, 17. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Venugopal, V.; Intes, X. Monte Carlo based method for fluorescence tomographic imaging with lifetime multiplexing using time gates. Biomed. Opt. Express 2011, 2, 871–886. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.; Perelman, L.; Dasari, R.R.; Feld, M.S. Fluorescence tomographic imaging in turbid media using early-arriving photons and Laplace transforms. Proc. Natl. Acad. Sci. USA 1997, 94, 8783–8788. [Google Scholar] [CrossRef] [PubMed]
- Niedre, M.J.; de Kleine, R.H.; Aikawa, E.; Kirsch, D.G.; Weissleder, R.; Ntziachristos, V. Early photon tomography allows fluorescence detection of lung carcinomas and disease progression in mice in vivo. Proc. Natl. Acad. Sci. USA 2008, 105, 19126–19131. [Google Scholar] [CrossRef] [PubMed]
- Zhao, L.; Yang, H.; Cong, W.; Wang, G.; Intes, X. Lp regularization for early gate fluorescence molecular tomography. Opt. Lett. 2014, 39, 4156–4159. [Google Scholar] [CrossRef] [PubMed]
- Valim, N.; Brock, J.; Leeser, M.; Niedre, M. The effect of temporal impulse response on experimental reduction of photon scatter in time-resolved diffuse optical tomography. Phys. Med. Biol. 2013, 58, 335–349. [Google Scholar] [CrossRef] [PubMed]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, S.-J.; Sinsuebphon, N.; Intes, X. Assessment of Gate Width Size on Lifetime-Based Förster Resonance Energy Transfer Parameter Estimation. Photonics 2015, 2, 1027-1042. https://doi.org/10.3390/photonics2041027
Chen S-J, Sinsuebphon N, Intes X. Assessment of Gate Width Size on Lifetime-Based Förster Resonance Energy Transfer Parameter Estimation. Photonics. 2015; 2(4):1027-1042. https://doi.org/10.3390/photonics2041027
Chicago/Turabian StyleChen, Sez-Jade, Nattawut Sinsuebphon, and Xavier Intes. 2015. "Assessment of Gate Width Size on Lifetime-Based Förster Resonance Energy Transfer Parameter Estimation" Photonics 2, no. 4: 1027-1042. https://doi.org/10.3390/photonics2041027



