Monolithically Integrated Ge-on-Si Active Photonics
Abstract
:1. Introduction
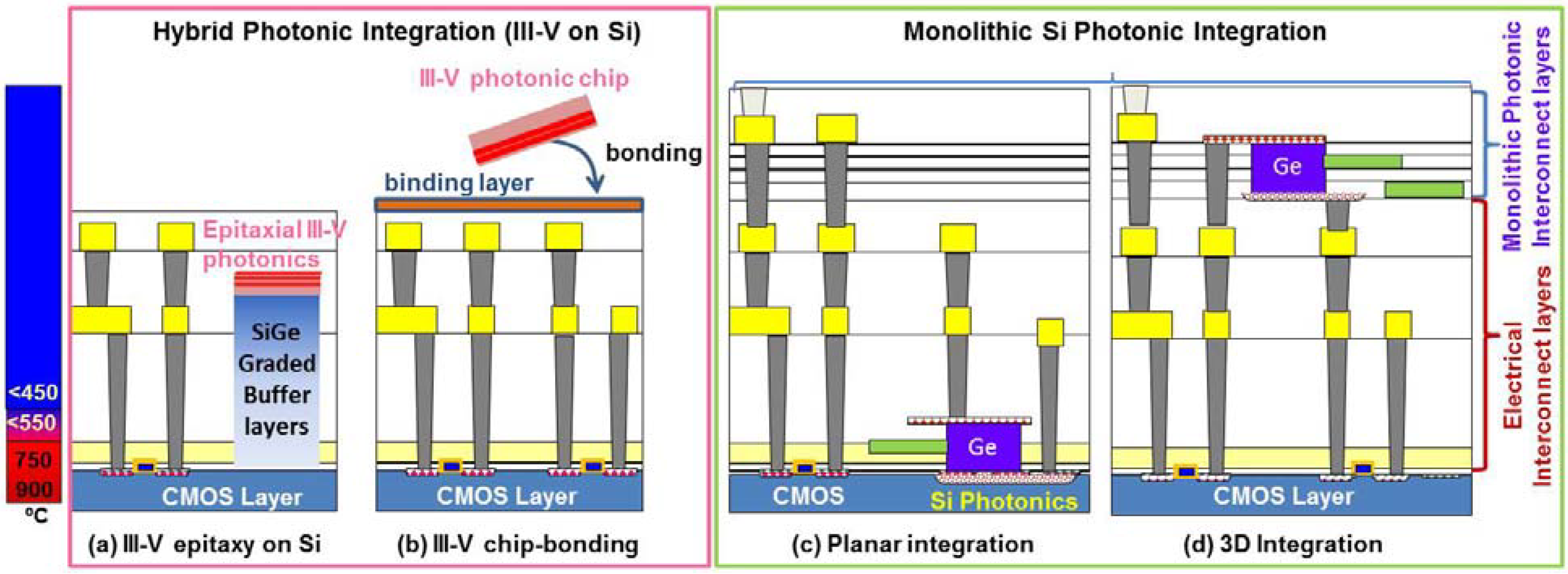
2. Band Structure and Band Engineering
2.1. Tensile Strain
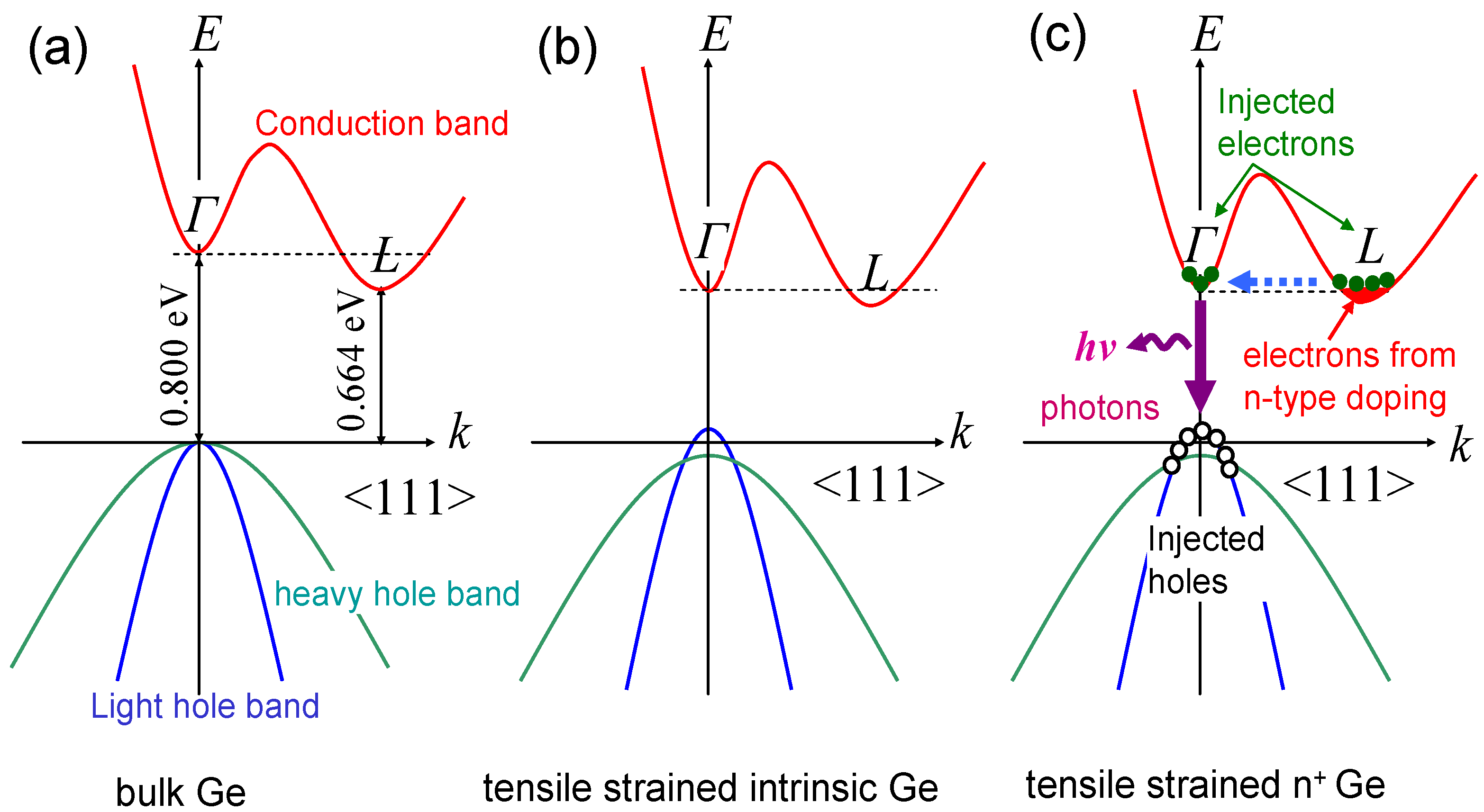
2.2. N-Type Doping
2.3. Sn Alloying
2.4. Cocktail Material Band Engineering Approaches for Optimal Ge-Based Gain Media

2.5. Separate Confinement of Γ. vs. L Electrons for Direct-Gap Ge Quantum Well (QW) Structures

3. Ge and GeSn Growth on Si
3.1. Epitaxy

3.2. Growth Methods towards 3D Photonic Integration


4. Ge-on-Si Active Photonic Devices
4.1. Waveguide Integration Schemes



4.2. Ge-on-Si PDs
| Responsivity (A/W) @ 1550 nm | 3dB Bandwidth (GHz) | Dark Current Density (mA/cm2) | Absolute Dark Current (μA)@ −1 V | Device Design | Reference | ||
|---|---|---|---|---|---|---|---|
| Max | 0 bias | Max | 0 bias | ||||
| 1.1 | - | 37@−3 V | 17.5 | 1.6 × 104 | 1.3 | butt p-i-n | [86] |
| 1@-4 V | 0.2 | 42@−4 V | 12 | 60 | 0.018 | butt p-i-n | [85] |
| >1.1 @ <1540 nm | - | 50@−5 V | - | 8900@ −5 V a | 4@−5 V | Bottom msm | [106] b |
| 0.42 | 0 | 40@−2.5 V | - | - | 90 | bottom msm | [75] c |
| 0.95 | - | 36 | - | 29 | 0.0046 | bottom p-i-n | [112] |
| 0.8 | 0.78 | >67; estimated 120 | 40 Gb/s | 8 × 104 | 4 | butt | [108] |
| 0.75@−2 V | - | 60@−2 V | - | 3750 | 3@−2 V | bottom p-i-n | [107] |
4.3. Ge and GeSi EAMs


| Reference | Optimal Wavelength Range (nm) | Coupling Method | Extinction Ratio (dB) | Insertion Loss (dB) | Bandwidth (GHz) | Vpp (V) | Active Device Area (μm2) | Average Dynamic Energy/bit 1/4 CVpp2 (fJ/bit) |
|---|---|---|---|---|---|---|---|---|
| Ge and GeSi FKE Modulators: | ||||||||
| [83] | 1539–1553 | butt | 8 | 3.7 | 1.2 | 3 (−4 to −7 V) | 0.6 × 50 | 25 a |
| [91] | 1580–1610 | evanescent | 10@ 1600 nm | 9.6 | 1.25 Gb/s | 5 | 0.8 × 20 | 102–103 |
| [119] | 1610–1640 | butt | 6.3@ 1620 nm | 3.6@ 1620 nm | 30 | 4 | 1 × 45 | ~70 |
| [120] | 1545–1581 | butt | 6 | 5 | 40.7 | 2.8 | 1 × 55 | 60 |
| [121] b | 1525–1555 | butt | 3 | 3 | >40; >10 Gb/s for 9 channels | 2 | - | 50 for EAM; 570 including driver |
| Ge QCSE Modulators: | ||||||||
| [122] | 1441–1461 | Side-entry | 7.3@ 1457 nm | ~9@ 1457 nm | - | 10 | 450 × 450 | - |
| [123] | 1415–440 | fiber coupled | 7/10@ 1420 nm | 3/7 dB@ 1420 nm | - | 6 | L = 34/64 μm | - |
| [124] | 1425–1446 | fiber coupled | 9@ 1435 nm Vpp = 1 V | 15@1435 nm, (−3 V) | 23 | 1 (−3 to −4 V) | 3 × 90 | 108 |
| [125] | 1450–1470@ −4 V DC bias c | butt | >3.2@ 1460 | ~15 | 3.5 | 1 (−3 to −5 V) | 0.8 × 10 | 0.75 |
| [126] | 1290–1310 | fiber coupled | 6@ 1293 nm | 2.5 | - | 7 | 3 × 150 | - |
4.4. Ge Gain Media and Lasers

5. Conclusions
Acknowledgments
Conflicts of Interest
References
- Lannoo, B.; Lambert, S.; van Heddeghem, W.; Pickavet, M.; Kuipers, F.; Koutitas, G.; Niavis, H.; Satsiou, A.; Beck, M.T.; Fischer, A.; et al. Overview of ICT Energy Consumption. Available online: http://www.internet-science.eu/sites/internet-science.eu/files/biblio/EINS_D8%201_final.pdf (accessed on 22 April 2014).
- Klein, T.E. Sustainable ICT Networks: The GreenTouch Vision. Green Research at Alcatel-Lucent. Available online: http://www.greentouch.org/uploads/documents/3%20Thierry%20Klein_EU%20SEW%20-%20The%20GT%20Vision%20-%20v2.pdf (accessed on 22 April 2014).
- Kimerling, L.C. Microphotonics: The Next Platform for the Information Age. 2011 MIT in Japan Conference. Available online: http://ilp.mit.edu/media/conferences/2011-japan/Kimerling.pdf (accessed on 22 April 2014).
- Soref, R.A. The past, present and future of silicon photonics. IEEE J. Sel. Top. Quantum Electron. 2006, 12, 1678–1687. [Google Scholar] [CrossRef]
- Kirchain, R.; Kimerling, L.C. A roadmap for nanophotonics. Nat. Photonics 2007, 1, 303–305. [Google Scholar] [CrossRef]
- Benner, A. Optical interconnect opportunities in supercomputers and high-end computing. In Proceedings of the 2012 Optical Fiber Communication Conference (OFC), Los Angeles, CA, USA, 4–8 March 2012.
- Liu, A.; Jones, R.; Liao, L.; Samara-Rubio, D.; Rubin, D.; Cohen, O.; Nicolaescu, R.; Paniccia, M. A high-speed silicon optical modulator based on metal-oxide-semiconductor capacitor. Nature 2004, 427, 615–618. [Google Scholar] [CrossRef]
- Xu, Q.; Schmidt, B.; Pradhan, S.; Lipson, M. Micrometre-scale silicon electro-optic modulator. Nature 2005, 435, 325–327. [Google Scholar] [CrossRef]
- Timurdogan, E.; Sorace-Agaskar, C.M.; Sun, J.; Hosseini, E.S.; Biberman, A.; Watts, M.R. A One Femtojoule Athermal Silicon Modulator. arXiv:1312.2683. Available online: http://arxiv.org/ftp/arxiv/papers/1312/1312.2683.pdf (accessed on 22 April 2014).
- Lin, H.; Ogbuu, O.; Liu, J.F.; Zhang, L.; Michel, J.; Hu, J.J. Breaking the Energy-Bandwidth Limit of Electrooptic Modulators: Theory and a Device Proposal. J. Light. Technol. 2013, 31, 4029–4036. [Google Scholar]
- Pavesi, L.; dal Negro, L.; Mazzoleni, C.; Franzo, G.; Priolo, F. Optical gain in silicon nanocrystals. Nature 2000, 408, 440–444. [Google Scholar] [CrossRef]
- Wilcoxon, J.P.; Samara, G.A. Tailorable, visible light emission from silicon nanocrystals. Appl. Phys. Lett. 1999, 74, 3164. [Google Scholar] [CrossRef]
- Geis, M.W.; Spector, S.J.; Grein, M.E.; Yoon, J.U.; Lennon, D.M.; Lyszczarz, T.M. Silicon waveguide infrared photodiodes with >35 GHz bandwidth and phototransistors with 50 AW-1 response. Opt. Express 2014, 22, 9150–9158. [Google Scholar]
- Souhan, B.; Grote, R.R.; Driscoll, J.B.; Lu, M.; Stein, A.; Bakhru, H.; Osgood, R.M. Metal-semiconductor-metal ion-implanted Si waveguide photodetectors for C-band operation. Opt. Express 2009, 17, 51–9158. [Google Scholar]
- Cheng, K.Y.; Anthony, R.; Kortshagen, U.R.; Holmes, R.J. High-efficiency silicon nanocrystal light-emitting devices. Nano Lett. 2011, 11, 1952–1956. [Google Scholar] [CrossRef]
- Physics of Group IV Elements and III–V Compounds, Landolt-Börnstein: Numerical Data and Functional Relationships in Science and Technology; Madelung, O. (Ed.) Springer: Berlin, Germany, 1982; Volume 17a.
- Lee, M.J.; Fitzgerald, E.A. Strained Si, SiGe, and Ge channels for high-mobility metal-oxide-semiconductor field-effect transistors. J. Appl. Phys. 2005, 97, 011101. [Google Scholar] [CrossRef]
- Liu, J.F.; Camacho-Aguilera, R.; Sun, X.; Wang, X.X.; Cai, Y.; Kimerling, L.C.; Michel, J. Reprinted from Thin Solid Films, Ge-on-Si Optoelectronics; Elsevier: Amsterdam, The Netherlands, 2011; Volume 520, pp. 3354–3360. [Google Scholar]
- Liu, J.F.; Sun, X.; Pan, D.; Wang, X.X.; Kimerling, L.C.; Koch, T.L.; Michel, J. Tensile-strained, n-type Ge as a gain medium for monolithic laser integration on Si. Opt. Express 2007, 15, 11272–11277. [Google Scholar]
- Soref, R.A.; Friedman, L. 1993b Direct gap Ge/GeSn/Si and GeSn/Ge/Si heterostructures. Superlattice Microstruct. 1993, 14, 189–193. [Google Scholar] [CrossRef]
- El Kurdi, M.; Fishman, G.; Sauvage, S.; Boucaud, P. Band structure and optical gain of tensile-strained germanium based on a 30 band k·p formalism. J. Appl. Phys. 2010, 107, 013710. [Google Scholar] [CrossRef]
- Aldaghri, O.; Ikonic, Z.; Kelsall, R.W. Optimum strain configurations for carrier injection in near infrared Ge lasers. J. Appl. Phys. 2012, 111, 053106. [Google Scholar] [CrossRef]
- Ishikawa, Y.; Wada, K.; Cannon, D.D.; Liu, J.F.; Luan, H.C.; Kimerling, L.C. Strain-induced direct bandgap shrinkage in Ge grown on Si substrate. Appl. Phys. Lett. 2003, 82, 2044–2046. [Google Scholar] [CrossRef]
- Liu, J.F.; Cannon, D.D.; Wada, K.; Ishikawa, Y.; Danielson, D.T.; Jongthammanurak, S.; Michel, J.; Kimerling, L.C. Deformation potential constants of biaxially tensile stressed Ge epitaxial films on Si(100). Phys. Rev. B 2004, 70, 155309. [Google Scholar] [CrossRef]
- Hartmann, J.M.; Abbadie, A.; Papon, A.M.; Holliger, P.; Roland, G.; Billon, T.; Fédéli, J.M.; Rouvière, M.; Vivien, L.; Laval, S. Reduced pressure-chemical vapor deposition of Ge thick layers on Si(001) for 1.3–1.55 µm photodetection. J. Appl. Phys. 2004, 95, 5905–5913. [Google Scholar] [CrossRef]
- Fang, Y.Y.; Tolle, J.; Roucka, R.; Chizmeshiya, A.V.G.; Kouvetakis, J.; D’Costa, V.R.; Menendez, J. Perfectly tetragonal, tensile-strained Ge on Ge1−ySny buffered Si(100). Appl. Phys. Lett. 2007, 90, 061915. [Google Scholar] [CrossRef]
- Takeuchi, S.; Shimura, Y.; Nakatsuka, O.; Zaima, S.; Ogawa, M.; Sakai, A. Growth of highly strain-relaxed Ge1−xSnx/virtual Ge by a Sn precipitation controlled compositionally step-graded method. Appl. Phys. Lett. 2008, 93, 231916. [Google Scholar]
- Liu, J.F.; Cannon, D.D.; Wada, K.; Ishikawa, Y.; Danielson, D.T.; Jongthammanurak, S.; Michel, J.; Kimerling, L.C. Silicidation-induced band gap shrinkage in Ge epitaxial films on Si. Appl. Phys. Lett. 2004, 84, 660–662. [Google Scholar] [CrossRef]
- Kuroyanagi, R.; Ishikawa, Y.; Tsuchizawa, T.; Wada, K. Controlling strain in Ge on Si for EA modulators. In Proceedings of the 8th IEEE International Conference on Group IV Photonics, London, UK, 14–16 September 2011.
- De Kersauson, M.; El Kurdi, M.; David, S.; Checoury, X.; Fishman, G.; Sauvage, S.; Jakomin, R.; Beaudoin, G.; Sagnes, I.; Boucaud, P. Optical gain in single tensile-strained germanium photonic wire. Opt. Express 2011, 19, 17925–17934. [Google Scholar]
- Jain, J.R.; Hryciw, A.; Baer, T.M.; Miller, D.A.B.; Brongersma, M.L.; Howe, R.T. A micromachining-based technology for enhancing germanium light emission via tensile strain. Nat. Photonics 2012, 6, 398–405. [Google Scholar] [CrossRef]
- Süess, M.J.; Geiger, R.; Minamisawa, R.A.; Schiefler, G.; Frigerio, J.; Chrastina, D.; Isella, G.; Spolenak, R.; Faist, J.; Sigg, H. Analysis of enhanced light emission from highly strained germanium microbridges. Nat. Photonics 2013, 7, 466–472. [Google Scholar] [CrossRef]
- Geiger, R.; Süess, M.J.; Bonzon, C.; Spolenak, R.; Faist, J.; Sigg, H. Strained Ge microbridges to obtain a direct bandgap laser. In Proceedings of the 7th International SiGe Technology and Device Meeting, Singapore, Singapore, 2–4 June 2014.
- Sukhdeo, D.S.; Nam, D.; Kang, J.H.; Brongersma, M.L.; Saraswat, K.C. Direct bandgap germanium-on-silicon inferred from 5.7% <100> uniaxial tensile strain. Photonics Res. 2014, 2, A8–A13. [Google Scholar] [CrossRef]
- Capellini, G.; Reich, C.; Guha, S.; Yamamoto, Y.; Lisker, M.; Virgilio, M.; Ghrib, A.; el Kurdi, M.; Boucaud, P.; Tillack, B.; et al. Tensile Ge microstructures for lasing fabricatedby means of a silicon complementary metal oxide-semiconductor process. Opt. Express 2014, 22, 399–410. [Google Scholar] [CrossRef]
- Haynes, J.R.; Nilsson, N.G. The direct radiative transitions in germanium and their use in the analysis of lifetime. In Proceedings of the VIIth International Conference on Physics of Semiconductors, Paris, France; 1964; pp. 21–31. [Google Scholar]
- Spitzer, W.G.; Trumbore, F.A.; Logan, R.A. Properties of heavily doped n-type germanium. J. Appl. Phys. 1961, 32, 1822–1830. [Google Scholar] [CrossRef]
- Newman, R.; Tyler, W.W. Effect of impurities on free-hole infrared absorption in p-type germanium. Phys. Rev. 1957, 105, 885–886. [Google Scholar] [CrossRef]
- Carroll, L.; Friedli, P.; Neuenschwander, S.; Sigg, H.; Cecchi, S.; Isa, F.; Chrastina, D.; Isella, G; Fedoryshyn, Y.; Faist, J. Direct-gap gain and optical absorption in germanium correlated to the density of photoexcited carriers doping, and strain. Phys. Rev. Lett. 2012, 109, 057402. [Google Scholar]
- Jenkins, J.W.; Dow, J.D. Electronic properties of metastable Ge1−xSnx alloys. Phys. Rev. B 1987, 36, 7994–8000. [Google Scholar] [CrossRef]
- He, G.; Atwater, H.A. Interband transitions in SnxGe1−x alloys. Phys. Rev. Lett. 1997, 79, 1937–1940. [Google Scholar] [CrossRef]
- Soref, R.; Kouvetakis, J.; Tolle, J.; Menendez, J.; D’Costa, V. Advances in SiGeSn technology. J. Mater. Res. 2007, 22, 3281–3291. [Google Scholar] [CrossRef]
- Mathews, J.; Roucka, R.; Xie, J.Q.; Yu, S.Q.; Menéndez, J.; and Kouvetakis, J. Extended performance GeSn/Si(100) p-i-n photodetectors for full spectral range telecommunication applications. Appl. Phys. Lett. 2009, 95, 133506. [Google Scholar]
- D’Costa, V.R.; Cook, C.S.; Birdwell, A.G.; Littler, C.L.; Canonico, M.; Zollner, S.; Kouvetakis, J.; Menéndez, J. Optical critical points of thin-film Ge1−ySny alloys: A comparative Ge1−ySny/Ge1−xSix study. Phys. Rev. B 2006, 73, 125207. [Google Scholar] [CrossRef]
- Chen, R.; Lin, H.; Huo, Y.; Hitzman, C.; Kamins, T.I.; Harris, J.S. Increased photoluminescence of strain-reduced, high-Sn composition Ge1−xSnx alloys grown by molecular beam epitaxy. Appl. Phys. Lett. 2011, 99, 181125. [Google Scholar]
- Oehme, M.; Buca, D.; Kostecki, K.; Wirths, S.; Hollaender, B.; Kasper, E.; Schulze, J. Epitaxial growth of highly compressively strained GeSn alloys up to 12.5% Sn. J. Cryst. Growth 2013, 384, 71–76. [Google Scholar] [CrossRef]
- Li, H.; Brouillet, J.; Salas, A.; Wang, X.X.; Liu, J.F. Low Temperature Growth of High Crystallinity GeSn on Amorphous Layers for Advanced Optoelectronics. Opt. Mater. Express 2013, 3, 1385–1396. [Google Scholar] [CrossRef]
- Oehme, M.; Kostecki, K.; Schmid, M.; Oliveira, F.; Kasper, E.; Schulze, J. Epitaxial growth of strained and unstrained GeSn alloys up to 25% Sn. Thin Solid Films 2014, 557, 169–172. [Google Scholar] [CrossRef]
- Van de Walle, C.G. Band lineups and deformation potentials in model-solid theory. Phys. Rev. B 1989, 39, 1871–1883. [Google Scholar] [CrossRef]
- Sun, X.; Liu, J.F.; Kimerling, L.C.; Michel, J. Direct gap photoluminescence of n-type tensile-strained Ge-on-Si. Appl. Phys. Lett. 2009, 95, 011911. [Google Scholar] [CrossRef]
- Bessette, J.; Camacho-Aguilera, R.; Cai, Y.; Kimerling, L.C.; Michel, J. Optical characterization of Ge-on-Si laser gain media. In Proceedings of the 8th IEEE International Conference on Group IV Photonics, London, UK, 14–16 September 2011. paper # P1.25.
- Sun, X.; Liu, J.F.; Kimerling, L.C.; Michel, J. Room-temperature direct bandgap electroluminesence from Ge-on-Si light-emitting diodes. Opt. Lett. 2009, 34, 1198–1200. [Google Scholar] [CrossRef]
- Cheng, S.L.; Lu, J.; Shambat, G.; Yu, H.Y.; Saraswat, K.; Vuckovic, J.; Nishi, Y. Room Temperature 1.6 μm electroluminescence from Ge light emitting Diode on Si Substrate. Opt. Express 2009, 17, 10019–10024. [Google Scholar]
- Arguirov, T.; Kittler, M.; Oehme, M.; Abrosimov, N.V.; Kasper, E.; Schulze, J. Room temperature direct band-gap emission from an unstrained Ge p-i-n LED on Si. Solid. State. Phenom. 2011, 178–179, 25–30. [Google Scholar] [CrossRef]
- Cai, Y.; Han, Z.; Wang, X.X.; Camacho-Aguilera, R.E.; Kimerling, L.C.; Michel, J.; Liu, J.F. Analysis of threshold current behavior for bulk and quantum well germanium laser structures. IEEE J. Sel. Top. Quantum Electron. 2013, 19, 1901009. [Google Scholar] [CrossRef]
- Froyen, S.; Wood, D.M.; Zunger, A. Electronic-structure of ultrathin SinGen strained superlattices—The possibility of direct band-gaps. Thin Solid Films 1989, 183, 33–48. [Google Scholar] [CrossRef]
- Kholod, A.N.; Ossicini, S.; Borisenko, V.E.; Arnaud d’Avitaya, F. True direct gap absorption in germanium quantum films. Phys. Rev. B. 2002, 65, 115315. [Google Scholar] [CrossRef]
- Virgilio, M.; Grosso, G. Type-I alignment and direct fundamental gap in SiGe based hetero-structures. J. Phys. C. Condens. Matter 2006, 18, 1021–1031. [Google Scholar] [CrossRef]
- Baribeau, J.M.; Jackman, T.E.; Houghton, D.C.; Maigné, P.; Denhoff, M.W. Growth and Characterization of Si1−xGex and Ge Epilayers on (100) Si. J. Appl. Phys. 1988, 63, 5738–5746. [Google Scholar] [CrossRef]
- Colace, L.; Masini, G.; Galluzzi, F.; Assanto, G.; Capellini, G.; di Gaspare, L.; Evangelisti, F. Ge/Si (001) photodetector for infrared light. Solid State Phenom. 1997, 54, 55–58. [Google Scholar] [CrossRef]
- Luan, H.C.; Lim, D.R.; Lee, K.K.; Chen, K.M.; Sandland, J.G.; Wada, K.; Kimerling, L.C. High-quality Ge epilayers on Si with low threading-dislocation densities. Appl. Phys. Lett. 1999, 75, 2909–2911. [Google Scholar] [CrossRef]
- Luan, H.-C. Ge Photodetectors for Si Microphotonics. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2001; pp. 74–76, 98–100. [Google Scholar]
- Tachikawa, M.; Yamaguchi, M. Film thickness dependence of dislocation reduction in GaAs-on-Si substrates. Appl. Phys. Lett. 1990, 54, 584–486. [Google Scholar]
- Romanova, A.E.; Pompe, W.; Beltz, G.E.; Speck, J.S. An approach to threading dislocation “reaction kinetics”. Appl. Phys. Lett. 1996, 69, 3342–3344. [Google Scholar] [CrossRef]
- Yamamoto, Y.; Kozlowski, G.; Zaumseil, P.; Tillack, B. Low threading dislocation Ge on Si by combining deposition and etching. Thin Solid Films 2012, 520, 3216–3221. [Google Scholar] [CrossRef]
- Liu, J.F.; Kimerling, L.C.; Michel, J. Monolithic Ge-on-Si lasers for large-scale electronic-photonic integration. Semicond. Sci. Technol. 2012, 27, 094006. [Google Scholar] [CrossRef]
- Liu, J.F.; Camacho-Aguilera, R.; Sun, X.; Wang, X.X.; Cai, Y.; Kimerling, L.C.; Michel, J. Ge-on-Si Optoelectronics. Thin Solid Films 2012, 520, 3354–3360. [Google Scholar] [CrossRef]
- Michel, J.; Liu, J.F.; Kimerling, L.C. High-Performance Ge-on-Si Photodetectors. Nat. Photonics 2010, 4, 527–534. [Google Scholar] [CrossRef]
- Camacho-Aguilera, R.E.; Cai, Y.; Bessette, J.T.; Kimerling, L.C.; Michel, J. High active carrier concentration in n-type, thin film Ge using delta-doping. Opt. Mater. Express 2012, 2, 1462–1469. [Google Scholar] [CrossRef]
- Cai, Y.; Camacho-Aguilera, R.E.; Bessette, J.T.; Kimerling, L.C.; Michel, J. High phosphorous doped germanium: Dopant diffusion and modeling. J. Appl. Phys. 2012, 112, 034509. [Google Scholar]
- Bauer, M.; Taraci, J.; Tolle, J.; Chizmeshya, A.V.G.; Zollner, S.; Smith, D. J.; Menendez, J.; Hu, C.W.; Kouvetakis, J. Ge-Sn semiconductors for band-gap and lattice engineering. Appl. Phys. Lett. 2002, 81, 2992–2994. [Google Scholar] [CrossRef]
- Mathews, J.; Beeler, R.T.; Tolle, J.; Xu, C.; Roucka, R.; Kouvetakis, J.; Menendez, J. Direct-gap photoluminescence with tunable emission wavelength in Ge1−ySny alloys on silicon. Appl. Phys. Lett. 2010, 97, 221912. [Google Scholar] [CrossRef]
- Liu, Y.; Deal, M.D.; Plummer, J.D. High-quality single-crystal Ge on insulator by liquid-phase epitaxy on Si substrate. Appl. Phys. Lett. 2004, 84, 2563–2565. [Google Scholar] [CrossRef]
- Miyao, M.; Toko, K.; Tanaka, T.; Sadohm, T. High-quality single-crystal Ge stripes on quartz substrate by rapid-melting-growth. Appl. Phys. Lett. 2009, 95, 022115. [Google Scholar] [CrossRef]
- Assefa, S.; Xia, F.N.; Bedell, S.W.; Zhang, Y.; Topuria, T.; Rice, P.M.; Vlasov, Y.A. CMOS-integrated high-speed MSM germanium waveguide photodetector. Opt. Express 2010, 18, 4986–4999. [Google Scholar]
- Matsue, M.; Yasutake, Y.; Fukatsu, S.; Hosoi, T.; Shimura, T.; Watanabe, H. Strain-induced direct band gap shrinkage in local Ge-on-insulator structures fabricated by lateral liquid-phase epitaxy. Appl. Phys. Lett. 2014, 104, 031106. [Google Scholar]
- Kanno, H.; Atsushi, K.; Sadoh, T.; Miyao, M. Ge-enhanced MILC velocity in a-Ge/a-Si/SiO2 layered structure. Mater. Sci. Semicond. Process. 2005, 8, 83–88. [Google Scholar] [CrossRef]
- Yu, C.H.; Yeh, P.H.; Cheng, S.L.; Chen, L.J.; Cheng, L.W. Metal-induced crystallization of amorphous Si1−xGex by rapid thermal annealing. Thin Solid Films 2004, 469–470, 356–360. [Google Scholar] [CrossRef]
- Yang, C.M.; Atwater, H.A. Selective solid phase crystallization for control of grain size and location in Ge thin films on silicon dioxide. Appl. Phys. Lett. 1996, 68, 3392–3394. [Google Scholar] [CrossRef]
- Schropp, R.E.I.; Carius, R.; Beaucarne, G. Amorphous silicon, microcrystalline silicon, and thin- film polycrystalline silicon solar cells. MRS Bull. 2007, 32, 219–224. [Google Scholar] [CrossRef]
- McComber, K.; Duan, X.; Liu, J.F.; Michel, J.; Kimerling, L.C. Single-crystal germanium growth on amorphous silicon. Adv. Funct. Mater. 2012, 22, 1048–1057. [Google Scholar] [CrossRef]
- Liu, J.F.; Dong, P.; Jongthammanurak, S.; Wada, K.; Kimerling, L.C.; and Michel, J. Design of monolithically integrated GeSi electroabsorption modulators and photodetectors on an SOI platform. Opt. Express 2007, 15, 623–628. [Google Scholar] [CrossRef]
- Liu, J.F.; Beals, M.; Pomerene, A.; Bernardis, S.; Sun, R.; Cheng, J.; Kimerling, L.C.; Michel, J. Waveguide integrated, ultra-low energy GeSi electro-absorption modulators. Nat. Photonics 2008, 2, 433–437. [Google Scholar] [CrossRef]
- Beals, M.; Michel, J.; Liu, J.F.; Ahn, D.H.; Sparacin, D.; Sun, R.; Hong, C.Y.; Kimerling, L.C.; Pomerene, A.; Carothers, D.; et al. Process flow innovations for photonic device integration in CMOS. Proc. Int. Soc. Opt. Eng. 2008, 6898, 689804. [Google Scholar]
- Vivien, L.; Osmond, J.; Fédéli, J.M.; Delphine, M.M.; Crozat, P.; Damlencourt, J.F.; Cassan, E.; Lecunff, Y.; Laval, S. 42 GHz p.i.n Germanium photodetector integrated in a silicon-on-insulator waveguide. Opt. Express 2009, 17, 6252–6257. [Google Scholar] [CrossRef]
- Feng, D.; Liao, S.; Dong, P.; Feng, N.N.; Liang, H.; Zheng, D.W.; Kung, C.C.; Fong, J.; Shafiiha, R.; Cunningham, J.; et al. High-speed Ge photodetector monolithically integrated with large cross-section silicon-on-insulator waveguide. Appl. Phys. Lett. 2009, 95, 261105. [Google Scholar] [CrossRef]
- Ren, S.; Kamins, T.I.; Miller, D.A.B. Thin dielectric spacer for the monolithic integration of bulk germanium or germanium quantum wells with silicon-on-insulator waveguides. IEEE. Photonics J. 2011, 3, 739–747. [Google Scholar] [CrossRef]
- Liu, J.F.; Pan, D.; Jongthammanurak, S.; Ahn, D.; Hong, C.Y.; Beals, M.; Kimerling, L.C.; Michel, J.; Pomerene, A.T.; Hill, C.; et al. Waveguide-Integrated Ge p-i-n Photodetectors on SOI Platform. In Proceedings of the 2006 IEEE International Conference on Group IV Photonics, Ottawa, ON, Canada, 13–15 September 2006. paper # ThA2.
- Ahn, D.; Kimerling, L.C.; Michel, J. Evanescent coupling device design for waveguide-integrated group IV photodetectors. J. Light. Technol. 2010, 28, 3387–3394. [Google Scholar]
- Ahn, D.H.; Kimerling, L.C.; Michel, J. Efficient evanescent wave coupling conditions for waveguide-integrated thin-film Si/Ge photodetectors on silicon-on-insulator/germanium-on-insulator substrates. J. Appl. Phys. 2011, 110, 083115. [Google Scholar] [CrossRef]
- Lim, A.E.-J.; Liow, T.Y.; Qing, F.; Duan, N.; Ding, L.; Yu, M.; Lo, G.-Q.; Kwong, D.L. Novel evanescent-coupled germanium electro-absorption modulator featuring monolithic integration with germanium p-i-n photodetector. Opt. Express 2011, 19, 5040–5046. [Google Scholar]
- Wang, X.X.; Liu, J.F. Step-coupler for efficient waveguide coupling to Ge/Si avalanche photodetectors. IEEE. Photonics Technol. Lett. 2011, 23, 146–148. [Google Scholar] [CrossRef]
- Liu, J.F.; Michel, J.; Giziewicz, W.; Pan, D.; Wada, K.; Cannon, D.D.; Kimerling, L.C.; Chen, J.; Ilday, F.O.; Kaertner, F.X.; et al. High-performance, tensile-strained Ge p-i-n photodetectors on a Si platform. Appl. Phys. Lett. 2005, 87, 103501. [Google Scholar] [CrossRef]
- Jutzi, M.; Berroth, M.; Wohl, G.; Oehme, M.; Kasper, E. Ge-on-Si vertical incidence photodiodes with 39-G Hz bandwidth. IEEE Photonics Technol. Lett. 2005, 17, 1510–1512. [Google Scholar] [CrossRef]
- Morse, M.; Dosunmu, O.; Sarid, G.; Chetrit, Y. IEEE. Photonics Technol. Lett. 2006, 18, 2442–2444. [CrossRef]
- Klinger, S.; Berroth, M.; Kaschel, M.; Oehme, M.; Kasper, E. Ge-on-Si p-i-n photodiodes with a 3-dB bandwidth of 49 GHz. IEEE Photonics Technol. Lett. 2009, 21, 920–922. [Google Scholar] [CrossRef]
- DiLello, N.A.; Johnstone, D.K.; Hoyt, J.L. Characterization of dark current in Ge-on-Si photodiodes. J. Appl. Phys. 2012, 112, 054506. [Google Scholar] [CrossRef]
- Colace, L.; Ferrara, P.; Assanto, G.; Fulgoni, D.; Nash, L. Low dark-current germanium-on silicon near-infrared detectors. IEEE. Photonics Technol. Lett. 2007, 19, 1813–1815. [Google Scholar] [CrossRef]
- Oehme, M.; Kostecki, K.; Ye, K.; Bechler, S.; Ulbricht, K.; Schmid, M.; Kaschel, M.; Gollhofer, M.; Körner, R.; Zhang, W.; et al. GeSn-on-Si normal incidence photodetectors with bandwidths more than 40 GHz. Opt. Express 2014, 22, 839–846. [Google Scholar] [CrossRef]
- Deliwala, S. Integrated optical receivers. In Proceedings of the 2011 IEEE International Conference on Group IV Photonics, London, UK, 14 September 2011.
- Kim, I.G.; Jang, K.S.; Joo, J.; Kim, S.; Kim, S.; Choi, K.S.; Oh, J.H.; Kim, S.A.; Kim, G. High-performance photoreceivers based on vertical-illumination type Ge-on-Si photodetectors operating up to 43 Gb/s at λ ~ 1550 nm. Opt. Express 2013, 21, 30718. [Google Scholar]
- Kang, Y.; Liu, H.D.; Morse, M.; Paniccia, M.J.; Zadka, M.; Litski, S.; Sarid, G.; Pauchard, A.; Kuo, Y.H.; Chen, H.W.; et al. Monolithic germanium/silicon avalanche photodiodes with 340 GHz gain-bandwidth product. Nat. Photonics 2009, 3, 59–63. [Google Scholar] [CrossRef]
- Huang, M.; Cai, P.; Wang, L.; Shi, T.; Chen, W.; Li, S.; Hou, G.; Hong, C.-Y.; Dong, P. Development of Si photonics technology: Ge/Si avalanche photodiode for PON applications. In Proceedings of the 2014 Optical Fiber Communication Conference (OFC 2014), San Francisco, CA, USA, 9–13 March 2014. paper # Tu2C2.
- Ahn, D.; Hong, C.Y.; Liu, J.F.; Giziewicz, W.; Beals, M.; Kimerling, L.C.; Michel, J. High performance, waveguide integrated Ge photodetectors. Opt. Express 2007, 15, 3916–3921. [Google Scholar]
- Vivien, L.; Rouvière, M.; Fédéli, J.M.; Marris-Morini, D.E.; Damlencourt, J.F.; Mangeney, J.; Crozat, P.; el Melhaoui, L.; Cassan, E.; le Roux, X.; et al. High speed and high responsivity germanium photodetector integrated in a silicon-on-insulator microwaveguide. Opt. Express 2007, 15, 9843–9848. [Google Scholar] [CrossRef]
- Chen, L.; Preston, K.; Manipatruni, S.; Lipson, M. Integrated GHz silicon photonic interconnect with micrometer-scale modulators and detectors. Opt. Express 2009, 18, 15248–15256. [Google Scholar]
- Novack, A.; Gould, M.; Yang, Y.; Xuan, Z.; Streshinsky, M.; Liu, Y.; Capellini, G.; Lim, A.E.J.; Lo, G.Q.; Baehr-Jones, T.; et al. Germanium photodetector with 60 GHz bandwidth using inductive gain peaking. Opt. Express 2013, 21, 28387–28393. [Google Scholar]
- Vivien, L.; Polzer, A.; Marris-Morini, D.; Osmond, J.; Hartmann, J.M.; Crozat, P.; Cassan, E.; Kopp, C.; Zimmermann, H.; Fédéli, J.M. Zero-bias 40 Gbit/s germanium waveguide photodetector on silicon. Opt. Express 2012, 20, 1096–1101. [Google Scholar] [CrossRef]
- Feng, D.D.; Qian, W.; Liang, H.; Luff, B.J.; Asghari, M. High-speed receiver technology on the SOI platform. IEEE. J. Sel. Top. Quantum Electron. 2013, 19, 3800108. [Google Scholar] [CrossRef]
- Kang, Y.M.; Morse, M.; Paniccia, M.J.; Zadka, M.; Saad, Y.; Sarid, G.; Pauchard, A.; Zaoui, W.S.; Chen, H.W.; Dai, D.; et al. Monolithic Ge/Si avalanche photodiodes. In Proceedings of the 2009 IEEE International Conference on Group IV Photonic, San Francisco, CA, USA, 9–11 September 2009; pp. 25–27.
- Assefa, S.; Xia, F.; Vlasov, Y.A. Reinventing germanium avalanche photodetector for nanophotonic on-chip optical interconnects. Nature 2010, 464, 80–85. [Google Scholar] [CrossRef]
- Liao, S.; Feng, N.-N.; Feng, D.; Dong, P.; Shafiiha, R.; Kung, C.-C.; Liang, H.; Qian, W.; Liu, Y.; Fong, J.; et al. 36 GHz submicron silicon waveguide germanium photodetector. Opt. Express 2011, 19, 10967–10972. [Google Scholar] [CrossRef]
- Pollak, F.H. Study of semiconductor surfaces and interfaces using electromodulation. Surf. Interface Anal. 2001, 31, 938–953. [Google Scholar] [CrossRef]
- Chuang, S.L. Physics of Optoelectronic Devices; Wiley: New York, NY, USA, 1995; Chapter 13. [Google Scholar]
- Jongthammanurak, S.; Liu, J.F.; Wada, K.; Cannon, D.D.; Danielson, D.T.; Pan, D.; Kimerling, L.C.; Michel, J. Large Electro-optic Effect in Tensile Strained Ge-on-Si Films. Appl. Phys. Lett. 2006, 89, 161115. [Google Scholar] [CrossRef]
- Kuo, Y.H.; Lee, Y.K.; Ge, Y.; Ren, S.; Roth, J.E.; Kamins, T.I.; Miller, D.A.B.; Harris, J.S. Strong quantum-confined Stark effect in germanium quantum-well structures on silicon. Nature 2005, 437, 1334–1336. [Google Scholar] [CrossRef]
- Edwards, E.H.; Lever, L.; Fei, E.T.; Kamins, T.I.; Ikonic, Z.; Harris, J.S.; Kelsall, R.W.; Miller, D.A.B. Low-voltage broad-band electroabsorption from thin Ge/SiGe quantum wells epitaxially grown on silicon. Opt. Express 2013, 21, 867–876. [Google Scholar] [CrossRef]
- Doerr, C.R.; Chen, L.Z.; Vermeulen, D.; Nielsen, T.; Azemati, S.; Stulz, S.; McBrien, G.; Xu, X.; Mikkelsen, B.; Givehchi, M.; et al. Single-chip silicon photonics 100-Gb/s coherent transceiver. In Proceedings of the 2014 Optical Fiber Communication Conference, San Francisco, CA, USA, 9–13 March 2014.
- Feng, N.N.; Feng, D.Z.; Liao, S.; Wang, X.; Dong, P.; Liang, H.; Kung, C.C.; Qian, W.; Fong, J.; Shafiiha, R.; et al. 30 GHz Ge electro-absorption modulator integrated with 3 μm silicon-on-insulator waveguide. Opt. Express 2011, 19, 7062–7067. [Google Scholar] [CrossRef]
- Feng, D.Z.; Liao, S.; Liang, H.; Fong, J.; Bijlani, B.; Shafiiha, R.; Luff, B.J.; Luo, Y.; Cunningham, J.E.; Krishnamoorthy, A.V.; et al. High speed GeSi electro-absorption modulator at 1550 nm wavelength on SOI waveguide. Opt. Express 2012, 20, 22224–22232. [Google Scholar] [CrossRef]
- Krishnamoorthy, A.V.; Zheng, X.; Feng, D.; Lexau, J.; Buckwalter, J.F.; Thacker, H.D.; Liu, F.; Luo, Y.; Chang, E.; Amberg, P.; et al. A low-power, high-speed, 9-channel germaniumsilicon electro-absorption modulator array integrated with digital CMOS driver and wavelength multiplexer. Opt. Express 2014, 22, 12289–12295. [Google Scholar] [CrossRef]
- Roth, J.E.; Fidaner, O.; Schaevitz, R.K.; Kuo, Y.H.; Kamins, T.I.; Harris, J.S.; Miller, D.A.B. Optical modulator on silicon employing germanium quantum wells. Opt. Express 2007, 15, 5851–5859. [Google Scholar]
- Chaisakul, P.; Marris-Morini, D.; Isella, G.; Chrastina, D.; le Roux, X.; Edmond, S.; Coudevylle, J.R.; Cassan, E.; Vivien, L. Polarization dependence of quantum-confined Stark effect in Ge/SiGe quantum well planar waveguides. Opt. Lett. 2011, 36, 1794–1796. [Google Scholar] [CrossRef]
- Chaisakul, P.; Marris-Morini, D.; Rouifed, M.-S.; Isella, G.; Chrastina, D.; Frigerio, J.; le Roux, X.; Edmond, S.; Coudevylle, J.-R.; Vivien, L. 23 GHz Ge/SiGe multiple quantum well electro-absorption modulator. Opt. Express 2012, 20, 3219–3224. [Google Scholar] [CrossRef]
- Ren, S.; Rong, Y.; Claussen, S.A.; Schaevitz, R.K.; Kamins, T.I.; Harris, J.S.; Miller, D.A.B. Ge/SiGe quantum well waveguide modulator monolithically integrated with SOI waveguides. IEEE Photonics Technol. Lett. 2012, 24, 461–463. [Google Scholar] [CrossRef]
- Rouifed, M.S.; Marris-Morini, D.; Chaisakul, P.; Frigerio, J.; Isella, G.; Chrastina, D.; Edmond, S.; Roux, X.L.; Coudevylle, J.R.; Bouville, D.; et al. Advances toward Ge/SiGe quantum-well waveguide modulators at 1.3 μm. IEEE. J. Sel. Top. Quantum Electron. 2014, 20, 3400207. [Google Scholar]
- Liu, J.F.; Sun, X.C.; Kimerling, L.C.; Michel, J. Direct-gap optical gain of Ge on Si at room temperature. Opt. Lett. 2009, 34, 1738–1740. [Google Scholar] [CrossRef]
- Liu, J.F.; Sun, X.; Camacho-Aguilera, R.; Kimerling, L.C.; Michel, J. Ge-on-Si laser operating at room temperature. Opt. Lett. 2010, 35, 679–681. [Google Scholar] [CrossRef]
- Camacho-Aguilera, R.E.; Cai, Y.; Patel, N.; Bessette, J.T.; Romagnoli, M.; Kimerling, L.C.; Michel, J. An electrically pumped germanium laser. Opt. Express 2012, 20, 11316–11320. [Google Scholar] [CrossRef]
- Wang, X.X.; Li, H.; Camacho-Aguilera, R.E.; Cai, Y.; Kimerling, L.C.; Michel, J.; Liu, J.F. Infrared absorption of n-type tensile-strained Ge-on-Si. Opt. Lett. 2013, 38, 652–654. [Google Scholar] [CrossRef]
- Tsai, C.-Y.; Tsai, C.-Y.; Chen, C.-H.; Sung, T.L.; Wu, T.-Y.; Shih, F.-P. Theoretical model for intravalley and intervalley free-Carrier absorption in semiconductor lasers: Beyond the classical Drude model. IEEE J. Quantun Electron. 1998, 34, 552–559. [Google Scholar] [CrossRef]
- Haug, A. Free carrier absorption in semiconductor lasers. Semicond. Sci. Technol. 1992, 7, 373–378. [Google Scholar] [CrossRef]
- Spitzer, W.G.; Whelan, J.M. Infrared absorption and electron effective mass in n-type gallium arsenide. Phys. Rev. 1959, 114, 59–63. [Google Scholar] [CrossRef]
- Boucaud, P.; el Kurdi, M.; Ghrib, A.; Prost, M.; de Kersauson, M.; Sauvage, S.; Aniel, F.; Checoury, X.; Beaudoin, G.; Largeau, L.; et al. Recent advances in germanium emission. Photonics Res. 2013, 1, 102–109. [Google Scholar]
- Tyulerev, V.G.; Obukhov, S.V.; Vast, M.; Sjakste, J. Ab initio calculation of electron-phonon scattering time in germanium. Phys. Rev. B 2011, 84, 035201. [Google Scholar]
- Wang, X.X.; Kimerling, L.C.; Michel, J.; Liu, J.F. Large inherent optical gain from the direct gap transition of Ge thin films. Appl. Phys. Lett. 2013, 102, 131116. [Google Scholar] [CrossRef]
- Stroscio, M.A.; Dutta, M. Phonons in Nanostructures; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Geiger, R.; Frigerio, J.; Süess, M.J.; Chrastina, D.; Isella, G.; Spolenak, R.; Faist, J.; Sigg, H. Excess carrier lifetimes in Ge layers on Si. Appl. Phys. Lett. 2014, 104, 062106. [Google Scholar]
- Langdo, T. Selective SiGe Nanostructures. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2001. [Google Scholar]
- Camacho-Aguilera, R.E.; Cai, Y.; Kimerling, L.C.; Michel, J. Ge-on-Si bufferless epitaxial growth for photonic devices. ECS Trans. 2012, 50, 469–473. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Liu, J. Monolithically Integrated Ge-on-Si Active Photonics. Photonics 2014, 1, 162-197. https://doi.org/10.3390/photonics1030162
Liu J. Monolithically Integrated Ge-on-Si Active Photonics. Photonics. 2014; 1(3):162-197. https://doi.org/10.3390/photonics1030162
Chicago/Turabian StyleLiu, Jifeng. 2014. "Monolithically Integrated Ge-on-Si Active Photonics" Photonics 1, no. 3: 162-197. https://doi.org/10.3390/photonics1030162
APA StyleLiu, J. (2014). Monolithically Integrated Ge-on-Si Active Photonics. Photonics, 1(3), 162-197. https://doi.org/10.3390/photonics1030162




