Optical Backplane Based on Ring-Resonators: Scalability and Performance Analysis for 10 Gb/s OOK-NRZ
Abstract
:1. Introduction
2. Optical Interconnection Architecture
 ℕ, then [N/(S-1)] cards will be connected to the first S-1 planes, while the remaining ones will occupy the first available positions within the last plane.
ℕ, then [N/(S-1)] cards will be connected to the first S-1 planes, while the remaining ones will occupy the first available positions within the last plane.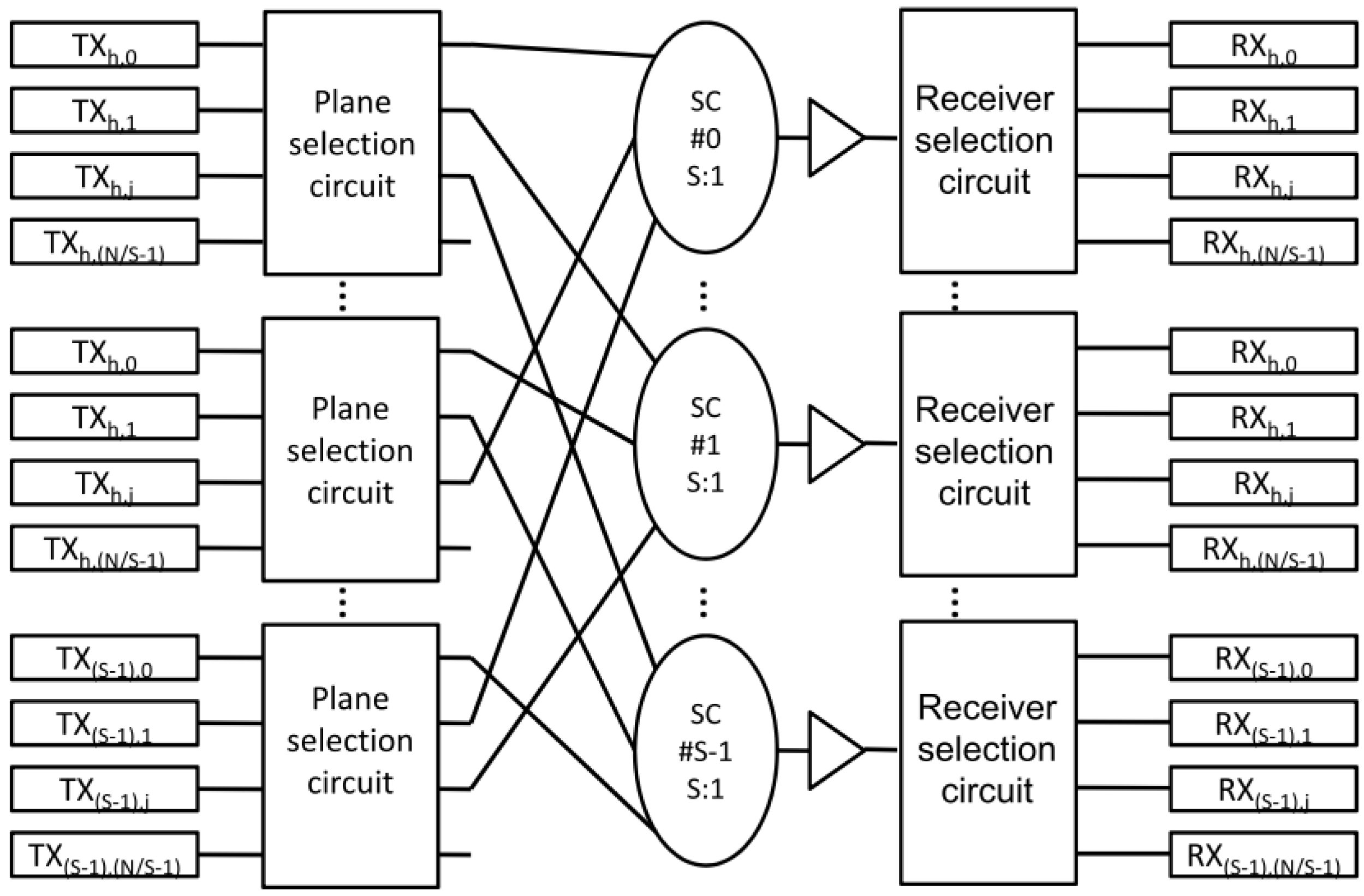
2.1. Ring Resonator Based Backplane
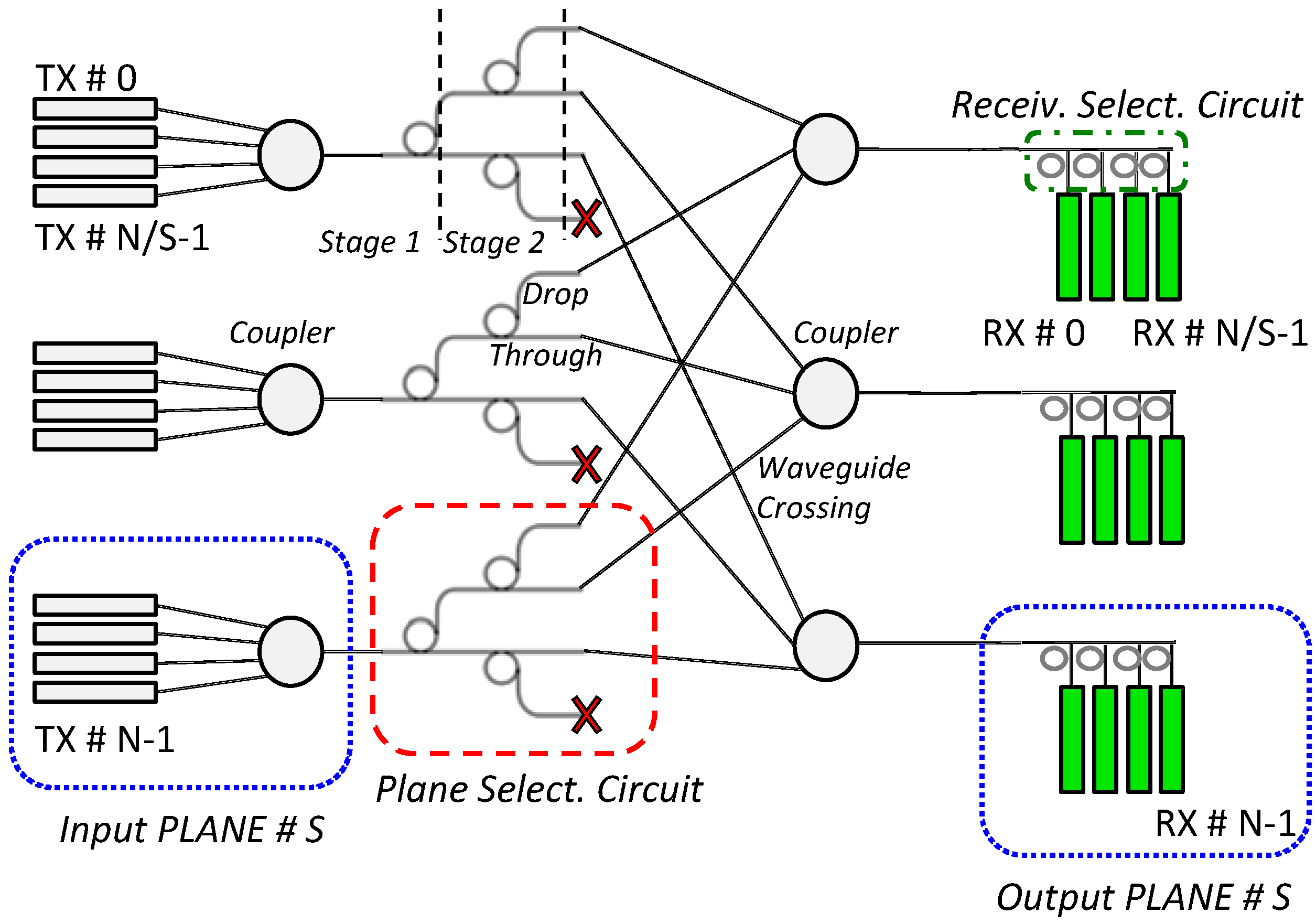

2.2. Backplane Transfer Function
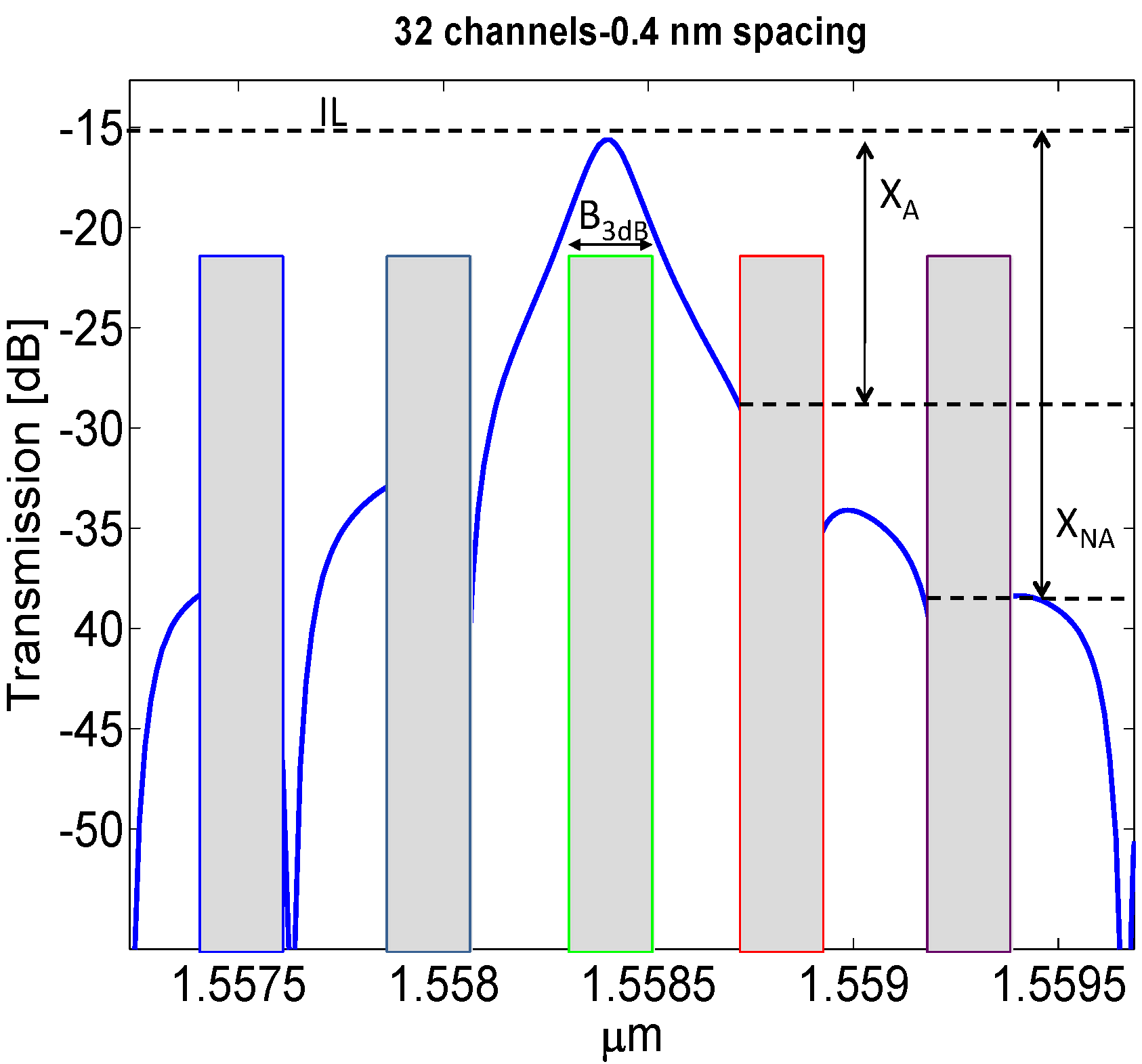


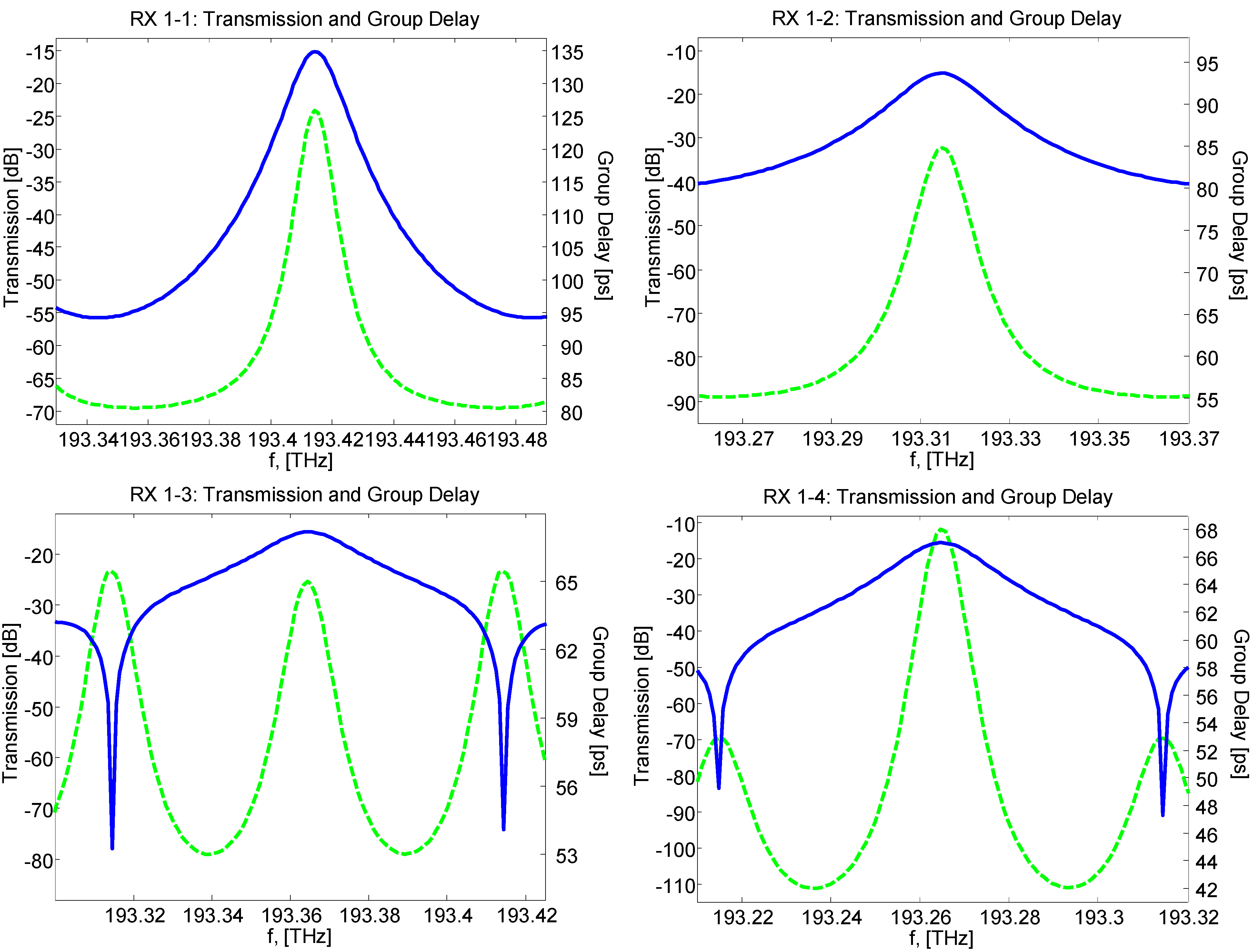
3. Illustrative Numerical Results
3.1. Number of Optical Channels (λ)
| λ | <IL> | ILm | ILM | Bm | BM | XA | XNA | XFL |
|---|---|---|---|---|---|---|---|---|
| Chan@GHz | [dB] | [dB] | [dB] | [GHz] | [GHz] | [dB] | [dB] | [dB] |
| 16@100 | −12.5 | −12 | −14 | 10.2 | 20.9 | −21.2 | −27.2 | −32 |
| 32@50 | −15.8 | −15 | −17.6 | 10.4 | 20.1 | −14 | −20.8 | −29 |
| 64@25 | −19.8 | −18 | −22.5 | 10.5 | 17.6 | −7.2 | −15.2 | −18 |
3.2. Roundtrip Loss of Ring Resonators (α)
| α | <IL> | ILm | ILM | Bm | BM | XA | XNA | XFL |
|---|---|---|---|---|---|---|---|---|
| [dB/turn] | [dB] | [dB] | [dB] | [GHz] | [GHz] | [dB] | [dB] | [dB] |
| 0 | −15.8 | −15 | −17.6 | 10.4 | 20.1 | −14 | −20.8 | −29 |
| 0.2 | −20.2 | −19.5 | −21.5 | 12.2 | 31.4 | −9.7 | −17.3 | −24 |
| 0.4 | −23 | −22.6 | −24.5 | 13.5 | 41.2 | −9.4 | −14.8 | −22 |
| 0.6 | −25.9 | −24.7 | −27.1 | 14.9 | 51.1 | −7.9 | −13 | −20 |
| 0.8 | −28 | −26.4 | −29.4 | 14.9 | 57 | −6.7 | −12.2 | −17 |
| 1.0 | −29.6 | −27.8 | −31.4 | 15.9 | 62 | −5.9 | −11.2 | −14 |
3.3. Thermal Variations (ΔT)
| ΔT | <IL> | ILm | ILM | Bm | BM | XA | XNA | XFL |
|---|---|---|---|---|---|---|---|---|
| [°C] | [dB] | [dB] | [dB] | [GHz] | [GHz] | [dB] | [dB] | [dB] |
| 0 | −15.8 | −15 | −17.6 | 10.4 | 20.1 | −14 | −20.8 | −29 |
| ±0.5 | −15.9 | −15.3 | −17.8 | 11.9 | 19.8 | −12.7 | −19.7 | −29 |
| ±1.0 | −16.2 | −16 | −18.4 | 11.6 | 20.1 | −12.2 | −20.4 | −27 |
| ±1.5 | −16.5 | −15.3 | −21.6 | 10.7 | 20.3 | −11.6 | −15.7 | −23 |
3.4. Waveguide Crossing
3.5. Technology Remarks
4. BER Performance Analysis
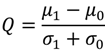
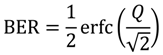
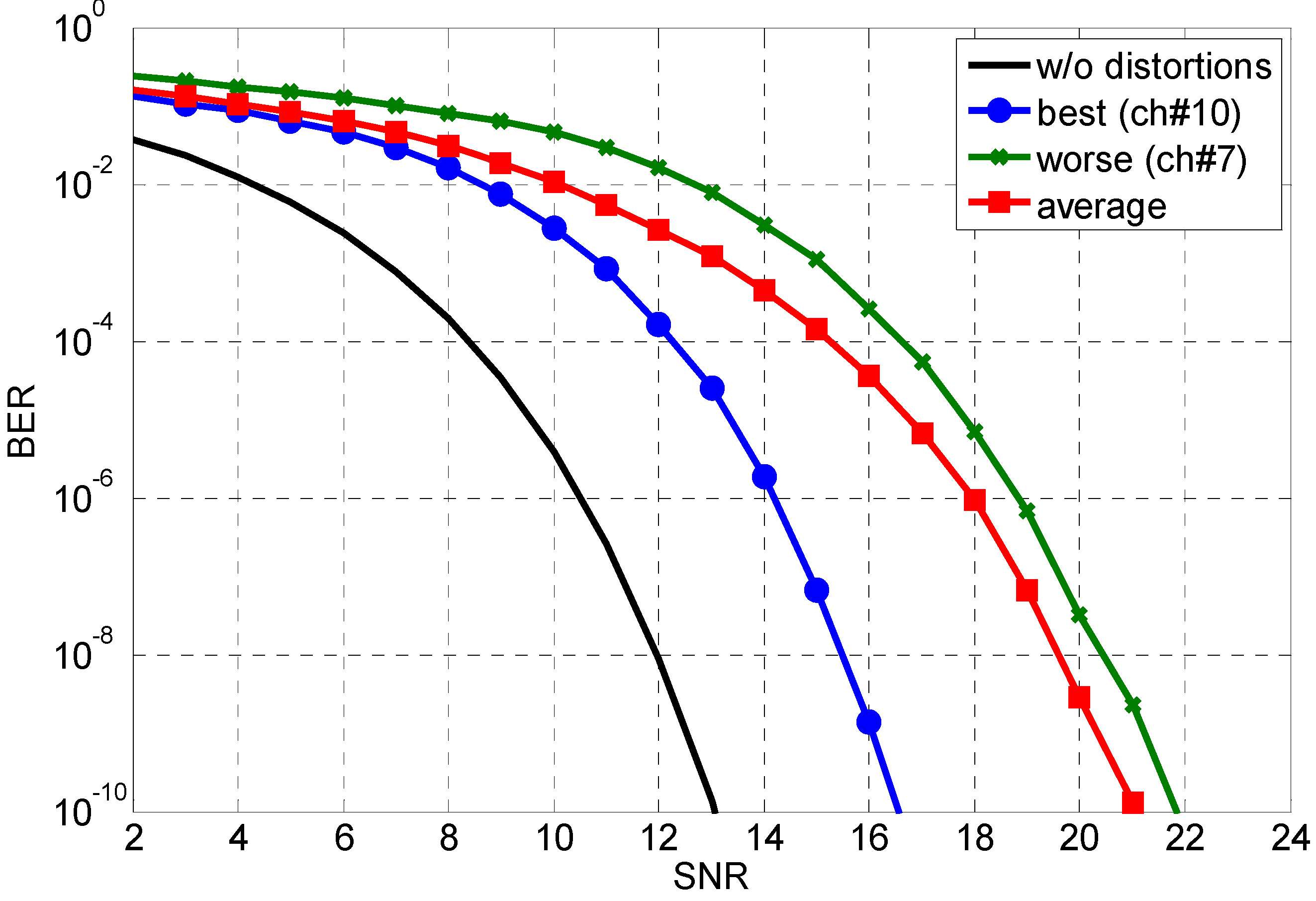
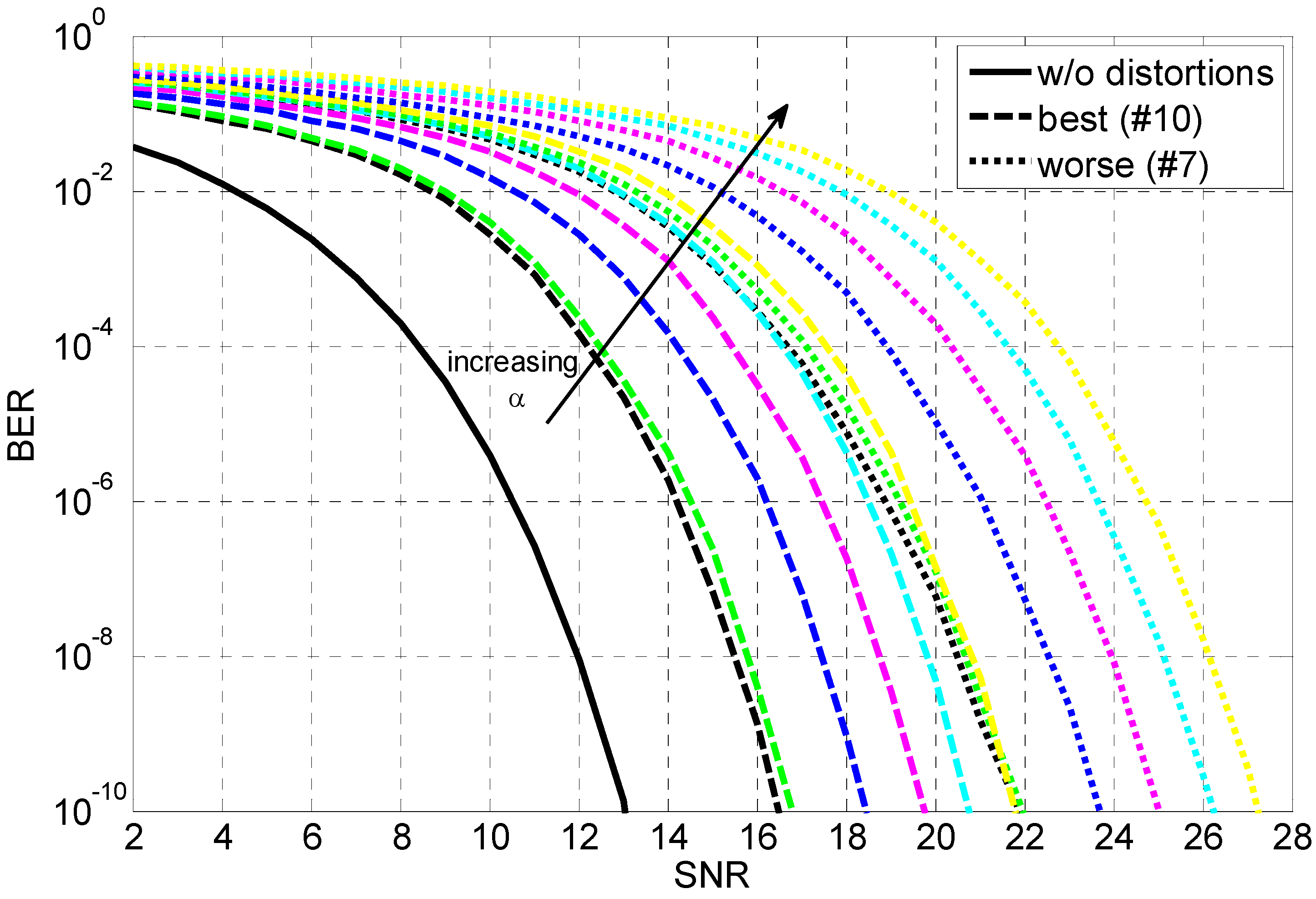
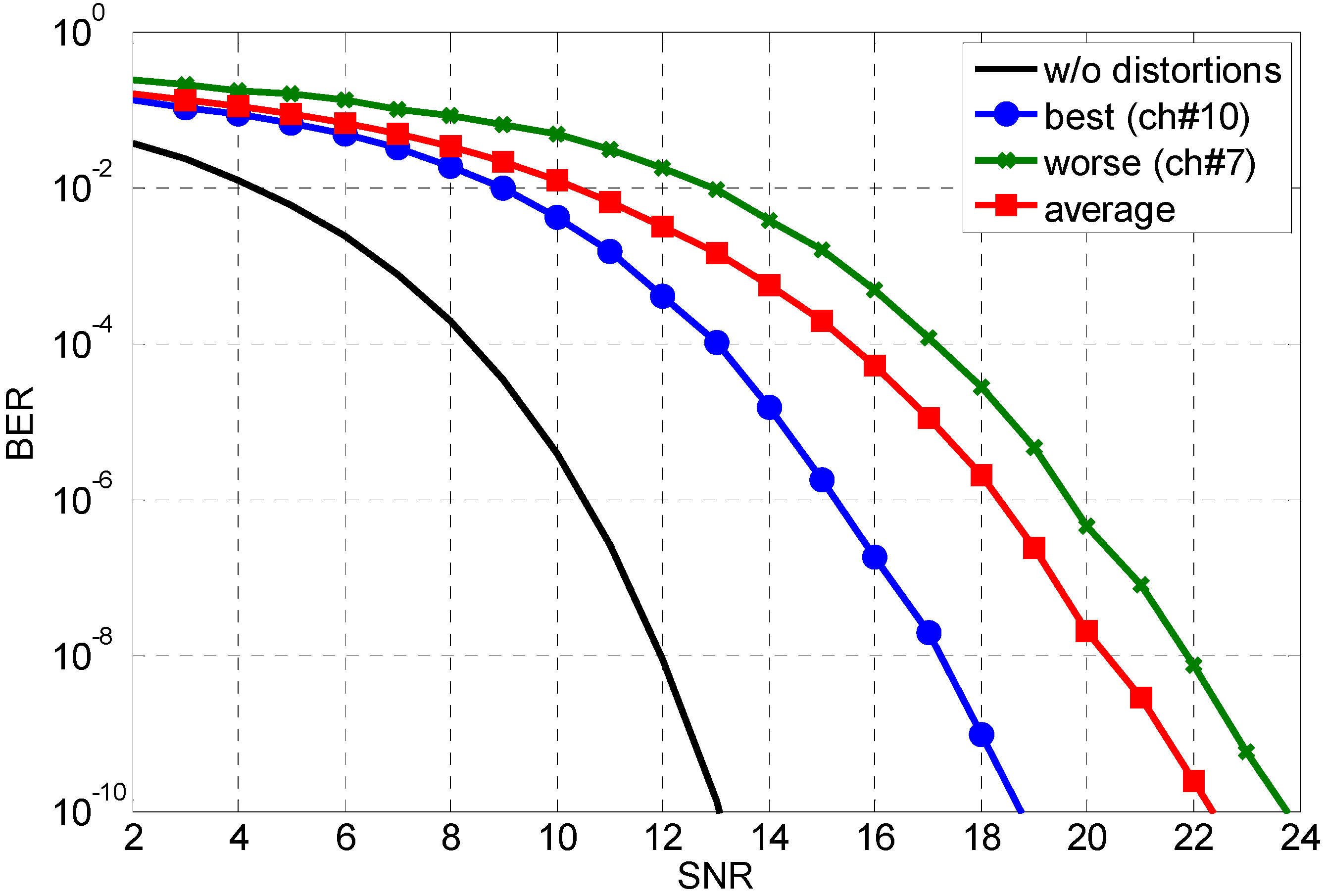
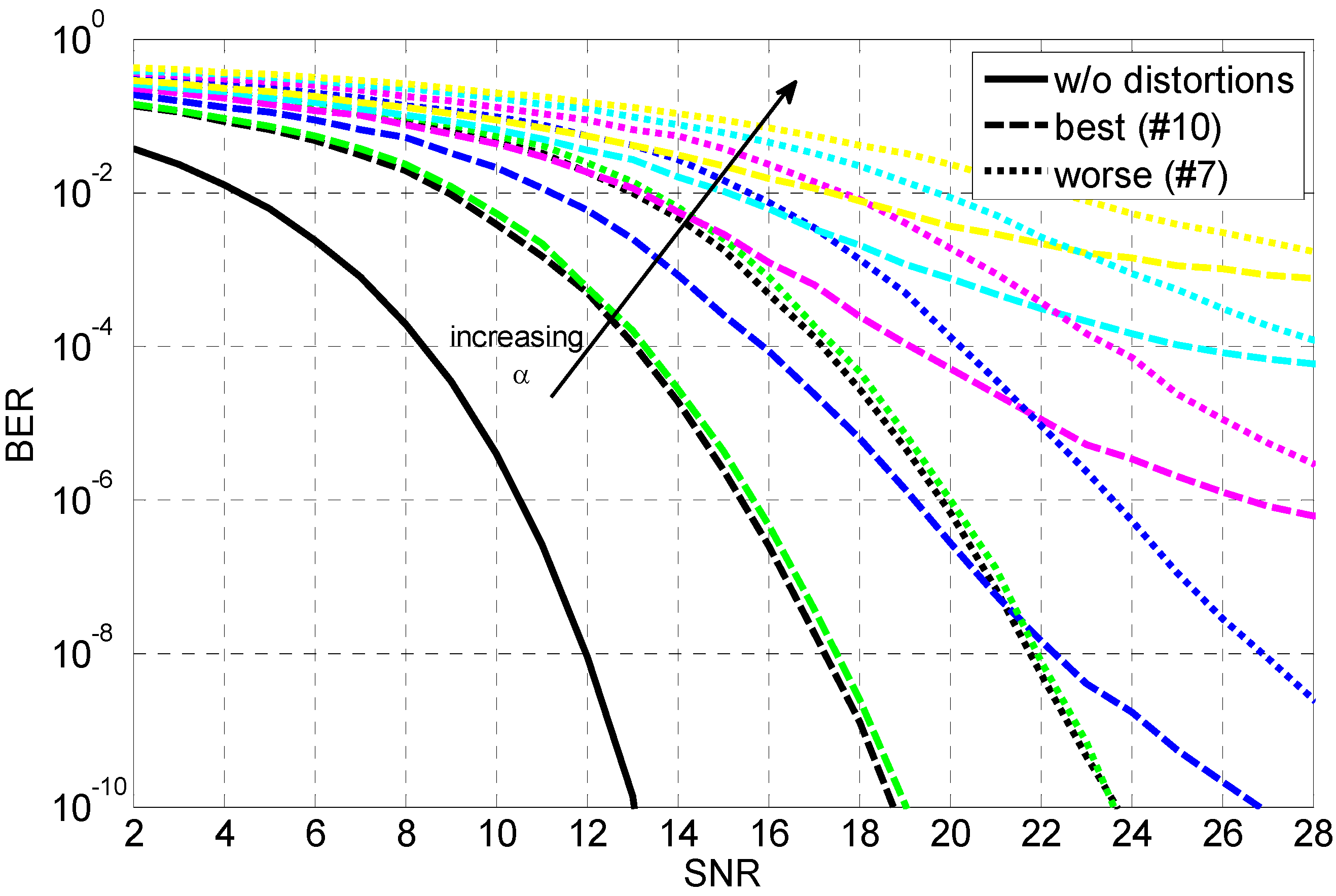
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Korotky, S.K. Traffic trends: Drivers and measures of cost-effective and energy-efficient technologies and architectures for backbone optical networks. In Proceedings of the Optical Fiber Communication Conference and Exposition and the National Fiber Optic Engineers Conference, Los Angeles, CA, USA, 4–8 March 2012; p. OM2G.1.
- Bianco, A.; Carta, E.; Cuda, D.; Finochietto, J.M.; Neri, F. An optical interconnection architecture for large packet switches. In Proceedings of the International Conference on Transparent Optical Networks, Rome, Italy, 1–5 July 2007; pp. 226–229.
- Siracusa, D.; Maier, G.; Linzalata, V.; Pattavina, A. Scalability of optical interconnections based on the arrayed waveguide grating in high capacity routers. In Proceedings of the IEEE International Conference on Optical Network Design and Modeling, Bologna, Italy, 8–10 February 2011; pp. 1–6.
- Klein, E.J. Densely Integrated Microring-Resonator Based Components for Fiber-to-the-Home Applications. Ph.D. Thesis, University of Twente, Enschede, The Netherlands, 2007. [Google Scholar]
- Melloni, A.; Martinelli, M. The ring-based resonant router. In Proceedings of the ICTON 2003; Warsaw, Poland: 29 June–3 July 2003.
- Cuda, D.; Gaudino, R.; Gavilanes, G.A.; Neri, F.; Maier, G.; Raffaelli, C.; Savi, M. Capacity/cost tradeoffs in optical switching fabrics for terabit packet switches. In Proceedings of the IEEE International Conference on Optical Network Design and Modeling, Braunschweig, Germany, 18–20 February 2009; 2009; pp. 1–6. [Google Scholar]
- Rizzelli, G.; Siracusa, D.; Maier, G.; Magarini, M.; Melloni, A. Performance of ring-resonator based optical backplane in high capacity routers. In Proceedings of the 15th International Conference on Transparent Optical Networks, Cartagena, Spain, 23–27 June 2013; pp. 1–4.
- Melloni, A.; Costa, R.; Cusmai, G.; Morichetti, F. The role of index contrast in dielectric optical waveguides. Int. J. Mater. Prod. Technol. 2009, 34, 421–437. [Google Scholar] [CrossRef]
- Filarete srl, Italy. Milano. Available online: http://www.aspicdesign.com (accessed on 11 April 2014).
- Melati, D.; Morichetti, F.; Canciamilla, A.; Roncelli, D.; Soares, F.; Bakker, A.; Melloni, A. Validation of the building-block-based approach for the design of photonic integrated circuits. J. Lightwave Technol. 2012, 30, 3610–3616. [Google Scholar] [CrossRef]
- “Dispersion”. In Fundamentals of Optical Fibers: Wiley Series in Pure and Applied Optics; Buck, J.A. (Ed.) Wiley-Interscience, John Wiley & Sons: Hoboken, NJ, USA, 2004.
- T Series Core Routers. Available online: http://www.juniper.net/ (accessed on 11 April 2014).
- Knights, A.P.; Jessop, P.E. Silicon waveguides for integrated optics. In Optical Waveguides: From Theory to Applied Technologies; Calvo, M.L., Lakshminarayanan, V., Eds.; Taylor and Francis: London, UK, 2007; pp. 231–270. [Google Scholar]
- Bukkems, H.G. Minimization of the loss of intersecting waveguides in inP-based photonic integrated circuits. Photonics Technol. Lett. 1999, 11, 1420–1422. [Google Scholar] [CrossRef]
- Downie, J.D. Relationship of Q penalty to eye-closure penalty for NRZ and RZ signals with signal-dependent noise. J. Lightwave Technol. 2005, 23, 2031–2038. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Rizzelli, G.; Siracusa, D.; Maier, G.; Magarini, M.; Alam, M.; Melloni, A. Optical Backplane Based on Ring-Resonators: Scalability and Performance Analysis for 10 Gb/s OOK-NRZ. Photonics 2014, 1, 131-145. https://doi.org/10.3390/photonics1020131
Rizzelli G, Siracusa D, Maier G, Magarini M, Alam M, Melloni A. Optical Backplane Based on Ring-Resonators: Scalability and Performance Analysis for 10 Gb/s OOK-NRZ. Photonics. 2014; 1(2):131-145. https://doi.org/10.3390/photonics1020131
Chicago/Turabian StyleRizzelli, Giuseppe, Domenico Siracusa, Guido Maier, Maurizio Magarini, Mehmood Alam, and Andrea Melloni. 2014. "Optical Backplane Based on Ring-Resonators: Scalability and Performance Analysis for 10 Gb/s OOK-NRZ" Photonics 1, no. 2: 131-145. https://doi.org/10.3390/photonics1020131






