1. Introduction
The classical “one-dimensional” Poisson distribution has historically been found to be useful in modeling a wide variety of “integer-valued” phenomena, such as the number of accidents and associated fatalities, disease advances, rate of rare event occurrences and so on. With regard to the Poisson model with concomitants, i.e., Poisson regression or count regression, its best known applications are in modeling counts of bacteria exposed to various environmental conditions and dilutions; modeling counts of infant mortality among groups with different demographics. All these examples are typically modeled under the assumption of equi-dispersion. However, count data also exhibits over and under dispersion. In this context, the one-dimensional Conway–Maxwell–Poisson model or its regression version fills the bill precisely by allowing us to model over, equi- and under-dispersion data.
In general, bivariate count data, along with having marginal over-, under- or equi-dispersion, will also exhibit a variety of dependence structures. In particular, for linear dependence, the possible relations are positive or negative correlation. The classical bivariate Poisson model is appropriate for data having equi-dispersed marginals with positive correlation. Here again, the bivariate Conway–Maxwell–Poisson is more flexible in that it can adapt to both under and over dispersed data, see Sellers et al. [
1]. Concerning bivariate Poisson regression models, the first version involving explanatory variables acting on the marginal means was introduced in Kocherlakota and Kocherlakota [
2] based on the classical bivariate Poisson model. In addition, the derivation of Wald, score and likelihood ratio test statistics for testing a single coefficient parameter vector are discussed in Riggs et al. [
3]. Zamani et al. [
4] proposed a bivariate Poisson model which can be fitted to both positive and negatively correlated data. Recently, Chowdhury et al. [
5] considered the Poisson–Poisson regression model (which is the particular case of the bivariate pseudo-Poisson model) to analyze the impact of covariates on the daily new cases and fatalities associated with the COVID-19 pandemic. Finally, we refer to Karlis and Ntzoufras [
6] and the R package
for maximum likelihood estimation, using an Expectation-Maximization (EM) algorithm, for diagonally inflated bivariate Poisson regression models.
In recent work, Arnold and Manjunath [
7] recommended the bivariate pseudo-Poisson model to fit data which have one marginal and other conditional of the Poisson form. Due to its straightforward structure with no restrictions on the conditional mean function, it allows us to include a variety of dependence structures, including positive and negative correlation. In the following, we introduce explanatory variables acting on the pseudo-Poisson parameters. Thanks to the simple structure, the concomitant effects can be introduced into each of the parameters to generate a family of models with a variety of dependence structures. We refer to Arnold et al. [
8] and Veeranna et al. [
9] on Bayesian and goodness-of-fit tests for the bivariate pseudo-Poisson model, respectively, which can also be adapted to accommodate the presence of concomitant variables. We refer to Arnold et al. [
10] and Filus et al. [
11] for further reading on conditional specified models and the triangular transformations, respectively. Finally, we refer Ghosh et al. [
12] on the recent results on bivariate count model which has both conditionals with a Poisson structure.
We next review the concept of multivariate pseudo-Poisson distributions, as discussed in Arnold and Manjunath [
7].
Definition 1. A k-dimensional random variable is said to have a k-dimensional pseudo-Poisson distribution if there exists a positive constant such thatand functions where, for each ℓ, such thatwhere. Note that there are no constraints on the forms of the functions that appear in the definition, save for measurability. In applications, it would typically be the case that the ’s would be chosen to be relatively simple functions depending on a limited number of parameters. Definition 2. A random pair of variables is said to have a bivariate pseudo-Poisson distribution if there exists a positive constant such thatand a function such that, for every non-negative integer , The fact that there are no constraints on the allows us to adapt to a variety of dependence structures including positive or negative correlation.
Example 1. A judicious choice of a parametric family for will admit positive and negative correlation between and . For example, if we considerFor , the above function will be increasing if , decreasing if and constant if . Consequently, and will have a positive correlation if , negative correlation if and will be uncorrelated if A more general model with the same properties can be obtained by replacing by , a parameterized family of distribution functions with support . 2. Incorporating Concomitant Variables
In many (perhaps, most) applications, in addition to the observed values of the
’s pairs, there will be available values of arrays of concomitant variables which are expected to influence the stochastic behavior of the observed data points. A straightforward manner in which to incorporate vectors of concomitant variables
into the model is as follows:
and
where
,
,
,
,
and
are
d-dimensional unknown parameters.
There are certainly many other manners in which one can model the influence of concomitant variables. If there is scientific justification for alternative models that do not introduce the concomitants via log-linear adjustments of the form specified in (
2) and (
3), then one should certainly utilize the scientifically appropriate link functions.
Just as in classical multiple regression, it is worthwhile to determine whether a simple linear dependence assumption for the effect of concomitants will be adequate to fit the data. In the remainder of this paper, we will focus on the simple model (
2) and (
3).
4. Statistical Inference
In this section, we obtain maximum likelihood estimators (m.l.e.) of parameters , , , , and . In addition, we construct the likelihood ratio test for the possible parallelism, coincidence and significance of each of the regression coefficients.
4.1. Estimation
Let
,
be a bivariate count sample from the pseudo-Poisson distribution (in
Section 2) and let
be
d-dimensional known covariates. Then, the log-likelihood function is
Partial differentiation with respect to each parameters
,
and
and equating to zero gives
Now, taking partial derivatives of
with respect to
,
and
for
and equating to zero yields
In particular, consider
and let
be the observed covariates. The likelihood equations from (
5) to (
10) simplify to become (with notation
,
and
)
In the same way,
Note that the equations from (
11) to (
16) do not yield explicit expressions for the maximum likelihood estimates. However, one can use numerical methods to solve the system of six equations with six unknown parameters.
4.2. Likelihood Ratio Test
The general form of a generalized likelihood ratio test statistic is of the form
Here,
is a subset of
and we envision testing
. We reject the null hypothesis for small values of
.
Now, for the bivariate pseudo-Poisson model, the natural parameter space under the full model is
. The m.l.e.’s under the complete parameter space are obtained by taking partial differentiation of Equation (
4) with respect to
and equating to zero. We denote the obtained numerical solution m.l.e.’s by
and
,
,
.
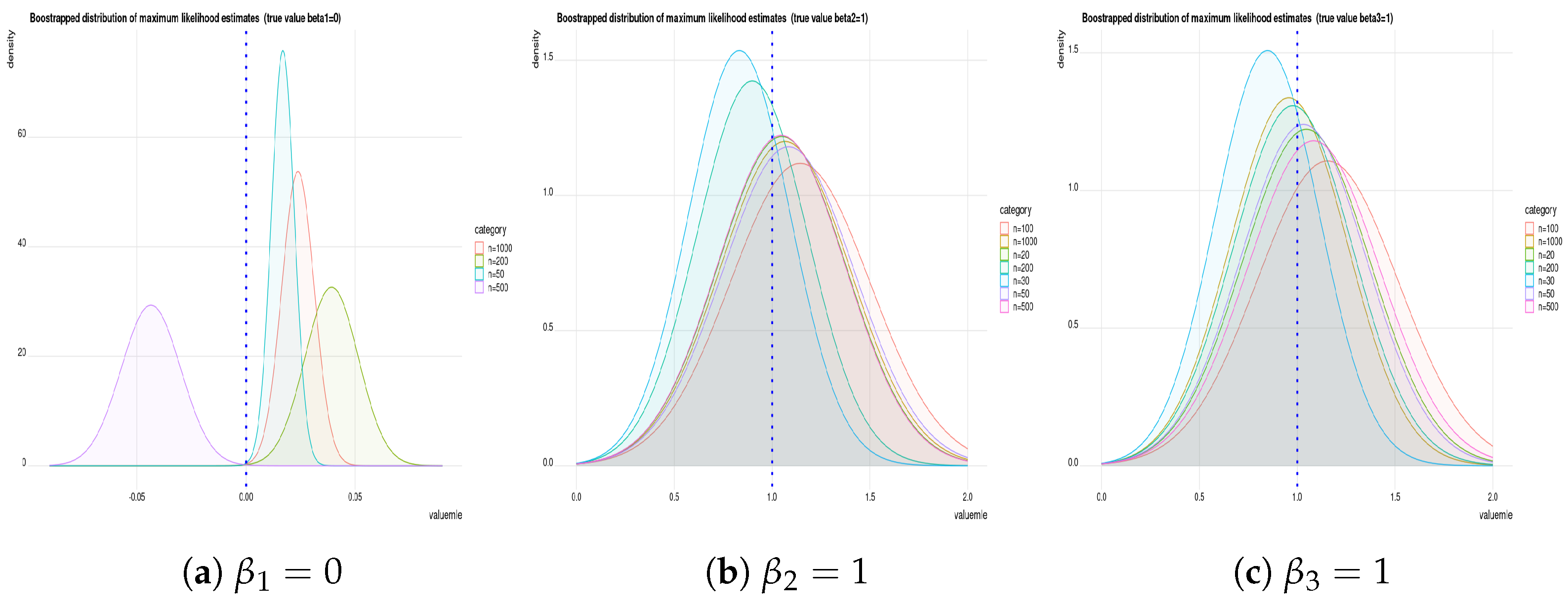
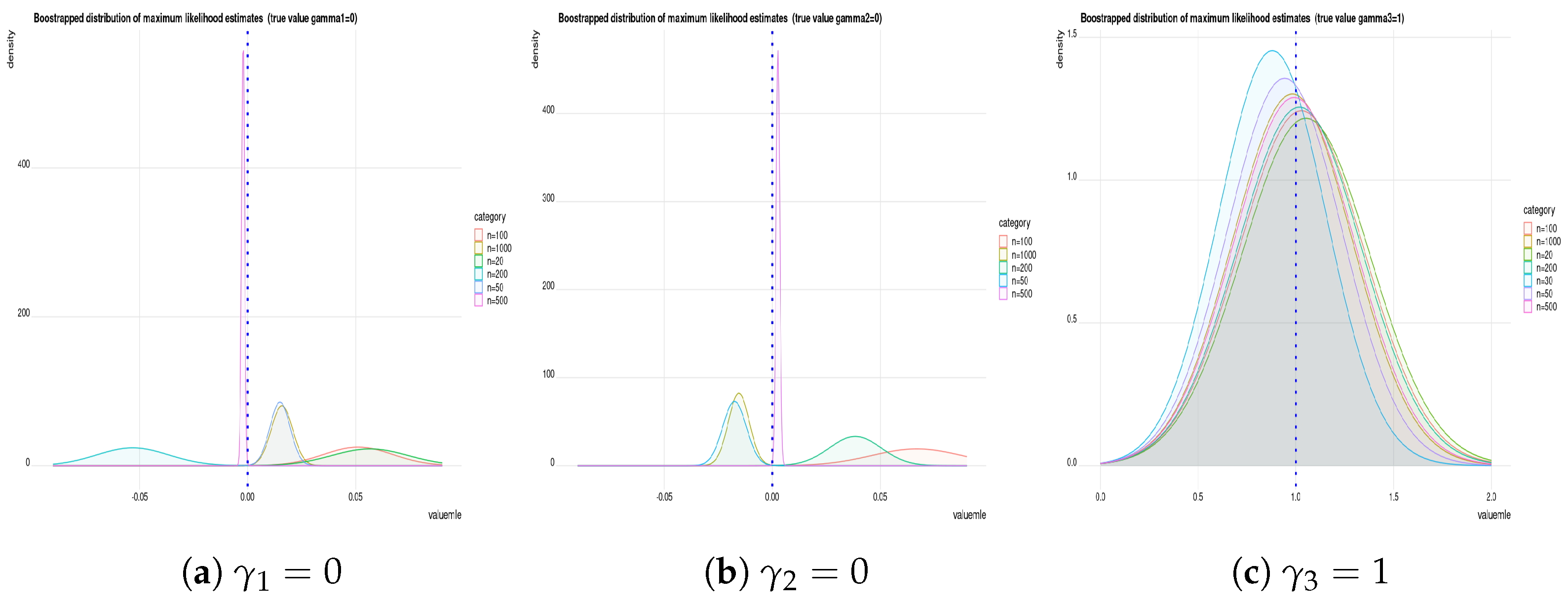
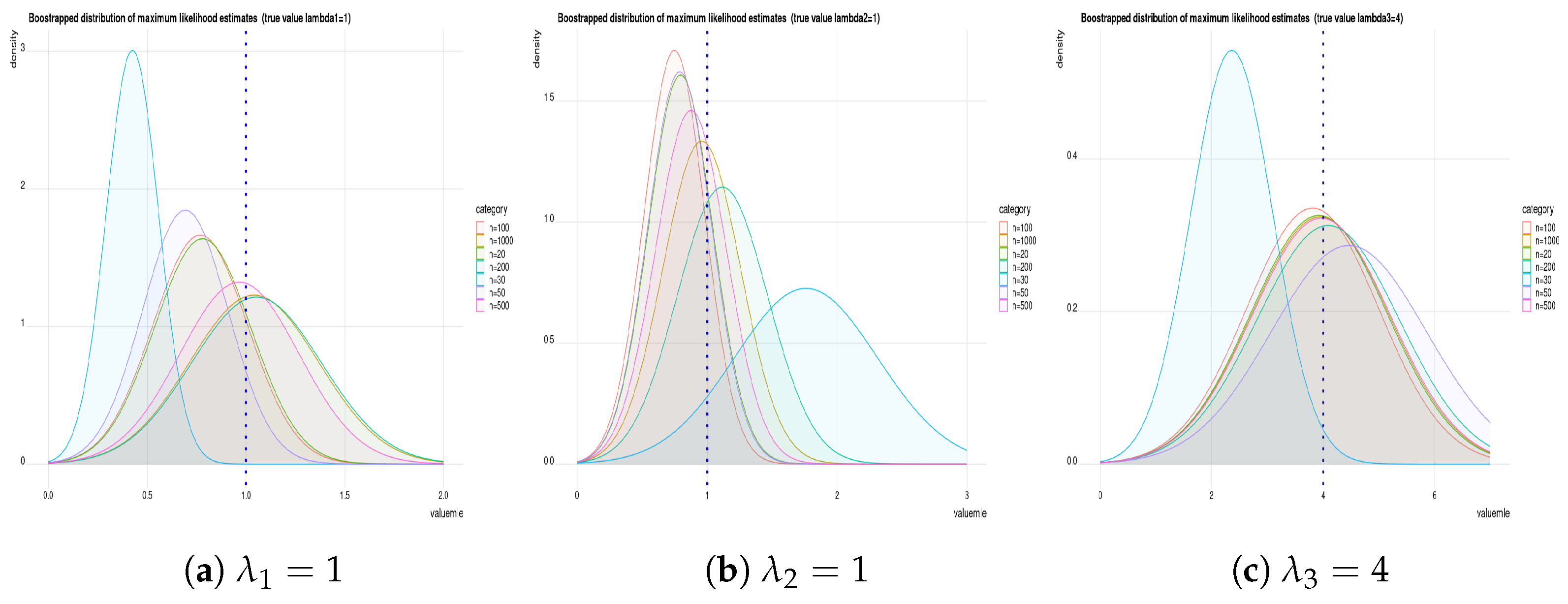
Remark 1. We used the “maxLik” optimization function in R (in the package “maxLik”) to obtain the m.l.e.’s by numerical solution. This function also allows us to use a different methods of optimization using algorithms such as Newton–Raphson, Broyden–Fletcher–Goldfarb–Shanno, Berndt–Hall–Hall–Hausman, Berndt–Hall–Hall–Hausman, Simulated Annealing, Conjugate Gradients and Nelder–Mead methods. In the current paper, we use the Newton–Raphson method to estimate parameters and to compute their standard errors.
4.2.1. Testing
In the following, we will construct a likelihood ratio test for testing whether the observed concomitant does not affect the distribution of
. Under the null hypothesis, the natural parameter space is
. Now, taking partial derivatives of Equation (
4) with respect to each parameters
,
,
and equating to zero yields
Equation (
18) is readily solved, to obtain the m.l.e. for
, namely,
. The remaining two Equations (19) and (20) must be solved numerically to obtain
,
.
Now let
and
,
,
be the m.l.e. estimates on unrestricted space. Then, the likelihood (as defined in Equation (
4)) ratio test statistic is
If n is large, then may be compared with a suitable percentile in order to decide whether should be rejected or not.
4.2.2. Testing
Here, we are testing that the observed concomitant does not affect the marginal distribution of
. Note that under the null hypothesis, the natural parameter space is
. Now, again taking partial derivatives of Equation (
4) with respect to parameters
,
,
&
,
and equating to zero gives m.l.e.’s, denoted by
,
,
,
and
, respectively. The likelihood ratio test statistic is
If n is large, then may be compared with a suitable percentile in order to decide whether should be rejected or not.
4.2.3. Testing
In this case, we are testing whether the observed concomitant does not affect the conditional distribution of
given
. Under the null hypothesis, the natural parameter space is
. Again, taking partial derivatives of Equation (
4) with respect to each parameters
,
,
&
and equating to zero gives to m.l.e.’s denoted by
,
,
,
. The likelihood ratio test statistic is
If n is large, then may be compared with a suitable percentile in order to decide whether should be rejected or not.
4.2.4. Testing
Here, we are interested in testing whether the observed concomitant does not affect the intercept term of the pseudo-Poisson model. Now, under the null hypothesis, the natural parameter space is
. Again, taking partial derivatives of Equation (
4) with respect to each parameters
,
,
&
,
and equating to zero gives to m.l.e.’s denoted by
,
,
,
,
. The likelihood ratio test statistic is
If n is large, then may be compared with a suitable percentile in order to decide whether should be rejected or not.
4.2.5. Testing
In this case, we wish to determine whether the concomitant does not affect the dependence structure of the pseudo-Poisson model. Thus, under the null hypothesis, parameter space is
. Now, taking partial derivatives of Equation (
4) with respect to the parameters
,
,
&
,
and equating to zero gives, m.l.e.’s denoted by
,
,
,
,
. The likelihood ratio test statistic is
If n is large, then may be compared with a suitable percentile in order to decide whether should be rejected or not.
In the next examples, we are interested in testing some hypotheses concerning the relationship between the explanatory and response variables. In particular, we are interested in testing whether the regression planes are parallel or if they are coincident. We illustrate the testing procedure using the simple sub-model given by
and
4.2.6. Testing for Parallelism
In the following, we are interested in testing whether the planes on which the means lie are parallel. If we set
for
then the two marginal means are
For the bivariate pseudo-Poisson regression model specified in (
26) and (
27), now it is interesting to examine the hypothesis that the planes on which the mean lies are parallel. This is equivalent to testing for the hypothesis
, for
. Under the null hypothesis, the pseudo-Poisson regression model will be
and
Note that testing for parallelism for the model specified in (
30) and (
31) is equivalent to testing for the observed concomitant and has no effect on the conditional distribution of
given
. Now, partial differentiation with respect to
and
,
and equating to zero gives us
Solving the above
d equations leads us to the m.l.e. of
denoted by
,
and the m.l.e. of
is
Now, we denote the obtained m.l.e.’s under the complete parameter space by
and
,
. The likelihood ratio test statistic is
where
is the likelihood of the model in (
26) & (
27) and (
30) & (
31). If
n is large, then
may be compared with a suitable
percentile in order to decide whether
should be rejected or not.
4.2.7. Testing for Coincidence
Here, we assume that the regression relationship does not change from time 1 to time 2 which will occur if the planes on which means lies are coincident. Now, for the given model in
and
, the two marginal means are
The assumption of coincidence leads us to test
, for
. Denote by
for
are m.l.e.’s under the null hypothesis and by
and
for
are m.l.e.’s under complete parameter space, for . Now, the likelihood ratio test statistic is
where
and
are likelihood under null and complete parameter space, respectively. If
n is large, then
may be compared with a suitable
percentile to decide whether
should be rejected or not.