Introducing BisQ, A Bicoherence-Based Nonlinear Index to Explore the Heart Rhythm
Abstract
:1. Introduction
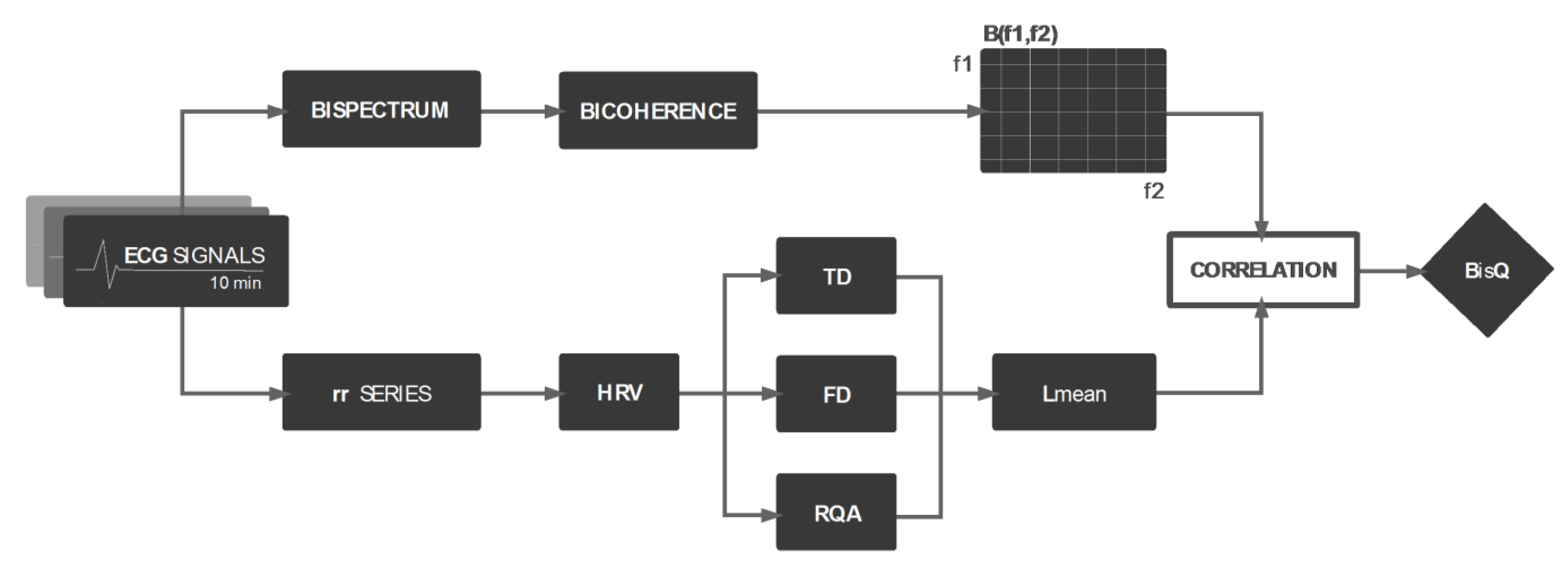
2. Materials and Methods
2.1. Relation Between Bicoherence Matrix Components and RQA-Derived Features
2.1.1. The Data
2.1.2. HRV Analysis
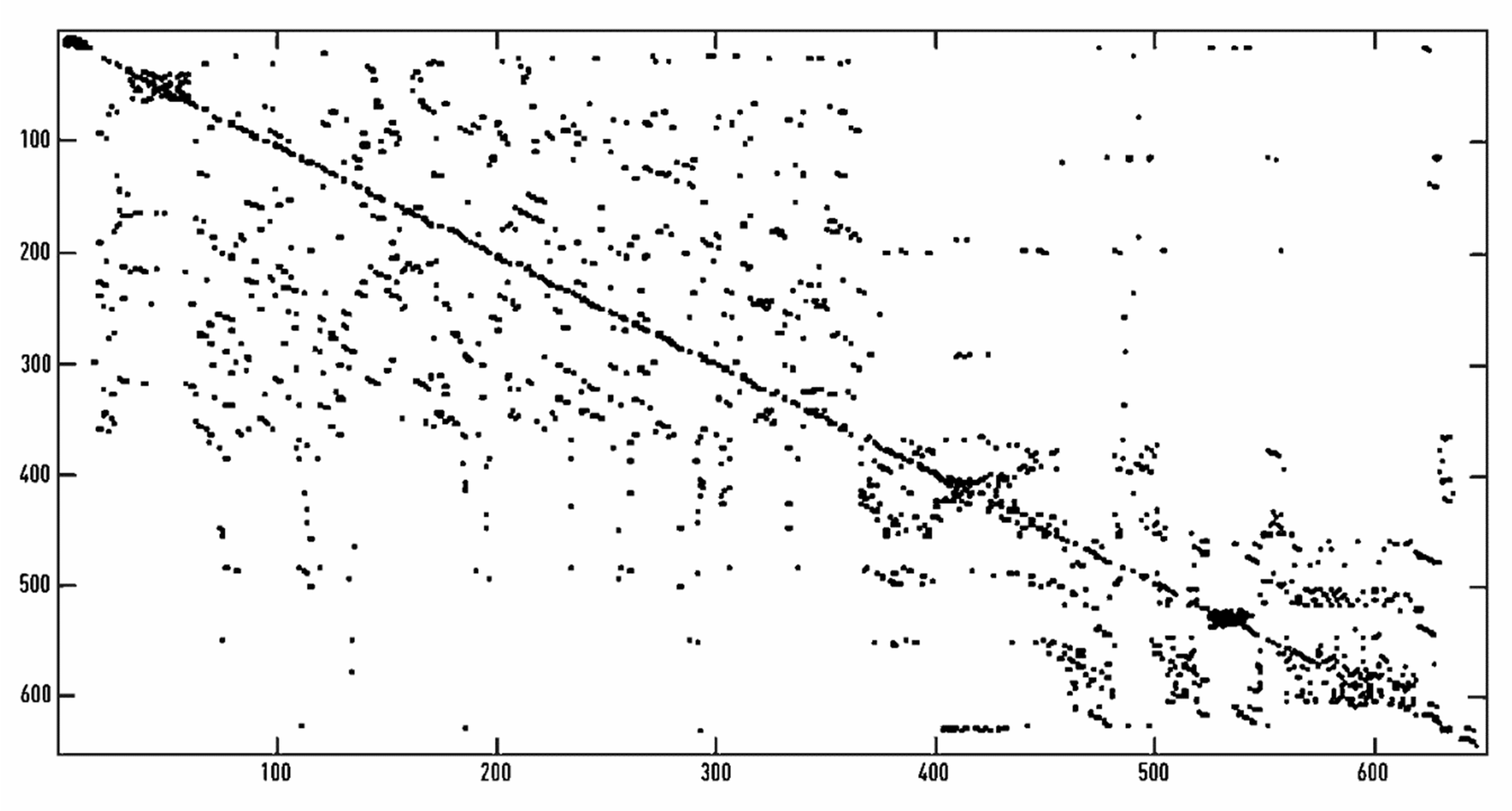
Recurrent Quantification Analysis (RQA)
2.1.3. Bispectral Analysis
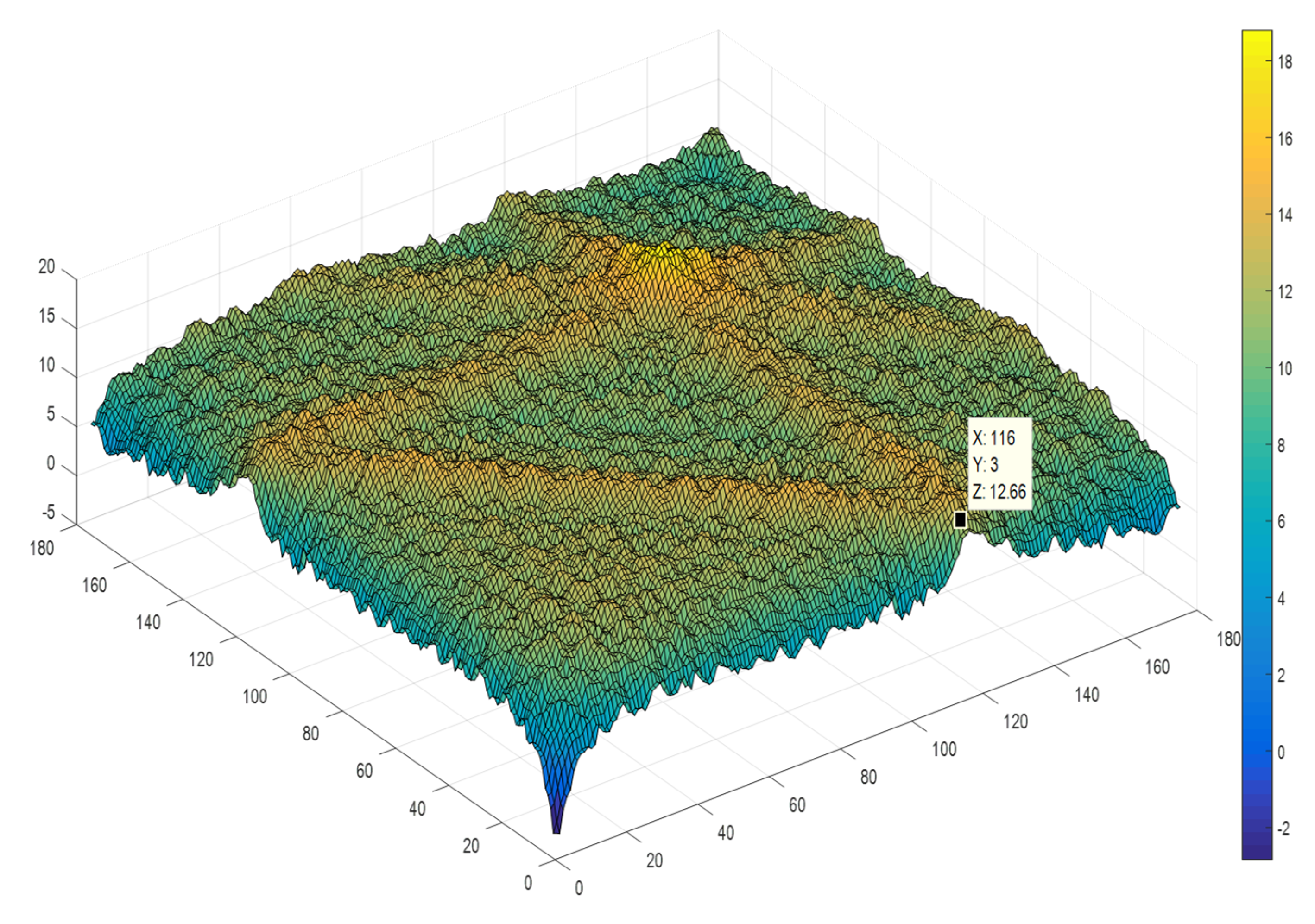
Bicoherence
2.1.4. Correlation Analysis
2.2. Bispectral Quotien (BisQ) Estimation
2.3. Evaluation of BisQ among Different Groups of ECG Recordings
Data
- Healthy (20 persons): Included 20 clinically healthy participants from the Fantasia data base. Recordings were taken in resting condition. Age ranged from 21 to 81 years Details about the database can be found in [29].
- Pre-Term Infants (7): Included seven preterm infants in the first year of life, also available on the Physionet site. This database contains simultaneous ECG and respiratory recordings from 10 preterm infants from the Neonatal Intensive Care Unit (NICU) of the University of Massachusetts Memorial Healthcare. The preterm infants were studied at conceptional ages between 29 and 35 weeks.
3. Results
3.1. HRV Recurrent Quantification Analysis (RQA)
3.2. Bicoherence Analysis
3.3. Correlation Analysis
F12b (1.19 Hz, 1.19 Hz); r = −0.3520,
F12c (1.05 Hz, 0.33 Hz); r = −0.3828.
3.4. Introducing BisQ
3.4.1. Correlation between BisQ and Lmean.
3.4.2. BisQ Correlation with Other HRV Variables
Principal Component Analysis (PCA)
Multivariate Regression
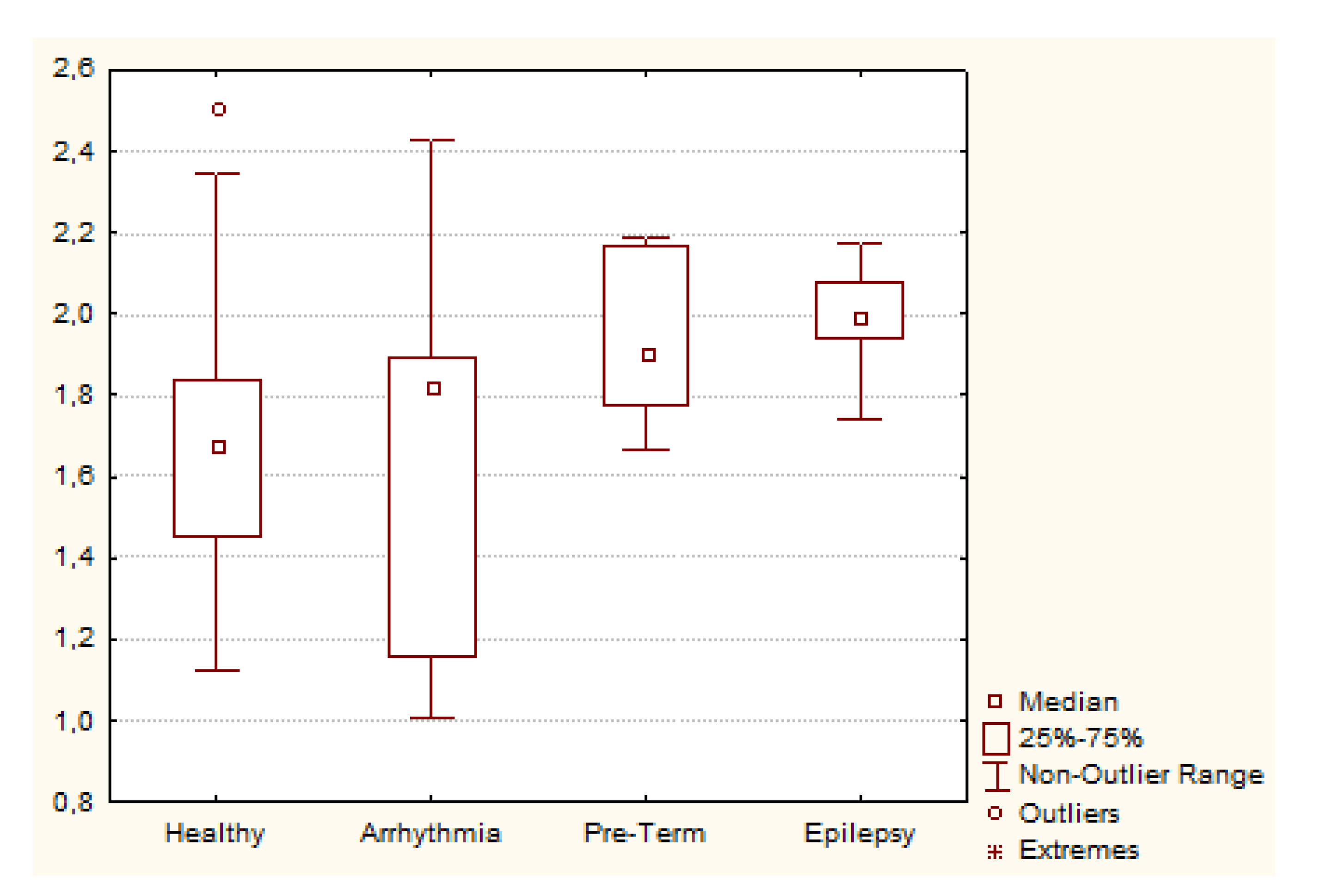
3.5. Comparing Real Data with BisQ
3.5.1. Correlation with Age
3.5.2. Comparing Groups
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Julian, G.; Ermesto, P. Applications of Fractal and Non-linear Time Series Analysis to the Study of Short-term Cardiovascular Control. Curr. Vasc. Pharmacol. 2004, 2, 149–162. [Google Scholar]
- Niskanen, J.-P.; Tarvainen, M.P.; Ranta-Aho, P.O.; Karjalainen, P.A. Software for advanced HRV analysis. Comput. Meth. Programs Biomed. 2004, 76, 73–81. [Google Scholar] [CrossRef] [PubMed]
- Young, H.; Benton, D. We should be using nonlinear indices when relating heart-rate dynamics to cognition and mood. Sci. Rep. 2015, 5, 16619–16622. [Google Scholar] [CrossRef] [Green Version]
- Quiroz-Juárez, M.A.; Jiménez-Ramírez, O.; Vázquez-Medina, R.; Breña-Medina, V.; Aragón, J.L.; Barrio, R.A. Generation of ECG signals from a reaction-diffusion model spatially discretized. Sci. Rep. 2019, 9, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Alliche, A.; Mokrani, K. Higher order statistics and EEG arrhythmia classification. In Proceedings of the 3rd IEEE International Symposium on Signal Processing and Information Technology (ISSPIT), Darmstadt, Germany, 17 December 2003; pp. 641–643. [Google Scholar]
- Webber, C.L.; Zbilut, J.P. Dynamical assessment of physiological systems and states using recurrence plot strategies. J. Appl. Physiol. 1994, 76, 965–973. [Google Scholar] [CrossRef] [PubMed]
- Brennan, M.; Palaniswami, M.; Kamen, P. Do existing measures of Poincaré plot geometry reflect nonlinear features of heart rate variability? IEEE Trans. Biomed. Eng. 2001, 48, 1342–1347. [Google Scholar] [CrossRef]
- Hoshi, R.A.; Pastre, C.M.; Marques Vanderlei, L.C.; Fernandes Godoy, M. Poincaré plot indexes of heart rate variability: Relationships with other nonlinear variables. Auton. Neurosci. 2013, 177, 271–274. [Google Scholar] [CrossRef]
- Calderón-Juárez, M.; González-Gómez, G.H.; Echeverría Pérez-Grovas, H.; Lerma, C. Association between Mean Heart Rate and Recurrence Quantification Analysis of Heart Rate Variability in End-Stage Renal Disease. Entropy 2020, 22, 114. [Google Scholar] [CrossRef] [Green Version]
- Chua, K.C.; Chandran, V.; Acharya, U.R.; Lim, C.M. Cardiac state diagnosis using higher order spectra of heart rate variability. J. Med. Eng. Tech. 2008, 32, 145–155. [Google Scholar] [CrossRef] [PubMed]
- Rastogil, M.; Nagchoudhuri, D.; Parikh, C.D. Quadratic Phase Coupling in ECG Signals. In Proceedings of the Asian Conference on Sensors and the International Conference on New Techniques in Pharmaceuticals and Biomedical Research, Kuala Lumpur, Malaysia, 5–7 September 2005. [Google Scholar]
- Lanata, A.; Valenza, G.; Mancuso, C.; Scilingo, E.P. Robust multiple cardiac arrhythmia detection through bispectrum analysis. Expert Syst. Appl. 2011, 38, 6798–6804. [Google Scholar] [CrossRef]
- Engin, M. ECG-Late Potential Extraction Using Averaged Singular—Values of Third-Order Cumulant (TOC) Based Bispectrum. Analog Integrated Circuits Signal Process. 2002, 33, 301–303. [Google Scholar] [CrossRef]
- Spaargaren, A.; English, M.J. Bispectral analysis of high resolution ECG. Electron. Lett. 1999, 35, 1216–1217. [Google Scholar] [CrossRef]
- Chamoun, N.G. Cardiac Biopotential Analysis System and Method. U.S. Patent No. 4,924,875, 15 May 1990. [Google Scholar]
- Martis, R.J.; Acharya, U.R.; Prasad, H.; Chua, C.K.; Lim, C.M.; Suri, J.S. Application of higher order statistics for atrial arrhythmia classification. Biomed. Signal Process. Control 2013, 8, 888–900. [Google Scholar] [CrossRef]
- Veerabhadrappa, S.T.; Vyas, A.L. Analysis and Classification of Three Trimesters During Normal Pregnancy Using Bispectrum. IETE J. Res. 2020, 1–10. [Google Scholar] [CrossRef]
- Swapna, G.; Soman, K.P.; Vinayakumar, R. Diabetes Detection Using ECG Signals: An Overview. In Deep Learning Techniques for Biomedical and Health Informatics; Springer: Cham, Switzerland, 2020; pp. 299–327. [Google Scholar]
- Toledo, E.; Pinhas, I.; Aravot, D.; Akselrod, S. Heart Transplantation—Spectral and Bispectral Analysis. In Proceedings of the 23rd Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Istanbul, Turkey, 25–26 October 2001. [Google Scholar]
- Penttonen, M.; Buzsáki, G. Natural logarithmic relationship between brain oscillators. Thalamus Relat. Syst. 2003, 2, 145–152. [Google Scholar] [CrossRef]
- Buzsáki, G.; Draguhn, A. Neuronal oscillations in cortical networks. Science 2004, 304, 1926–1929. [Google Scholar] [CrossRef] [Green Version]
- Belluscio, M.A.; Mizuseki, K.; Schmidt, R.; Kempter, R.; Buzsáki, G. Cross-frequency phase–phase coupling between theta and gamma oscillations in the hippocampus. J. Neurosci. 2012, 32, 423–435. [Google Scholar] [CrossRef]
- Varon, C.; Jansen, K.; Lagae, L.; Faes, L.; Van Huffel, S. Transient behavior of cardiorespiratory interactions towards the onset of epileptic seizures. Comput. Cardiol. 2014, 41, 917–920. [Google Scholar]
- Hagiwara, Y.; Faust, O. Nonlinear Analysis of Coronary Artery Disease, Myocardial Infarction, and Normal ECG Signals. J. Mech. Med. Biol. 2017, 17, 1740006. [Google Scholar] [CrossRef]
- Task Force of the European Society of Cardiology the North American Society of Pacing Electrophysiology. Heart Rate Variability: Standards of Measurement, Physiological Interpretation, and Clinical Use. Circulation 1996, 93, 1043–1065. [Google Scholar] [CrossRef] [Green Version]
- Mahdiani, S.; Jeyhani, V.; Peltokangas, M.; Vehkaoja, A. Is 50 Hz high enough ECG sampling frequency for accurate HRV analysis? In Proceedings of the 37th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Milan, Italy, 25–29 August 2015; pp. 5948–5951. [Google Scholar] [CrossRef]
- Zou, Y.; Donner, R.V.; Donges, J.F.; Marwan, N.; Kurths, J. Identifying shrimps in continuous dynamical systems using recurrence based methods. EGUGA 2010, 20, 8226. [Google Scholar]
- Shahbazi, F.; Ewald, A.; Nolte, G. Univariate normalization of bispectrum using Hölder’s inequality. J. Neurosci. Methods 2014, 15, 177–186. [Google Scholar] [CrossRef] [PubMed]
- Iyengar, N.; Peng, C.-K.; Morin, R.; Goldberger, A.L.; Lipsitz, L.A. Age-related alterations in the fractal scaling of cardiac interbeat interval dynamics. Am. J. Physiol. 1996, 271, R1078–R1084. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Trulla, L.L.; Giuliani, A.; Zbilut, J.P.; Webber, C.L. Recurrence quantification analysis of the logistic equation with transients. Phys. Lett. A 1996, 223, 255–260. [Google Scholar] [CrossRef]
- Schwartz, T.H. Neurovascular coupling and epilepsy: Hemodynamic markers for localizing and predicting seizure onset. Epilepsy Curr. 2007, 7, 91–94. [Google Scholar] [CrossRef] [PubMed]
- Billeci, L.; Marino, D.; Insana, L.; Vatti, G.; Varanini, M. Patient-specific seizure prediction based on heart rate variability and recurrence quantification analysis. PLoS ONE 2018, 13, e0204339. [Google Scholar] [CrossRef]
- Goldenholz, D.M.; Kuhn, A.; Austermuehle, A.; Bachler, M.; Mayer, C.; Wassertheurer, S.; Inati, S.K.; Theodore, W.H. Long-term monitoring of cardiorespiratory patterns in drug-resistant epilepsy. Epilepsia 2017, 58, 77–84. [Google Scholar] [CrossRef] [Green Version]
- Platiša, M.M.; Bojić, T.; Pavlović, S.U.; Radovanović, N.N.; Kalauzi, A. Uncoupling of cardiac and respiratory rhythm in atrial fibrillation. Biomed. Eng. Biomed. Tech. 2016, 61, 657–663. [Google Scholar] [CrossRef]
- Radovanovic, N.N.; Pavlovic, S.U.; Milašinovic, G.; Kircanski, B.; Platiša, M.M. Bidirectional Cardio-Respiratory Interactions in Heart Failure. Front. Physiol. 2018, 9, 165–169. [Google Scholar] [CrossRef] [Green Version]
- Ahn, S.; Sol fest, J.; Rubchinsky, L.L. Fine temporal structure of cardiorespiratory synchronization. Am. J. Physiol. Heart Circ. Physiol. 2014, 306, H755–H763. [Google Scholar] [CrossRef] [Green Version]
- Faes, L.; Marinazzo, D.; Montalto, A.; Nollo, G. Lag-specific transfer entropy as a tool to assess cardiovascular and cardiorespiratory information transfer. IEEE Trans. Biomed. Eng. 2014, 61, 2556–2568. [Google Scholar] [CrossRef] [PubMed]
| Feature Type | Description | Acronym |
|---|---|---|
| Time domain | Mean value of RR intervals | |
| Standard deviation of RR intervals | ||
| Root mean square of successive differences | ||
| Relative amount of NN50 | pNN50 | |
| Mean of the standard deviation | ||
| Frequency domain | Power law scaling exponent | BetaFD |
| Absolute power in the very low frequency range 0–0.04 Hz | ||
| Normalized power in the very low frequency range 0–0.04 Hz | VLFnorm | |
| Absolute power in the low frequency range 0.04–0.15 Hz | ||
| Normalized power in the low frequency range 0.04–0.15 Hz | LFnorm | |
| Low frequency peak position | LF_Peak, | |
| Absolute power in the high frequency range 0.15–0.4 Hz | ||
| Normalized power in the high frequency range 0.15–0. 4 Hz | HFnorm | |
| High frequency peak position | HF-Peak | |
| LF/HF power ratio | ||
| Total area under the spectral curve |
| Healthy (20;10f) | Arrhythmia (21;10f) | Pre-Term (7) | Epilepsy (9;4f) | |
|---|---|---|---|---|
| Age Group (y) | ||||
| 0 to 1 | 7 | |||
| 10to 19 | 3(2f) | |||
| 20 to 29 | 5 (4f) | 1 (1f) | 4(1f) | |
| 30 to 39 | 5(2f) | 1 (1f) | 2(1f) | |
| 40 to 49 | 2(1f) | |||
| 50 to 59 | 1 (0f) | |||
| 60 to 69 | 1(0f) | 9 (1f) | ||
| 70 to 79 | 8(4f) | 3 (4f) | ||
| >80 | 1(0f) | 4 (2f) |
| BisQ | |
|---|---|
| SDNN | −0.32 |
| SEM | −0.31 |
| Tot PW | −0.23 |
| VLFP | −0.20 |
| DET | −0.37 |
| Entr | −0.43 |
| Lmean | −0.51 |
| PC# | % Variance | Correlation with BisQ |
|---|---|---|
| 1 | 99.25 | −0.1817 |
| 6 | 0.006 | −0.2621 |
| 12 | 0.002 | 0.2115 |
| 14 | 0.0001 | −0.2732 |
| A | E | PI | |
|---|---|---|---|
| H | 0.3640 | 0.00137 | 0.0224 |
| A | 0.018265 | 0.4079 | |
| E | 0.1662 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hernández-Caceres, J.L.; González-Fernández, R.I.; Ontivero-Ortega, M.; Nolte, G. Introducing BisQ, A Bicoherence-Based Nonlinear Index to Explore the Heart Rhythm. Math. Comput. Appl. 2020, 25, 45. https://doi.org/10.3390/mca25030045
Hernández-Caceres JL, González-Fernández RI, Ontivero-Ortega M, Nolte G. Introducing BisQ, A Bicoherence-Based Nonlinear Index to Explore the Heart Rhythm. Mathematical and Computational Applications. 2020; 25(3):45. https://doi.org/10.3390/mca25030045
Chicago/Turabian StyleHernández-Caceres, José Luis, René Iván González-Fernández, Marlis Ontivero-Ortega, and Guido Nolte. 2020. "Introducing BisQ, A Bicoherence-Based Nonlinear Index to Explore the Heart Rhythm" Mathematical and Computational Applications 25, no. 3: 45. https://doi.org/10.3390/mca25030045
APA StyleHernández-Caceres, J. L., González-Fernández, R. I., Ontivero-Ortega, M., & Nolte, G. (2020). Introducing BisQ, A Bicoherence-Based Nonlinear Index to Explore the Heart Rhythm. Mathematical and Computational Applications, 25(3), 45. https://doi.org/10.3390/mca25030045





