3-Homogeneous Groups and Block-Transitive 7–(v, k, 3) Designs

Abstract

The classification of a block-transitive designs is an important subject on algebraic combinatorics. With the aid of MATLAB software, using the classification theorem of 3-homogeneous permutation groups, we look at the classification problem of block-transitive 7–(v, k, 3) design and prove our main theorem: If the automorphism group of a 7–(v, k, 3) design is block-transitive, then it is neither isomorphic to Affine Type Groups nor Almost Simple Type Groups.

1. Introduction

A $t-$design is a finite incidence structure $D=(X,\mathrm{{\rm B}})$, where $X$ is a set of points and $\mathrm{{\rm B}}$ a set of blocks, such that (1) each block is incident with k points and (2) each t-subset of $X$ is incident with $\lambda$ blocks. If $\left|X\right|=v$, then we call D a $t-(v,k,\lambda )$ design [1].

Usually we denote $\left|\mathrm{{\rm B}}\right|=b$. A t-design D is trivial, if each t-subset of X is a block and all t-subsets of X are contained in B. If any two blocks of D are different, then D is called simple. If a permutation of X preserves a block of D to a block of itself, the permutation is called an automorphism of D, and all the automorphisms of D form a group G, called the automorphism group of D, and we denote it $G\le Aut(D)$. A group of automorphism of D is block-transitive if G acts transitively on the blocks of D. This is equivalent to that group G is transitive on the blocks and a block stable subgroup of G is also transitive on the blocks. Here we are interested in a design that is nontrivial and simple.

How to construct a block design with given parameters is one of the most important topics of combinatorial mathematics. It is especially difficult to construct a t–design with larger parameters. By [2], we have the following result: if D is a nontrivial $t-(v,k,\lambda )$ design with a block-transitive automorphism group, then $t\le 7$. Thus, it is necessary to discuss block-transitive designs with $t\le 7$.

Praeger and Cameron proved a very meaningful theorem in 1993 [2]: when t > 8, there is no non-trivial block-transitive t-design, and when t > 7, there is no non-trivial flag-transitive t-design. At present, the research results of flag-transitive design are relatively perfect. However, the research on block-transitive t-designs is scarce. In 2010, Huber completed the proof that there is no block-transitive Steiner 6-design (unless $G=P\Gamma L(2,p^e),$ $p=2,3$, and e is odd prime) [3]. However, when $\lambda \ge 2$, the current research progress is slow and has yielded few results. In this paper, we are going to study the existence of block-transitive $7-(v,k,3)$ designs. The main results are as follows.

Theorem. 

Let $D$ be a non-trivial $7-(v,k,3)$ design and G be an automorphism group of D. If G acts block-transitively on D, then G is neither isomorphic to Affine Type Groups nor Almost Simple Type Groups.

2. Preliminary Results

Lemmas 1–5 can be found in the results of Beth et al. [4].

Lemma 1. 

Let $D$ be a $t-(v,k,\lambda )$ design, where $t\ge 2$ and $G\le Aut(D)$ [4]. Therefore, the following holds:

1. 

If $G$ acts block-transitively on $D$ , then G acts point $\left[t/2\right]$ -homogeneously on $D$.

2. 

If $G$ acts flag-transitively on $D$ , then $G$ acts point $\left[(t+1)/2\right]$-homogeneously on $D$.

In particular, when $t=7,\lambda =3$ and $G$ acts block-transitively on $D$, then $G$ acts point 3-homogeneously on $D$. We can use the classification of finite 3-homogeneous permutation groups to discuss a block-transitive $7-(v,k,3)$ design.

Lemma 2. 

Let $D$ be a $t-(v,k,\lambda )$ design. Therefore, the following holds:

1. 

$bk=vr$

2. 

$\left(\begin{array}{c}v\\ t\end{array}\right)\lambda =b\left(\begin{array}{c}k\\ t\end{array}\right)$

3. 

For any 1 $\le s<t$ , a $t-(v,k,\lambda )$ design is also a $s-(v,k,{\lambda }_s)$ design, where:

$${\lambda }_s=\lambda \frac{(v-s)(v-s-1)\dots (v-t+1)}{(k-s)(k-s-1)\dots (k-t+1)}$$

4. 

If t = 7, then

$$r(k-1)(k-2)(k-3)(k-4)(k-5)(k-6)=\lambda (v-1)(v-2)(v-3)(v-4)(v-5)(v-6)$$

Lemma 3. 

If $D$ is a non-trivial $t-(v,k,\lambda )$ design, then

$$\lambda \left(\begin{array}{c}v-s\\ t-s\end{array}\right)\equiv 0\left(\mathrm{mod}\left(\begin{array}{c}k-s\\ t-s\end{array}\right)\right),0\le s\le t$$

Lemma 4. 

If $D$ is a non-trivial $t-(v,k,\lambda )$ design, then $v>k+t$.

Lemma 5. 

If $D$ is a $t-(v,k,\lambda )$ design, then

$$\lambda (v-t+1)\ge (k-t+1)(k-t+2),t>2.$$

In this case, when $t=7$, we deduce from Lemma 5 the following upper bound for the positive integer $k$.

Lemma 6. 

Let $D$ be a non-trivial $7-(v,k,3)$ design, then

$$k\le \left[\sqrt{3v-\frac{71}{4}}+\frac{11}{2}\right]$$

Proof. 

By Lemma 5, when $t=7,\lambda =3$, we have $3(v-7+1)\ge (k-7+1)(k-7+2),$ then

$$k\le \left[\sqrt{3v-\frac{71}{4}}+\frac{11}{2}\right]$$

☐

Lemma 7. 

Let $D$ be a non-trivial $t-(v,k,\lambda )$ design and G be an automorphism group of D [2]. If $G$ acts block-transitively on $D$, then $b=\frac{\left|G\right|}{\left|G_B\right|}.$

Lemma 8. 

Let G be a finite 3-homogeneous permutation group on a set X with $\left|X\right|\ge 4$ , then G is either of Affine Type or Almost Simple Type [5].

Lemma 9. 

In finite 3-homogeneous permutation groups, the classification of Affine Type Group is one of the following [5]:

1. 

$G\cong AGL(1,8),A\Gamma L(1,8)orA\Gamma L(1,32)$

2. 

$G\cong SL(d,2),d\ge 2$

3. 

$G\cong A_7,v=2^4$

Lemma 10. 

In finite 3-homogeneous permutation groups on a set X with $\left|X\right|\ge 4$, let G be of Almost Simple Type [4]. Therefore, G contains a simple normal subgroup N, where N is the socle of group G and $N\le G\le Aut(N)$. Thus, N and $v=\left|X\right|$ are given as follows:

1. 

$A_v,v\ge 5$

2. 

$PLS(2,q),v=q+1,q>3$

3. 

$M_v,v=11,12,22,23,24$

4. 

$M_{11},v=12$

Lemma 11. 

Let $\epsilon$ be a 3-dimensional subspace in vector space $V=V(d,2)$, then $GL(d,2)=SL(d,2)$ acts point-transitively on $V\backslash \epsilon$ ([6]).

3. Proof of the Main Theorem

Let $D$ be a non-trivial $7-(v,k,3)$ design, the automorphism group $G$ of D acts block-transitively on $D$, then $G$ is a finite 3-homogeneous permutation group. Using Lemma 8, we know that a permutation group of a $7-(v,k,3)$ design is either Affine Type or Almost Simple Type. For $D$ is non-trivial, then we can suppose $k>7$. Now we are going to discuss the problem in two cases.

3.1. G Is an Affine Type Group

Corollary 1. 

G is not isomorphic to $AGL(1,8),A\Gamma L(1,8)orA\Gamma L(1,32)$.

If $v=8$, then $k<v-t=8-7=1$, which is a contradiction to the condition of $k>7$.

If $v=32$ and $\left|G\right|=\left|A\Gamma L(1,32)\right|=4960$, by Lemma 6, we have $k\le \left[\sqrt{3v-\frac{71}{4}}+\frac{11}{2}\right]\le 14,$ and combining the condition of $k>7,$ the parameter $k$ satisfies condition $8\le k\le 14$. It is clear here that these are not possible if $10\le k\le 14$. Because of Lemma 2 (2), we have 29|b, but $29\perp \left|G\right|$ (where $29\perp \left|G\right|$ means that $\left|G\right|$ cannot be divisible by 29), which leads to a contradiction. Corollary 1 is impossible.

Corollary 2. 

G is not isomorphic to $SL(d,2),d\ge 2$.

Here $\left|V\right|=\left|V(d,2)\right|=2^d$. If $d=2,3,$ then $v=\left|V\right|=4,8,$ and by the proof of the above Corollary 1, none of the designs satisfying the above conditions exist. Now we assume $d>3$. Let $e_1,e_2,\cdots ,e_d$ be a set of bases of vector space $V(d,2)$. Therefore, the dimension of the subspace generated by any 7 points in vector space $V(d,2)$ is at least 3. Let $\epsilon =<e_1,e_2,e_3>$ be a vector subspace generated by the base vectors $e_1,e_2,e_3$ and $\mathrm{S}=\text{{}0,e_1,e_2,e_3,e_1+e_2,e_1+e_3,e_2+e_3\text{}}$ be any 7-subset of $\epsilon$. By the definition of t-design, for a 7-design, each 7-subset is contained in exactly 3 blocks and we record these three blocks as $B_1,B_2,B_3.$ Thus, $\mathrm{S}\subseteq B_1\cap B_2\cap B_3.$ If $B_1$ contains a vector $\alpha$ and $\alpha \in V(d,2)\backslash \epsilon$, then by the transitivity of $SL{(d,2)}_{\epsilon }$ on the vector space $V(d,2)$, we have ${\alpha }^{SL{(d,2)}_{\epsilon }}=V(d,2)\backslash S$ and $\epsilon \cup V(d,2)\backslash S\subseteq B_1^{{}^{SL{(d,2)}_{\epsilon }}}\subseteq B_1\cup B_2\cup B_3.$

Therefore, we have $2^d-8\le 3(k-7)$ or $v=2^d\le 3k-13$, on the other hand, by Lemma 5, we have $3(v-6)$ $\ge (k-6)(k-5)$, so $k<14$. As the same proof method of Corollary 1, we can rule out this case.

Corollary 3. 

G is not isomorphic to $A_7,v=2^4$.

Here $v=2^4=16,$ and for $k\le \left[\sqrt{3v-\frac{71}{4}}+\frac{11}{2}\right]\le 11$ and $k\ge 8,$ the possible value of k is 8, 9, 10, or 11 by calculation. The corresponding r are not positive integers. This is impossible.

Thus, Corollary 3 is not possible.

3.2. G Is an Almost Simple Type

Corollary 4. 

G is not isomorphic to $A_v,v\ge 5.$

Since D is a non-trivial 7-design, then, by Lemma 4, $k<v-7$. Of course, we have $k\le v-2$, so $A_v(v\ge 5)$ acts v-2-transitively on D, and then G is k-transitive on D. It means that D contains all k-subsets and D is a trivial design, a contradiction.

Corollary 5. 

G is not isomorphic to $N=PSL(2,q),v=q+1,q=p^e\ge 3.$

Here, $N\le G\le Aut(N)$ and $Aut(N)=P\Gamma L(2,q).$ For $\left|N\right|=\left|PSL(2,q)\right|=\frac{(q+1)q(q-1)}{n}$, $n=(2,q-1)$.

$$\left|PGL(2,q)\right|=(q+1)q(q-1),\left|P\Gamma L(2,q)\right|=\left|PGL(2,q)\right|\cdot e=e(q+1)q(q-1)$$

Then

$$\left|G\right|=\frac{a(q+1)q(q-1)}{n},q=p^e,a|ne$$

For $v=q+1>k\ge 8,$ then $q\ge 8$. By Lemmas 2 (1) and 7, we have

$$b=\frac{\left|G\right|}{\left|G_B\right|}=\lambda \frac{\left(\begin{array}{c}v\\ t\end{array}\right)}{\left(\begin{array}{c}k\\ t\end{array}\right)}$$

and

$$\frac{a(q+1)(q-1)q}{\left|G_B\right|n}=\frac{3(v-1)(v-2)(v-3)(v-4)(v-5)(v-6)}{k(k-1)(k-2)(k-3)(k-4)(k-5)(k-6)}$$

(1)

For v = q + 1, we have

$$\frac{a(q+1)(q-1)q}{\left|G_B\right|n}=\frac{3(q-1)(q-2)(q-3)(q-4)(q-5)(q+1)q}{k(k-1)(k-2)(k-3)(k-4)(k-5)(k-6)}$$

(2)

After simplification, we obtain the following:

$$3(q-2)(q-3)(q-4)(q-5)\left|G_B\right|n=ak(k-1)(k-2)(k-3)(k-4)(k-5)(k-6)$$

(3)

Using Lemma 5 again, then

$$3(q-5)\ge (k-6)(k-5)$$

(4)

Add Equation (4) into Equation (3), we have

$$(q-2)(q-3)(q-4)\left|G_B\right|n\le ak(k-1)(k-2)(k-3)(k-4)$$

(5)

Additionally, by Equation (4), we can obtain an Inequality (6) under the conditions of $k\ge 27$,

$$k(k-1)(k-2)(k-3)\le 2{[(k-6)(k-5)]}^2$$

(6)

By Equations (5) and (6) and Lemma 6, we have

$$\left|{\mathrm{G}}_B\right|n\text{<}\frac{18a{(q-5)}^2(\sqrt{3q-\frac{59}{4}}+\frac{3}{2})}{(q-2)(q-3)(q-4)}$$

(7)

Now we are going to discuss it in three steps.

1. $p=2,q=2^{\mathrm{e}}.$

Here $n=(2,q-1)=1$. By $a|ne$, we know $a\le e$, so

$$\left|{\mathrm{G}}_B\right|\text{<}\frac{18e{(2^e-5)}^2(\sqrt{3\cdot 2^e-\frac{59}{4}}+\frac{3}{2})}{(2^e-2)(2^e-3)(2^e-4)}$$

(8)

Now, we construct an auxiliary function as follows:

$$y=f(e)=\frac{18e{(2^e-5)}^2(\sqrt{3\cdot 2^e-\frac{59}{4}}+\frac{3}{2})}{(2^e-2)(2^e-3)(2^e-4)}$$

(9)

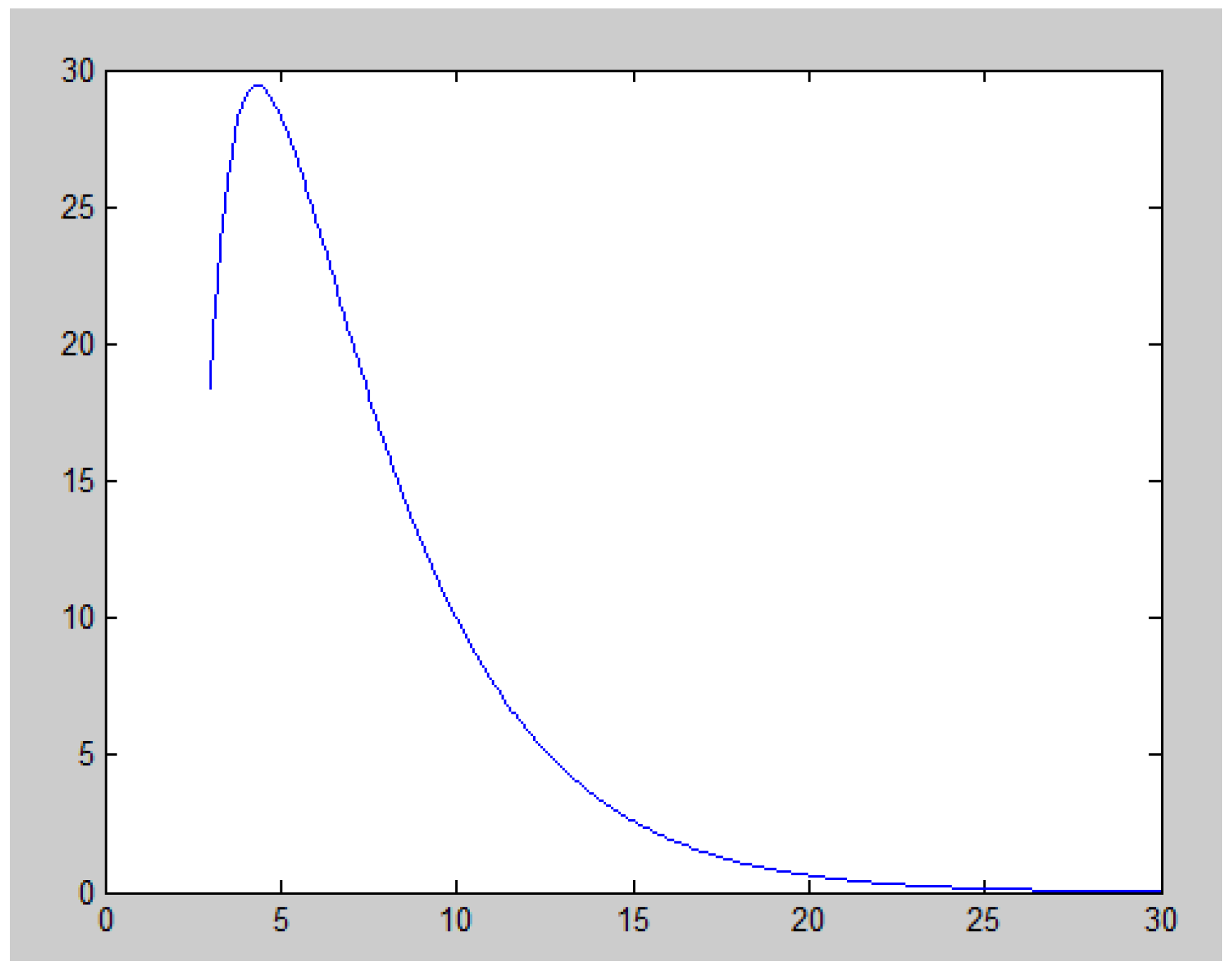
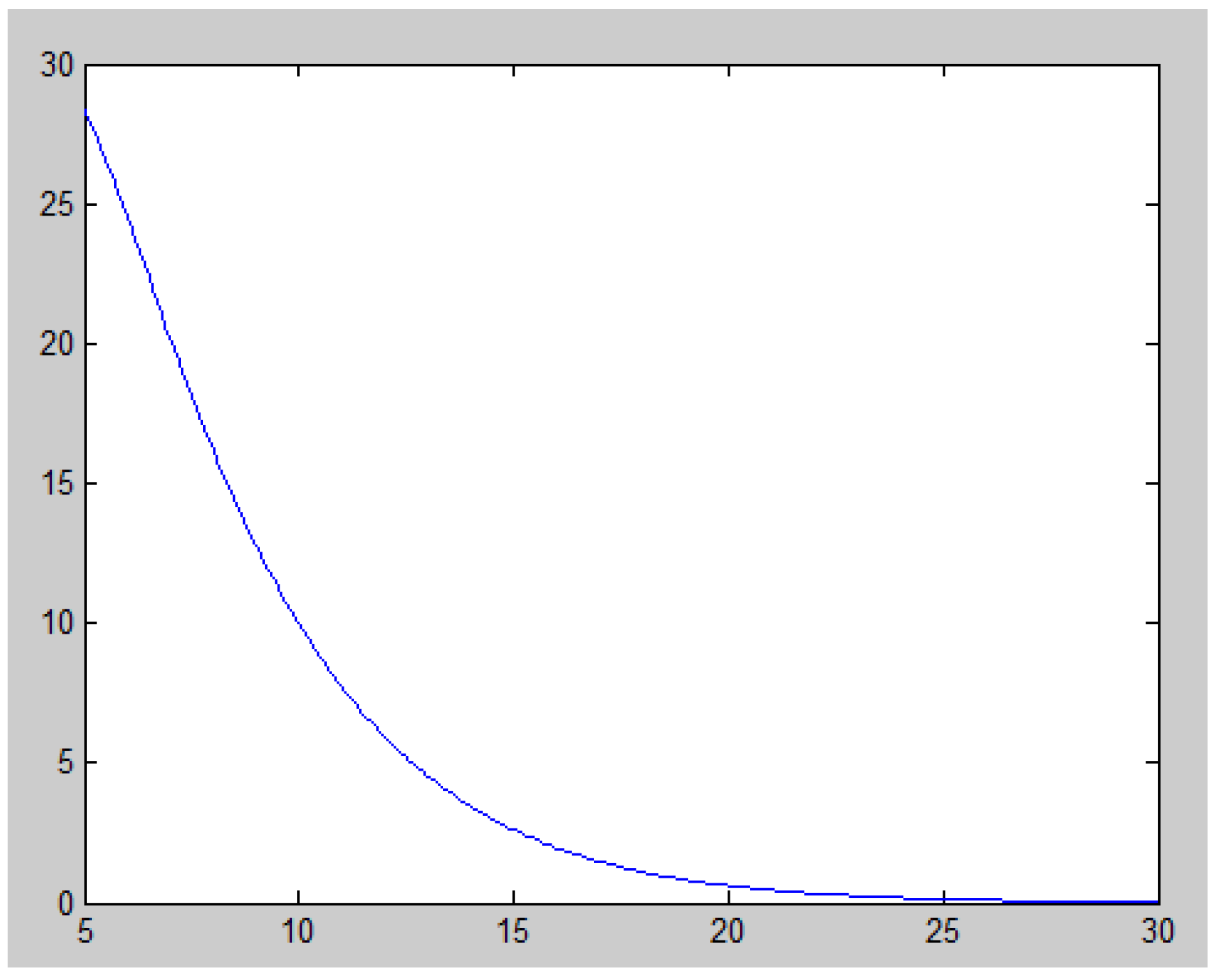
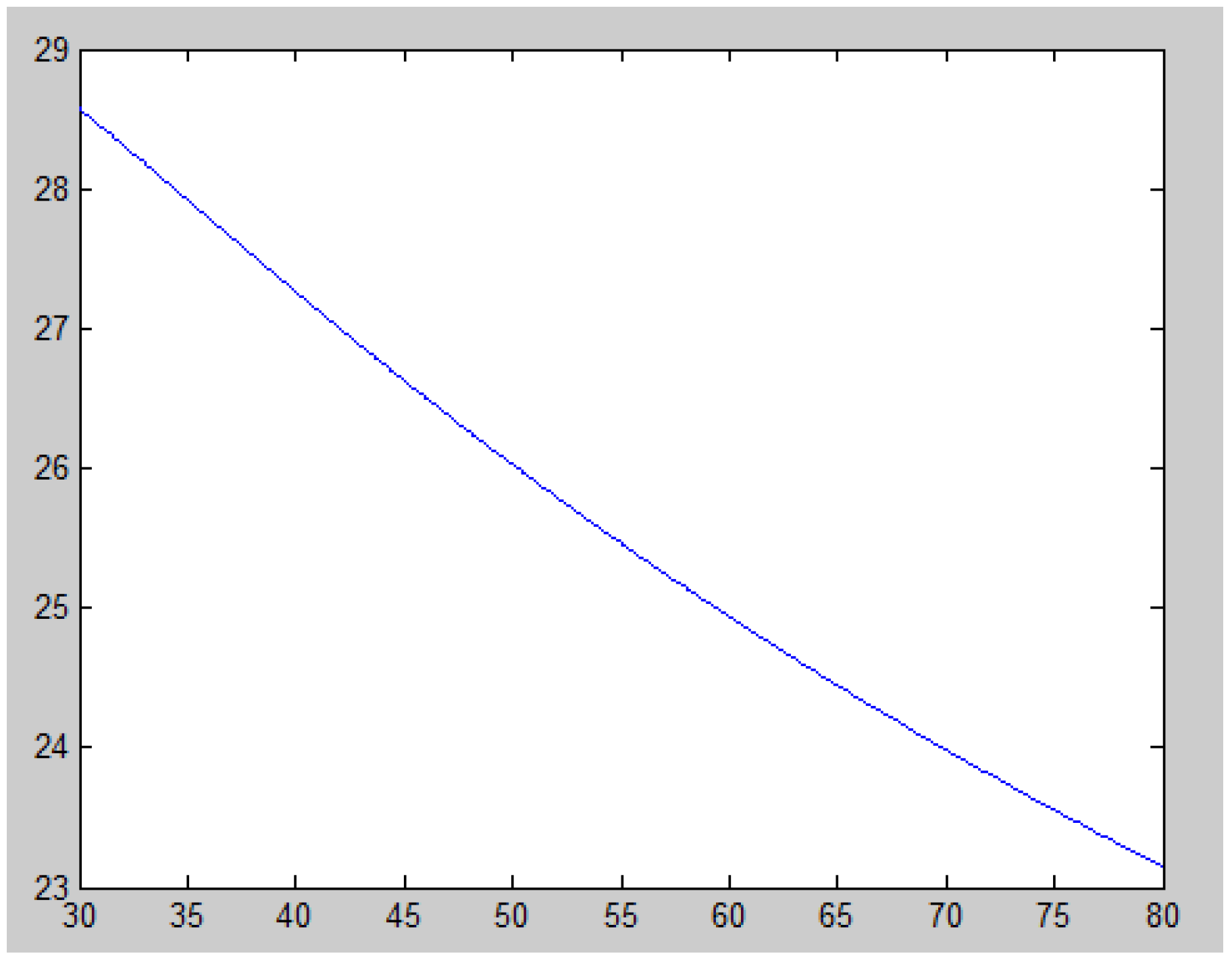
Equation (9) is a decreasing function of e ($e\ge 3$). Using a computer to calculate, we find that $f(18)\approx 1.0979006,f(19)\approx 0.8190221<1$. Using MATLAB software, we map Figure 1 and Figure 2 as follows (see Appendix A and Appendix B):

For $\left|G_B\right|\ge 1$, by properties of a decreasing function, we obtain $e\le 18$. As a result, the corresponding values of q and v are as shown in

Table 1. Values of q and v.

e	q	v
3	8	9
4	16	17
5	32	33
6	64	65
7	128	129
8	256	257
9	512	513
10	1024	1025
11	2048	2049
12	4096	4097
13	8192	8193
14	16,384	16,385
15	32,768	32,769
16	65,536	65,537
17	131,072	131,073
18	262,144	262,145

.

Since $8\le k\le \left[\sqrt{3v-\frac{71}{4}}+\frac{11}{2}\right]$ and $v=q+1\ge 15$. By Equation (3), the possible values of v and k are only one of the following three kinds $(v,k)=(65537,8)$, (131073,8), and (262145,8). They are all in contradiction with the hypothesis $k\ge 26$.

Now, we are going to discuss the case that k is less than 27. We can introduce Inequality (10) with Equation (3) and $\left|G_B\right|\ge 1$:

$$\frac{3(2^e-2)(2^e-3)(2^e-4)(2^e-5)}{e}\le k(k-1)(k-2)(k-3)(k-4)(k-5)(k-6).$$

(10)

Let

$$f(e)=\frac{3(2^e-2)(2^e-3)(2^e-4)(2^e-5)}{e}$$

and

$$h(k)=k(k-1)(k-2)(k-3)(k-4)(k-5)(k-6)$$

Then, $f(e)$ is an increasing function of e, and the maximum value of $h(k)$ is $h{(k)}_{max}=$$h(26)=552,552,000.$ It can be calculated that the maximum value of e is $e_{max}=9$. Due to $k\ge 8$ and $v=2^e+1>k+t\ge 15,$ the minimum value of e is $e_{\min }=4$.

Again, with Equation (3), we have

$$(q-2)(q-3)(q-4)(q-5)|k(k-1)(k-2)(k-3)(k-4)(k-5)(k-6)e,$$

(11)

and

$$(q-2)(q-3)(q-4)(q-5)\le k(k-1)(k-2)(k-3)(k-4)(k-5)(k-6)e$$

(12)

The admissible parameter sets (with Inequality (12) and Lemmas 3–6) are shown in

Table 2. Values of q, v and k.

e	q	v	k
4	16	17	8, 9
5	32	33	8, 9, 10, 11, 12, 13, 14
6	64	65	12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24
7	128	129	16, 17, 18, 19, 20, 21, 22, 23, 24
8	256	257	21, 22, 23, 24, 25, 26
9	512	513	k is at least equal to 29, contradiction.

.

At last, the admissible parameter sets (v, k) in Table 2 do not satisfy Equation (11). Therefore, we show that it does not occur.

2. $p=3,q=3^{\mathrm{e}}.$

The proof is similar to the above. However, here $n=(2,q-1)=2$, and by $a|ne$, we have $a\le 2e$. Correspondingly, we can construct the following auxiliary function:

$$y=f(e)=\frac{36e{(3^e-5)}^2(\sqrt{3\cdot 3^e-\frac{59}{4}}+\frac{3}{2})}{(3^e-2)(3^e-3)(3^e-4)}$$

(13)

Similar to the proof method of the above, we can rule out it.

3. $p\ge 5,q=p^e$ and p is a prime.

Since $n=(2,q-1)=2$ and $a|ne,$ then $a\le 2e.$ If $p\ge 5,q=p^e\ge 5^e,$ then $q=p^e\ge 5^e\ge 5^{\frac{a}{2}}>2^a$, and $a<{\log }_{2}q$. By Inequality (7), we have

$$2\le \left|G_B\right|n<\frac{18e{(q-5)}^2(\sqrt{3q-\frac{59}{4}}+\frac{3}{2}){\log }_{2}q}{(q-2)(q-3)(q-4)}$$

(14)

Let

$$f(q)=\frac{18{(q-5)}^2(\sqrt{3q-\frac{59}{4}}+\frac{3}{2}){\log }_{2}q}{(q-2)(q-3)(q-4)}$$

(15)

since $f(q)$ is a reduced function when q is greater than 28 (Figure 3 and Figure 4) (see Appendix C and Appendix D).

For $f(65000)=1.9617,f(60000)=2.0273,$ binding Inequality (11), the range of possible values of q is $28<q<60000$. Accordingly, the values of k satisfy the condition $13<k<430$. For each pair (q, k), there is no corresponding $7-(q+1,k,3)$ design by Lemma 2.

In a word, if $N=PLS(2,q),v=q+1,q=p^e\ge 3$, and $k\ge 26$, $G$ cannot act block-transitively on any $7-(v,k,3)$ designs.

Now, we discuss the case of $8\le k<26$. By Equation (3),

$$\frac{3(q-2)(q-3)(q-4)(q-5)}{{\log }_{2}q}\le k(k-1)(k-2)(k-3)(k-4)(k-5)(k-6)$$

After calculating, the prime number that is suitable for the above inequality does not exist.

In summary, Corollary 2 is not possible.

Corollary 6. 

G is not isomorphic to $N=M_v,v=11,12,22,23,24$.

By inequality $8\le k\le \left[\sqrt{3v-\frac{71}{4}}+\frac{11}{2}\right]$ and Lemma 2 (4), we know that admissible parameter sets are 7–(11, 8, 3), 7–(12, 8, 3), 7–(22, 8, 3), 7–(23, 8, 3), 7–(24, 8, 3), and 7–(22, 9, 3), 7–(22, 10, 3).

By Lemma 3, if $t=7,\lambda =3$, we have

$$3\left(\begin{array}{c}v-s\\ 7-s\end{array}\right)\equiv 0\left(\mathrm{mod}\left(\begin{array}{c}k-s\\ 7-s\end{array}\right)\right),0\le s\le 7$$

(16)

• For parameter set 7–(11, 8, 3), Equation (16) does not hold if we take , and 7–(11, 8, 3) design does not exist.
• For parameter sets 7–(12, 8, 3), 7–(22, 8, 3), 7–(22, 9, 3), and 7–(22, 10, 3), Equation (16) does not hold if we take $s=3$ , thus neither of these four designs exist.
• For parameter sets 7–(23, 8, 3), Equation (16) does not hold when $s=2$, and this design does not exist.

At last, using Lemma 2, we have

$$bk(k-1)(k-2)(k-3)(k-4)(k-5)(k-6)=3v(v-1)(v-2)(v-3)(v-4)(v-5)(v-6)$$

(17)

For parameter sets 7–(24, 8, 3), the right side of Equation (17) can be divisible by 19, so b can be divisible by 19. By Lemma 7, $\left|G\right|$ can be divisible by 19, but if $\left|G\right|=244823040a$ (where a = 1 or 2), this is impossible. Therefore, the 7–(24, 8, 3) design does not exist.

Corollary 7. 

G is not isomorphic to $N=M_{11},v=12$.

By the proof of Corollary 3, we know that this case will not occur. In this way, we have completed the proof of the main theorem.

4. Conclusions

With the aid of the MATLAB software, using the classification theorem of 3-homogeneous permutation groups, we have proved that a block-transitive automorphism group of a 7–(v, k, 3) design is neither isomorphic to Affine Type Groups nor Almost Simple Type Groups.