A New Algorithm for the Numerical Solution of Telegraph Equations by Using Fibonacci Polynomials

Abstract

In this study, we present a numerical scheme to solve the telegraph equation by using Fibonacci polynomials. This method is based on the Fibonacci collocation method which transforms the equation into a matrix equation, and the unknown of this equation is a Fibonacci coefficients matrix. Some numerical examples with comparisons are included to demonstrate the validity and applicability of the proposed method. The results show the efficiency and accuracy of this paper.

1. Introduction

Linear partial differential equations play an important role in the modelling of engineering problems and in many areas of science. Especially, hyperbolic type partial differential equations (PDEs) is a significant class of the PDEs because of a wide range of applications in many fields.

The hyperbolic type PDEs model atomic physics, aerospace, industry, biology and engineering problems such as vibrations of structures, beams and buildings [1,2].

In this paper, we show a new algorithm for the numerical solutions of the Telegraph equation which is a typical example of the hyperbolic type PDEs. This equation is commonly used in signal analysis for transmission and propagation of electrical signals and also has applications in other fields. Telegraph equation models mix diffusion and wave propagation by introducing a term that accounts for effects of finite velocity to standard heat or mass transport equation [2,3,4,5,6].

In recent years, some authors have shown interest in the numerical solution of telegraph type PDEs, using various methods such as: Radial basis function approximation [1], Chebyshev Tau method [2], He’s variational iteration method [7], Laguerre-Legendre spectral collocation method [8], differential quadrature method [9] and differential transform method [10].

We consider the second-order linear hyperbolic partial differential Telegraph equation.

$$\frac{{\partial }^{2}u\left(x,t\right)}{\partial t^2}+\alpha \frac{\partial u\left(x,t\right)}{\partial t}+\beta u\left(x,t\right)=\frac{{\partial }^{2}u\left(x,t\right)}{\partial x^2}+g\left(x,t\right), 0<x<l, 0<t\le \tau$$

(1)

with the initial conditions.

$$\begin{gathered} u\left(x,0\right)=k_1\left(x\right), 0<x<l \\ {u}_t\left(x,0\right)=k_2\left(x\right), 0<x<l \end{gathered}$$

(2)

and Dirichlet boundary conditions.

$$\begin{gathered} u\left(0,t\right)=h_1\left(t\right), 0<t\le \tau \\ u\left(l,t\right)=h_2\left(t\right), 0<t\le \tau \end{gathered}$$

(3)

where $\alpha , \beta$ are known constant coefficients, $g, k_1, k_2, h_1$ and $h_2$ are known functions and the function $u\left(x,t\right)$ is unknown.

In this study, we introduce Fibonacci collocation method based on matrix relations which has been used to find the approximate solutions of differential, integral and integro-differential equations, differential- difference equations, Fredholm integro differential-difference equations, Pantograph-type functional differential equations and linear Volterra integro differential equations [11,12,13,14,15]. Because Fibonacci polynomials are orthogonal polynomials and the collocation method is easily programmable by symbolic computation programs, this method is preferable [15]. Also, recently, several researchers have used other collocation methods to solve different types of the partial differential equations by using various special polynomials without Fibonacci polynomials [16,17,18,19,20]. On the other hand, these matrix methods were used for the numerical analysis of the longitudinal vibration of rods [21]. In addition to this, Shaban et al. [22] use the homotopy analysis method based on the operational matrix with Chebyshev polynomials.

In this paper, by developing the Fibonacci collocation method studied in [11,12,13,14,15], we will obtain the approximate solution of Equation (1) in the truncated Fibonacci series form.

$$u_N\left(x,t\right)={\displaystyle \sum }_{m=1}^N{\displaystyle \sum }_{n=1}^N{a}_{mn}{F}_m\left(x\right)F_n\left(t\right)$$

(4)

where $a_{mn};m,n=1,\dots ,N$ are the unknown Fibonacci coefficients and $F_m\left(x\right),n=1,\dots ,N$ are the Fibonacci functions defined by,

$$F_n\left(x\right)={\displaystyle \sum }_{j=0}^{\left[\left(n-1\right)/2\right]}\left(\begin{array}{c}n-j-1\\ j\end{array}\right)x^{n-2j-1}, \left[\left(n-1\right)/2\right]=\{\begin{array}{c}\frac{n-2}{2},n even \\ \frac{n-1}{2},n odd\end{array}$$

2. Fundamental Relations

To obtain the numerical solution of hyperbolic partial differential Telegraph equation with Fibonacci Collocation Method, we first evaluate the Fibonacci coefficients of the unknown function. For convenience, the solution function Equation (4) can be written in the matrix form

$$u_N\left(x,t\right)=\mathit{F}\left(x\right)\overline{\mathit{F}}\left(t\right)\mathit{A}$$

(5)

where

$$\mathit{F}\left(x\right)={\left[\begin{array}{ccc}{F}_1\left(x\right)& F_2\left(x\right)& \begin{array}{cc}\cdots & F_N\left(x\right)\end{array}\end{array}\right]}_{1\times N}$$

$$\overline{\mathit{F}}\left(t\right)={\left[\begin{array}{c}\mathit{F}\left(t\right)\\ \mathbf{0}\\ \begin{array}{c}⋮\\ \mathbf{0}\end{array}\end{array} \begin{array}{ccc}\mathbf{0}& \cdots & \mathbf{0}\\ \mathit{F}\left(t\right)& \cdots & \mathbf{0}\\ \begin{array}{c}⋮\\ \mathbf{0}\end{array}& \begin{array}{c}\ddots \\ \cdots \end{array}& \begin{array}{c}⋮\\ \mathit{F}\left(t\right)\end{array}\end{array}\right]}_{N\times N^2}$$

such that $\mathit{F}\left(t\right)={\left[\begin{array}{ccc}{F}_1\left(x\right)& F_2\left(x\right)& \begin{array}{cc}\cdots & F_N\left(x\right)\end{array}\end{array}\right]}_{1\times N}$ and

$$\mathit{A}={\left[\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & \begin{array}{ccc}{a}_{1N}& a_{21}& \begin{array}{ccc}{a}_{22}& \cdots & \begin{array}{cccccc}{a}_{2N}& \cdots & a_{N1}& a_{N2}& \cdots & a_{NN}\end{array}\end{array}\end{array}\end{array}\right]}_{1\times N^2}^T$$

In there, the matrix form $\mathit{F}\left(x\right)$ can be written as

$${\mathit{F}}^T\left(x\right)=\mathit{C}{\mathit{X}}^T\left(x\right)\iff \mathit{F}\left(x\right)=\mathit{X}\left(x\right){\mathit{C}}^T$$

(6)

So that

$$\mathit{F}\left(x\right)=\left[\begin{array}{ccc}{F}_1\left(x\right)& F_2\left(x\right)& \begin{array}{cc}\cdots & F_N\left(x\right)\end{array}\end{array}\right],\mathit{X}\left(x\right)=\left[\begin{array}{ccc}1& x& \begin{array}{cc}\cdots & x^{N-1}\end{array}\end{array}\right]$$

If $\mathit{N}$is even,

$$\mathit{C}=\left[\begin{array}{cccccc}\left(\begin{array}{c}0\\ 0\end{array}\right)& 0& 0& 0& \cdots & 0\\ 0& \left(\begin{array}{c}1\\ 0\end{array}\right)& 0& 0& \cdots & 0\\ \left(\begin{array}{c}1\\ 1\end{array}\right)& 0& \left(\begin{array}{c}2\\ 0\end{array}\right)& 0& \cdots & 0\\ 0& \left(\begin{array}{c}2\\ 1\end{array}\right)& 0& \left(\begin{array}{c}3\\ 0\end{array}\right)& \cdots & 0\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ \left(\begin{array}{c}\left(n-2\right)/2\\ \left(n-2\right)/2\end{array}\right)& 0& \left(\begin{array}{c}n/2\\ \left(n-4\right)/2\end{array}\right)& 0& \cdots & 0\\ 0& \left(\begin{array}{c}n/2\\ \left(n-2\right)/2\end{array}\right)& 0& \left(\begin{array}{c}\left(n+2\right)/2\\ \left(n-4\right)/2\end{array}\right)& \cdots & \left(\begin{array}{c}n-1\\ 0\end{array}\right)\end{array}\right]$$

If $\mathit{N}$is odd,

$$\mathit{C}=\left[\begin{array}{cccccc}\left(\begin{array}{c}0\\ 0\end{array}\right)& 0& 0& 0& \cdots & 0\\ 0& \left(\begin{array}{c}1\\ 0\end{array}\right)& 0& 0& \cdots & 0\\ \left(\begin{array}{c}1\\ 1\end{array}\right)& 0& \left(\begin{array}{c}2\\ 0\end{array}\right)& 0& \cdots & 0\\ 0& \left(\begin{array}{c}2\\ 1\end{array}\right)& 0& \left(\begin{array}{c}3\\ 0\end{array}\right)& \cdots & 0\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ 0& \left(\begin{array}{c}\left(n-1\right)/2\\ \left(n-3\right)/2\end{array}\right)& 0& \left(\begin{array}{c}\left(n+1\right)/2\\ \left(n-5\right)/2\end{array}\right)& \cdots & 0\\ \left(\begin{array}{c}\left(n-1\right)/2\\ \left(n-1\right)/2\end{array}\right)& 0& \left(\begin{array}{c}\left(n+1\right)/2\\ \left(n-3\right)/2\end{array}\right)& 0& \cdots & \left(\begin{array}{c}n-1\\ 0\end{array}\right)\end{array}\right]$$

$\mathit{C}$ is the characteristic matrix of the matrix relations [11].

$$\overline{\mathit{F}}\left(t\right)=\overline{\mathit{X}}\left(t\right){\overline{\mathit{C}}}^T$$

(7)

where

$$\overline{\mathit{X}}\left(t\right)=\left[\begin{array}{c}X\left(t\right)\\ 0\\ \begin{array}{c}⋮\\ 0\end{array}\end{array} \begin{array}{ccc}0& \cdots & 0\\ X\left(t\right)& \cdots & 0\\ \begin{array}{c}⋮\\ \cdots \end{array}& \begin{array}{c}\ddots \\ 0\end{array}& \begin{array}{c}⋮\\ X\left(t\right)\end{array}\end{array}\right],{\overline{\mathit{C}}}^T=\left[\begin{array}{c} {\mathit{C}}^T\\ \mathbf{0}\\ \begin{array}{c}⋮\\ \mathbf{0}\end{array}\end{array} \begin{array}{ccc}\mathbf{0}& \cdots & \mathbf{0}\\ {\mathit{C}}^T& \cdots & \mathbf{0}\\ \begin{array}{c}⋮\\ \mathbf{0}\end{array}& \begin{array}{c}\ddots \\ \cdots \end{array}& \begin{array}{c}⋮\\ {\mathit{C}}^T\end{array}\end{array}\right]$$

3. Method of Solution

We can compute the matrix forms of the terms $u\left(x,t\right), u_x\left(x,t\right), u_t\left(x,t\right), u_{xx}\left(x,t\right),u_{tt}\left(x,t\right)$. of Equation (1) now. From the relations Equations (5)–(7) we obtain the matrix forms.

$$u\left(x,t\right)=\mathit{X}\left(x\right) {\mathit{C}}^T \overline{\mathit{X}}\left(t\right) {\overline{\mathit{C}}}^T\mathit{A}$$

(8)

$$u_x\left(x,t\right)=\mathit{X}\left(x\right)\mathit{B} {\mathit{C}}^T \overline{\mathit{X}}\left(t\right) {\overline{\mathit{C}}}^T\mathit{A}$$

(9)

$$u_t\left(x,t\right)=\mathit{X}\left(x\right) {\mathit{C}}^T \overline{\mathit{X}}\left(t\right) \overline{\mathit{B}} {\overline{\mathit{C}}}^T\mathit{A}$$

(10)

$$u_{xx}\left(x,t\right)=\mathit{X}\left(x\right){\mathit{B}}^2 {\mathit{C}}^T \overline{\mathit{X}}\left(t\right) {\overline{\mathit{C}}}^T\mathit{A}$$

(11)

$$u_{tt}\left(x,t\right)=\mathit{X}\left(x\right) {\mathit{C}}^T \overline{\mathit{X}}\left(t\right){\overline{\mathit{B}}}^2{\overline{\mathit{C}}}^T\mathit{A}$$

(12)

where

$$\mathit{B}=\left[\begin{array}{ccc}\begin{array}{ccc}0& 1& 0\\ 0& 0& 2\end{array}& \cdots & \begin{array}{c}0\\ 0\end{array}\\ ⋮& \ddots & ⋮\\ \begin{array}{ccc}0& 0& 0\\ 0& 0& 0\end{array}& \cdots & \begin{array}{c}N-1\\ 0\end{array}\end{array}\right],\overline{\mathit{B}}=\left[\begin{array}{c}\mathit{B}\\ \mathbf{0}\\ \begin{array}{c}⋮\\ \mathbf{0}\end{array}\end{array} \begin{array}{ccc}\mathbf{0}& \cdots & \mathbf{0}\\ \mathit{B}& \cdots & \mathbf{0}\\ \begin{array}{c}⋮\\ \mathbf{0}\end{array}& \begin{array}{c}\ddots \\ \cdots \end{array}& \begin{array}{c}⋮\\ \mathit{B}\end{array}\end{array}\right]$$

where all $\mathbf{0}$ matrix is $N\times N$.

By substituting the expressions Equations (5)–(12) into Equation (1), we have the matrix equation.

$$\begin{gathered} \{\mathit{X}\left(x\right) {\mathit{C}}^T \overline{\mathit{X}}\left(t\right) \overline{\mathit{B}} {\overline{\mathit{C}}}^T+\alpha \mathit{X}\left(x\right) {\mathit{C}}^T \overline{\mathit{X}}\left(t\right) \overline{\mathit{B}} {\overline{\mathit{C}}}^T+ \beta \mathit{X}\left(x\right) {\mathit{C}}^T \overline{\mathit{X}}\left(t\right) {\overline{\mathit{C}}}^T \\ -\mathit{X}\left(x\right) \mathit{B}{ }^2 {\mathit{C}}^T \overline{\mathit{X}}\left(t\right) {\overline{\mathit{C}}}^T\}= g\left(x,t\right) \end{gathered}$$

(13)

Shortly, Equation (13) can be written as

$$\mathit{W}\left(x,t\right)\mathit{A}=g\left(x,t\right)$$

(14)

where $\mathit{W}\left(x,t\right)=\left[w_{ij}\right], i,j=1,2,\dots , N^2 .$

By using in Equation (14) the collocation points $\left(x_i, t_j\right)$ defined by

$$\begin{gathered} x_i=\frac{l}{N-1}\left(i-1\right), i=1, 2, \dots , N \\ {t}_j=\frac{\tau }{N-1}\left(j-1\right), j=1, 2, \dots , N \end{gathered}$$

(15)

So, the system of the matrix equations can be written as

$$\underset{\mathit{W}}{\underbrace{\left[\begin{array}{c}\mathit{W}\left(x_1,t_1\right)\\ \mathit{W}\left(x_1,t_2\right)\\ ⋮\\ \mathit{W}\left(x_1,t_N\right)\\ \mathit{W}\left(x_2,t_1\right)\\ \mathit{W}\left(x_2,t_2\right)\\ ⋮\\ \mathit{W}\left(x_2,t_N\right)\\ ⋮\\ \mathit{W}\left(x_N,t_1\right)\\ \mathit{W}\left(x_N,t_2\right)\\ \begin{array}{c}⋮\\ \mathit{W}\left(x_N,t_N\right)\end{array}\end{array}\right]}} [\mathit{A}]=\underset{\mathit{G}}{\underbrace{\left[\begin{array}{c}g\left(x_1,t_1\right)\\ g\left(x_1,t_2\right)\\ ⋮\\ g\left(x_1,t_N\right)\\ g\left(x_2,t_1\right)\\ g\left(x_2,t_2\right)\\ ⋮\\ g\left(x_2,t_N\right)\\ ⋮\\ g\left(x_N,t_1\right)\\ g\left(x_N,t_2\right)\\ \begin{array}{c}⋮\\ g\left(x_N,t_N\right)\end{array}\end{array}\right]}}$$

Or, in summary, the fundamental matrix equation is

$$WA=G$$

(16)

By means of the relation Equations (8) and (10) for the conditions Equation (2), we can obtain the matrix forms.

$$u\left(x,0\right)=k_1\left(x\right)\Rightarrow \mathit{X}\left(x\right) {\mathit{C}}^T \overline{\mathit{X}}\left(0\right) {\overline{\mathit{C}}}^T\mathit{A}=k_1\left(x\right)$$

(17)

$$u_t\left(x,0\right)=k_2\left(x\right)\Rightarrow \mathit{X}\left(x\right) {\mathit{C}}^T \overline{\mathit{X}}\left(0\right) \overline{\mathit{B}} {\overline{\mathit{C}}}^T\mathit{A}=k_2\left(x\right)$$

(18)

By substituting the collocation points Equation (15) into Equations (17) and (18), we have the fundamental matrix equations of the initial conditions.

$$\underset{{\mathit{U}}_{\mathbf{1}}}{\underbrace{\left[\begin{array}{c}\mathit{X}\left(x_1\right) {\mathit{C}}^T \overline{\mathit{X}}\left(0\right) {\overline{\mathit{C}}}^T\\ \mathit{X}\left(x_2\right) {\mathit{C}}^T \overline{\mathit{X}}\left(0\right) {\overline{\mathit{C}}}^T\\ ⋮\\ \mathit{X}\left(x_N\right) {\mathit{C}}^T \overline{\mathit{X}}\left(0\right) {\overline{\mathit{C}}}^T\end{array}\right]}} \underset{\mathit{A}}{\underbrace{\left[\begin{array}{c}{a}_{11}\\ a_{12}\\ ⋮\\ a_{NN}\end{array}\right] }}= \underset{{\mathit{K}}_{\mathbf{1}}}{\underbrace{\left[\begin{array}{c}{k}_1\left(x_1\right)\\ k_1\left(x_2\right)\\ ⋮\\ k_1\left(x_N\right)\end{array}\right]}}, U_{\mathbf{1}}A=K_{\mathbf{1}}$$

$$\underset{{\mathit{U}}_{\mathbf{2}}}{\underbrace{\left[\begin{array}{c}\mathit{X}\left(x_1\right) {\mathit{C}}^T \overline{\mathit{X}}\left(0\right) \overline{\mathit{B}} {\overline{\mathit{C}}}^T\\ \mathit{X}\left(x_2\right) {\mathit{C}}^T \overline{\mathit{X}}\left(0\right) \overline{\mathit{B}} {\overline{\mathit{C}}}^T\\ ⋮\\ \mathit{X}\left(x_N\right) {\mathit{C}}^T \overline{\mathit{X}}\left(0\right) \overline{\mathit{B}} {\overline{\mathit{C}}}^T\end{array}\right]}} \underset{\mathit{A}}{\underbrace{\left[\begin{array}{c}{a}_{11}\\ a_{12}\\ ⋮\\ a_{NN}\end{array}\right] }}= \underset{{\mathit{K}}_{\mathbf{2}}}{\underbrace{\left[\begin{array}{c}{k}_2\left(x_1\right)\\ k_2\left(x_2\right)\\ ⋮\\ k_2\left(x_N\right)\end{array}\right]}}, U_{\mathbf{2}}A=K_{\mathbf{2}}$$

Similarly, by using Equation (8) for the conditions Equation (3), we can have the matrix forms as follow

$$u\left(0,t\right)=h_1\left(t\right)\Rightarrow \mathit{X}\left(0\right) {\mathit{C}}^T \overline{\mathit{X}}\left(t\right) {\overline{\mathit{C}}}^T\mathit{A}=h_1\left(t\right)$$

(19)

$$u\left(l,t\right)=h_2\left(t\right)\Rightarrow \mathit{X}\left(l\right) {\mathit{C}}^T \overline{\mathit{X}}\left(t\right) {\overline{\mathit{C}}}^T\mathit{A}=h_2\left(t\right)$$

(20)

On the other hand, by substituting the collocation points Equation (16) into Equations (19) and (20), we obtain the fundamental matrix equations of the Dirichlet boundary conditions

$$\underset{{\mathit{V}}_{\mathbf{1}}}{\underbrace{\left[\begin{array}{c}\mathit{X}\left(0\right) {\mathit{C}}^T \overline{\mathit{X}}\left(t_1\right) {\overline{\mathit{C}}}^T\\ \mathit{X}\left(0\right) {\mathit{C}}^T \overline{\mathit{X}}\left(t_2\right) {\overline{\mathit{C}}}^T\\ ⋮\\ \mathit{X}\left(0\right) {\mathit{C}}^T \overline{\mathit{X}}\left(t_N\right) {\overline{\mathit{C}}}^T\end{array}\right]}} \underset{\mathit{A}}{\underbrace{\left[\begin{array}{c}{a}_{11}\\ a_{12}\\ ⋮\\ a_{NN}\end{array}\right] }}= \underset{{\mathit{H}}_{\mathbf{1}}}{\underbrace{\left[\begin{array}{c}{h}_1\left(t_1\right)\\ h_1\left(t_2\right)\\ ⋮\\ h_1\left(t_N\right)\end{array}\right], }} V_{\mathbf{1}}A=H_{\mathbf{1}}$$

$$\underset{{\mathit{V}}_{\mathbf{2}}}{\underbrace{\left[\begin{array}{c}\mathit{X}\left(l\right) {\mathit{C}}^T \overline{\mathit{X}}\left(t_1\right) {\overline{\mathit{C}}}^T\\ \mathit{X}\left(l\right) {\mathit{C}}^T \overline{\mathit{X}}\left(t_2\right) {\overline{\mathit{C}}}^T\\ ⋮\\ \mathit{X}\left(l\right) {\mathit{C}}^T \overline{\mathit{X}}\left(t_N\right) {\overline{\mathit{C}}}^T\end{array}\right]}} \underset{\mathit{A}}{\underbrace{\left[\begin{array}{c}{a}_{11}\\ a_{12}\\ ⋮\\ a_{NN}\end{array}\right] }}= \underset{{\mathit{H}}_{\mathbf{2}}}{\underbrace{\left[\begin{array}{c}{h}_2\left(t_1\right)\\ h_2\left(t_2\right)\\ ⋮\\ h_2\left(t_N\right)\end{array}\right]}}, V_{\mathbf{2}}A=H_{\mathbf{2}}$$

To obtain the approximate solution of Equation (1) under conditions Equations (2) and (3), the augmented matrix is formed as follows

$$\left[\begin{array}{ccc}\check{\mathit{W}}& ;& \check{\mathit{G}}\end{array}\right]=\left[\begin{array}{ccc}\begin{array}{c}{\mathit{U}}_{\mathbf{1}}\\ {\mathit{U}}_{\mathit{2}}\\ \begin{array}{c}{\mathit{V}}_{\mathit{1}}\\ {\mathit{V}}_{\mathit{2}}\\ \mathit{W}\end{array}\end{array}& \begin{array}{c};\\ ;\\ \begin{array}{c};\\ ;\\ ;\end{array}\end{array}& \begin{array}{c}{K}_{\mathbf{1}}\\ K_{\mathbf{2}}\\ \begin{array}{c}{H}_{\mathbf{1}}\\ H_{\mathbf{2}}\\ \mathit{G}\end{array}\end{array}\end{array}\right]$$

So, the unknown Fibonacci coefficients are obtained as

$$\mathit{A}={\left(\check{\stackrel{ˇ}{\mathit{W}}}\right)}^{-1}\check{\stackrel{ˇ}{\mathit{G}}}$$

where $\left[\begin{array}{ccc}\check{\stackrel{ˇ}{\mathit{W}}}& ;& \check{\stackrel{ˇ}{\mathit{G}}}\end{array}\right]$ is generated by using the Gauss elimination method and then removing zero rows of the augmented matrix $[\begin{array}{ccc}\check{\mathit{W}}& ;& \check{\mathit{G}}\end{array}]$.

4. Error Estimation Algorithm

In this section, we introduce an error estimation algorithm for obtaining the Fibonacci polynomial solution giving last sections and use this technique to obtain the corrected solution of the problem. This algorithm is based on residual function [23,24,25], so we define residual function as follows:

$$R_N\left(x,t\right)=L\left[u_N\left(x,t\right)\right]-g\left(x,t\right)$$

(21)

where

$$L\left[u_N\left(x,t\right)\right]=\frac{{\partial }^2{u}_N\left(x,t\right)}{\partial t^2}+\alpha \frac{\partial u_N\left(x,t\right)}{\partial t}+\beta u_N\left(x,t\right)-\frac{{\partial }^2{u}_N\left(x,t\right)}{\partial x^2}$$

(22)

From Equations (21) and (22),

$$\frac{{\partial }^2{u}_N\left(x,t\right)}{\partial t^2}+\alpha \frac{\partial u_N\left(x,t\right)}{\partial t}+\beta u_N\left(x,t\right)-\frac{{\partial }^2{u}_N\left(x,t\right)}{\partial x^2} =g\left(x,t\right)+R_N\left(x,t\right)$$

(23)

with the initial conditions

$$\begin{gathered} u_N\left(x,0\right)=k_1\left(x\right), 0<x<l \\ {(u_N)}_t\left(x,0\right)=k_2\left(x\right), 0<x<l \end{gathered}$$

(24)

and Dirichlet boundary conditions

$$\begin{gathered} u_N\left(0,t\right)=h_1\left(t\right), 0<t\le \tau \\ {u}_N\left(l,t\right)=h_2\left(t\right), 0<t\le \tau \end{gathered}$$

(25)

Also, the error function $e_N\left(x,t\right)$ is defined as follows:

$$e_N\left(x,t\right)=u\left(x,t\right)-u_N\left(x,t\right)$$

(26)

Because of the fact that $L$ is linear operator, error problem can be defined by using error function as

$$\frac{{\partial }^2{e}_N\left(x,t\right)}{\partial t^2}+\alpha \frac{\partial e_N\left(x,t\right)}{\partial t}+\beta e_N\left(x,t\right)-\frac{{\partial }^2{e}_N\left(x,t\right)}{\partial x^2} =-R_N\left(x,t\right)$$

(27)

with homogenous conditions

$$\begin{array}{c}{e}_N\left(x,0\right)=0, 0<x<l\\ {(e_N)}_t\left(x,0\right)=0, 0<x<l\\ e_N\left(0,t\right)=0, 0<t\le \tau \\ e_N\left(l,t\right)=0, 0<t\le \tau \end{array}$$

(28)

The problem (27) under conditions (28) was solved by Fibonacci collocation method given by Section 3. When we solve the Equation (28) for $M>N$ which is a truncated number, we get the approximation $e_{N,M}\left(x,t\right)$ to $e_N\left(x,t\right)$ even if the exact solution of the problem is unknown.

Consequently, by means of the error estimation function $e_{N,M}\left(x,t\right)$, we obtain the corrected Fibonacci polynomial solution.

$$u_{N,M}\left(x,t\right)=u_N\left(x,t\right)+e_{N,M}\left(x,t\right).$$

(29)

5. Numerical Examples

In this section, we will give several examples to illustrate the applicability of the Fibonacci matrix method and all of them are performed on the computer. Maximum absolute error $L_{\infty }$ is defined as

$$L_{\infty }={\parallel u-u_N\parallel }_{\infty }=\begin{array}{c}max\\ j\end{array}\left|u_j-{\left(u_N\right)}_j\right|$$

(30)

Example 1. 

First, let us consider the hyperbolic Telegraph Equation [2]

$$\frac{{\partial }^{2}u\left(x,t\right)}{\partial t^2}+\frac{\partial u\left(x,t\right)}{\partial t}+u\left(x,t\right)-\frac{{\partial }^{2}u\left(x,t\right)}{\partial x^2}=x^2+t-1, 0<x<1, 0<t\le 1$$

with the initial conditions

$$\begin{gathered} u\left(x,0\right)=x^2, 0<x<1 \\ {u}_t\left(x,0\right)=1, 0<x<1 \end{gathered}$$

and Dirichlet boundary conditions

$$\begin{gathered} u\left(0,t\right)=t, 0<t\le 1 \\ u\left(1,t\right)=1+t, 0<t\le 1. \end{gathered}$$

Here $l=1,\tau =1,\alpha =1,\beta =1$,$k_1\left(x\right)=x^2,k_2\left(x\right)=1,g\left(x,t\right)=x^2+t-1.$

By using the solution algorithm in given Section 3, we find the Fibonacci polynomial solution of the problem is $u_5\left(x,t\right)=x^2+t$, which is the exact solution of the problem. Further, we can obtain the exact solution of the problem for the any value of $N.$

Example 2. 

Consider the following Telegraph Equation [5]

$$\frac{{\partial }^{2}u\left(x,t\right)}{\partial t^2}+ \alpha \frac{\partial u\left(x,t\right)}{\partial t}+\beta u\left(x,t\right)-\frac{{\partial }^{2}u\left(x,t\right)}{\partial x^2}=g\left(x,t\right), 0<x<\pi , 0<t\le 2$$

with the initial conditions

$$u_t\left(x,0\right)=-\sin \left(x\right), 0<x<\pi$$

and Dirichlet boundary conditions

$$\begin{gathered} u\left(0,t\right)=0,0<t\le 2 \\ u\left(\pi ,t\right)=0,0<t\le 2. \end{gathered}$$

The exact solution is given by $u\left(x,t\right)=e^{\left(-t\right)}\sin \left(x\right).$

Note that $l=\pi ,\tau =2$, $k_1\left(x\right)=\sin \left(x\right),k_2\left(x\right)=-\sin \left(x\right).$

$$g\left(x,t\right)=\left(2-\alpha + \beta \right)e^{\left(-t\right)}\sin \left(x\right), h_1\left(t\right)= h_2\left(t\right)=0$$

In Table 1 shows a comparison of the absolute errors values of Fibonacci polynomial solution and corrected Fibonacci polynomial solution with Taylor Matrix Method and Legendre Multiwavelet Method. Also, Figure 1 clearly shows when the $N$ values increase, and when the absolute error function values rapidly decrease.

Table 1. Comparison of the absolute errors values of Fibonacci polynomial solution and corrected Fibonacci polynomial solution with Taylor Matrix Method and Legendre Multiwavelet Method for Example 1 and$\alpha =4,\beta =2$.

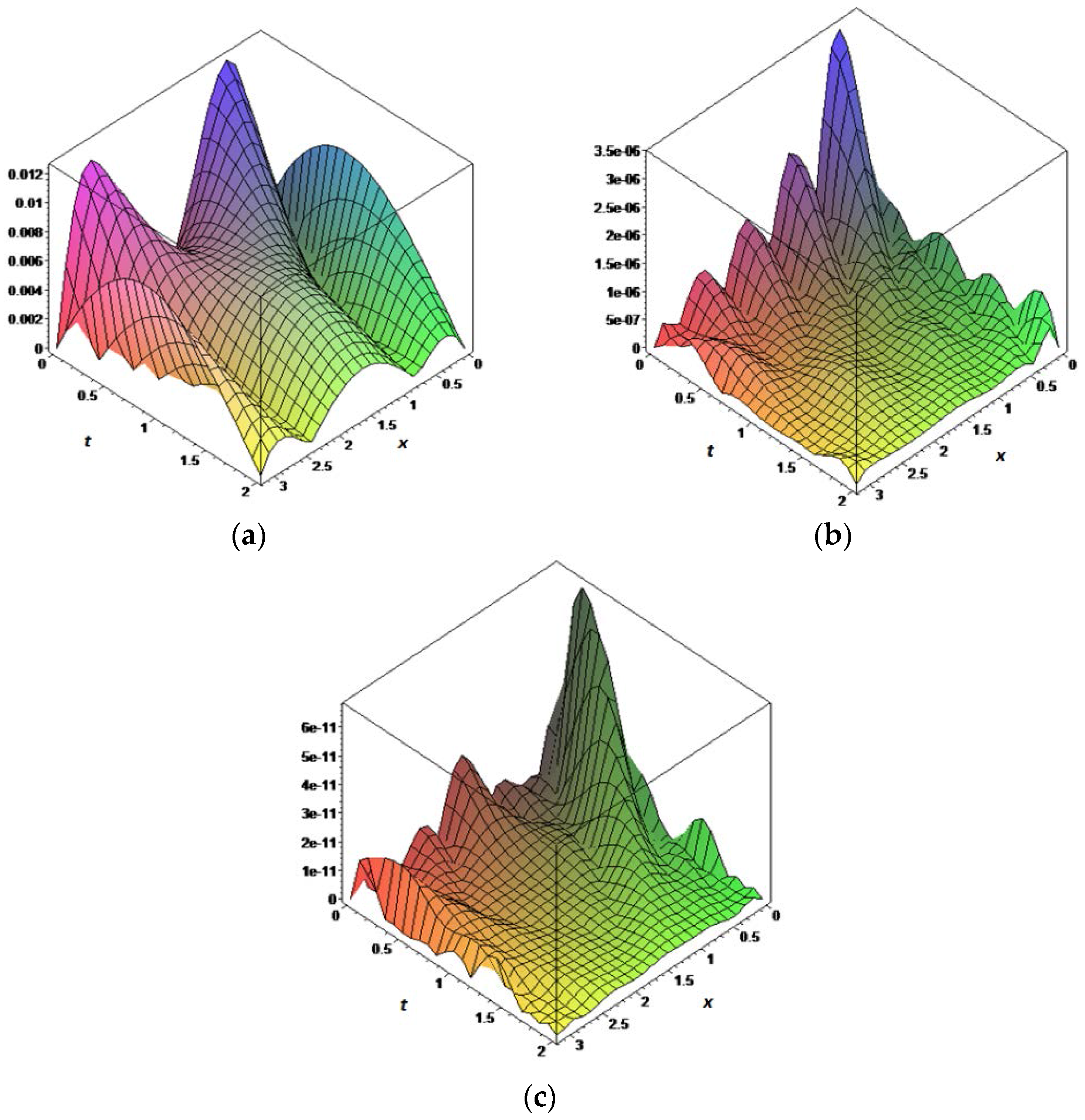
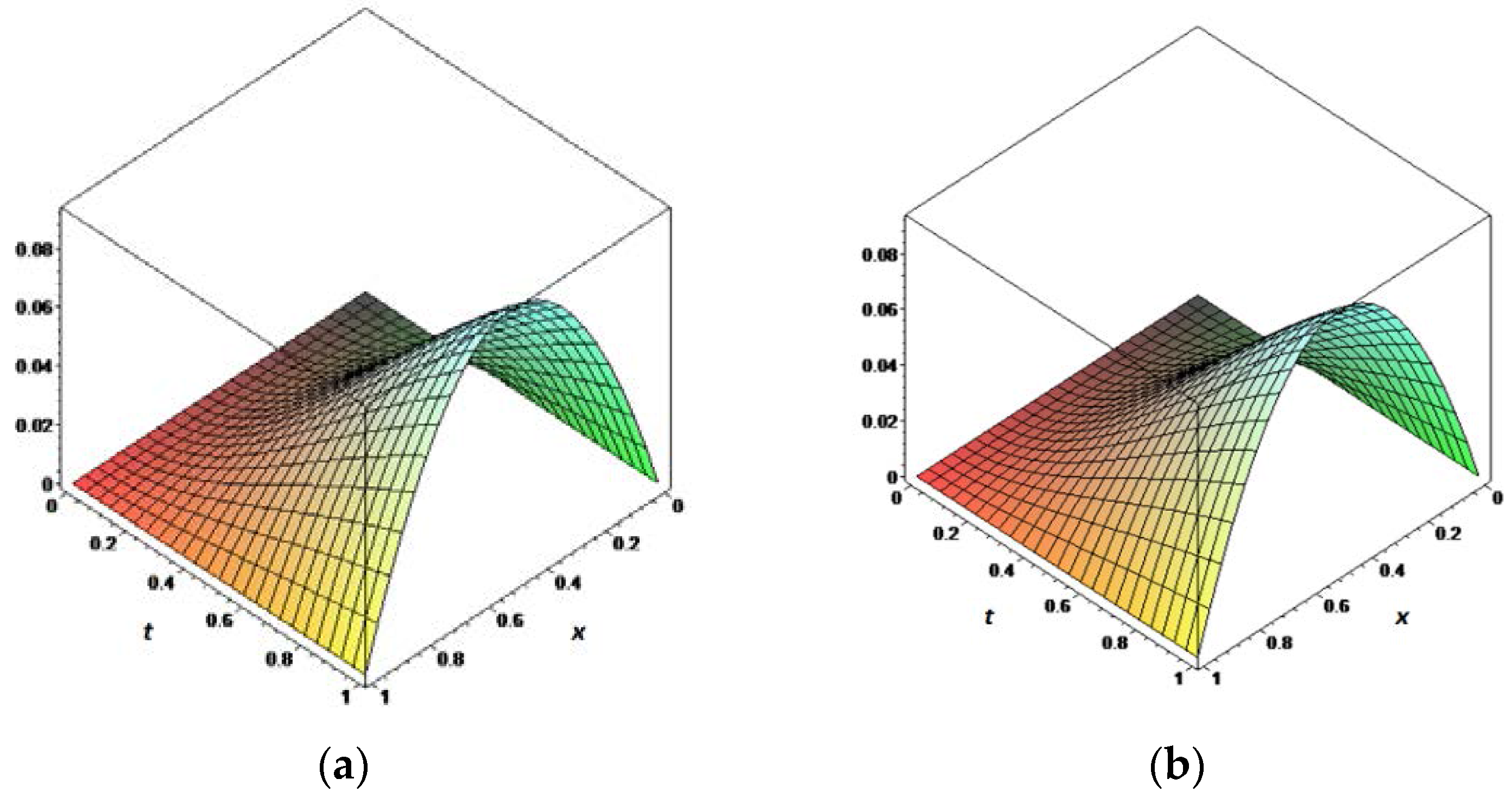
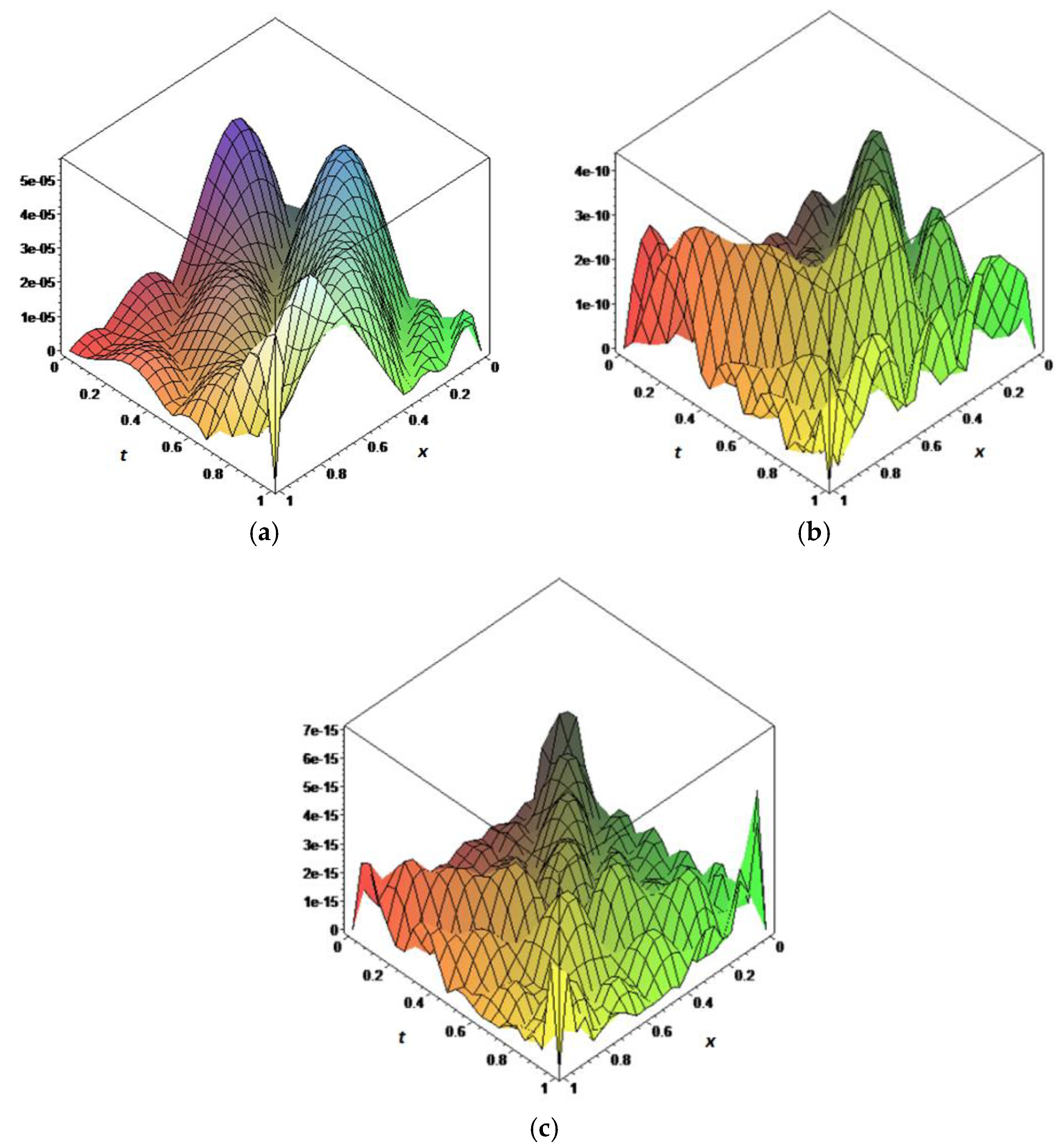
Values	Taylor Matrix Method [16]	Legendre Multiwavelet [26]	Fibonacci Polynomial Solution	Corrected Fibonacci Polynomial Solution
$(x_r,t_r)$	$N=11$		$N=12$	$N=12, M=14$
$\left(0.1,0.1\right)$	$7.68e-20$	$8.31e-10$	$1.19e-10$	$4.28e-12$
$\left(0.2,0.2\right)$	$7.34e-16$	$2.00e-10$	$7.00e-11$	$5.93e-13$
$\left(0.3,0.3\right)$	$1.66e-13$	$1.00e-10$	$5.32e-10$	$3.56e-12$
$\left(0.4,0.4\right)$	$8.12e-12$	$4.00e-09$	$7.68e-10$	$6.13e-12$
$\left(0.5,0.5\right)$	$1.71e-10$	$1.11e-09$	$5.04e-10$	$7.07e-12$
$\left(0.6,0.6\right)$	$2.11e-09$	$5.00e-10$	$1.93e-10$	$6.62e-12$
$\left(0.7,0.7\right)$	$1.81e-09$	$3.36e-08$	$1.02e-09$	$4.93e-12$
$\left(0.8,0.8\right)$	$1.18e-07$	$8.32e-07$	$1.63e-09$	$2.39e-12$
$\left(0.9,0.9\right)$	$6.03e-07$	$2.80e-06$	$1.35e-09$	$2.40e-13$

Figure 1. Graphs of the absolute error functions of Exp. 2 for $N=5,10,13$ and $\alpha =6,\beta =2$. (a) The absolute error function for $N=5$; (b) The absolute error function for $N=10$; (c) The absolute error function for$N=13.$

Example 3. 

[1] As a final example, we solve the hyperbolic Telegraph Equation

$$\frac{{\partial }^{2}u\left(x,t\right)}{\partial t^2}+\frac{\partial u\left(x,t\right)}{\partial t}+u\left(x,t\right)-\frac{{\partial }^{2}u\left(x,t\right)}{\partial x^2}=(2-2t+t^2)\left(x-x^2\right)e^{\left(-t\right)}+2t^2{e}^{\left(-t\right)},$$

$$0<x<1, t\ge 0$$

with the initial conditions

$$\begin{gathered} u\left(x,0\right)=0, 0<x<2 \\ {u}_t\left(x,0\right)=0, 0<x<2 \end{gathered}$$

and Dirichlet boundary conditions

$$\begin{gathered} u\left(0,t\right)=0,t\ge 0 \\ u\left(1,t\right)=0,t\ge 0. \end{gathered}$$

The exact solution of this problem is

$$u\left(x,t\right)=t^2\left(x-x^2\right)e^{\left(-t\right)}$$

where $l=1,\tau =1,\alpha =1,\beta =1$, $k_1\left(x\right)=k_2\left(x\right)=0.$

$$g\left(x,t\right)=(2-2t+t^2)\left(x-x^2\right)e^{\left(-t\right)}2t^2{e}^{\left(-t\right)}, h_1\left(t\right)= h_2\left(t\right)=0$$

Exact solution and numerical solution for $N=11$ are plotted in Figure 2. On the other hand, taking $N=7, 11, 14$, we compared the absolute error functions in Figure 3 and Table 2.

Figure 2. Exact solution and Fibonacci polynomial solution of Example 3 for $N=11$. (a) Exact solution; (b) Present method for $N=11.$

Figure 3. Graphs of the absolute errors functions of Example 3 for $N=7, 11, 14$. (a) The absolute error function for N = 7; (b) The absolute error function for N = 11; (c) The absolute error function for N = 14.

Table 2. Comparison of the absolute error values $E_{N }\left(x_r,1\right)$ of Example 3 for $N=7, 11, 14$.

	Present Method
$x_i$	$N=7$	$N=11$	$N=14$
$0.1$	$8.875e-6$	$2.140e-10$	$2.454e-15$
$0.2$	$1.283e-6$	$2.713e-10$	$4.741e-16$
$0.3$	$3.515e-6$	$1.435e-10$	$1.363e-15$
$0.4$	$4.354e-6$	$1.400e-10$	$1.414e-16$
$0.5$	$1.644e-5$	$2.330e-10$	$1.187e-16$
$0.6$	$2.848e-5$	$1.464e-11$	$5.275e-17$
$0.7$	$4.052e-5$	$2.135e-10$	$5.596e-16$
$0.8$	$5.250e-5$	$1.539e-10$	$3.518e-16$
$0.9$	$5.283e-5$	$1.011e-10$	$1.438e-15$

Table 3 shows a comparison of the $L_{\infty }$ values of Fibonacci polynomial solution and corrected Fibonacci polynomial solution with B-spline Collocation Method and Tau Method for Example 3.

Table 3. Comparison of the $L_{\infty }$ values of Fibonacci polynomial solution and corrected Fibonacci polynomial solution with B-spline Collocation Method and Tau Method for Example 3.

	B-Spline Collocation Method [27]	Tau Method [1]	Fibonacci Polynomial Solution	Corrected Fibonacci Polynomial Solution
	$h=0.01$$\mathrm{\Delta }t=0.001$		$N=8$	$N=8, M=10$
$t$	$L_{\infty }$	$L_{\infty }$	$L_{\infty }$	$L_{\infty }$
$1$	$5.9153e-5$	$1.8479e-5$	$4.9393e-6$	$3.9524e-9$
$2$	$1.7864e-5$	$1.0713e-5$	$3.6458e-5$	$1.3181e-6$

6. Conclusions

In this article, we have presented a new approach using the Fibonacci polynomials to solve the Telegraph equation which is a typical example of the hyperbolic type PDEs. The solution of this equation is expressed as a truncated series of Fibonacci polynomials, which are then transformed from algebraic form to matrix form. The new method has been applied to three illustrative examples. Illustrated examples are contained to demonstrate the applicability and the validity of the method and the obtained results are compared with the different methods in literature. The results show the efficiently and the accuracy of the present work. Moreover, it is well seen from these examples that the method yields either the exact solution or a high accuracy approximate solution for the telegraph equations. Also, as N increases, the errors decrease more rapidly. One of the considerable advantages of this technique is that the approximate solutions are found very easily by using the computer programs. As seen from this study, the new approach with Fibonacci polynomial is a good approximation for solving the Telegraph equations.