Modelling Sessile Droplet Profile Using Asymmetrical Ellipses
Abstract
:1. Introduction
2. Theoretical Background
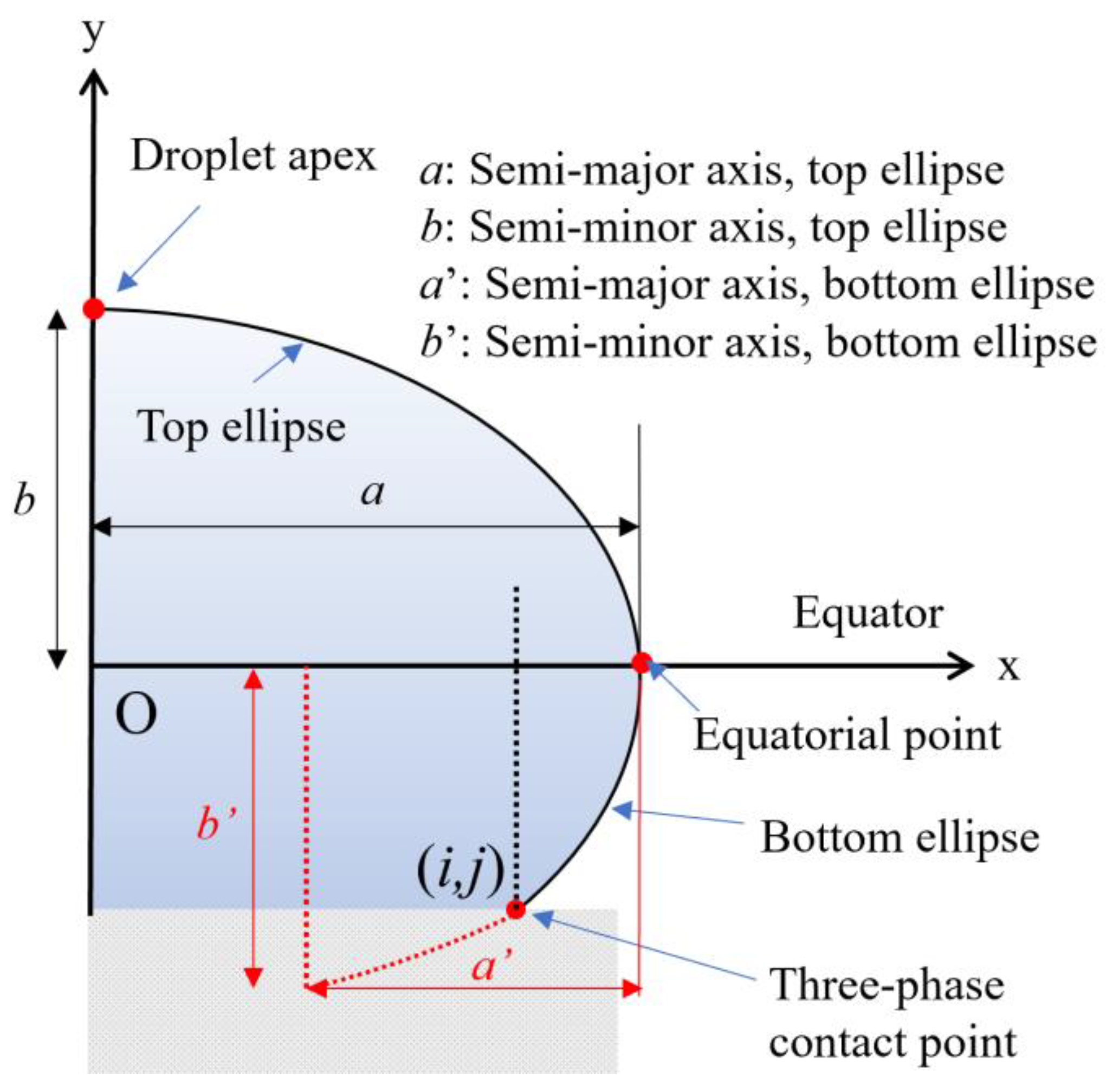
2.1. Defining the Ellipses
2.2. Determining Surface Tension Using Droplet Apex and Equatorial Point
2.3. Determining Contact Angles
- (i)
- y0 = 0, since the bottom ellipse foci are located on the x-axis;
- (ii)
- When x = a, y = b, since the equatorial point is known;
- (iii)
- When x = i, y = j, since the three-phase contact point is known;
- (iv)
- from the radius of curvature.
3. Methods
4. Results and Discussion
4.1. Surface Tension Determination
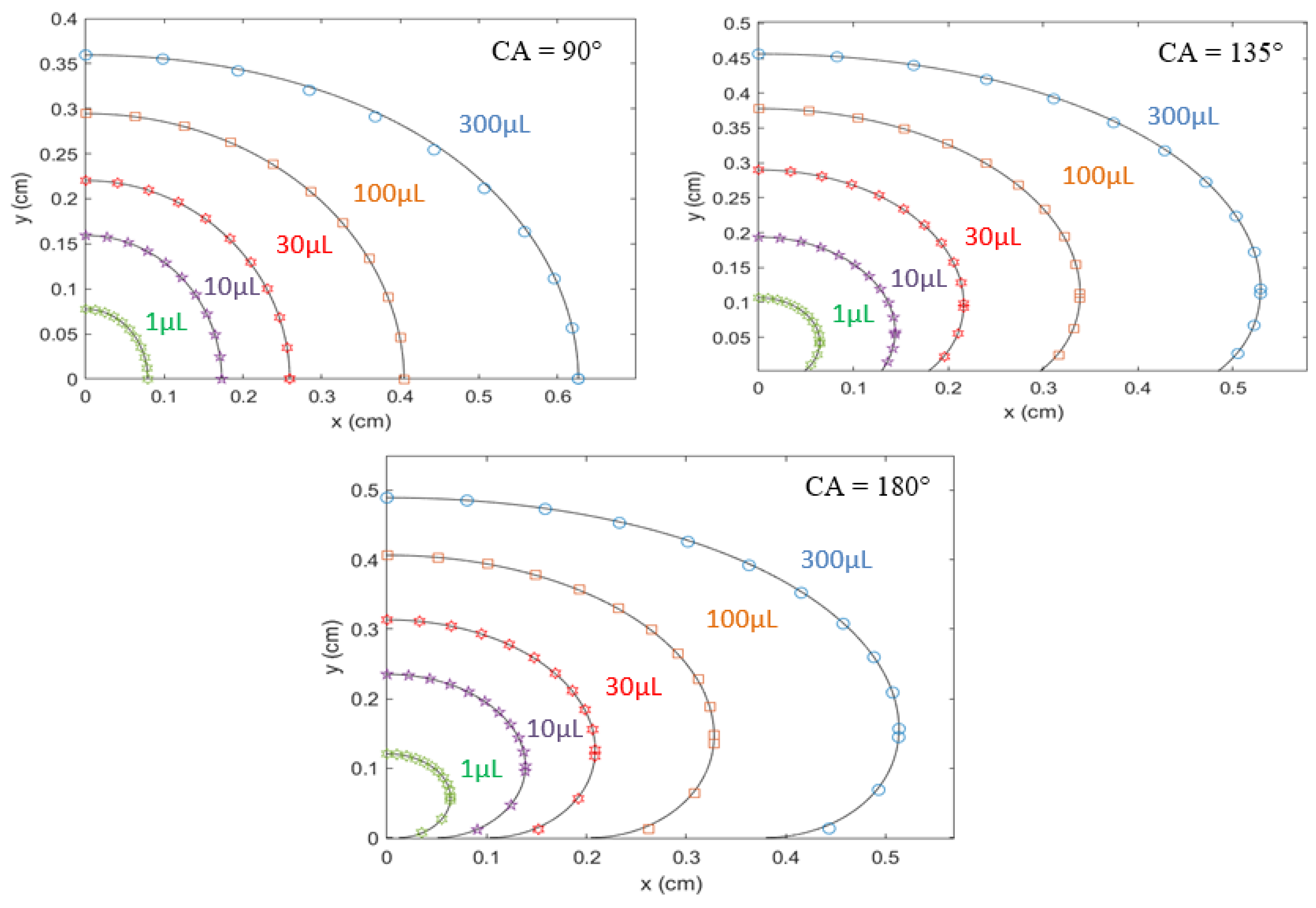
4.2. Generation of Elliptic Droplet Profile and Contact Angle
4.3. Compatibility of Elliptic Model with Actual Sessile Droplet
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lubarda, V.A.; Talke, K.A. Analysis of the Equilibrium Droplet Shape Based on an Ellipsoidal Droplet Model. Langmuir 2011, 27, 10705–10713. [Google Scholar] [CrossRef]
- Dixit, S.S.; Pincus, A.; Guo, B.; Faris, G.W. Droplet Shape Analysis and Permeability Studies in Droplet Lipid Bilayers. Langmuir 2012, 28, 7442–7451. [Google Scholar] [CrossRef] [Green Version]
- Zhou, W.; Loney, D.; Degertekin, F.L.; Rosen, D.W.; Fedorov, A.G. What controls dynamics of droplet shape evolution upon impingement on a solid surface? AIChE J. 2013, 59, 3071–3082. [Google Scholar] [CrossRef]
- Saad, S.M.I.; Policova, Z.; Neumann, A.W. Design and accuracy of pendant drop methods for surface tension measurement. Colloids Surf. A Physicochem. Eng. Asp. 2011, 384, 442–452. [Google Scholar] [CrossRef]
- Berry, J.D.; Neeson, M.J.; Dagastine, R.R.; Chan, D.Y.C.; Tabor, R.F. Measurement of surface and interfacial tension using pendant drop tensiometry. J. Colloid Interface Sci. 2015, 454, 226–237. [Google Scholar] [CrossRef] [PubMed]
- Brandon, S.; Marmur, A. Simulation of Contact Angle Hysteresis on Chemically Heterogeneous Surfaces. J. Colloid Interface Sci. 1996, 183, 351–355. [Google Scholar] [CrossRef] [PubMed]
- He, B.; Yang, S.; Qin, Z.; Wen, B.; Zhang, C. The roles of wettability and surface tension in droplet formation during inkjet printing. Sci. Rep. 2017, 7, 11841. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jain, V.; Raj, T.P.; Deshmukh, R.; Patrikar, R. Design, fabrication and characterization of low cost printed circuit board based EWOD device for digital microfluidics applications. Microsyst. Technol. 2017, 23, 389–397. [Google Scholar] [CrossRef]
- Nguyen, C.T.; Kim, B. Stress and surface tension analyses of water on graphene-coated copper surfaces. Int. J. Precis. Eng. Manuf. 2016, 17, 503–510. [Google Scholar] [CrossRef]
- Gates, C.H.; Perfect, E.; Lokitz, B.S.; Brabazon, J.W.; McKay, L.D.; Tyner, J.S. Transient analysis of advancing contact angle measurements on polished rock surfaces. Adv. Water Resour. 2018, 119, 142–149. [Google Scholar] [CrossRef]
- Hünnekens, B.; Peters, F.; Avramidis, G.; Krause, A.; Militz, H.; Viöl, W. Plasma treatment of wood–polymer composites: A comparison of three different discharge types and their effect on surface properties. J. Appl. Polym. Sci. 2016, 133. [Google Scholar] [CrossRef]
- Bashforth, F.; Adams, J. An Attempt to Test the Theory of Capillary Action; Cambridge University: Cambridge, UK, 1892. [Google Scholar]
- Shanahan, M.E.R. An approximate theory describing the profile of a sessile drop. J. Chem. Soc. Faraday Trans. 1 Phys. Chem. Condens. Phases 1982, 78, 2701–2710. [Google Scholar] [CrossRef]
- Joshi, Y.P. Shape of a liquid surface in contact with a solid. Eur. J. Phys. 1990, 11, 125–129. [Google Scholar] [CrossRef]
- Yildiz, B.; Bashiry, V. Shape analysis of a sessile drop on a flat solid surface. J. Adhes. 2019, 95, 929–942. [Google Scholar] [CrossRef]
- Hartland, S.; Hartley, R.W. Axisymmetric Fluid-Liquid Interfaces: Tables Giving the Shape of Sessile and Pendant Drops and External Menisci, with Examples of Their Use; Elsevier Science Limited: Amsterdam, The Netherlands, 1976. [Google Scholar]
- Jennings, J.W.; Pallas, N.R. An efficient method for the determination of interfacial tensions from drop profiles. Langmuir 1988, 4, 959–967. [Google Scholar] [CrossRef]
- Yu, K.; Yang, J.; Zuo, Y.Y. Automated Droplet Manipulation Using Closed-Loop Axisymmetric Drop Shape Analysis. Langmuir 2016, 32, 4820–4826. [Google Scholar] [CrossRef] [Green Version]
- Skinner, F.K.; Rotenberg, Y.; Neumann, A.W. Contact angle measurements from the contact diameter of sessile drops by means of a modified axisymmetric drop shape analysis. J. Colloid Interface Sci. 1989, 130, 25–34. [Google Scholar] [CrossRef]
- Río, O.I.D.; Neumann, A.W. Axisymmetric Drop Shape Analysis: Computational Methods for the Measurement of Interfacial Properties from the Shape and Dimensions of Pendant and Sessile Drops. J. Colloid Interface Sci. 1997, 196, 136–147. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Aussillous, P.; Quéré, D. Liquid marbles. Nature 2001, 411, 924–927. [Google Scholar] [CrossRef] [PubMed]
- Aussillous, P.; Quéré, D. Properties of liquid marbles. Proc. R. Soc. A Math. Phys. Eng. Sci. 2006, 462, 973–999. [Google Scholar] [CrossRef]
- Singha, P.; Ooi, C.H.; Nguyen, N.-K.; Sreejith, K.R.; Jin, J.; Nguyen, N.-T. Capillarity: Revisiting the fundamentals of liquid marbles. Microfluid. Nanofluidics 2020, 24, 81. [Google Scholar] [CrossRef]
- Singha, P.; Nguyen, N.-K.; Sreejith, K.R.; An, H.; Nguyen, N.-T.; Ooi, C.H. Effect of Core Liquid Surface Tension on the Liquid Marble Shell. Adv. Mater. Interfaces 2021, 8, 2001591. [Google Scholar] [CrossRef]
- Ooi, C.H.; Vadivelu, R.; Jin, J.; Sreejith, K.R.; Singha, P.; Nguyen, N.-K.; Nguyen, N.-T. Liquid marble-based digital microfluidics—Fundamentals and applications. Lab Chip 2021, 21, 1199–1216. [Google Scholar] [CrossRef]
- Ooi, C.H.; Singha, P.; Nguyen, N.-K.; An, H.; Nguyen, V.T.; Nguyen, A.V.; Nguyen, N.-T. Measuring the effective surface tension of a floating liquid marble using X-ray imaging. Soft Matter 2021, 17, 4069–4076. [Google Scholar] [CrossRef]
- Singha, P.; Nguyen, N.-K.; Zhang, J.; Nguyen, N.-T.; Ooi, C.H. Oscillating sessile liquid marble—A tool to assess effective surface tension. Colloids Surf. A Physicochem. Eng. Asp. 2021, 627, 127176. [Google Scholar] [CrossRef]
- Ooi, C.H.; Vadivelu, R.K.; St John, J.; Dao, D.V.; Nguyen, N.-T. Deformation of a floating liquid marble. Soft Matter 2015, 11, 4576–4583. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cengiz, U.; Erbil, H.Y. The lifetime of floating liquid marbles: The influence of particle size and effective surface tension. Soft Matter 2013, 9, 8980–8991. [Google Scholar] [CrossRef]
- Jin, J.; Nguyen, N.-T. Manipulation schemes and applications of liquid marbles for micro total analysis systems. Microelectron. Eng. 2018, 197, 87–95. [Google Scholar] [CrossRef]
- Nguyen, N.-K.; Singha, P.; Zhang, J.; Phan, H.-P.; Nguyen, N.-T.; Ooi, C.H. Digital Imaging-based Colourimetry for Enzymatic Processes in Transparent Liquid Marbles. ChemPhysChem 2021, 22, 99–105. [Google Scholar] [CrossRef]
- Nguyen, N.-K.; Ooi, C.H.; Singha, P.; Jin, J.; Sreejith, K.R.; Phan, H.-P.; Nguyen, N.-T. Liquid Marbles as Miniature Reactors for Chemical and Biological Applications. Processes 2020, 8, 793. [Google Scholar] [CrossRef]
- Nguyen, N.-K.; Singha, P.; An, H.; Phan, H.-P.; Nguyen, N.-T.; Ooi, C.H. Electrostatically excited liquid marble as a micromixer. React. Chem. Eng. 2021, 6, 1386–1394. [Google Scholar] [CrossRef]
- Ooi, C.H.; Nguyen, N.-T. Manipulation of liquid marbles. Microfluid. Nanofluidics 2015, 19, 483–495. [Google Scholar] [CrossRef]
- Arbatan, T.; Li, L.; Tian, J.; Shen, W. Liquid Marbles as Micro-bioreactors for Rapid Blood Typing. Adv. Healthc. Mater. 2012, 1, 80–83. [Google Scholar] [CrossRef] [PubMed]
- Zang, D.; Li, J.; Chen, Z.; Zhai, Z.; Geng, X.; Binks, B.P. Switchable Opening and Closing of a Liquid Marble via Ultrasonic Levitation. Langmuir 2015, 31, 11502–11507. [Google Scholar] [CrossRef] [PubMed]
- Sato, E.; Yuri, M.; Fujii, S.; Nishiyama, T.; Nakamura, Y.; Horibe, H. Liquid marbles as a micro-reactor for efficient radical alternating copolymerization of diene monomer and oxygen. Chem. Commun. 2015, 51, 17241–17244. [Google Scholar] [CrossRef] [PubMed]
- Han, X.; Koh, C.S.L.; Lee, H.K.; Chew, W.S.; Ling, X.Y. Microchemical Plant in a Liquid Droplet: Plasmonic Liquid Marble for Sequential Reactions and Attomole Detection of Toxin at Microliter Scale. ACS Appl. Mater. Interfaces 2017, 9, 39635–39640. [Google Scholar] [CrossRef]
- Tian, J.; Fu, N.; Chen, X.D.; Shen, W. Respirable liquid marble for the cultivation of microorganisms. Colloids Surf. B Biointerfaces 2013, 106, 187–190. [Google Scholar] [CrossRef] [PubMed]
- Sheng, Y.; Sun, G.; Wu, J.; Ma, G.; Ngai, T. Silica-Based Liquid Marbles as Microreactors for the Silver Mirror Reaction. Angew. Chem. Int. Ed. 2015, 54, 7012–7017. [Google Scholar] [CrossRef] [PubMed]
- Gu, H.; Ye, B.; Ding, H.; Liu, C.; Zhao, Y.; Gu, Z. Non-iridescent structural color pigments from liquid marbles. J. Mater. Chem. C 2015, 3, 6607–6612. [Google Scholar] [CrossRef]
- McHale, G.; Elliott, S.J.; Newton, M.I.; Herbertson, D.L.; Esmer, K. Levitation-Free Vibrated Droplets: Resonant Oscillations of Liquid Marbles. Langmuir 2009, 25, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Farid, M. A new approach to modelling of single droplet drying. Chem. Eng. Sci. 2003, 58, 2985–2993. [Google Scholar] [CrossRef]
- Hu, H.; Larson, R.G. Evaporation of a Sessile Droplet on a Substrate. J. Phys. Chem. B 2002, 106, 1334–1344. [Google Scholar] [CrossRef]
- Marinaro, G.; Riekel, C.; Gentile, F. Size-Exclusion Particle Separation Driven by Micro-Flows in a Quasi-Spherical Droplet: Modelling and Experimental Results. Micromachines 2021, 12, 185. [Google Scholar] [CrossRef] [PubMed]
- Marchese, A.J.; Dryer, F.L.; Nayagam, V. Numerical modeling of isolated n-alkane droplet flames: Initial comparisons with ground and space-based microgravity experiments. Combust. Flame 1999, 116, 432–459. [Google Scholar] [CrossRef]

| Volume (µL) | Input Parameters (cm) | Surface Tension (mN/m) | ||
|---|---|---|---|---|
| a | b | Generated | Error (%) | |
| 1 | 0.0636 | 0.0628 | 72.00 | 0.000 |
| 10 | 0.1388 | 0.1314 | 72.29 | 0.403 |
| 30 | 0.2087 | 0.1866 | 73.69 | 2.347 |
| 100 | 0.3280 | 0.2589 | 71.99 | 0.139 |
| 300 | 0.5135 | 0.3323 | 70.47 | 2.125 |
| Pre-Defined Volume (µL) | Contact Angle (°) | Volume (µL) | Surface Area (cm2) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| (i) | (ii) | Error (%) | (i) | (ii) | Error (%) | (i) | (ii) | Error (%) | |
| 1 | 90 | 90 | 0 | 1.0 | 1.0 | 0 | 0.039 | 0.039 | 0 |
| 135 | 134.13 | 0.65 | 1.0 | 1.0 | 0 | 0.044 | 0.043 | 0.23 | |
| 180 | 174.75 | 3 | 1.0 | 1.0 | 0 | 0.050 | 0.049 | 0.41 | |
| 10 | 90 | 90 | 0 | 9.9 | 10.0 | 1.00 | 0.178 | 0.178 | 0.28 |
| 135 | 137.12 | 1.55 | 10.4 | 10.4 | 0 | 0.199 | 0.199 | 0.10 | |
| 180 | 179.21 | 0.44 | 10.0 | 10.0 | 0 | 0.218 | 0.219 | 0.23 | |
| 30 | 90 | 90 | 0 | 30.8 | 30.8 | 0 | 0.379 | 0.379 | 0.03 |
| 135 | 138.76 | 2.71 | 31.6 | 31.7 | 0.32 | 0.410 | 0.410 | 0.19 | |
| 180 | 180.00 | 0 | 30.9 | 31.1 | 0.64 | 0.452 | 0.454 | 0.57 | |
| 100 | 90 | 90 | 0 | 100.7 | 101.0 | 0.30 | 0.846 | 0.848 | 0.19 |
| 135 | 141.35 | 4.49 | 101.2 | 101.5 | 0.30 | 0.871 | 0.871 | 0.01 | |
| 180 | 180.00 | 0.00 | 100.4 | 101.3 | 0.89 | 0.963 | 0.972 | 0.88 | |
| 300 | 90 | 90 | 0 | 300.7 | 294.4 | 2.14 | 1.821 | 1.801 | 1.10 |
| 135 | 139.82 | 3.45 | 298.9 | 297.0 | 0.64 | 1.784 | 1.772 | 0.67 | |
| 180 | 180.00 | 0 | 300.8 | 300.0 | 0.27 | 1.959 | 1.964 | 0.28 | |
| Pre-Defined Volume (µL) | Bond Number | ||
|---|---|---|---|
| (i) | (ii) | Error (%) | |
| 1 | 0.0536 | 0.0534 | 0.374 |
| 10 | 0.2461 | 0.2462 | 0.041 |
| 30 | 0.5195 | 0.5201 | 0.115 |
| 100 | 1.1423 | 1.1444 | 0.184 |
| 300 | 2.3654 | 2.3505 | 0.64 |
| Run | Volume (µL) | Surface Area (cm2) | Contact Angle (°) | Surface Tension (mN/m) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (i) | (ii) | Error (%) | (i) | (ii) | Error (%) | (i) | (ii) | Error (%) | (i) | (ii) | Error (%) | |
| 1 | 10.7 | 10.7 | 0 | 0.203 | 0.204 | 0.49 | 137 | 138.46 | 1.07 | 81.75 | 78.7 | 3.87 |
| 2 | 10.5 | 10.6 | 0.95 | 0.201 | 0.202 | 0.5 | 137.72 | 139.46 | 1.26 | 72.67 | 69.6 | 4.41 |
| 3 | 10.8 | 10.8 | 0 | 0.205 | 0.206 | 0.49 | 138.91 | 140.84 | 1.39 | 72.67 | 70 | 3.81 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tran, D.T.; Nguyen, N.-K.; Singha, P.; Nguyen, N.-T.; Ooi, C.H. Modelling Sessile Droplet Profile Using Asymmetrical Ellipses. Processes 2021, 9, 2081. https://doi.org/10.3390/pr9112081
Tran DT, Nguyen N-K, Singha P, Nguyen N-T, Ooi CH. Modelling Sessile Droplet Profile Using Asymmetrical Ellipses. Processes. 2021; 9(11):2081. https://doi.org/10.3390/pr9112081
Chicago/Turabian StyleTran, Du Tuan, Nhat-Khuong Nguyen, Pradip Singha, Nam-Trung Nguyen, and Chin Hong Ooi. 2021. "Modelling Sessile Droplet Profile Using Asymmetrical Ellipses" Processes 9, no. 11: 2081. https://doi.org/10.3390/pr9112081
APA StyleTran, D. T., Nguyen, N.-K., Singha, P., Nguyen, N.-T., & Ooi, C. H. (2021). Modelling Sessile Droplet Profile Using Asymmetrical Ellipses. Processes, 9(11), 2081. https://doi.org/10.3390/pr9112081








