On the Use of Nonlinear Model Predictive Control without Parameter Adaptation for Batch Processes
Abstract
:1. Introduction
2. Problem Formulation—Model Predictive Control without Parameter Adaptation
3. Variational Analysis of Model Predictive Control without Parameter Adaptation
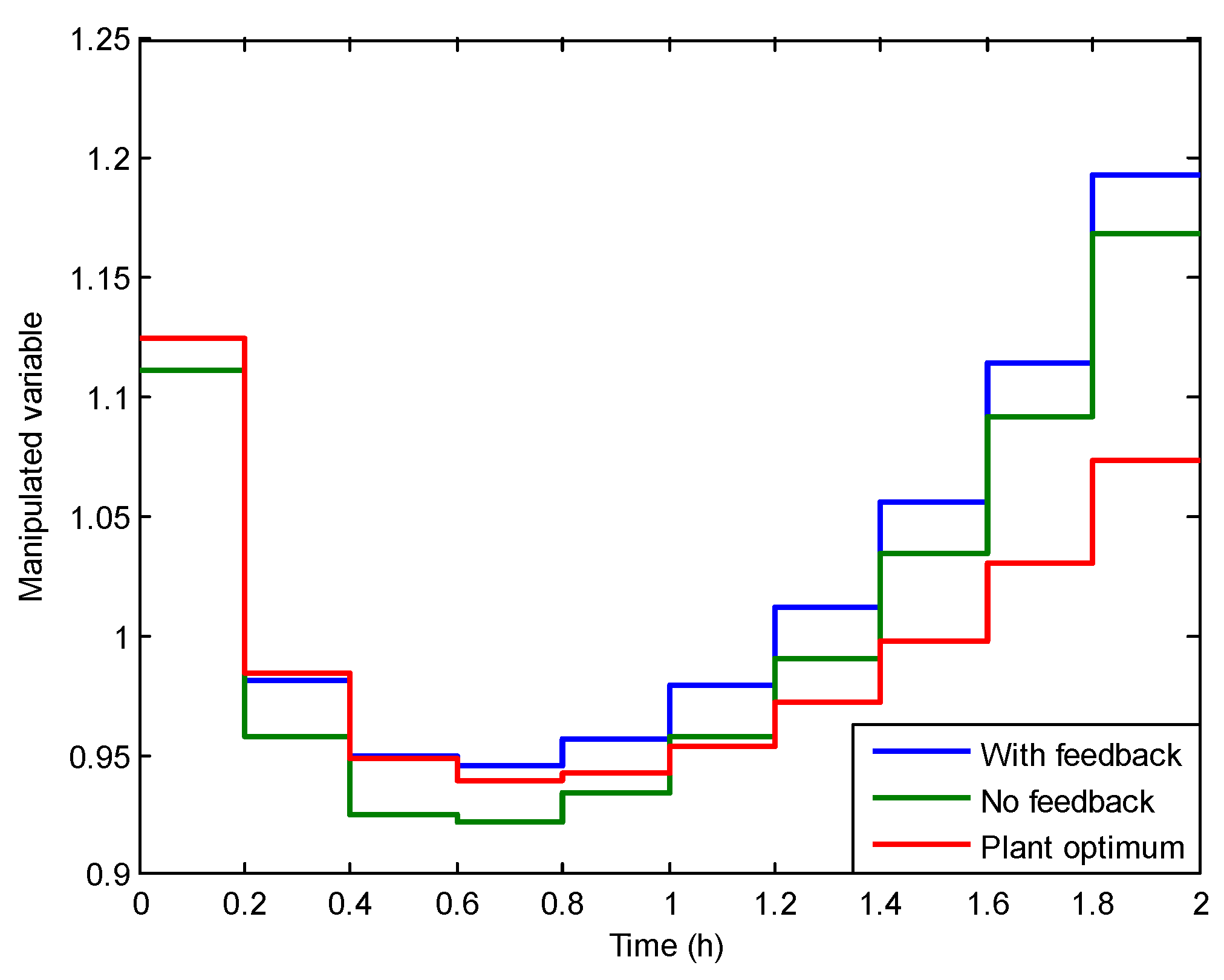
4. Results and Discussion
4.1. Illustrative Example
4.2. Results
5. Conclusions
Acknowledgment
Author Contributions
Conflicts of Interest
Abbreviations
| MPC | Model predictive control |
| NMPC | Nonlinear MPC |
| D-RTO | Dynamic real-time optimization |
References
- Peters, N.; Guay, M.; DeHaan, D. Real-time dynamic optimization of batch systems. J. Process Control 2007, 17, 261–271. [Google Scholar] [CrossRef]
- Srinivasan, B.; Palanki, S.; Bonvin, D. Dynamic optimization of batch processes—I. Characterization of the nominal solution. Comput. Chem. Eng. 2003, 27, 1–26. [Google Scholar] [CrossRef]
- Bonvin, D.; Srinivasan, B.; Hunkeler, D. Control and optimization of batch processes—Improvement of process operation in the production of specialty chemicals. IEEE Control Syst. Mag. 2006, 26, 34–45. [Google Scholar] [CrossRef]
- De Souza, G.; Odloak, D.; Zanin, A.C. Real time optimization (RTO) with model predictive control (MPC). Comput. Chem. Eng. 2010, 34, 1999–2006. [Google Scholar] [CrossRef]
- Diehl, M.; Bock, H.G.; Schlöder, J.P.; Findeisen, R.; Nagy, Z.; Allgöwer, F. Real-time optimization and nonlinear model predictive control of processes governed by differential-algebraic equations. J. Process Control 2002, 12, 577–585. [Google Scholar] [CrossRef]
- Lu, J. Challenging control problems and emerging technologies in enterprise optimization. Control Eng. Pract. 2003, 11, 847–858. [Google Scholar] [CrossRef]
- Würth, L.; Hannemann, R.; Marquardt, W. Neighboring-extremal updates for nonlinear model-predictive control and dynamic real-time optimization. J. Process Control 2009, 19, 1277–1288. [Google Scholar] [CrossRef]
- Aravind, P.; Valluvan, M.; Saranya, M. Simulation based modeling and implementation of adaptive control technique for Non Linear process tank. Int. J. Comput. Appl. 2013, 68, 16. [Google Scholar] [CrossRef]
- Dostal, P.; Bobal, V.; Vojtesek, J.; Chramcov, B. Adaptive control of nonlinear processes using two methods of parameter estimation. WSEAS Trans. Syst. 2014, 13, 292–301. [Google Scholar]
- Paz Suárez, L.A.; Georgieva, P.; de Feyo Azevedo, S. Nonlinear MPC for fed-batch multiple stages sugar crystallization. Chem. Eng. Res. Des. 2011, 89, 753–767. [Google Scholar] [CrossRef]
- Revollar, S.; Vega, P.; Vilanova, R. Economic optimization of wastewater treatment plants using Non Linear model predictive control. In Proceedings of the 19th International Conference on System Theory, Control and Computing (ICSTCC), Cheile Gradistei, Romania, 14–16 October 2015.
- Kamaraju, V.K.; Chiu, M.S.; Srinivasan, B. Reformulating real-time optimal feedback based on model uncertainty. In Proceedings of the 10th IFAC Symposium on Dynamics and Control of Process Systems, Mumbai, India, 18–20 December 2013; pp. 756–761.
- Yuan, C.; Wang, C. Persistency of excitation and performance of deterministic learning. In Proceedings of the 30th Chinese Control Conference, Yantai, China, 22–24 July 2011.
- Pahija, E.; Manenti, F.; Mujtaba, I.M.; Rossi, F. Assessment of control techniques for the dynamic optimization of (semi-)batch reactors. Comput. Chem. Eng. 2014, 66, 269–275. [Google Scholar] [CrossRef]
- Jamaludin, M.Z.; Swartz, C.L.E. A bilevel programming formulation for dynamic real-time optimization. IFAC-PapersOnLine 2015, 48, 906–911. [Google Scholar] [CrossRef]
- Nagy, Z.K.; Braatz, R.D. Open-loop and closed-loop robust optimal control of batch processes using distributional and worst-case analysis. J. Process Control 2004, 14, 411–422. [Google Scholar] [CrossRef]
- Kadam, J.V.; Schlegel, M.; Srinivasan, B.; Bonvin, D.; Marquardt, W. Dynamic optimization in the presence of uncertainty: From off-line nominal solution to measurement-based implementation. J. Process Control 2007, 17, 389–398. [Google Scholar] [CrossRef]
- Lucia, S.; Finkler, T.; Engell, S. Multi-stage nonlinear model predictive control applied to a semi-batch polymerization reactor under uncertainty. J. Process Control 2013, 23, 1306–1319. [Google Scholar] [CrossRef]
- Mesbah, A.; Streif, S.; Findeisen, R.; Braatz, R.D. Stochastic nonlinear model predictive control with probabilistic constraints. In Proceedings of the 2014 American Control Conference (ACC), Portland, OR, USA, 4–6 June 2014.
- Morari, M.; Lee, J.H. Model predictive control: Past, present and future. Comput. Chem. Eng. 1999, 23, 667–682. [Google Scholar] [CrossRef]
- Nagy, Z.K.; Allgöwer, F. A nonlinear model predictive control approach for robust end-point property control of a thin-film deposition process. Int. J. Robust Nonlinear Control 2007, 17, 1600–1613. [Google Scholar] [CrossRef]
| Parameter | Value | Units |
|---|---|---|
| 5 | mol/L | |
| 0 | mol/L | |
| 5 × 103 | h−1 | |
| 7 × 1016 | - | |
| 2 × 104 | J/mol | |
| 1 × 105 | J/mol | |
| 8.314 | J/mol.K | |
| 5 | - | |
| 1 | - | |
| 0.0224 | - | |
| 2 | H | |
| 1.25 | - | |
| 0.1 | mol/L | |
| 0.001 | - | |
| 0.999 | - |
| Case | Parametric Error | Cost | ||
|---|---|---|---|---|
| Offline | Re-Optimization | Plant Optimum | ||
| 1. Unconstrained, Economic cost | -- | 4.03 | 4.03 | 4.03 |
| : −20%; : −20% | 3.70 | 3.71 | 3.72 | |
| : −20%; : +20% | 3.691 | 3.686 | 3.697 | |
| 2. Terminal constraint Economic cost | -- | 3.71 | 3.71 | 3.71 |
| : −20%; : −20% | 1.29 | 2.03 | 3.35 | |
| : −20%; : +20% | 3.01 | 2.93 | 3.06 | |
| 3. Path constraints Economic cost | -- | 3.80 | 3.80 | 3.80 |
| : −50%; : −50% | 3.079 | 3.079 | 3.17 | |
| : −50%; : +50% | 2.39 | 2.37 | 2.40 | |
| 4. Unconstrained Trajectory cost | -- | 0.00 | 0.00 | 0.00 |
| : −20%; : −20% | 1.16 | 0.303 | 0.03 | |
| : −20%; : +20% | 1.10 | 0.30 | 0.00 | |
| 5. Terminal constraint Trajectory cost | -- | 0.00 | 0.00 | 0.00 |
| : −20%; : −20% | 2.84 | 1.49 | 0.03 | |
| : −20%; : +20% | 1.80 | 1.38 | 0.36 | |
| 6. Path constraint Trajectory cost | -- | 0.21 | 0.21 | 0.21 |
| : −20%; : −20% | 0.20 | 0.16 | 0.02 | |
| : −20%; : +20% | 2.060 | 1.48 | 0.47 | |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Binette, J.-C.; Srinivasan, B. On the Use of Nonlinear Model Predictive Control without Parameter Adaptation for Batch Processes. Processes 2016, 4, 27. https://doi.org/10.3390/pr4030027
Binette J-C, Srinivasan B. On the Use of Nonlinear Model Predictive Control without Parameter Adaptation for Batch Processes. Processes. 2016; 4(3):27. https://doi.org/10.3390/pr4030027
Chicago/Turabian StyleBinette, Jean-Christophe, and Bala Srinivasan. 2016. "On the Use of Nonlinear Model Predictive Control without Parameter Adaptation for Batch Processes" Processes 4, no. 3: 27. https://doi.org/10.3390/pr4030027





