A Continuous Formulation for Logical Decisions in Differential Algebraic Systems using Mathematical Programs with Complementarity Constraints
Abstract
:1. Introduction
2. Background
2.1. Logical Disjunctions in Optimization
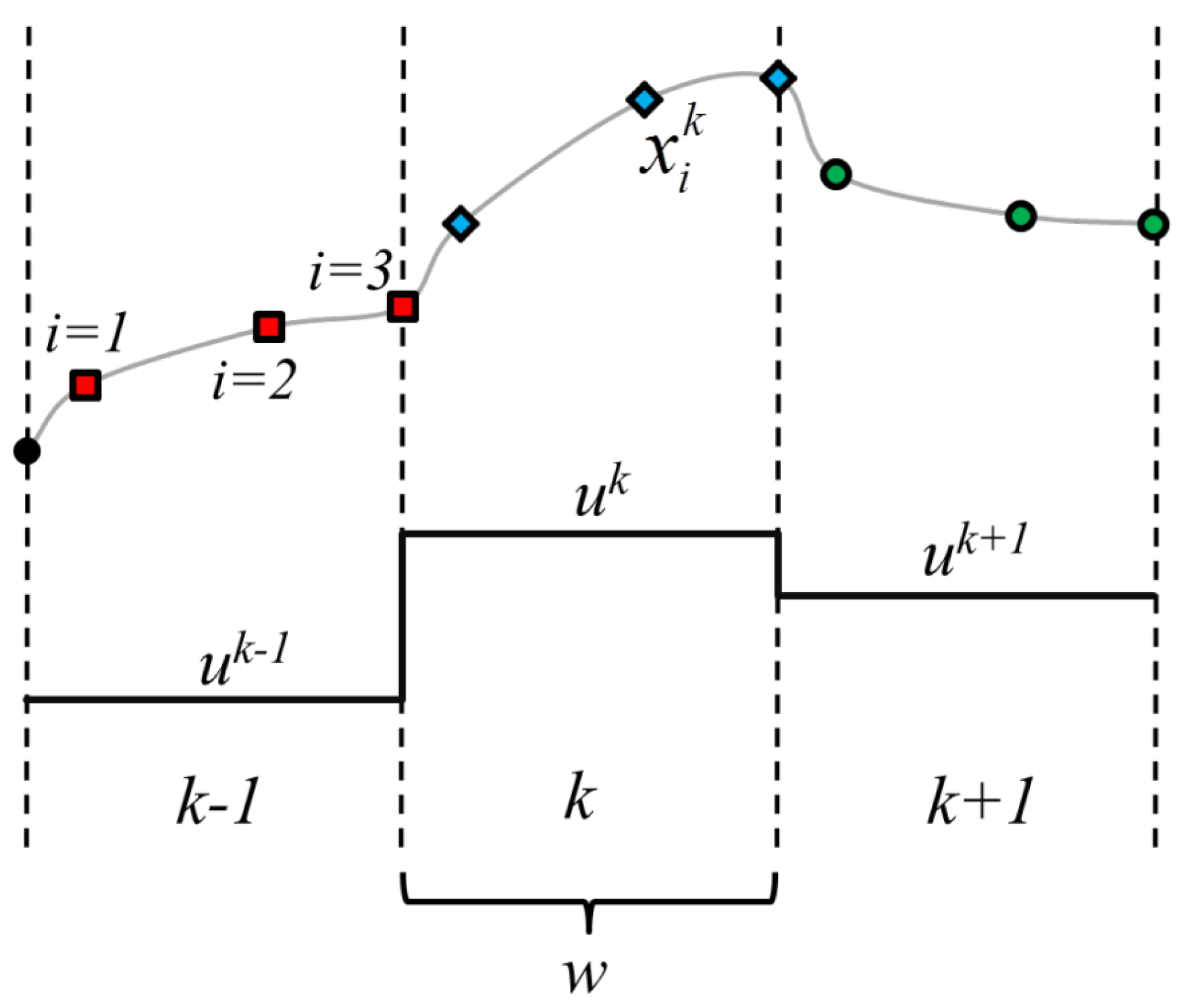
2.2. Sequential Solution Method
2.3. Simultaneous Solution Method
2.4. Embedding MPECs with Complementarity into Simultaneous Equations
2.4.1. Absolute Value Operator
2.4.2. Min/Max Operator
2.4.3. Signum Operator
3. MPEC Formulations with Complementarity to Represent Logical Statements
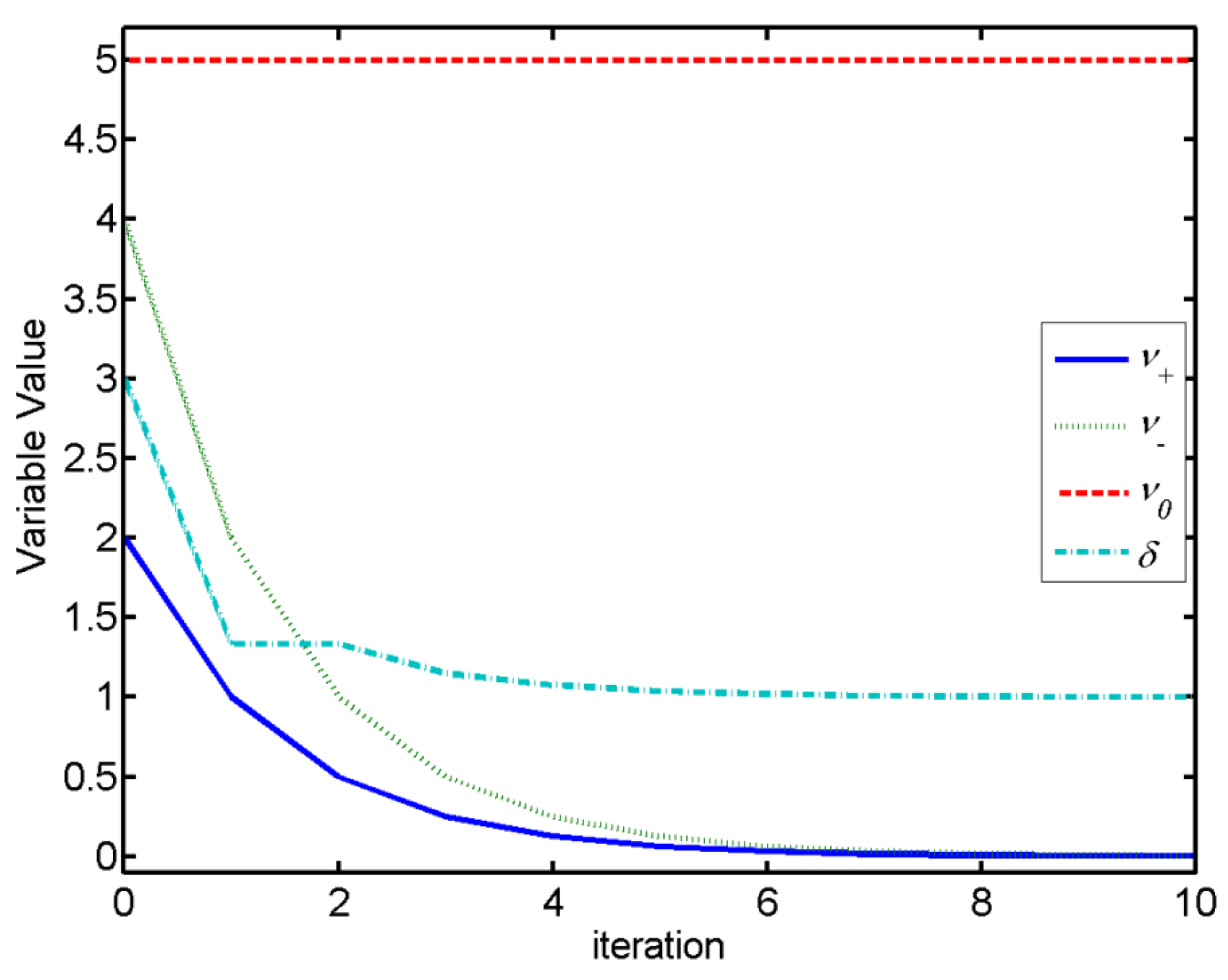
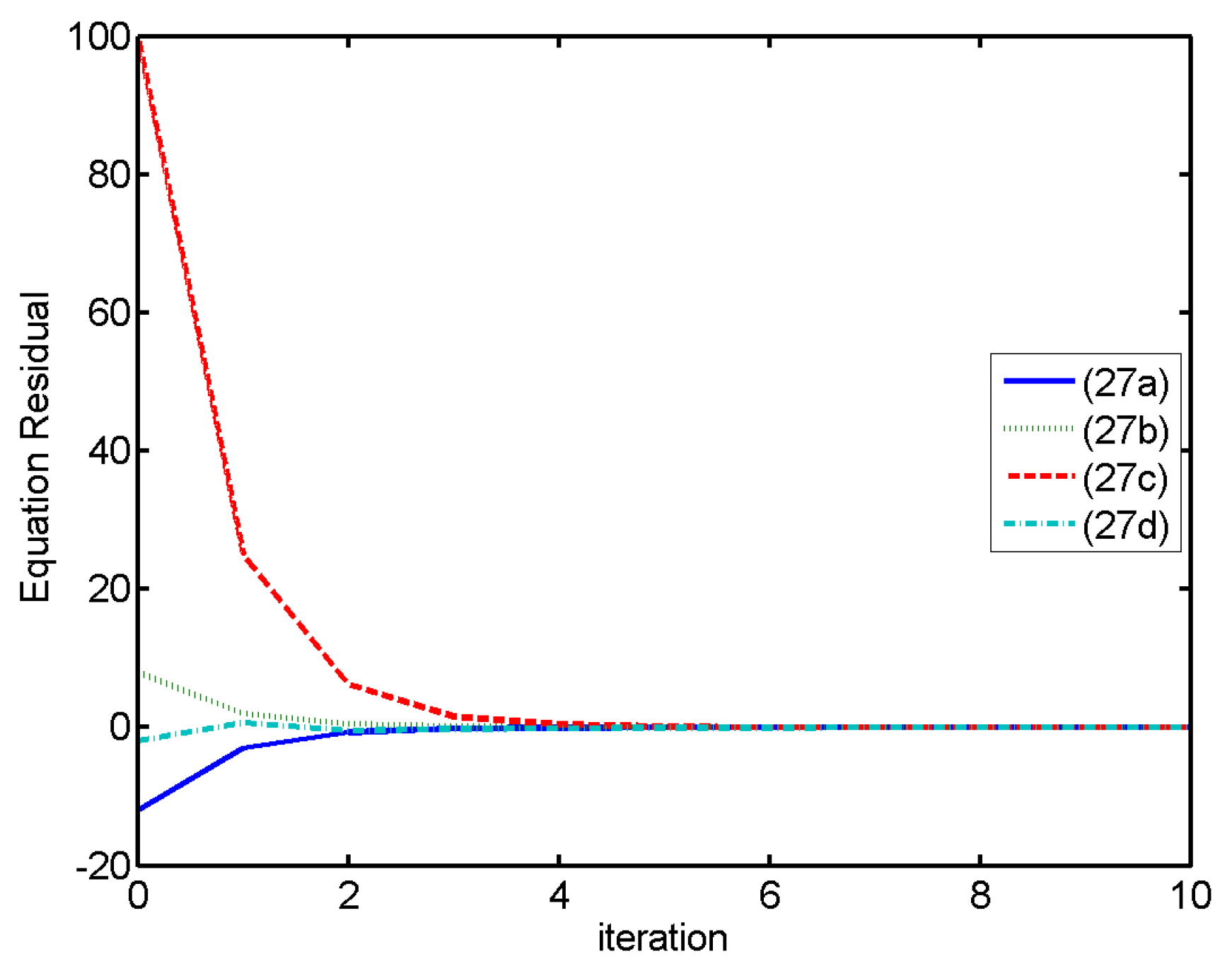
3.1. Jump Function
3.2. Heaviside Function
4. Continuous Logic in Dynamic Systems
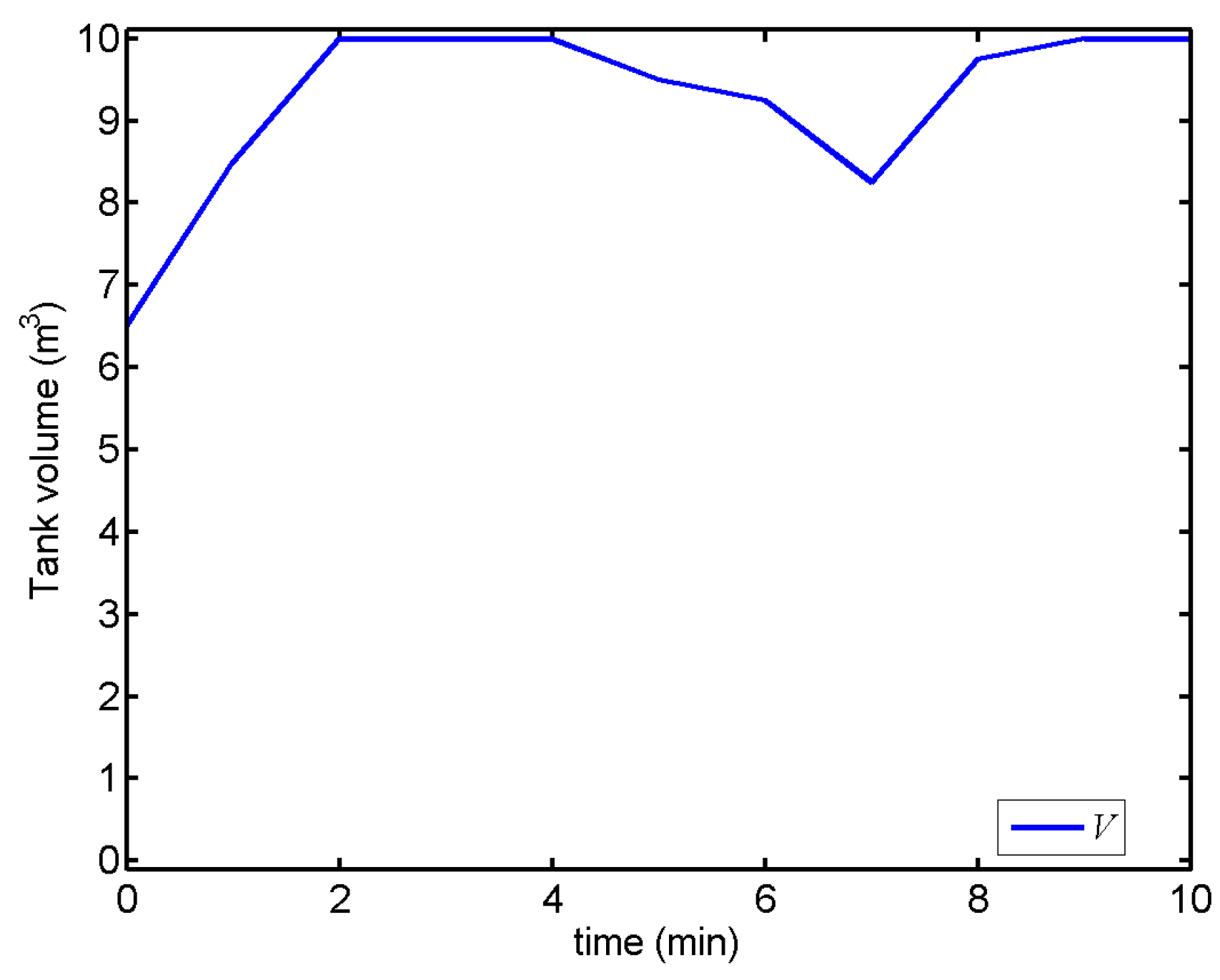
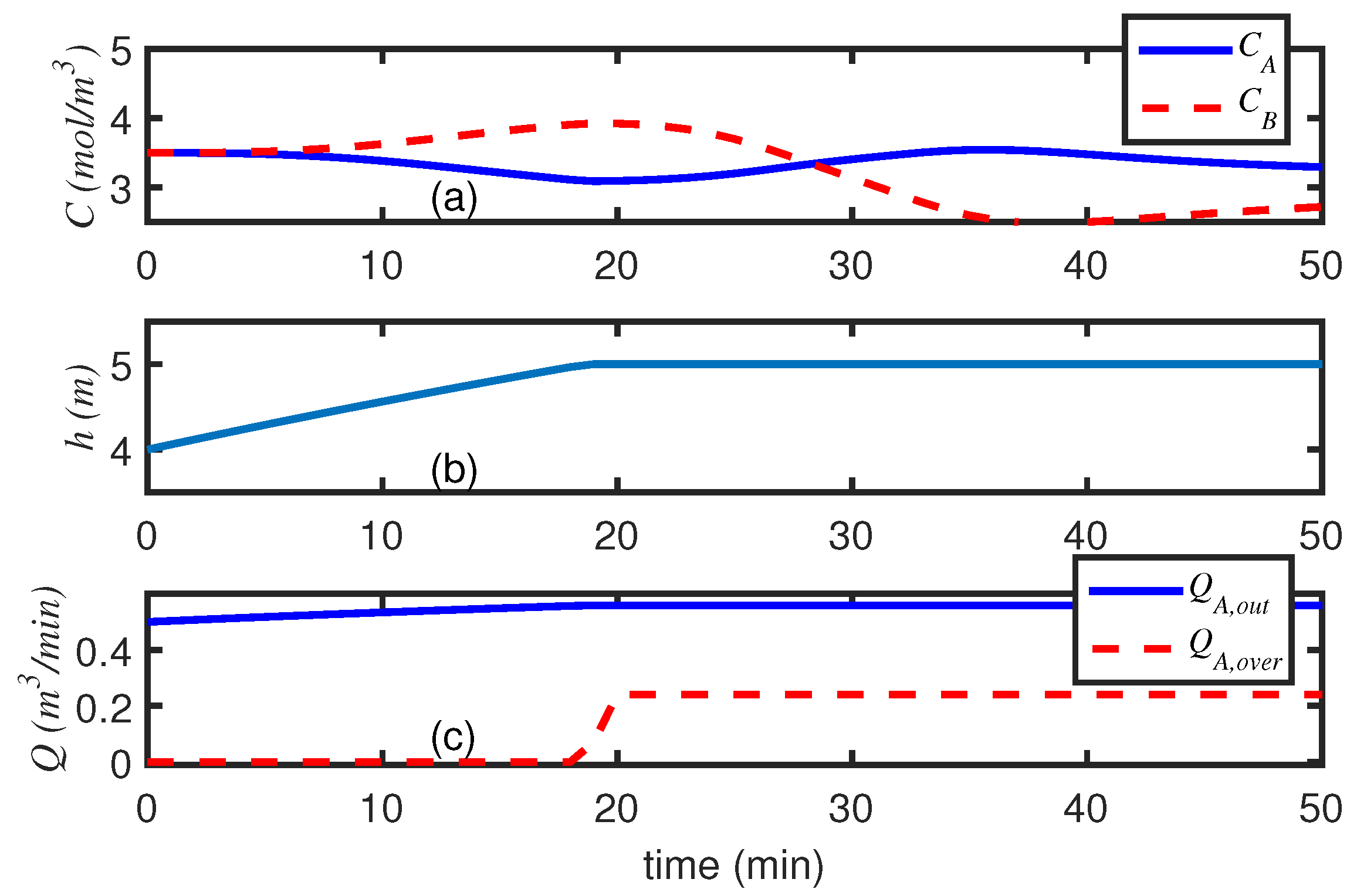
4.1. Tank with Overflow
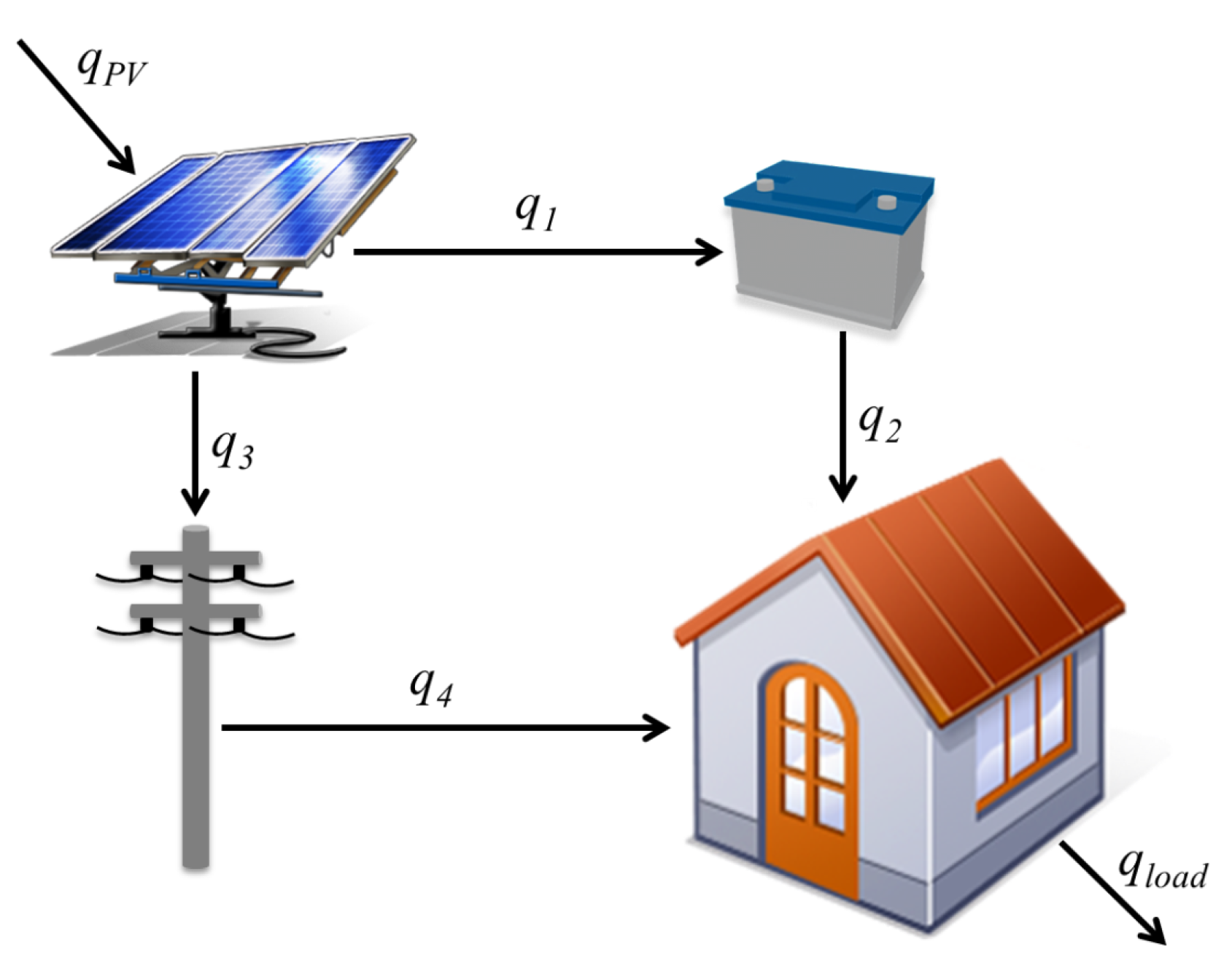
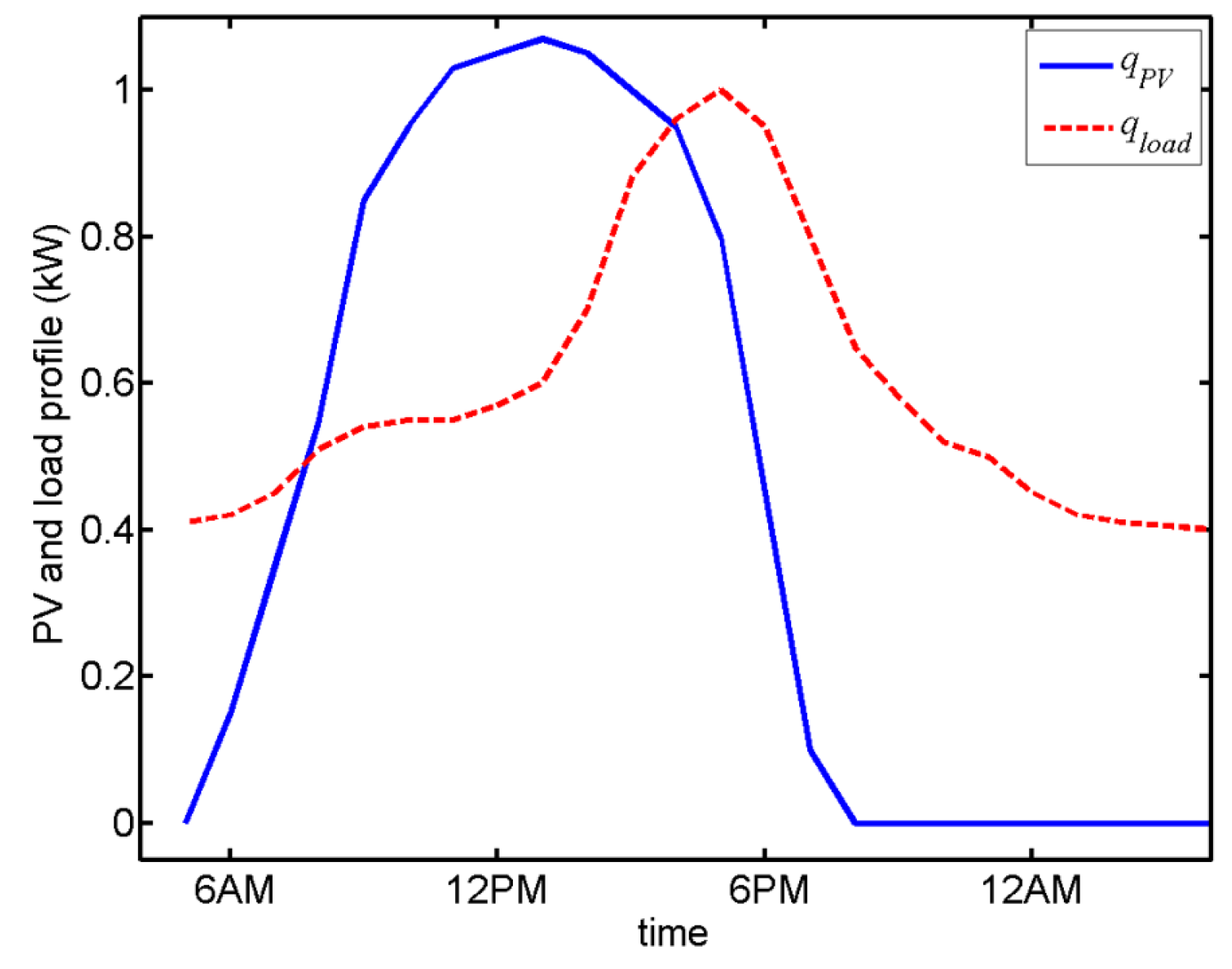
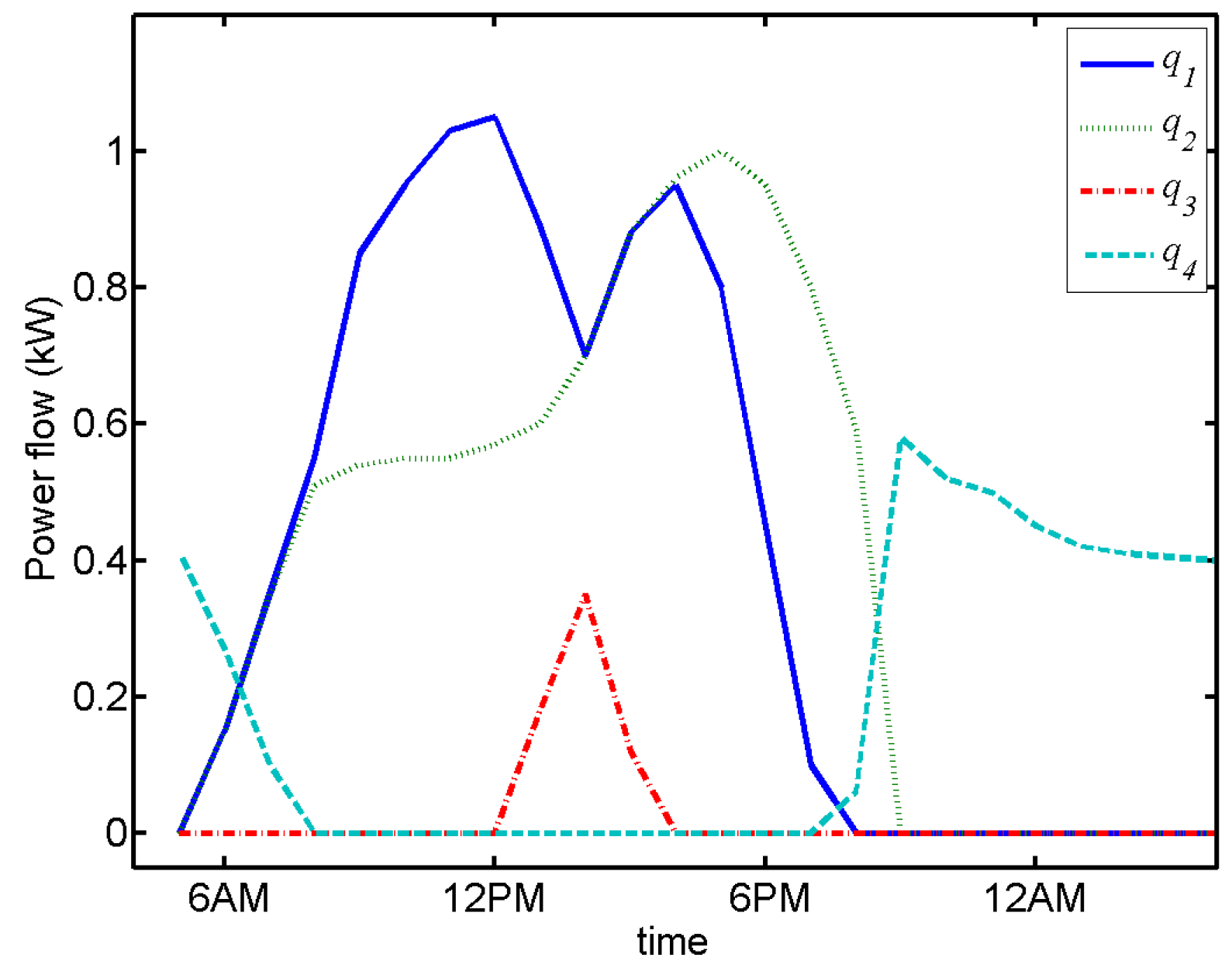
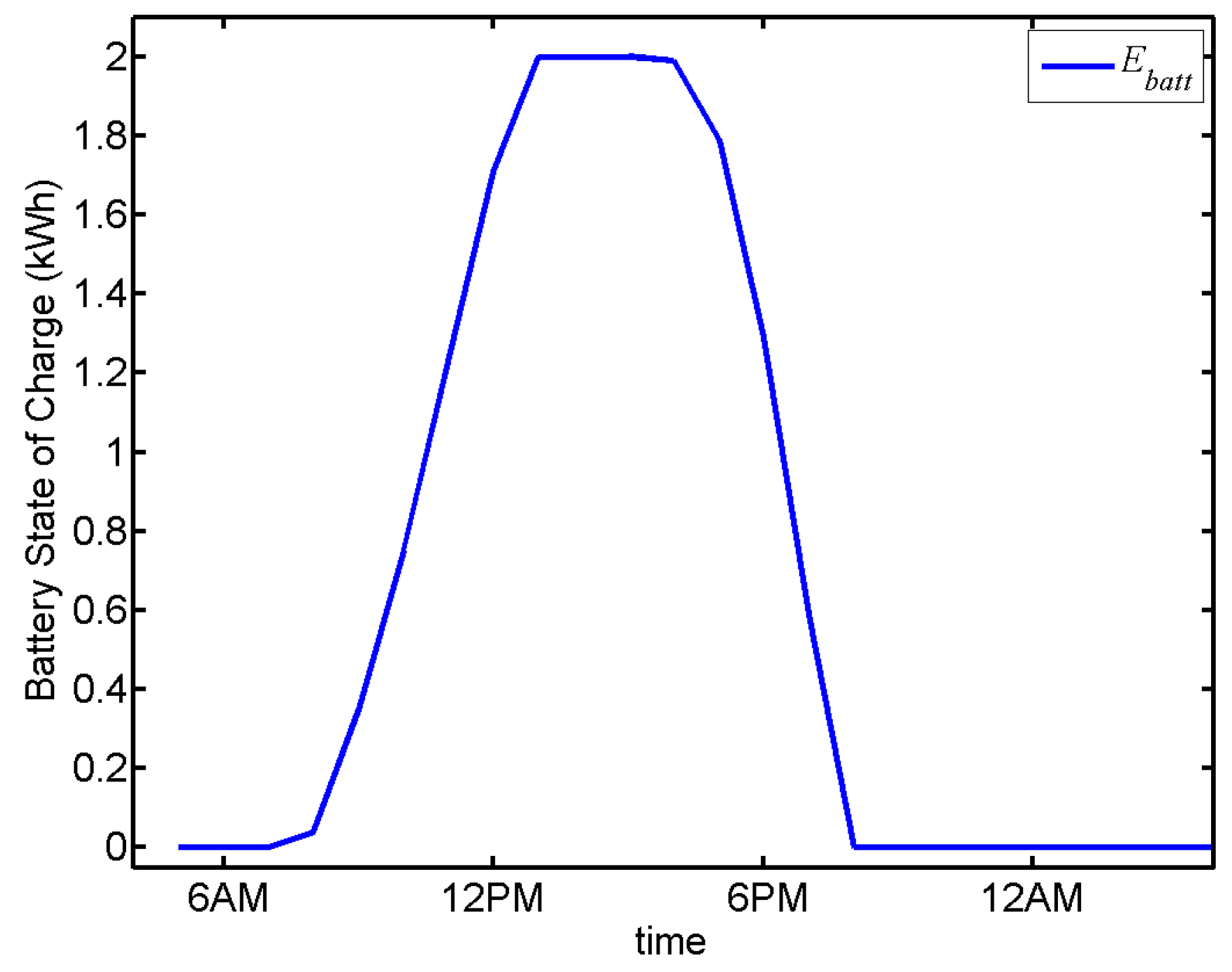
4.2. Power Flow System
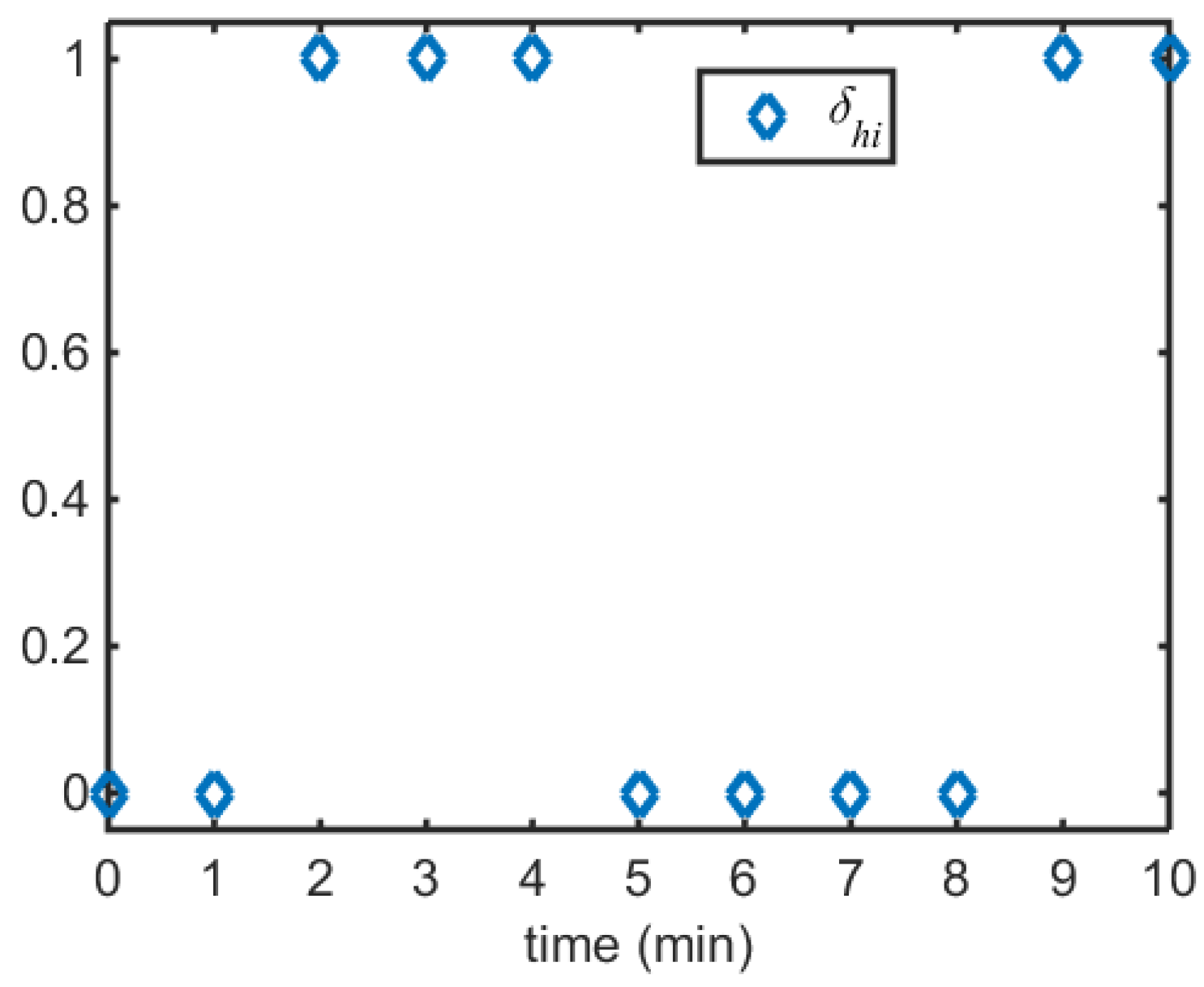
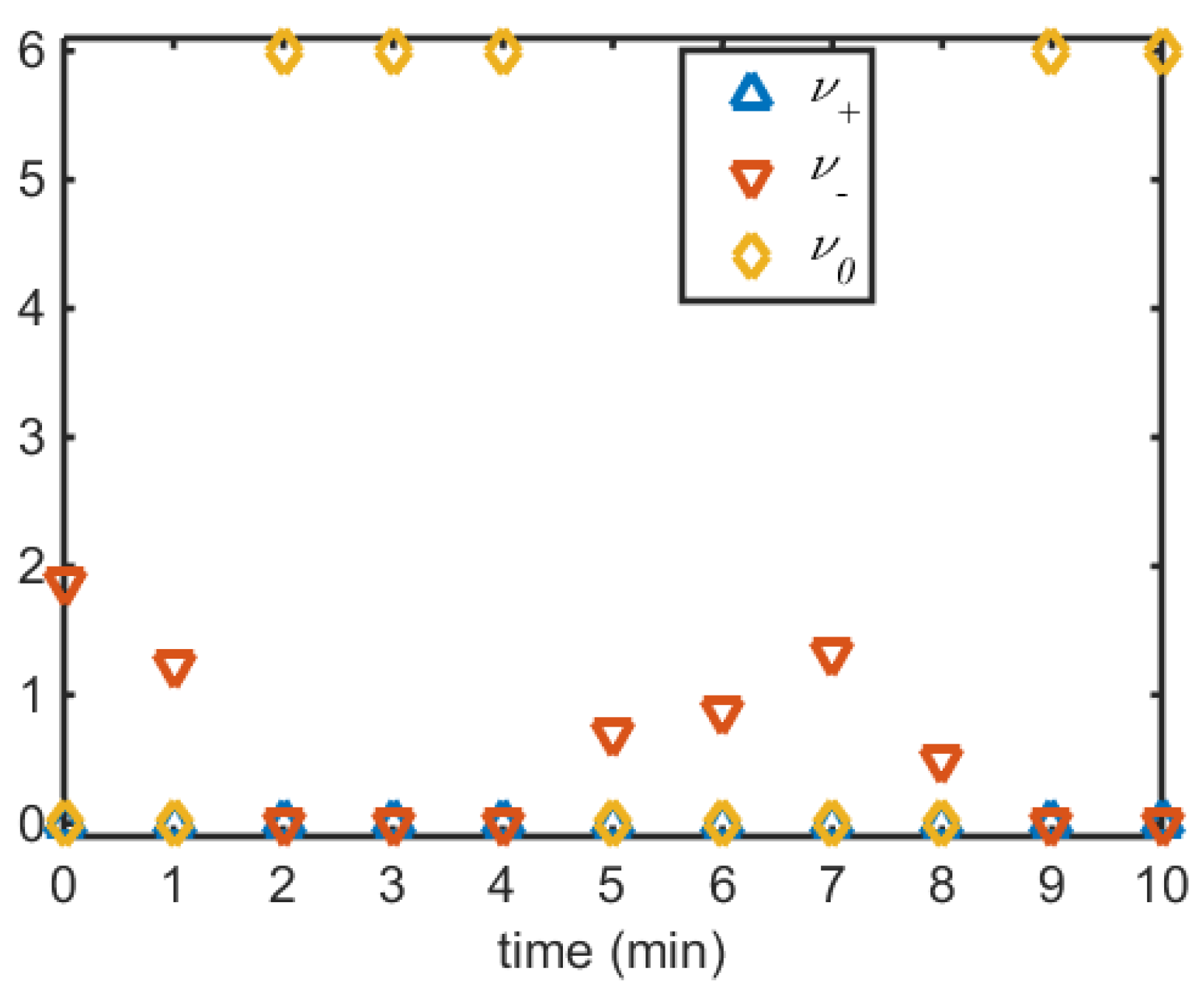
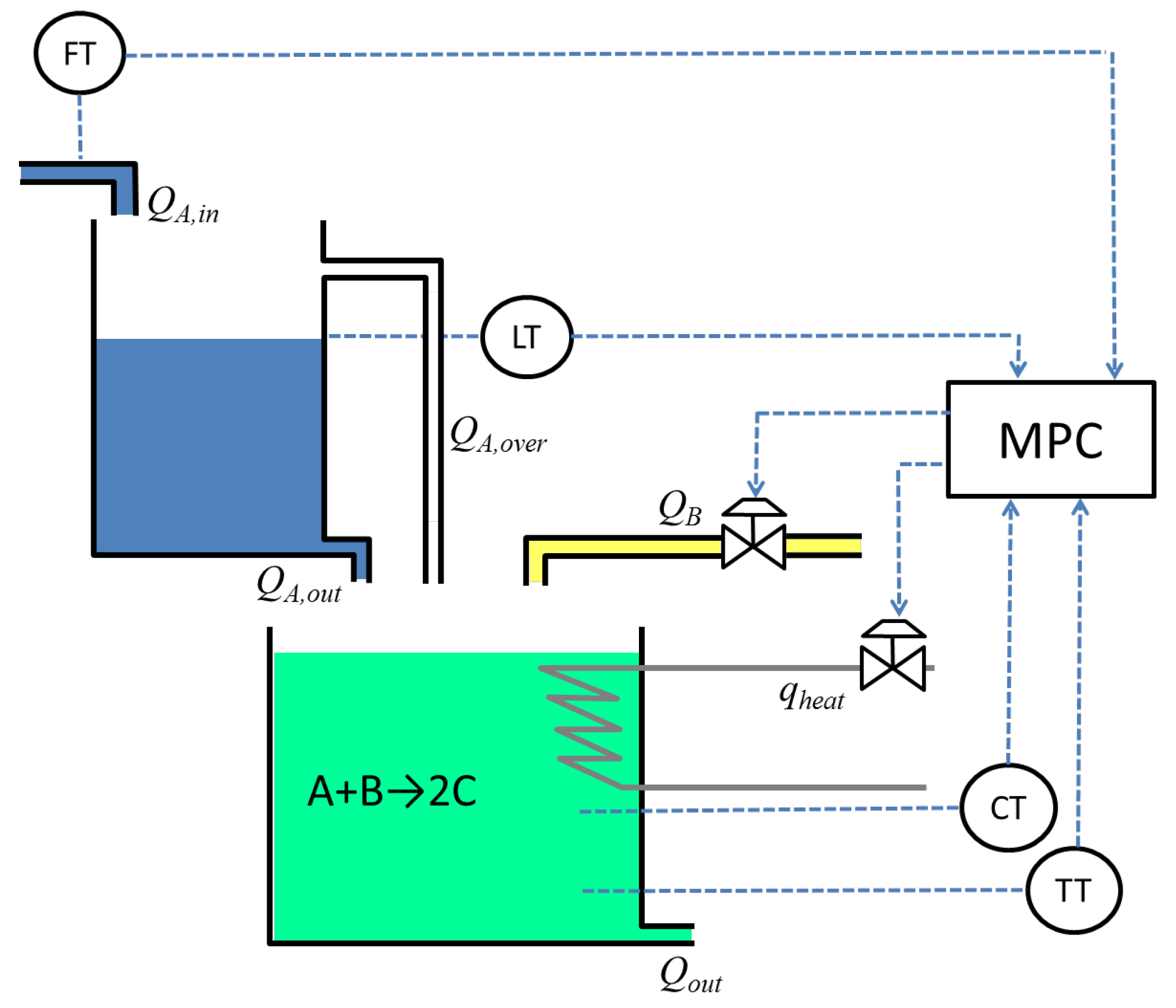
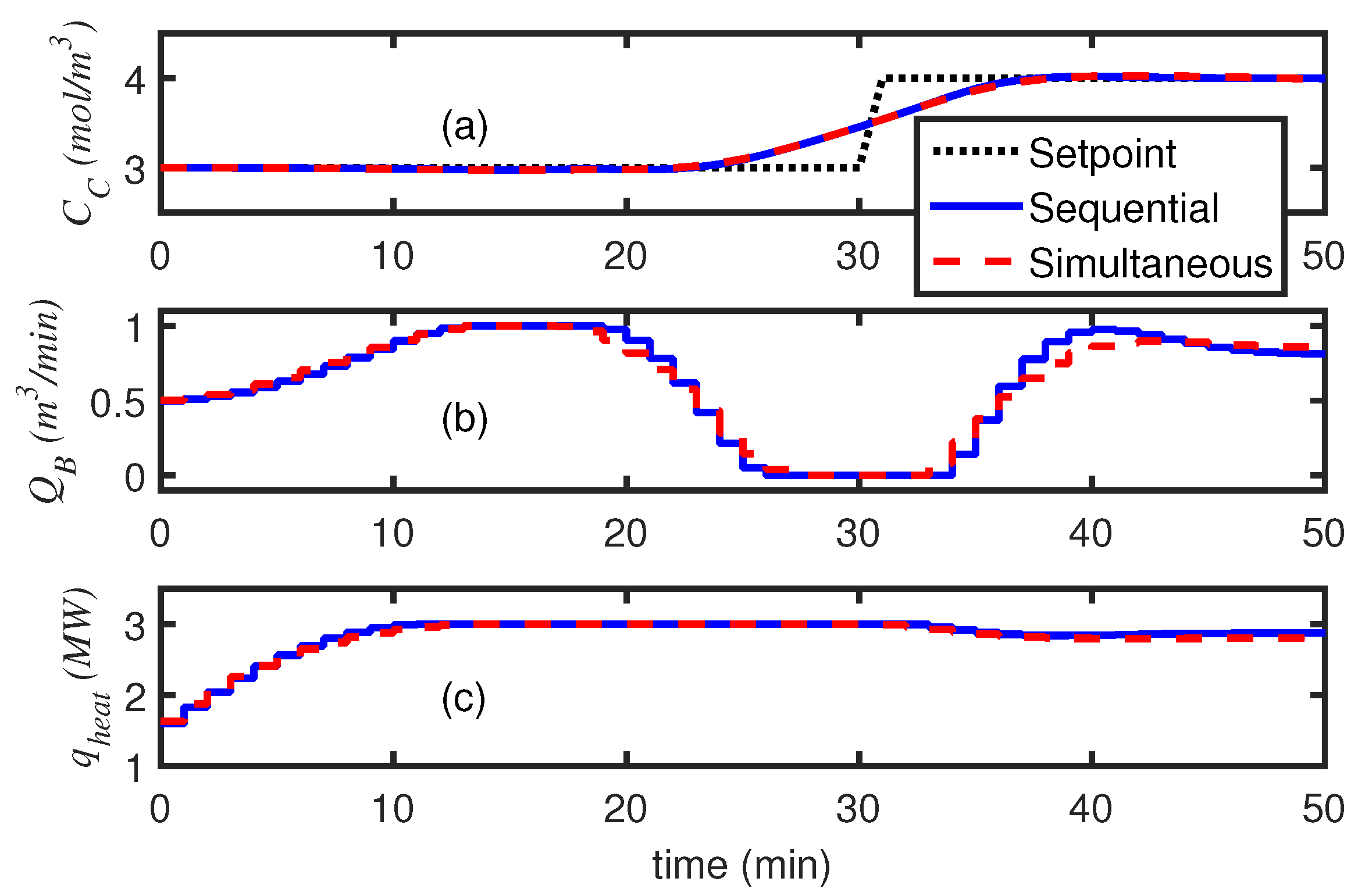
5. Continuous Logic in an NMPC Problem
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Trespalacios, F.; Grossmann, I.E. Algorithmic Approach for Improved Mixed-Integer Reformulations of Convex Generalized Disjunctive Programs. INFORMS J. Comput. 2015, 27, 59–74. [Google Scholar] [CrossRef]
- Movahedian, N.; Nobakhtian, S. Necessary and sufficient conditions for nonsmooth mathematical programs with equilibrium constraints. Nonlinear Anal. Theory Methods Appl. 2010, 72, 2694–2705. [Google Scholar] [CrossRef]
- Yin, H.; Ding, F.; Zhang, J. Active set algorithm for mathematical programs with linear complementarity constraints. Appl. Math. Comput. 2011, 217, 8291–8302. [Google Scholar] [CrossRef]
- Tangaramvong, S.; Tin-Loi, F. An FE-MPEC approach for limit load evaluation in the presence of contact and displacement constraints. Int. J. Solids Struct. 2012, 49, 1753–1763. [Google Scholar] [CrossRef]
- Tangaramvong, S.; Tin-Loi, F.; Senjuntichai, T. An MPEC approach for the critical post-collapse behavior of rigid-plastic structures. Int. J. Solids Struct. 2011, 48, 2732–2742. [Google Scholar] [CrossRef]
- Baumrucker, B.; Renfro, J.; Biegler, L.T. MPEC problem formulations and solution strategies with chemical engineering applications. Comput. Chem. Eng. 2008, 32, 2903–2913. [Google Scholar] [CrossRef]
- Raghunathan, A.U.; Biegler, L.T. Mathematical programs with equilibrium constraints (MPECs) in process engineering. Comput. Chem. Eng. 2003, 27, 1381–1392. [Google Scholar] [CrossRef]
- Raghunathan, A.U.; Diaz, M.S.; Biegler, L.T. An MPEC formulation for dynamic optimization of distillation operations. Comput. Chem. Eng. 2004, 28, 2037–2052. [Google Scholar] [CrossRef]
- Zhou, L.; Liao, Z.; Wang, J.; Jiang, B.; Yang, Y.; Du, W. Energy configuration and operation optimization of refinery fuel gas networks. Appl. Energy 2015, 139, 365–375. [Google Scholar] [CrossRef]
- Gabriel, S.A.; Leuthold, F.U. Solving discretely-constrained MPEC problems with applications in electric power markets. Energy Econ. 2010, 32, 3–14. [Google Scholar] [CrossRef]
- Chen, Y.H.H.; Paltsev, S.; Reilly, J.M.; Morris, J.F.; Babiker, M.H. Long-term economic modeling for climate change assessment. Econ. Model. 2016, 52, 867–883. [Google Scholar] [CrossRef]
- Walpen, J.; Mancinelli, E.; Lotito, P. A heuristic for the OD matrix adjustment problem in a congested transport network. Eur. J. Oper. Res. 2015, 242, 807–819. [Google Scholar] [CrossRef]
- Kovacevic, R.; Pflug, G. Electricity swing option pricing by stochastic bilevel optimization: A survey and new approaches. Eur. J. Oper. Res. 2014, 237, 389–403. [Google Scholar] [CrossRef]
- Júdice, J. Optimization with linear complementarity constraints. Pesquisa Oper. 2014, 34, 559–584. [Google Scholar] [CrossRef]
- Baumrucker, B.; Biegler, L. MPEC strategies for optimization of a class of hybrid dynamic systems. J. Process Control 2009, 19, 1248–1256. [Google Scholar] [CrossRef]
- Baumrucker, B.; Biegler, L.T. MPEC strategies for cost optimization of pipeline operations. Comput. Chem. Eng. 2010, 34, 900–913. [Google Scholar] [CrossRef]
- Hedengren, J.D. MPEC: Mathematical Programs with Equilibrium Constraints. Available online: http://apmonitor.com/wiki/index.php/Apps/MpecExamples (Accessed on 31 December 2015).
- Björkqvist, J.; Westerlund, T. Automated reformulation of disjunctive constraints in MINLP optimization. Comput. Chem. Eng. 1999, 23, S11–S14. [Google Scholar] [CrossRef]
- Grossmann, I.E. Review of nonlinear mixed-integer and disjunctive programming techniques. Optim. Eng. 2002, 3, 227–252. [Google Scholar] [CrossRef]
- Belotti, P.; Kirches, C.; Leyffer, S.; Linderoth, J.; Luedtke, J.; Mahajan, A. Mixed-integer nonlinear optimization. Acta Numer. 2013, 22, 1–131. [Google Scholar] [CrossRef]
- Grossmann, I.E.; Türkay, M. Solution of algebraic systems of disjunctive equations. Comput. Chem. Eng. 1996, 20, S339–S344. [Google Scholar] [CrossRef]
- Liu, G.; Zhang, J. A new branch and bound algorithm for solving quadratic programs with linear complementarity constraints. J. Comput. Appl. Math. 2002, 146, 77–87. [Google Scholar] [CrossRef]
- Sawaya, N.W.; Grossmann, I.E. A cutting plane method for solving linear generalized disjunctive programming problems. Comput. Chem. Eng. 2005, 29, 1891–1913. [Google Scholar] [CrossRef]
- Andreani, R.; Júdice, J.J.; Martínez, J.M.; Martini, T. Feasibility Problems with Complementarity Contraints. Eur. J. Oper. Res. 2016, 249, 41–54. [Google Scholar] [CrossRef]
- Biegler, L.T. An overview of simultaneous strategies for dynamic optimization. Chem. Eng. Process.: Process Int. 2007, 46, 1043–1053. [Google Scholar] [CrossRef]
- Diehl, M.; Ferreau, H.J.; Haverbeke, N. Nonlinear Model Predictive Control: Towards New Challenging Applications; Springer Berlin Heidelberg: Berlin, Heidelberg, Germany, 2009; Chapter Efficient Numerical Methods for Nonlinear MPC and Moving Horizon Estimation; pp. 391–417. [Google Scholar]
- Bertsekas, D.P. Dynamic Programming and Suboptimal Control: A Survey from ADP to MPC. Eur. J. Control 2005, 11, 310–334. [Google Scholar] [CrossRef]
- Su, J.; Renaud, J. Automatic Differentiation in Robust Optimization. AIAA J. 1997, 35, 1072–1079. [Google Scholar] [CrossRef]
- Tanartkit, P.; Biegler, L.T. Stable decomposition for dynamic optimization. Ind. Eng. Chem. Res. 1995, 34, 1253–1266. [Google Scholar] [CrossRef]
- Hedengren, J.D.; Allsford, K.V.; Ramlal, J. Moving horizon estimation and control for an industrial gas phase polymerization reactor. In Proceedings of the IEEE American Control Conference (ACC’07), Marriott Marquis Hotel at Times Square, New York City, NY, USA, 11–13 July 2007; pp. 1353–1358.
- Leibman, M.; Edgar, T.; Lasdon, L. Efficient data reconciliation and estimation for dynamic processes using nonlinear programming techniques. Comput. Chem. Eng. 1992, 16, 963–986. [Google Scholar] [CrossRef]
- Spivey, B.J.; Hedengren, J.D.; Edgar, T.F. Constrained nonlinear estimation for industrial process fouling. Ind. Eng. Chem. Res. 2010, 49, 7824–7831. [Google Scholar] [CrossRef]
- Carey, G.; Finlayson, B.A. Orthogonal collocation on finite elements. Chem. Eng. Sci. 1975, 30, 587–596. [Google Scholar] [CrossRef]
- Finlayson, B.A. Orthogonal collocation on finite elements-progress and potential. Math. Comput. Simul. 1980, 22, 11–17. [Google Scholar] [CrossRef]
- Bequette, B.W. Nonlinear control of chemical processes: A review. Ind. Eng. Chem. Res. 1991, 30, 1391–1413. [Google Scholar] [CrossRef]
- Zavala, V.M. Computational Strategies for the Optimal Operation of Large-Scale Chemical Processes. PhD dissertation, Carnegie Mellon University, 2008. [Google Scholar]
- Biegler, L.T.; Cervantes, A.M.; Wächter, A. Advances in simultaneous strategies for dynamic process optimization. Chem. Eng. Sci. 2002, 57, 575–593. [Google Scholar] [CrossRef]
- Hughes, T.J.; Reali, A.; Sangalli, G. Efficient quadrature for NURBS-based isogeometric analysis. Comput. Methods Appl. Mech. Eng. 2010, 199, 301–313. [Google Scholar] [CrossRef]
- Safdarnejad, S.M.; Hedengren, J.D.; Lewis, N.R.; Haseltine, E.L. Initialization strategies for optimization of dynamic systems. Comput. Chem. Eng. 2015, 78, 39–50. [Google Scholar] [CrossRef]
- Hedengren, J.D.; Shishavan, R.A.; Powell, K.M.; Edgar, T.F. Nonlinear modeling, estimation and predictive control in APMonitor. Comput. Chem. Eng. 2014, 70, 133–148. [Google Scholar] [CrossRef]
- Spivey, B.; Hedengren, J.; Edgar, T. Constrained Control and Optimization of Tubular Solid Oxide Fuel Cells for Extending Cell Lifetime. In Proceedings of the American Control Conference (ACC’12), Fairmont Queen Elizabeth Hotel, Montreal, QC, Canada, 27–29 June 2012; pp. 1356–1361.
- Jacobsen, L.; Spivey, B.; Hedengren, J. Model Predictive Control with a Rigorous Model of a Solid Oxide Fuel Cell. In Proceedings of the American Control Conference (ACC’13), Renaissance Downtown Hotel, Washington, DC, USA, 17–19 June 2013; pp. 3747–3752.
- Hedengren, J. APMonitor Modeling Language for Mixed-Integer Differential Algebraic Systems. In Proceedings of the Computing Society Session on Optimization Modeling Software: Design and Applications, INFORMS National Meeting, Phoenix Convention Center, Phoenix, AZ, USA, 14–17 October 2012.
- Hedengren, J.D.; Eaton, A.N. Overview of Estimation Methods for Industrial Dynamic Systems. Optim. Eng. 2015. [Google Scholar] [CrossRef]
- Hedengren, J.; Mojica, J.; Cole, W.; Edgar, T. APOPT: MINLP Solver for Differential and Algebraic Systems with Benchmark Testing. In Proceedings of the INFORMS National Meeting, Phoenix Convention Center, Phoenix, AZ, USA, 14–17 October 2012.
- Wächter, A.; Biegler, L.T. On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming. Math. Program. 2006, 106, 25–57. [Google Scholar] [CrossRef]
- Powell, K.M.; Sriprasad, A.; Cole, W.J.; Edgar, T.F. Heating, cooling, and electrical load forecasting for a large-scale district energy system. Energy 2014, 74, 877–885. [Google Scholar] [CrossRef]
- Powell, K.M.; Cole, W.J.; Ekarika, U.F.; Edgar, T.F. Optimal chiller loading in a district cooling system with thermal energy storage. Energy 2013, 50, 445–453. [Google Scholar] [CrossRef]
- Powell, K.M.; Edgar, T.F. Modeling and control of a solar thermal power plant with thermal energy storage. Chem. Eng. Sci. 2012, 71, 138–145. [Google Scholar] [CrossRef]
- Cole, W.J.; Powell, K.M.; Edgar, T.F. Optimization and advanced control of thermal energy storage systems. Energy Build. 2012, 28, 81–99. [Google Scholar] [CrossRef]
- Powell, K.; Hedengren, J.; Edgar, T. Dynamic Optimization of a Solar Thermal Energy Storage System over a 24 Hour Period using Weather Forecasts. In Proceedings of the American Control Conference (ACC’13), Renaissance Downtown Hotel, Washington, DC, USA, 17–19 June 2013; pp. 2952–2957.
- Powell, K.M.; Hedengren, J.D.; Edgar, T.F. Dynamic optimization of a hybrid solar thermal and fossil fuel system. Solar Energy 2014, 108, 210–218. [Google Scholar] [CrossRef]
- MATLAB. Version 8.5.0 (R2015a), The MathWorks Inc.: Natick, MA, USA, 2015.
- Lewis, N.R.; Hedengren, J.D.; Haseltine, E.L. Hybrid Dynamic Optimization Methods for Systems Biology with Efficient Sensitivities. Processes 2015, 3, 701–729. [Google Scholar] [CrossRef]



© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Powell, K.M.; Eaton, A.N.; Hedengren, J.D.; Edgar, T.F. A Continuous Formulation for Logical Decisions in Differential Algebraic Systems using Mathematical Programs with Complementarity Constraints. Processes 2016, 4, 7. https://doi.org/10.3390/pr4010007
Powell KM, Eaton AN, Hedengren JD, Edgar TF. A Continuous Formulation for Logical Decisions in Differential Algebraic Systems using Mathematical Programs with Complementarity Constraints. Processes. 2016; 4(1):7. https://doi.org/10.3390/pr4010007
Chicago/Turabian StylePowell, Kody M., Ammon N. Eaton, John D. Hedengren, and Thomas F. Edgar. 2016. "A Continuous Formulation for Logical Decisions in Differential Algebraic Systems using Mathematical Programs with Complementarity Constraints" Processes 4, no. 1: 7. https://doi.org/10.3390/pr4010007
APA StylePowell, K. M., Eaton, A. N., Hedengren, J. D., & Edgar, T. F. (2016). A Continuous Formulation for Logical Decisions in Differential Algebraic Systems using Mathematical Programs with Complementarity Constraints. Processes, 4(1), 7. https://doi.org/10.3390/pr4010007








