Dynamic Optimization in JModelica.org †
Abstract
:1. Introduction
2. Dynamic Optimization
2.1. Problem Formulation
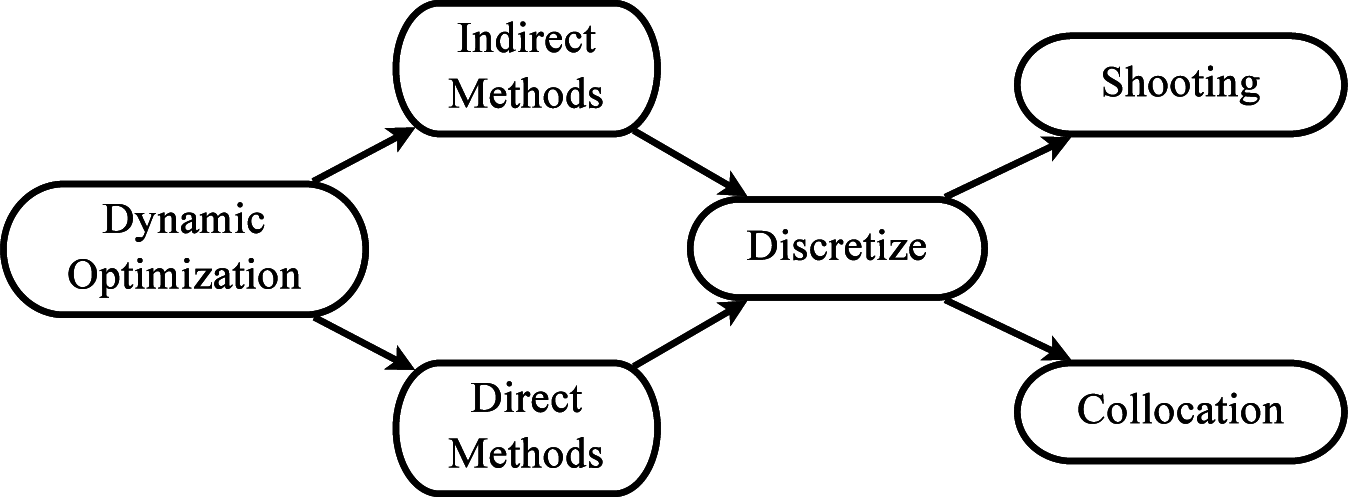
2.2. Numerical Methods
3. Related Software and Languages
3.1. Tools for Dynamic Optimization
3.2. Modelica and Optimica
3.3. Software Used to Implement Framework
3.3.1. CasADi
3.3.2. The JModelica.org Compiler
3.3.3. Nonlinear Programming and Linear Solvers
4. Direct Local Collocation
4.1. Collocation Polynomials
4.2. Transcription of the Dynamic Optimization Problem
5. Practical Aspects and Additional Features
5.1. Initialization
5.2. Problem Scaling
Time-Invariant Linear Scaling
Time-Invariant Affine Scaling
Time-Variant Linear Scaling
5.3. Discretization Verification
5.4. Control Discretization
5.5. Algorithmic Differentiation Graphs
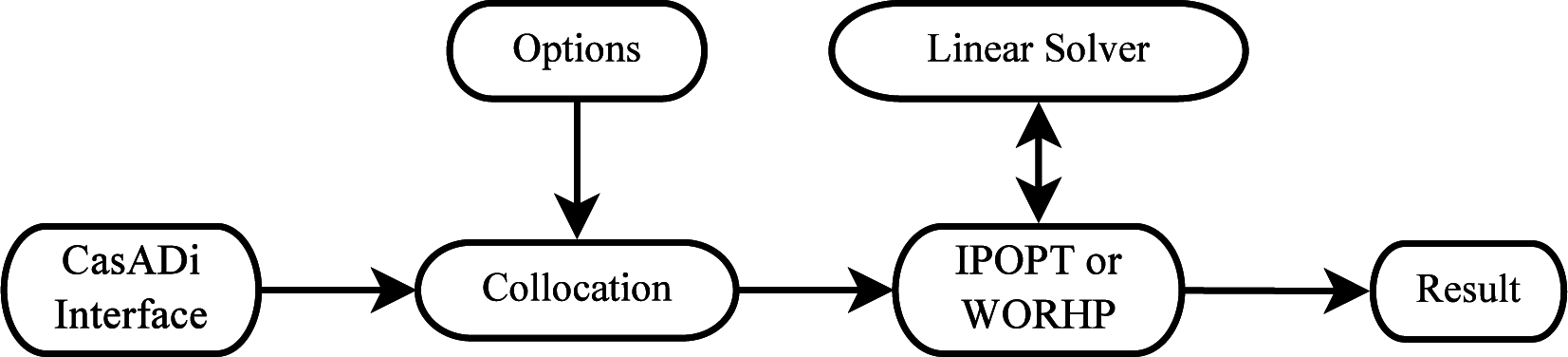
6. Implementation
7. Examples
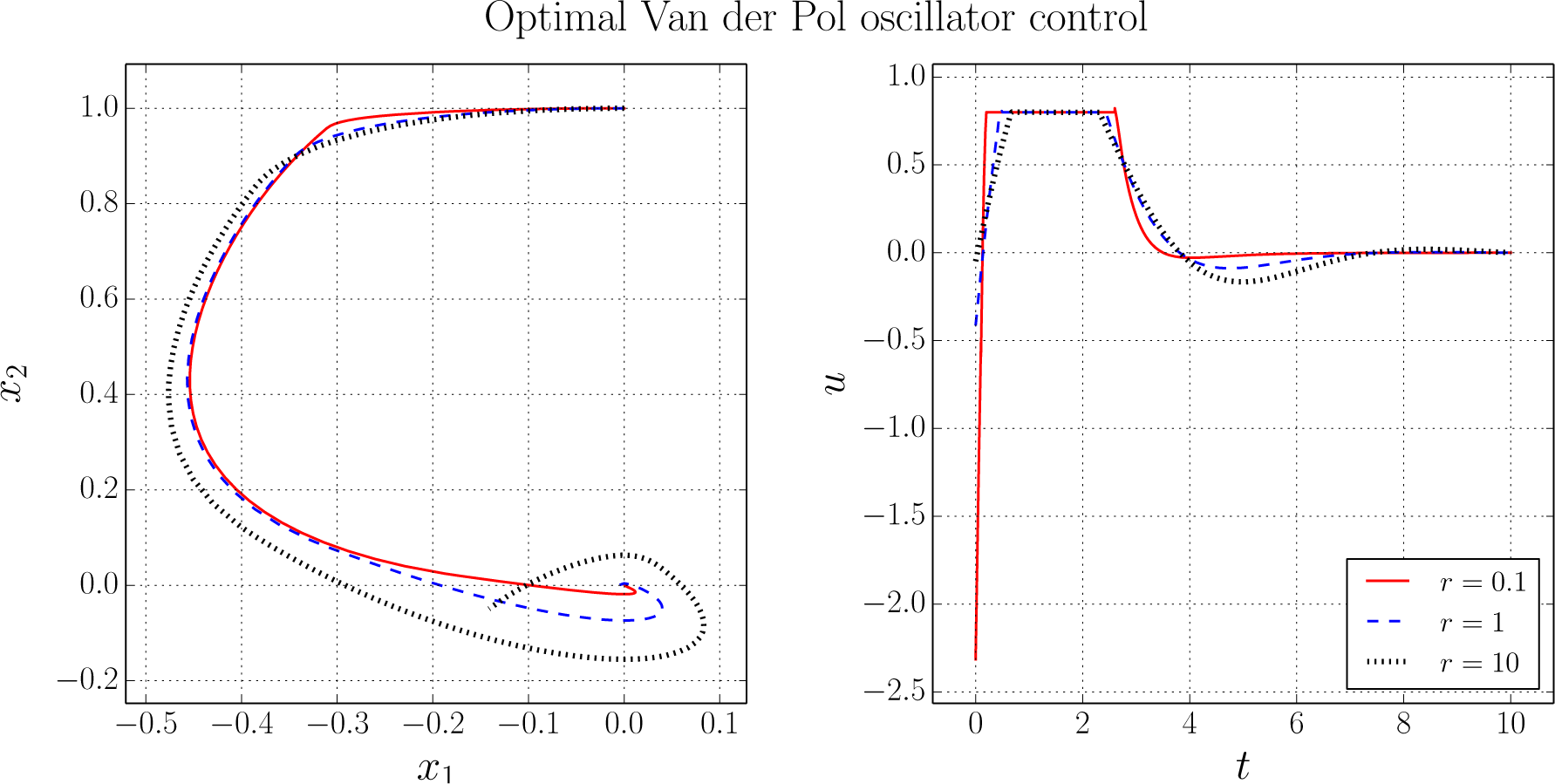
7.1. Van der Pol Oscillator


7.2. Distillation Column
8. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Sällberg, E.; Lind, A.; Velut, S.; Åkesson, J.; Gallardo Yances, S.; Link, K. Start-Up Optimization of a Combined Cycle Power Plant, Proceedings of the 9th International Modelica Conference, Munich, Germany, 3–5 September 2012.
- Prata, A.; Oldenburg, J.; Kroll, A.; Marquardt, W. Integrated scheduling and dynamic optimization of grade transitions for a continuous polymerization reactor. Comput. Chem. Eng. 2008, 32, 463–476. [Google Scholar]
- Ilzhoefer, A.; Houska, B.; Diehl, M. Nonlinear MPC of kites under varying wind conditions for a new class of large-scale wind power generators. Int. J. Robust Nonlinear Control 2007, 17, 1590–1599. [Google Scholar]
- Zavala, V.M. Inference of building occupancy signals using moving horizon estimation and Fourier regularization. J. Proc. Cont. 2014, 24, 714–722. [Google Scholar]
- Allgöwer, F.; Badgwell, T.A.; Qin, J.S.; Rawlings, J.B.; Wright, S.J. Nonlinear Predictive Control and Moving Horizon Estimation—An Introductory Overview. In Advances in Control: Highlights of ECC ’99; Frank, P.M., Ed.; Springer: Berlin, Germany, 1999; pp. 391–449. [Google Scholar]
- Åkesson, J.; Årzén, K.E.; Gäfvert, M.; Bergdahl, T.; Tummescheit, H. Modeling and optimization with Optimica and JModelica.org—Languages and tools for solving large-scale dynamic optimization problems. Comput. Chem. Eng. 2010, 34, 1737–1749. [Google Scholar]
- JModelica.org User Guide. Available online: http://www.jmodelica.org/page/236 accessed on 16 June 2015.
- Fritzson, P. Principles of Object-Oriented Modeling and Simulation with Modelica 2.1; Wiley-IEEE Press: Piscataway, NJ, USA, 2004. [Google Scholar]
- Åkesson,, J. Optimica—An Extension of Modelica Supporting Dynamic Optimization, Proceedings of the 6th International Modelica Conference, Bielefeld, Germany, 3–4 March 2008.
- Wächter, A.; Biegler, L.T. On the implementation of a primal-dual interior point filter line search algorithm for large-scale nonlinear programming. Math. Program. 2006, 106, 25–57. [Google Scholar]
- Büskens, C.; Wassel, D. The ESA NLP Solver WORHP. In Modeling and Optimization in Space Engineering; Fasano, G., Pintér, J.D., Eds.; Springer: New York, NY, USA, 2013; Volume 73, pp. 85–110. [Google Scholar]
- Liberzon, D. Calculus of Variations and Optimal Control Theory: A Concise Introduction; Princeton University Press: Princeton, NJ, USA, 2012. [Google Scholar]
- Betts, J.T. Practical Methods for Optimal Control and Estimation Using Nonlinear Programming, 2nd ed; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2010. [Google Scholar]
- Bertsekas, D.P. Dynamic Programming and Optimal Control, 3rd ed; Athena Scientific: Belmont, MA, USA, 2005; Volume 1. [Google Scholar]
- Betts, J.T. Survey of numerical methods for trajectory optimization. J. Guid. Contr. Dynam. 1998, 21, 193–207. [Google Scholar]
- Rao, A.V. A Survey of Numerical Methods for Optimal Control, Proceedings of the 2009 AAS/AIAA Astrodynamics Specialists Conference, Pittsburgh, PA, USA, 9–13 August 2009.
- Fourer, R.; Gay, D.M.; Kernighan, B.W. AMPL: A Modeling Language for Mathematical Programming; Duxbury Press Brooks Cole Publishing: Pacific Grove, CA, USA, 2003. [Google Scholar]
- Brooke, A.; Kendrick, D.A.; Meeraus, A.; Rosenthal, R.E. GAMS: A User’s Guide; Scientific Press: Redwood City, CA, USA, 1988. [Google Scholar]
- Hart, W.E.; Laird, C.; Watson, J.P.; Woodruff, D.L. Pyomo – Optimization Modeling in Python; Springer: Berlin, Germany, 2012. [Google Scholar]
- Houska, B.; Ferreau, H.J.; Diehl, M. ACADO toolkit—An open-source framework for automatic control and dynamic optimization. Optimal Control Appl. Methods 2011, 32, 298–312. [Google Scholar]
- Tomlab Optimization. PROPT. Available online: http://tomdyn.com accessed on 16 June 2015.
- Holmström, K. The TOMLAB Optimization Environment in Matlab. Adv. Model. Optim. 1999, 1, 47–69. [Google Scholar]
- Hedengren, J.D. APMonitor. Available online: http://apmonitor.com accessed on 16 June 2015.
- Process Systems Enterprise. gPROMS. Available online: http://www.psenterprise.com/gproms accessed on 16 June 2015.
- Bachmann, B.; Ochel, L.; Ruge, V.; Gebremedhin, M.; Fritzson, P.; Nezhadali, V.; Eriksson, L.; Sivertsson, M. Parallel Multiple-Shooting and Collocation Optimization with OpenModelica, Proceedings of the 9th International Modelica Conference, Munich, Germany, 3–5 September 2012.
- Pytlak, R.; Tarnawski, T.; Fajdek, B.; Stachura, M. Interactive dynamic optimization server—connecting one modelling language with many solvers. Optim. Methods Softw. 2014, 29, 1118–1138. [Google Scholar]
- ITEA. Model Driven Physical Systems Operation. Available online: https://itea3.org/project/modrio.html accessed on 16 June 2015.
- Andersson, J. A General-Purpose Software Framework for Dynamic Optimization. Ph.D. Thesis, KU Leuven, Leuven, Belgium, October 2013. [Google Scholar]
- Andersson, J.; Åkesson, J.; Casella, F.; Diehl, M. Integration of CasADi and JModelica.org, Proceedings of the 8th International Modelica Conference, Dresden, Germany, 20–22 March 2011.
- Magnusson, F.; Åkesson, J. Collocation Methods for Optimization in a Modelica Environment, Proceedings of the 9th International Modelica Conference, Munich, Germany, 3–5 September 2012.
- Åkesson, J.; Ekman, T.; Hedin, G. Implementation of a Modelica compiler using JastAdd attribute grammars. Sci. Comput. Program. 2010, 75, 21–38. [Google Scholar]
- Ekman, T.; Hedin, G. The JastAdd system—modular extensible compiler construction. Sci. Comput. Program. 2007, 69, 14–26. [Google Scholar]
- Mattsson, S.E.; Söderlind, G. Index Reduction in Differential-Algebraic Equations Using Dummy Derivatives. SIAM J. Sci. Comput. 1993, 14, 677–692. [Google Scholar]
- Lennernäs, B. A CasADi Based Toolchain for JModelica.org. M.Sc. Thesis, Lund University, Lund, Sweden, 2013. [Google Scholar]
- HSL. A collection of Fortran codes for large scale scientific computation. Available online: http://www.hsl.rl.ac.uk accessed on 16 June 2015.
- Biegler, L.T. Nonlinear Programming: Concepts, Algorithms, and Applications to Chemical Processes; Mathematical Optimization Society and the Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2010. [Google Scholar]
- Hairer, E.; Wanner, G. Solving Ordinary Differential Equations II: Stiff and Differential-Algebraic Problems, 2nd ed; Springer-Verlag: Berlin, Germany, 1996. [Google Scholar]
- Rodriguez, J.S. Large-scale dynamic optimization using code generation and parallel computing. M.Sc. Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2014. [Google Scholar]
- Magnusson, F. Collocation Methods in JModelica.org. M.Sc. Thesis, Lund University, Lund, Sweden, February 2012. [Google Scholar]
- Betts, J.T.; Huffman, W.P. Mesh refinement in direct transcription methods for optimal control. Optim. Control Appl. Methods 1998, 19, 1–21. [Google Scholar]
- Vasantharajan, S.; Biegler, L.T. Simultaneous strategies for optimization of differential-algebraic systems with enforcement of error criteria. Comput. Chem. Eng. 1990, 14, 1083–1100. [Google Scholar]
- JModelica.org source code. Available online: https://svn.jmodelica.org and in particular https://svn.jmodelica.org/trunk/Python/src/pyjmi/optimization/casadi_collocation.py?p=6606 accessed on 16 June 2015.
- Dassault Systèmes. Dymola. Available online: http://www.dymola.com accessed on 16 June 2015.
- Pfeiffer, A.; Bausch-Gall, I.; Otter, M. Proposal for a Standard Time Series File Format in HDF5, Proceedings of the 9th International Modelica Conference, Munich, Germany, 3–5 September 2012.
- Holmqvist, A.; Törndahl, T.; Magnusson, F.; Zimmermann, U.; Stenström, S. Dynamic parameter estimation of atomic layer deposition kinetics applied to in situ quartz crystal microbalance diagnostics. Chem. Eng. Sci. 2014, 111, 15–33. [Google Scholar]
- De Coninck, R.; Magnusson, F.; Åkesson, J.; Helsen, L. Grey-Box Building Models for Model Order Reduction and Control, Proceedings of the 10th International Modelica Conference, Lund, Sweden, 10–12 March 2014.
- Vande Cavey, M.; De Coninck, R.; Helsen, L. Setting Up a Framework for Model Predictive Control with Moving Horizon State Estimation Using JModelica, Proceedings of the 10th International Modelica Conference, Lund, Sweden, 10–12 March 2014.
- Larsson, P.O.; Casella, F.; Magnusson, F.; Andersson, J.; Diehl, M.; Akesson, J. A Framework for Nonlinear Model-Predictive Control Using Object-Oriented Modeling with a Case Study in Power Plant Start-Up, Proceedings of the 2013 IEEE Multi-Conference on Systems and Control, Hyderabad, India, 27–30 August 2013.
- Berntorp, K.; Olofsson, B.; Lundahl, K.; Nielsen, L. Models and methodology for optimal trajectory generation in safety-critical road-vehicle manoeuvres. Veh. Syst. Dyn. 2014, 52, 1304–1332. [Google Scholar]
- Hunter, J.D. Matplotlib: A 2D Graphics Environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar]
- Diehl, M. Real-Time Optimization for Large Scale Nonlinear Processes. Ph.D. Thesis, Heidelberg University, Heidelberg, Germany, July 2001. [Google Scholar]
- Hedengren, J.D. A Nonlinear Model Library for Dynamics and Control, 2008. Available online: http://www.hedengren.net/research/Publications/Cache_2008/NonlinearModelLibrary.pdf accessed on 16 June 2015.
- Magnusson, F.; Berntorp, K.; Olofsson, B.; Åkesson, J. Symbolic Transformations of Dynamic Optimization Problems, Proceedings of the 10th International Modelica Conference, Lund, Sweden, 10–12 March 2014.


© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Magnusson, F.; Åkesson, J. Dynamic Optimization in JModelica.org. Processes 2015, 3, 471-496. https://doi.org/10.3390/pr3020471
Magnusson F, Åkesson J. Dynamic Optimization in JModelica.org. Processes. 2015; 3(2):471-496. https://doi.org/10.3390/pr3020471
Chicago/Turabian StyleMagnusson, Fredrik, and Johan Åkesson. 2015. "Dynamic Optimization in JModelica.org" Processes 3, no. 2: 471-496. https://doi.org/10.3390/pr3020471




