Interpretation of Cellular Imaging and AQP4 Quantification Data in a Single Cell Simulator
Abstract
:1. Introduction
2. Method and Experimental Section
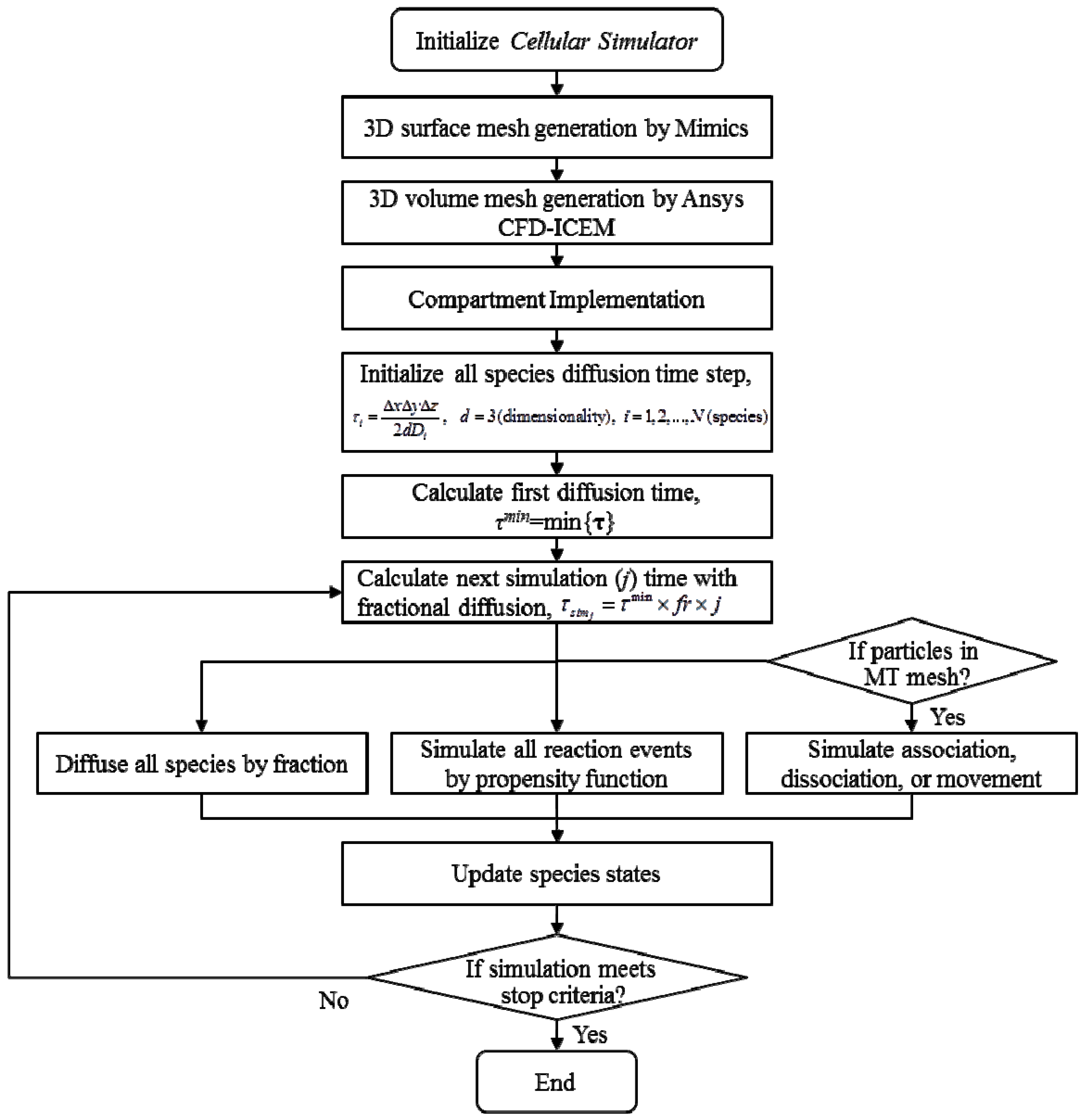
2.1. Prototype Cell Simulator
| Author, year | Cell simulator | Simulation event | Mathematical model | Transport on cytoskeleton | Natural cell structure | 3d Visualization | ||
|---|---|---|---|---|---|---|---|---|
| Diffusion | Reaction | Deterministic | Stochastic | |||||
| Kim, 2013 | This work | ■ | ■ | ■ | ■ | ■ | ■ | ■ |
| Loew, 2001 [23] | VCell | ■ | ■ | ■ | ■ | ■ | ■ | |
| Tomita, 1999 [24] | ECell | ■ | ■ | ■ | ||||
| Hattne, 2005 [21] | MesoRD | ■ | ■ | ■ | ■ | ■ | ||
| Raymond, 2003 [27] | JSim | ■ | ■ | |||||
| Ander, 2004 [28] | SmartCell | ■ | ■ | ■ | ■ | |||
| Stiles, 1996 [22] | MCell | ■ | ■ | ■ | ■ | ■ | ||
| Plimpton, 2003 [29] | ChemCell | ■ | ■ | ■ | ■ | ■ | ||
| Andrews, 2004 [30] | Smoldyn | ■ | ■ | ■ | ■ | |||
| Boulianne, 2008 [31] | GridCell | ■ | ■ | |||||
| Le Novère, 2001 [32] | StochSim | ■ | ■ | |||||
2.2. Geometry Reconstruction of the Astrocyte Model

2.3. Implementation of Cell Compartments

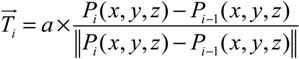
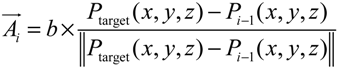
- Step 1. Select a starting mesh of MT growth (the MTOC) and a target mesh located at the endfoot.
- Step 2. Generate the first growth step with a random direction, with the length of the segment equal to the distance to the connecting mesh.
- Step 3. Grow a segment to the neighboring mesh adjusting its direction and length with the information of tangent vector and target vector (direction to the final destination).
- Step 4. Repeat step 3 until it encounters the boundary of the endfoot process.
- Step 5. If the growth does not encounter the boundary of an endfoot process, the growth will be terminated and a new MT growth will start from step 1. Otherwise, the MT segment grows into the process which contains a target mesh selected in step 1.
- Step 6. Grow a segment to the neighboring mesh adjusting its direction and length with the information of tangent vector, target vector, and distance to the normal surface.
- Step 7. Repeat step 6 until it comes into contact with the endfoot boundary.
- Step 8.Upon reaching a member of the mesh at the endfoot boundary, the smooth and shortest path finding algorithm will stop and finalize the trajectory to the target mesh selected in step 1.
- Step 9. The defined end criterion for the total number of MTs will terminate the algorithm.
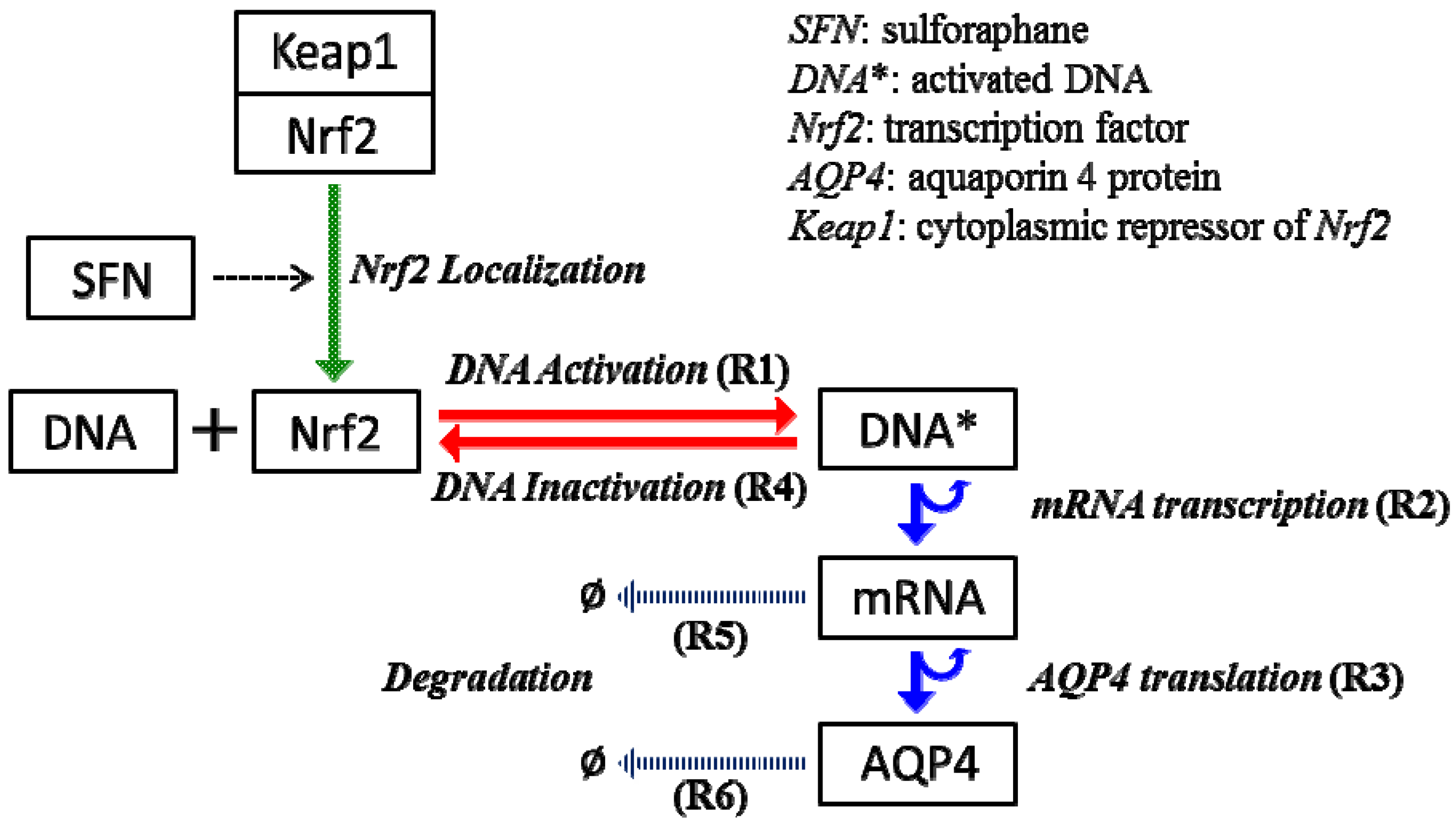
2.4. Stochastic Model and Simulation of Biochemical Kinetics and Transport
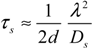
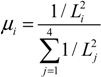
2.5. Comparison with Deterministic Kinetic Model
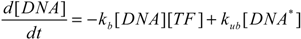
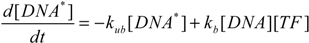
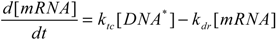
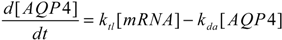
3. Results and Discussion
3.1. Kinetic Rates for the Steady State System
| Parameters | Values (s−1) |
|---|---|
| Transcription rate with no SFN treatment | 5.55 × 10−4 |
| Transcription rate with SFN treatment | 2.08 × 10−3 |
| Translation rate | 0.25 |
| Degradation rate of mRNA | 4.01 × 10−5 |
| Degradation rate of AQP4 | 8.02 × 10−6 |
3.2. Increased Transcription upon Sulforaphane Stimulation
3.3. Dynamic Behavior of the System
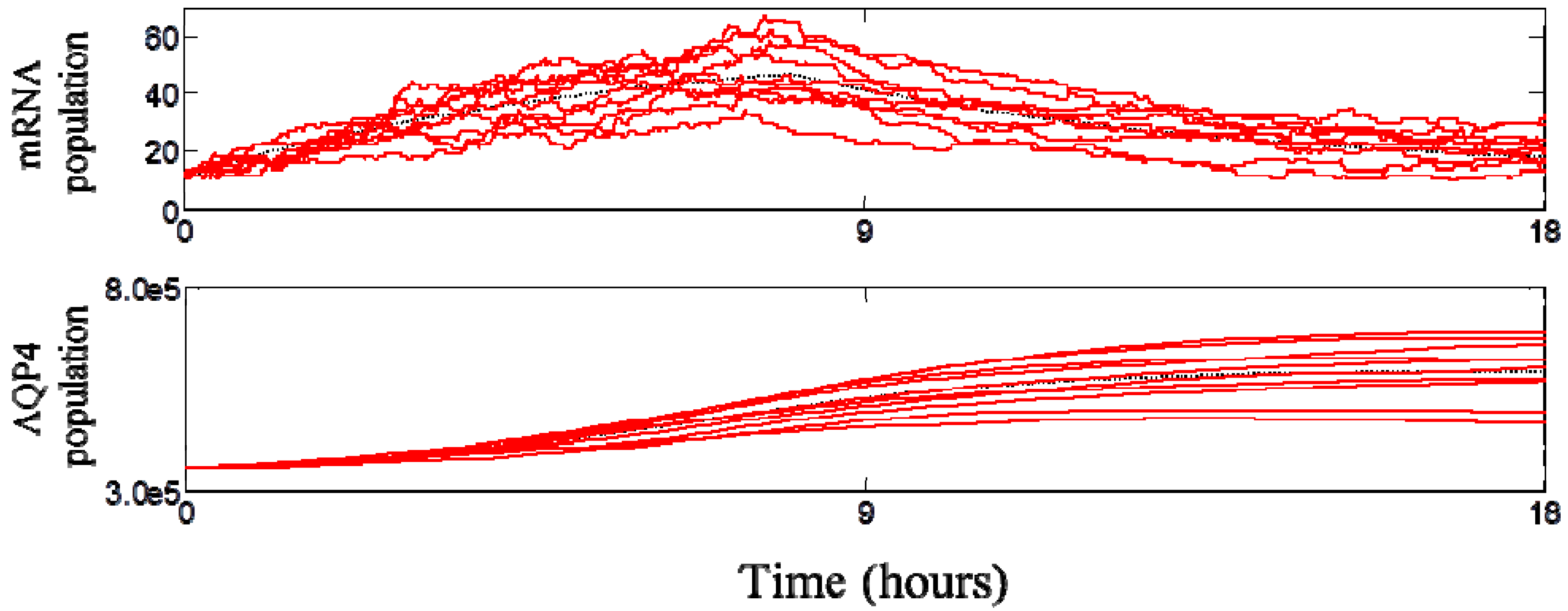
3.4. Spatial Translocation of Aquaporin 4
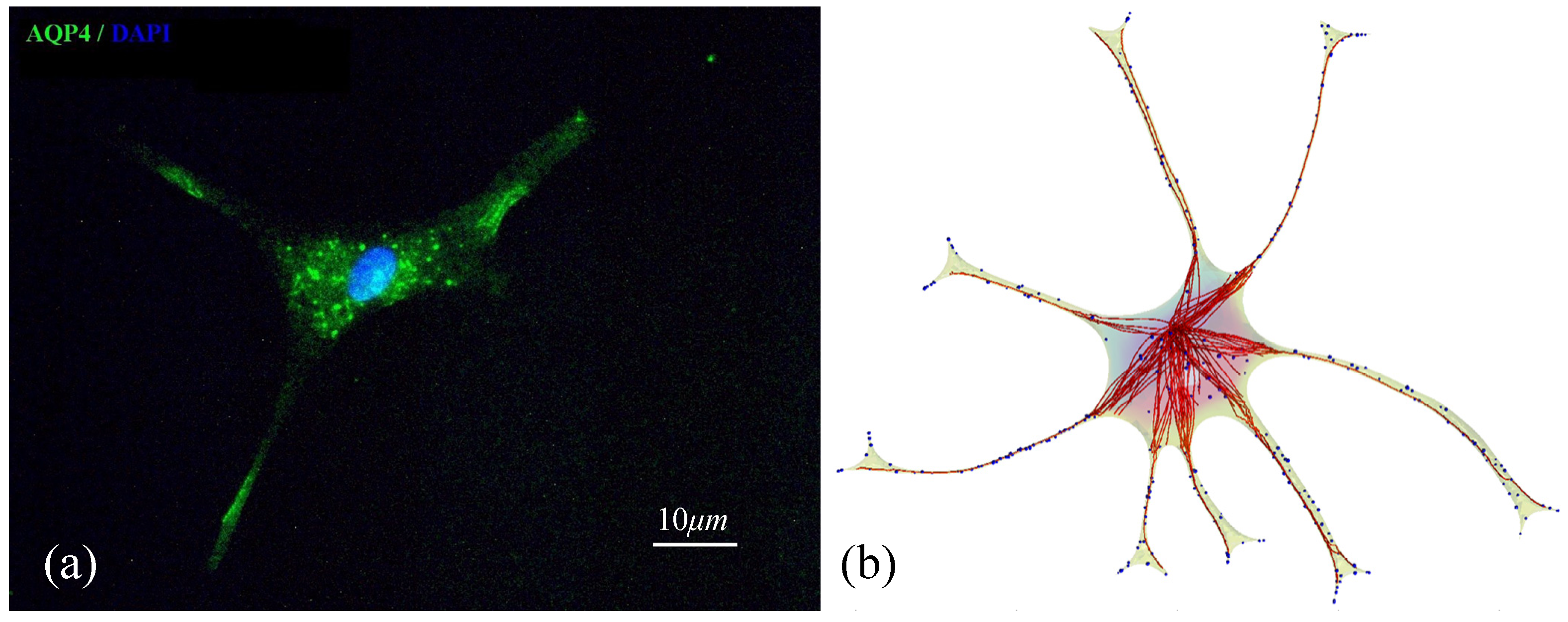
3.5. Validation of the Model
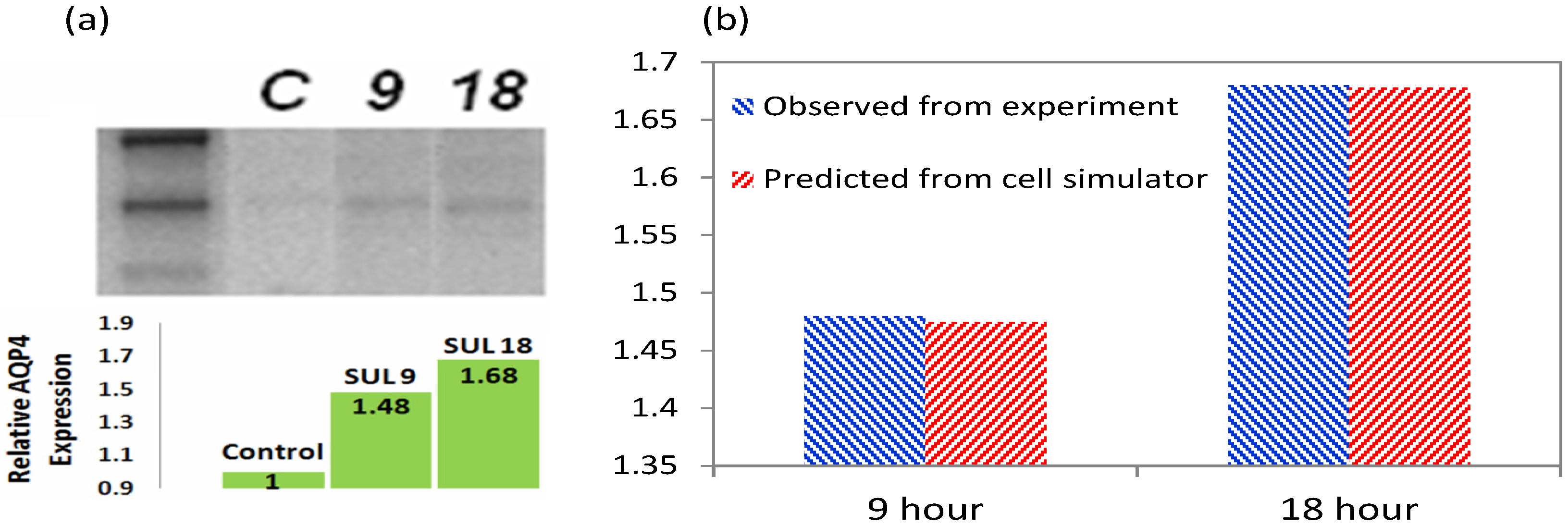
4. Conclusions
Nomenclature
| kb | DNA activation rate |
| kub | DNA inactivation rate |
| ktc | mRNA transcription rate |
| ktl | AQP4 translation rate |
| kdr | mRNA decay rate |
| kda | AQP4 decay rate |
| DNA* | activated DNA molecule |
Acknowledgments
Conflicts of Interest
Appendix
A. Nuclear Translocation of Nrf2
B. Quantification of AQP4 Expression
C. Determination of Diffusivity
References
- Wacker, I.; Kaether, C.; Kromer, A.; Migala, A.; Almers, W.; Gerdes, H.H. Microtubule-dependent transport of secretory vesicles visualized in real time with a GFP-tagged secretory protein. J. Cell Sci. 1997, 110, 1453–1463. [Google Scholar]
- Balla, T.; Varnai, P. Visualizing cellular phosphoinositide pools with GFP-fused protein-modules. Sci. STKE 2002, 2002, pl3. [Google Scholar]
- Cui, B.X.; Wu, C.B.; Chen, L.; Ramirez, A.; Bearer, E.L.; Li, W.P.; Mobley, W.C.; Chu, S. One at a time, live tracking of NGF axonal transport using quantum dots. Proc. Natl. Acad. Sci. USA 2007, 104, 13666–13671. [Google Scholar]
- Dahan, M.; Levi, S.; Luccardini, C.; Rostaing, P.; Riveau, B.; Triller, A. Diffusion dynamics of glycine receptors revealed by single-quantum dot tracking. Science 2003, 302, 442–445. [Google Scholar] [CrossRef]
- Howarth, M.; Takao, K.; Hayashi, Y.; Ting, A.Y. Targeting quantum dots to surface proteins in living cells with biotin ligase. Proc. Natl. Acad. Sci. USA 2005, 102, 7583–7588. [Google Scholar] [CrossRef]
- Courty, S.; Luccardini, C.; Bellaiche, Y.; Cappello, G.; Dahan, M. Tracking individual kinesin motors in living cells using single quantum-dot imaging. Nano Lett. 2006, 6, 1491–1495. [Google Scholar] [CrossRef]
- Seitz, A.; Surrey, T. Processive movement of single kinesins on crowded microtubules visualized using quantum dots. EMBO J. 2006, 25, 267–277. [Google Scholar] [CrossRef]
- Schwartz, A.L. Cell biology of intracellular protein trafficking. Annu. Rev. Immunol. 1990, 8, 195–229. [Google Scholar] [CrossRef]
- Klann, M. Development of a Stochastic Multi-scale Simulation Method for the Analysis of Spatiotemporal Dynamics in Cellular Transport and Signaling Processes. Ph.D. Thesis, University of Stuttgart, Stuttgart, Germany, 2011. [Google Scholar]
- Klann, M.T.; Lapin, A.; Reuss, M. Stochastic simulation of signal transduction: Impact of the cellular architecture on diffusion. Biophys. J. 2009, 96, 5122–5129. [Google Scholar] [CrossRef]
- Verkman, A.S. Aquaporins at a glance. J. Cell Sci. 2011, 124, 2107–2112. [Google Scholar] [CrossRef]
- Nielsen, S.; Nagelhus, E.A.; Amiry-Moghaddam, M.; Bourque, C.; Agre, P.; Ottersen, O.P. Specialized membrane domains for water transport in glial cells: High-resolution immunogold cytochemistry of aquaporin-4 in rat brain. J. Neurosci. 1997, 17, 171–180. [Google Scholar]
- Manley, G.T.; Fujimura, M.; Ma, T.; Noshita, N.; Filiz, F.; Bollen, A.W.; Chan, P.; Verkman, A.S. Aquaporin-4 deletion in mice reduces brain edema after acute water intoxication and ischemic stroke. Nat. Med. 2000, 6, 159–163. [Google Scholar] [CrossRef]
- Papadopoulos, M.C.; Manley, G.T.; Krishna, S.; Verkman, A.S. Aquaporin-4 facilitates reabsorption of excess fluid in vasogenic brain edema. FASEB. J. 2004, 18, 1291–1293. [Google Scholar]
- Zhao, H.D.; Zhang, F.; Shen, G.; Li, Y.B.; Li, Y.H.; Jing, H.R.; Ma, L.F.; Yao, J.H.; Tian, X.F. Sulforaphane protects liver injury induced by intestinal ischemia reperfusion through Nrf2-ARE pathway. World J. Gastroenterol. 2010, 16, 3002–3010. [Google Scholar] [CrossRef]
- Thimmulappa, R.K.; Mai, K.H.; Srisuma, S.; Kensler, T.W.; Yamamato, M.; Biswal, S. Identification of Nrf2-regulated genes induced by the chemopreventive agent sulforaphane by oligonucleotide microarray. Cancer Res. 2002, 62, 5196–5203. [Google Scholar]
- Kraft, A.D.; Johnson, D.A.; Johnson, J.A. Nuclear factor e2-related factor 2-dependent antioxidant response element activation by tert-butylhydroquinone and sulforaphane occurring preferentially in astrocytes conditions neurons against oxidative insult. J. Neurosci. 2004, 24, 1101–1112. [Google Scholar] [CrossRef]
- Zhao, J.; Moore, A.N.; Clifton, G.L.; Dash, P.K. Sulforaphane enhances aquaporin-4 expression and decreases cerebral edema following traumatic brain injury. J. Neurosci. Res. 2005, 82, 499–506. [Google Scholar]
- Umenishi, F.; Verkman, A.S. Isolation and functional analysis of alternative promoters in the human aquaporin-4 water channel gene. Genomics 1998, 50, 373–377. [Google Scholar] [CrossRef]
- Yenkie, K.M.; Diwekar, U.; Linninger, A.A.; Kim, S. A New Method for Parameter Estimation in Stochastic Differential Equations. In Proceedings of the AICHE Annual Meeting, San Fracisco, CA, USA, 3–8 November 2013; p. 589.
- Hattne, J.; Fange, D.; Elf, J. Stochastic reaction-diffusion simulation with mesoRD. Bioinformatics 2005, 21, 2923–2924. [Google Scholar] [CrossRef]
- Stiles, J.R.; Van Helden, D.; Bartol, T.M.; Salpeter, E.E.; Salpeter, M.M. Miniature endplate current rise times <100 mu s from improved dual recordings can be modeled with passive acetylcholine diffusion from a synaptic vesicle. Proc. Natl. Acad. Sci. USA 1996, 93, 5747–5752. [Google Scholar] [CrossRef]
- Loew, L.M.; Schaff, J.C. The virtual cell: A software environment for computational cell biology. Trends Biotechnol. 2001, 19, 401–406. [Google Scholar] [CrossRef]
- Tomita, M.; Hashimoto, K.; Takahashi, K.; Shimizu, T.S.; Matsuzaki, Y.; Miyoshi, F.; Saito, K.; Tanida, S.; Yugi, K.; Venter, J.C.; et al. E-cell: Software environment for whole-cell simulation. Bioinformatics 1999, 15, 72–84. [Google Scholar] [CrossRef]
- Birbaumer, M.; Schweitzer, F. Agent-based modeling of intracellular transport. Eur. Phys. J. B 2011, 82, 245–255. [Google Scholar] [CrossRef]
- De Heras Ciechomski, P.; Klann, M.; Mange, R.; Koeppl, H. From Biochemical Reaction Networks to 3D Dynamics in the Cell: The Zigcell3d Modeling, Simulation and Visualisation Framework. In Proceedings of the 2013 IEEE Symposium on Biological Data Visualization (BioVis), Atlanta, GA, USA, 13–14 October 2013; pp. 41–48.
- Raymond, G.M.; Butterworth, E.; Bassingthwaighte, J.B. Jsim: Free software package for teaching physiological modeling and research. FASEB J. 2003, 17, A390. [Google Scholar]
- Ander, M.; Beltrao, P.; Ventura, B.D.; Ferkinghoff-Borg, J.; Foglierini, M.; Lemerle, C.; Tomás-Oliveira, I.; Serrano, L. Smartcell, a framework to simulate cellular processes that combines stochastic approximation with diffusion and localisation: Analysis of simple networks. Syst. Biol. 2004. [Google Scholar] [CrossRef]
- Plimpton, S.J.; Slepoy, A. Chemcell: A Particle-Based Model of Protein Chemistry and Diffusion in Microbial Cells; Department of Energy: Albuquerque, NM, USA, 2003. [Google Scholar]
- Andrews, S.S.; Bray, D. Stochastic simulation of chemical reactions with spatial resolution and single molecule detail. Phys. Biol. 2004, 1, 137. [Google Scholar] [CrossRef]
- Boulianne, L.; Al Assaad, S.; Dumontier, M.; Gross, W.J. Gridcell: A stochastic particle-based biological system simulator. BMC Syst. Biol. 2008, 2, 66. [Google Scholar] [CrossRef]
- Le Novere, N.; Shimizu, T.S. Stochsim: Modelling of stochastic biomolecular processes. Bioinformatics 2001, 17, 575–576. [Google Scholar] [CrossRef]
- Arkin, A.; Ross, J.; McAdams, H.H. Stochastic kinetic analysis of developmental pathway bifurcation in phage λ-infected escherichia coli cells. Genetics 1998, 149, 1633–1648. [Google Scholar]
- Khanin, R.; Higham, D.J. Chemical master equation and langevin regimes for a gene transcription model. Theor. Comput. Sci. 2008, 408, 31–40. [Google Scholar] [CrossRef]
- Paulsson, J.; Berg, O.G.; Ehrenberg, M. Stochastic focusing: Fluctuation-enhanced sensitivity of intracellular regulation. Proc. Natl. Acad. Sci. USA 2000, 97, 7148–7153. [Google Scholar] [CrossRef]
- Isaacson, S.A.; Isaacson, D. Reaction-diffusion master equation, diffusion-limited reactions, and singular potentials. Phys. Rev. E 2009, 80, 066106. [Google Scholar] [CrossRef]
- Baras, F.; Mansour, M.M. Reaction-diffusion master equation: A comparison with microscopic simulations. Phys. Rev. E 1996, 54, 6139–6148. [Google Scholar] [CrossRef]
- Gillespie, D.T. Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem. 1977, 81, 2340–2361. [Google Scholar] [CrossRef]
- Rodríguez, J.V.; Kaandorp, J.A.; Dobrzyński, M.; Blom, J.G. Spatial stochastic modelling of the phosphoenolpyruvate-dependent phosphotransferase (pts) pathway in Escherichia coli. Bioinformatics 2006, 22, 1895–1901. [Google Scholar] [CrossRef]
- Vale, R.D.; Reese, T.S.; Sheetz, M.P. Identification of a novel force-generating protein, kinesin, involved in microtubule-based motility. Cell 1985, 42, 39–50. [Google Scholar] [CrossRef]
- Steinberg, G.; Schliwa, M. Characterization of the biophysical and motility properties of kinesin from the fungus neurospora crassa. J. Biol. Chem. 1996, 271, 7516–7521. [Google Scholar] [CrossRef]
- Von Massow, A.; Mandelkow, E.M.; Mandelkow, E. Interaction between kinesin, microtubules, and microtubule-associated protein 2. Cell Motil. Cytoskeleton 1989, 14, 562–571. [Google Scholar] [CrossRef]
- Schwanhausser, B.; Busse, D.; Li, N.; Dittmar, G.; Schuchhardt, J.; Wolf, J.; Chen, W.; Selbach, M. Global quantification of mammalian gene expression control. Nature 2011, 473, 337–342. [Google Scholar] [CrossRef]
- Neely, J.D.; Amiry-Moghaddam, M.; Ottersen, O.P.; Froehner, S.C.; Agre, P.; Adams, M.E. Syntrophin-dependent expression and localization of aquaporin-4 water channel protein. Proc. Natl. Acad. Sci. USA 2001, 98, 14108–14113. [Google Scholar]
- Jain, A.K.; Bloom, D.A.; Jaiswal, A.K. Nuclear import and export signals in control of Nrf2. J. Biol. Chem. 2005, 280, 29158–29168. [Google Scholar] [CrossRef]
- Rash, J.E.; Yasumura, T.; Hudson, C.S.; Agre, P.; Nielsen, S. Direct immunogold labeling of aquaporin-4 in square arrays of astrocyte and ependymocyte plasma membranes in rat brain and spinal cord. Proc. Natl. Acad. Sci. USA 1998, 95, 11981–11986. [Google Scholar] [CrossRef]
- Rossi, A.; Baumgart, F.; van Hoek, A.N.; Verkman, A.S. Post-Golgi supramolecular assembly of aquaporin-4 in orthogonal arrays. Traffic 2012, 13, 43–53. [Google Scholar] [CrossRef]
- Furman, C.S.; Gorelick-Feldman, D.A.; Davidson, K.G.V.; Yasumura, T.; Neely, J.D.; Agre, P.; Rash, J.E. Aquaporin-4 square array assembly: Opposing actions of M1 and M23 isoforms. Proc. Natl. Acad. Sci. USA 2003, 100, 13609–13614. [Google Scholar] [CrossRef]
- Niture, S.K.; Jain, A.K.; Jaiswal, A.K. Antioxidant-induced modification of iNrf2 cysteine 151 and PKC-δ-mediated phosphorylation of Nrf2 serine 40 are both required for stabilization and nuclear translocation of Nrf2 and increased drug resistance. J. Cell Sci. 2009, 122, 4452–4464. [Google Scholar] [CrossRef]
- Rasband, W.S. Imagej; US National Institutes of Health: Bethesda, MA, USA, 1997. [Google Scholar]
- Swaminathan, R.; Hoang, C.P.; Verkman, A.S. Photobleaching recovery and anisotropy decay of green fluorescent protein GFP-s65t in solution and cells: Cytoplasmic viscosity probed by green fluorescent protein translational and rotational diffusion. Biophys. J. 1997, 72, 1900–1907. [Google Scholar] [CrossRef]
- Adams, C.L.; Chen, Y.-T.; Smith, S.J.; Nelson, W.J. Mechanisms of epithelial cell-cell adhesion and cell compaction revealed by high-resolution tracking of E-cadherin-green fluorescent protein. J. Cell Biol. 1998, 142, 1105–1119. [Google Scholar] [CrossRef]
- Phair, R.D.; Misteli, T. High mobility of proteins in the mammalian cell nucleus. Nature 2000, 404, 604–609. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Kim, S.B.; Hsu, Y.; Linninger, A.A. Interpretation of Cellular Imaging and AQP4 Quantification Data in a Single Cell Simulator. Processes 2014, 2, 218-237. https://doi.org/10.3390/pr2010218
Kim SB, Hsu Y, Linninger AA. Interpretation of Cellular Imaging and AQP4 Quantification Data in a Single Cell Simulator. Processes. 2014; 2(1):218-237. https://doi.org/10.3390/pr2010218
Chicago/Turabian StyleKim, Seon B., Ying Hsu, and Andreas A. Linninger. 2014. "Interpretation of Cellular Imaging and AQP4 Quantification Data in a Single Cell Simulator" Processes 2, no. 1: 218-237. https://doi.org/10.3390/pr2010218
APA StyleKim, S. B., Hsu, Y., & Linninger, A. A. (2014). Interpretation of Cellular Imaging and AQP4 Quantification Data in a Single Cell Simulator. Processes, 2(1), 218-237. https://doi.org/10.3390/pr2010218




