Next Article in Journal
Absorption and Chemisorption of Small Levitated Single Bubbles in Aqueous Solutions
Previous Article in Journal
Towards a Tissue-Engineered Ligament: Design and Preliminary Evaluation of a Dedicated Multi-Chamber Tension-Torsion Bioreactor
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Processes
Volume 2
Issue 1
10.3390/pr2010180
processes-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Analysis of Multi-Loop Control Structures of Dividing-Wall Distillation Columns Using a Fundamental Model

by
Salvador Tututi-Avila
1,2,
Arturo Jiménez-Gutiérrez
2 and
Juergen Hahn
1,*
1
Department of Biomedical Engineering, Department of Chemical & Biological Engineering, Rensselaer Polytechnic Institute, Troy, NY 12180-3590, USA
2
Departamento de Ingeniería Química, Instituto Tecnológico de Celaya, Ave. Tecnológico y García Cubas S/N, Celaya 38010, Gto., Mexico
*
Author to whom correspondence should be addressed.
Processes 2014, 2(1), 180-199; https://doi.org/10.3390/pr2010180
Submission received: 11 November 2013 / Revised: 23 January 2014 / Accepted: 11 February 2014 / Published: 24 February 2014
Browse Figures
Versions Notes

Abstract

:
Dividing-wall columns (DWCs) have significant potential as energy-efficient processes for the separation of multicomponent mixtures. However, in addition to an efficient steady state design, dynamics and control also play a major part for the success of a technology. This is especially so for complex distillation systems. This paper investigates the dynamics of a dividing wall column used for the separation of ternary mixtures. A detailed dynamic first principles-based model of the column I s developed in gPROMS. The model is used to generate data used for control loop pairing via the Relative Gain Array (RGA), and controller parameters are found by using Internal Model Control (IMC) tuning. The best control structures for DWC systems, involving four different ternary mixtures, and two different feed compositions for each mixture, are investigated.

1. Introduction

Separation by distillation, the most common separation process in the chemical and petrochemical industries, consumes a significant amount of energy. In order to address this point, new distillation structures, which hold the promise to be more energy-efficient, have been recently considered.
The conventional distillation designs for separation of ternary mixtures are the direct and indirect sequences. Alternative options, such as thermally coupled arrangements, have been shown to provide significant energy savings over the conventional sequences, and, in some cases, even lower capital costs. In particular, the fully thermally coupled structure, or Petlyuk column (Figure 1) [1,2], has received special attention. The Petlyuk arrangement consists of a prefractionator coupled to the main column, using two recycle streams. An implementation of Petlyuk columns that has been used in some production facilities consists of a dividing wall column (DWC). DWCs are thermodynamically equivalent to the Petlyuk system [3]. DWCs split the middle section of a single vessel into two sections by inserting a vertical wall, thus, implementing the Petlyuk configuration in a single shell [4,5,6,7,8].
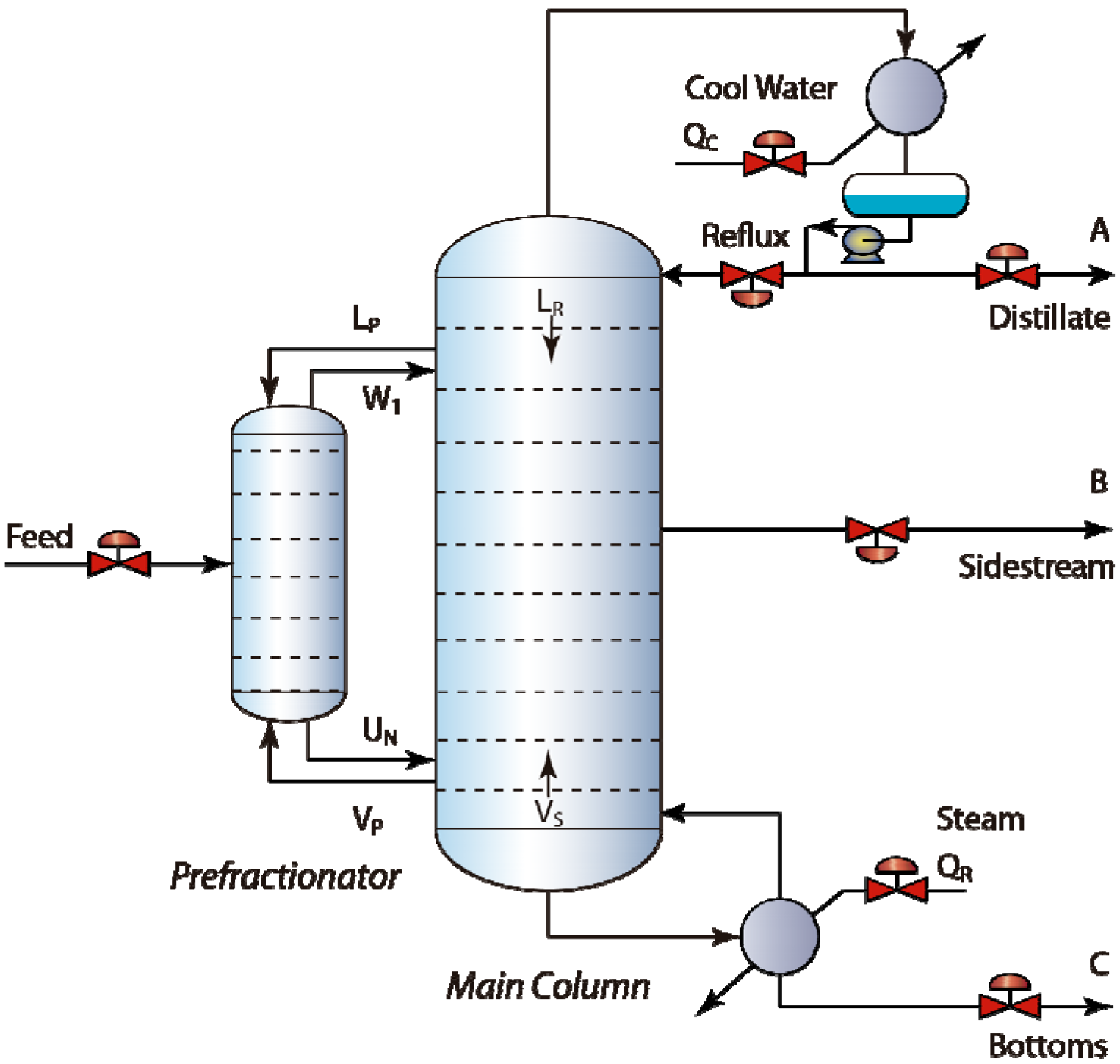
Processes 02 00180 g001 1024
Figure 1. Petlyuk column.
Figure 1. Petlyuk column.
Processes 02 00180 g001
Dividing-wall columns represent a typical example of process intensification since they can bring significant reductions in both capital investment and energy costs of up 30% [8,9,10]. In the last couple of decades, there have been over 100 DWCs found in industrial use worldwide [3]. DWC technology has proven to be a feasible option, not only to separate multicomponent mixtures, but also for processes involving azeotropic, extractive, and reactive distillation.
The benefits of DWC technology can only be achieved with proper control structures that provide a stable and robust operation of the separation process. Control of conventional distillation columns has been extensively studied in the literature, but fewer studies on the control of DWCs have been reported. Compared to a conventional distillation system, the control of a DWC is more difficult due to increased interaction among the controlled and manipulated variables. Nevertheless, it has been reported that thermally coupled sequences have good controllability properties [11,12], provided that an appropriate control structure is selected [9]. Controllability and the effect of optimal operation on different control structures have been investigated in several papers [13,14,15,16,17]. One particularly relevant study is the one by Ling and Luyben [18], where they proposed a control structure that adds an additional control loop to the three point DB-LSV control structure used by Wolff and Skogestad [19], in order to lower energy requirements. Mutalib and Smith [20] investigated the operation and control of DWCs, with control configurations determined by Relative Gain array (RGA). They reported that DWCs achieve stable operation with DB-LSV and LB-DSV multiloop control configurations. Recently Kim et al. [21] investigated two-point temperature control structures for three different systems under different feed conditions. They recommended the (L,S) and (V,S) control structures. PI controllers have been reported to provide stable operation in DWC [16,20]. Ling and Luyben [18] used a sequential methodology to tune the Proportional-Integral (PI) controllers. Other authors have used different tuning methodologies and techniques, e.g., tuning based on minimizing convergence indices [22,23]. IMC tuning of PI/PIDs has also been considered to control hypothetical ternary systems in DWCs [24,25]. One key aspect for evaluating the performance of control systems applied to DWCs is the rigor of the model that the controllers are applied to. The most commonly used dynamic models involve several simplifying assumptions, which may not provide the most realistic scenario for evaluating control structures.
This work seeks to address this last point in that a rigorous, first principles-based dynamic model of a DWC is used for separation of ternary mixtures. Different control structures are analyzed to identify the best-performing structure for this complex distillation system. In addition, different mixtures and feed compositions are considered in order to explore how the mixture properties affect the selection of the best control structure.

2. Design and Modeling of DWCs

2.1. Design of DWCs

The energy savings reported for DWCs are achieved because of the reduction or elimination of the remixing of the intermediate component observed in conventional distillation sequences. Different approaches have been reported in the literature for designing energy-efficient Petlyuk or DWC columns. For example, Triantafyllou and Smith [26], and Hernández and Jiménez [27], have presented systematic methodologies, while Dünnebier and Pantelides [28], and Grossman et al. [29], have used mathematical programming techniques. In this work the methodology proposed by Hernández and Jiménez [27,30] for the design of dividing wall columns with minimum energy consumption is used. A basic design is first obtained from the use of shortcut methods for a nonintegrated counterpart, based on conventional columns (a prefractionator followed by two binary distillation columns). Steady-state rigorous simulations of the thermally coupled structure are then conducted using gPROMS to test the preliminary design; in this step, adjustments to the tray structure are made as required so that the design meets the specified product purities. Finally, two degrees of freedom remain to be specified, which are used to obtain the conditions that provide minimum energy consumption. In this case, the search procedure provides the optimal values of the interconnecting vapor flowrate (VP) and the interconnecting liquid flowrate (LP).

2.2. Model Equations

Dynamic modeling of DWCs has received significant attention over the last two decades. Halvorsen and Skogestad [31,32] presented a simplified model that has been used in several control studies [24,33,34,35]. They assumed constant relative volatility, no energy balances and changes in enthalpy, a linearized liquid dynamics, no vapor flow dynamics, and a constant pressure drop. Hernandez and Jimenez [30] presented a dynamic model based on an equilibrium stage using mass and energy balances assuming ideal vapor liquid equilibrium, algebraic energy balances, and constant pressure. This model was also used in control studies [11,22]. In contrast to these models, a rigorous dynamic first principles-based model is developed in this work and implemented in gPROMS. The details of the model are given in the Appendix.

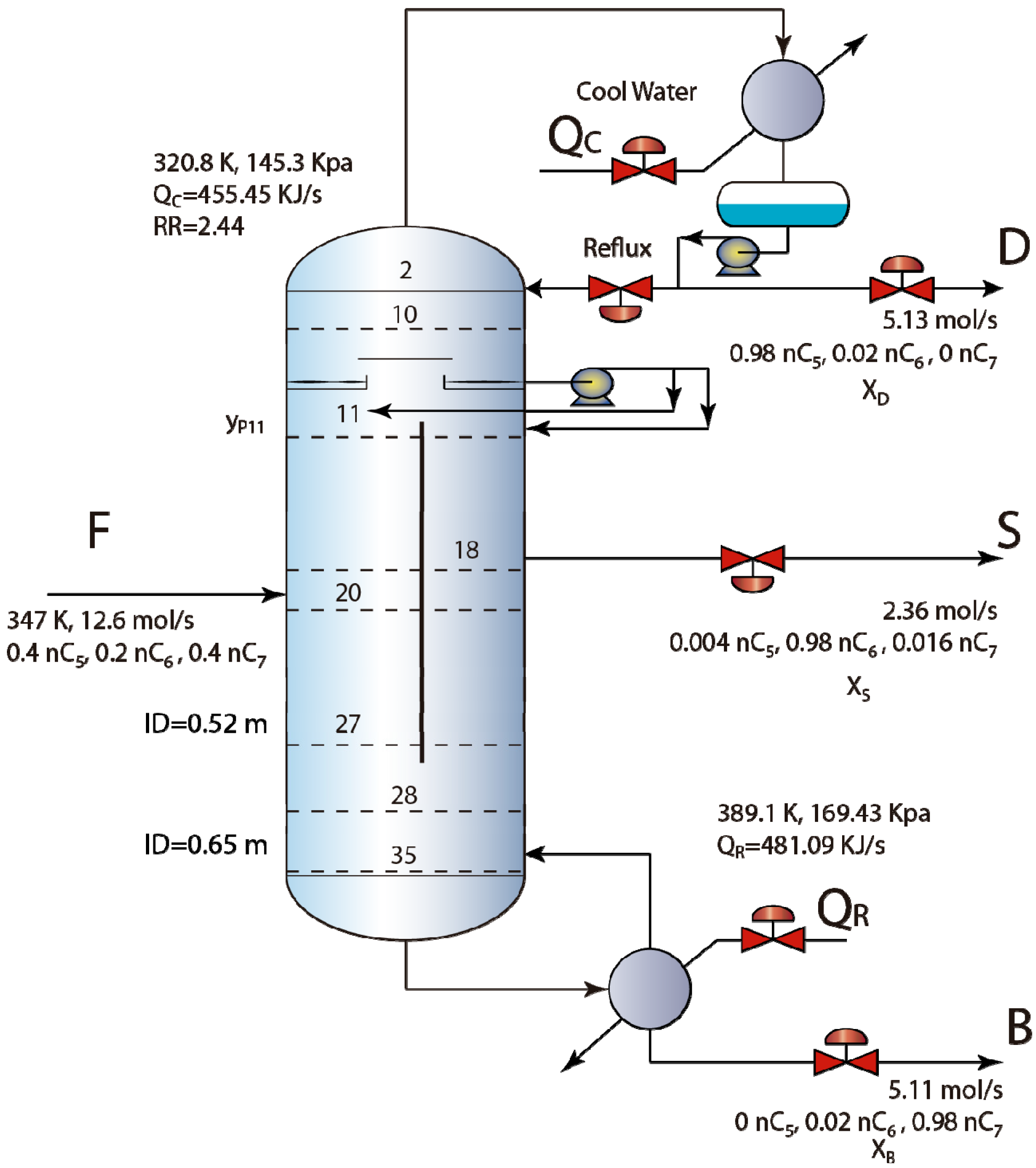
3. Investigated Column and Controller Design

Simulation studies require a column design and a specified mixture for dynamic simulations. This study is based on ternary mixtures ABC, with A being the most volatile component and C the heaviest component. Four mixtures with three significantly different values of their ease of separability index (ESI) [36] are considered. Table 1 gives the mixtures investigated in this work, along with their ESI values. A mixture of n-pentane (nC5), n-hexane (nC6), and n-heptane (nC7), which has been used in several studies from the literature [22,23,37] (with an ESI value of approximately 1.0), serves to illustrate in detail the procedure used for design and control. The results for the other mixtures are summarized in Section 4.
Table
Table 1. Ternary mixtures considered in this work.
Table 1. Ternary mixtures considered in this work.
MixtureComponents (A,B,C)ESI
M1n-pentane, n-hexane, n-heptane1.04
M2n-butane, i-pentane, n-pentane1.86
M3i-pentane, n-pentane, n-hexane0.47
M4benzene, toluene, ethylbenzene0.98
The feed flow rate is taken as 12.6 mol/s of a saturated liquid, with a molar composition of 40%, 20%, and 40% for the components nC5, nC6, and nC7, respectively. Specified product purities of 98 mol% for all components were assumed. The pressure design was set so as to ensure the use of cooling water in the condenser. Thermodynamic properties were estimated using the SRK equation of state. The details of the resulting design and operating conditions in both sections of the column are presented in Figure 2.
Processes 02 00180 g002 1024
Figure 2. Dividing wall column flowsheet.
Figure 2. Dividing wall column flowsheet.
Processes 02 00180 g002
Figure 3 illustrates the liquid composition profiles of the column. It can be observed that the side stream, which provides the production of the intermediate component, is drawn from the tray with the maximum composition of this component; this is consistent with the principles behind a proper design of energy-efficient Petlyuk columns.
Processes 02 00180 g003 1024
Figure 3. Comparison of liquid composition profiles of the main column and of the prefractionator computed by the gPROMS model, an Aspen Plus model, and a simplified model from the literature.
Figure 3. Comparison of liquid composition profiles of the main column and of the prefractionator computed by the gPROMS model, an Aspen Plus model, and a simplified model from the literature.
Processes 02 00180 g003
To compare the gPROMS results with models from other commercial tools (Aspen Plus by AspenTech) and with the use of a reported simplified model [31,32], composition profiles from each model were obtained. Figure 3 shows that the profiles obtained with Aspen Plus are basically identical to those obtained with gPROMS; the profiles obtained with the simplified model, on the other hand, clearly differ at some points from the rigorous model. The difference between the rigorous model from this work and simplified models from the literature will become more noticeable for non-ideal mixtures, although simplified models are commonly used for preliminary-design studies; in such a case, a next design step would require the rigorous determination of temperatures, pressures, stream flow rates, stream compositions, and heat-transfer rates at each stage, by solving material-balance, energy-balance, and equilibrium relations for each stage. As far as the steady state model from Aspen Plus is concerned, it was obtained only for comparison purposes of the steady state, with no further use in this work as dynamic simulations were carried out next.

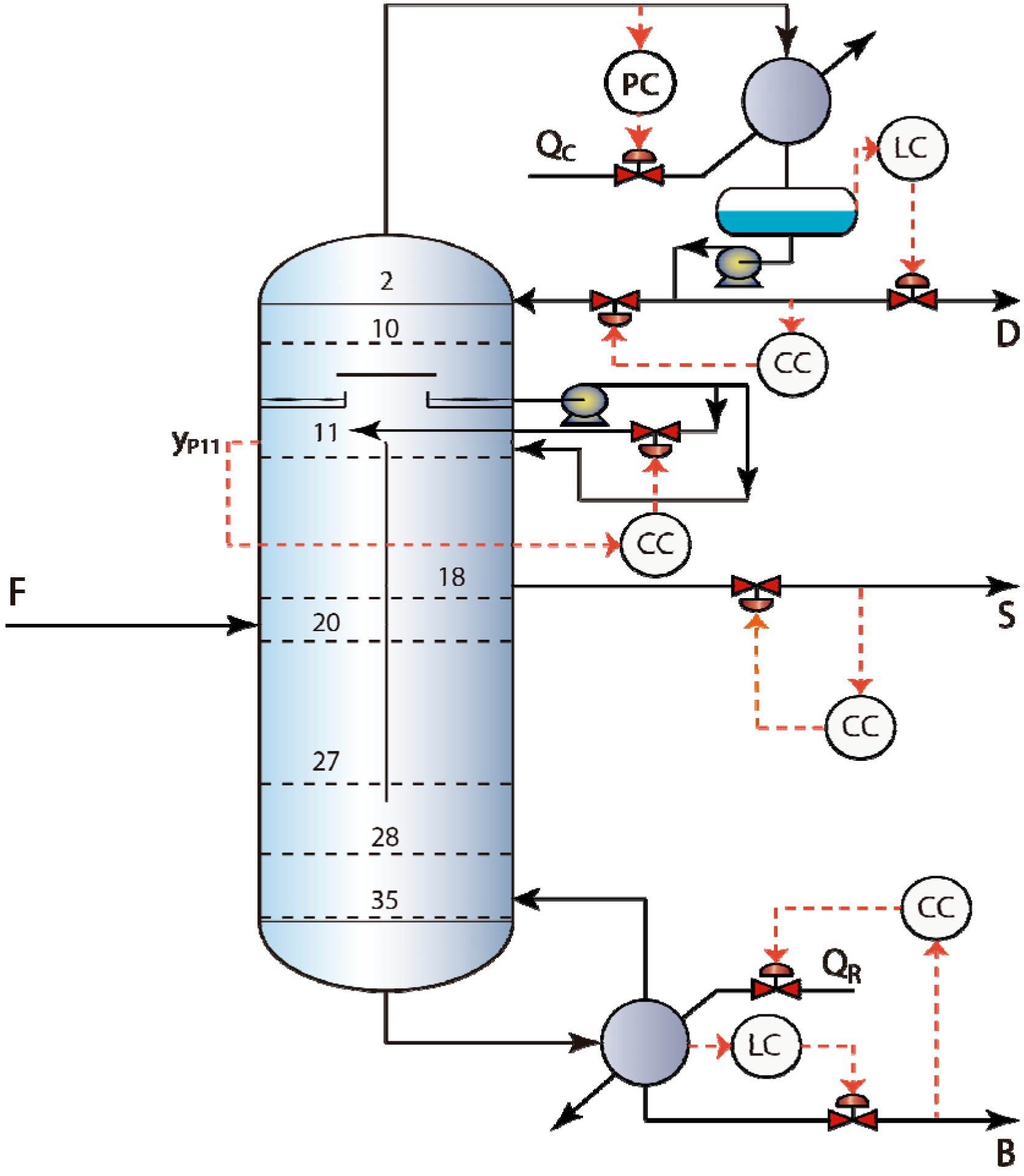
3.1. RGA Analysis and PI Controller Tuning

The design task of the DWC control system involves the selection of controlled and manipulated variables and the control structure design via input-output pairing. DWC operation includes seven variables that can be manipulated: reflux flow rate (L1), sidestream flow rate (S), reboiler duty (QR), condenser duty (Qc), liquid split ratio (βL), distillate flow rate (D), and bottoms flow rate (B). These variables can be used to control seven process variables, which are the purities of the three product streams (xA, xB, xC), the heavy component impurity at the top of the prefractionator (yp11(nc7)), the hold up in the reflux drum (MD), and the hold up in the reboiler (MNT). The column pressure is commonly controlled by the heat removal (Qc) obtained to close the heat balance, as condenser cooling tends to be quite variable and difficult to measure [38]. Two additional degrees of freedom are fixed with the control of the liquid levels in the reflux drum and in the column reboiler. The level (or hold up) of the reflux drum and the reboiler can be controlled with the variables L1 (reflux) or D (distillate), and V (vapor boil-up) or B (bottoms), respectively. Consequently, there are four inventory control options to stabilize the column and to control the hold up (or level) in the reflux tank and the hold up (or level) in the reboiler, namely the combinations DB, DV, LB, and LV [39]. For conventional distillation columns, the hold-up of the reflux drum (MD) is typically controlled by manipulating the distillate flow rate (D), and the liquid hold up in the column base (MNT) by manipulating the bottoms flow rate (B) [40].
Controllability indices can be applied to obtain information about the process behavior to determine an appropriate control structure [17]. In this study, the relative gain array (RGA) is employed [41,42] to determine the pairing of the controlled and manipulated variables. In order to identify the parameters of the process dynamics, step changes of 0.1% of the steady-state value in the input variables were implemented and the open loop dynamic responses were recorded. The dynamic responses were fitted to transfer functions and arranged into a transfer function matrix, after which the RGA was calculated.
For the common DB stabilization already reported for this particular mixture [22,37], the transfer function matrix is given in Table 2.
Table
Table 2. Transfer function matrix for DB stabilization.
Table 2. Transfer function matrix for DB stabilization.
L1SQRβL
xA Processes 02 00180 i001 Processes 02 00180 i002 Processes 02 00180 i003 Processes 02 00180 i004
xB Processes 02 00180 i005 Processes 02 00180 i006 Processes 02 00180 i007 Processes 02 00180 i008
xc Processes 02 00180 i009 Processes 02 00180 i010 Processes 02 00180 i011 Processes 02 00180 i012
yp11 Processes 02 00180 i013 Processes 02 00180 i014 Processes 02 00180 i015 Processes 02 00180 i016
The values of the RGA for this control structure are given in Table 3. RGA analysis for the DB stabilization control indicates that the three manipulated variables to be used for the control of the three product streams are the reflux flow rate (L1), the side stream flow rate (S) and the reboiler heat duty (QR); an additional control loop is given by manipulating a liquid split ratio (βL) for the control of the heavy component composition (yp11(nC7)) at the top of the prefractionator, which has been reported to minimize the energy consumption during transient operation [18]. The result is the DB-LSV structure used in several works [14,19,22], with an additional loop to help minimize energy requirements. Figure 4 depicts the DB-LSV control structure with the additional loop.
Table
Table 3. Relative Gain array (RGA) for DB stabilization control.
Table 3. Relative Gain array (RGA) for DB stabilization control.
L1SQRβL
xA1.1938−0.0015−0.1880−0.0043
xB0.24090.8407−0.0688−0.0127
xc−0.30740.16291.3019−0.1574
yp11−0.1273−0.0021−0.04491.1743
Processes 02 00180 g004 1024
Figure 4. DB-LSV control structure of the DWC.
Figure 4. DB-LSV control structure of the DWC.
Processes 02 00180 g004
To compare the DB-LSV with other control structures, only practical configurations will be considered. Thus, the multi-loop control structures considered here are DB-LSV, DV-LSB, LB-DSV, and LV-DSB [34], with the additional control loop for the heavy component composition (yp11(nC7)) at the top of the prefractionator. All the control structures are based on PI loops in a multi-loop framework. PI controller settings were determined by using IMC tuning rules [43,44,45,46]. Proportional controllers are used for the level controllers, as no integrating action is required for level control [18]. The pressure controllers are of PI type with Kc = 20 and τI = 12 min [47]. Table 4 shows the controller parameter values for the PI controllers for each control loop.
Table
Table 4. Parameter values of the PI controllers obtained using IMC tuning.
Table 4. Parameter values of the PI controllers obtained using IMC tuning.
Control structure-Controlled variableManipulated variableτc (min)Kc (%/%)τI(min)
DB-LSV
xD(nC5)L113.652.77846.77
xS(nC6)S14.688.61373.43
xB(nC7)QR7.723.55341.38
yp11(nC7)βL16.570.385183.38
DV-LSB
xD(nC5)L115.872.93839.68
xS(nC6)S10.0165.9833.35
xB(nC7)B6.7713.8345.14
yp11(nC7)βL16.560.382582.83
LB-DSV
xD(nC5)D29.503.85559.01
xS(nC6)S39.7654.8879.52
xB(nC7)QR7.884.98352.57
yp11(nC7)βL16.590.388583.02
LV-DSB
xD(nC5)D28.384.4456.77
xS(nC6)S13.86176.327.72
xB(nC7)B18.1814.990.94
yp11(nC7)βL16.590.387382.24

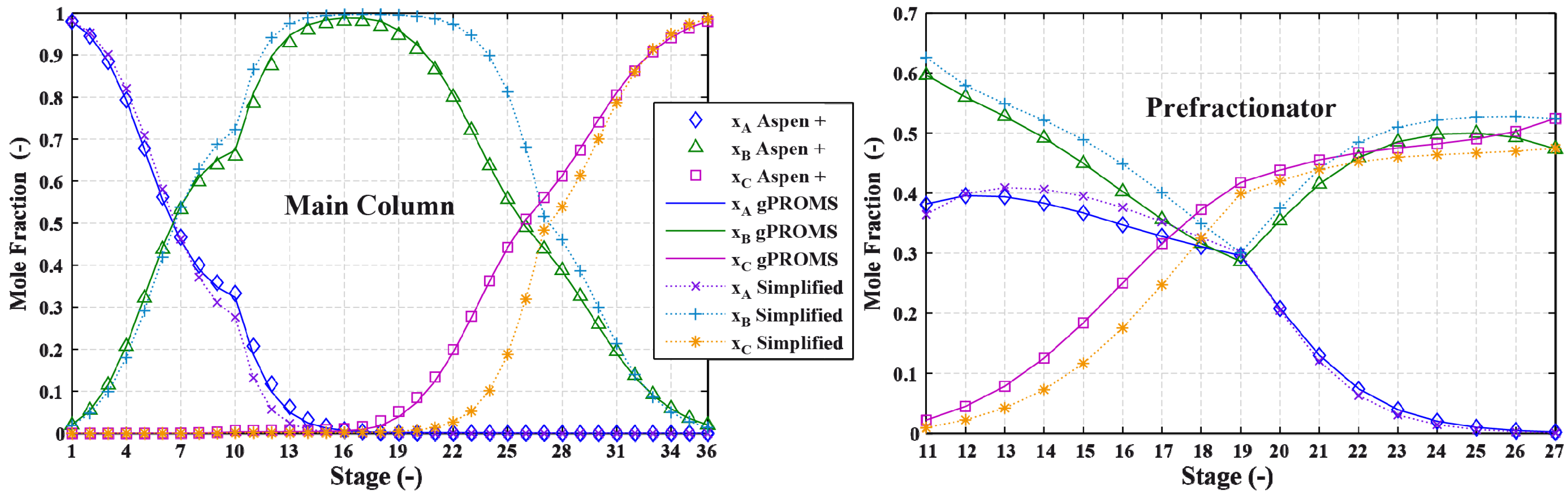
3.2. Results and Discussion

The DWC dynamic simulation requires the solution of a system of 1011 differential and algebraic equations in gPROMS. Additionally, the model includes many function evaluations for thermodynamic properties, which are not separately counted as equations. The model also includes the implemented control loops.
Figure 5 shows the responses of the DWC system for the DB-LSV configuration. Figure 6a illustrates the dynamic responses of the system under a regulatory test by assuming a disturbance of +10% in the feed flow rate at time = 0.5 h. Figure 6b displays the dynamic results obtained for a feed composition disturbance, where the composition of the light component was changed by +10% with a proportional adjustment of the other two components. The three product compositions with this control configuration return to their set-point within three hours or less.
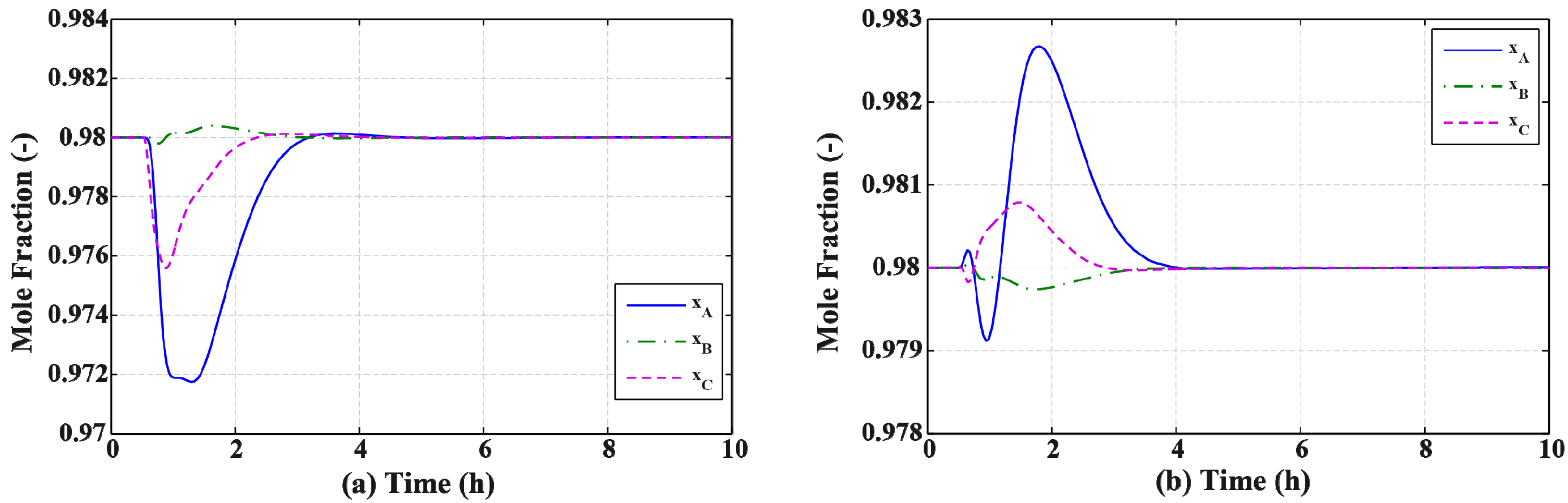
Processes 02 00180 g005 1024
Figure 5. Dynamic response of DB-LSV control structure, under a disturbance of (a) +10% in the feed flow rate and (b) +10% xA in the feed composition.
Figure 5. Dynamic response of DB-LSV control structure, under a disturbance of (a) +10% in the feed flow rate and (b) +10% xA in the feed composition.
Processes 02 00180 g005
The dynamic responses of the DV-LSB structure shown in Figure 6 produce similar settling times to the DB-LSV structure for the disturbances discussed above.
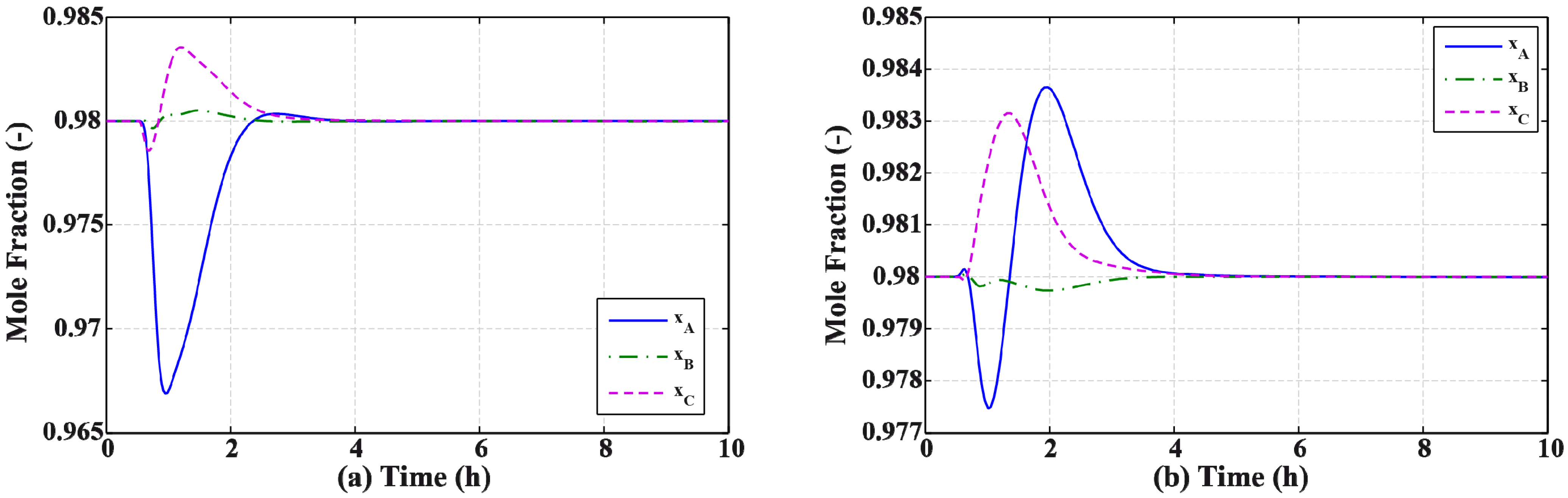
Processes 02 00180 g006 1024
Figure 6. Dynamic response of DV-LSB control structure, under a disturbance of (a) +10% in the feed flow rate and (b) +10% xA in the feed composition.
Figure 6. Dynamic response of DV-LSB control structure, under a disturbance of (a) +10% in the feed flow rate and (b) +10% xA in the feed composition.
Processes 02 00180 g006
Figure 7 depicts the dynamic responses of the LB-DSV, which shows longer settling time, as well as overshoot compared to the DB-LSV and DV-LSB structures. The compositions for the three product streams return to their set point values in 10 h or more. The LV-DSB structure exhibits similar behavior to the LB-DSV structure with even longer settling time (Figure 8).
The dynamic simulations show that all the investigated control structures can reject disturbances in the feed flow rate and in the feed composition. However, the LB-DSV and LV-DSB control structures showed longer settling times than the DB-LSV and the DV-LSB structures. The main difference among these control structures is the control of the reflux drum level by using the reflux (L) or the distillate (D) flow rates. Here, the so-called “Richardson’s rule” is compatible with the results; it suggests to use the distillate flow rate for reflux ratio columns (RR < 4) to control the reflux drum level [40], which favors the DB-LSV and DV-LSB structures.
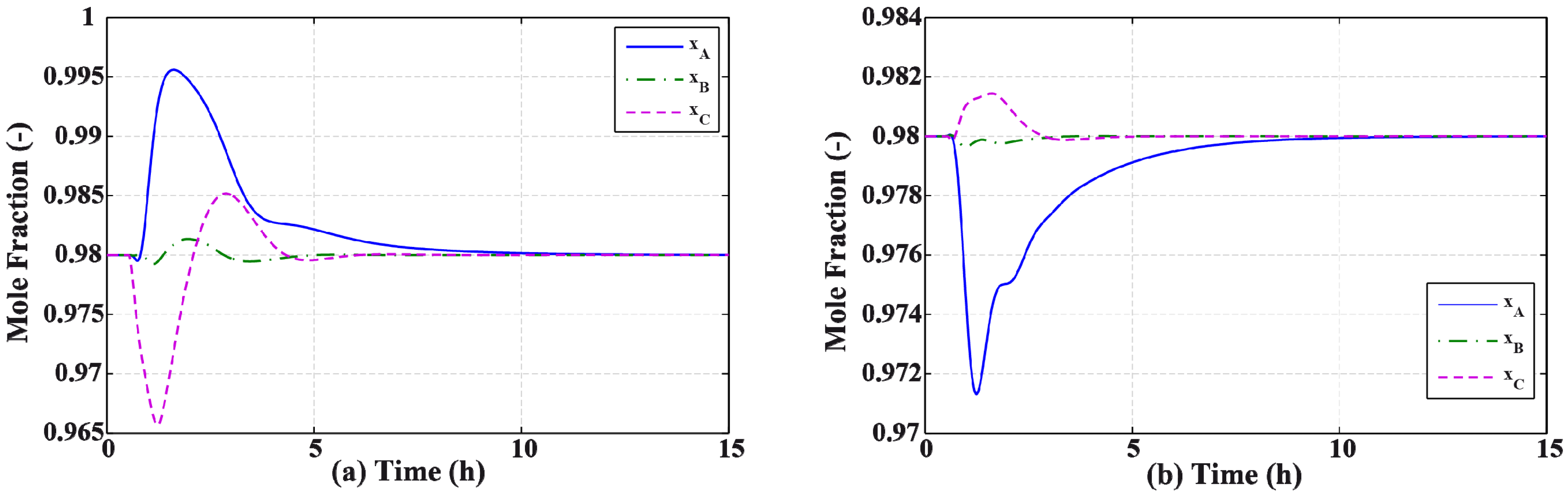
Processes 02 00180 g007 1024
Figure 7. Dynamic response of LB-DSV control structure, under a disturbance of (a) +10% in the feed flow rate and (b) +10% xA in the feed composition.
Figure 7. Dynamic response of LB-DSV control structure, under a disturbance of (a) +10% in the feed flow rate and (b) +10% xA in the feed composition.
Processes 02 00180 g007
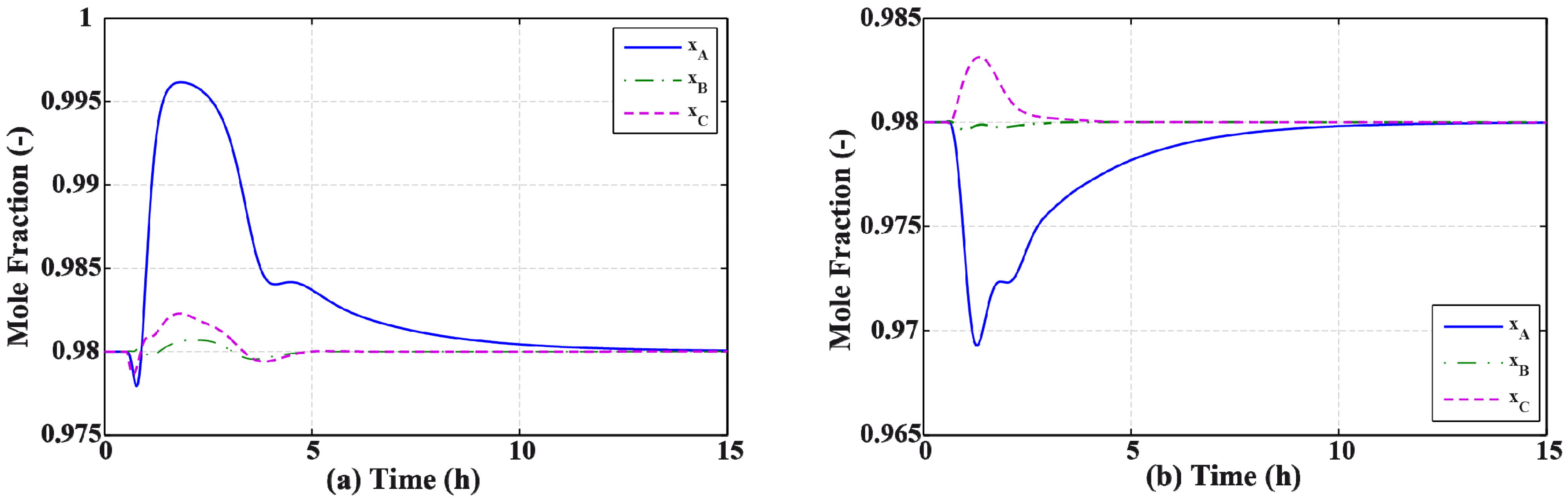
Processes 02 00180 g008 1024
Figure 8. Dynamic response of LV-DSB control structure, under a disturbance of (a) +10% in the feed flow rate and (b) +10% xA in the feed composition.
Figure 8. Dynamic response of LV-DSB control structure, under a disturbance of (a) +10% in the feed flow rate and (b) +10% xA in the feed composition.
Processes 02 00180 g008
For a final comparison of the effectiveness of the control structures, Figure 9 gives a summary of the overall performance by evaluating the integral of the absolute error (IAE) for the regulatory tasks. The superior performance of the DB-LSV control structure is supported by the lower IAE values.
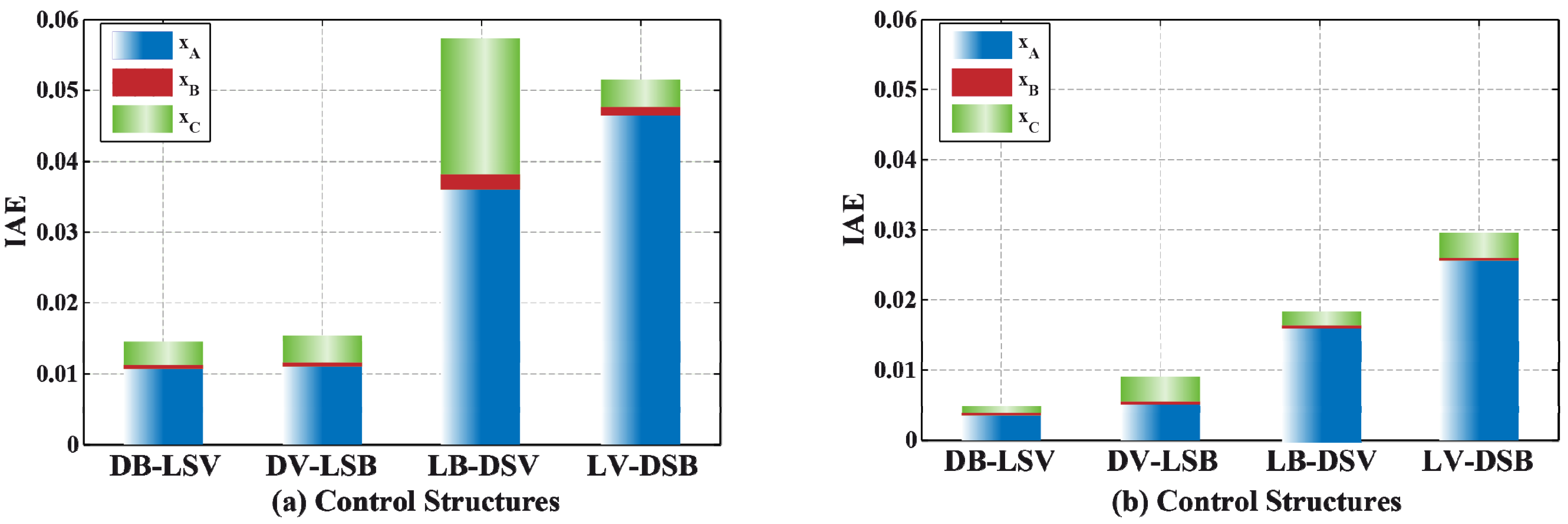
Processes 02 00180 g009 1024
Figure 9. Comparison of the performance of the control structures in terms of the Integral of Absolute Error (IAE) for a disturbance of (a) +10% in the feed flow rate and (b) +10% in the light component composition.
Figure 9. Comparison of the performance of the control structures in terms of the Integral of Absolute Error (IAE) for a disturbance of (a) +10% in the feed flow rate and (b) +10% in the light component composition.
Processes 02 00180 g009
To complement this study, Figure 10a shows the dynamic responses of the DB-LSV control structure when a simultaneous disturbance in the feed flow rate (+10% F) and feed composition of the light component (+10% xA) was considered. The settling times of the controlled variables are short, illustrating the good performance of the presented control scheme and controller tuning. Figure 10b displays the set point tracking test, where the compositions for the three product streams reach the new set point values in approximately eight hours.
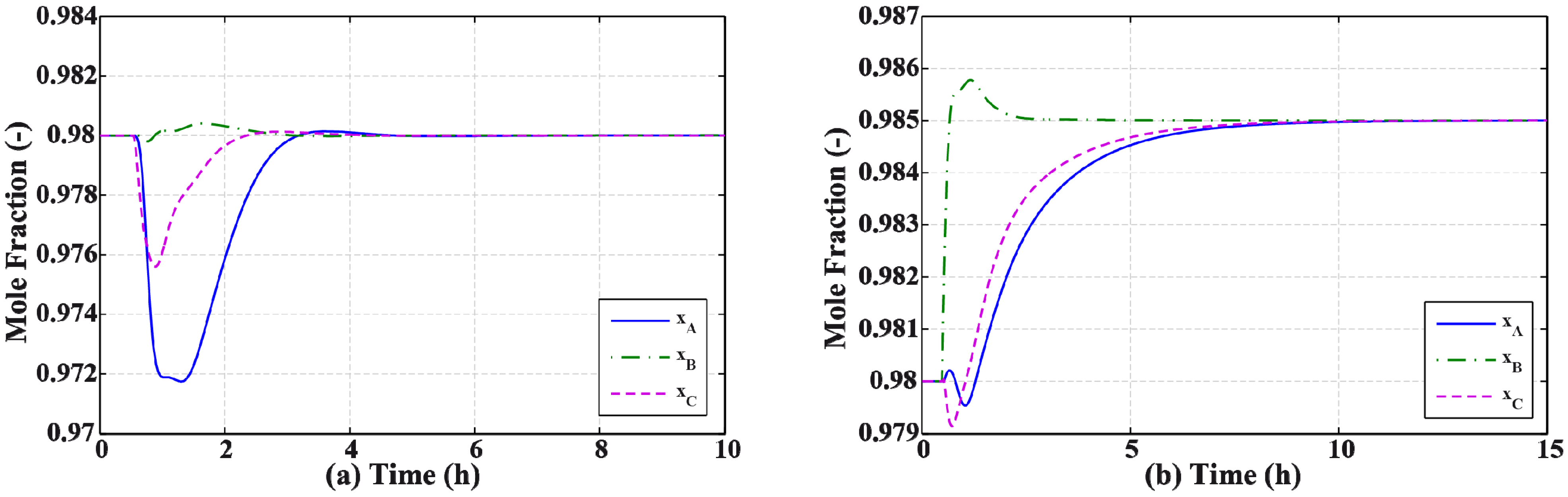
Processes 02 00180 g010 1024
Figure 10. Dynamic response of DB-LSV control structure, (a) at a simultaneous disturbance of +10% in the feed flow rate and +10% in the light component composition and (b) +0.5% change of the setpoint.
Figure 10. Dynamic response of DB-LSV control structure, (a) at a simultaneous disturbance of +10% in the feed flow rate and +10% in the light component composition and (b) +0.5% change of the setpoint.
Processes 02 00180 g010

4. Effect of Mixture Properties on Control Structure Selection

Mixtures of n-butane, i-pentane, n-pentane, and, separately, of i-pentane, n-pentane, n-hexane, with ESI values higher and lower than 1.0 were considered next. Additionally, a mixture of benzene, toluene, and ethylbenzene was considered in order to also investigate a mixture that does not only consist of aliphatic compounds. Because of the nature of this particular mixture, the NRTL model was used to estimate its thermodynamic properties. In addition, two different feed conditions, F1 = [0.40 0.20 0.40] and F2 = [0.15 0.7 0.15], were used for each mixture to explore the effect of this variable. The results for the first part of the analysis, dealing with the column design for each case study, are summarized in Table 5.
Table
Table 5. Design structure of dividing-wall columns (DWCs) for different mixtures and feeds.
Table 5. Design structure of dividing-wall columns (DWCs) for different mixtures and feeds.
MixtureRRNmainNprefracNLNVNSQR/[KW]βLβV
M1F12.443617112818481.090.38490.6571
M1F210.193737112817576.230.36110.6947
M2F116.6293211160211839.670.14970.1893
M2F243.7299211166211732.190.12510.1619
M3F18.4880623373631147.890.16800.3035
M3F229.1880593372621243.350.14570.2733
M4F12.053718102717526.230.49600.7548
M4F29.16421693117634.770.22680.5570
Table
Table 6. Best control structures for the case studies.
Table 6. Best control structures for the case studies.
MixtureComponents (A,B,C)ESIBEST CONTROL STRUCTURE
F1F2
M1n-pentane, n-hexane, n-heptane1.04DB-LSVLB-DSV
M2n-butane, i-pentane, n-pentane1.86LB-DSVLB-DSV
M3i-pentane, n-pentane, n-hexane0.47DB-LSVDV-LSB
M4benzene, toluene, ethylbenzene0.98DB-LSVDV-LSB
Table
Table 7. Integral of Absolute Error (IAE) values for all case studies.
Table 7. Integral of Absolute Error (IAE) values for all case studies.
Mixture/Feed CompositionControlled variableFlow Rate DisturbanceComposition Disturbance
StructureDB-LSVDV-LSBLB-DSVLV-DSBDB-LSVDV-LSBLB-DSVLV-DSB
M1F1xA0.010770.011070.036610.049630.003550.005070.015950.02560
xB0.000500.000530.002180.001440.000390.000390.000410.00043
xC0.003280.003760.019310.004330.000940.003580.001990.00357
Overall0.014550.015360.058110.055410.004880.009030.018350.02960
M1F2xA0.027010.019820.004490.063400.003310.002590.002020.02894
xB0.002310.002070.002310.002470.000270.000290.000290.00050
xC0.006580.002390.006920.003370.000500.002630.000560.00274
Overall0.035900.024280.013720.069240.004090.005510.002870.03219
M2F1xA0.148020.147600.002930.002640.20397*0.001720.00162
xB0.109820.109650.001870.001819.84515*0.000830.00083
xC0.002690.000880.000800.002510.00374*0.000190.00091
Overall0.260530.258130.005590.0069710.05287*0.002740.00335
M2F2xA0.28814*0.01153*0.32005*0.00568*
xB0.00764*0.00268*0.01081*0.00094*
xC0.02220*0.00569*0.02285*0.00153*
Overall0.31799*0.01989*0.35371*0.00815*
M3F1xA0.008520.004540.024300.024240.00037*0.027630.02796
xB0.020750.011460.068750.060740.00037*0.018320.01832
xC0.013750.028580.019600.016860.00139*0.006250.00348
Overall0.043030.044580.112640.101850.00213*0.052190.04976
M3F2xA0.027140.00742**0.008570.00283**
xB0.015510.00813**0.003100.00141**
xC0.069550.00859**0.027070.00280**
Overall0.112200.02414**0.038730.00705**
M4F1xA0.042060.040840.061670.055240.016310.012110.023100.02050
xB0.015270.049950.070690.074440.002000.001460.000990.00132
xC0.022810.023860.026780.023530.002680.002250.002040.00225
Overall0.080140.114650.159140.153210.020990.015820.026130.02407
M4F2xA0.053960.023530.010040.009780.018360.007590.018310.01031
xB0.003620.004440.001830.003030.000620.001170.000430.00054
xC0.029570.008750.017050.006210.004530.004230.002610.00258
Overall0.087150.036720.028930.019010.023510.013000.021350.01343
* The control configuration could not handle the disturbance imposed (i.e., unstable regulatory control).
After the control analysis was carried out, the best control structures for each mixture with its corresponding feed conditions were identified. Table 6 reports the best structure obtained for each case. The reported control structures achieved the best dynamic performance, in terms of the lowest IAE values, for disturbances in both feed flow rate and feed composition. To identify the best control structure of mixture M4, an extra disturbance test was carried out, which considered a combined effect of +10% in the feed flow rate and +10% in the feed composition. Table 7 contains the IAE values for all mixtures, operating conditions, and different control structures.
It can be observed that both ESI values and feed composition affect the dynamic performance of and control structure selected for the separation system. For mixtures with ESI values approximately equal to or lower than 1.0 and feeds with low concentration of the intermediate component, the DB-LSV structure provided the best control strategy. This behavior could also be explained by the reflux ratio required for the separation of these mixtures, which was the lowest out of the eight case studies analyzed here. For the case of feeds with high concentration of the intermediate component, the LB-DSV system gave the best performance for mixtures with ESI values equal or higher than 1.0; for mixtures M3, with an ESI value lower than 1.0, the preferred control structure changed to the DV-LSB arrangement. For mixture M4 a nonideal mixture with an ESI value close to 1.0, the best control structure for this first test was the DB-LSV arrangement, consistent with that for the other mixture (M1) with an ESI value of 1.0; however, for the second test, the best dynamic behavior was obtained under the DV-LSB structure, which was also the preferred control option for mixture M3 with an ESI value lower than 1.0. Even though no universally optimal control structure can be obtained for the different mixtures and conditions, one can identify the combination of mixture properties and feed composition that provided the best control structure, i.e., mixtures with low (high) concentration of the B component and ESI values lower or equal to (higher or equal to) than 1.0 shared the DB-LSV (LB-DSV or DV-LSB) as the control structure with the best dynamic performance. It should be noted that these are initial observations and future work is required to generalize these findings.

5. Conclusions

This paper presented a rigorous dynamic model of a DWC. The model was implemented in the dynamic simulator gPROMS, and a noticeable difference was found when the profiles of the rigorous model were compared with those obtained from a simplified model. One part of the contribution of this work includes the analysis of different control structures and the detection of the best structure as a function of the separation properties of the mixture and its feed composition.
The approach consisted of developing a dynamic first principles-based model, which was used in simulations to derive transfer functions between the controlled and manipulated variables of the process. RGA was then used for selecting the variables for control loop pairing and the controllers were tuned using IMC. The separation properties of the ternary mixture were characterized by their ease of separability (ESI) factor. Several control structures were analyzed, and the results showed that for mixtures with ESI values equal to or lower than 1.0, the widely known DB-LSV structure from the literature, with an additional loop to implicitly minimize energy requirements, gave the best closed-loop performance in the face of disturbances in feed flow rate and feed composition. Another structure that gave outstanding results was the LV-DSB closed loop arrangement, which provided the best dynamic responses for mixtures with ESI values higher than 1.0 and low concentration of the intermediate component, and with ESI values equal to or higher than 1.0 and high concentration of the intermediate component. The DV-LSB control structure produced good results for mixtures with ESI values lower than 1.0 and high concentration of the intermediate component. Such trends provided by this initial study can be used as a basis for further control studies to validate these heuristic rules.

Nomenclature

Aholes
total area of all active holes
Atray
tray active area
B
bottoms flow rate
D
distillate flow rate
F
feed flow rate
g
Gravity
H
enthalpy of vapor
h
enthalpy of liquid
hweir
liquid height on weir
L
liquid flow rate
L1
reflux flow rate
Lp
liquid flow rate fed to the prefractionator
LR
total liquid leaving the bottom tray in the rectifying section
K
vapor-liquid equilibrium constant
Kc
proportional gain
S
side product
Lweir
weir length
Nc
number of components in the mixture
Nmain
number of stages in the Main Column
Nprefrac
number of stages in the Prefractionator
NL
liquid interconnecting stage
NV
vapor interconnecting stage
NS
side stream stage
M
moles of liquid retained
MD
moles of liquid retained in the reflux drum
MNT
moles of liquid retained in the base of the column
Q
heat transferred
QC
condenser heat duty
QR
reboiler heat duty
RR
reflux ratio
U
liquid sidestream
V
vapor flow rate fed to the prefractionator
Vp
vapor flow rate
VS
total vapor leaving the top tray in the stripping section
W
vapor sidestream
x
liquid mole fraction
xA
mole fraction of A in the top product
xB
mole fraction of B in the sidestream product
xC
mole fraction of C in the bottoms product
y
vapor mole fraction
yp11
mole fraction of the heavy component on stage 11 at the top of the prefractionator
z
mole fraction of the feed

Greek Symbols 

α
dry-hole pressure drop coefficient
βL
liquid split
βV
vapor split
β
aeration factor
ρ
molar density
φL
liquid fugacity coefficient
φV
vapor fugacity coefficient
γ
liquid molar volume
τc
filter parameter
τp
time constant
τI
integral time
θ
dead time

Subscripts and Superscripts 

L
liquid phase
V
vapor phase
i
component
NT
total number of stages
j
stage number

Acknowledgments

Financial support from Conacyt, Mexico, through project CB-84493 is gratefully acknowledged. Also, S. Tututi was supported through a postdoctoral fellowship “Estancias Posdoctorales y Sabáticas al Extranjero para la Consolidación de Grupos de Investigación 2011 (Register No. 184961)” given by Conacyt.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix

The dynamic model of the DWC was developed assuming a generic equilibrium stage (Figure 11). The equations of the model include mass and energy balances, closure equations, thermodynamic relationships, tray hydraulics, variable-pressure, and liquid and vapor splitting relationships (Equations (1–12)). The column contains a total of NT theoretical trays. The liquid holdup on each tray, including the downcomer, is Mj. The liquid on each tray is assumed to be perfectly mixed with composition xi,j.
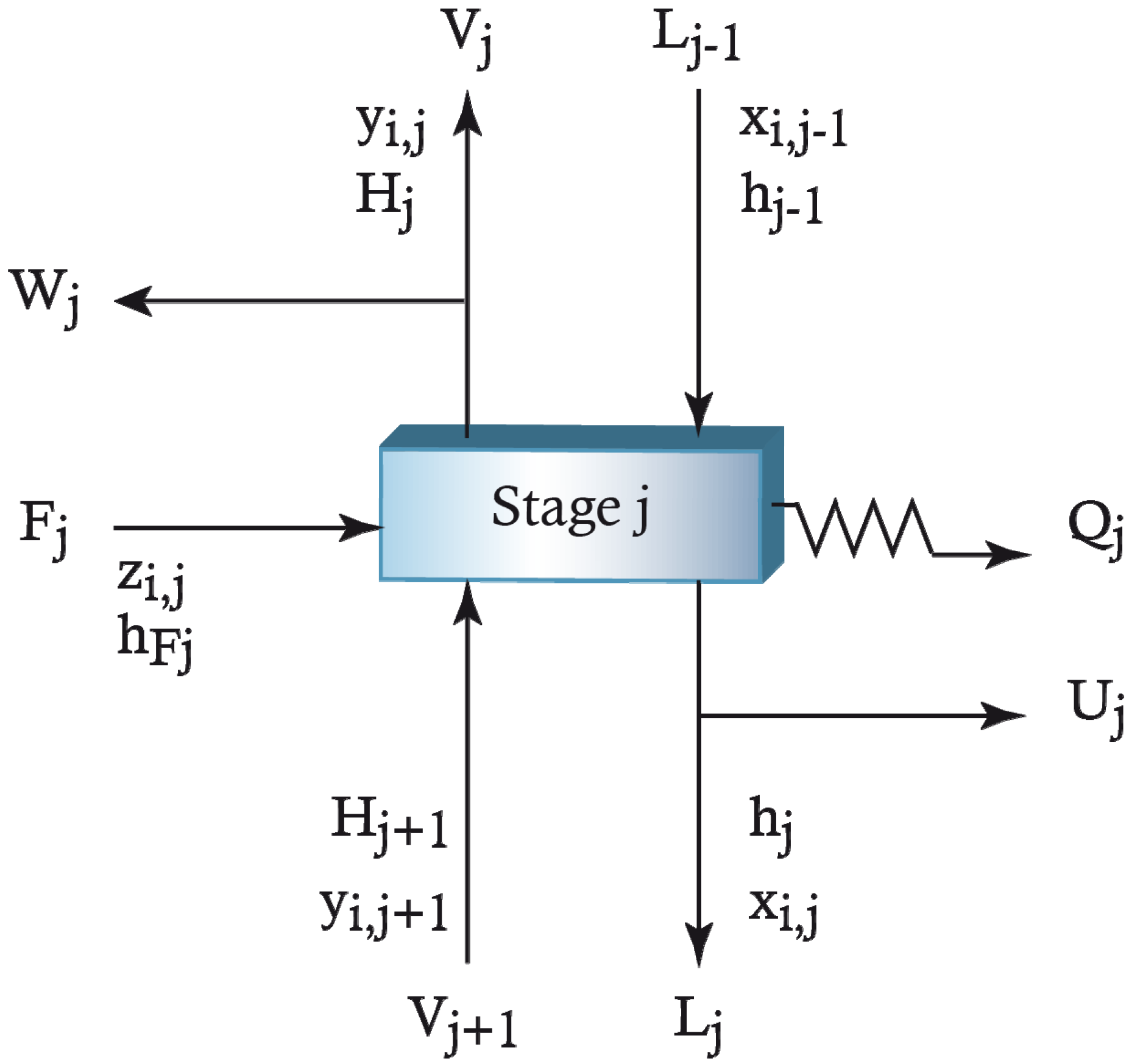
Processes 02 00180 g011 1024
Figure 11. A generic equilibrium stage for the DWC model.
Figure 11. A generic equilibrium stage for the DWC model.
Processes 02 00180 g011
The overhead vapor is sent to a total condenser and from there to the reflux drum with a liquid holdup MD (in moles). The content of the drum is assumed to be perfectly mixed with composition xi,D. The liquid in the drum is at its bubblepoint. The reflux is pumped back to the top stage (j = 2) of the column at a rate L1. The overhead distillate product is removed at a rate D. The reflux drum (j = 1) dynamics are described by Equations (1–3):
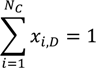
Processes 02 00180 i017
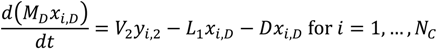
Processes 02 00180 i018
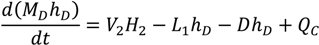
Processes 02 00180 i019
A single or two phase feed of molar flow rate Fj enters the feed stage j, with overall mole fraction composition zi,j of component i and corresponding overall molar enthalpy hFj. Also entering stage j is interstage liquid from stage j − 1 above of molar flow rate Lj−1, with composition in mole fractions xi,j and enthalpy hj−1 Similarly, interstage vapor with molar flow rate Vj+1, composition in mole fractions yi,j+1 and enthalpy Hj+1 is coming from stage j + 1 below. Leaving stage is vapor with yi,j,Hj. This stream can be divided into a vapor sidestream of molar flow rate Wj and an interstage stream of molar flow rate Vj that goes to stage j − 1. Also leaving stage j is a liquid stream, given by xi,j and hj, in equilibrium with the vapor (Vj + Wj); the liquid stream is divided into a sidestream of molar flow rate Uj and an interstage stream of molar flow rate Lj that goes to stage j + 1. Heat can be transferred at a rate Qj from or to stage j to simulate stage intercoolers, interheaters, intercondensers, interreboilers, condensers, or reboilers. The mass and energy balances for any stage (2 < j < NT−1) including the feed streams are given by the following:
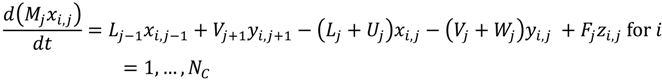
Processes 02 00180 i020
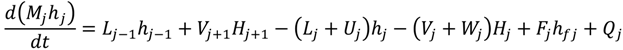
Processes 02 00180 i021
At the base of the column, liquid product is removed at a rate LNT with a composition xi,NT. Vapor boilup is generated in a reboiler at a rate VNT. The liquids in the reboiler and in the base of the column are perfectly mixed with the same composition xi,NT and total holdup MNT. Equations (6 and 7) describe the mass and energy balances in the reboiler:
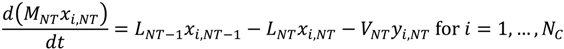
Processes 02 00180 i022
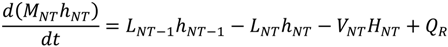
Processes 02 00180 i023
Mole fraction summations (2 < j < NT):
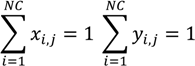
Processes 02 00180 i024
Each tray and the base of the column use an equilibrium relationship (2 < j < NT):
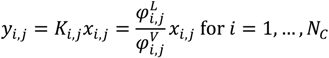
Processes 02 00180 i025
The liquid flow rates throughout the column will depend on the fluid mechanics of each stage and will not be constant throughout the column. The modified Francis weir formula (Equation 10) provides a relationship between the tray liquid holdup [48,49], Mj, and the liquid molar flow rate leaving the j-th stage Lj, (2 < j < NT−1):
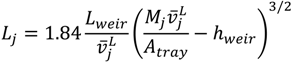
Processes 02 00180 i026
An equation linking the pressure driving force to the vapor flow is given by (2 < j < NT−1) [50,51]:
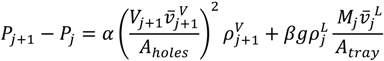
Processes 02 00180 i027
where Aholes is the total area of all active holes; α and β are parameters; and ρ refers to molar density. Tray geometry and sizing were configured as in Georgiadis et al. [49].
Equations (1–11) describe the model of the main column; the prefractionator equations are similar to the main column, but do not contain a condenser or a reboiler. The equations for the prefractionator and the main column must be solved simultaneously because of the recycle streams. The prefractionator and the main column are interconnected by the side extractions from the prefractionator (W1,UNT) and vapor and liquid side streams from the main column (VP and LP) (see Figure 1). Equation (12) provides the liquid and vapor relationships between the main column and the prefractionator.
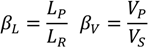
Processes 02 00180 i028
Enthalpies, fugacity coefficients and molar volumes of liquid and vapor streams are calculated as functions of temperature, pressure, and composition. Vapor hold-up is neglected here, although it can be important for columns operating at very high pressure [52]. Additionally, a dynamic energy balance is included. A common simplification found in the literature is to use an algebraic form [11,22,30]; however, neglecting the energy balance dynamics can result in abnormal dynamic responses in flow rates and compositions [53]. Therefore, this assumption is not made in this work and a dynamic energy balance is used as part of the model. The rigorous dynamic model was implemented in gPROMS and solved for steady state, as well as for dynamic conditions.

References

  1. Petlyuk, F.B.; Platonov, V.M.; Slavinskii, D.M. Thermodynamically optimal method for separating multicomponent mixtures. Int. Chem. Eng. 1965, 5, 555–561. [Google Scholar]
  2. Agrawal, R. A method to draw fully thermally coupled distillation column configurations for multicomponent distillation. Chem. Eng. Res. Des. 2000, 78, 454–464. [Google Scholar] [CrossRef]
  3. Dejanović, I.; Matijašević, L.; Olujić, Ž. Dividing wall column—A breakthrough towards sustainable distilling. Chem. Eng. Process.: Process Intensif. 2010, 49, 559–580. [Google Scholar] [CrossRef]
  4. Ben-Guang, R. Synthesis of dividing-wall columns (DWC) for multicomponent distillations—A systematic approach. Chem. Eng. Res. Des. 2011, 89, 1281–1294. [Google Scholar] [CrossRef]
  5. Kaibel, G. Distillation columns with vertical partitions. Chem. Eng. Technol. 1987, 10, 92–98. [Google Scholar] [CrossRef]
  6. Kaibel, B.; Jansen, H.; Zich, E.; Olujic, Z. Unfixed dividing wall technology for packed and tray distillation columns. IChemE Trans. Sympos. Ser. No. 152 2006, 15, 252. [Google Scholar]
  7. Kolbe, B.; Wenzel, S. Novel distillation concepts using one-shell columns. Chem. Eng. Process.: Process Intensif. 2004, 43, 339–346. [Google Scholar] [CrossRef]
  8. Christiansen, A.C.; Skogestad, S.; Lien, K. Complex distillation arrangements: Extending the petlyuk ideas. Comput. Chem. Eng. 1997, 21, S237–S242. [Google Scholar] [CrossRef]
  9. Kiss, A.A.; Bildea, C.S. A control perspective on process intensification in dividing-wall columns. Chem. Eng. Process.: Process Intensif. 2011, 50, 281–292. [Google Scholar] [CrossRef]
  10. Errico, M.; Tola, G.; Rong, B.-G.; Demurtas, D.; Turunen, I. Energy saving and capital cost evaluation in distillation column sequences with a divided wall column. Chem. Eng. Res. Des. 2009, 87, 1649–1657. [Google Scholar] [CrossRef]
  11. Hernández, S.; Jiménez, A. Controllability analysis of thermally coupled distillation systems. Ind. Eng. Chem. Res. 1999, 38, 3957–3963. [Google Scholar] [CrossRef]
  12. Jiménez, A.; Hernández, S.; Montoy, F.A.; Zavala-García, M. Analysis of control properties of Conventional and nonconventional distillation sequences. Ind. Eng. Chem. Res. 2001, 40, 3757–3761. [Google Scholar] [CrossRef]
  13. Serra, M.; Perrier, M.; Espuna, A.; Puigjaner, L. Study of the divided wall column controllability: Influence of design and operation. Comput. Chem. Eng. 2000, 24, 901–907. [Google Scholar] [CrossRef]
  14. Serra, M.; Perrier, M.; Espuña, A.; Puigjaner, L. Analysis of different control possibilities for the divided wall column: Feedback diagonal and dynamic matrix control. Comput. Chem. Eng. 2001, 25, 859–866. [Google Scholar] [CrossRef]
  15. Serra, M.; Espuña, A.; Puigjaner, L. Controllability of different multicomponent distillation arrangements. Ind. Eng. Chem. Res. 2003, 42, 1773–1782. [Google Scholar] [CrossRef]
  16. Segovia-Hernández, J.G.; Hernández, S.; Rico-Ramı́rez, V.; Jiménez, A. A comparison of the feedback control behavior between thermally coupled and conventional distillation schemes. Comput. Chem. Eng. 2004, 28, 811–819. [Google Scholar] [CrossRef]
  17. Segovia-Hernández, J.G.; Hernández-Vargas, E.A.; Márquez-Muñoz, J.A. Control properties of thermally coupled distillation sequences for different operating conditions. Comput. Chem. Eng. 2007, 31, 867–874. [Google Scholar] [CrossRef]
  18. Ling, H.; Luyben, W.L. New control structure for divided-wall columns. Ind. Eng. Chem. Res. 2009, 48, 6034–6049. [Google Scholar] [CrossRef]
  19. Wolff, E.A.; Skogestad, S. Operation of integrated three-product (Petlyuk) distillation columns. Ind. Eng. Chem. Res. 1995, 34, 2094–2103. [Google Scholar] [CrossRef]
  20. Mutalib, M.I. A.; Smith, R. Operation and control of dividing wall distillation columns: Part 1: Degrees of freedom and dynamic simulation. Chem. Eng. Res. Des. 1998, 76, 308–318. [Google Scholar] [CrossRef]
  21. Kim, K.; Lee, M.; Park, S. Two-point temperature control structure selection for dividing-wall distillation columns. Ind. Eng. Chem. Res. 2012, 51, 15683–15695. [Google Scholar] [CrossRef]
  22. Segovia-Hernández, J.G.; Hernández, S.; Femat, R.; Jiménez, A. Control of thermally coupled distillation arrangements with dynamic estimation of load disturbances. Ind. Eng. Chem. Res. 2006, 46, 546–558. [Google Scholar] [CrossRef]
  23. Tututi-Avila, S.; Jiménez-Gutiérrez, A. Control of dividing-wall columns via fuzzy logic. Ind. Eng. Chem. Res. 2013, 52, 7492–7503. [Google Scholar] [CrossRef]
  24. Dwivedi, D.; Halvorsen, I.J.; Skogestad, S. Control structure selection for three-product Petlyuk (dividing-wall) column. Chem. Eng. Process.: Process Intensif. 2013, 64, 57–67. [Google Scholar] [CrossRef]
  25. Zumoffen, D.; Gonzalo, M.; Basualdo, M. Improvements on multivariable control strategies tested on the Petlyuk distillation column. Chem. Eng. Sci. 2013, 93, 292–306. [Google Scholar] [CrossRef]
  26. Triantafyllou, C.; Smith, R. The design and optimisation of fully thermally coupled distillation columns: Process design. Chem. Eng. Res. Des. 1992, 70, 118–132. [Google Scholar]
  27. Hernández, S.; Jiménez, A. Design of energy-efficient Petlyuk systems. Comput. Chem. Eng. 1999, 23, 1005–1010. [Google Scholar] [CrossRef]
  28. Dünnebier, G.; Pantelides, C.C. Optimal design of thermally coupled distillation columns. Ind. Eng. Chem. Res. 1998, 38, 162–176. [Google Scholar]
  29. Grossmann, I.E.; Aguirre, P.A.; Barttfeld, M. Optimal synthesis of complex distillation columns using rigorous models. Comput. Chem. Eng. 2005, 29, 1203–1215. [Google Scholar] [CrossRef]
  30. Hernández, S.; Jiménez, A. Design of optimal thermally-coupled distillation systems using a dynamic model. Chem. Eng. Res. Design 1996, 74, 357–362. [Google Scholar]
  31. Halvorsen, I.J.; Skogestad, S. Optimal operation of Petlyuk distillation: Steady-state behavior. J. Process Control 1999, 9, 407–424. [Google Scholar] [CrossRef]
  32. Halvorsen, I.J.; Skogestad, S. Optimizing control of Petlyuk distillation: Understanding the steady-state behavior. Comput. Chem. Eng. 1997, 21, S249–S254. [Google Scholar] [CrossRef]
  33. Rewagad, R.R.; Kiss, A.A. Dynamic optimization of a dividing-wall column using model predictive control. Chem. Eng. Sci. 2012, 68, 132–142. [Google Scholar] [CrossRef]
  34. Serra, M.; Espuña, A.; Puigjaner, L. Control and optimization of the divided wall column. Chem. Eng. Process.: Process Intensif. 1999, 38, 549–562. [Google Scholar] [CrossRef]
  35. van Diggelen, R.C.; Kiss, A.A.; Heemink, A.W. Comparison of control strategies for dividing-wall columns. Ind. Eng. Chem. Res. 2009, 49, 288–307. [Google Scholar] [CrossRef]
  36. Tedder, D.W.; Rudd, D.F. Parametric studies in industrial distillation: Part I. Design comparisons. AIChE J. 1978, 24, 303–315. [Google Scholar] [CrossRef]
  37. Segovia-Hernández, J.G.; Hernández, S.; Jiménez, A. Control behaviour of thermally coupled distillation sequences. Chem. Eng. Res. Des. 2002, 80, 783–789. [Google Scholar] [CrossRef]
  38. Liptak, B.G. Instrument Engineers’ Handbook: Vol. 2 Process Control and Optimization, 4th ed.; CRC/Taylor & Francis: Boca Raton, FL, USA, 2006; p. 2387. [Google Scholar]
  39. Kiss, A.A.; Rewagad, R.R. Energy efficient control of a BTX dividing-wall column. Comput. Chem. Eng. 2011, 35, 2896–2904. [Google Scholar] [CrossRef]
  40. Luyben, W.L.; Tyréus, B.D.; Luyben, M.L. Plantwide Process Control; McGraw-Hill: New York, NY, USA, 1999; p. 395. [Google Scholar]
  41. Gross, F.; Baumann, E.; Geser, A.; Rippin, D.W.T.; Lang, L. Modelling, simulation and controllability analysis of an industrial heat-integrated distillation process. Comput. Chem. Eng. 1998, 22, 223–237. [Google Scholar] [CrossRef]
  42. Skogestad, S.; Postlethwaite, I. Multivariable Feedback Control: Analysis and Design; Wiley: Chichester, UK; New York, NY, USA, 1996; p. 559. [Google Scholar]
  43. Morari, M.; Zafiriou, E. Robust Process Control; Prentice Hall: Englewood Cliffs, NJ, USA, 1989; p. 488. [Google Scholar]
  44. Rivera, D.E.; Morari, M.; Skogestad, S. Internal model control: PID controller design. Ind. Eng. Chem. Process Des. Dev. 1986, 25, 252–265. [Google Scholar] [CrossRef]
  45. Seborg, D.E. Process Dynamics and Control, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2011; p. 514. [Google Scholar]
  46. Skogestad, S. Simple analytic rules for model reduction and PID controller tuning. J. Process Control 2003, 13, 291–309. [Google Scholar] [CrossRef]
  47. Luyben, W.L. Distillation Design and Control using Aspen Simulation; Wiley-Interscience: Hoboken, NJ, USA, 2006. [Google Scholar]
  48. Coulson, J.M.; Richardson, J.F. Coulson & Richardson’s Chemical Engineering. Volume 1,Fluid Flow,Heat Transfer and Mass Transfer; Butterworth-Heinemann: Amsterdam, The Netherlands; Boston, MA, USA, 2009; p. 895. [Google Scholar]
  49. Georgiadis, M.C.; Schenk, M.; Pistikopoulos, E.N.; Gani, R. The interactions of design control and operability in reactive distillation systems. Comput. Chem. Eng. 2002, 26, 735–746. [Google Scholar] [CrossRef]
  50. McCabe, W.L.; Smith, J.C.; Harriott, P. Unit Operations of Chemical Engineering, 5th ed.; McGraw-Hill: New York, NY, USA, 1992; p. 1130. [Google Scholar]
  51. Luyben, W.L. Process Modeling, Simulation, and Control for Chemical Engineers, 2nd ed.; McGraw-Hill: New York, NY, USA, 1990; p. 725. [Google Scholar]
  52. Choe, Y.S.; Luyben, W.L. Rigorous dynamic models of distillation columns. Ind. Eng. Chem. Res. 1987, 26, 2158–2161. [Google Scholar] [CrossRef]
  53. Fuentes, C.; Luyben, W.L. Comparison of energy models for distillation columns. Ind. Eng. Chem. Fundam. 1982, 21, 323–325. [Google Scholar] [CrossRef]

Share and Cite

MDPI and ACS Style

Tututi-Avila, S.; Jiménez-Gutiérrez, A.; Hahn, J. Analysis of Multi-Loop Control Structures of Dividing-Wall Distillation Columns Using a Fundamental Model. Processes 2014, 2, 180-199. https://doi.org/10.3390/pr2010180

AMA Style

Tututi-Avila S, Jiménez-Gutiérrez A, Hahn J. Analysis of Multi-Loop Control Structures of Dividing-Wall Distillation Columns Using a Fundamental Model. Processes. 2014; 2(1):180-199. https://doi.org/10.3390/pr2010180

Chicago/Turabian Style

Tututi-Avila, Salvador, Arturo Jiménez-Gutiérrez, and Juergen Hahn. 2014. "Analysis of Multi-Loop Control Structures of Dividing-Wall Distillation Columns Using a Fundamental Model" Processes 2, no. 1: 180-199. https://doi.org/10.3390/pr2010180

Article Metrics

Back to TopTop