An Adaptive Peak Power Prediction Method for Power Lithium-Ion Batteries Considering Temperature and Aging Effects
Abstract
:1. Introduction
2. Battery Modeling and Parameter Identification
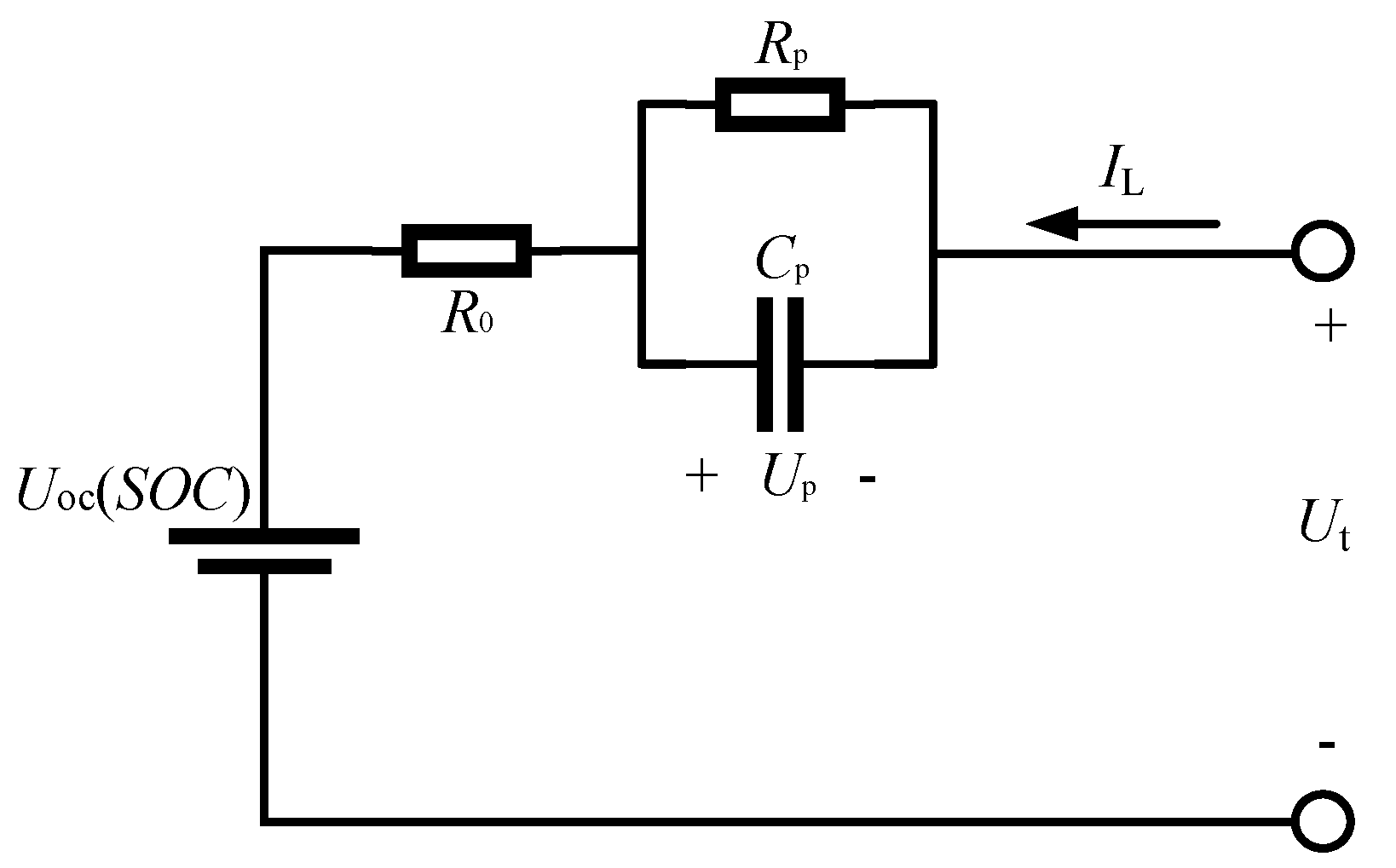
2.1. Battery Equivalent Circuit Model
2.2. Online Identification of Model Parameters
- (1)
- Parameter initialization. represents the parameters identified by VFF-RLS, I0 is the identity matrix, P is the covariance matrix, δ is a constant:
- (2)
- Calculate estimation error e(k):
- (3)
- Calculate gain matrix , among λ It’s a forgetting factor ():
- (4)
- Update Covariance matrix :
- (5)
- Parameter estimation:
- (6)
- Update forgetting factor:
3. Battery State Estimation and Power Prediction
3.1. SOC Estimation Method
- (1)
- For state variable assign initial value, Assign initial value to error covariance matrix , and . is the process excitation noise covariance matrix of the state vector; is the observation noise Covariance matrix of the state vector.
- (2)
- Calculate Kalman gain :
- (3)
- Posteriori estimation of state variables, is posteriori estimation of state variable:
- (4)
- Posteriori estimate of the error Covariance matrix, is prior estimation of error covariance matrix:
3.2. Battery Power Prediction Method
3.2.1. Voltage Constraint
3.2.2. SOC Constraint
3.2.3. SOP under Multiple Constraints
4. Experimental Verification
4.1. Experimental Subjects and Platforms
4.2. Battery OCV-SOC Curve
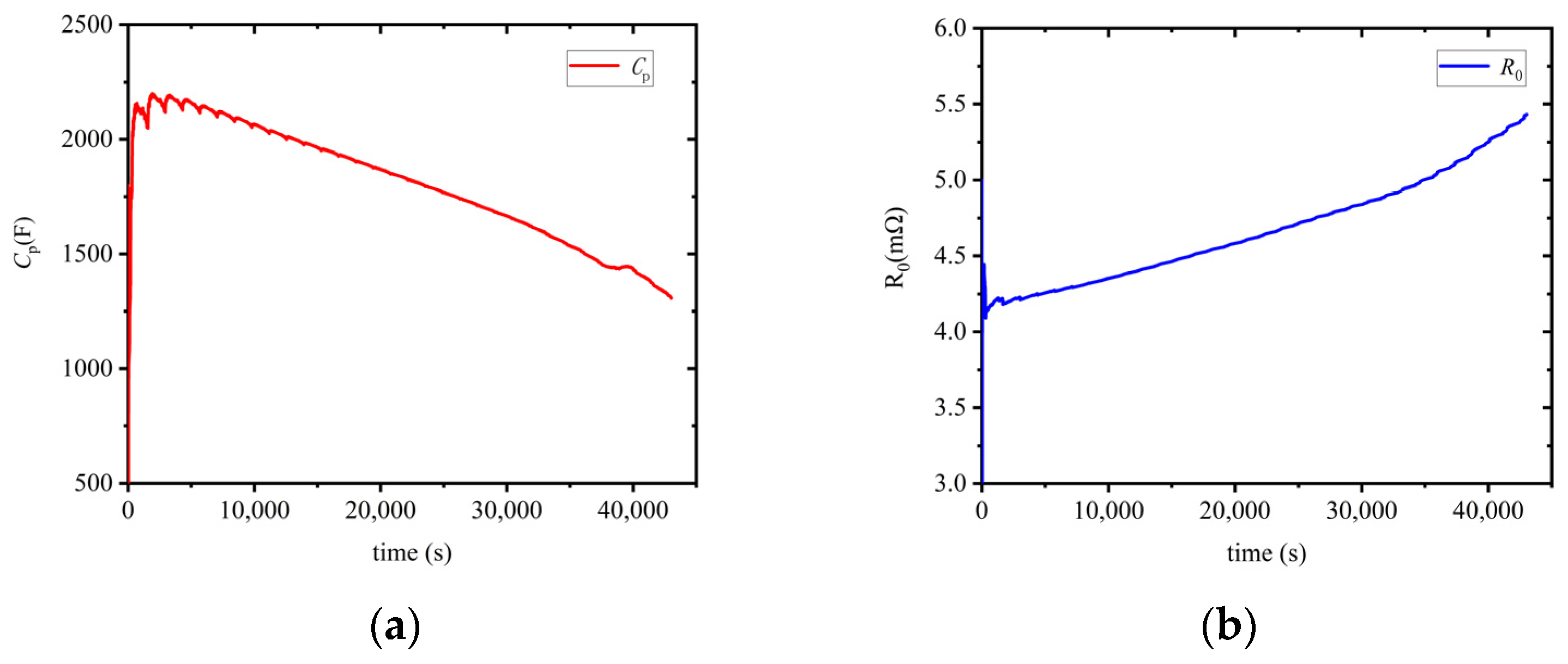
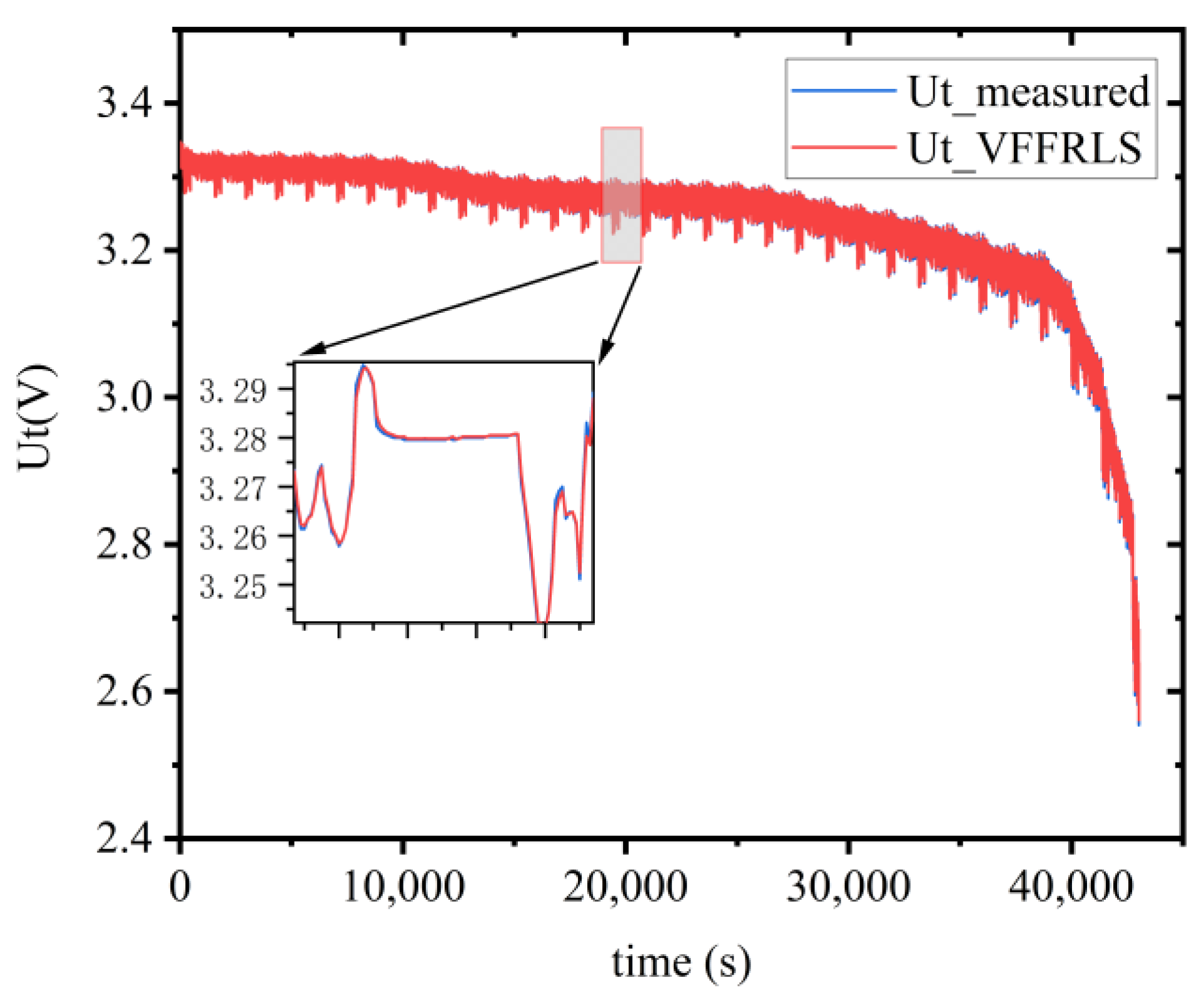
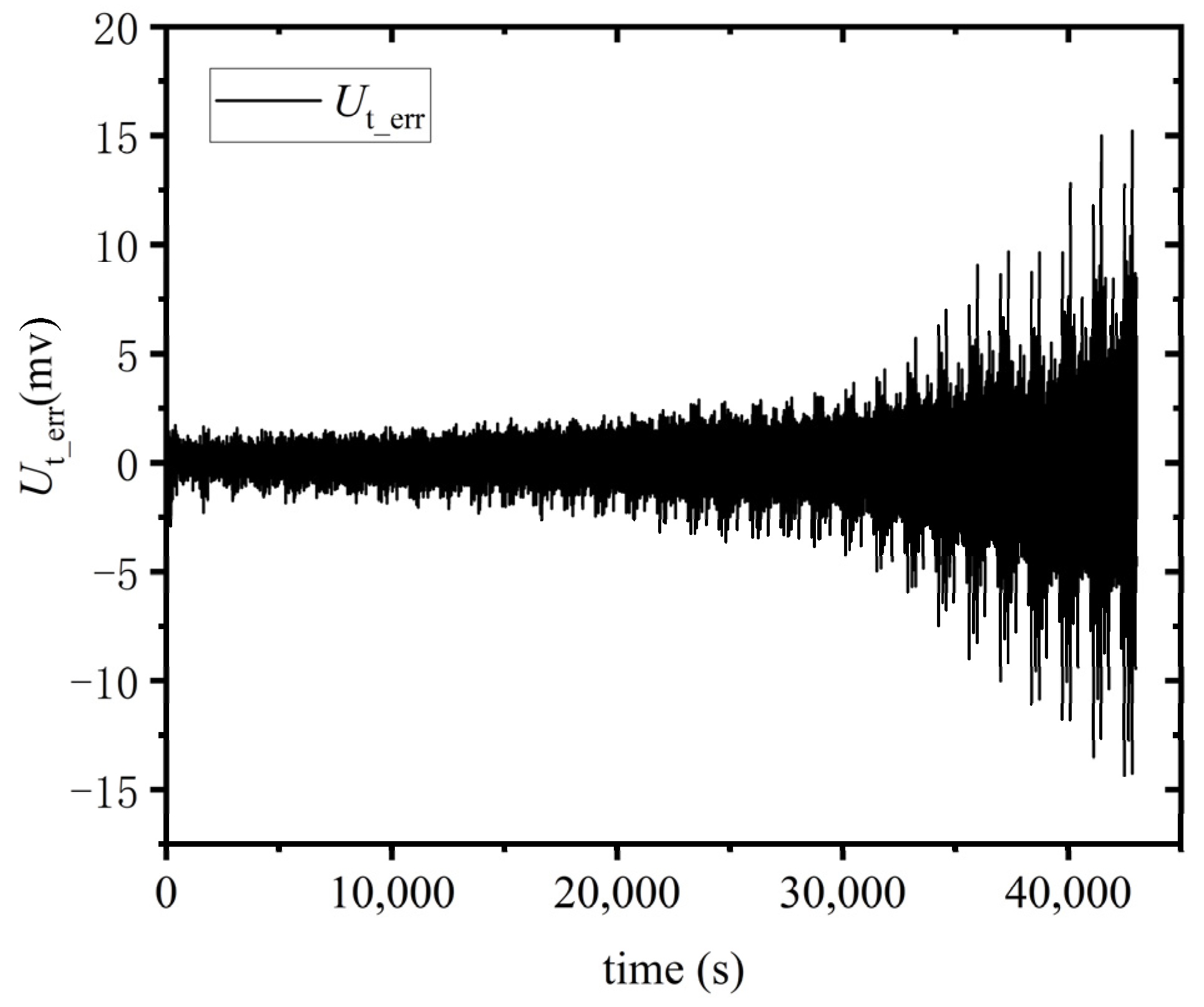
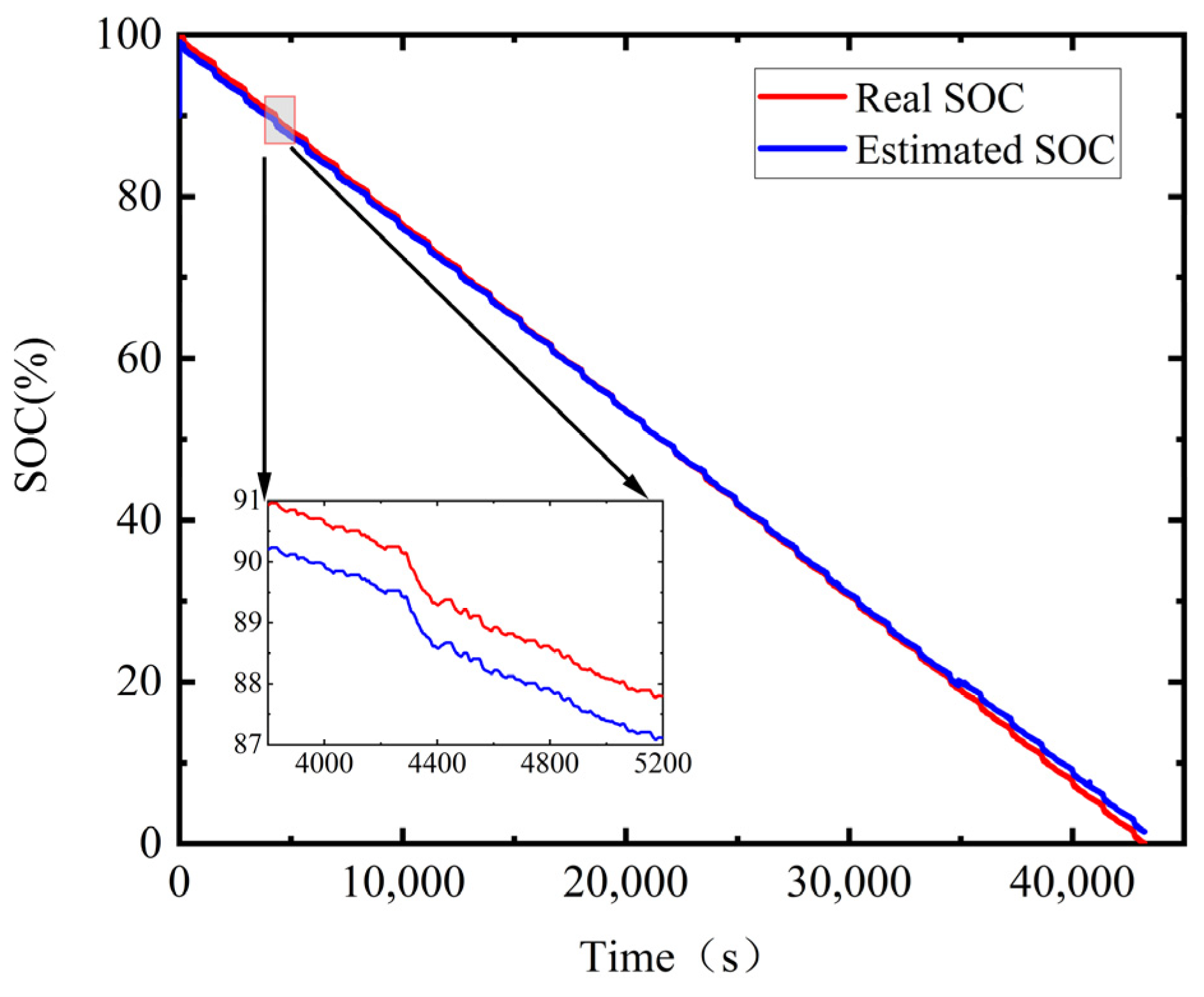
4.3. Online Parameter Identification and SOC Estimation Results
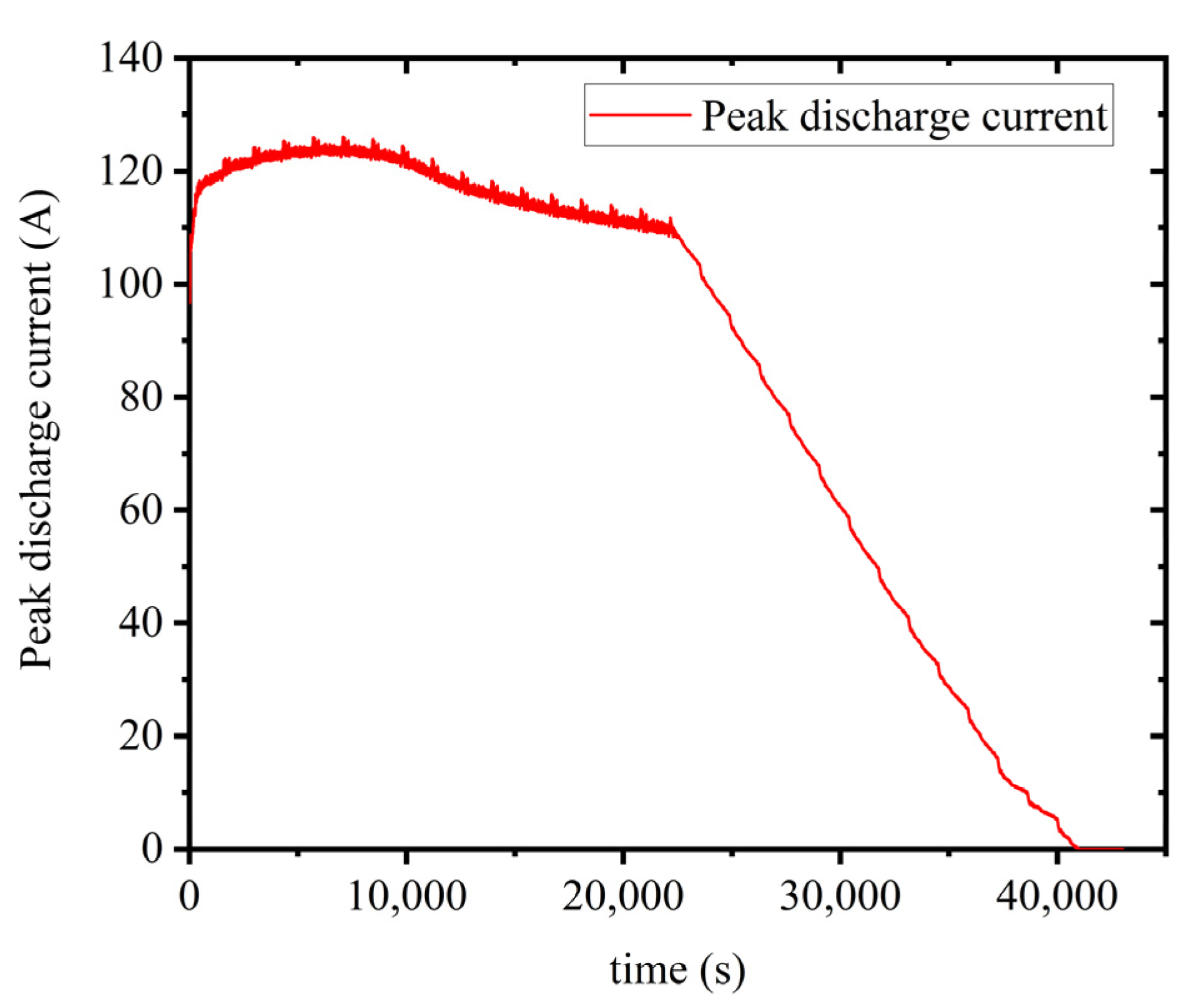
4.4. SOP Prediction Verification
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, Z.; Khajepour, A.; Song, J. A Comprehensive Review of the Key Technologies for Pure Electric Vehicles. Energy 2019, 182, 824–839. [Google Scholar]
- Selvakumar, S.G. Electric and Hybrid Vehicles—A Comprehensive Overview. In Proceedings of the 2021 IEEE 2nd International Conference On Electrical Power and Energy Systems (ICEPES), Bhopal, India, 10–11 December 2021; pp. 1–6. [Google Scholar]
- Lu, L.; Han, X.; Li, J.; Hua, J.; Ouyang, M. A Review on the Key Issues for Lithium-Ion Battery Management in Electric Vehicles. J. Power Sources 2013, 226, 272–288. [Google Scholar]
- Barelli, L.; Bidini, G.; Cardelli, E.; Ciupageanu, D.-A.; Ottaviano, A.; Pelosi, D.; Castellini, S.; Lazaroiu, G. Adaptive Voltage Control of Islanded RES-Based Residential Microgrid with Integrated Flywheel/Battery Hybrid Energy Storage System. In Proceedings of the 2020 22nd European Conference on Power Electronics and Applications (EPE’20 ECCE Europe), Lyon, France, 7–11 September 2020; pp. 1–10. [Google Scholar]
- Barelli, L.; Bidini, G.; Pelosi, D.; Ciupageanu, D.A.; Cardelli, E.; Castellini, S.; Lăzăroiu, G. Comparative Analysis of AC and DC Bus Configurations for Flywheel-Battery HESS Integration in Residential Micro-Grids. Energy 2020, 204, 117939. [Google Scholar]
- Ciupageanu, D.-A.; Barelli, L.; Ottaviano, A.; Pelosi, D.; Lazaroiu, G. Innovative Power Management of Hybrid Energy Storage Systems Coupled to RES Plants: The Simultaneous Perturbation Stochastic Approximation Approach. In Proceedings of the 2019 IEEE PES Innovative Smart Grid Technologies Europe (ISGT-Europe), Bucharest, Romania, 29 September–2 October 2019; pp. 1–5. [Google Scholar]
- Zhang, T.; Guo, N.; Sun, X.; Fan, J.; Yang, N.; Song, J.; Zou, Y. A Systematic Framework for State of Charge, State of Health and State of Power Co-Estimation of Lithium-Ion Battery in Electric Vehicles. Sustainability 2021, 13, 5166. [Google Scholar] [CrossRef]
- Ma, J.; Chen, B.; Wang, L.; Cui, G. Progress and Prospect on Failure Mechanisms of Solid-State Lithium Batteries. J. Power Sources 2018, 392, 94–115. [Google Scholar]
- Liu, Y. The Development History of Cathode and Anode Materials of Lithium Ion Battery. In Proceedings of the 7th International Conference on Education, Management, Information and Mechanical Engineering (EMIM 2017), Shenyang, China, 28–30 April 2017; Jing, W., Ning, X., Huiyu, Z., Eds.; Atlantis Press: Paris, France, 2017; Volume 76, pp. 1399–1402. [Google Scholar]
- Guo, R.; Shen, W. An Enhanced Multi-Constraint State of Power Estimation Algorithm for Lithium-Ion Batteries in Electric Vehicles. J. Energy Storage 2022, 50, 104628. [Google Scholar] [CrossRef]
- Lai, X.; He, L.; Wang, S.; Zhou, L.; Zhang, Y.; Sun, T.; Zheng, Y. Co-Estimation of State of Charge and State of Power for Lithium-Ion Batteries Based on Fractional Variable-Order Model. J. Clean. Prod. 2020, 255, 120203. [Google Scholar] [CrossRef]
- Farmann, A.; Sauer, D.U. A Comprehensive Review of On-Board State-of-Available-Power Prediction Techniques for Lithium-Ion Batteries in Electric Vehicles. J. Power Sources 2016, 329, 123–137. [Google Scholar]
- Shen, X.; Sun, B.; Qi, H.; Shen, X.; Su, X. Research on Peak Power Test Method for Lithium Ion Battery. Energy Procedia 2018, 152, 550–555. [Google Scholar] [CrossRef]
- Jin, C.; Sun, Y.; Zheng, Y.; Yang, X.; Lai, X.; Gu, H.; Feng, X. Experimental Investigation of State-of-Power Measurement for Lithium-Ion Batteries. Int. J. Energy Res. 2021, 45, 7549–7560. [Google Scholar] [CrossRef]
- Guo, R.; Shen, W. A Data-Model Fusion Method for Online State of Power Estimation of Lithium-Ion Batteries at High Discharge Rate in Electric Vehicles. Energy 2022, 254, 124270. [Google Scholar] [CrossRef]
- Tang, X.; Yao, K.; Liu, B.; Hu, W.; Gao, F. Long-Term Battery Voltage, Power, and Surface Temperature Prediction Using a Model-Based Extreme Learning Machine. Energies 2018, 11, 86. [Google Scholar] [CrossRef] [Green Version]
- Plett, G.L. High-Performance Battery-Pack Power Estimation Using a Dynamic Cell Model. IEEE Trans. Veh. Technol. 2004, 53, 1586–1593. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.; Wang, L.; Wang, L.; Liao, C.; Zhang, Y. Joint State-of-Charge and State-of-Available-Power Estimation Based on the Online Parameter Identification of Lithium-Ion Battery Model. IEEE Trans. Ind. Electron. 2022, 69, 3677–3688. [Google Scholar] [CrossRef]
- Yang, L.; Cai, Y.; Yang, Y.; Deng, Z. Supervisory Long-Term Prediction of State of Available Power for Lithium-Ion Batteries in Electric Vehicles. Appl. Energy 2020, 257, 114006. [Google Scholar] [CrossRef]
- Lin, P.; Jin, P.; Hong, J.; Wang, Z. Battery Voltage and State of Power Prediction Based on an Improved Novel Polarization Voltage Model. Energy Rep. 2020, 6, 2299–2308. [Google Scholar] [CrossRef]
- Liu, C.; Hu, M.; Jin, G.; Xu, Y.; Zhai, J. State of Power Estimation of Lithium-Ion Battery Based on Fractional-Order Equivalent Circuit Model. J. Energy Storage 2021, 41, 102954. [Google Scholar] [CrossRef]
- Tan, Y. Joint Estimation of Ternary Lithium-Ion Battery State of Charge and State of Power Based on Dual Polarization Model. Int. J. Electrochem. Sci. 2020, 1128–1147. [Google Scholar] [CrossRef]
- Pei, L.; Zhu, C.; Wang, T.; Lu, R.; Chan, C.C. Online Peak Power Prediction Based on a Parameter and State Estimator for Lithium-Ion Batteries in Electric Vehicles. Energy 2014, 66, 766–778. [Google Scholar] [CrossRef]
- Wei, C.; Benosman, M.; Kim, T. Online Parameter Identification for State of Power Prediction of Lithium-Ion Batteries in Electric Vehicles Using Extremum Seeking. Int. J. Control Autom. Syst. 2019, 17, 2906–2916. [Google Scholar] [CrossRef]
- Wang, J.; Wang, S.; Yu, C.; Li, B.; He, M. An Online Method for Power State Estimation of Lithium-Ion Batteries under the Constraints of the Fusion Model Considering Temperature Effect. Int. J. Electrochem. Sci. 2022, 17, 220764. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Y.; Wu, J.; Chen, Z. A Novel Method for Lithium-Ion Battery State of Energy and State of Power Estimation Based on Multi-Time-Scale Filter. Appl. Energy 2018, 216, 442–451. [Google Scholar] [CrossRef]
- Waag, W.; Fleischer, C.; Sauer, D.U. Adaptive On-Line Prediction of the Available Power of Lithium-Ion Batteries. J. Power Sources 2013, 242, 548–559. [Google Scholar] [CrossRef]









| Current | 4 | 20 | 40 | 60 | 80 | 100 | 120 |
|---|---|---|---|---|---|---|---|
| IR (lnA/A) | 0.402 | 0.152 | 0.0928 | 0.0685 | 0.0549 | 0.0461 | 0.0399 |
| Rp (mΩ) | 7.16 | 4.67 | 3.11 | 2.58 | 2.24 | 2.32 | 2.35 |
| Items | Parameter |
|---|---|
| Working voltage | 3.2 V |
| Nominal capacity | 8 Ah |
| Charging cutoff voltage | 3.65 V |
| Discharge cutoff Voltage | 2.5 V |
| Maximum charging current | 10 C |
| Maximum discharge current | 30 C |
| Operating temperature range | Discharge: 0~30 °C Charge: −20~60 °C |
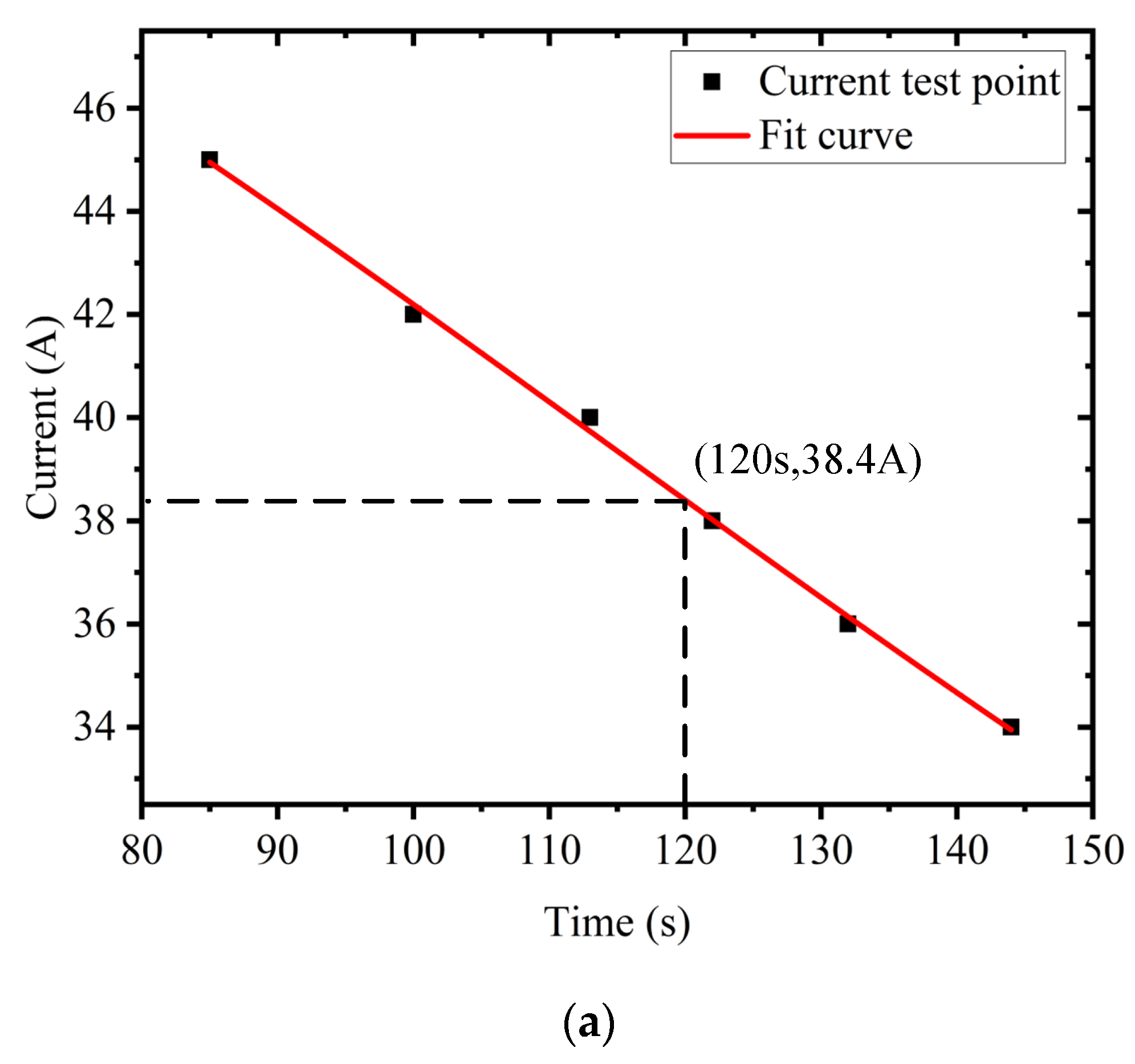
| SOC (%) | Discharge Current (A) | Discharge Time (s) |
|---|---|---|
| 70 | 129 | 115 |
| 127 | 117 | |
| 124 | 119 | |
| 120 | 124 | |
| 117 | 126 | |
| 115 | 129 | |
| 50 | 120 | 105 |
| 110 | 107 | |
| 105 | 114 | |
| 103 | 116 | |
| 100 | 125 | |
| 95 | 138 | |
| 20 | 45 | 85 |
| 42 | 100 | |
| 40 | 113 | |
| 38 | 122 | |
| 36 | 132 | |
| 34 | 144 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, J.; Wu, C.; Ma, C.; Yuan, Z.; Guo, Y.; Wang, R.; Wu, Y.; Sun, J.; Liu, L. An Adaptive Peak Power Prediction Method for Power Lithium-Ion Batteries Considering Temperature and Aging Effects. Processes 2023, 11, 2449. https://doi.org/10.3390/pr11082449
Ye J, Wu C, Ma C, Yuan Z, Guo Y, Wang R, Wu Y, Sun J, Liu L. An Adaptive Peak Power Prediction Method for Power Lithium-Ion Batteries Considering Temperature and Aging Effects. Processes. 2023; 11(8):2449. https://doi.org/10.3390/pr11082449
Chicago/Turabian StyleYe, Jilei, Chao Wu, Changlong Ma, Zijie Yuan, Yilong Guo, Ruoyu Wang, Yuping Wu, Jinlei Sun, and Lili Liu. 2023. "An Adaptive Peak Power Prediction Method for Power Lithium-Ion Batteries Considering Temperature and Aging Effects" Processes 11, no. 8: 2449. https://doi.org/10.3390/pr11082449
APA StyleYe, J., Wu, C., Ma, C., Yuan, Z., Guo, Y., Wang, R., Wu, Y., Sun, J., & Liu, L. (2023). An Adaptive Peak Power Prediction Method for Power Lithium-Ion Batteries Considering Temperature and Aging Effects. Processes, 11(8), 2449. https://doi.org/10.3390/pr11082449








