Seepage Simulation of Conglomerate Reservoir Based on Digital Core: A Case Study of the Baikouquan Formation in Mahu Sag, Junggar Basin
Abstract
:1. Introduction
2. Samples and Methods
3. Results and Discussion
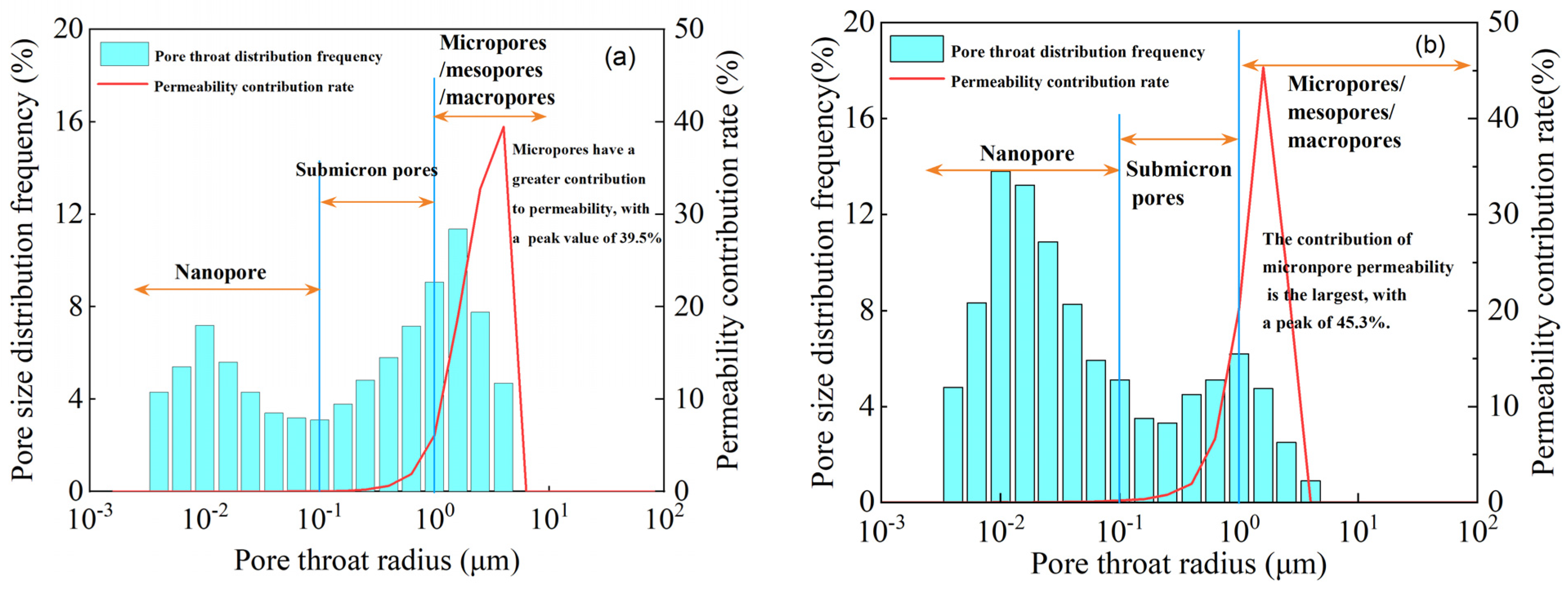
3.1. Pore Structure Characteristics
3.2. Micron CT Scale Pore Network Model
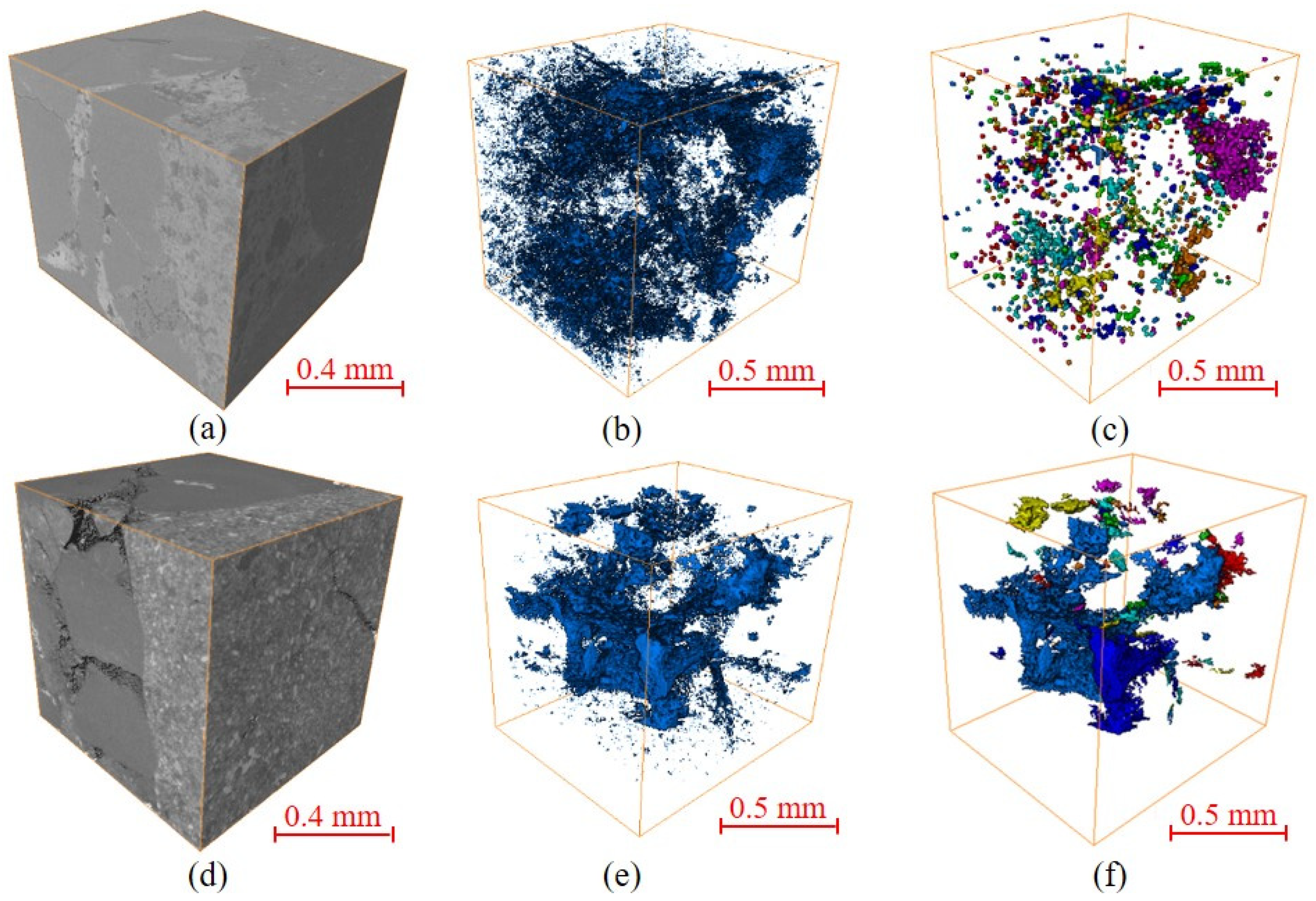
3.2.1. Characteristics of Micron-Scale 2-D Pore Structure
3.2.2. Characteristics of Micron-Scale 3-D Pore Structure
3.2.3. Pore Network Modeling
3.3. Fine-Scale Pore Network Model Based on MAPS
3.3.1. Nano-Submicron Pore Characteristics
3.3.2. Fine-Scale Pore Network Modeling
3.4. Construction of Two-Scale Pore Network Model
3.5. Pore Scale Seepage Simulation
3.5.1. Permeability Calculation
3.5.2. Pore Scale Flooding Simulation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhong, X.; Liu, L.; Wang, H.; Xu, Z.; Chen, H.; Wang, X.; Zhu, Y. Characteristics and origins of the modal pore throat structure in weakly cemented sandy conglomerate reservoirs. J. Pet. Sci. Eng. 2022, 208, 109470. [Google Scholar] [CrossRef]
- Xiao, M.; Wu, S.; Yuan, X.; Cao, Z.; Xie, Z. Diagenesis effects on the conglomerate reservoir quality of the Baikouquan Formation, Junggar Basin, China. J. Pet. Sci. Eng. 2020, 195, 107599. [Google Scholar] [CrossRef]
- Li, L.; Hao, Y.; Lv, Y.; Wang, C.; Yao, C.; Zhao, Q.; Xiao, P. Experimental investigation on low-velocity seepage characteristics and influencing factors in a shale oil reservoir. J. Pet. Sci. Eng. 2020, 195, 107732. [Google Scholar] [CrossRef]
- Lv, W.; Chen, S.; Gao, Y.; Kong, C.; Jia, N.; He, L.; Wang, R.; Li, J. Evaluating seepage radius of tight oil reservoir using digital core modeling approach. J. Pet. Sci. Eng. 2019, 178, 609–615. [Google Scholar] [CrossRef]
- Meng, M.; Peng, J.; Ge, H.; Ji, W.; Li, X.; Wang, Q. Rock Fabric of Lacustrine Shale and Its Influence on Residual Oil Distribution in the Upper Cretaceous Qingshankou Formation, Songliao Basin. Energy Fuels 2023, 37, 7151–7160. [Google Scholar] [CrossRef]
- Wei, J.; Zhang, A.; Li, J.; Liu, X.; Wang, A.; Yang, Y.; Zhou, X.; Zeng, Q.; Niu, Y. Study on oil seepage mechanisms in lamellar shale by using the lattice Boltzmann method. Fuel 2023, 351, 128939. [Google Scholar] [CrossRef]
- Dang, W.; Gao, G.; You, X.; Wu, J.; Liu, S.; Yan, Q.; He, W.; Guo, L. Genesis and distribution of oils in Mahu Sag, Junggar Basin, NW China. Pet. Explor. Dev. 2023, 50, 840–850. [Google Scholar] [CrossRef]
- Li, J.; Tang, Y.; Tao, W.; Zhao, J.; Wu, H.; Wu, W.; Bai, Y. Overpressure origin and its effects on petroleum accumulation in the conglomerate oil province in Mahu Sag, Junggar Basin, NW China. Pet. Explor. Dev. 2020, 47, 726–739. [Google Scholar] [CrossRef]
- Pal, A.K.; Garia, S.; Ravi, K.; Nair, A.M. Pore scale image analysis for petrophysical modelling. Micron 2022, 154, 103195. [Google Scholar] [CrossRef]
- Al-Kharusi, A.S.; Blunt, M.J. Network extraction from sandstone and carbonate pore space images. J. Pet. Sci. Eng. 2007, 56, 219–231. [Google Scholar] [CrossRef]
- Fan, N.; Wang, J.; Deng, C.; Fan, Y.; Guo, X. Quantitative characterization of coal microstructure and visualization seepage of macropores using CT-based 3D reconstruction. J. Nat. Gas Sci. Eng. 2020, 81, 103384. [Google Scholar] [CrossRef]
- Tan, M.; Su, M.; Liu, W.; Song, X.; Wang, S. Digital core construction of fractured carbonate rocks and pore-scale analysis of acoustic properties. J. Pet. Sci. Eng. 2021, 196, 107771. [Google Scholar] [CrossRef]
- Hasnan, H.K.; Sheppard, A.; Hassan, M.H.A.; Knackstedt, M.; Abdullah, W.H. Digital core analysis: Improved connectivity and permeability characterization of thin sandstone layers in heterolithic rocks. Mar. Pet. Geol. 2020, 120, 104549. [Google Scholar] [CrossRef]
- Dixon, M.; Newton, B.; Schwartz, A.; Smart, E.; Hooghan, K. Use of Digital Imaging for Improved Evaluation of Unconventional Reservoirs. In Proceedings of the SPE Reservoir Characterisation and Simulation Conference and Exhibition, Abu Dhabi, United Arab Emirates, 16–18 September 2013. [Google Scholar]
- Yuan, H.; You, Z.; Shapiro, A.; Bedrikovetsky, P. Improved population balance model for straining-dominant deep bed filtration using network calculations. Chem. Eng. J. 2013, 226, 227–237. [Google Scholar] [CrossRef]
- Yang, H.; Balhoff, M.T. Pore-network modeling of particle retention in porous media. AIChE J. 2017, 63, 3118–3131. [Google Scholar] [CrossRef]
- Naik, S.; Gerke, K.M.; You, Z.; Bedrikovetsky, P. Application of percolation, critical-path, and effective-medium theories for calculation of two-phase relative permeability. Phys. Rev. E 2021, 103, 043306. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Zhang, Y.; Wang, B. Evolution of the effective permeability for transient and pore-scale two-phase flow in real porous media. Int. J. Heat Mass Transf. 2017, 113, 1093–1105. [Google Scholar] [CrossRef]
- Van Dijke, M.I.J.; Sorbie, K.S.; Sohrabi, M.; Danesh, A. Three-phase flow WAG processes in mixed-wet porous media: Pore-scale network simulations and comparison with water-wet micromodel experiments. SPE J. 2004, 9, 57–66. [Google Scholar] [CrossRef]
- Lie, K.A.; Juanes, R. A front-tracking method for the simulation of three-phase flow in porous media. Comput. Geosci. 2005, 9, 29–59. [Google Scholar] [CrossRef]
- Wu, J.; Yang, S.; Gan, B.; Cao, Y.; Zhou, W.; Kou, G.; Zhao, B. Pore structure and movable fluid characteristics of typical sedimentary lithofacies in a tight conglomerate reservoir, Mahu depression, northwest China. ACS Omega 2021, 6, 23243–23261. [Google Scholar] [CrossRef]
- Zhou, Y.; Wu, S.; Li, Z.; Zhu, R.; Xie, S.; Zhai, X.; Lei, L. Investigation of microscopic pore structure and permeability prediction in sand-conglomerate reservoirs. J. Earth Sci. 2021, 32, 818–827. [Google Scholar] [CrossRef]
- Zhou, Y.; Wu, S.; Li, Z.; Zhu, R.; Xie, S.; Jing, C.; Lei, L. Multifractal study of three-dimensional pore structure of sand-conglomerate reservoir based on CT images. Energy Fuels 2018, 32, 4797–4807. [Google Scholar] [CrossRef]
- Xu, J.; Wu, K.; Li, R.; Li, Z.; Li, J.; Xu, Q.; Chen, Z. Real gas transport in shale matrix with fractal structures. Fuel 2018, 219, 353–363. [Google Scholar] [CrossRef]
- Xu, J.; Wu, K.; Yang, S.; Cao, J.; Chen, Z.; Pan, Y.; Yan, B. Real gas transport in tapered noncircular nanopores of shale rocks. AIChE J. 2017, 63, 3224–3242. [Google Scholar] [CrossRef]
- Andrä, H.; Combaret, N.; Dvorkin, J.; Glatt, E.; Han, J. Digital rock physics benchmarks—Part I: Imaging and segmentation. Comput. Geosci. 2013, 50, 25–32. [Google Scholar] [CrossRef]
- Dong, H.; Blunt, M.J. Pore-network extraction from micro-computerized-tomography images. Phys. Rev. E 2009, 80, 036307. [Google Scholar] [CrossRef] [PubMed]

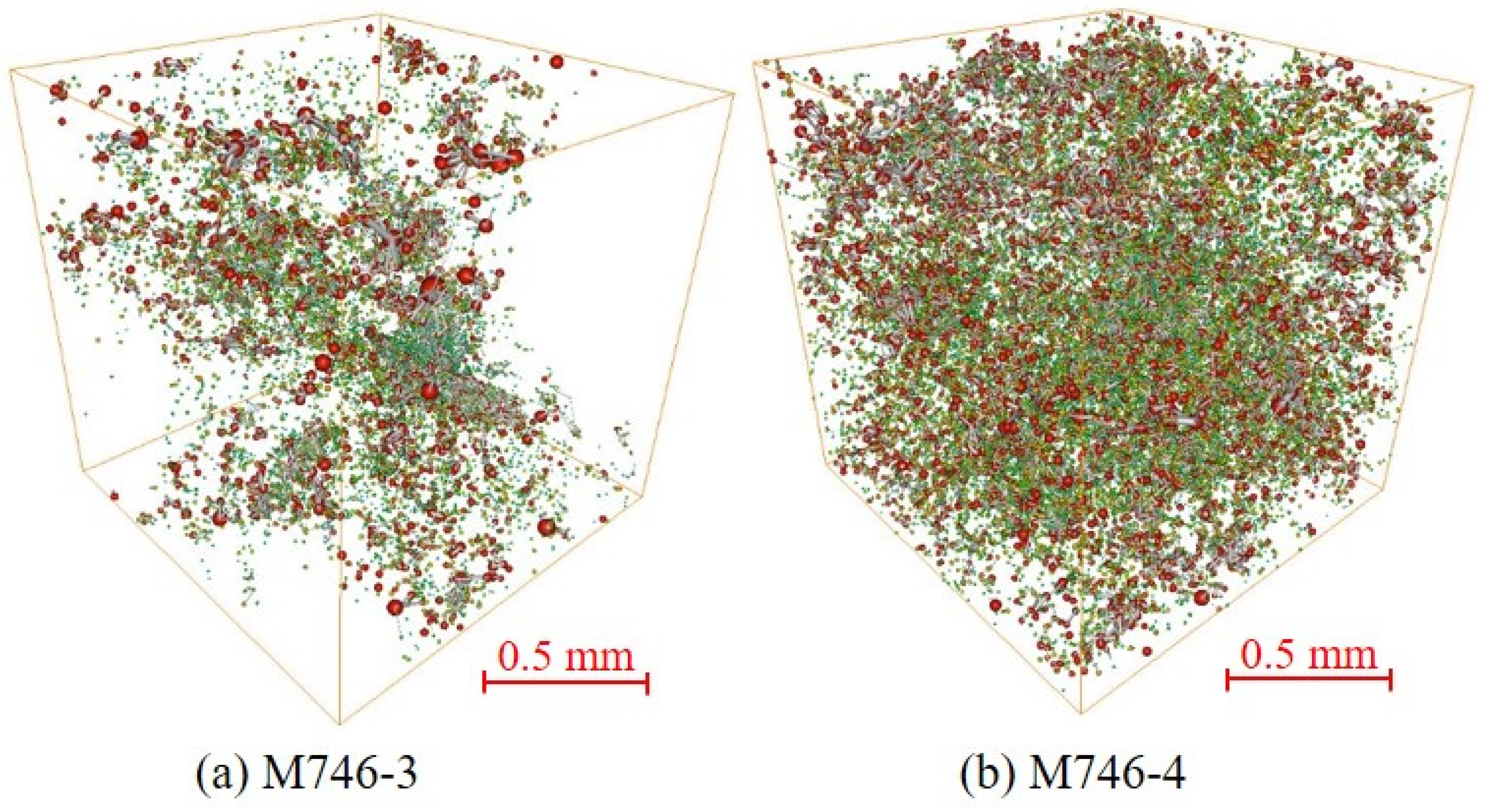




| Sample Number | Length (mm) | Diameter (mm) | Porosity (%) | Permeability (10−3 μm2) |
|---|---|---|---|---|
| M746-3 | 52.22 | 24.91 | 6.7 | 0.601 |
| M746-4 | 50.34 | 25.28 | 5.6 | 0.598 |
| Samples | Porosity (%) | Experimental Permeability (mD) | Simulated Permeability (mD) |
|---|---|---|---|
| M746-3 | 6.7 | 0.601 | 0.403 |
| M746-4 | 5.6 | 0.598 | 0.485 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, D.; Hu, H.; Dong, Y.; Wang, Y.; Liu, D.; Liu, H.; Du, M. Seepage Simulation of Conglomerate Reservoir Based on Digital Core: A Case Study of the Baikouquan Formation in Mahu Sag, Junggar Basin. Processes 2023, 11, 3185. https://doi.org/10.3390/pr11113185
Zhang D, Hu H, Dong Y, Wang Y, Liu D, Liu H, Du M. Seepage Simulation of Conglomerate Reservoir Based on Digital Core: A Case Study of the Baikouquan Formation in Mahu Sag, Junggar Basin. Processes. 2023; 11(11):3185. https://doi.org/10.3390/pr11113185
Chicago/Turabian StyleZhang, Daiyan, Haisheng Hu, Yan Dong, Yingwei Wang, Dunqing Liu, Hongxian Liu, and Meng Du. 2023. "Seepage Simulation of Conglomerate Reservoir Based on Digital Core: A Case Study of the Baikouquan Formation in Mahu Sag, Junggar Basin" Processes 11, no. 11: 3185. https://doi.org/10.3390/pr11113185





