Fracture Process and Failure Characteristics of Sandstone with Different Height-to-Diameter Ratios
Abstract
:1. Introduction
2. Size Effect Theory of Rock Masses
3. Mechanical Property Testing of Sandstone with Different Height-to-Diameter Ratios
3.1. Test Plan
3.2. Test Equipment
3.3. Sample Processing
3.4. Test Results and Analysis
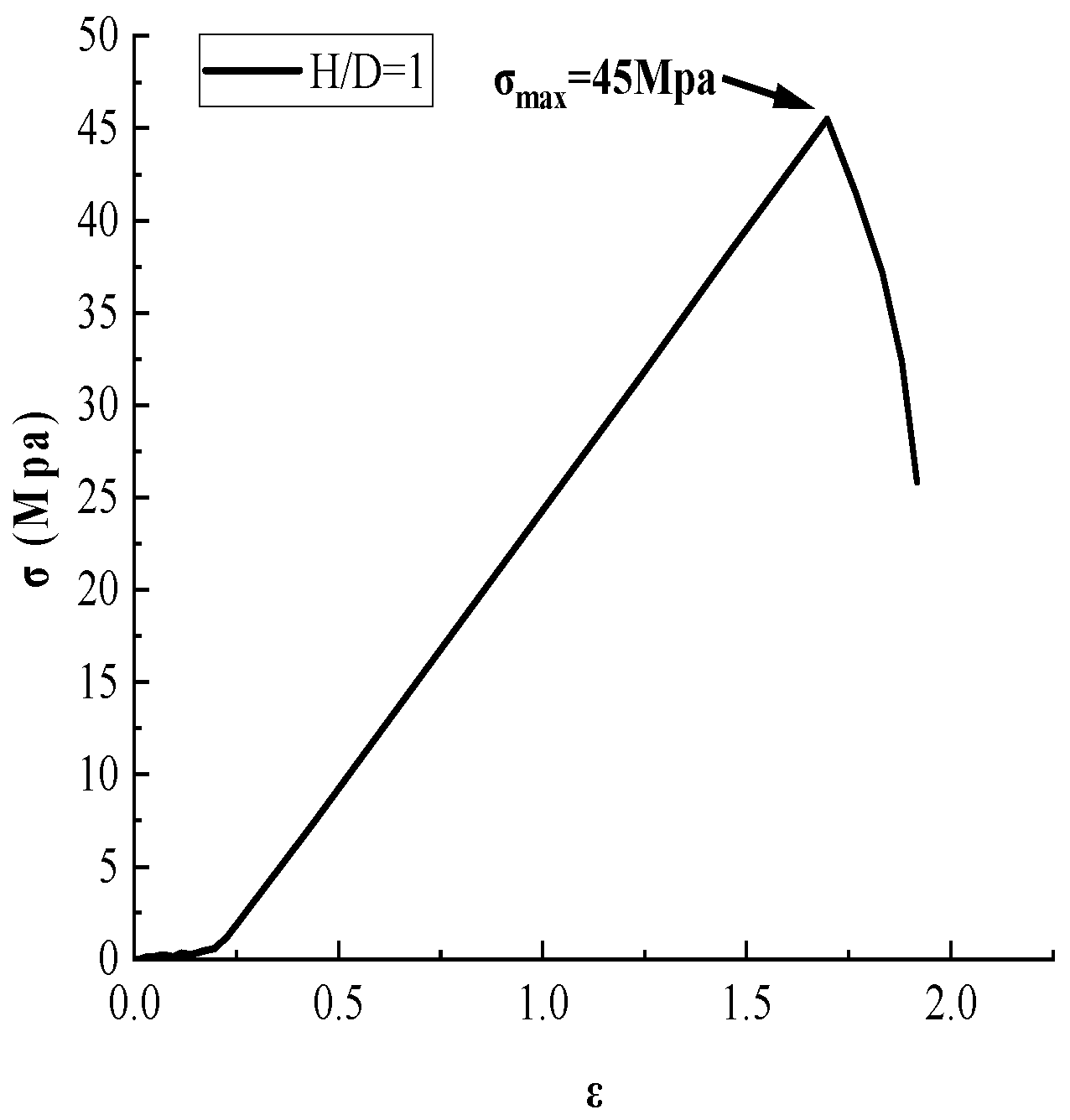
3.4.1. Analysis of Rock Failure Characteristics with a Height-to-Diameter Ratio of 1:1
3.4.2. Analysis of Rock Failure Characteristics with a Height-to-Diameter Ratio of 2:1
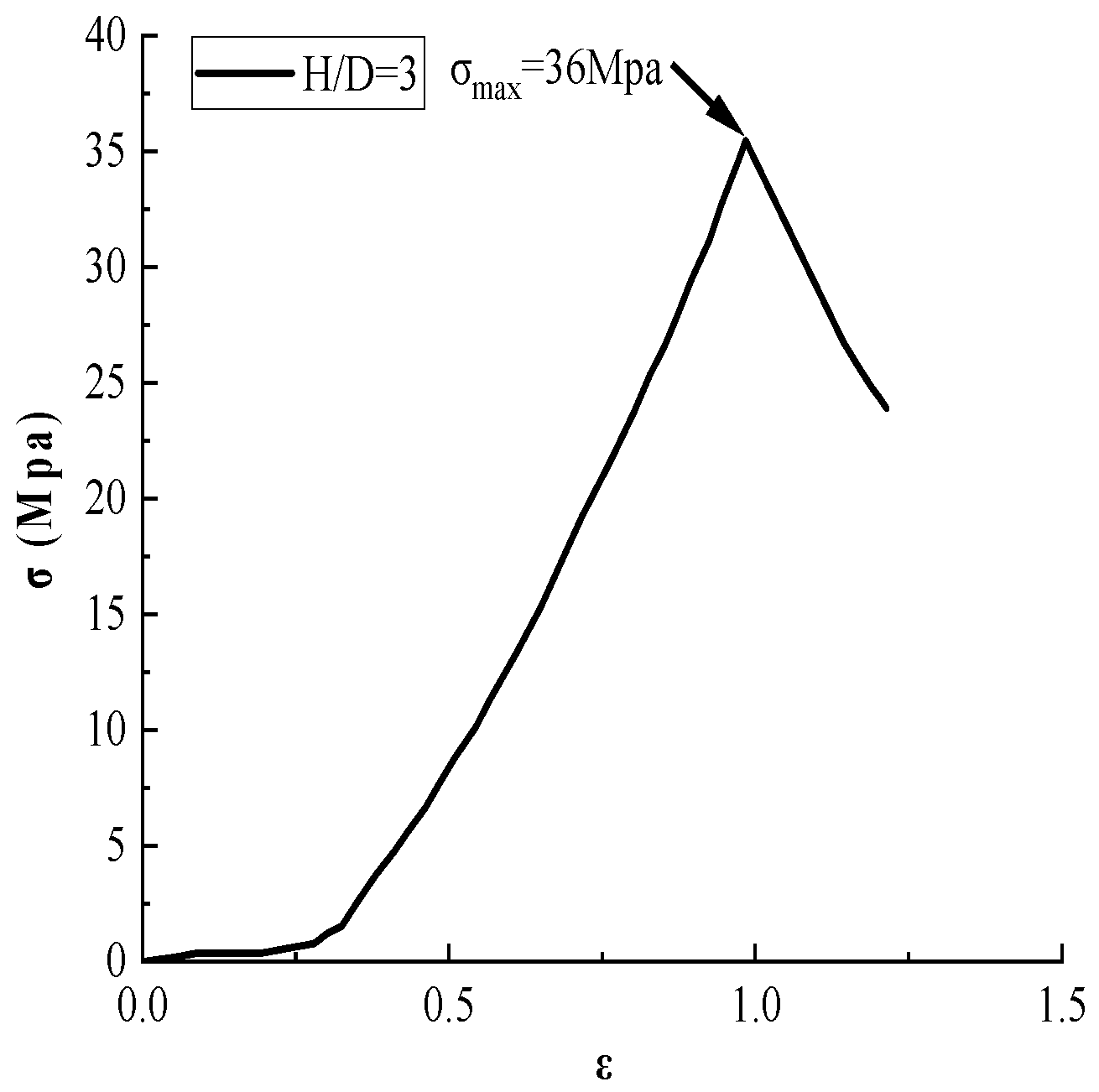
3.4.3. Analysis of Rock Failure Characteristics with a Height-to-Diameter Ratio of 3:1
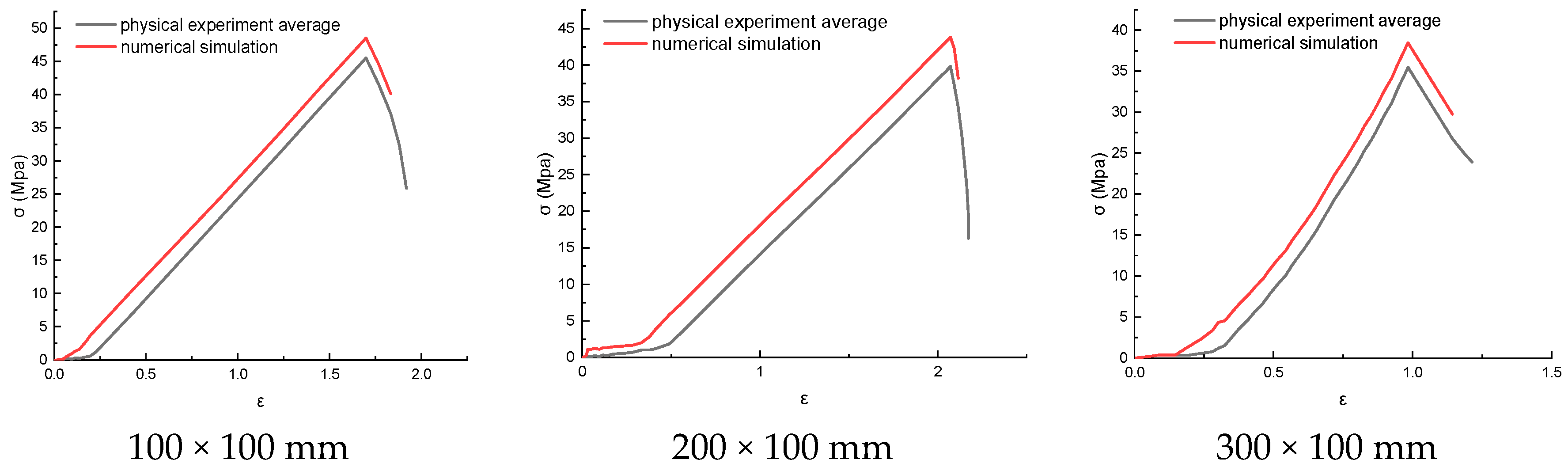
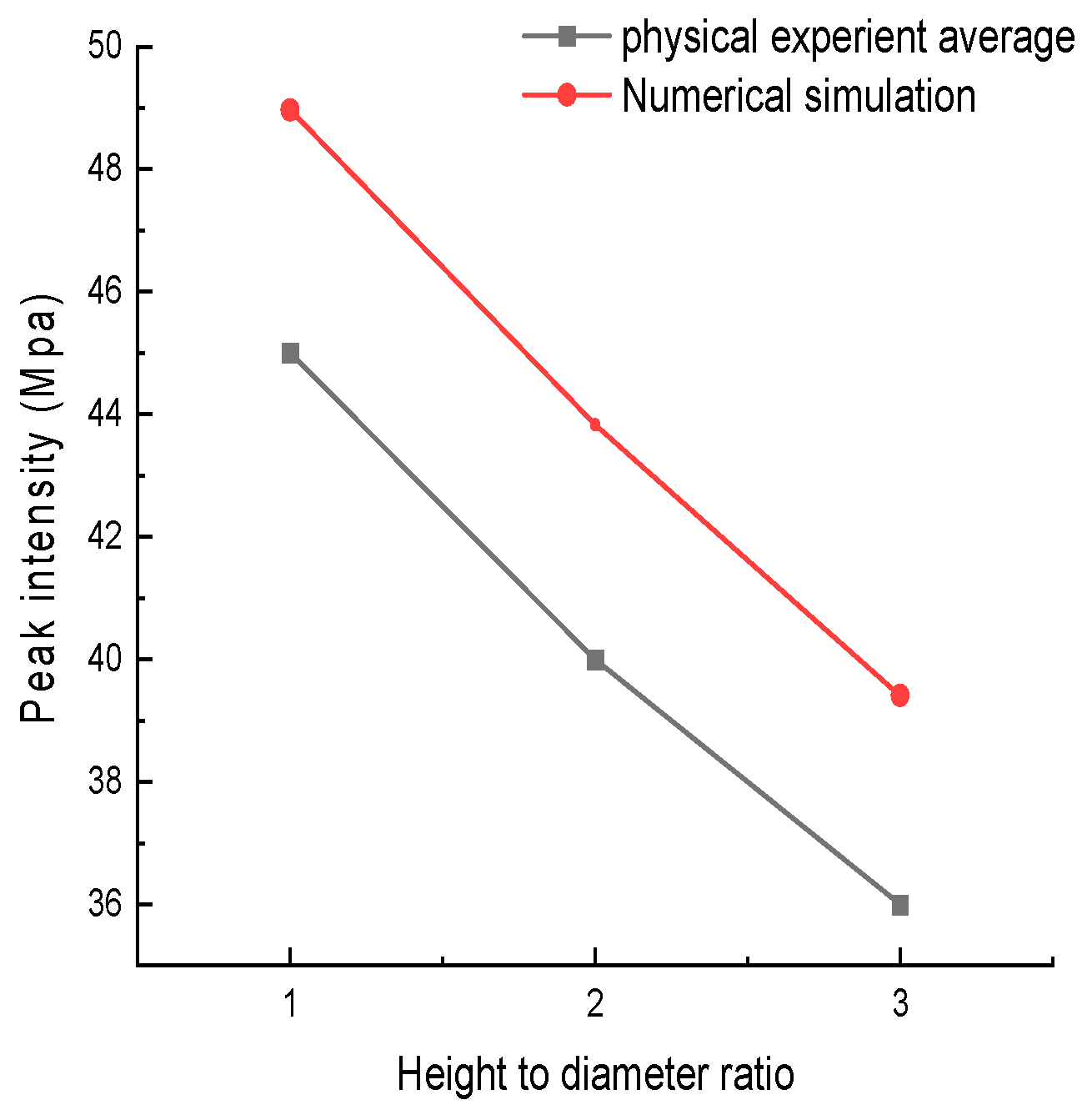
3.4.4. Comparative Analysis of Failure Characteristics of Rocks with Different Height-to-Diameter Ratios
4. Analysis of the Fracture Process of Rock Masses with Different Height-to-Diameter Ratios
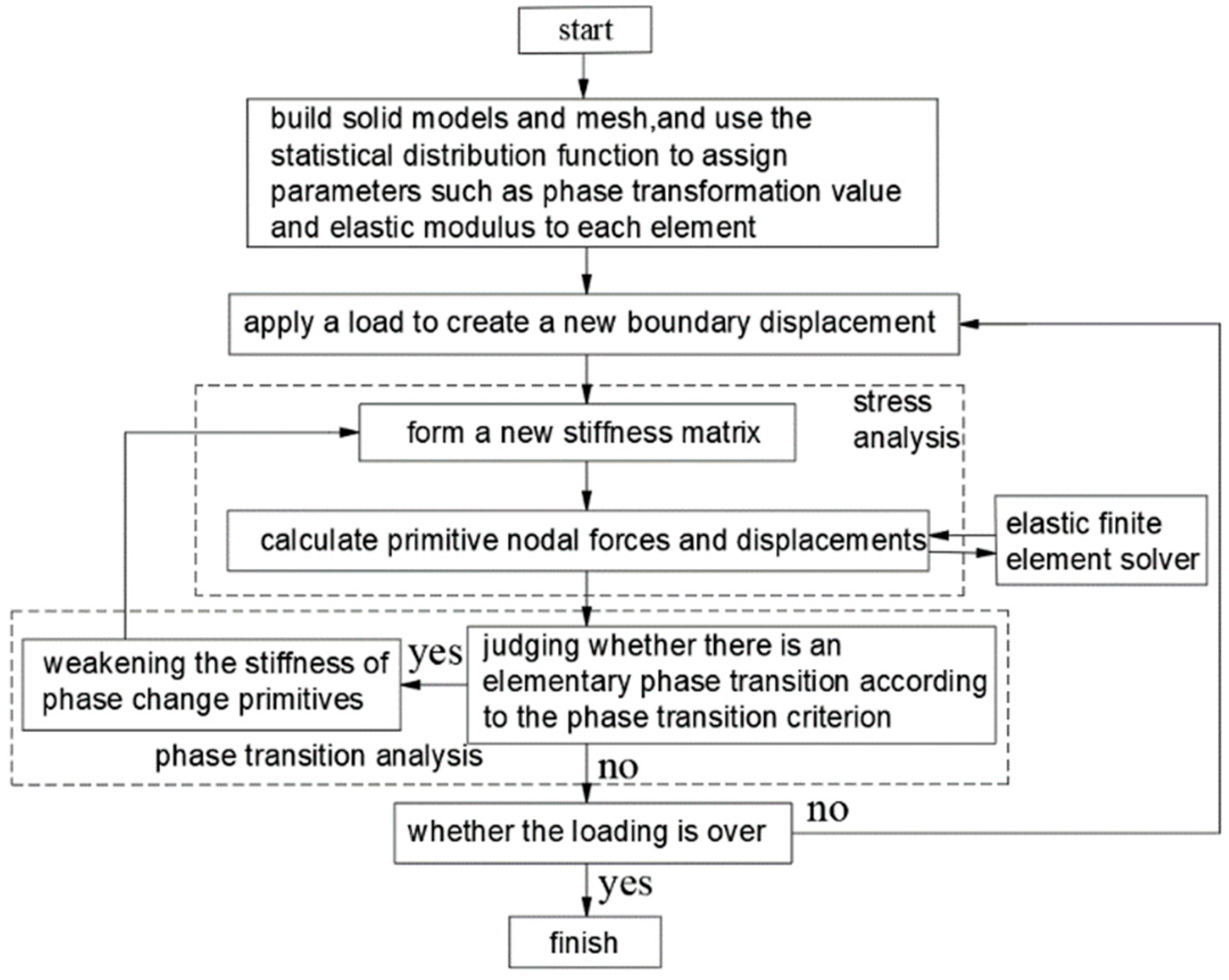
4.1. Real Rock Fracture Analysis System
4.2. Model Test Scheme Design
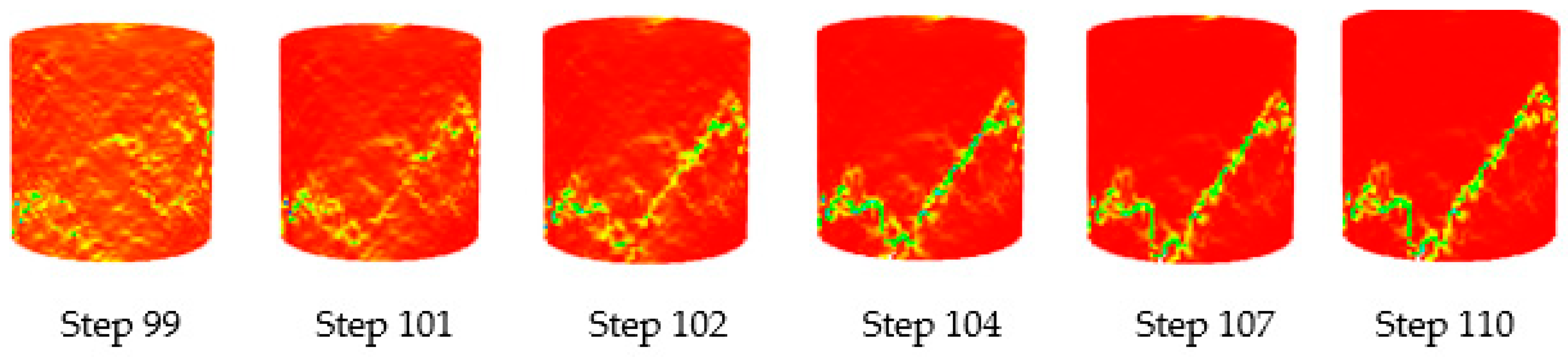
4.2.1. Analysis of Rock Failure Characteristics with a Height-to-Diameter Ratio of 1:1
4.2.2. Analysis of Rock Failure Characteristics with a Height-to-Diameter Ratio of 2:1
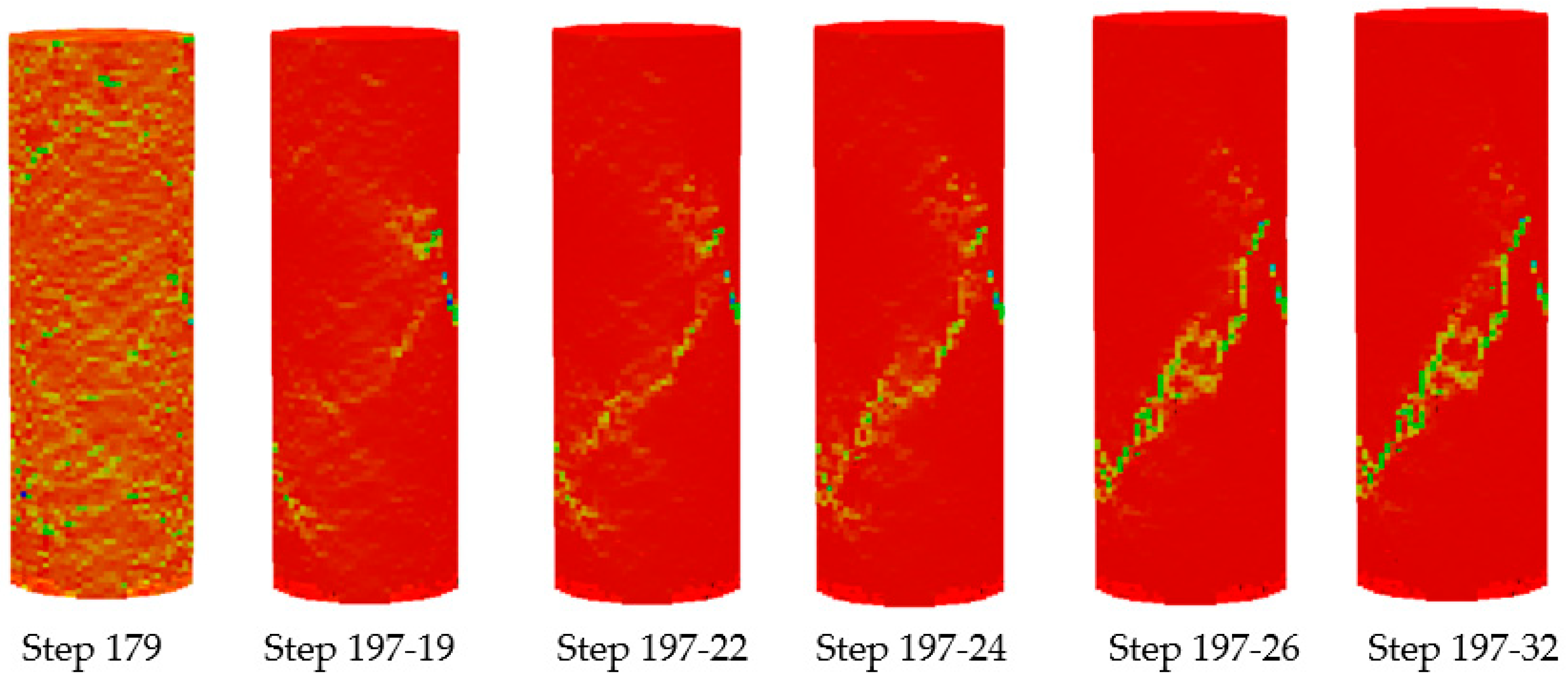
4.2.3. Analysis of Rock Failure Characteristics with a Height-to-Diameter Ratio of 3:1
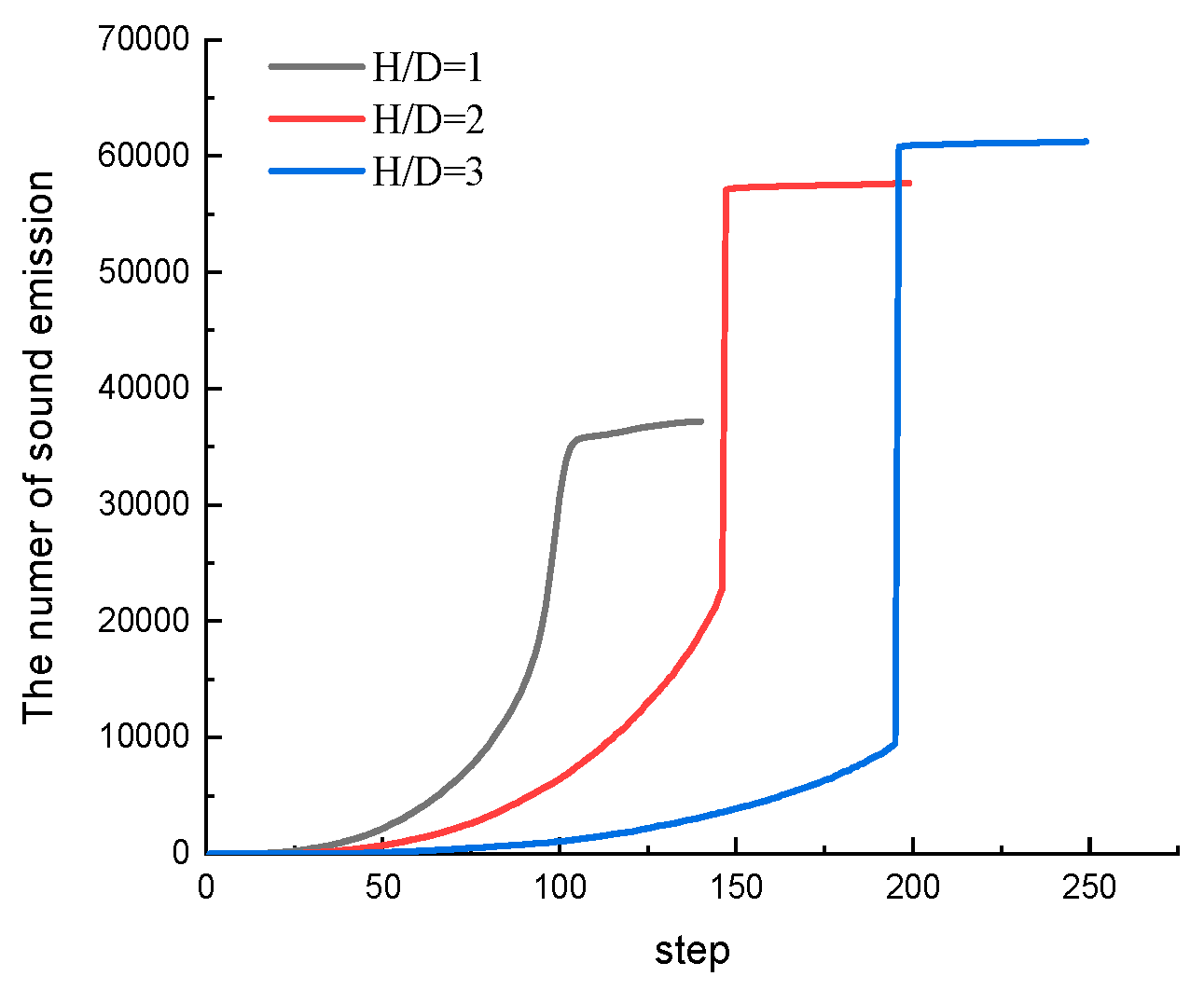
4.2.4. Comparative Analysis of Failure Characteristics of Rock Specimens with Different Height-to-Diameter Ratios
5. Conclusions
6. Future Work and Prospects
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ye, D. Stability Analysis and Reinforcement Measures of Road Tunnels crossing Coal Seam Goaf Groups. Ph.D. Dissertation, Kunming University of Science and Technology, Kunming, China, 2021. [Google Scholar]
- Hosung, S.; Carlos, J.S. Numerical study of fractured rock masses: Transverse isotropy vs. implicit joint-continuum models. Comput. Geotech. 2021, 138, 104317. [Google Scholar]
- Yan, B.; Qi, Q.; Liu, J.; Cai, M.; Li, X.; Wang, P. Fracture propagation and permeability evolution mechanism of jointed rock mass in coastal mines. Rock Mech. Rock Eng. 2022, 56, 2763–2778. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, S.; Zheng, R.; Li, H. Quantitative Characterization of Tight Rock Microstructure of Digital Core. Geofluids 2022, 2022, 3554563. [Google Scholar] [CrossRef]
- Kumar, A.G.; Kanti, M.M. Evaluating Road-Cut Slope Stability Using Newly Proposed Stability Charts and Rock Microstructure: An Example from Dharasu-Uttarkashi Roadway, Lesser Himalayas, India. Rock Mech. Rock Eng. 2022, 55, 3959–3995. [Google Scholar]
- Huang, D.; Chang, X.; Tan, Y.; Fang, K.; Yin, Y. From rock microstructure to macromechanical properties based on fractal dimensions. Adv. Mech. Eng. 2019, 11, 1–13. [Google Scholar] [CrossRef]
- You, M.; Hua, A. Scale effect of uniaxial compression of rock samples and pillar bearing performance. Chin. J. Coal 1997, 22, 39–43. [Google Scholar]
- Das, A.J.; Mandal, P.K.; Ghosh, N.; Singh, A.P.; Kumar, R.; Tewari, S.; Bhattacharjee, R. Evaluation of energy accumulation, strain burst potential and stability of rock mass during underground extraction of a highly stressed coal seam under massive strata—A field study. Eng. Geol. 2023, 322, 107178. [Google Scholar] [CrossRef]
- Jiang, Z.; Guo, W.; Xie, S. Coal Pillar Size Determination and Surrounding Rock Control for Gob-Side Entry Driving in Deep Soft Coal Seams. Processes 2023, 11, 2331. [Google Scholar] [CrossRef]
- Li, Q.; Li, J.; Wang, Z.; Li, K.; Zhang, C. Study on Coal Pillar Size Design Based on Non-integral Contact Structure of Coal and Rock Under Static and Dynamic Loads. Front. Mater. 2021, 8, 721713. [Google Scholar] [CrossRef]
- Yang, R.; Zhu, Y.; Li, Y.; Li, W.; Lin, H. Coal pillar size design and surrounding rock control techniques in deep longwall entry. Arab. J. Geosci. 2020, 13, 453. [Google Scholar] [CrossRef]
- Meng, Z.X. Optimization Studies on Pillar Size of Fully Mechanized Caving Face. Adv. Mater. Res. 2014, 3384, 1010–1012. [Google Scholar] [CrossRef]
- Zhang, G.C.; He, F.L.; Jia, H.G.; Lai, Y.H. Analysis of Gateroad Stability in Relation to Yield Pillar Size: A Case Study. Rock Mech. Rock Eng. 2017, 50, 1263–1278. [Google Scholar] [CrossRef]
- Zhou, J.; Zhao, G.; Meng, X.; Liu, C.; Ma, L.; Xu, W.; Cheng, X. Experimental Investigation of the Size Effect of Rock under Impact Load. Minerals 2022, 13, 43. [Google Scholar] [CrossRef]
- Zhao, Y.; Mishra, B.; Shi, Q.; Zhao, G. A Size-Dependent Bonded-Particle Model for Transversely Isotropic Rock and its Application in Studying the Size Effect of Shale. Geotech. Geol. Eng. 2022, 40, 5437–5453. [Google Scholar] [CrossRef]
- Kun, Q. Pillar Design Based on Sandstone Pillar Strength Characteristics and Failure Mechanism. Ph.D. Dissertation, China University of Mining and Technology, Beijing, China, 2015. [Google Scholar]
- Ohtsu, M. Acoustic emission theory for moment tensor analysis. Res. Nondestruct. Valuat. 1995, 6, 169–184. [Google Scholar] [CrossRef]
- Chang, S.H.; Lee, C.I. Estimation of cracking and damage mechanisms in rock under triaxial compression by moment tensor analysis of acoustic emission. Int. J. Rock Mech. Min. Sci. 2004, 41, 1069–1086. [Google Scholar] [CrossRef]
- Jansen, D.P.; Carlson, S.R.; Young, R.P.; Hutchins, D.A. Ultrasonic imaging, and acoustic emission monitoring of thermally induced microcracks in Lac du Bonnet granite. J. Geophys. Res. Solid Earth 1993, 98, 22231. [Google Scholar] [CrossRef]
- Du, K.; Su, R.; Tao, M.; Yang, C.; Momeni, A.; Wang, S. Specimen shape and cross-section effects on the mechanical properties of rocks under uniaxial compressive stress. Bull. Eng. Geol. Environ. 2019, 78, 6061–6074. [Google Scholar] [CrossRef]
- Komurlu, E. Loading rate conditions and specimen size effect on strength and deformability of rock materials under uniaxial compression. Int. J. Geo-Eng. 2018, 9, 1–11. [Google Scholar] [CrossRef]
- Daraei, A.; Sharifi, F.; Qader, D.N.; Hama Ali, H.F.; Kolivand, F. Prediction of the static elastic modulus of limestone using downhole seismic test in Asmari formation. Acta Geophys. 2023, 1–9. [Google Scholar] [CrossRef]
- Daraei, A.; Zare, S. Determination of critical saturation degree in rocks based on maximum loss of uniaxial compression strength and deformation modulus. Geomech. Geophys. Geo-Energy Geo-Resour. 2018, 4, 343–353. [Google Scholar] [CrossRef]
- Su, H.J.; Jing, H.W.; Mao, X.B.; Zhao, H.H.; Yin, Q.; Wang, C. Size effect of sandstone after high temperature under uniaxial compression. J. Cent. South Univ. 2015, 22, 1901–1908. [Google Scholar] [CrossRef]
- Wang, Q.; Chen, J.; Guo, J.; Luo, Y.; Wang, H.; Liu, Q. Acoustic emission characteristics and energy mechanism in karst limestone failure under uniaxial and triaxial compression. Bull. Eng. Geol. Environ. 2019, 78, 1427–1442. [Google Scholar] [CrossRef]
- Gong, F.; Yan, J.; Li, X. Criteria for rockburst tendency based on linear energy storage law and residual elastic energy index. Chin. J. Rock Mech. Eng. 2018, 37, 1993–2014. [Google Scholar]
- Wang, J.; Zuo, T.; Li, X.; Tao, Z.; Ma, J. Study on the fractal characteristics of the pomegranate biotite schist under impact loading. Geofluids 2021, 2021, 1570160. [Google Scholar] [CrossRef]
- Zhang, Z.; Qian, Q.; Wang, H.; Huang, Y.; Wang, J.; Liu, H. Study on the dynamic mechanical properties of metamorphic limestone under impact loading. Lithosphere 2021, 2021, 8403502. [Google Scholar] [CrossRef]
- Zuo, T.; Zhao, Z.; Wang, J.; Li, X.; Tao, Z.; Yang, C. Analysis of dynamic damage fractal and energy consumption characteristics of dolomite marble. Shock Vib. 2022, 2022, 9440222. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, C.; Jiang, J.; Huang, W.; Guo, D.; Sheng, T. Vibration characteristics and isolation in vibration-sensitive areas under moving vehicle load. Soil Dyn. Earthq. Eng. 2022, 153, 107077. [Google Scholar] [CrossRef]
- Honglu, F.; Xiaohe, X.; Chunan, T. Application of catastrophe theory on unstable failure of rock and experimental verification. China Mining Magazine, 1995. [Google Scholar]
- Li, Y. Numerical simulation of rock sample fracture process based on multifractal theory. J. Liaoning Univ. Sci. Technol. 2016, 39, 76–80. [Google Scholar]
- Jia, G.; Kang, L. Study on the stability of coal pillars for roadway protection in fully mechanized caving mining. Chin. J. Coal 2002, 1, 6–10. [Google Scholar]
- Zhang, P. Simulation study on size effect of large-section rectangular roadway. Coal Technol. 2018, 37, 119–122. [Google Scholar] [CrossRef]
- You, M.; Hua, A. The failure mode and bearing capacity reduction of rock samples under uniaxial compression. Chin. J. Rock Mech. Eng. 1998, 3, 292–296. [Google Scholar]
- Guo, Y.; Zhao, Y.; Feng, G.; Ran, H.; Zhang, Y. Study on the damage size effect of gangue cemented backfill under uniaxial compression damage. Chin. J. Rock Mech. Eng. 2021, 40, 2434–2444. [Google Scholar]
- Wang, L.; Xiong, Z.; Su, C. Analysis of Size Effect and Failure Characteristics of Modified High-Water Filling Pillar Materials. Coal Sci. Technol. 2021, 49. [Google Scholar]
- Fu, W. Experimental study on size effect of uniaxial compressive strength of rocks with different aspect ratios. Resour. Environ. Eng. 2019, 33, 232–234. [Google Scholar]
- Han, S. Research on Scale Effect and Slenderness Ratio Effect of Rock Mass Characteristics. Ph.D. Dissertation, Taiyuan University of Technology, Taiyuan, China, 2007. [Google Scholar]
- Xiong, Q.; Lin, Q.; Hampton, J.C. Temporal evolution of a shear-type rock fracture process zone (FPZ) along continuous, sequential and spontaneously well-separated laboratory instabilities—From intact rock to thick gouged fault. Geophys. J. Int. 2021, 226, 351–367. [Google Scholar] [CrossRef]
- Zhang, H.; Sun, Q.; Ge, Z. Analysis of the characteristics of magnetic properties change in the rock failure process. Acta Geophys. 2020, 68, 289–302. [Google Scholar] [CrossRef]











| Height-to-Diameter Ratio H/D | Numbering | H (mm) | D (mm) | Actual Aspect Ratio H/D |
|---|---|---|---|---|
| 1 | 10A | 100.1 | 99.8 | 1.0 |
| 10B | 100.2 | 99.8 | 1.0 | |
| 10C | 100.2 | 99.8 | 1.0 | |
| 2 | 20A | 200.2 | 99.8 | 2.0 |
| 20B | 200.3 | 99.8 | 2.0 | |
| 20C | 200.2 | 99.8 | 2.0 | |
| 3 | 30A | 300.1 | 99.8 | 3.0 |
| 30B | 300.3 | 99.8 | 3.0 | |
| 30C | 300.2 | 99.8 | 3.0 |
| Numbering | Elastic Modulus (Gpa) | Compressive Strength (MPa) | Average Strength (MPa) |
|---|---|---|---|
| 10A | 29.7 | 45.3 | 45.0 |
| 10B | 29.8 | 47.5 | |
| 10C | 29.9 | 42.2 | |
| 20A | 24.6 | 43.5 | 40.0 |
| 20B | 25.4 | 39.8 | |
| 20C | 25.0 | 36.7 | |
| 30A | 20.7 | 34.6 | 36.0 |
| 30B | 21.4 | 38.4 | |
| 30C | 20.9 | 35.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, C.; Li, M.; Yan, X.; Deng, T.; Zhang, J. Fracture Process and Failure Characteristics of Sandstone with Different Height-to-Diameter Ratios. Processes 2023, 11, 3069. https://doi.org/10.3390/pr11113069
Zhang C, Li M, Yan X, Deng T, Zhang J. Fracture Process and Failure Characteristics of Sandstone with Different Height-to-Diameter Ratios. Processes. 2023; 11(11):3069. https://doi.org/10.3390/pr11113069
Chicago/Turabian StyleZhang, Chengliang, Mingjian Li, Xiang Yan, Tao Deng, and Jinrui Zhang. 2023. "Fracture Process and Failure Characteristics of Sandstone with Different Height-to-Diameter Ratios" Processes 11, no. 11: 3069. https://doi.org/10.3390/pr11113069





