Laser Doppler Velocimetry Test of Flow Characteristics in Draft Tube of Model Pump Turbine
Abstract
:1. Introduction
2. Materials and Methods
2.1. Draft Tube Testing Program
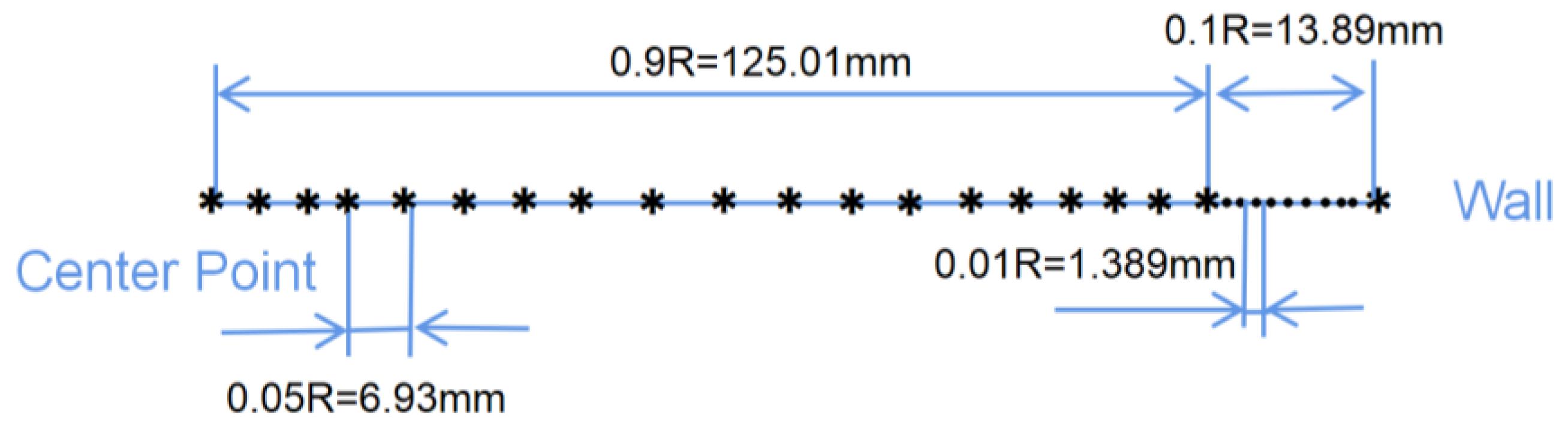
2.1.1. Test Location and Distribution of Test Points
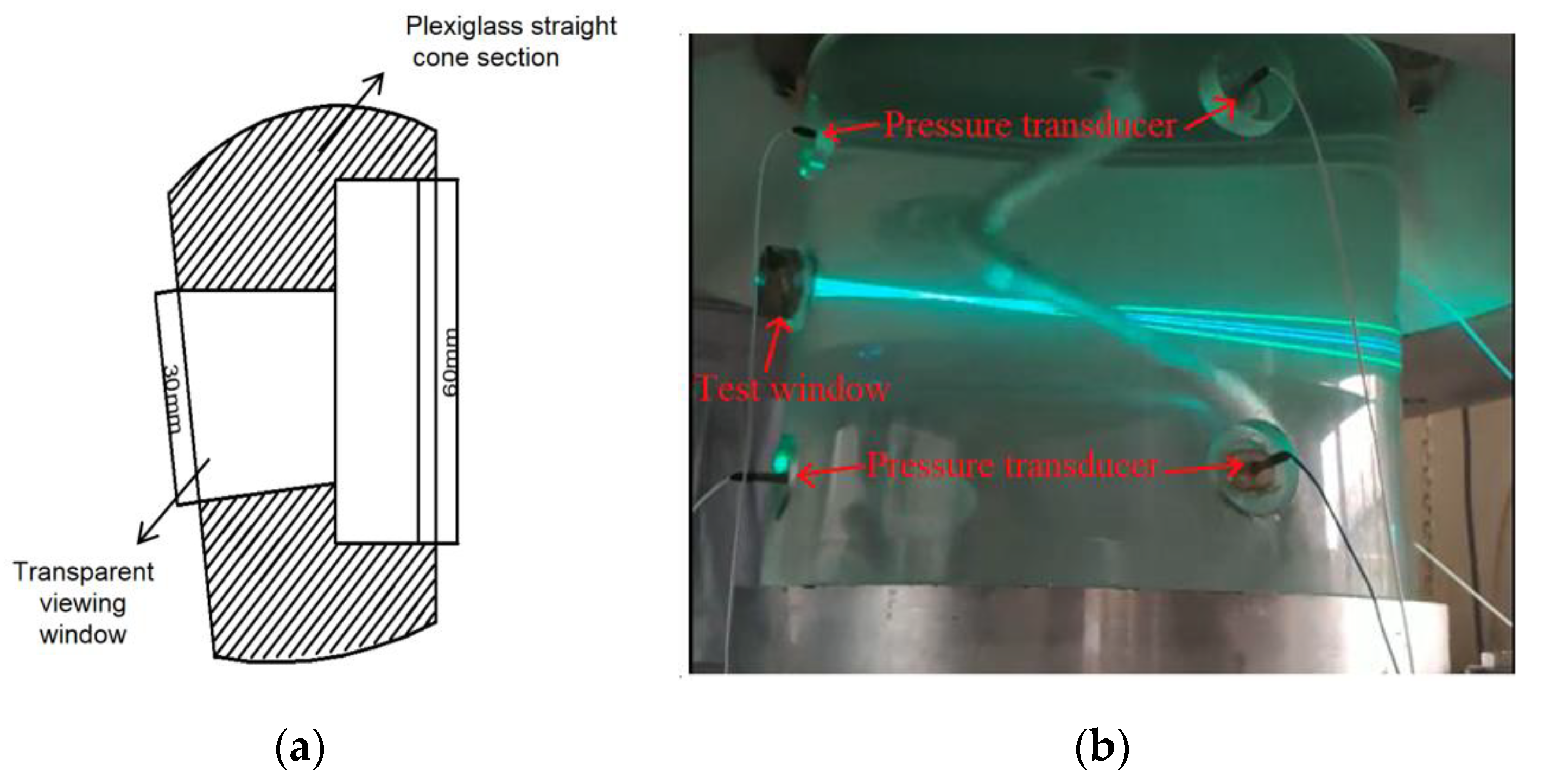
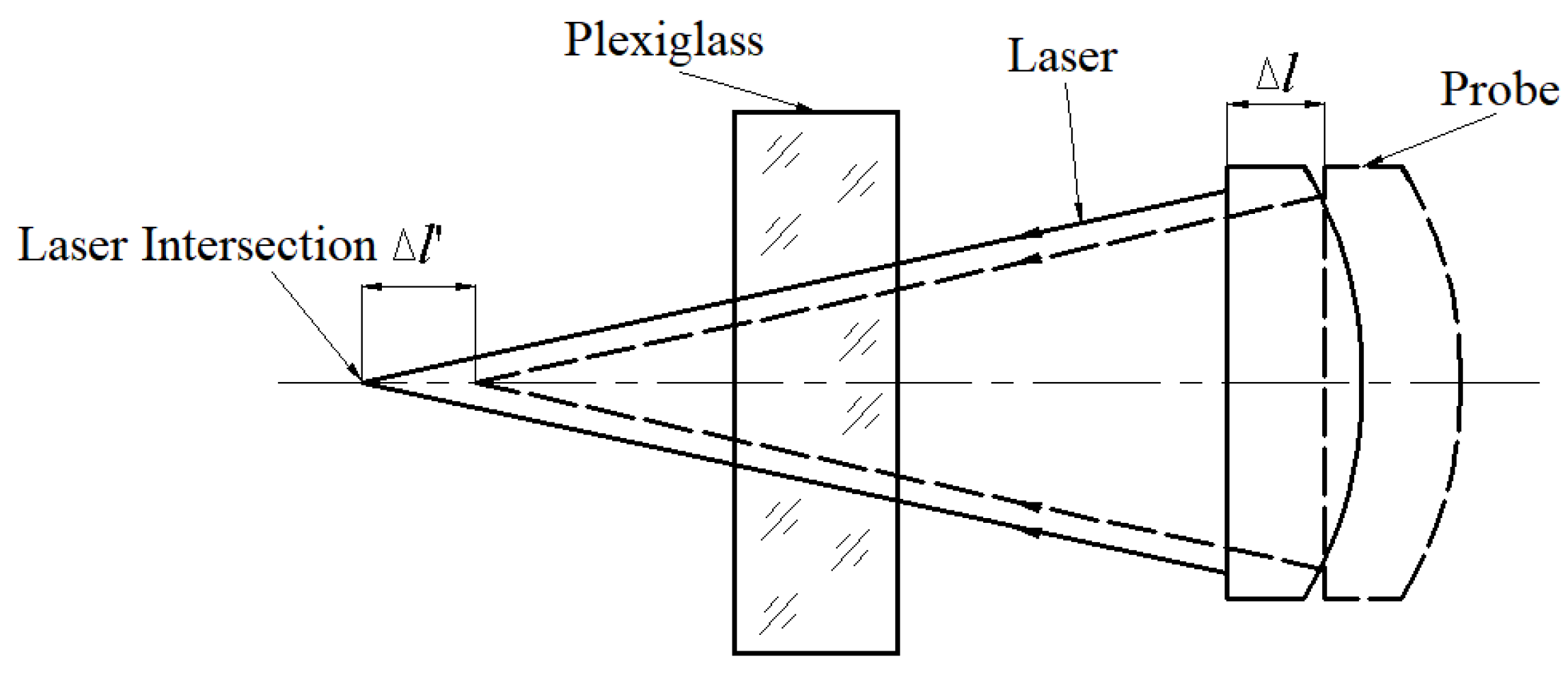
2.1.2. Draft Tube Transparency and Light Path Positioning
2.2. LDV Test Measurement Error Analysis
2.2.1. Repeatability Test
2.2.2. Integral Flow Rate and Flow Meter Flow Deviation
2.2.3. Error Analysis
3. Results
3.1. Analysis of LDV Test Results
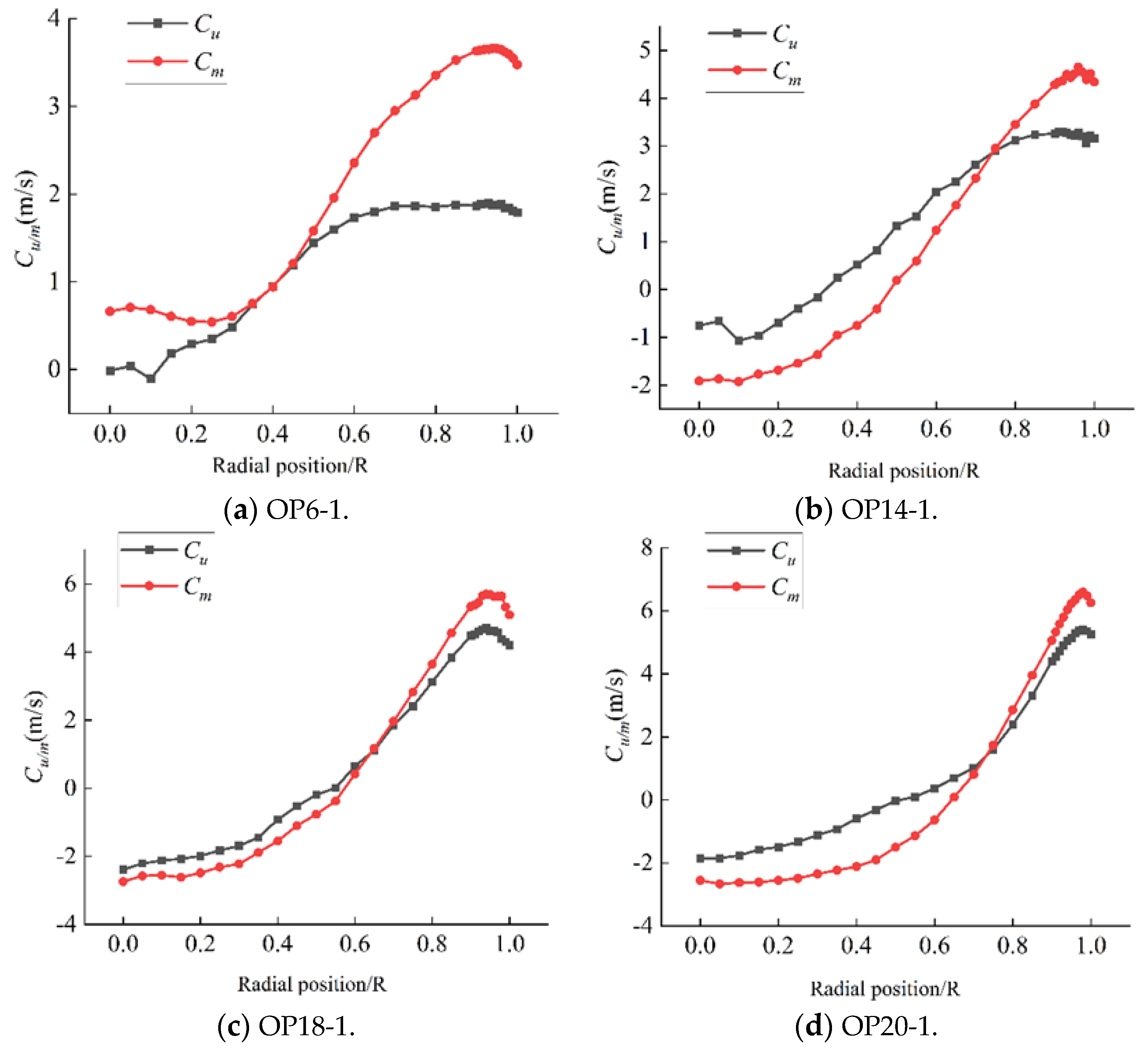
3.1.1. LDV Testing for Hydraulic Turbine Operating Conditions
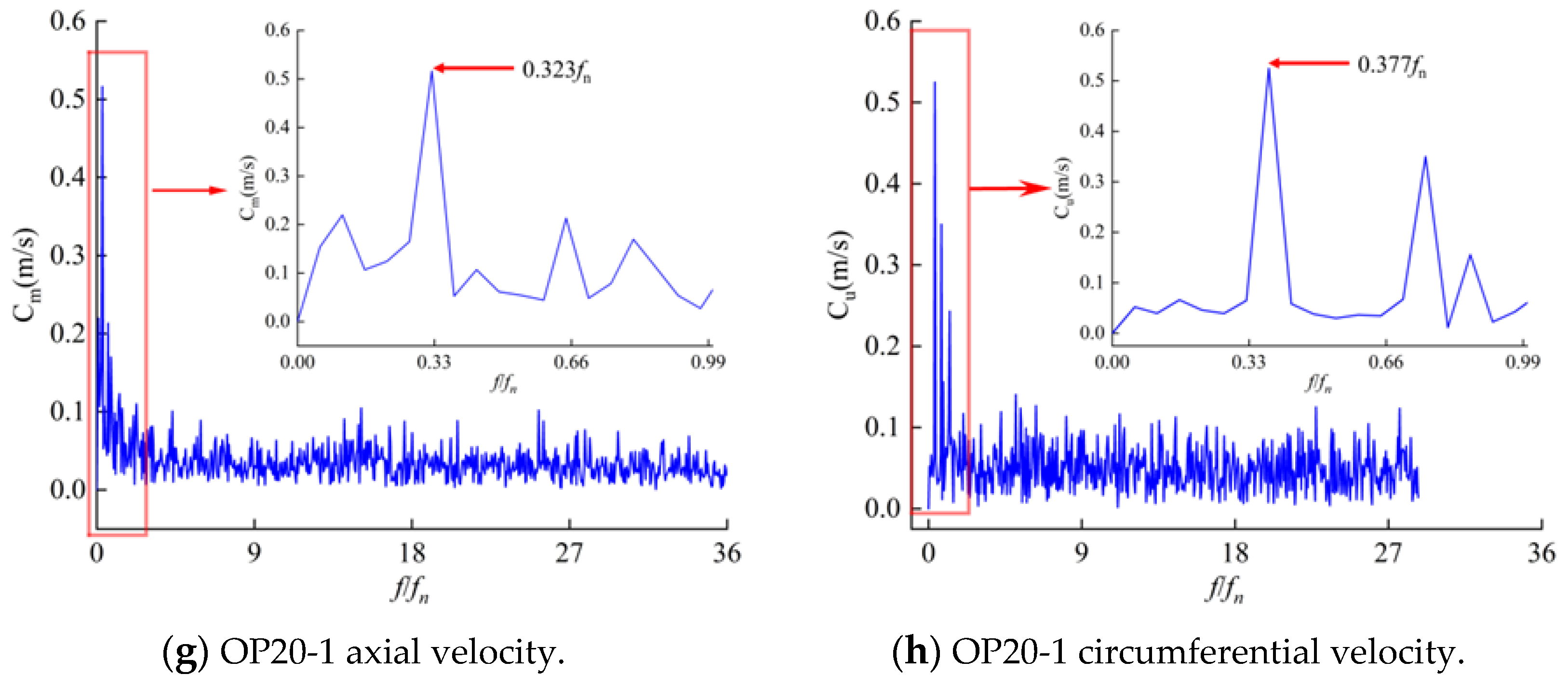
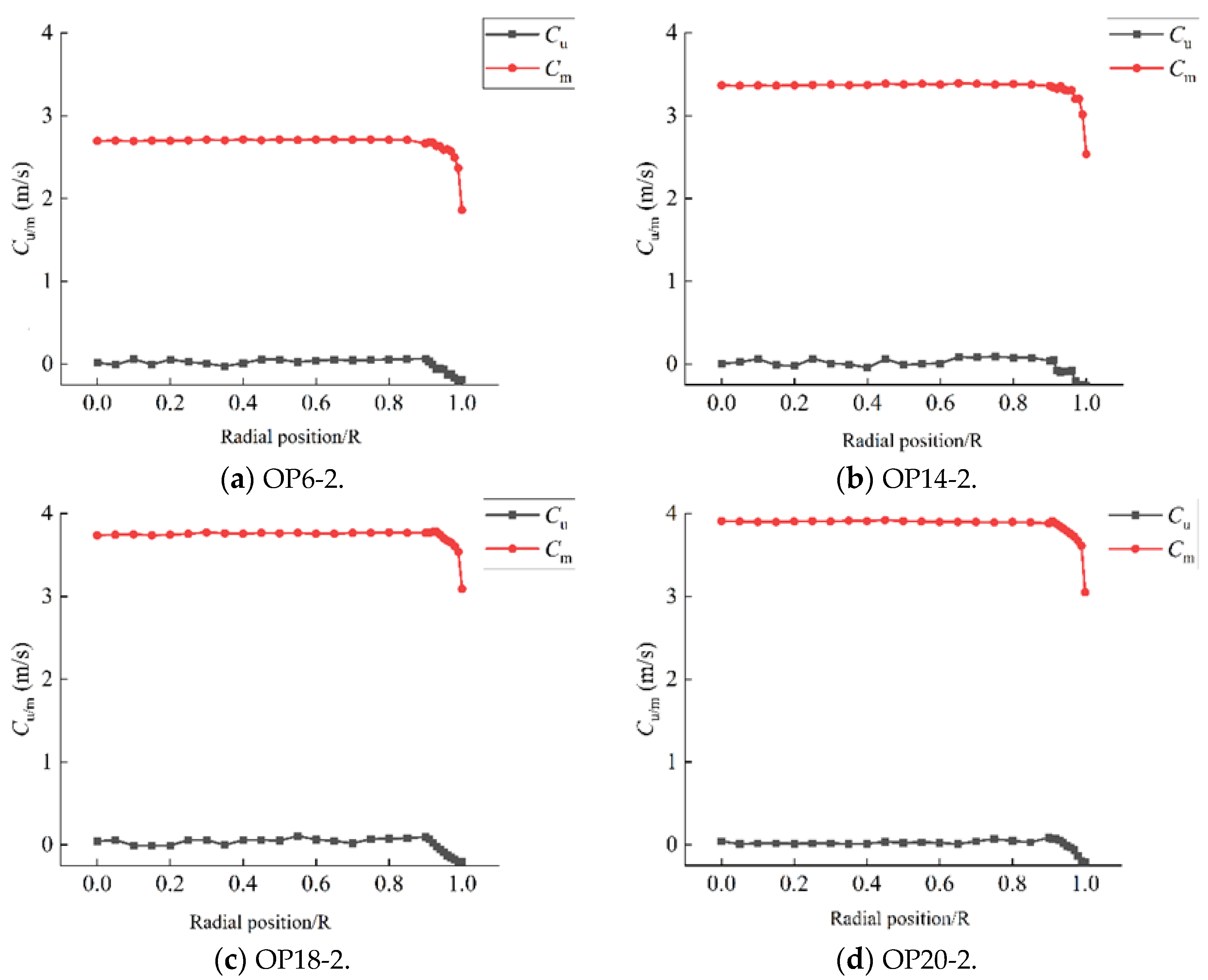
3.1.2. LDV Test for Water Pump Conditions
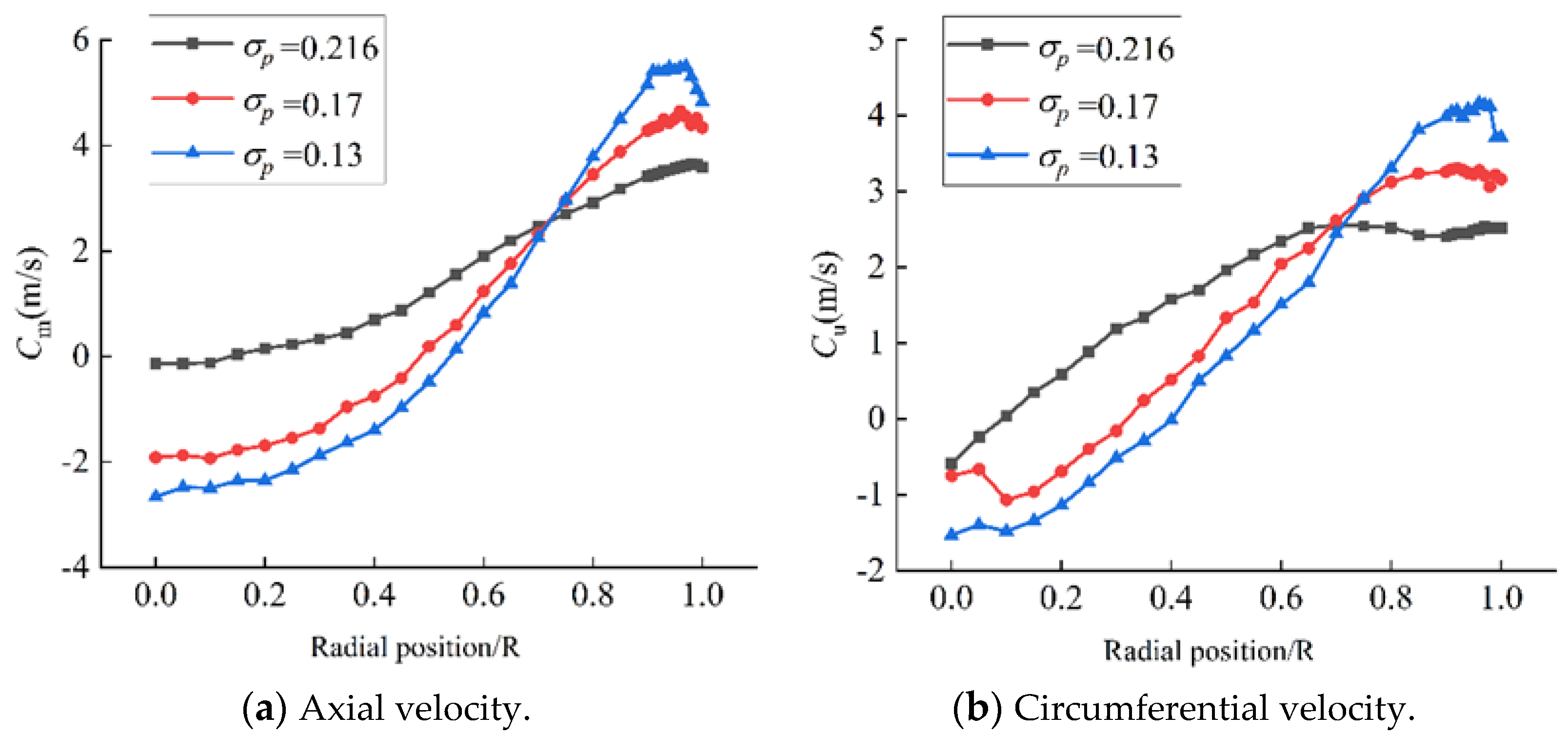
3.1.3. LDV Test of Hydraulic Turbine Operating Conditions with Different Cavitation Coefficients
4. Conclusions
- 1.
- Under turbine operating conditions, the draft tube vortex rope created a backflow area in the center region of the draft tube, and the circumferential velocity pulsation and axial velocity pulsation caused by the periodic rotation of the vortex rope were the direct causes of pressure pulsation in the draft tube.
- 2.
- The range affected by the draft tube vortex rope rotation was related to the opening degree and cavitation factor. Under the three cavitation coefficient conditions tested, it was observed that, as the cavitation coefficient increased, the axial velocity and the principal frequency associated with it both decreased, while the degree of pulsation of the axial velocity and circumferential velocity also decreased.
- 3.
- LDV testing techniques on draft tubes can be used to optimize the runner design of pump turbines. They enable the performance of the runner to be tested in the design process through model tests.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Schleicher, W.C.; Oztekin, A. Hydraulic design and optimization of a modular pump-turbine runner. Energy Convers. Manag. 2015, 93, 388–398. [Google Scholar] [CrossRef] [Green Version]
- Li, D.; Wang, H.; Qin, Y.; Li, Z.; Wei, X.; Qin, D. Mechanism of high amplitude low frequency fluctuations in a pump-turbine in pump mode. Renew. Energy 2018, 126, 668–680. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, D.; Wu, C.; Wang, X.; Lee, J.M.; Jung, K.H. Dynamic modeling and dynamical analysis of pump-turbines in S-shaped regions during runaway operation. Energy Convers. Manag. 2017, 138, 375–382. [Google Scholar] [CrossRef] [Green Version]
- Liu, S.; Shao, J.; Wu, S.; Wu, Y. Numerical simulation of pressure fluctuation in Kaplan turbine. Sci. China Technol. Sci. 2008, 51, 1137–1148. [Google Scholar] [CrossRef]
- Guo, L.; Liu, J.; Wang, L.; Qin, D.; Wei, X. Pressure fluctuation propagation of a pump turbine at pump mode under low head condition. Sci. China Technol. Sci. 2014, 57, 811–818. [Google Scholar] [CrossRef]
- Ge, M.; Petkovšek, M.; Zhang, G.; Jacobs, D.; Coutier-Delgosha, O. Cavitation dynamics and thermodynamic effects at elevated temperatures in a small Venturi channel. Int. J. Heat Mass Transf. 2021, 170, 120970. [Google Scholar] [CrossRef]
- Ge, M.; Sun, C.; Zhang, G.; Coutier-Delgosha, O.; Fan, D. Combined suppression effects on hydrodynamic cavitation performance in Venturi-type reactor for process intensification. Ultrason. Sonochem. 2022, 86, 106035. [Google Scholar] [CrossRef]
- Zhang, G.; Khlifa, I.; Fezzaa, K.; Ge, M.; Coutier Delgosha, O. Experimental investigation of internal two-phase flow structures and dynamics of quasi-stable sheet cavitation by fast synchrotron x-ray imaging editors-pick. Phys. Fluids 2020, 32, 113310. [Google Scholar] [CrossRef]
- Li, W.; Li, Z.; Qin, Z.; Yan, S.; Wang, Z.; Peng, S. Influence of the solution pH on the design of a hydro-mechanical magneto-hydraulic sealing device. Eng. Fail. Anal. 2022, 135, 106091. [Google Scholar] [CrossRef]
- Li, Z.; Li, W.; Wang, Q.; Xiang, R.; Cheng, J.; Han, W.; Yan, Z. Effects of medium fluid cavitation on fluctuation characteristics of magnetic fluid seal interface in agricultural centrifugal pump. Int. J. Agric. Biol. Eng. 2021, 14, 85–92. [Google Scholar] [CrossRef]
- Husmatuchi, V.; Farhat, M. Experiment investigation of a pump turbine at off design operating conditions. In Proceedings of the 3rd IAHR International Meeting of the Working Group on Cavitation and Dynamic Problems in Hydraulic Machinery and Systems, Brno, Czech Republic, 14–16 October 2009; pp. 339–347. [Google Scholar]
- Bergan, C.; Amiri, K.; Cervantes, M.J. Preliminary measurements of the radial velocity in the Francis-99 draft tube cone. J. Phys. Conf. Ser. 2015, 579, 012014. [Google Scholar] [CrossRef]
- Sundstrom, L.R.J.; Amiri, K.; Bergan, C. LDA measurements in the Francis-99 draft tube cone. In Proceedings of the 27th IAHR Symposium on Hydraulic Machinery and Systems, Montreal, QC, Canada, 22–26 September 2014. [Google Scholar]
- Jese, U.; Fortes-Patella, R.; Antheaume, S. High head pump-turbine: Pumping mode numerical simulations with a cavitation model for off-design conditions. In Proceedings of the 28th IAHR Symposium on Hydraulic Machinery and Systems, Grenoble, France, 4–8 July 2016. [Google Scholar]
- Zhang, X.; Burgstaller, R.; Lai, X.D. Experimental and numerical analysis of performance discontinuity of a pump-turbine under pumping mode. In Proceedings of the 28th IAHR Symposium on Hydraulic Machinery and Systems, Grenoble, France, 4–8 July 2016. [Google Scholar]
- Gentner, C. Numerical and experimental analysis of instability phenomena in pump-turbines. In Proceedings of the 26th IAHR Symposium on Hydraulic Machinery and Systems, Beijing, China, 19–23 August 2012. [Google Scholar]
- Trivedi, C.; Cervantes, M.; Gandhi, B.; Dahlhaug, O. Experimental and numerical studies for a high head Francis turbine at several operating points. J. Fluid. Eng. 2013, 135, 111102. [Google Scholar] [CrossRef]
- Krappel, T.; Riedelbauch, S.; Jester-Zuerker, R.; Jung, A.; Flurl, B.; Unger, F.; Galpin, P. Turbulence resolving flow simulations of a Francis turbine in part load using highly parallel CFD simulations. In Proceedings of the 28th IAHR Symposium on Hydraulic Machinery and Systems, Grenoble, France, 4–8 July 2016. [Google Scholar]
- Sheng, S. New development in the technology of flow measurement over the last decade. Mech. Eng. 2002, 24, 1–14. [Google Scholar]
- Ge, M.; Manikkam, P.; Ghossein, J.; Subramanian, R.K.; Coutier-Delgosha, O.; Zhang, G. Dynamic mode decomposition to classify cavitating flow regimes induced by thermodynamic effects. Energy 2022, 254 Pt C, 124426. [Google Scholar] [CrossRef]
- Ge, M.; Zhang, G.; Petkovšek, M.; Long, K.; Coutier-Delgosha, O. Intensity and regimes changing of hydrodynamic cavitation considering temperature effects. J. Clean. Prod. 2022, 338, 130470. [Google Scholar] [CrossRef]
- Deng, W.; Xu, L.; Li, Z.; Tang, W.; Wang, X.; Shang, L.; Liu, D.; Liu, X. Stability Analysis of Vaneless Space in High-Head Pump-Turbine under Turbine Mode: Computational Fluid Dynamics Simulation and Particle Imaging Velocimetry Measurement. Machines 2022, 10, 143. [Google Scholar] [CrossRef]
- Xu, L.; Jin, X.; Li, Z.; Deng, W.; Liu, D.; Liu, X. Particle Image Velocimetry Test for the Inter-Blade Vortex in a Francis Turbine. Processes 2021, 9, 1968. [Google Scholar] [CrossRef]
- Liu, D.M.; Zhao, Y.Z.; Zuo, Z.G. Experimental research on flow field in the draft tube of pump turbines based on LDV. IOP Conf. Ser. Earth Environ. Sci. 2019, 240, 072030. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z. Rotating stall mechanism and stability control in the pump flows. IOP Conf. Ser. Earth Environ. Sci. 2010, 12, 012010. [Google Scholar] [CrossRef] [Green Version]
- Edinger, G.; Erne, S.; Doujak, E.; Bauer, C. Flow determination of a pump-turbine at zero discharge. IOP Conf. Ser. Earth Environ. Sci. 2014, 22, 032051. [Google Scholar] [CrossRef] [Green Version]
- Ji, L.; Xu, L.; Peng, Y.; Zhao, X.; Li, Z.; Tang, W.; Liu, D.; Liu, X. Experimental and Numerical Simulation Study on the Flow Characteristics of the Draft Tube in Francis Turbine. Machines 2022, 10, 230. [Google Scholar] [CrossRef]
- Liu, S.-B.; Shi, G.-T.; Liu, D.-M. Hydraulic Turbine Pressure Pulsation and Hydraulic Vibration; China Water Conservancy and Hydropower Press: Beijing, China, 2020. [Google Scholar]






| Group | Group | ||||
|---|---|---|---|---|---|
| Group 1 | 160 | 131.50 | Group 2 | 140 | 103.34 |
| 130 | 107.49 | 130 | 95.15 | ||
| 105 | 78.76 | 115 | 84.02 | ||
| 75 | 56.22 | 80 | 58.48 |
| Parameters | Information |
|---|---|
| Test range | −150~1000 m/s |
| Precision | 0.1% |
| Scope of application | 3D measurement of gas, liquid, or multiphase flows |
| Sampling frequency | 400~800 MHz |
| Maximum processing frequency | 175 MHz |
| Minimum processing frequency | 300 Hz |
| Dynamic range | 8-bit |
| Frequency Shift | Built-in |
| Minimum Time | 50 ns |
| Maximum sampling rate | 800 MHz |
| Distance/mm | Number of Repetitions | Cu (m/s) | Cm (m/s) | Cu Repeatability/% | Cm Repeatability/% |
|---|---|---|---|---|---|
| 18 | 1 | 1.179 | 0.7849 | 96.452 | 97.054 |
| 2 | 1.1172 | 0.7254 | 98.120 | 95.142 | |
| 3 | 1.1088 | 0.7711 | 97.383 | 98.864 | |
| 4 | 1.1205 | 0.7775 | 98.410 | 98.025 | |
| 5 | 1.1675 | 0.7533 | 97.462 | 98.801 | |
| 36 | 1 | 1.9698 | 3.7116 | 98.931 | 99.277 |
| 2 | 1.9543 | 3.7656 | 99.726 | 99.279 | |
| 3 | 1.9400 | 3.7234 | 99.540 | 99.592 | |
| 4 | 1.9472 | 3.7635 | 99.910 | 99.335 | |
| 5 | 1.9335 | 3.7291 | 99.207 | 99.745 | |
| 54 | 1 | 1.478 | 3.7446 | 99.586 | 99.856 |
| 2 | 1.5028 | 3.7261 | 98.743 | 99.650 | |
| 3 | 1.4748 | 3.7545 | 99.371 | 99.591 | |
| 4 | 1.4905 | 3.7450 | 99.571 | 99.845 | |
| 5 | 1.4746 | 3.7258 | 99.357 | 99.642 | |
| 72 | 1 | 1.5128 | 3.7672 | 99.324 | 99.885 |
| 2 | 1.5231 | 3.7453 | 100.000 | 99.533 | |
| 3 | 1.5302 | 3.7535 | 99.534 | 99.751 | |
| 4 | 1.5300 | 3.7835 | 99.547 | 99.451 | |
| 5 | 1.5194 | 3.7648 | 99.757 | 99.948 | |
| 90 | 1 | 2.2578 | 3.1054 | 98.988 | 99.995 |
| 2 | 2.2241 | 3.0730 | 99.504 | 98.952 | |
| 3 | 2.2530 | 3.1177 | 99.203 | 99.608 | |
| 4 | 2.2159 | 3.1148 | 99.137 | 99.702 | |
| 5 | 2.2251 | 3.1168 | 99.549 | 99.637 |
| Operating Point | Q11/(L/s) | n11/(r/min) | n/(r/min) |
|---|---|---|---|
| OP6-1 | 237.28 | 31.60 | 599.91 |
| OP14-1 | 524.09 | 33.53 | 599.86 |
| OP18-1 | 636.4 | 34.30 | 599.95 |
| OP20-1 | 667.8 | 36.27 | 599.92 |
| OP6-2 | −348.46 | −38.01 | −639.87 |
| OP14-2 | −504.33 | −37.78 | −599.85 |
| OP18-2 | −540.4 | −38.32 | −599.84 |
| OP20-2 | −704.83 | −40.17 | −599.92 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, W.; Li, Z.; Ji, L.; Shang, L.; Liu, D.; Liu, X. Laser Doppler Velocimetry Test of Flow Characteristics in Draft Tube of Model Pump Turbine. Processes 2022, 10, 1323. https://doi.org/10.3390/pr10071323
Deng W, Li Z, Ji L, Shang L, Liu D, Liu X. Laser Doppler Velocimetry Test of Flow Characteristics in Draft Tube of Model Pump Turbine. Processes. 2022; 10(7):1323. https://doi.org/10.3390/pr10071323
Chicago/Turabian StyleDeng, Wanquan, Zhen Li, Lei Ji, Linmin Shang, Demin Liu, and Xiaobing Liu. 2022. "Laser Doppler Velocimetry Test of Flow Characteristics in Draft Tube of Model Pump Turbine" Processes 10, no. 7: 1323. https://doi.org/10.3390/pr10071323





