Prediction and Control of Input and Output for Industry–University–Research Collaboration Network in Construction Industry
Abstract
:1. Introduction
2. Related Work
2.1. Feedback Control and Feedforward Control
2.2. Innovation Output Prediction
2.3. Controller Structure
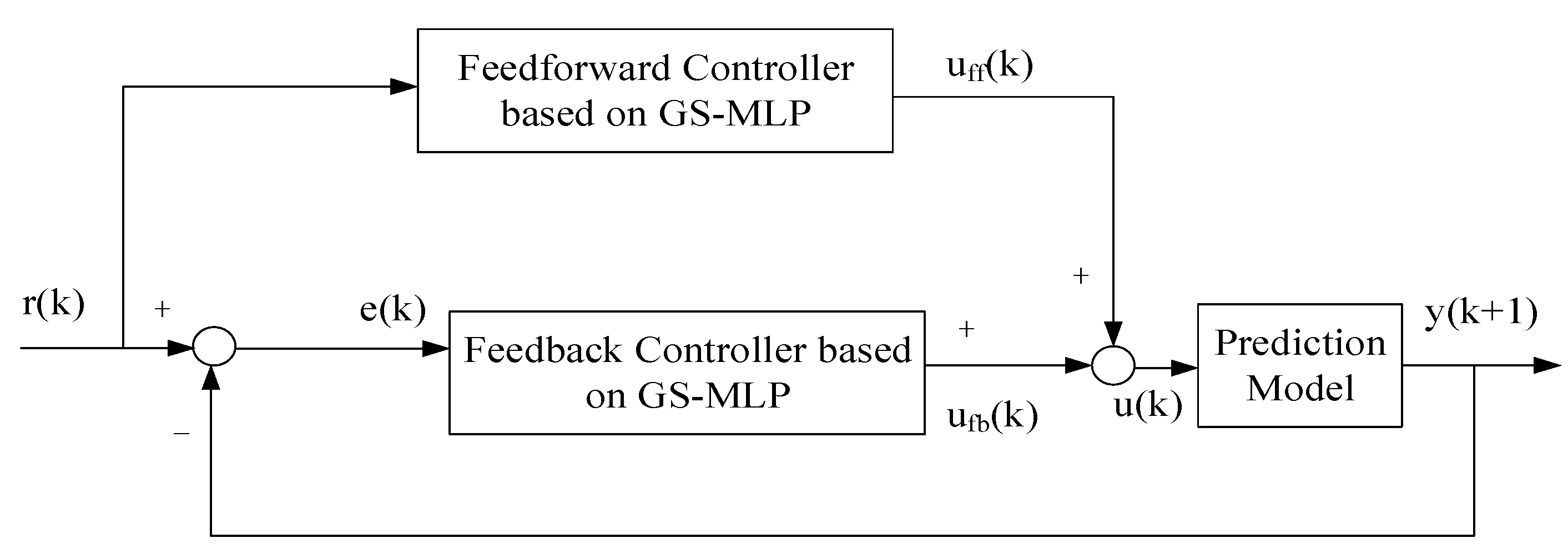
3. FCFCM-MLP
3.1. FCFCM-MLP and Its Components
- (1)
- Structure of the controllers—GS-MLP
- (2)
- Prediction model
- (3)
- Feedforward controller
- (4)
- Feedback controller
3.2. Control Process
- (1)
- Feedforward control, to generate , namely, the , according to Equation (3);
- (2)
- Predict, to generate according to Equation (1);
- (3)
- Calculate the control error , put it into the FCFC, and then repeat the following procedures:
- Put into the FFC to generate the ;
- Put the and the into the FBC to generate the ;
- and take the as the input of the prediction model.
- (1)
- Train the prediction model:
- Input X into the prediction model to generate the output Y;
- Optimize and train the prediction models (HHO-SVR, ELM, etc.);
- Calculate the training error of the prediction model.
- (2)
- Train the FFC:
- Input X into the FFC to generate the output Y;
- Optimize and train the FFC (GS-MLP).
- (3)
- Train the FBC:
- Input X into the FBC to generate the output Y;
- Optimize and train the FBC (GS-MLP).
- (1)
- Predict X with the trained FFC;
- (2)
- Predict Y with the trained prediction model;
- (3)
- Compute the error between the real Y and the predicted Y;
- (4)
- Put the error into the FCFC to predict X;
- (5)
- Compute the mean value of the output generated in Step (1) and Step (4) and take it as the input of the prediction model in the next step;
- (6)
- Input the control signal obtained in the previous step to generate a new output Y;
4. Tests and Analysis
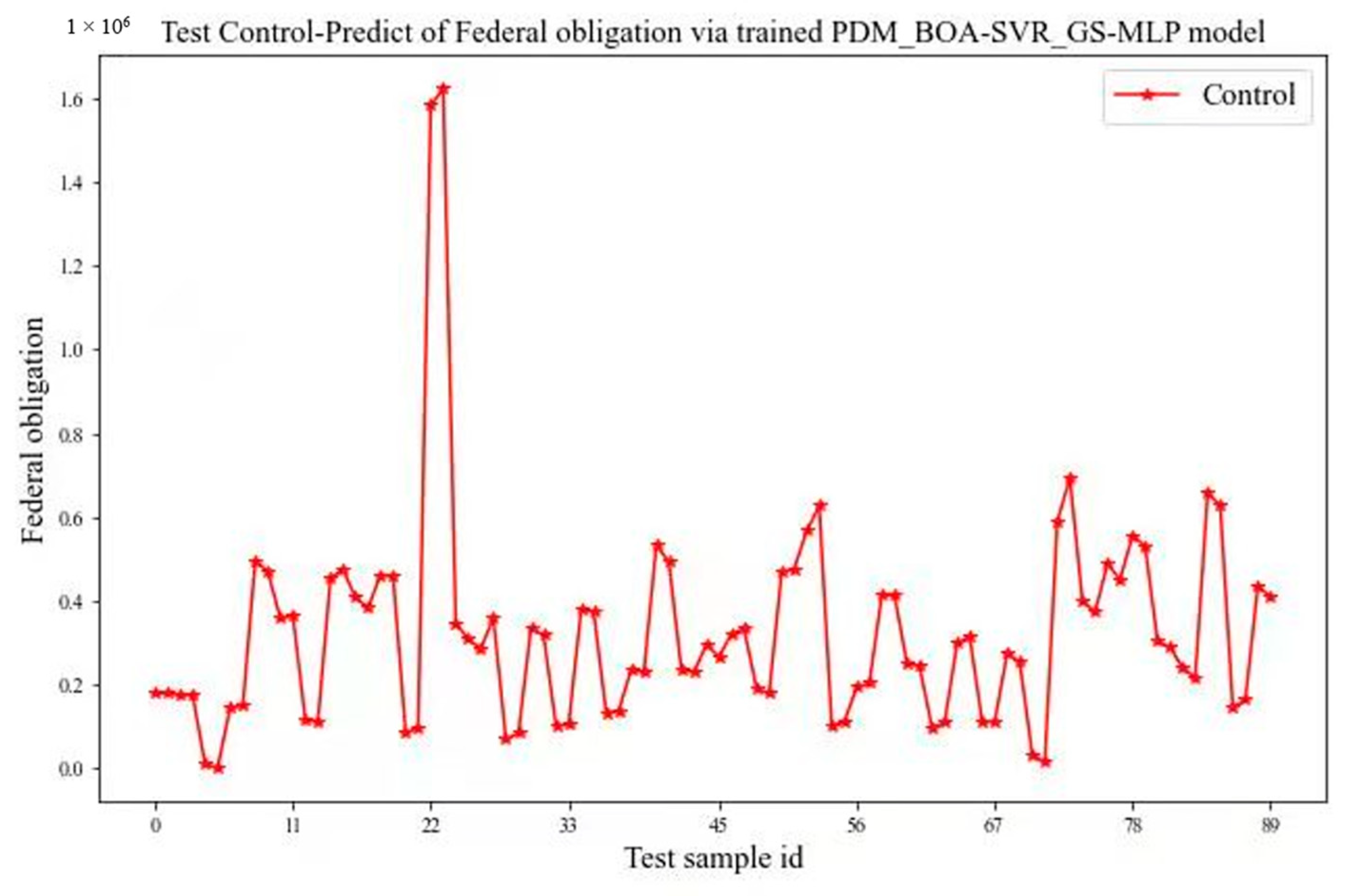
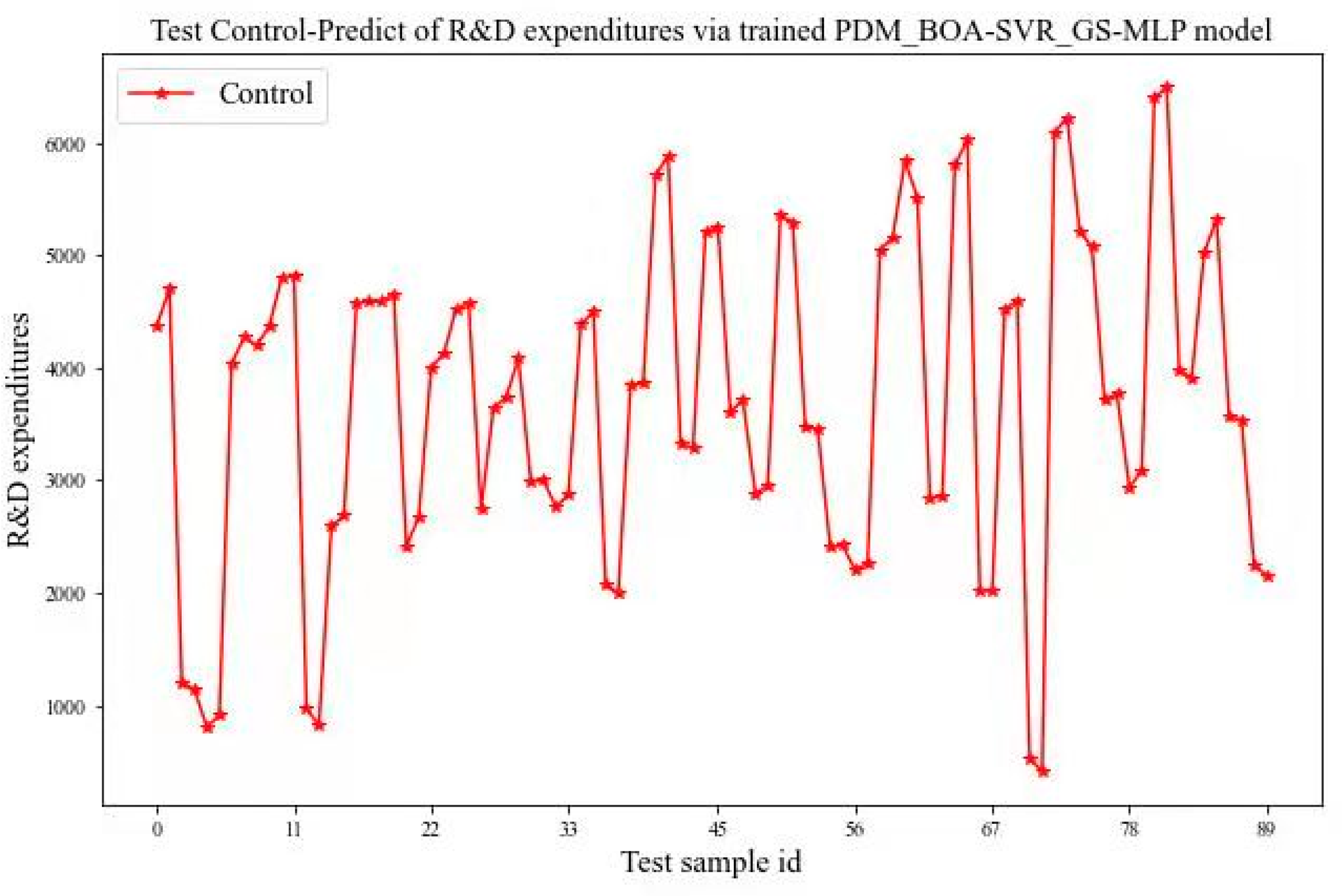
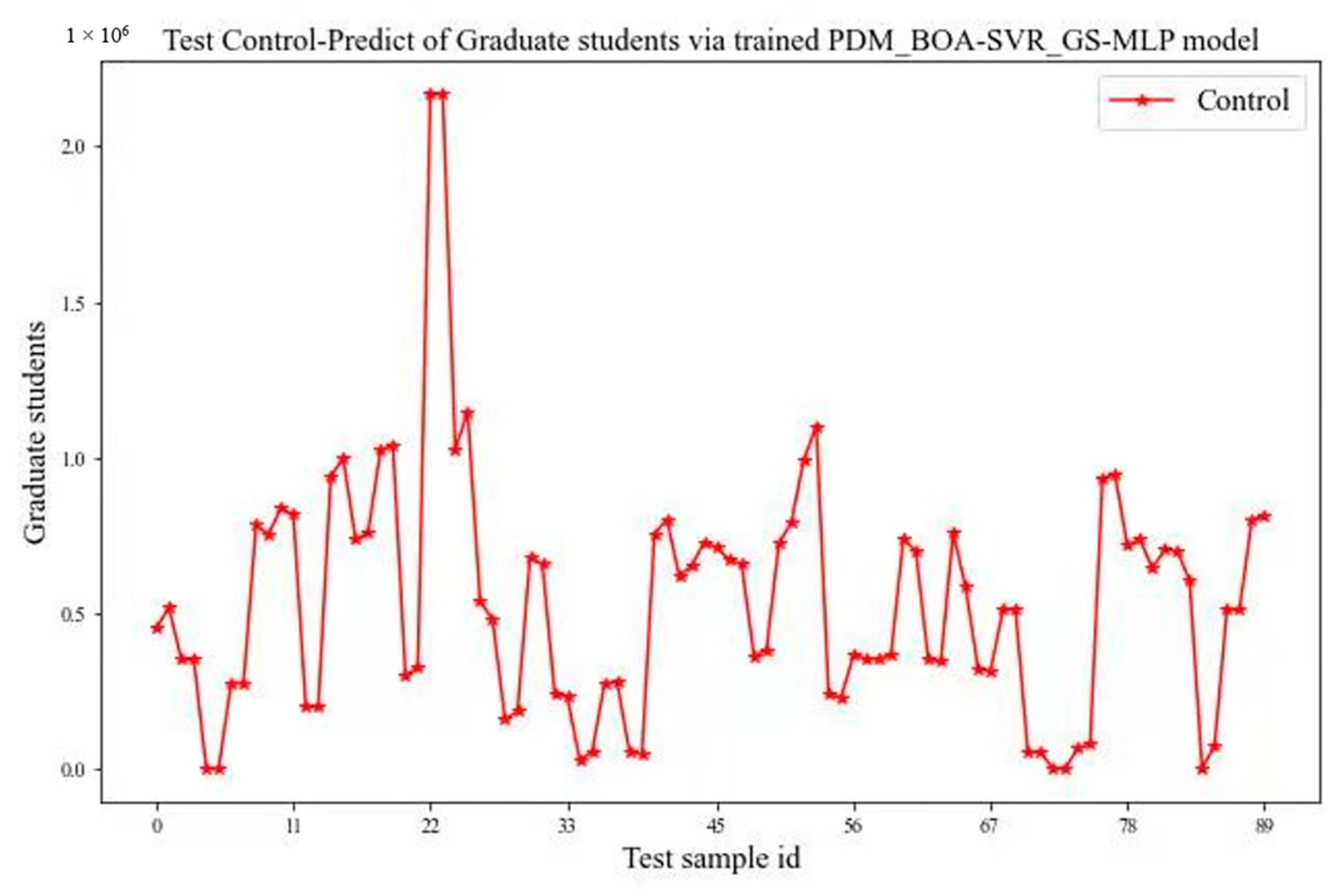
4.1. Datasets and the Index System
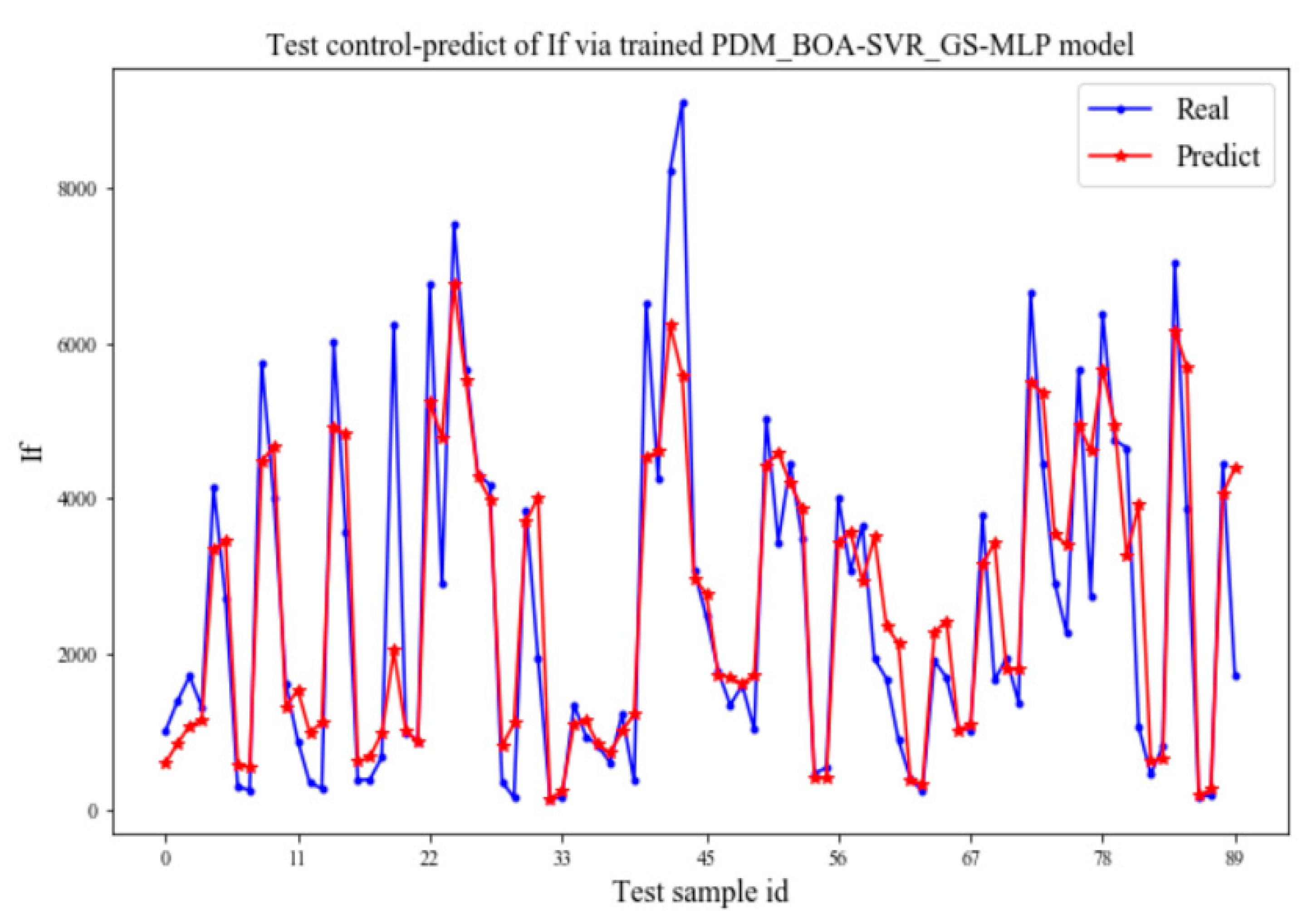
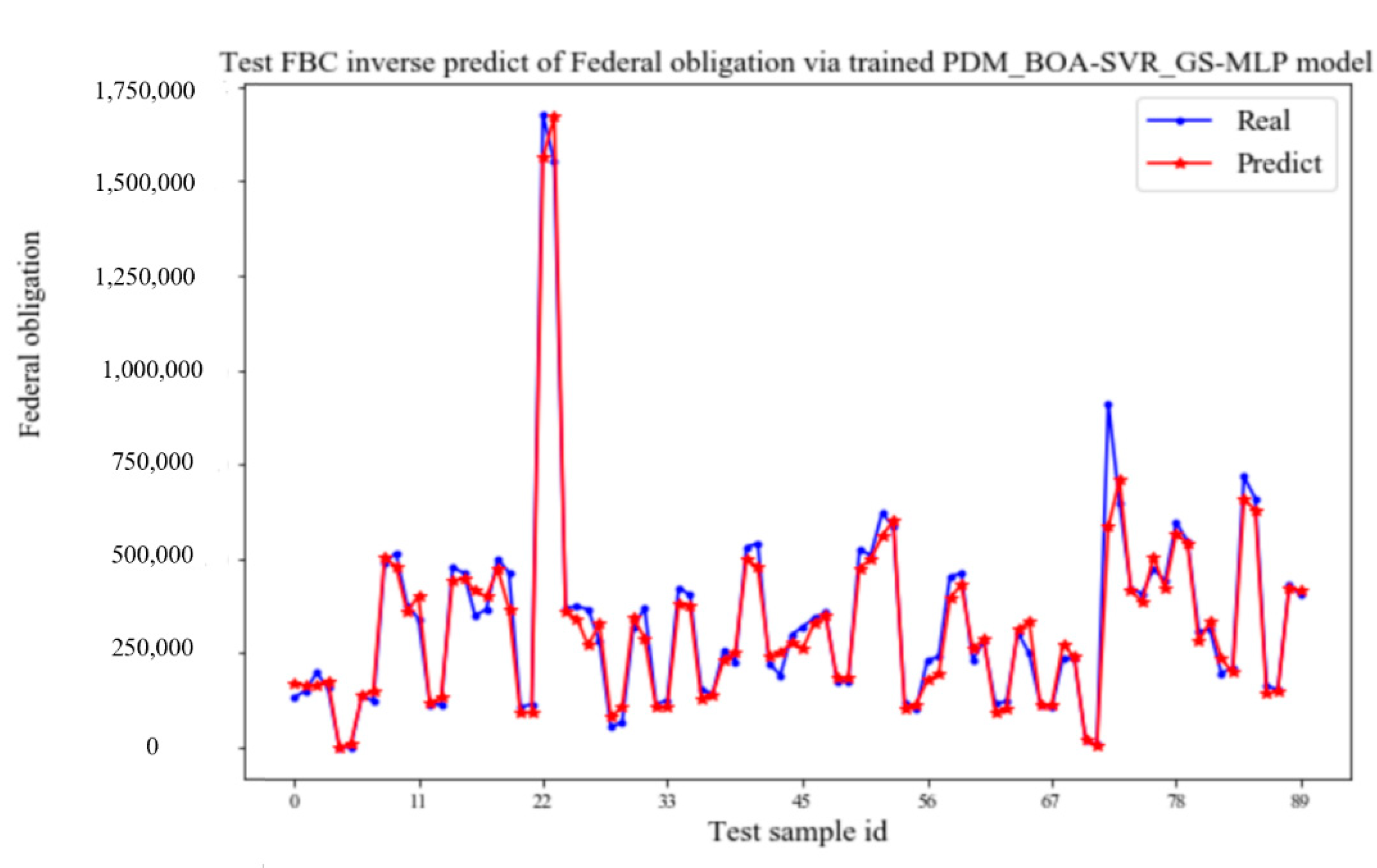
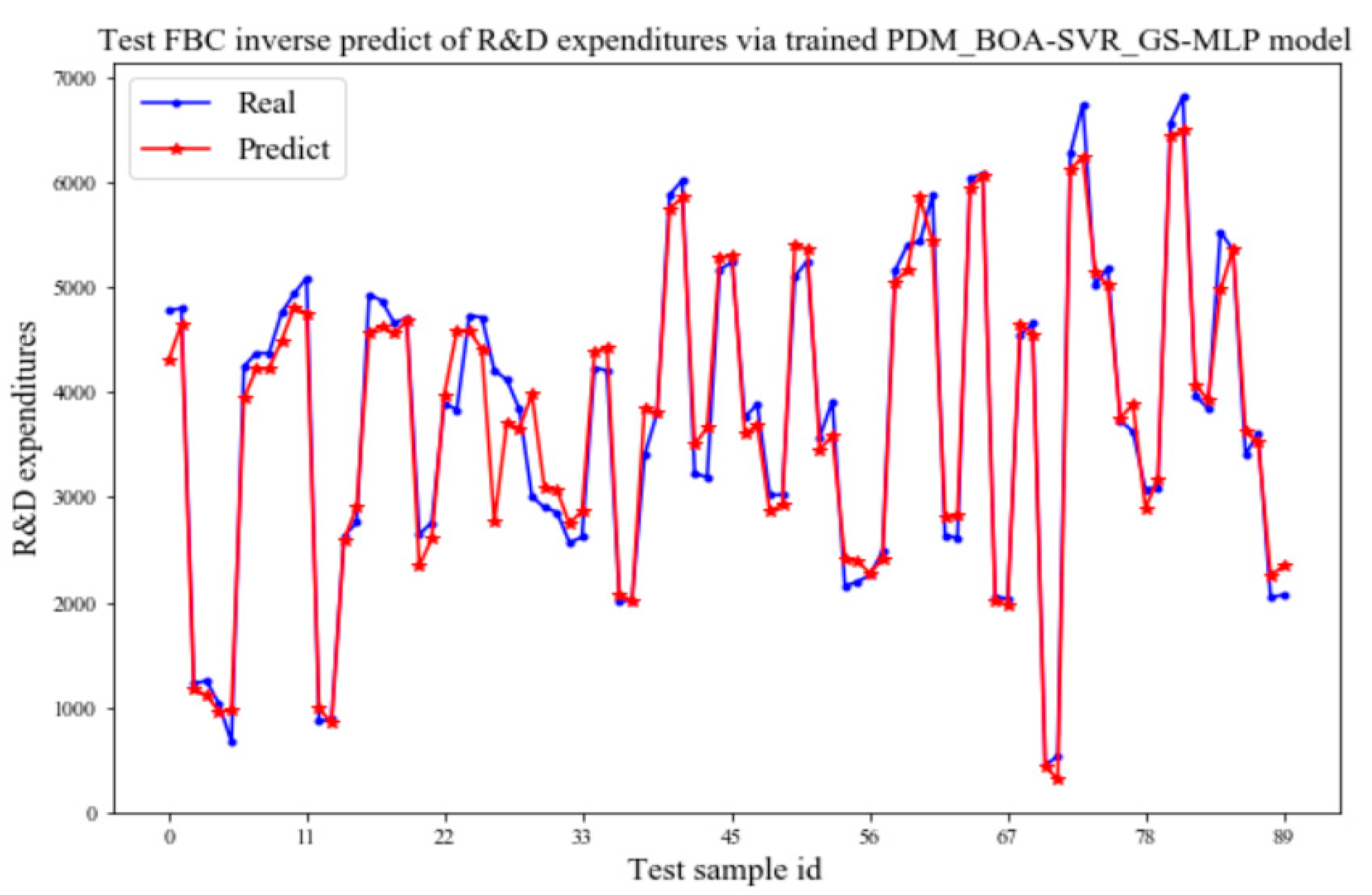
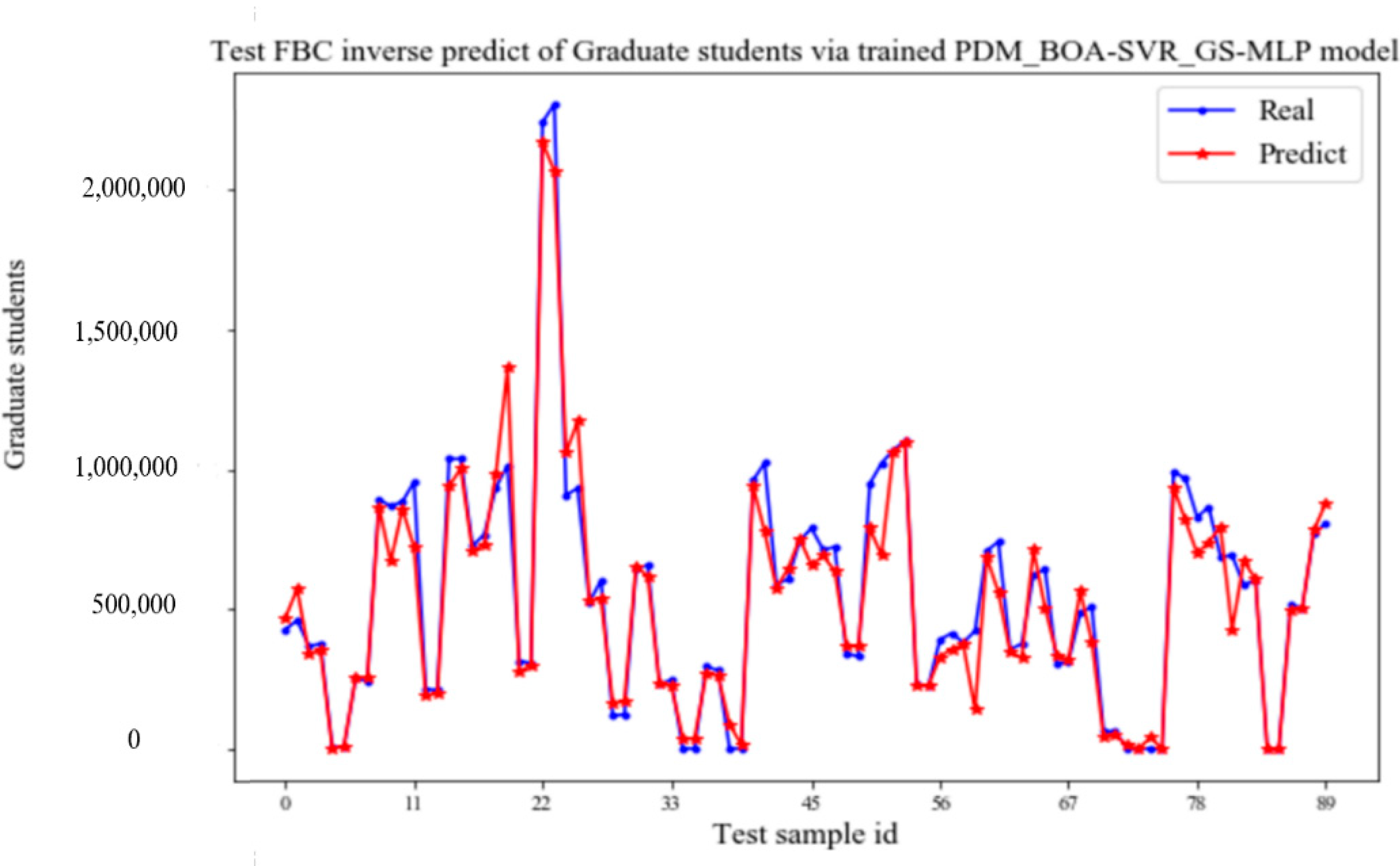
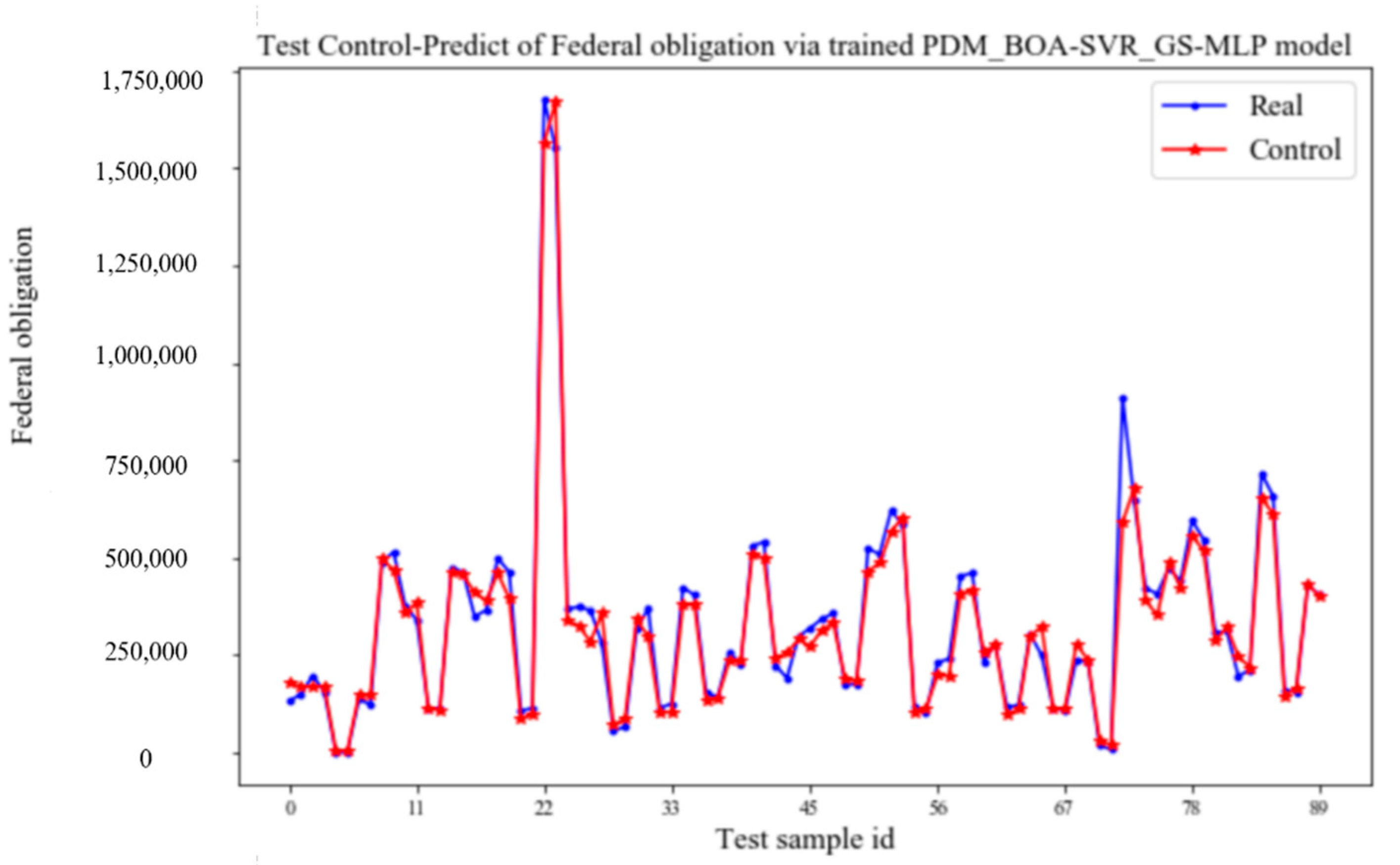
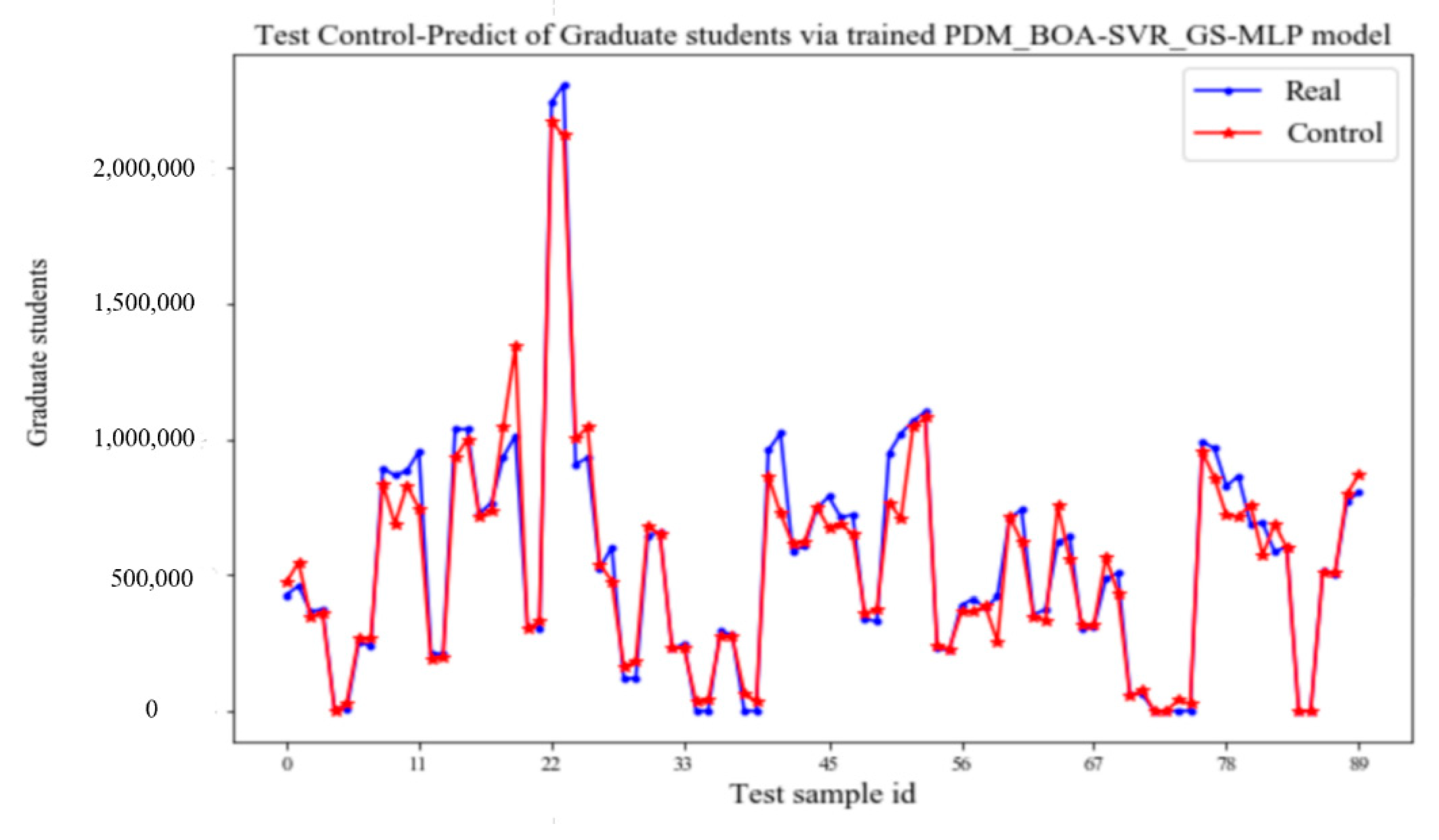
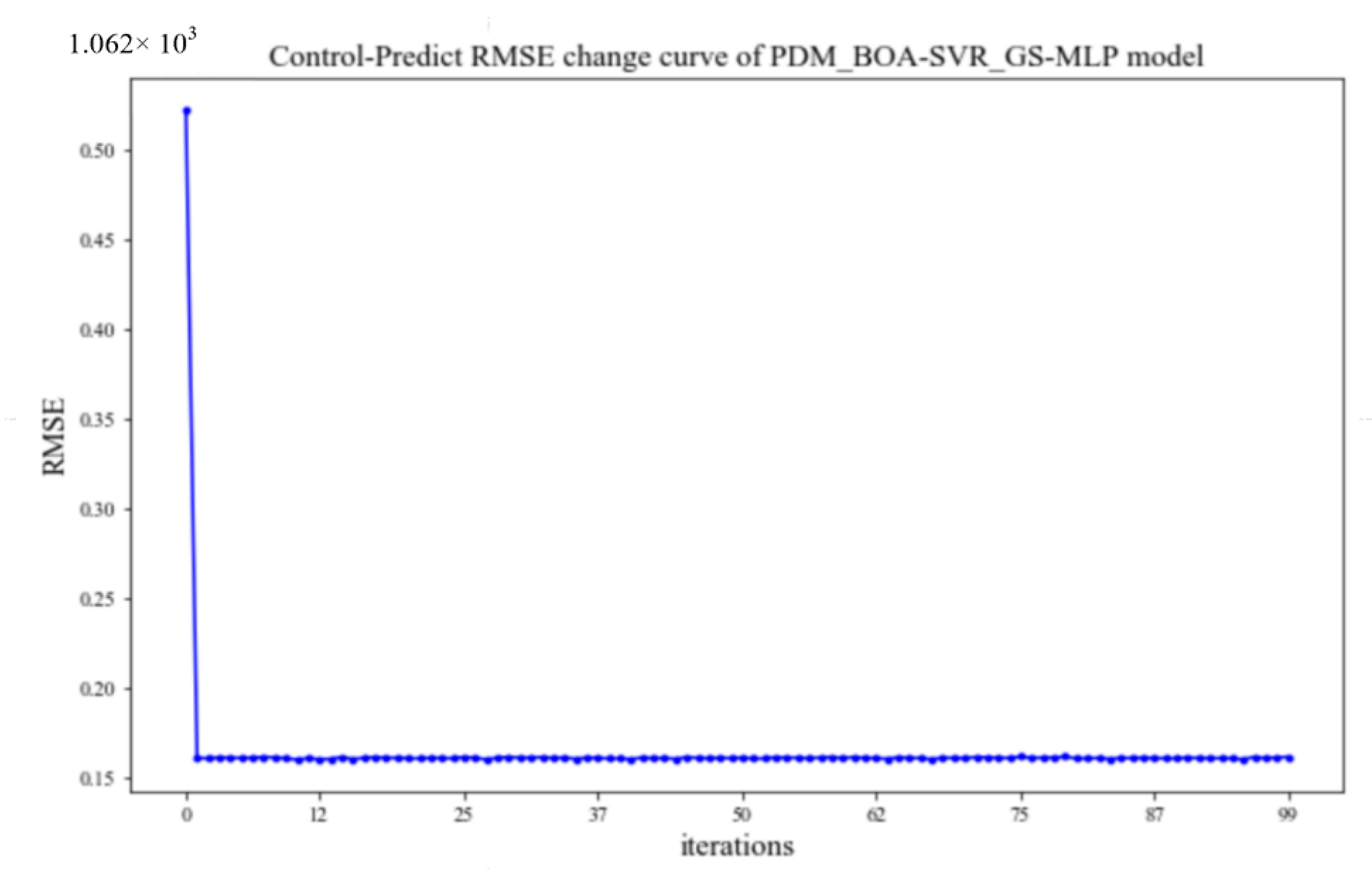
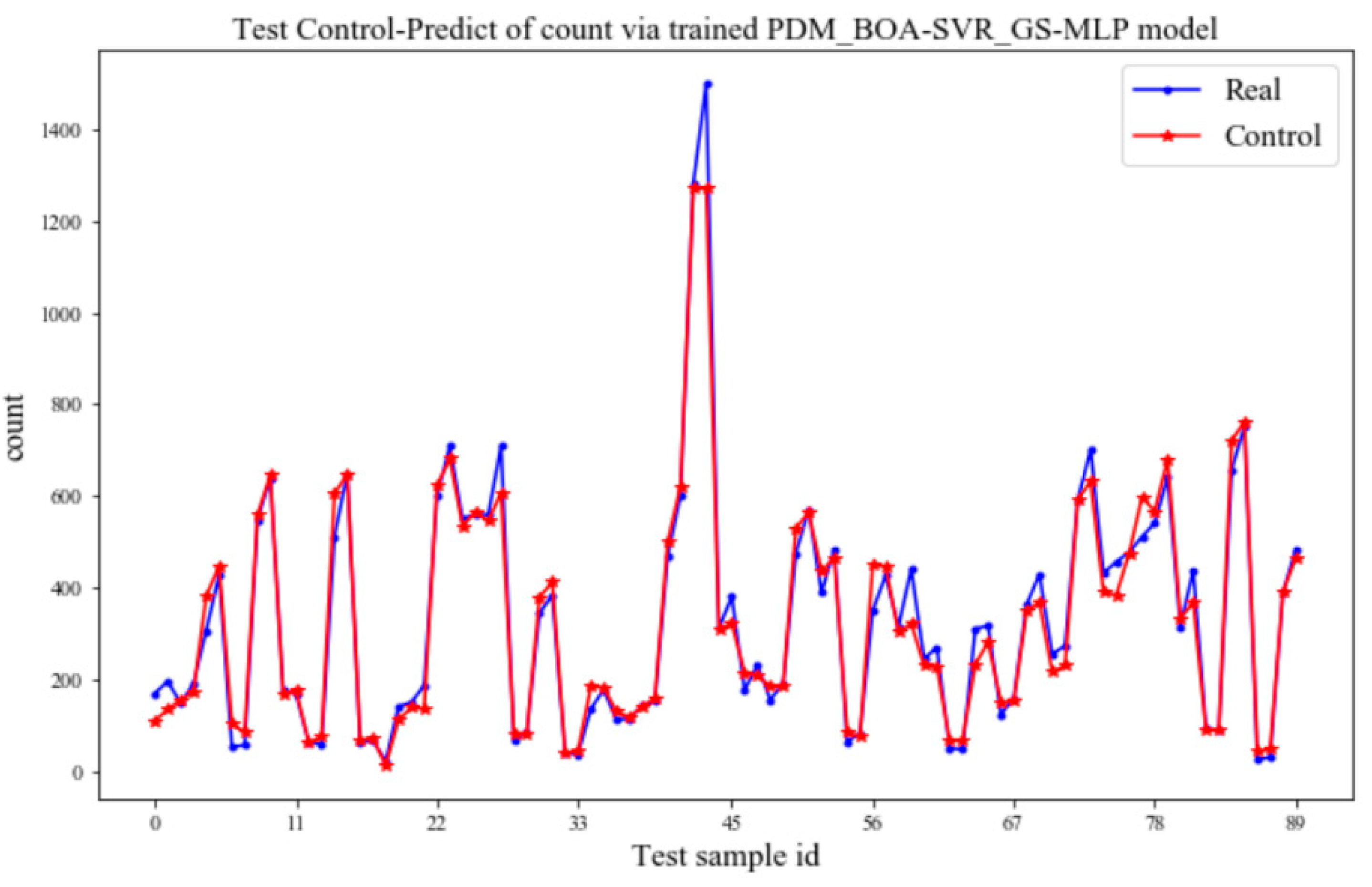
4.2. Tests of Output—Track Control Performance
- (1)
- The prediction performance of the prediction-control model on the test set.
- (2)
- The prediction performance of the feedback controller on the test set.
- (3)
- The control performance of the prediction-control model on the test set.
- (i)
- Feedback control with capital input and personnel input as independent variables.
- (ii)
- Feedback control with network connection density.
- (4)
- Comparison results of performance of models.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, H.Y. Research on Coordinated Development of Technological Innovation Ecosystem; Central South University: Changsha, China, 2014. [Google Scholar]
- Cao, X.; Liu, G.W. Collaborative evolution path of industry university research cooperative innovation network under the guidance of resource allocation. J. Syst. Manag. 2015, 24, 769–777. [Google Scholar]
- Chen, F.; Jin, Z.; Wang, E.; Wang, L.; Jiang, Y.; Guo, P.; Guo, X.; He, X. Relationship model between surface strain of concrete and expansion force of reinforcement rust. Sci. Rep. 2021, 11, 4208. [Google Scholar] [CrossRef] [PubMed]
- Chen, F.X.; Zhong, Y.C.; Gao, X.Y.; Jin, Z.Q.; Wang, E.D.; Zhu, F.P.; Shao, X.X.; He, X.Y. Non-uniform Model of Relationship Between Surface Strain and Rust Expansion Force of Reinforced Concrete. Sci. Rep. 2020, 11, 8741. [Google Scholar] [CrossRef] [PubMed]
- Cao, Q.W.; Duan, W.C. Paradox of scale economies and multi-dimensional performance analysis in scientific research. Sci. Res. 2021, 3, 1–19. [Google Scholar]
- Yang, X.J. Analysis on the allocation optimization of resources for the integration of industry, university and research in universities. Cult. Educ. Mater. 2008, 24, 129–131. [Google Scholar]
- Wu, M.; Zhang, B.; Zhou, Y.; Huang, K. A Double-Fold 7×8 Butler Matrix-Fed Multibeam Antenna with a Boresight Beam for 5G Applications. IEEE Antennas Wirel. Propag. Lett. 2022, 21, 516–520. [Google Scholar] [CrossRef]
- Cao, J.H. ADRC of Ship Course and its Parameter Optimization; Dalian Maritime University: Dalian, China, 2020. [Google Scholar]
- Jiang, Y.; Li, X. Broadband cancellation method in an adaptive co-site interference cancellation system. Int. J. Electron. 2022, 109, 854–874. [Google Scholar] [CrossRef]
- Meng, Q.; Ma, Q.; Zhou, G. Adaptive Output Feedback Control for Stochastic Uncertain Nonlinear Time-delay Systems. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 3289–3293. [Google Scholar] [CrossRef]
- Zheng, Y. Research on Prediction-Control Model of Hydropower Unit Regulation System; Huazhong University of Science and Technology: Wuhan, China, 2018. [Google Scholar]
- Sahoo, H.K.; Dash, P.K.; Rath, N.P. NARX model based nonlinear dynamic system identification using low complexity neural networks and robust H∞ Filter. Appl. Soft Comput. 2013, 13, 3324–3334. [Google Scholar] [CrossRef]
- Xi, Y.; Jiang, W.; Wei, K.; Hong, T.; Cheng, T.; Gong, S. Wideband RCS Reduction of Microstrip Antenna Array Using Coding Metasurface with Low Q Resonators and Fast Optimization Method. IEEE Antennas Wirel. Propag. Lett. 2022, 21, 656–660. [Google Scholar] [CrossRef]
- Hong, T.; Guo, S.; Jiang, W.; Gong, S. Highly Selective Frequency Selective Surface with Ultrawideband Rejection. IEEE Trans. Antennas Propag. 2022, 70, 3459–3468. [Google Scholar] [CrossRef]
- Xu, K.; Weng, X.; Li, J.; Guo, Y.; Wu, R.; Cui, J.; Chen, Q. 60-GHz third-order on-chip bandpass filter using GaAs pHEMT technology. Semicond. Sci. Technol. 2022, 37, 055004. [Google Scholar] [CrossRef]
- Zhou, T.H.; Zhu, C.S. Design of Robust Output Controller for an Active Magnetic Bearing High-speed Motor Rigid Rotor System Based on Eigenstructure Assignment. Proc. CSEE 2022, 42, 3775–3785. [Google Scholar]
- Mao, Y.Z.; Feng, Z.Y.; Guo, H.R. Static output feedback control of vehicle’s active front wheel steering considering multi-performance constraints. J. Shanghai Jiaotong Univ. 2022, 2, 156–164. [Google Scholar] [CrossRef]
- Wu, Z.L.; Huo, B.Y.; Qin, Y.H.; Liu, Y.H.; Li, D.H. Conditional feedback control of limb rehabilitation system based on functional electricity stimulation. Control. Theory Appl. 2022, 39, 1079–1087. [Google Scholar]
- Zuo, Y.; Dai, C.H.; Guo, A.; Chen, W.R. PEMFC air supply regulation system based on improved EKF algorithm and stack power demand. Proc. CSEE 2021, 41, 6550–6560. [Google Scholar]
- Pizarro-Lerma, A.; Santibañez, V.; Garcia-Hernandez, R.; Villalobos-Chin, J. Sectorial fuzzy controller plus feedforward for the trajectory tracking of robotic arms in joint space. Mathematics 2021, 9, 616. [Google Scholar] [CrossRef]
- Niu, Z.; Zhang, B.; Dai, B.; Zhang, J.; Shen, F.; Hu, Y.; Zhang, Y. 220 GHz Multi Circuit Integrated Front End Based on Solid-State Circuits for High Speed Communication System. Chin. J. Electron. 2022, 31, 569–580. [Google Scholar] [CrossRef]
- Cao, Z.; Wang, Y.; Zheng, W.; Yin, L.; Tang, Y.; Miao, W.; Yang, B. The algorithm of stereo vision and shape from shading based on endoscope imaging. Biomed. Signal Process. Control. 2022, 76, 103658. [Google Scholar] [CrossRef]
- Sabahi, K.; Ghaemi, S.; Pezeshki, S. Application of type-2 fuzzy logic system for load frequency control using feedback error learning approaches. Appl. Soft Comput. 2014, 21, 1–11. [Google Scholar] [CrossRef]
- Xie, Y.; Alleyne, A. Robust, Two Degree-of-freedom control for MIMO System with both model and signal uncertainties. IFAC Proc. Vol. 2014, 47, 9313–9320. [Google Scholar] [CrossRef]
- Wei, X.Y. Research on Core Patent Prediction from the Perspective of Technology Field Segmentation; Shanxi University: Taiyuan, China, 2018. [Google Scholar]
- Hu, Z.W.; Wu, Y.S. Analysis and prediction of influence factors of scientific and technological output—An approach based on multiple regression and BP neural network. Sci. Res. 2012, 30, 992–1004. [Google Scholar]
- Ma, C.; Zhou, D.Q.; Zhang, Y. BP neural network based on improved whale algorithm for water demand prediction. Comput. Sci. 2020, 47, 32–36. [Google Scholar]
- Zheng, W.; Zhou, Y.; Liu, S.; Tian, J.; Yang, B.; Yin, L. A Deep Fusion Matching Network Semantic Reasoning Model. Appl. Sci. 2022, 12, 3416. [Google Scholar] [CrossRef]
- Wang, J.; Tian, J.; Zhang, X.; Yang, B.; Liu, S.; Yin, L.; Zheng, W. Control of Time Delay Force Feedback Teleoperation System with Finite Time Convergence. Front. Neurorobot. 2022, 16, 877069. [Google Scholar] [CrossRef]
- Yang, J.; Liu, H.; Ma, K.; Yang, B.; Guerrero, M.J. An Optimization Strategy of Price and Conversion Factor Considering the Coupling of Electricity and Gas Based on Three-Stage Game. IEEE Trans. Autom. Sci. Eng. 2022, 1–14. [Google Scholar] [CrossRef]
- Ndofor, H.A.; Sirmon, D.G.; He, X.M. Firm resources, competitive actions and performance: Investigation a mediated model with evidence from the in-vitro diagnostics industry. Strateg. Manag. J. 2011, 23, 640–657. [Google Scholar] [CrossRef]
- Li, J.; Xu, K.; Chaudhuri, S.; Yumer, E.; Zhang, H.; Guibas, L. GRASS: Generative recursive autoencoders for shape structures. ACM Trans. Graph. 2017, 36, 1–14. [Google Scholar] [CrossRef]
- Lin, Y.; Song, H.; Ke, F.; Yan, W.; Liu, Z.; Cai, F. Optimal caching scheme in D2D networks with multiple robot helpers. Comput. Commun. 2022, 181, 132–142. [Google Scholar] [CrossRef]

| Symbols | Definitions |
|---|---|
| Output value, namely, the composite value of papers jointly produced by universities, enterprises, and scientific research institutes; k indicates which year | |
| Expected output value | |
| Control error, namely, the error between the expected output and the real output; k indicates which year | |
| Output of the feedforward controller; ff means feedforward control; k indicates which year | |
| Output of the feedback controller; fb means feedback control; k indicates which year | |
| , total output of the controller, and part of inputs of the prediction model Grid Search Multilayer Perceptron | |
| Structure of the feedforward controller and the feedback controller based on MLP, and GS is used to improve control accuracy | |
| Feedforward Controller | |
| Feedback Controller | |
X Y | Feedforward Controller–Feedback Controller: a controller based on FFC and FBC Feedforward-Control–Feedback-Control-Model-based Multilayer Perceptron, namely, the name of the control model Innovation input value including x1, x2, and x3; according to actual needs, the network structure value x4–x7 can also be includedInnovation output representing a y (k) |
| Variables | Indexes | Sources |
|---|---|---|
| Innovation input | x1: capital input | Government capital |
| x2: capital input | R&D expenditures | |
| x3: personnel input | Number of postgraduates | |
| Network centrality | x4: closeness centrality | Processed collaboration network built by year with Python |
| x5: betweenness centrality | ||
| x6: degree centrality | ||
| Network connection density | x7: connection density | Processed with Python |
| Innovation output | y: composite value of papers jointly produced by different institutes | Composite value of influence factors |
| Model | RMSE | Model | RMSE |
|---|---|---|---|
| ELM_MLP | 1408.991751 | HHO-SVR_GS-MLP | 1092.937662 |
| ELM_GS-MLP | 1383.816101 | BOA-SVR_GS-MLP | 1106.277331 |
| SVR_MLP | 1169.163554 | PSO_BOA-SVR_GS-MLP | 1084.636205 |
| SVR_GS-MLP | 1160.010254 | PDM_BOA-SVR_GS-MLP | 1075.364392 |
| ALO-SVR_GS-MLP | 1113.07555 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhong, R.; Wang, D.; Hu, C.; Li, Y.; Feng, G. Prediction and Control of Input and Output for Industry–University–Research Collaboration Network in Construction Industry. Processes 2022, 10, 2037. https://doi.org/10.3390/pr10102037
Zhong R, Wang D, Hu C, Li Y, Feng G. Prediction and Control of Input and Output for Industry–University–Research Collaboration Network in Construction Industry. Processes. 2022; 10(10):2037. https://doi.org/10.3390/pr10102037
Chicago/Turabian StyleZhong, Ruiqiong, Dong Wang, Cheng Hu, Yuxin Li, and Gege Feng. 2022. "Prediction and Control of Input and Output for Industry–University–Research Collaboration Network in Construction Industry" Processes 10, no. 10: 2037. https://doi.org/10.3390/pr10102037





