Complex Nonlinear Behavior in Metabolic Processes: Global Bifurcation Analysis of Escherichia coli Growth on Multiple Substrates
Abstract
:1. Introduction
2. Metabolic Model
2.1. The HCM Framework
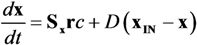
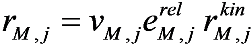
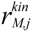 is the kinetic term, and
is the kinetic term, and 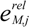 is the relative enzyme level to its theoretical maximum, i.e., eM,j/
is the relative enzyme level to its theoretical maximum, i.e., eM,j/ 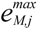 .
. 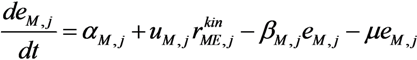
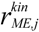 is the kinetic part of the inducible enzyme synthesis rate, βM,j is the degradation rate and µ is the specific growth rate. The four terms of the right-hand side denote constitutive and inducible rates of enzyme synthesis and the decrease of enzyme levels by degradation and dilution, respectively. The cybernetic control variables, uM,j and vM,j, are computed from the Matching and Proportional laws [21,22], respectively:
is the kinetic part of the inducible enzyme synthesis rate, βM,j is the degradation rate and µ is the specific growth rate. The four terms of the right-hand side denote constitutive and inducible rates of enzyme synthesis and the decrease of enzyme levels by degradation and dilution, respectively. The cybernetic control variables, uM,j and vM,j, are computed from the Matching and Proportional laws [21,22], respectively:
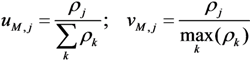
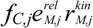 , and fC,j denotes the factor converting EM flux to the carbon uptake rate. Dynamic shifts among different pathways are realized by two controlling variables, uM,j and vM,j.
, and fC,j denotes the factor converting EM flux to the carbon uptake rate. Dynamic shifts among different pathways are realized by two controlling variables, uM,j and vM,j. 2.2. HCM for Anaerobic E. coli Growth
3. Methods
3.1. Rigorous Combinatoric Analysis
| Variables or parameters | Equations or parameter values |
|---|---|
| Extracellular metabolites and biomass | Glucose:  Pyruvate:  Acetate:  Ethanol:  Formate: 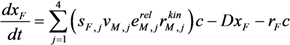 Biomass: 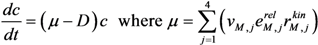 |
| Enzymes | 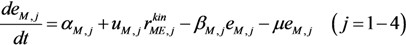 |
| Cybernetic variables | 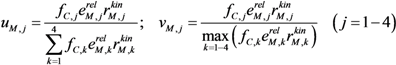 |
| Kinetics | 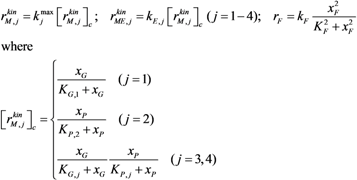 |
| Parameters and stoichiometric coefficients |  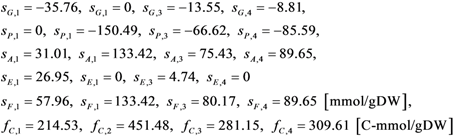 |
| Notations | c: biomass concentration, g/L D: dilution rate, 1/h eM,j, 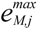 : level of enzyme that catalyzes the jth EM flux and its maximal level : level of enzyme that catalyzes the jth EM flux and its maximal level fC,j: factor converting the EM flux (i.e., growth rate) to the carbon uptake rate, C-mmol/gDW (DW = dry weight) kF: rate constant for formate decomposition 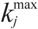 : maximal rate constant for the jth EM flux, 1/h : maximal rate constant for the jth EM flux, 1/h KF: Michaelis constant for formate decomposition, mM KG,j, KP,j: Michaelis constants for the jth EM flux, mM rF: specific rate of formate decomposition into CO2 and H2, mmol/(gDW℘h) rM,j, 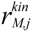 : regulated and unregulated fluxes through the jth EM, mmol/(gDW h) : regulated and unregulated fluxes through the jth EM, mmol/(gDW h) 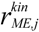 : kinetic part of inducible enzyme synthesis rate, 1/h : kinetic part of inducible enzyme synthesis rate, 1/h sA,j, sE,j, sF,j, sG,j, sP,j: stoichiometric coefficients, mmol/gDW t: time, h uM,j: cybernetic variable regulating the enzyme induction vM,j: cybernetic variable regulating the enzyme activity xA, xE, xF, xG, xP: concentrations of acetate, ethanol, formate, glucose and pyruvate, mM xIN,G, xIN,P: feed concentration of glucose and pyruvate, mM Greek letters αM,j: constitutive enzyme synthesis rate, 1/h βM,j: rate of enzyme degradation, 1/h µ: growth rate, 1/h |
| Case | vM,1 | vM,2 | vM,3 | vM,4 |
|---|---|---|---|---|
| I | 1 | ≤1 | ≤1 | ≤1 |
| II | ≤1 | 1 | ≤1 | ≤1 |
| III | ≤1 | ≤1 | 1 | ≤1 |
| IV | ≤1 | ≤1 | ≤1 | 1 |
 , with
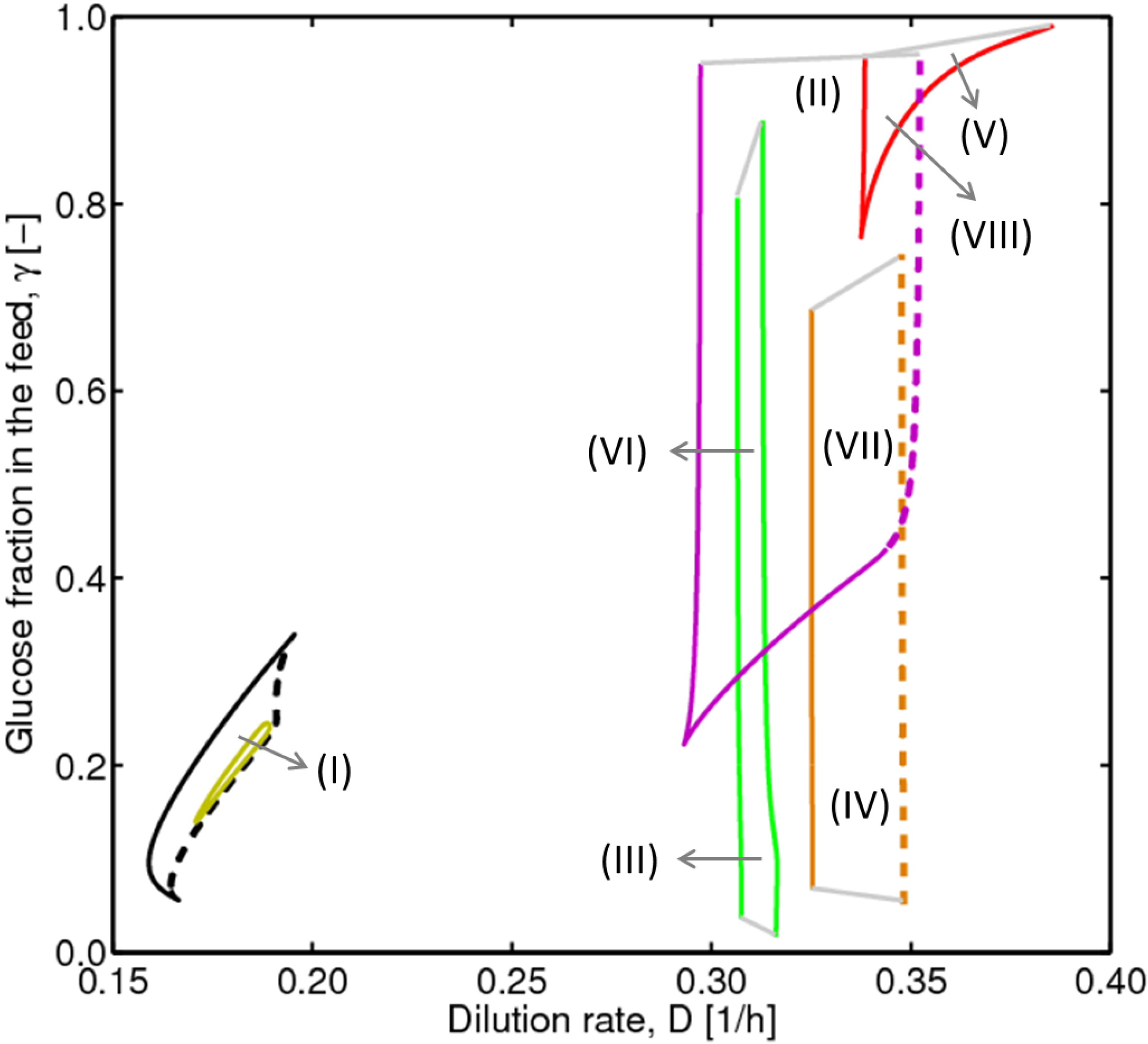
, with 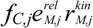 , leading to four independent sets of model equations. Figure 1 shows the resulting four hysteresis curves in the D − c space with a fixed value of γ (i.e., 0.2), obtained from the analysis of Cases I to IV, respectively. Segments highlighted in color represent feasible branches satisfying the constraint, i.e., vM,j = 1 (j = 1 − 4), i.e., green (b), cyan (c) and magenta (d), respectively. Note that no such colored branch is found in Figure 1a, indicating that there exists no feasible solution satisfying vM,1 = 1 along the whole profile.
, leading to four independent sets of model equations. Figure 1 shows the resulting four hysteresis curves in the D − c space with a fixed value of γ (i.e., 0.2), obtained from the analysis of Cases I to IV, respectively. Segments highlighted in color represent feasible branches satisfying the constraint, i.e., vM,j = 1 (j = 1 − 4), i.e., green (b), cyan (c) and magenta (d), respectively. Note that no such colored branch is found in Figure 1a, indicating that there exists no feasible solution satisfying vM,1 = 1 along the whole profile. 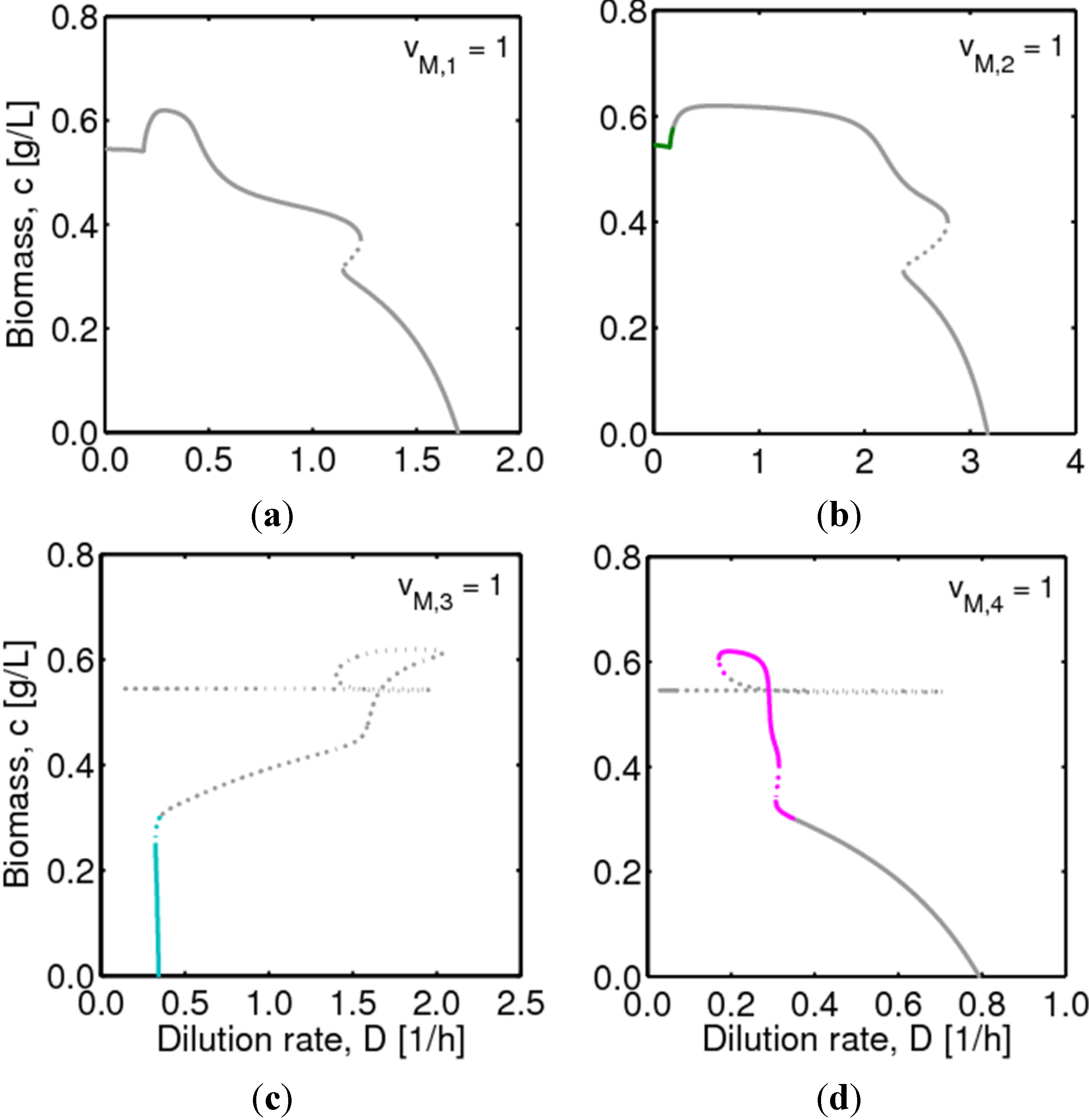
3.2. Smooth Approximation to the Max Function
 with
with 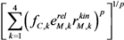 .
. 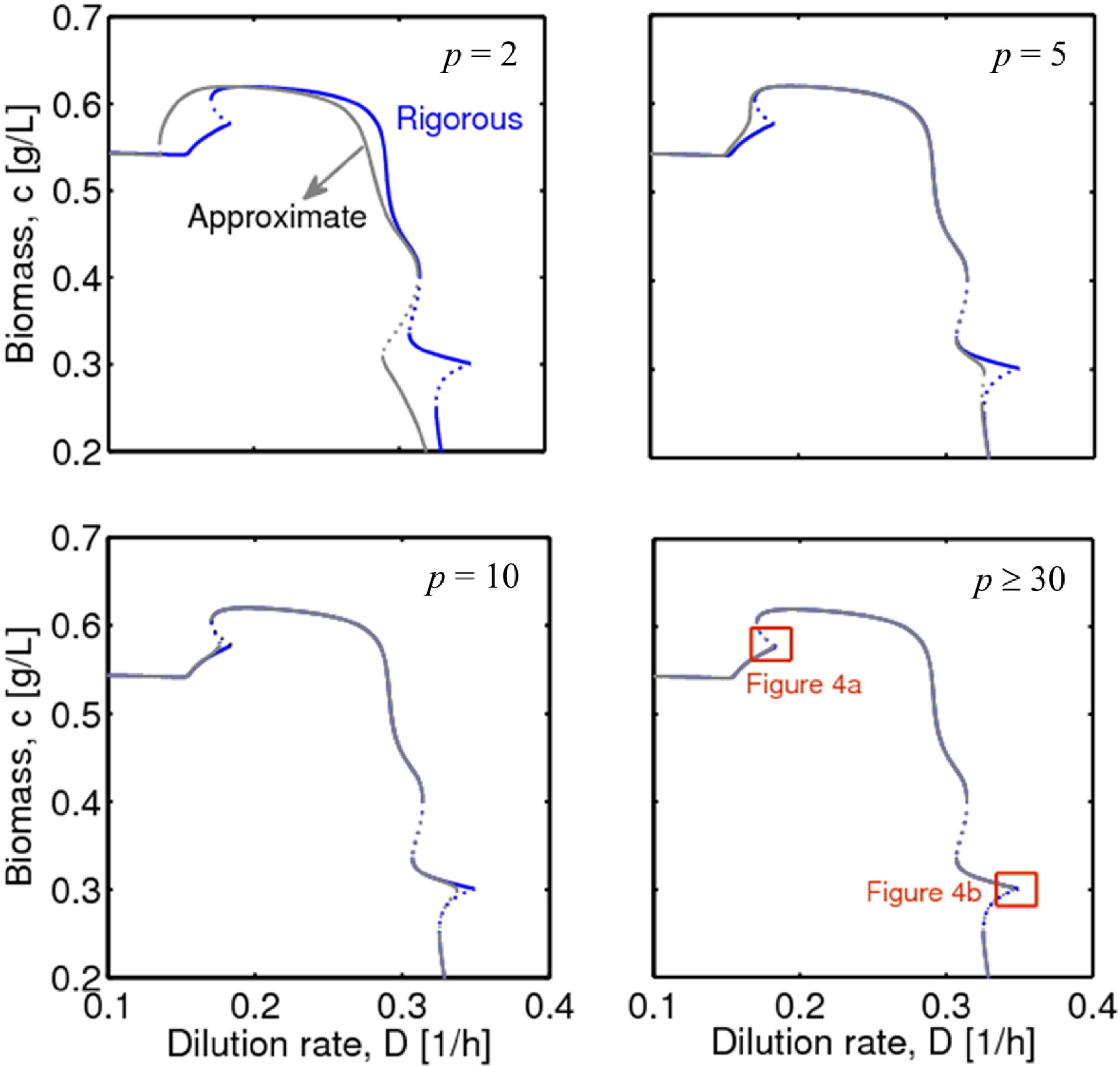
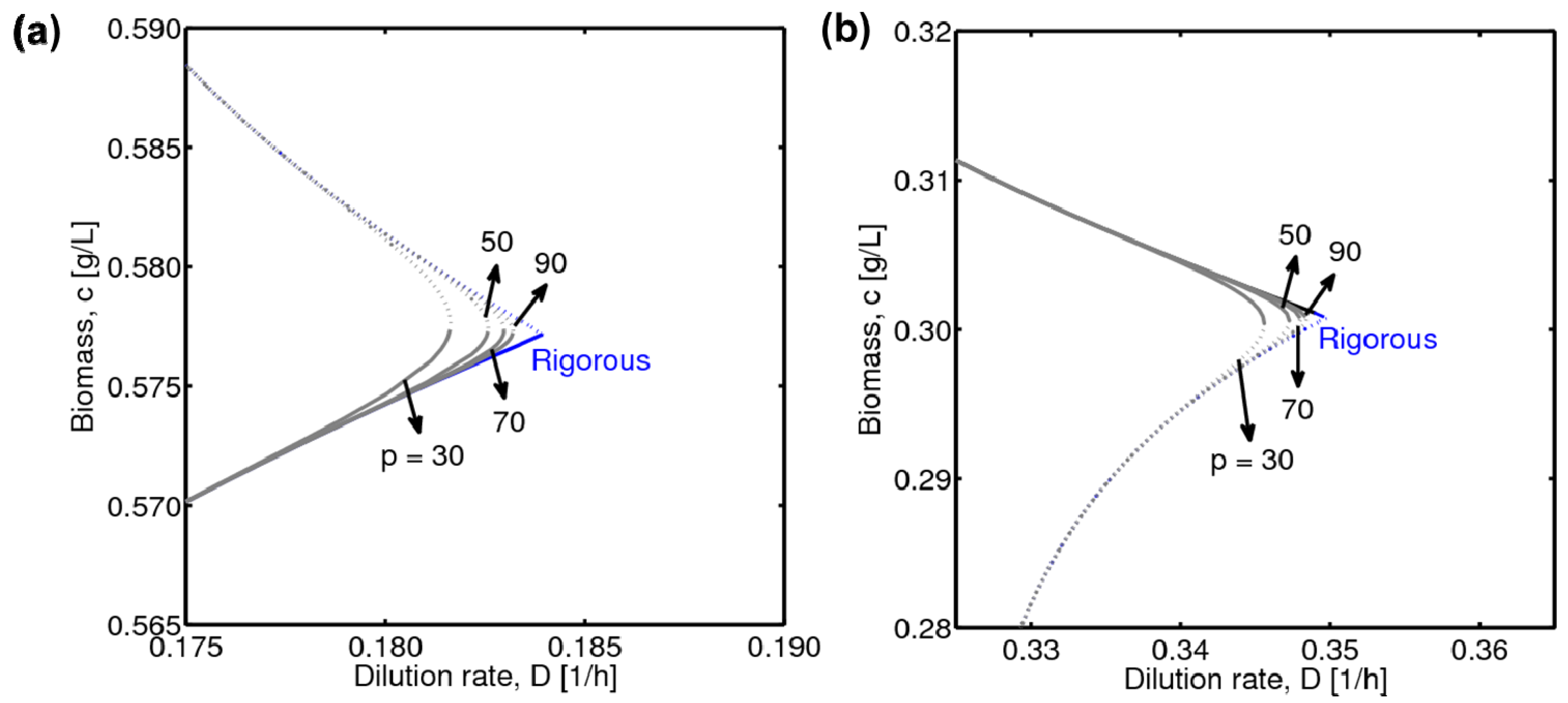
3.3. Integration of Two Methods
4. Results and Discussion
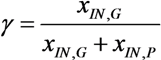
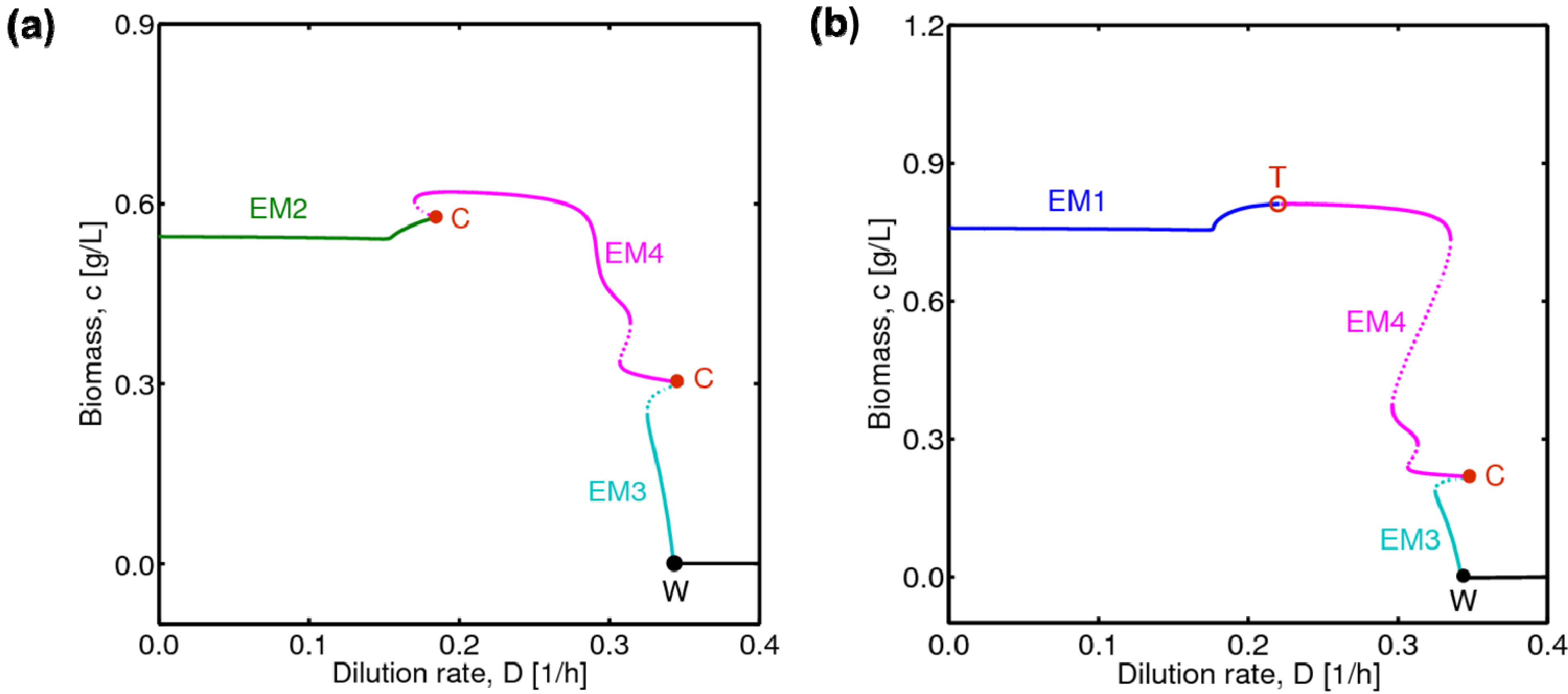
4.1. Hysteresis Behaviors and Bifurcation Diagram
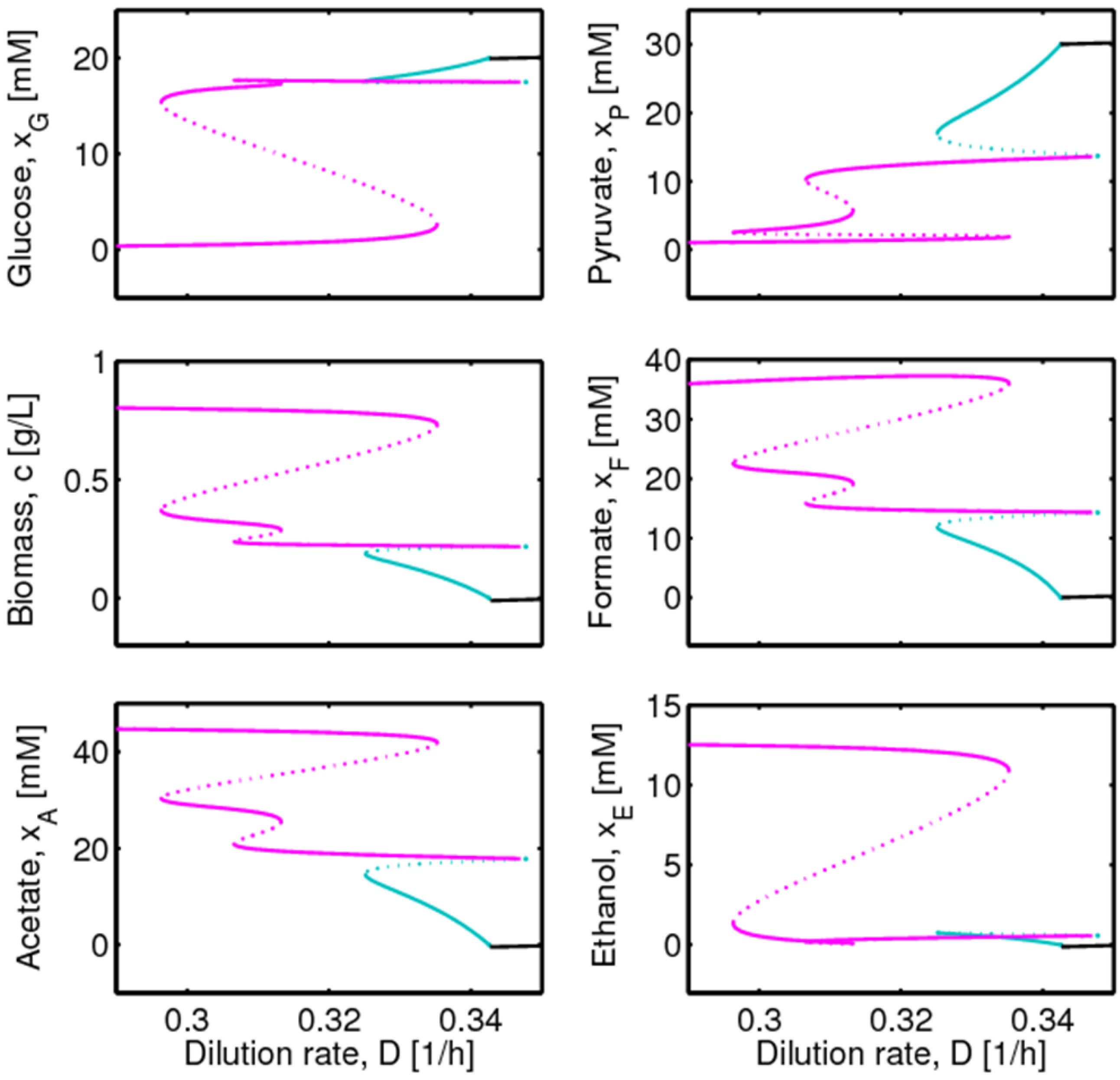
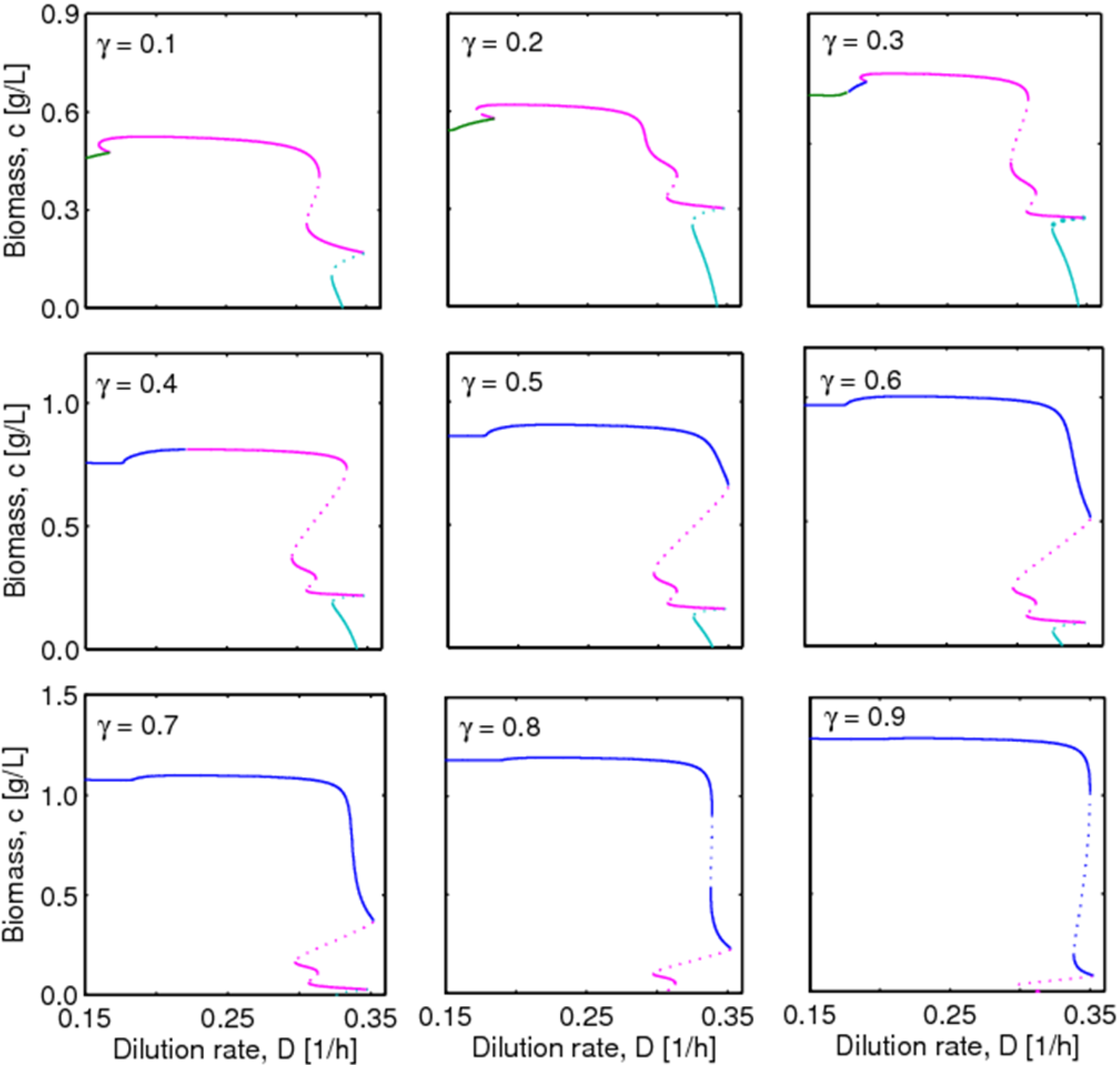
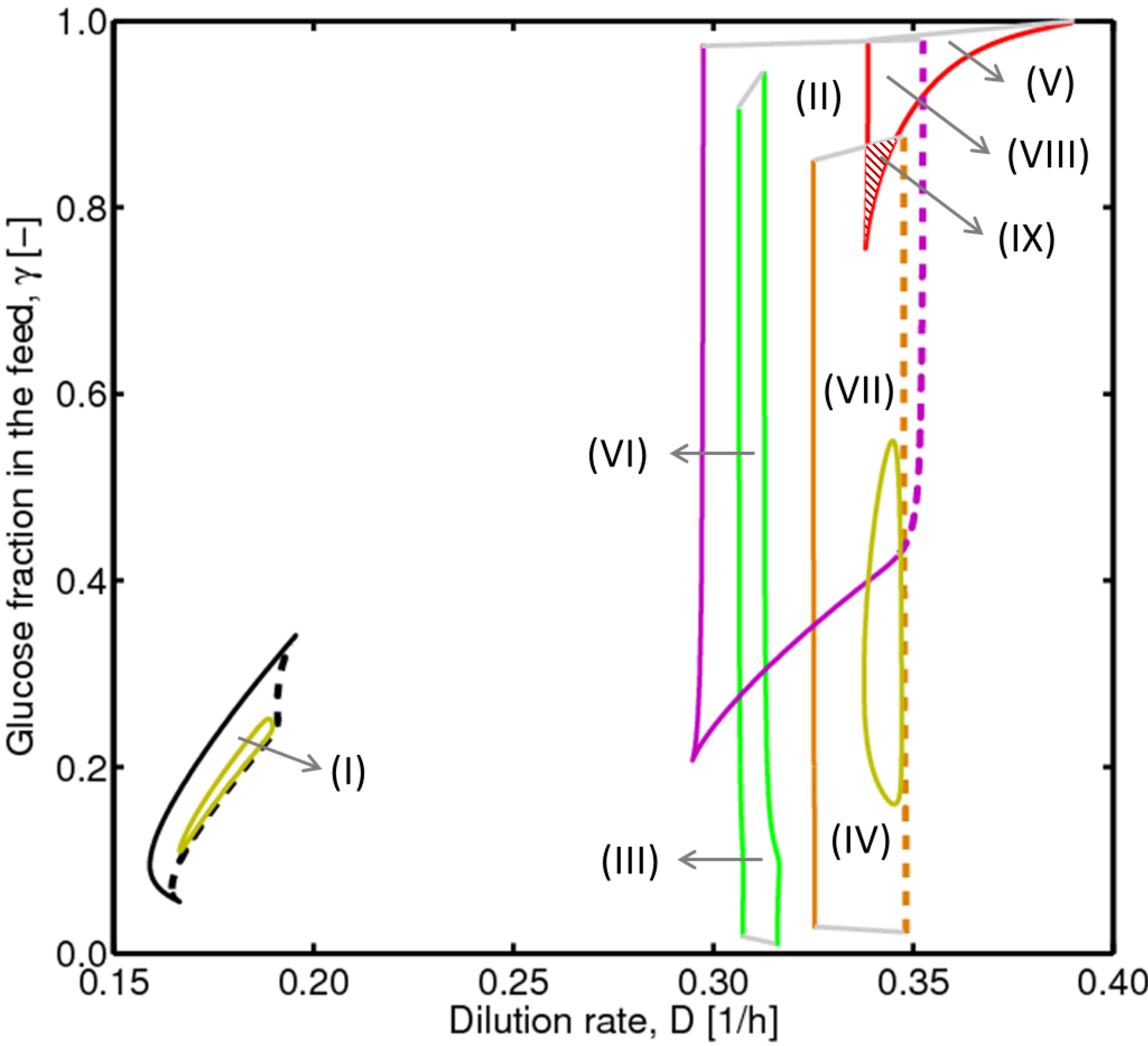
4.2. Bifurcation Diagram at a Higher Sugar Concentration in the Feed
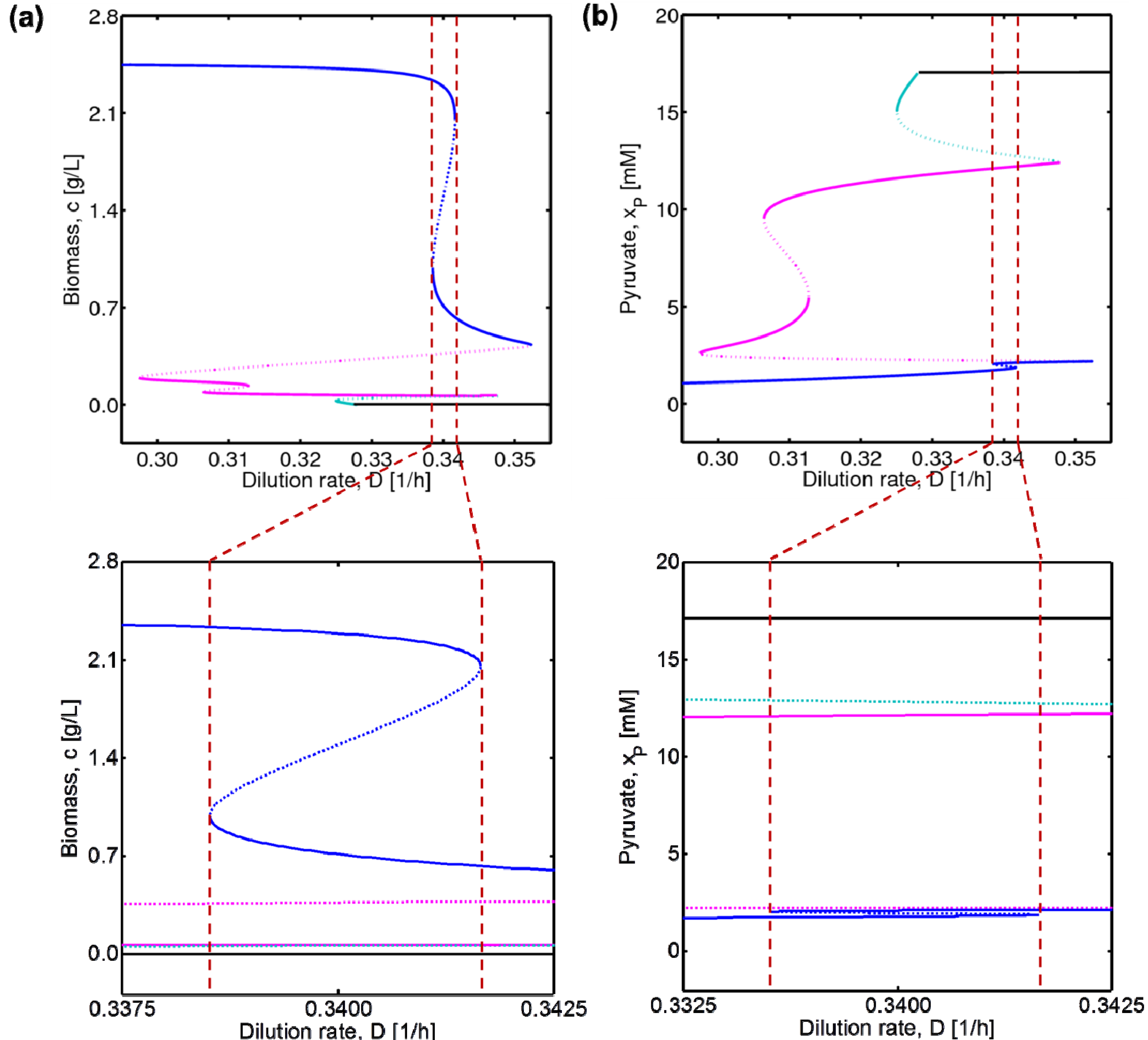
4.3. Experimental Validation
5. Conclusions
Acknowledgments
Conflicts of Interest
References
- Alzate, C.A.C.; Astudillo, I.C.P. Importance of stability study of continuous systems for ethanol production. J. Biotechnol. 2011, 151, 43–55. [Google Scholar]
- Elnashaie, S.S.; Grace, J.R. Complexity, bifurcation and chaos in natural and man-made lumped and distributed systems. Chem. Eng. Sci. 2007, 62, 3295–3325. [Google Scholar] [CrossRef]
- Trinh, C.T.; Wlaschin, A.; Srienc, F. Elementary mode analysis: A useful metabolic pathway analysis tool for characterizing cellular metabolism. Appl. Microbiol. Biotechnol. 2009, 81, 813–826. [Google Scholar]
- Wagner, C.; Urbanczik, R. The geometry of the flux cone of a metabolic network. Biophys. J. 2005, 89, 3837–3845. [Google Scholar] [CrossRef]
- Orth, J.D.; Thiele, I.; Palsson, B.O. What is flux balance analysis? Nat. Biotechnol. 2010, 28, 245–248. [Google Scholar]
- Reed, J.L.; Palsson, B.O. Thirteen years of building constraint-based in silico models of Escherichia coli. J. Bacteriol. 2003, 185, 2692–2699. [Google Scholar]
- Wiechert, W.; Noack, S. Mechanistic pathway modeling for industrial biotechnology: Challenging but worthwhile. Curr. Opin. Biotechnol. 2011, 22, 604–610. [Google Scholar] [CrossRef]
- Ramkrishna, D.; Song, H.S. Dynamic models of metabolism: Review of the cybernetic approach. AIChE J. 2012, 58, 986–997. [Google Scholar] [CrossRef]
- Song, H.S.; DeVilbiss, F.; Ramkrishna, D. Modeling metabolic systems: The need for dynamics. Curr. Opin. Chem. Eng. 2013, in press. [Google Scholar] [Green Version]
- Namjoshi, A.A.; Ramkrishna, D. Multiplicity and stability of steady states in continuous bioreactors: Dissection of cybernetic models. Chem. Eng. Sci. 2001, 56, 5593–5607. [Google Scholar] [CrossRef]
- Namjoshi, A.A.; Hu, W.S.; Ramkrishna, D. Unveiling steady-state multiplicity in hybridoma cultures: The cybernetic approach. Biotechnol. Bioeng. 2003, 81, 80–91. [Google Scholar] [CrossRef]
- Simpson, D.J.; Kompala, D.S.; Meiss, J.D. Discontinuity induced bifurcations in a model of Saccharomyces cerevisiae. Math. Biosci. 2009, 218, 40–49. [Google Scholar] [CrossRef]
- Kim, J.I.; Varner, J.D.; Ramkrishna, D. A hybrid model of anaerobic E. coli GJT001: Combination of elementary flux modes and cybernetic variables. Biotechnol. Prog. 2008, 24, 993–1006. [Google Scholar] [CrossRef]
- Song, H.S.; Morgan, J.A.; Ramkrishna, D. Systematic development of hybrid cybernetic models: Application to recombinant yeast co-consuming glucose and xylose. Biotechnol. Bioeng. 2009, 103, 984–1002. [Google Scholar] [CrossRef]
- Song, H.S.; Ramkrishna, D. Reduction of a set of elementary modes using yield analysis. Biotechnol. Bioeng. 2009, 102, 554–568. [Google Scholar] [CrossRef]
- Kim, J.I.; Song, H.S.; Sunkara, S.R.; Lali, A.; Ramkrishna, D. Exacting predictions by cybernetic model confirmed experimentally: Steady state multiplicity in the chemostat. Biotechnol. Prog. 2012, 28, 1160–1166. [Google Scholar] [CrossRef]
- Seydel, R. Practical Bifurcation and Stability Analysis; Springer Verlag: New York, NY, USA, 2009; Volume5. [Google Scholar] [Green Version]
- Dhooge, A.; Govaerts, W.; Kuznetsov, Y.A. MATCONT: A MATLAB package for numerical bifurcation analysis of ODEs. ACM Trans. Math. Softw. (TOMS) 2003, 29, 141–164. [Google Scholar] [CrossRef]
- Dhooge, A.; Govaerts, W.; Kuznetsov, Y.A.; Meijer, H.; Sautois, B. New features of the software MatCont for bifurcation analysis of dynamical systems. Math. Comput. Model. Dyn. Syst. 2008, 14, 147–175. [Google Scholar] [CrossRef]
- Schuster, S.; Fell, D.A.; Dandekar, T. A general definition of metabolic pathways useful for systematic organization and analysis of complex metabolic networks. Nat. Biotechnol. 2000, 18, 326–332. [Google Scholar] [CrossRef]
- Kompala, D.S.; Ramkrishna, D.; Jansen, N.B.; Tsao, G.T. Investigation of bacterial-growth on mixed substrates—Experimental evaluation of cybernetic models. Biotechnol. Bioeng. 1986, 28, 1044–1055. [Google Scholar]
- Young, J.D.; Ramkrishna, D. On the matching and proportional laws of cybernetic models. Biotechnol. Prog. 2007, 23, 83–99. [Google Scholar]
- Von Kamp, A.; Schuster, S. Metatool 5.0: Fast and flexible elementary modes analysis. Bioinformatics 2006, 22, 1930–1931. [Google Scholar] [CrossRef]
- Kim, J.I. A Hybrid Cybernetic Modeling for the Growth of Escherichia coli in Glucose-Pyruvate Mixtures. Ph.D. Thesis, Purdue University, West Lafayette, IN, USA, May 2008. [Google Scholar] [Green Version]
- Simpson, D.J.W. Bifurcations in Piecewise-Smooth Continuous Systems; World Scientific Publishing Co.: Hackensack, NJ, USA, 2010. [Google Scholar] [Green Version]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Song, H.-S.; Ramkrishna, D. Complex Nonlinear Behavior in Metabolic Processes: Global Bifurcation Analysis of Escherichia coli Growth on Multiple Substrates. Processes 2013, 1, 263-278. https://doi.org/10.3390/pr1030263
Song H-S, Ramkrishna D. Complex Nonlinear Behavior in Metabolic Processes: Global Bifurcation Analysis of Escherichia coli Growth on Multiple Substrates. Processes. 2013; 1(3):263-278. https://doi.org/10.3390/pr1030263
Chicago/Turabian StyleSong, Hyun-Seob, and Doraiswami Ramkrishna. 2013. "Complex Nonlinear Behavior in Metabolic Processes: Global Bifurcation Analysis of Escherichia coli Growth on Multiple Substrates" Processes 1, no. 3: 263-278. https://doi.org/10.3390/pr1030263
APA StyleSong, H.-S., & Ramkrishna, D. (2013). Complex Nonlinear Behavior in Metabolic Processes: Global Bifurcation Analysis of Escherichia coli Growth on Multiple Substrates. Processes, 1(3), 263-278. https://doi.org/10.3390/pr1030263





