Artery Segmentation in Ultrasound Images Based on an Evolutionary Scheme
Abstract
:1. Introduction

2. Materials and Methods
2.1. Evaluated Segmentation Methods
2.1.1. Parametric Active Contour

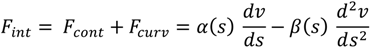
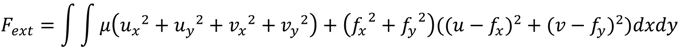
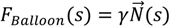
2.1.2. Region-Based Active Contour Model (ACM)
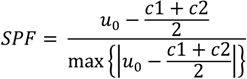
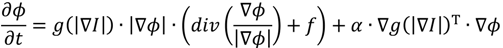
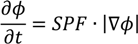
2.1.3. Segmentation Based on Fuzzy C-Mean Clustering
2.1.4. Active Shape Models (ASMs)
2.2. Proposed Segmentation Method
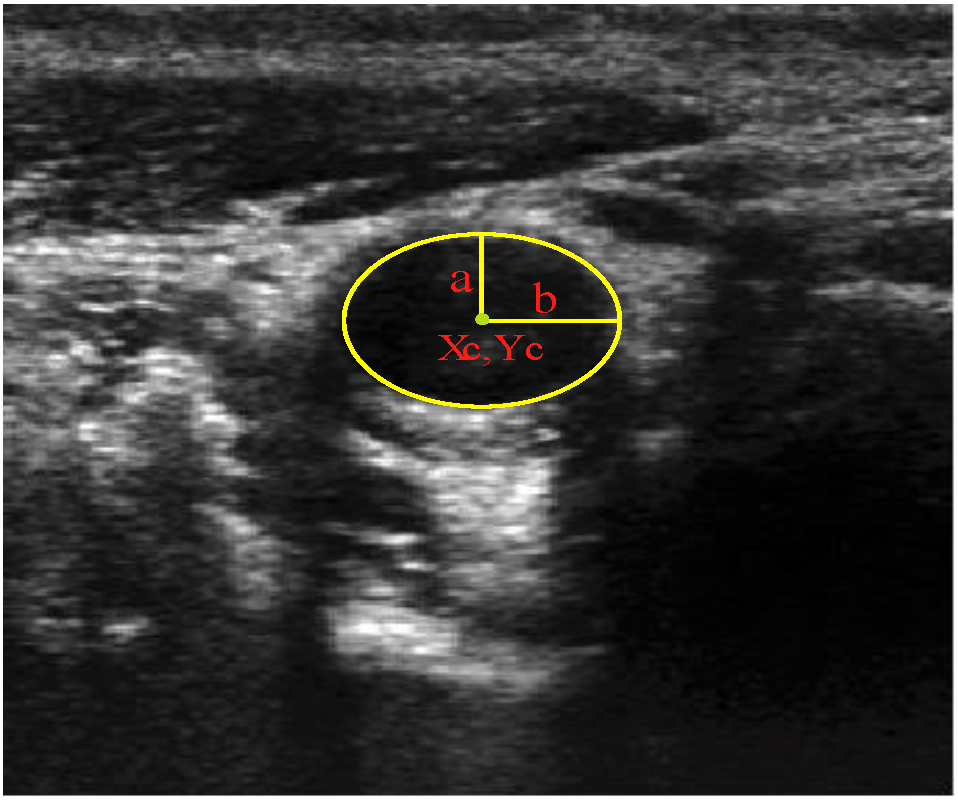
y(t) = yc + a ∙ cost ∙ sinθ − b ∙ sint ∙ cosθ
 ) are used to estimate the new one, with a desired mutation factor (F). Different approaches of this operator will be evaluated in Section 3. Another important exploration mechanism is the one provided by the cross-operator (Cross), where the mutated agents will be mixed with the current generation with a probability factor, CR (Cross Rate).
) are used to estimate the new one, with a desired mutation factor (F). Different approaches of this operator will be evaluated in Section 3. Another important exploration mechanism is the one provided by the cross-operator (Cross), where the mutated agents will be mixed with the current generation with a probability factor, CR (Cross Rate).

- 1 Population = InitPopulation(MaxPar,MinPar);
- 2 FitPop = GetFitness(Population);
- 3 BestAgent = GetBestAgent(Population);
- 4 while (NumIter < NumIterMax)
- 5 MutPop = Mutate(Population,BestAgent,F);
- 6 CrPop = Cross(Population,MutPop,CR);
- 7 FitCr = GetFitness(CrPop);
- 8 Population = Replace(Population,CRPop,FitCr,FitPop);
- 9 BestAgent = GetBestAgent(Population);
- 10 NumIter = NumIter + 1;
- 11 end while
- 12 return BestAgent
2.2.1. Feature Extraction
 , and the magnitude projection image,
, and the magnitude projection image,  .
.
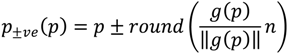
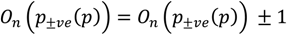

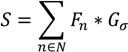
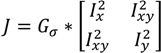
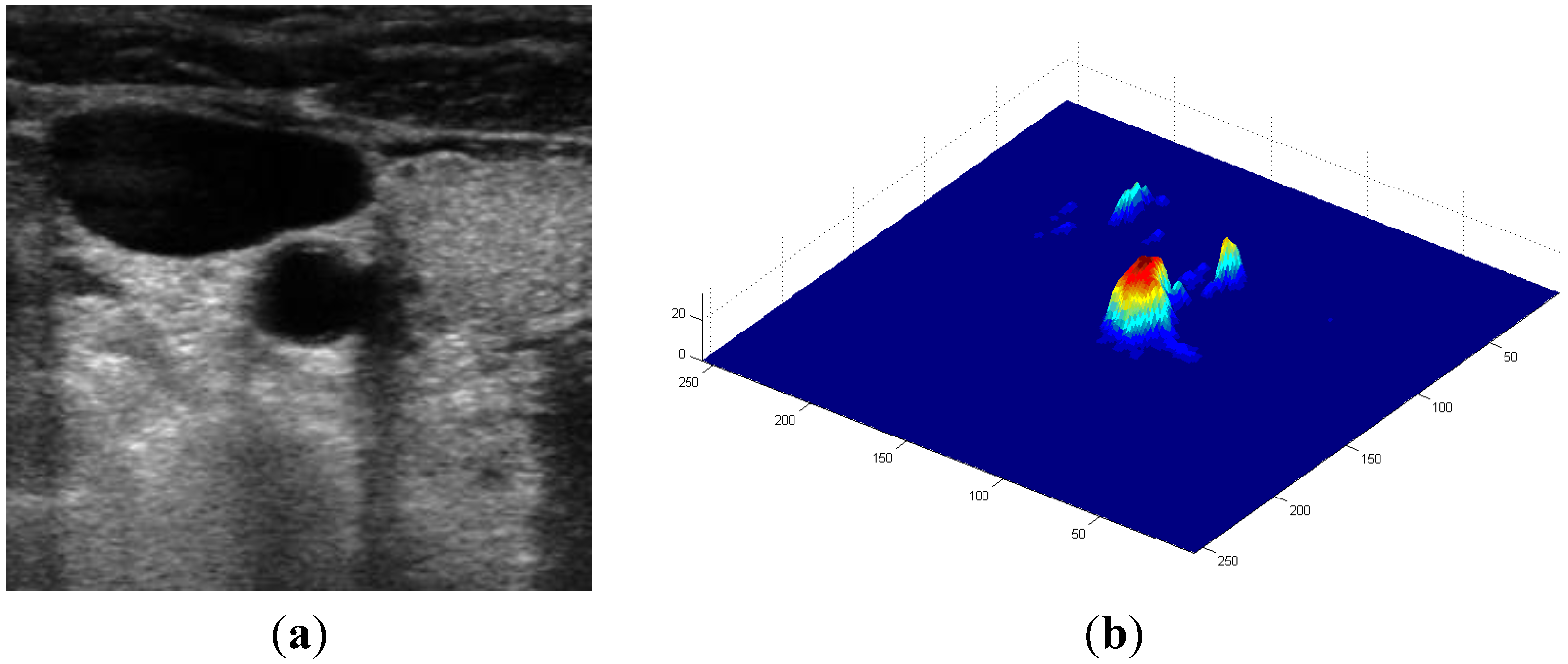
 determinates the level of speckle noise, and therefore, it allows the control of the diffusion over time in Image (I).
determinates the level of speckle noise, and therefore, it allows the control of the diffusion over time in Image (I).
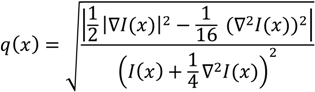
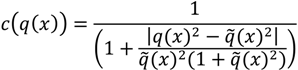

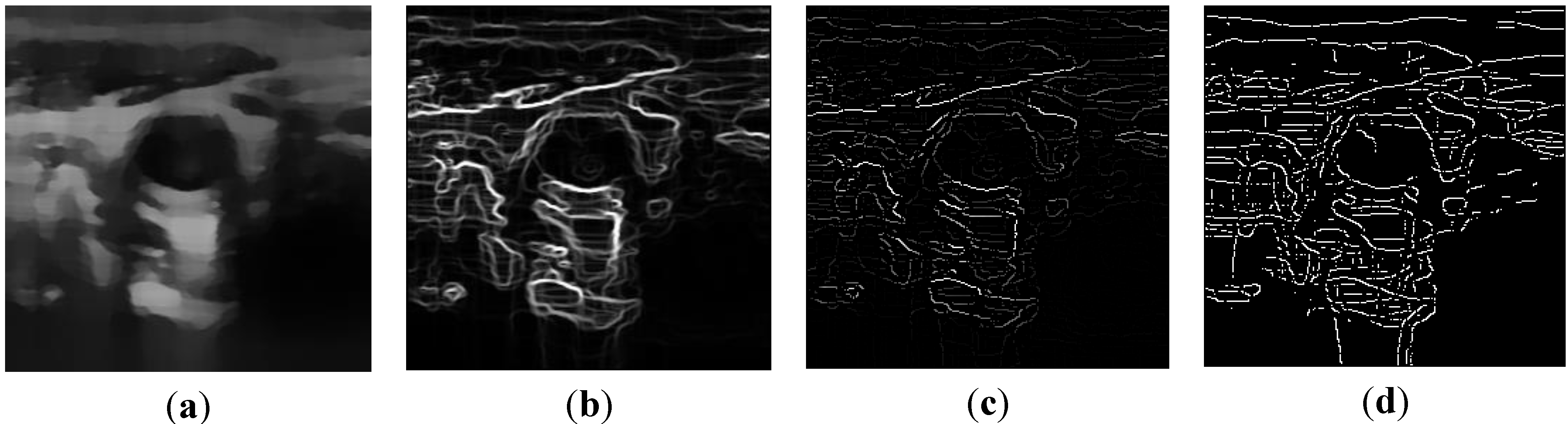
2.2.2. Ellipse Parameter Estimation
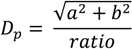
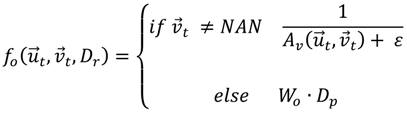
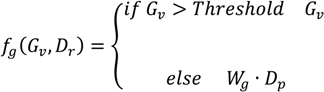
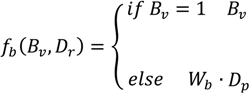
 ), and the pixel orientation, (
), and the pixel orientation, (  ), vector by means of function Av, which defines the angle between both vectors. The second objective function, f𝑔, Equation (22), aims to find shapes with a higher echogenicity given by the LIP-Sobel gra2-dient, Gv. To avoid the gradient generated by small variations in the intensity of the image, a threshold scheme is utilized. The function is set to the gradient if the threshold is higher than a defined value; otherwise, a penalization is applied to avoid the discontinuity in the shape of the ellipse and the gradient map. The third objective function, fb, Equation (23), acts in a similar way as the previous one, but in this case, a binary map, Bv, is used. Finally, the fourth objective function, fFRS, Equation (24), will guide the ellipse into the center of the artery using the FRS map. Once all the objective functions have been defined, the fitness function can be expressed as shown in Equation (25), where the weights, α1,α2,α3,α4, are incorporated for each respective objective function. After empirical tests, it was found that those values fixed to α1 = 100, α2 = 2, α3 = 100, α4 = 30 of the proposed method achieve satisfactory results.
), vector by means of function Av, which defines the angle between both vectors. The second objective function, f𝑔, Equation (22), aims to find shapes with a higher echogenicity given by the LIP-Sobel gra2-dient, Gv. To avoid the gradient generated by small variations in the intensity of the image, a threshold scheme is utilized. The function is set to the gradient if the threshold is higher than a defined value; otherwise, a penalization is applied to avoid the discontinuity in the shape of the ellipse and the gradient map. The third objective function, fb, Equation (23), acts in a similar way as the previous one, but in this case, a binary map, Bv, is used. Finally, the fourth objective function, fFRS, Equation (24), will guide the ellipse into the center of the artery using the FRS map. Once all the objective functions have been defined, the fitness function can be expressed as shown in Equation (25), where the weights, α1,α2,α3,α4, are incorporated for each respective objective function. After empirical tests, it was found that those values fixed to α1 = 100, α2 = 2, α3 = 100, α4 = 30 of the proposed method achieve satisfactory results.
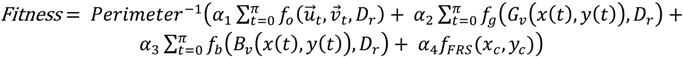
2.3. GPU Implementation
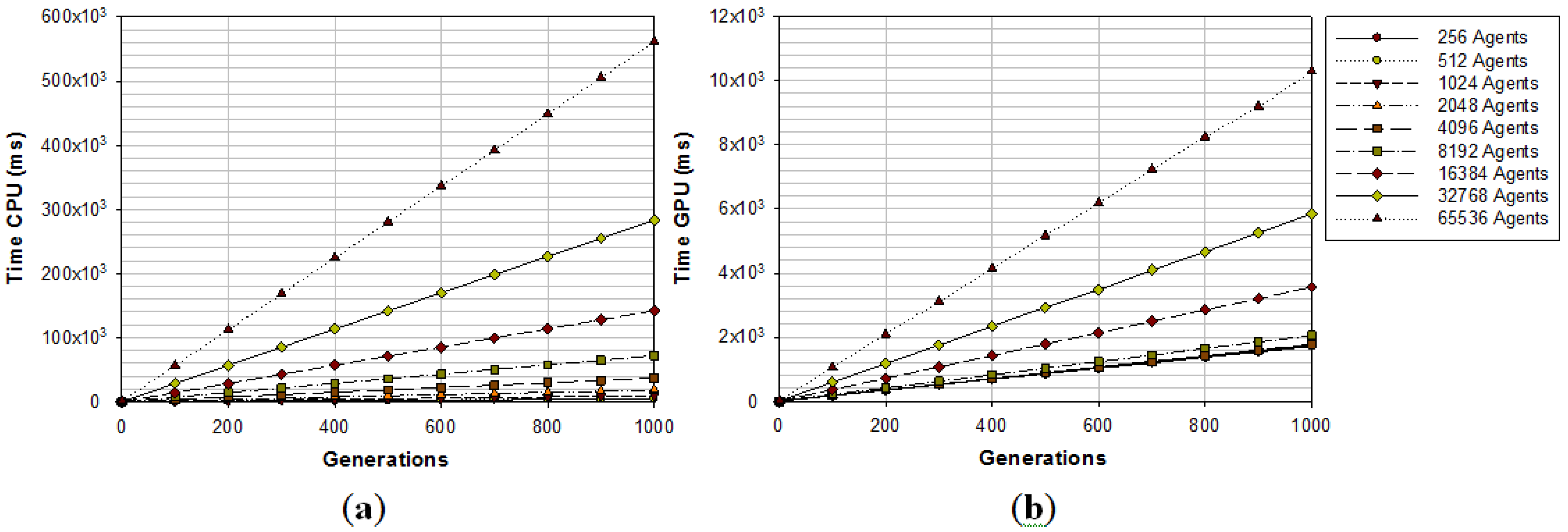

| Method | GPU Time | CPU (8 cores) Time |
|---|---|---|
| SRAD (AOS)5 Iterations | 7.65 ms | 13.58 ms |
| FRS | 3.78 ms | - |
| Pixel Orientation | 1.14 ms | 6.95 ms |
| Non-Max Suppression | 0.16 ms | 2.29 ms |
| LIP-Sobel Gradient | 0.11 ms | 1.42 ms |
3. Results
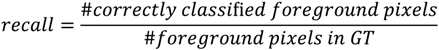
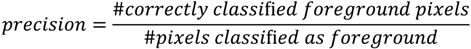

- (1)
- DE/Best/1
- (2)
- DE/Current to Best/1
- (3)
- DE/Current to Best/2
- (4)
- DE/Rand/1
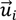 , denotes the mutated vector,
, denotes the mutated vector, 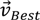 the best agent in the current generation,
the best agent in the current generation, 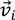 the current agent and
the current agent and 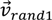 and
and 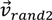 the random vectors in the evaluated generation. Figure 8 shows the obtained segmentation results with different mutation operators. To perform this test, the experiment has been repeated 10 times (per each operator) and the mean of the obtained results has been computed. It can be observed that the best mutation operation can have an impact of about 3% in precision and almost 1% in the F-measure with respect to the worst case.
the random vectors in the evaluated generation. Figure 8 shows the obtained segmentation results with different mutation operators. To perform this test, the experiment has been repeated 10 times (per each operator) and the mean of the obtained results has been computed. It can be observed that the best mutation operation can have an impact of about 3% in precision and almost 1% in the F-measure with respect to the worst case.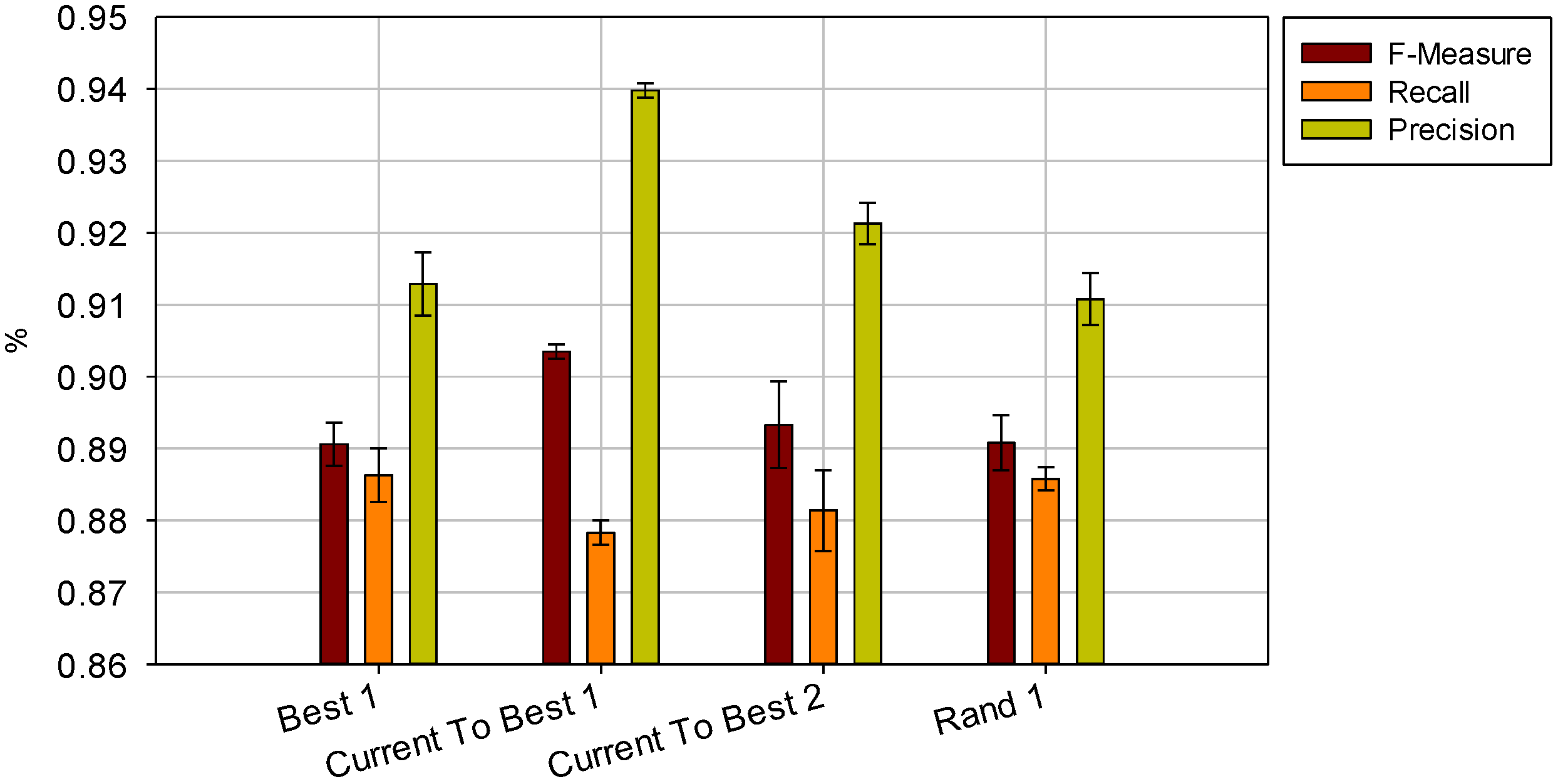
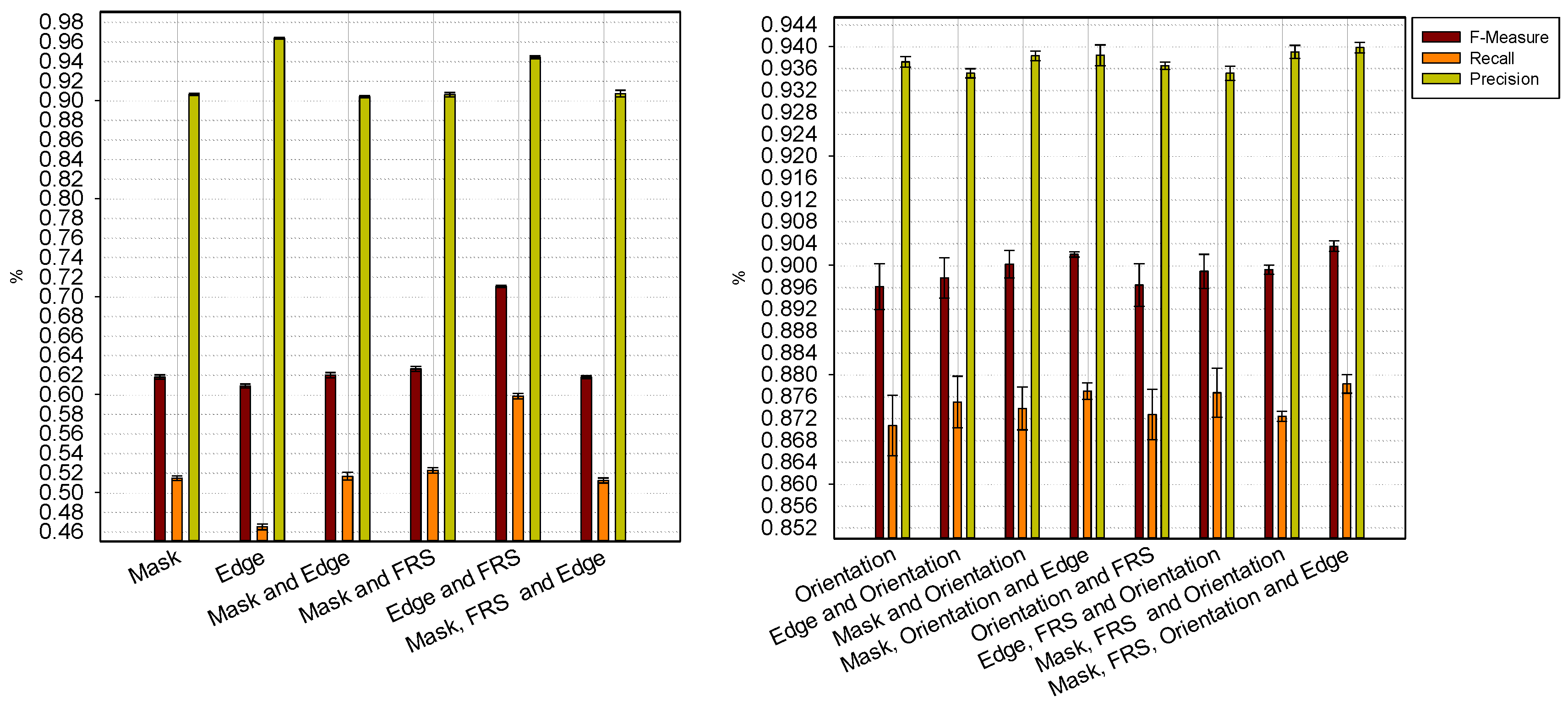
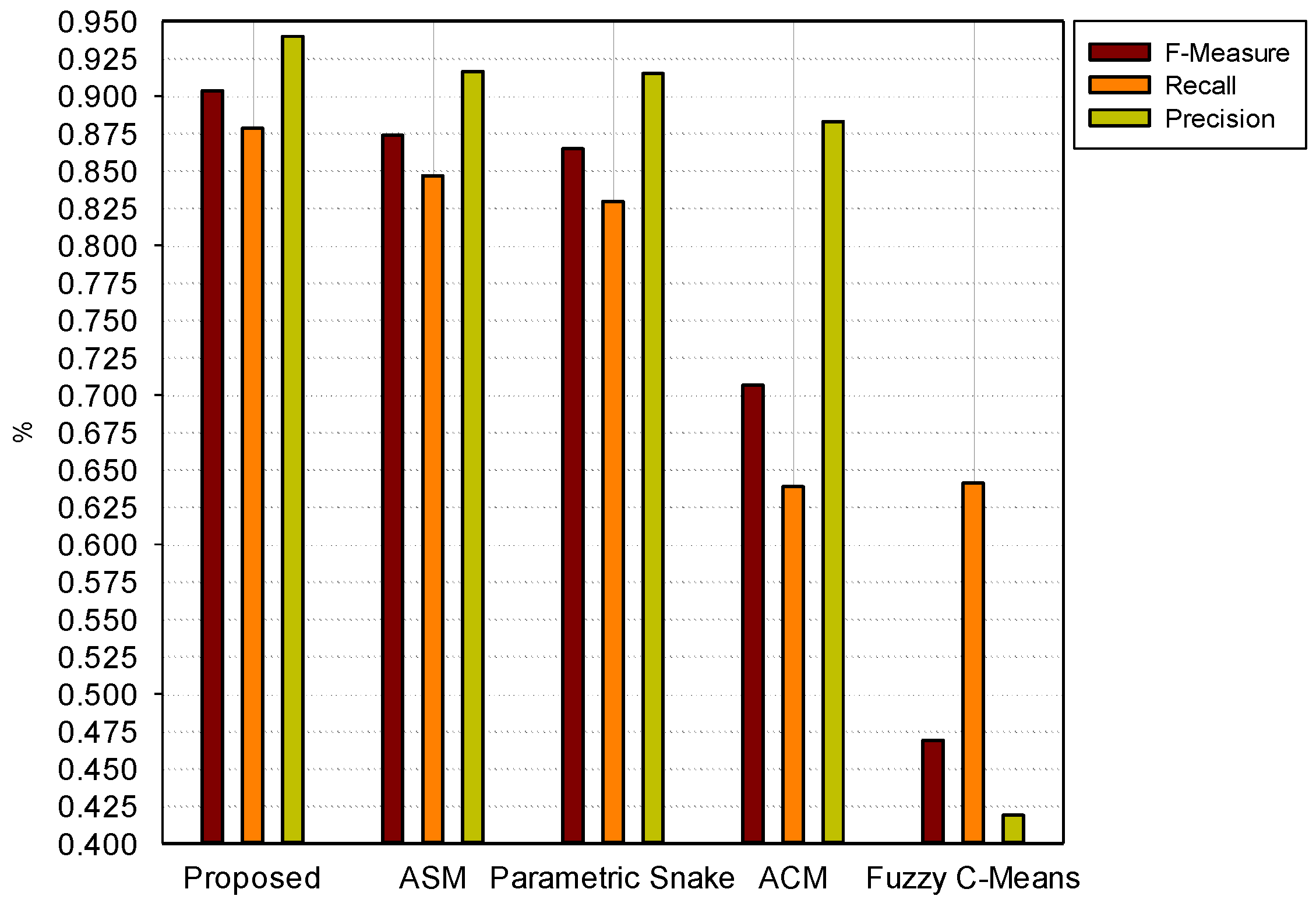
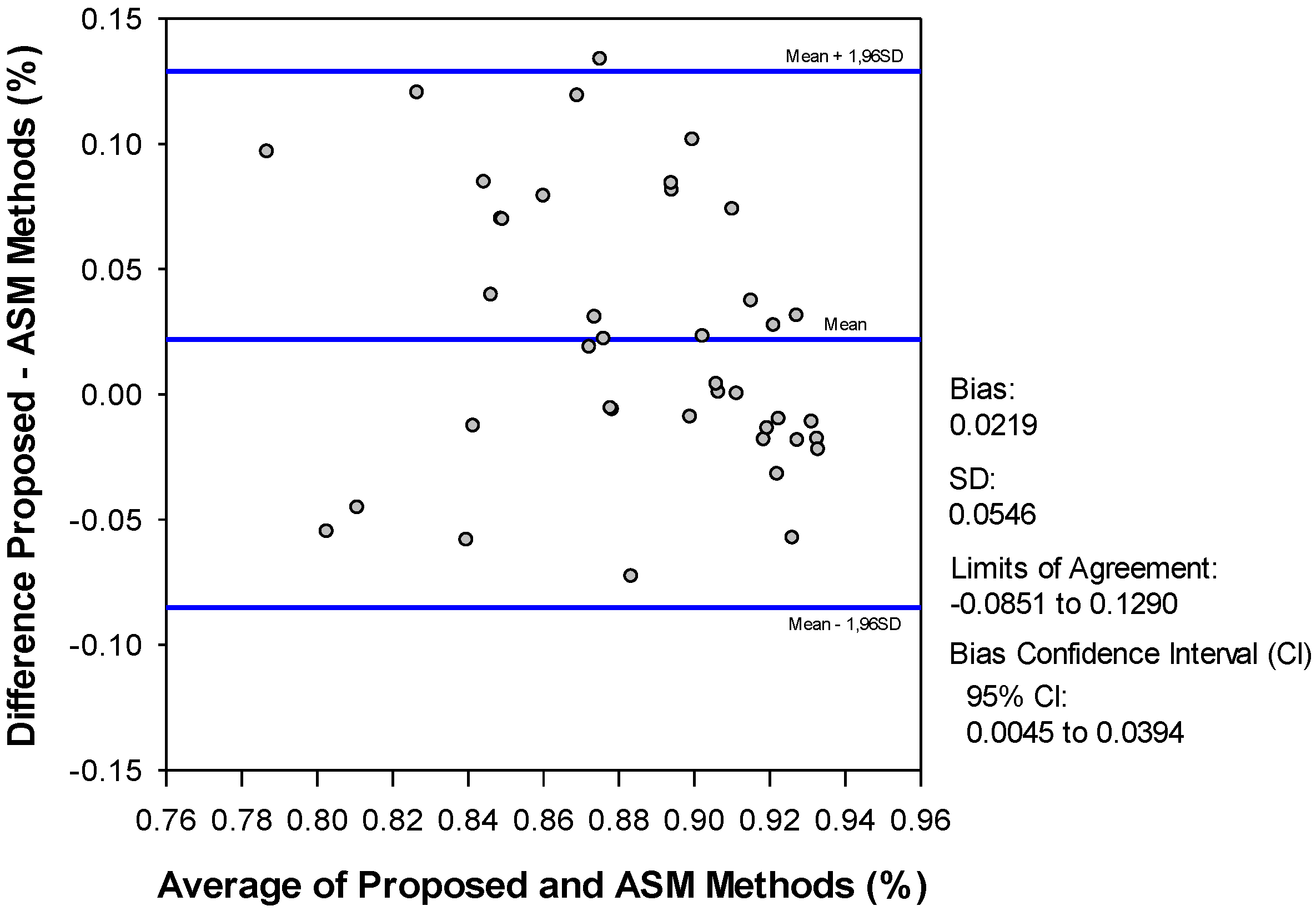
4. Discussion
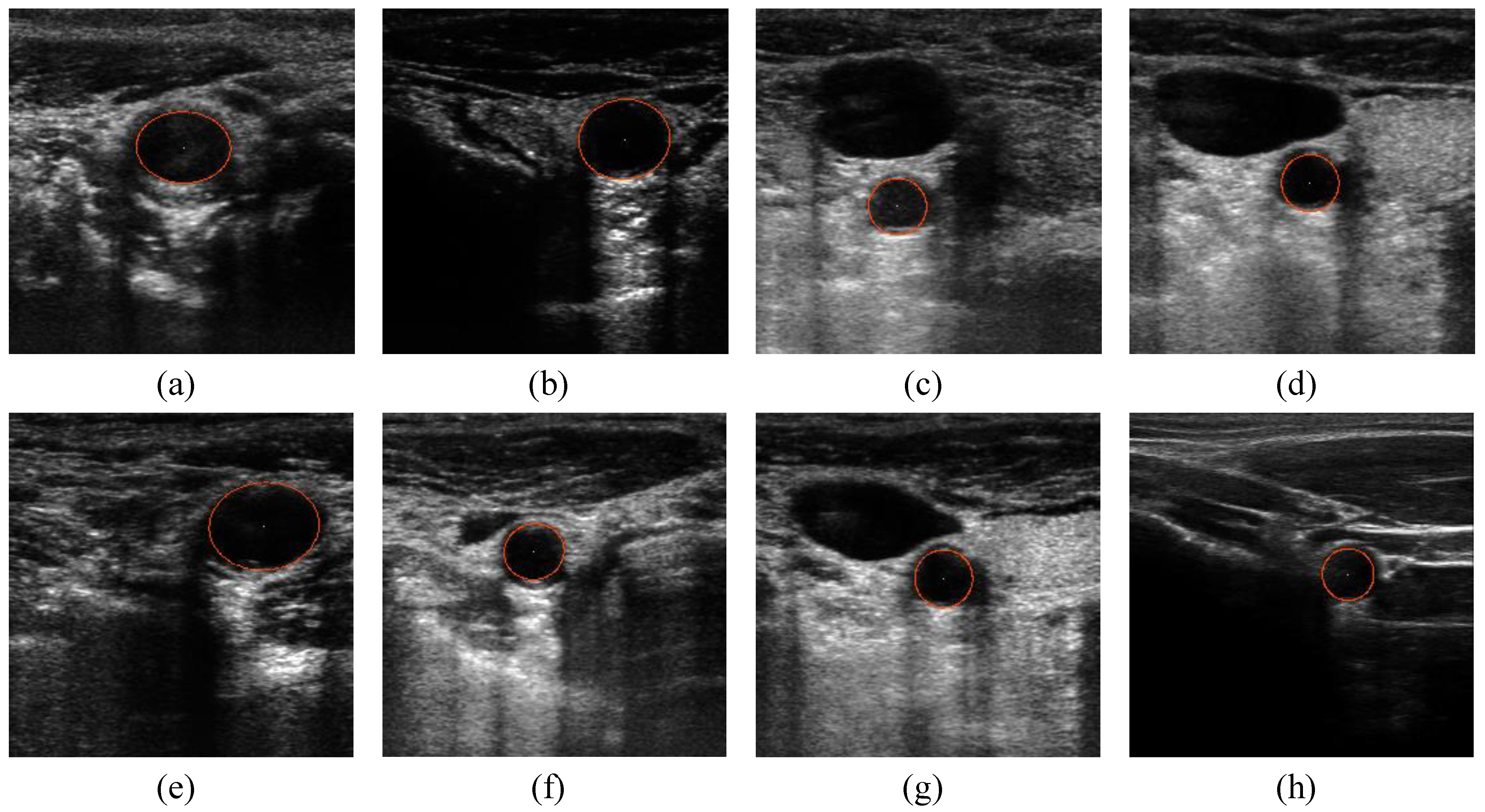
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Yao, J.; Kharma, N.; Grogono, P. A multi-population genetic algorithm for robust and fast ellipse detection. Pattern Anal. Appl. 2005, 8, 149–162. [Google Scholar] [CrossRef]
- McLaughlin, R.A. Randomized Hough transform: Improved ellipse detection with comparison. Pattern Recogn. Lett. 1998, 19, 299–305. [Google Scholar] [CrossRef]
- Lutton, E.; Martinez, P. A Genetic Algorithm for the Detection of 2D Geometric Primitives in Images. In Proceedings of the 12th International Conference on Pattern Recognition, Jerusalem, Israel, 9–13 October 1994; pp. 526–528.
- Mainzer, T. Genetic Algorithm for Shape Detection. Technical Report No. DCSE/TR-2002-06. University of West Bohemia: Pilsen, Czech Republic, 2002. [Google Scholar]
- Moursi, S.G.; Sakka, M.R.E. Semi-automatic snake based segmentation of carotid artery ultrasound images. Commun. Arab Comput. Soc. (ACS) 2009, 2, 1–32. [Google Scholar]
- Kass, M.; Witkin, A.; Terzopoulos, D. Snakes: Active contour models. Int. J. Comput. Vis. 1987, 1, 321–331. [Google Scholar]
- Xu, C.; Prince, J.L. Snakes, shapes, and gradient vector flow. IEEE T. Image Process. 1998, 7, 359–369. [Google Scholar] [CrossRef]
- Cohen, L.D.; Cohen, I. Finite-element methods for active contour models and balloons for 2-D and 3-D images. IEEE T. Pattern Anal. 1993, 15, 1131–1147. [Google Scholar] [CrossRef]
- Ciecholewski, M. Gallbladder Boundary Segmentation from Ultrasound Images Using Active Contour Model. In Intelligent Data Engineering and Automated Learning–IDEAL; Springer: Berlin/Heidelberg, Germany, 2010; pp. 63–69. [Google Scholar]
- Cvancarova, M.; Albregtsen, F.; Brabrand, K.; Samset, E. Segmentation of Ultrasound Images of Liver Tumors Applying Snake Algorithms and GVF. In Proceedings of the 19th International Congress and Exhibition: Computer Assisted Radiology and Surgery (CARS 2005), Berlin, Germany, 22–25 June 2005; pp. 218–223.
- Tang, J. A multi-direction GVF snake for the segmentation of skin cancer images. Pattern Recogn. 2009, 42, 1172–1179. [Google Scholar] [CrossRef]
- Zhang, K.; Zhang, L.; Song, H.; Zhou, W. Active contours with selective local or global segmentation: A new formulation and level set method. Image Vis. Comput. 2010, 28, 668–676. [Google Scholar] [CrossRef]
- Caselles, V.; Kimmel, R.; Sapiro, G. Geodesic active contours. Int. J. Comput. Vis. 1997, 22, 61–79. [Google Scholar] [CrossRef]
- Chan, T.F.; Vese, L.A. Active contours without edges. IEEE T. Image Process. 2001, 10, 266–277. [Google Scholar] [CrossRef]
- Dunn, J.C. A fuzzy relative of the isodata process and its use in detecting compact well-separated clusters. J. Cybernet. 1973, 3, 32–57. [Google Scholar] [CrossRef]
- Abdel-Dayem, A.; El-Sakka, M. Fuzzy c-Means Clustering for Segmenting Carotid Artery Ultrasound Images. In Proceedings of the International Conference on Image Analysis and Recognition (ICIAR 2007), Montreal, Canada, 22–24 August 2007; pp. 933–948.
- Vincent, L. Morphological grayscale reconstruction in image analysis: Applications and efficient algorithms. IEEE T. Image Process. 1993, 2, 176–201. [Google Scholar] [CrossRef]
- Cootes, T.F.; Taylor, C.J.; Cooper, D.H.; Graham, J. Active shape models—Their training and application. Comput. Vis. Image Underst. 1995, 61, 38–59. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Hansen, N. Compilation of results on the 2005 CEC benchmark function set. Tech. Rep. Institute of Computational Science ETH Zurich. 2006. [Google Scholar]
- Loy, G.; Zelinsky, A. Fast radial symmetry for detecting points of interest. IEEE T. Pattern Anal. 2003, 25, 959–973. [Google Scholar] [CrossRef]
- Yongjian, Y.; Acton, S.T. Speckle reducing anisotropic diffusion. IEEE T. Image Process. 2002, 11, 1260–1270. [Google Scholar] [CrossRef]
- Palomares, J.M.; Gonzalez, J.; Ros, E.; Prieto, A. General logarithmic image processing. IEEE T. Image Process. 2006, 15, 3602–3608. [Google Scholar] [CrossRef]
- Deng, G.; Cahill, L.W.; Tobin, G.R. The study of logarithmic image processing model and its application to image enhancement. IEEE T. Image Process. 1995, 506–512. [Google Scholar] [CrossRef]
- Canny, J.F. A computational approach to edge detection. IEEE T. Pattern Anal. 1986, 8, 679–698. [Google Scholar] [CrossRef]
- Hajela, P.; Lin, C.Y. Genetic search strategies in multicriterion optimal design. Struct. Optim. 1992, 4, 99–107. [Google Scholar] [CrossRef]
- De Veronses, L.; Krohling, R. Differential Evolution Algorithm on the GPU with C-CUDA. In Proceedings of the IEEE Congress on Evolutionary Computation (CEC), Barcelona, Spain, 18–23 July 2010; pp. 1–7.
- Zhu, W. Massively parallel differential evolution-pattern search optimization with graphics hardware acceleration: An investigation on bound constrained optimization problems. J. Glob. Optim. 2011, 50, 417–437. [Google Scholar] [CrossRef]
- Zhu, W.; Li, Y. GPU-Accelerated Differential Evolutionary Markov Chain Monte Carlo Method for Multi-Objective Optimization over Continuous Space. In Proceedings of the 2nd Workshop on Bio-Inspired Algorithms for Distributed Systems (BADS), New York, NY, USA, 7–11 June 2010; pp. 1–8.
- Marsaglia, G. Xorshift RNGs. J. Stat. Softw. 2003, 8, 1–6. [Google Scholar]
- Mallipeddi, R.; Suganthan, P.N. Empirical Study on the Effect of Population Size on Differential Evolution Algorithm. In Proceedings of the IEEE Congress on Evolutionary Computation (CEC), Hong Kong, China, 1–6 June 2008; pp. 3664–3671.
- Weichert, J. Anisotropic Diffusion in Image Processing; BG Teubner: Stuttgart, Germany, 2008; pp. 278–290. [Google Scholar]
- Weickert, J.; Romeny, B.H.; Viergever, M.A. Efficient and reliable schemes for nonlinear diffusion filtering. IEEE T. Image Process. 1998, 7, 398–409. [Google Scholar] [CrossRef]
- Cao, T.; Wang, B.; Liu, D.C. Optimized GPU Framework for Semi-Implicit AOS Scheme Based Speckle Reducing Nolinear Diffusion. In Proceedings of the SPIE Medical Imaging; Lake Buena Vista, FL, USA: 8–12 February 2009.
- Hockney, R.W. A fast direct solution of Poisson’s equation using Fourier analysis. J. ACM 1965, 12, 95–113. [Google Scholar] [CrossRef]
- Hockney, R.W.; Jesshope, C.R. Parallel Computers; Adam Hilger: London, UK, 1981. [Google Scholar]
- Zhang, Y.; Cohen, J.; Owens, J.D. Fast Tridiagonal Solvers on the GPU. In Proceedings of the 15th ACM SIGPLAN Symposium Principles and Practice of Parallel Programming (PPoPP ’10), Bangalore, India, 9–14 January 2010; pp. 127–136.
- Glavtchev, V.; Muyan-Ozcelik, P.; Ota, J.M.; Owens, J.D. Feature-Based Speed Limit Sign Detection Using a Graphics Processing Unit. In Proceedings of the IEEE on Intelligent Vehicles Symposium (IV), Baden-Baden, Germany, 5–9 June 2011; pp. 195–200.
- Palomar, R.; Palomares, J.M.; Castillo, J.M.; Olivares, J.; Gómez-Luna, J. Parallelizing and Optimizing LIP-Canny Using Nvidia Cuda. In Trends in Applied Intelligent Systems; Springer: Berlin/Heidelberg, Germany, 2010; pp. 389–398. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Guzman, P.; Ros, R.; Ros, E. Artery Segmentation in Ultrasound Images Based on an Evolutionary Scheme. Informatics 2014, 1, 52-71. https://doi.org/10.3390/informatics1010052
Guzman P, Ros R, Ros E. Artery Segmentation in Ultrasound Images Based on an Evolutionary Scheme. Informatics. 2014; 1(1):52-71. https://doi.org/10.3390/informatics1010052
Chicago/Turabian StyleGuzman, Pablo, Rafael Ros, and Eduardo Ros. 2014. "Artery Segmentation in Ultrasound Images Based on an Evolutionary Scheme" Informatics 1, no. 1: 52-71. https://doi.org/10.3390/informatics1010052
APA StyleGuzman, P., Ros, R., & Ros, E. (2014). Artery Segmentation in Ultrasound Images Based on an Evolutionary Scheme. Informatics, 1(1), 52-71. https://doi.org/10.3390/informatics1010052








