Dependence Uncertainty Bounds for the Expectile of a Portfolio
Abstract
:1. Introduction and Preliminaries
2. Bounds when Only the Marginal Distributions Are Known
2.1. Upper Bound with Marginal Information
2.2. Lower Bound with Marginal Information
2.2.1. Rearrangement Algorithm
| Standard RA: | , | . |
| Midpoint RA: | , | . |
| Expectation RA: | , | , |
| , |
| Standard RA | ||||||||||||
| d | 1 | 2 | 3 | 4 | 5 | 8 | 1 | 2 | 3 | 4 | 5 | 8 |
| 0.1 | 0.2 | 0.2 | 0.2 | 0.3 | 0.4 | 0.3 | 0.5 | 0.6 | 0.7 | 0.8 | 1.2 | |
| 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 1.0 | 0.7 | 1.1 | 1.4 | 1.7 | 1.9 | 2.6 | |
| 0.5 | 0.7 | 0.9 | 1.0 | 1.2 | 1.5 | 1.2 | 1.7 | 2.2 | 2.6 | 2.9 | 3.8 | |
| 1.2 | 1.6 | 1.9 | 2.2 | 2.5 | 3.1 | 2.5 | 3.4 | 4.2 | 4.9 | 5.4 | 6.9 | |
| 5.3 | 6.6 | 7.6 | 8.3 | 9.0 | 10.6 | 9.0 | 11.5 | 13.4 | 14.9 | 16.2 | 19.4 | |
| Midpoint RA | ||||||||||||
| d | 1 | 2 | 3 | 4 | 5 | 8 | 1 | 2 | 3 | 4 | 5 | 8 |
| 0.0 | 0.0 | 0.0 | 0.0 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.2 | 0.2 | |
| 0.1 | 0.1 | 0.1 | 0.2 | 0.2 | 0.3 | 0.2 | 0.3 | 0.4 | 0.5 | 0.5 | 0.7 | |
| 0.2 | 0.2 | 0.3 | 0.3 | 0.4 | 0.5 | 0.4 | 0.6 | 0.7 | 0.8 | 1.0 | 1.3 | |
| 0.5 | 0.7 | 0.8 | 0.9 | 1.0 | 1.3 | 1.0 | 1.4 | 1.7 | 2.0 | 2.2 | 2.8 | |
| 3.0 | 3.8 | 4.3 | 4.7 | 5.1 | 6.0 | 5.1 | 6.5 | 7.5 | 8.3 | 9.0 | 10.6 | |
| Expectation RA | ||||||||||||
| d | 1 | 2 | 3 | 4 | 5 | 8 | 1 | 2 | 3 | 4 | 5 | 8 |
| 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | |
| 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | |
| 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.1 | |
| 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.1 | 0.1 | 0.1 | 0.1 | |
| 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.2 | |
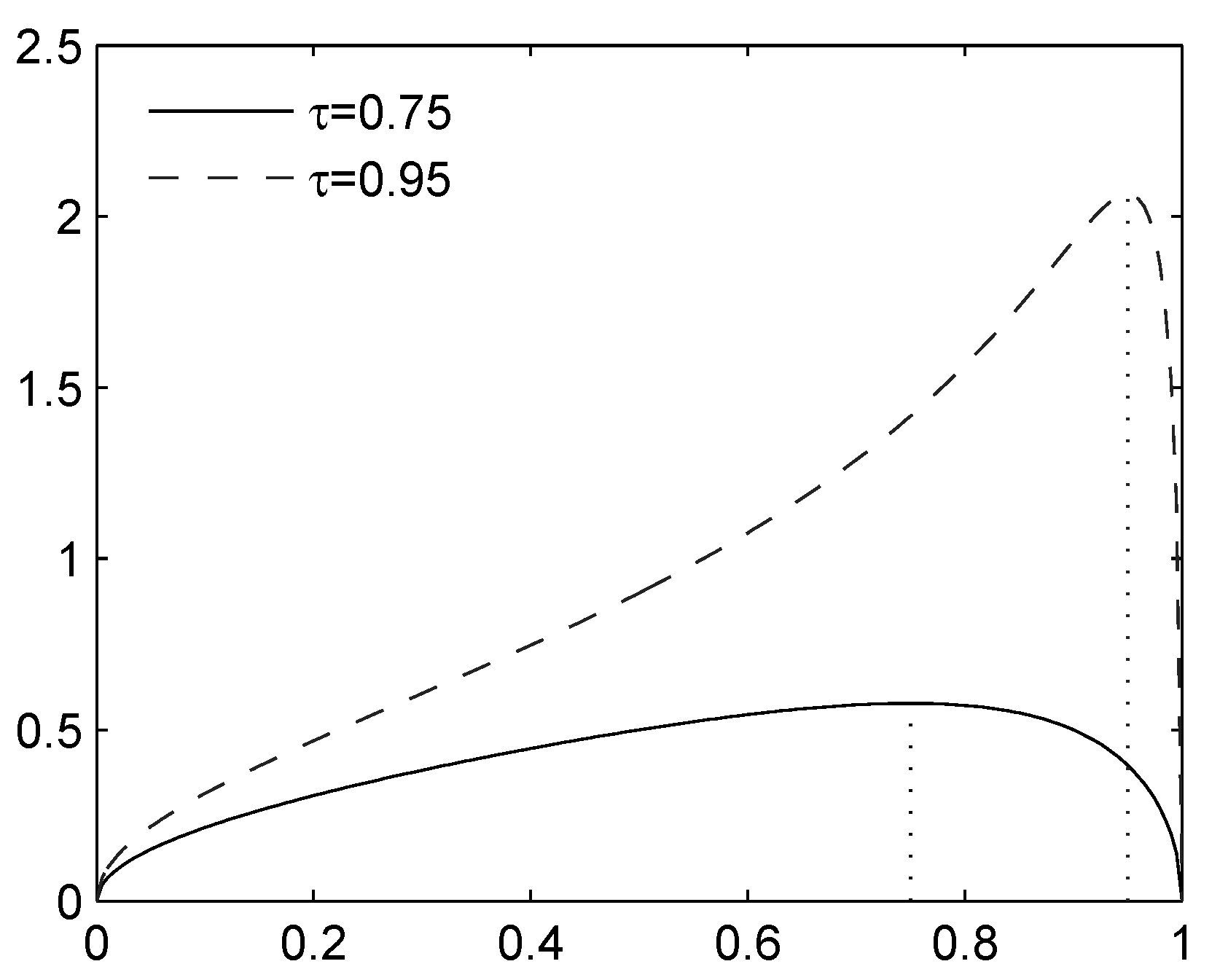
2.3. Example: Location-Scale Family
2.3.1. Upper Bound
2.3.2. Lower Bound
- (i)
- If , then a minimal element in in convex order is:Correspondingly,
- (ii)
- Otherwise, if F furthermore admits a unimodal density, then the minimal element in the admissible class is the constant , and thus, .
3. Bounds when the Mean and Variance of the Sum Are Known
3.1. Upper Bound with Variance Constraint
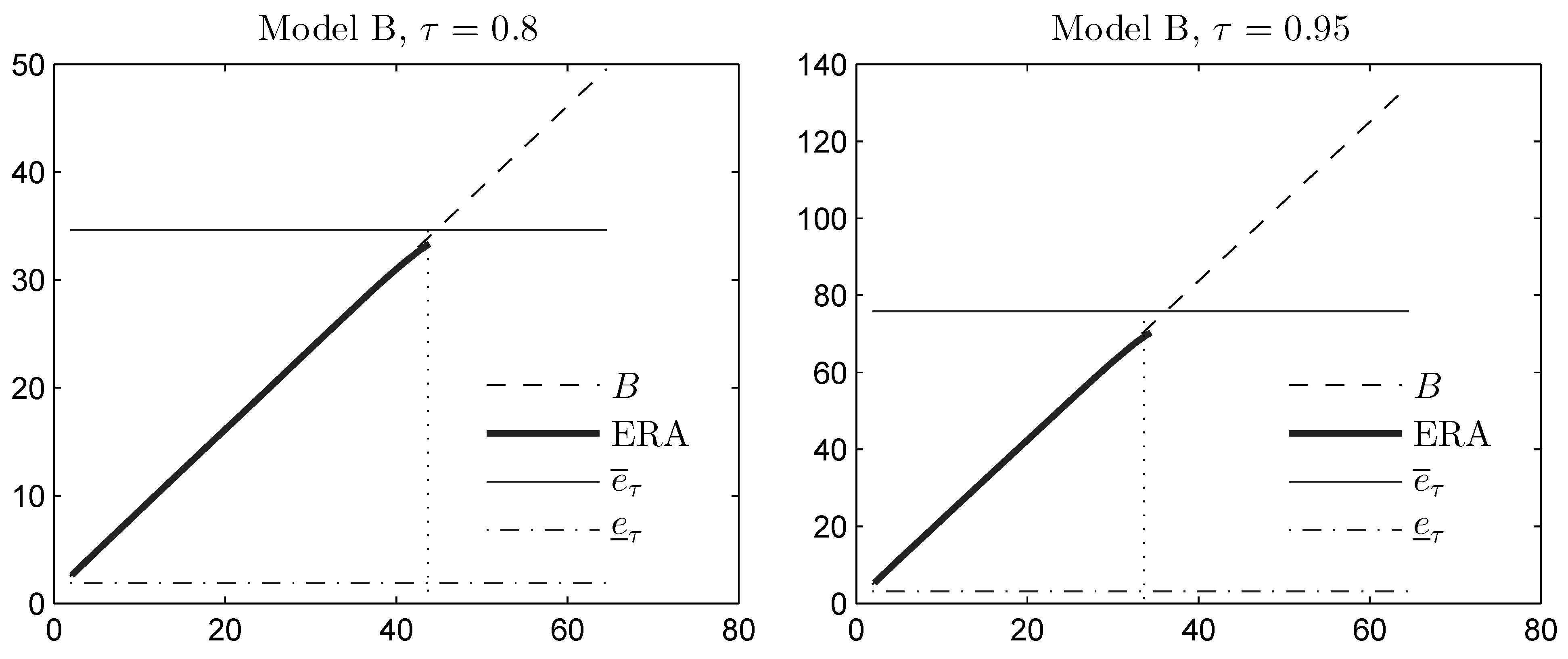
- (i)
- A procedure called the extended rearrangement algorithm (ERA) was introduced in [30] and makes it possible to compute an approximation of from below, using both the marginal, as well as the variance information. This algorithm will be applied in an example in Section 4.3.
- (ii)
- Denote by and by . A similar proof as in Theorem 5 shows that C and D are attained by the same diatomic variable that attains the bound B; see also [30]. We find that:and, thus, that . On the other hand, the numerical value of these upper bounds would coincide for , and , if we set .
3.2. Lower Bound with Variance Constraint
4. Bounds for Factor Models
4.1. Upper Bound
4.2. Lower Bound
4.3. Example: Skewed Student t Distribution
| Model A. | ||||||
|---|---|---|---|---|---|---|
| 0.8 | 1.24 | 2.16 | 13.70 | 35.58 | 35.62 | 35.63 |
| 0.9 | 1.24 | 3.02 | 21.63 | 57.14 | 57.21 | 57.22 |
| 0.95 | 1.24 | 4.14 | 29.65 | 78.73 | 78.85 | 78.87 |
| 0.99 | 1.25 | 8.44 | 51.18 | 135.63 | 135.98 | 136.02 |
| 0.999 | 1.30 | 23.30 | 96.78 | 251.11 | 252.65 | 252.84 |
| Model B. | ||||||
| τ | ||||||
| 0.8 | 1.91 | 2.18 | 19.34 | 34.58 | 34.61 | 34.62 |
| 0.9 | 2.50 | 3.01 | 30.68 | 55.29 | 55.36 | 55.37 |
| 0.95 | 3.15 | 3.99 | 41.90 | 75.74 | 75.84 | 75.86 |
| 0.99 | 5.15 | 7.34 | 70.80 | 128.00 | 128.28 | 128.31 |
| 0.999 | 10.05 | 17.51 | 126.92 | 228.06 | 229.15 | 229.29 |
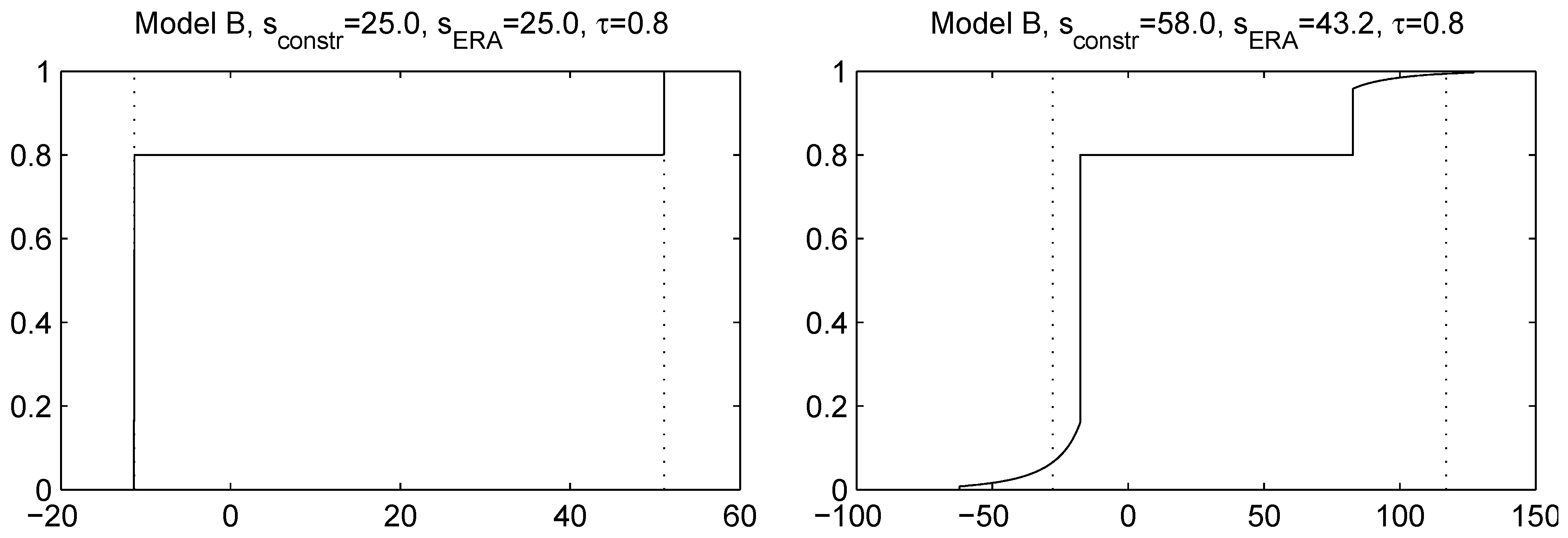
- (i)
- (ii)
- The most time-consuming quantity to compute was the unconstrained lower bound on the expectile, because the RA requires a discretization of the margins, i.e., calculating the skew-t inverse df times (each margin took about 10 min on an Intel i5 2.5 GHz desktop with ). A similar calculation with Pareto dfs as in Table 1 was done for this discretization size. The maximum error using the expectation RA was 0.4% for and 1.5% for ; hence, this discretization size was deemed sufficient for our purposes.
- (iii)
- Due to the mixture form of GH distributions, a faster method for discretizing the margins could be using a Monte Carlo sample. Since GH dfs can have heavy tails, a similar approach to the “expectation” discretization for RA was considered, specifically, rejecting any sample points that lie below or above and adding two points equal to the expectations over the corresponding intervals. However, this method resulted in a large variance over repeated trials, so the obtained bounds were not used.
4.4. Adding Variance Information
5. Dependence Uncertainty Spread Comparison

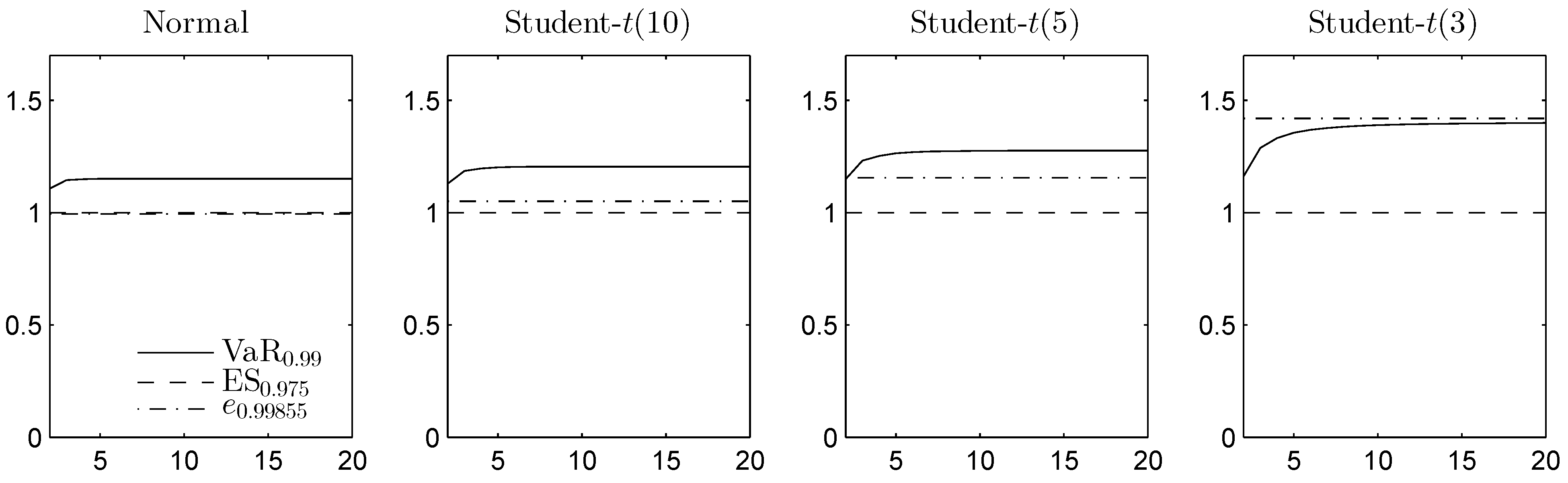
6. Final Remarks
Acknowledgments
Author Contributions
Conflicts of Interest
References
- P. Embrechts, G. Puccetti, L. Rüschendorf, R. Wang, and A. Beleraj. “An academic response to Basel 3.5.” Risks 2 (2014): 25–48. [Google Scholar] [CrossRef] [Green Version]
- S. Emmer, M. Kratz, and D. Tasche. “What is the best risk measure in practice? A comparison of standard measures.” J. Risk 18 (2015): 31–60. [Google Scholar] [CrossRef]
- P. Artzner, F. Delbaen, J.M. Eber, and D. Heath. “Coherent measures of risk.” Math. Financ. 9 (1999): 203–228. [Google Scholar] [CrossRef]
- T. Gneiting. “Making and evaluating point forecasts.” J. Am. Stat. Assoc. 106 (2011): 746–762. [Google Scholar] [CrossRef]
- S. Kou, and X. Peng. “Expected shortfall or median shortfall.” J. Financ. Eng. 1 (2014): 1450007. [Google Scholar] [CrossRef]
- J.M. Chen. “Measuring Market Risk Under the Basel Accords: VaR, Stressed VaR, and Expected Shortfall.” Aestimatio IEB Int. J. Financ. 8 (2014): 184–201. [Google Scholar]
- C. Acerbi, and B. Szekely. “Back-testing expected shortfall.” Risk 27 (2014): 76–81. [Google Scholar]
- T. Fissler, and J.F. Ziegel. “Higher order elicitability and Osband’s principle.” Available online: arxiv.org/abs/1503.08123 (accessed on 30 September 2015).
- J.F. Ziegel. “Coherence and elicitability.” Math. Financ., 2014. [Google Scholar] [CrossRef]
- F. Bellini, and V. Bignozzi. “On elicitable risk measures.” Quant. Financ. 15 (2015): 725–733. [Google Scholar] [CrossRef]
- F. Delbaen, F. Bellini, V. Bignozzi, and J.F. Ziegel. “Risk measures with the CxLS property.” Financ. Stoch., 2015. [Google Scholar] [CrossRef]
- W.K. Newey, and J.L. Powell. “Asymmetric least squares estimation and testing.” Econom.: J. Econom. Soc. 55 (1987): 819–847. [Google Scholar] [CrossRef]
- F. Delbaen. “A remark on the structure of expectiles.” Available online: arxiv.org/abs/1307.5881 (accessed on 22 July 2013).
- B. Efron. “Regression percentiles using asymmetric squared error loss.” Stat. Sin. 1 (1991): 93–125. [Google Scholar]
- Q. Yao, and H. Tong. “Asymmetric least squares regression estimation: A nonparametric approach.” J. Nonparametr. Stat. 6 (1996): 273–292. [Google Scholar] [CrossRef]
- G. De Rossi, and A. Harvey. “Quantiles, expectiles and splines.” J. Econom. 152 (2009): 179–185. [Google Scholar] [CrossRef]
- C.W. Granger, and C.Y. Sin. “Modelling the absolute returns of different stock indices: exploring the forecastability of an alternative measure of risk.” J. Forecast. 19 (2000): 277–298. [Google Scholar] [CrossRef]
- J.W. Taylor. “Estimating value at risk and expected shortfall using expectiles.” J. Financ. Econom. 6 (2008): 231–252. [Google Scholar] [CrossRef]
- S. Manganelli. “Asset allocation by penalized least squares.” Available online: www.ecb.europa.eu/pub/pdf/scpwps/ecbwp723.pdf (accessed on 6 February 2007).
- C. Keating, and W.F. Shadwick. “A universal performance measure.” J. Perform. Meas. 6 (2002): 59–84. [Google Scholar]
- B. Rémillard. In Statistical Methods for Financial Engineering. Boca Raton, FL, USA: CRC Press, 2013. [Google Scholar]
- C.M. Kuan, J.H. Yeh, and Y.C. Hsu. “Assessing value at risk with CARE, the conditional autoregressive expectile models.” J. Econom. 150 (2009): 261–270. [Google Scholar] [CrossRef]
- G. De Rossi. “Staying ahead on downside risk.” In Optimizing Optimization: The Next Generation of Optimization Applications and Theory. Edited by S. Satchell. Waltham, MA, USA: Academic Press, 2009, pp. 143–160. [Google Scholar]
- F. Bellini, and E. di Bernardino. “Risk management with expectiles.” Eur. J. Financ., 2015. [Google Scholar] [CrossRef]
- Y. Aıt-Sahalia, and A.W. Lo. “Nonparametric risk management and implied risk aversion.” J. Econom. 94 (2000): 9–51. [Google Scholar] [CrossRef]
- A. Ahmadi-Javid. “Entropic value-at-risk: A new coherent risk measure.” J. Optim. Theory Appl. 155 (2012): 1105–1123. [Google Scholar] [CrossRef]
- F. Bellini, B. Klar, A. Müller, and E.R. Gianin. “Generalized quantiles as risk measures.” Insur.: Math. Econ. 54 (2014): 41–48. [Google Scholar] [CrossRef]
- A.J. McNeil, R. Frey, and P. Embrechts. Quantitative Risk Management: Concepts, Techniques and Tools, 2nd ed. Princeton, NJ, USA: Princeton University Press, 2015. [Google Scholar]
- A. Van Heerwaarden, and R. Kaas. “The Dutch premium principle.” Insur.: Math. Econ. 11 (1992): 129–133. [Google Scholar] [CrossRef]
- C. Bernard, L. Rüschendorf, and S. Vanduffel. “Value-at-Risk bounds with variance constraints.” J. Risk Insur., 2015. forthcoming. [Google Scholar] [CrossRef]
- V. Bignozzi, G. Puccetti, and L. Rüschendorf. “Reducing model risk via positive and negative dependence assumptions.” Insur.: Math. Econ. 61 (2015): 17–26. [Google Scholar] [CrossRef]
- C. Bernard, L. Rüschendorf, S. Vanduffel, and R. Wang. “Risk bounds for factor models.” Available online: papers.ssrn.com/sol3/papers.cfm?abstract_id=2572508 (accessed on 26 February 2015).
- G. Puccetti, L. Rüschendorf, D. Small, and S. Vanduffel. “Reduction of Value-at-Risk bounds via independence and variance information.” Scand. Actuar. J., 2015. forthcoming. [Google Scholar] [CrossRef]
- C. Bernard, and S. Vanduffel. “Quantile of a mixture with application to model risk assessment.” Depend. Model. 3 (2015): 172–181. [Google Scholar] [CrossRef]
- C. Bernard, L. Rüschendorf, S. Vanduffel, and J. Yao. “How robust is the value-at-risk of credit risk portfolios? ” Eur. J. Financ., 2015. [Google Scholar] [CrossRef]
- C. Bernard, and S. Vanduffel. “A new approach to assessing model risk in high dimensions.” J. Bank. Financ. 58 (2015): 166–178. [Google Scholar] [CrossRef]
- N. Bäuerle, and A. Müller. “Stochastic orders and risk measures: consistency and bounds.” Insur.: Math. Econ. 38 (2006): 132–148. [Google Scholar] [CrossRef]
- E. Jouini, W. Schachermayer, and N. Touzi. “Law invariant risk measures have the Fatou property.” In Advances in Mathematical Economics. Edited by S. Kusuoka and A. Yamazaki. Berlin, Germany: Springer, 2006, pp. 49–71. [Google Scholar]
- F. Bellini. “Isotonicity properties of generalized quantiles.” Stat. Probab. Lett. 82 (2012): 2017–2024. [Google Scholar] [CrossRef]
- A.H. Tchen. “Inequalities for distributions with given marginals.” Ann. Probab. 8 (1980): 814–827. [Google Scholar] [CrossRef]
- B. Wang, and R. Wang. “Joint mixability.” Math. Oper. Res., 2015. forthcoming. [Google Scholar] [CrossRef]
- B. Wang, and R. Wang. “The complete mixability and convex minimization problems with monotone marginal densities.” J. Multivar. Anal. 102 (2011): 1344–1360. [Google Scholar] [CrossRef]
- G. Puccetti, and R. Wang. “Extremal dependence concepts.” Stat. Sci., 2015. forthcoming. [Google Scholar]
- J. Dhaene, and M. Denuit. “The safest dependence structure among risks.” Insur.: Math. Econ. 25 (1999): 11–21. [Google Scholar] [CrossRef]
- C. Bernard, X. Jiang, and R. Wang. “Risk aggregation with dependence uncertainty.” Insur.: Math. Econ. 54 (2014): 93–108. [Google Scholar] [CrossRef]
- E. Jakobsons, X. Han, and R. Wang. “General convex order on risk aggregation.” Scand. Actuar. J., 2015. [Google Scholar] [CrossRef]
- P. Embrechts, G. Puccetti, and L. Rüschendorf. “Model uncertainty and VaR aggregation.” J. Bank. Financ. 37 (2013): 2750–2764. [Google Scholar] [CrossRef]
- G. Puccetti. “Sharp bounds on the expected shortfall for a sum of dependent random variables.” Stat. Probab. Lett. 83 (2013): 1227–1232. [Google Scholar] [CrossRef]
- G. Puccetti, and L. Rüschendorf. “Computation of sharp bounds on the expected value of a supermodular function of risks with given marginals.” Commun. Stat.—Simul. Comput. 44 (2015): 705–718. [Google Scholar] [CrossRef]
- P. Embrechts, and E. Jakobsons. “Dependence uncertainty for aggregate risk: Examples and simple bounds.” In The Fascination of Probability, Statistics and their Applications: In Honour of Ole E. Barndorff-Nielsen. Edited by M. Podolskij, R. Stelzer, S. Thorbjørnsen and A. Veraart. Berlin, Germany: Springer, 2016. [Google Scholar]
- M. Hofert, A. Memartoluie, D. Sunders, and T. Wirjanto. “Improved algorithms for computing worst Value-at-Risk: Numerical challenges and the Adaptive Rearrangement Algorithm.” Available online: arxiv.org/abs/1505.02281 (accessed on 9 May 2015).
- M. Shaked, and J.G. Shanthikumar. Stochastic Orders. Berlin, Germany: Springer, 2007. [Google Scholar]
- L. Rüschendorf, and L. Uckelmann. “Variance minimization and random variables with constant sum.” In Distributions with Given Marginals and Statistical Modelling. Berlin, Germany: Springer, 2002, pp. 211–222. [Google Scholar]
- F. De Vylder, and M.J. Goovaerts. “Analytical best upper bounds on stop-loss premiums.” Insur.: Math. Econ. 1 (1982): 163–175. [Google Scholar] [CrossRef]
- O.E. Barndorff-Nielsen. “Exponentially decreasing distributions for the logarithm of particle size.” In Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences; 1977, Volume 353, pp. 401–419. [Google Scholar]
- O.E. Barndorff-Nielsen. “Hyperbolic distributions and distributions on hyperbolae.” Scand. J. Stat. 5 (1978): 151–157. [Google Scholar]
- O.E. Barndorff-Nielsen. “Normal inverse Gaussian distributions and stochastic volatility modeling.” Scand. J. Stat. 24 (1997): 1–13. [Google Scholar] [CrossRef]
- E. Eberlein, and U. Keller. “Hyperbolic distributions in finance.” Bernoulli 1 (1995): 281–299. [Google Scholar] [CrossRef]
- E. Eberlein, U. Keller, and K. Prause. “New insights into smile, mispricing, and value at risk: The hyperbolic model.” J. Bus. 71 (1998): 371–405. [Google Scholar] [CrossRef]
- K. Aas, I. Hobæk Haff, and X.K. Dimakos. “Risk estimation using the multivariate normal inverse Gaussian distribution.” J. Risk 8 (2005): 39–60. [Google Scholar]
- D.B. Madan, and E. Seneta. “The variance gamma (VG) model for share market returns.” J. Bus. 63 (1990): 511–524. [Google Scholar] [CrossRef]
- D.B. Madan, P.P. Carr, and E.C. Chang. “The variance gamma process and option pricing.” Eur. Financ. Rev. 2 (1998): 79–105. [Google Scholar] [CrossRef]
- S. Demarta, and A.J. McNeil. “The t copula and related copulas.” Int. Stat. Rev. 73 (2005): 111–129. [Google Scholar] [CrossRef]
- K. Aas, and I. Hobæk Haff. “The generalized hyperbolic skew Student’s t-distribution.” J. Financ. Econom. 4 (2006): 275–309. [Google Scholar] [CrossRef]
- S. Dokov, S.V. Stoyanov, and S. Rachev. “Computing VaR and AVaR of skewed-t distribution.” J. Appl. Funct. Anal. 3 (2008): 189–209. [Google Scholar]
- O.E. Barndorff-Nielsen, and C. Halgreen. “Infinite divisibility of the hyperbolic and generalized inverse Gaussian distributions.” Probab. Theory Relat. Fields 38 (1977): 309–311. [Google Scholar] [CrossRef]
- Y.S. Kim, S.T. Rachev, M.L. Bianchi, and F.J. Fabozzi. “Computing VaR and AVaR in infinitely divisible distributions.” Probab. Math. Stat. 30 (2010): 223–245. [Google Scholar] [CrossRef]
- P. Embrechts, B. Wang, and R. Wang. “Aggregation-robustness and model uncertainty of regulatory risk measures.” Financ. Stoch. 19 (2015): 763–790. [Google Scholar] [CrossRef]
- Basel Committee on Banking Supervision. Fundamental Review of the Trading Book. Basel, Switzerland: Bank of International Settlements, 2012. [Google Scholar]
- N. Costanzino, and M. Curran. “Backtesting general spectral risk measures with application to Expected Shortfall.” Available online: papers.ssrn.com/sol3/papers.cfm?abstract_id=2514403 (accessed on 21 February 2015).
- Basel Committee on Banking Supervision. Fundamental Review of the Trading Book: A Revised Market Risk Framework. Basel, Switzerland: Bank of International Settlements, 2013. [Google Scholar]
- 1.Note that for a continuous rv X, .
- 2.Likewise, the study of VaR bounds is connected to identifying (in an appropriate admissible class) the elements that are minimum in the sense of convex order, a feature that points to a similarity between the study of bounds on the expectile and the study of bounds on VaR; see Section 2.3 in [30] for these results.
- 3.Note that Equation (4) also follows from the more general results in [37,38]. Indeed, [37] has shown that any convex risk measure ρ with the Fatou property is consistent with the convex order, meaning that implies . Furthermore, [38] shows that law-invariant risk measures have the Fatou property. Since the expectile is convex and law invariant, it is consistent with the convex order. See [39] for further results on the properties of the expectile and other generalized quantiles with respect to various stochastic orders.
- 4.Note indeed that the admissible class reflects constraints rendering optimization difficult. By relaxing the d (infinite dimensional) constraints on the marginal distributions and substituting them by the portfolio mean constraint, we enlarge the class (as there are many marginal distributions that yield the same portfolio mean) and effectively obtain two constraints only, which greatly facilitates the optimization.
- 5.Assuming a compact support would improve the lower bound, but we do not elaborate on this case here and refer to [54].
- 6.This upper bound can also be derived using the reasoning in the proof of Theorem 5. Indeed, one shows that the upper bound is attained by a diatomic variable (with mean and variance ). Next, one optimizes over to obtain Equation (18).
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jakobsons, E.; Vanduffel, S. Dependence Uncertainty Bounds for the Expectile of a Portfolio. Risks 2015, 3, 599-623. https://doi.org/10.3390/risks3040599
Jakobsons E, Vanduffel S. Dependence Uncertainty Bounds for the Expectile of a Portfolio. Risks. 2015; 3(4):599-623. https://doi.org/10.3390/risks3040599
Chicago/Turabian StyleJakobsons, Edgars, and Steven Vanduffel. 2015. "Dependence Uncertainty Bounds for the Expectile of a Portfolio" Risks 3, no. 4: 599-623. https://doi.org/10.3390/risks3040599






