An Improved Model for the Steric-Entropic Effect on the Retention of Rod-like Particles in Field-Flow Fractionation: Discussion of Aspect Ratio-Based Separation

Abstract

We developed an improved model for predicting the steric-entropic effect on the separation behaviors of rod-like particles in flow field-flow fractionation. Our new model incorporates the “pole-vault” rotation of a rod-like particle near a wall under shear flow into the original model developed by Beckett and Giddings which considered only Brownian rotation. We investigated the effect of the aspect ratio on the retention ratios and the cross-sectional concentration distribution in the separation of rods in field-flow fractionation (FFF). Our analyses involved comparing the results predicted using the original model and those from the new model under various rod geometries and flow conditions. We found that the new model can show the aspect ratio-enhanced elution trend in certain flow conditions for the assumption of non-constant cloud thickness (ratio between the cross flow rate and the rod diffusivity). We also deducted that the flow conditions allowing for the aspect ratio-enhanced elution are related to the interplay among the axial flow rate, cloud thickness, and rod geometry. The new model can be viewed as a prototype to qualitatively show the aspect ratio-enhanced trend since its quantitative agreement with the experimental data must be improved for our future work.

1. Introduction

Field-flow fractionation (FFF) is a particle separation technique which utilizes a parabolic channel flow and a cross-force field. As particles are flowing in the channel flow, the cross force pushes them towards the bottom of the channel (“accumulation wall”). However, the particles form a concentration distribution in the cross-sectional direction near the wall according to their physical properties in response to the force field. Thus, particle mixtures with different physical properties result in different concentration distributions and subsequently a different elution time due to the parabolic channel flow. In other words, particles whose concentrations are distributed farther away from the wall tend to elute faster. Therefore, correctly modeling the concentration distribution by incorporating the response of a particle of interest to a particular force field is a key to predicting the separation behaviors of particles in FFF. Based on the types of responsive forces, separation mechanisms in FFF are classified as “normal mode” for particle diffusivity, “steric mode” for excluded volume effect, and “lift-hyperlayer mode” for shear-induced migration [1].

Shape-based particle separation using FFF has gained attention due to the rapid development in the applications of micro/nanorods, in which shape-specific physico-chemical properties are important. Examples can be found in biomedical applications of gold nanorods (GNR) [2] and polystyrene (PS) rods [3,4], where the aspect ratio (the ratio between the length of the long principal axis and the diameter of a rod-like particle: Ar = L/d) characterizes the property utilized. Our interest in this work is focused on the dynamics of rod-like particles in flow-FFF (Fl-FFF), in which the cross-force field is the flow field. For the sake of clarity and convenience, FFF, throughout the rest of this study, will be referred to as Fl-FFF.

The majority of theories about FFF has been developed based on the assumption that particles are spherical in shape. Studies on the shape effect of non-spherical particles on FFF separation have been limited. Beckett and Giddings proposed a separation mechanism called the “steric-entropic mode,” which considers the shape effects of rod and disk-like particles on the cross-sectional concentration distribution very near the accumulation wall [5]. The numerical simulation performed by Phelan and Bauer compared the normal and steric modes of rod-like particles and spherical particles [6]. Alfi and Park developed a model that can predict the concentration distribution of rod-like particles by considering the average orientation correction for the normal mode as well as the shear-induced rod migration for the lift-hyperlayer mode [7].

Experimental studies on rod-like particle separation have been performed on single-walled carbon nanotubes (SWNT) and GNRs. Chun and coworkers separated SWNTs according to their lengths. The lengths of SWNTs were estimated by comparing the elution times of polystyrene spherical particles of known sizes and light-scattering data [8]. The separation of GNRs has been performed for various sizes and shapes using asymmetric flow FFF (AF4), which is a commercialized variation of Fl-FFF [9,10,11]. Although experimental results have shown many examples of separation by sizes and shapes, theoretical explanation of those experimental observations has yet to be elucidated. One noteworthy experimental observation is the Ar-based separation by Gigault and coworkers [9]: The results of GNR elution times showed that higher Ar rods elute faster. However, this Ar-enhanced elution trend cannot be explained by the normal mode, whether based on typical FFF theory or the recent model for rod-like particles [7], which will be demonstrated and discussed in later sections. Although Gigault and coworkers discussed the Ar-enhanced elution by referring to the steric-entropic mode, no quantitative or qualitative analysis using the concentration distribution of the steric-entropic mode has yet been performed [9].

Based on the theory of the steric-entropic mode, the orientation distribution of a non-spherical particle is restricted by the excluded volume effect caused by the interplay between the particle configuration and the accumulation wall, which results in entropy loss and subsequent faster elution (Figure 1). The equation for the derived cross-sectional concentration distribution, c(x), for rod-like particles is given as

$$\text{c}\left(x\right)=c_0\text{exp}\left(\frac{x}{l_c}\right)\frac{x}{2L}.$$

(1)

Here, c₀ is the particle concentration at the wall (x = 0) and l_c is the cloud thickness which can be expressed as l_c = D_⊥/U_x for a rod with a translational diffusivity in the perpendicular direction to its long axis, D_⊥, under the cross-flow field of flow rate U_x. Equation (1) predicts that increasing values of L/2l_c will lift c(x) away from a wall for the condition of L > 2l_c > d, where l_c is assumed to be constant (see Figure 2 of [5]) . In other words, it suggests that rods with longer L should show the Ar-enhanced elution, as discussed in [9].

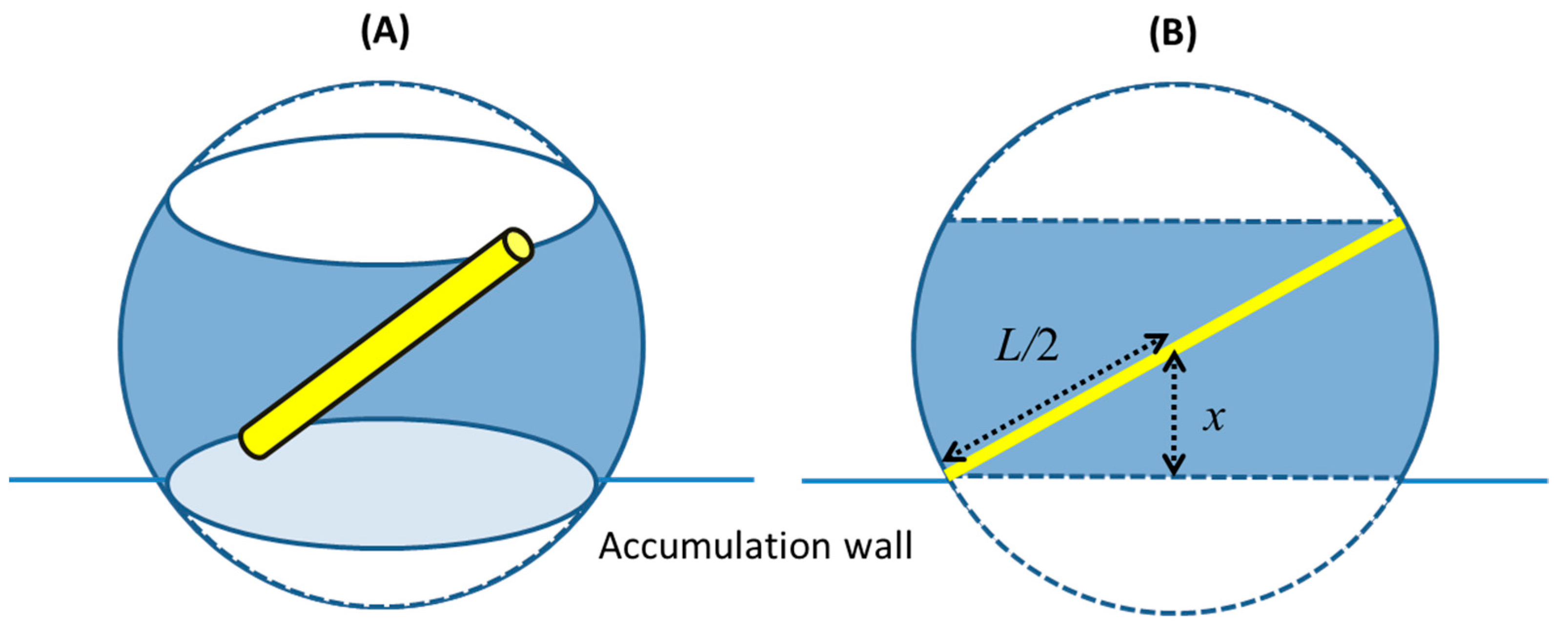
Figure 1. (A) A schematic demonstration of the restricted orientation configuration (shaded region on the sphere) of a Brownian rod with length L and its center-of-mass position at x. (B) the same demonstration in the z-direction view (redrawn from [5]).

Figure 1. (A) A schematic demonstration of the restricted orientation configuration (shaded region on the sphere) of a Brownian rod with length L and its center-of-mass position at x. (B) the same demonstration in the z-direction view (redrawn from [5]).

In this study, we investigated the Ar-dependent separation trend by applying the steric-entropic mode to the model equation for c(x) developed by [7]. It is important to note here that we released the constant l_c assumption by actually evaluating it for each D_⊥/U_x. The results from our analysis did not find the Ar-enhanced elution under any flow conditions. Therefore, we propose an improved mechanism for the steric-entropic mode that identifies some cases reproducing the Ar-enhanced elution trend. This study is organized as follows: Section 2 describes the mathematical models and numerical calculations used; Section 3 demonstrates the results of each model and discusses the Ar-dependent trend by comparing those results to each other; Section 4 summarizes the findings and future works.

2. Model Description

In this study, we analyze the separation behaviors of rod-like particles in FFF by comparing the distributions of c(x) and the retention ratios, R, predicted by each model. R, which has a physical meaning of the dimensionless elution time of a solute relative to that of a carrier liquid, can be obtained using the formula:

$$R=\frac{\langle c\left(x\right)v\left(x\right)\rangle }{\langle c\left(x\right)v\left(x\right)\rangle }$$

(2)

Here, <…> indicates the cross-sectional average. The velocity profile, v(x), (y-direction as axial flow direction) of the parabolic channel flow of its thickness, w, is known as:

$$v\left(x\right)=6\langle v\left(x\right)\rangle \left[\left(\frac{x}{w}\right)-{\left(\frac{x}{w}\right)}^2\right]$$

(3)

subsequently, <v(x)> or <v>, the cross-sectional average of v(x), indicates the axial flow rate.

Note here that we have assumed a Newtonian incompressible fluid in the Stokes flow region as a condition of the carrier liquid, as well as a rectangular FFF channel with sufficiently large breadth (neglecting the effect in the z-direction), and, finally, rod-like particles as the slender-body model (Ar > 5) [12]. The following subsections describe how to get c(x) using each model under the aforementioned assumptions.

2.1. Concentration Profile of Rod-like Particles

A model to predict c(x) for rod-like particles in FFF was derived [7], which is given as:

$$c\left(x\right)=c_{0}exp\left[{{\displaystyle \int }}_{d/2}^x\frac{U_x/D_{\perp }+M\left(\overline{x}\right)}{1+\langle \langle p_x^2\rangle \rangle }d\overline{x}\right]S\left(x\right)$$

(4)

Here, $\overline{x}$ is a dummy variable for the integration. The integration range (d/2 < x < w-d/2) is modified by the rod radius to incorporate the steric mode. The lift-hyperlayer mode is incorporated by M(x) which represents shear-induced migration [13,14,15]. The correction of D_⊥ for the cross-sectional direction (x-direction) is made by <<p_x²>>, which represents the orientation average of the square of the x-component of the orientation unit vector, p. The steric-entropic correction, S(x), is added for this study. More details of this term will be derived and explained in the next sections.

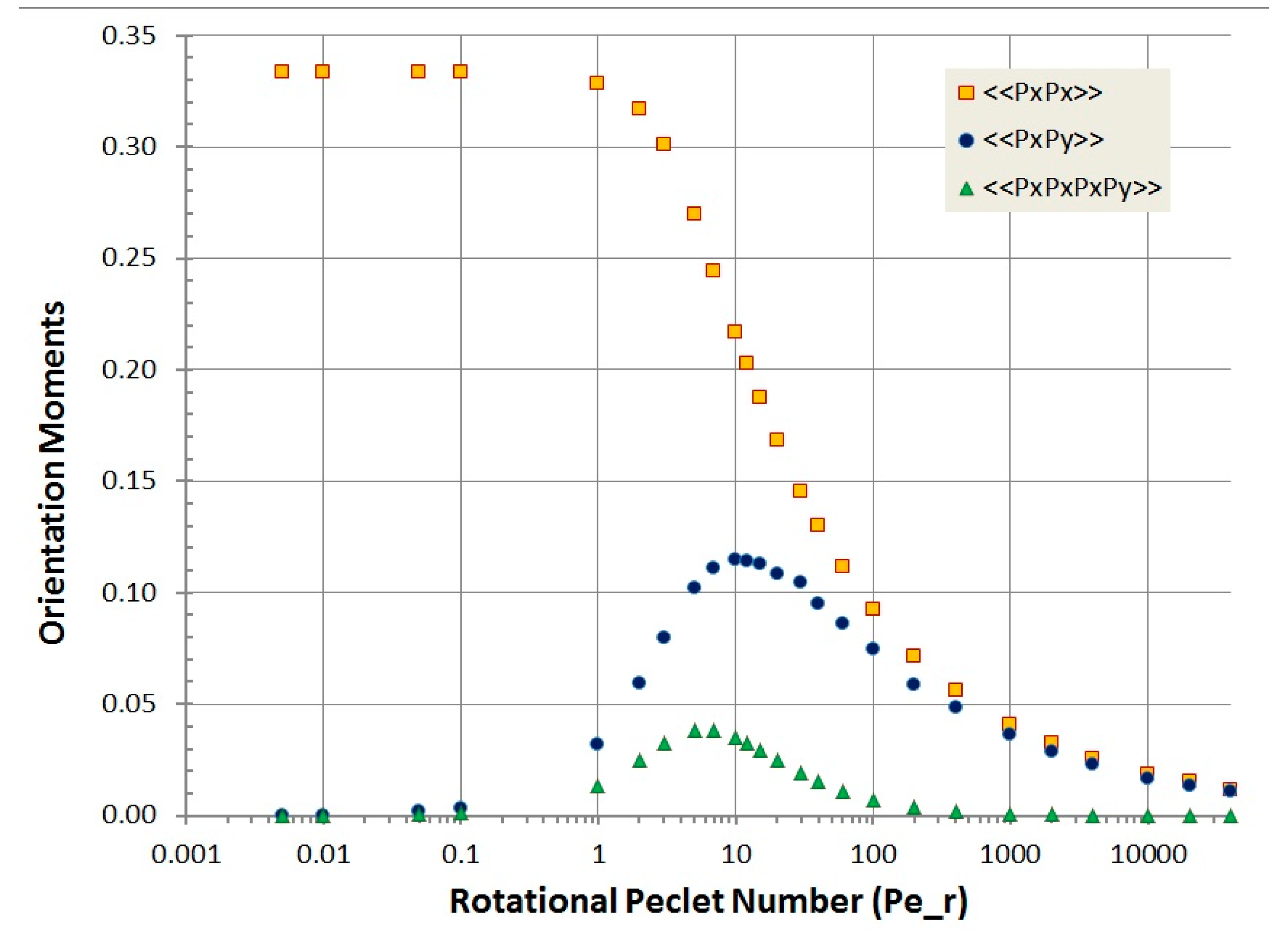
Note here that the terms M(x) and <<p_x²>> are both functions of the Peclet number, Pe_s, which is defined as the ratio between shear rate, $\dot{\gamma }$, and D_⊥:

$$P{e}_s=\frac{\dot{\gamma }{L}^2}{D_{\perp }}$$

(5)

Since $\dot{\gamma }$ is a function of x for parabolic flow, M(x) and <<p_x²>> are eventually dependent on the x position, evaluations of which are summarized in the Appendix. More details are described in [13]. Considering the slender-body expression [12] for D_⊥ and the parabolic flow profile (3), (5) can be also written as:

$$P{e}_s=\frac{4\pi \mu \dot{\gamma }{L}^3}{k_{B}T\ln \left(2Ar\right)}$$

(6)

Here, k_BT is the thermal energy and μ is the solvent viscosity. According to the slender-body approximation, the rotational diffusivity is D_R = D_⊥ /12L² [12,13,14,15]. Therefore, (5) can be rewritten in terms of the rotational Peclet number, Pe_r:

$$P{e}_s=12P{e}_r$$

(7)

It is also noteworthy that (4) can be reduced to the typical exponentially decaying function of c(x) for spherical particles in the normal mode if the diffusivity of the spherical particles is D_⊥ and all the corrections are neglected (d/2→ 0: no excluded volume effect, M(x)→0: no migration, <<p_x²>>→0: perfectly aligned in the axial flow direction, S(x) →1 for no steric-entropic effect):

$$c\left(x\right)=c_0\text{exp}\left[{{\displaystyle \int }}_0^x\frac{U_x}{D_{\perp }}d\overline{x}\right]=c_0\text{exp}\left(x\frac{U_x}{D_{\perp }}\right)$$

(8)

2.2. The Original Model for the Steric-Entropic Mode

Beckett and Giddings derived (1) by applying S(x) to (8). As demonstrated in Figure 1A, their original form of S(x) was derived by considering the configuration of a rod with Brownian rotation restricted by a wall. Considering that the orientation distribution of a Brownian rod in a free space is like the surface of a sphere with its radius equal to L, the orientation distribution restricted by the rod-wall excluded volume effect can be obtained by the area swiped by the tip of a rod with its center-of-mass position at x. S(x) is the ratio of the area where the rod rotation is allowed to the spherical surface area, of which the final form is:

$$S\left(x\right)=\frac{2x}{L} \equiv S_0\left(x\right)$$

(9)

In this study, we apply (9) to (4) to investigate the effect of the steric-entropic mode by the original model on the Ar-dependent separation behavior as discussed in [9]. Note here that the definition of S₀(x) will be used in the new model in the next section.

2.3. Improved Model for the Steric-Entropic Mode

We introduce a new model for evaluating S(x) by considering the “pole-vault” rotation of a rod. It has been known that a non-Brownian rod under a shear flow rotates following a trajectory called the Jeffery orbit [16]. However, it also has been observed that a non-Brownian rod near a wall rotates in a different way, called a “pole-vault” rotation, which is accompanied by a center-of-mass change, as shown in Figure 2 [17,18,19].

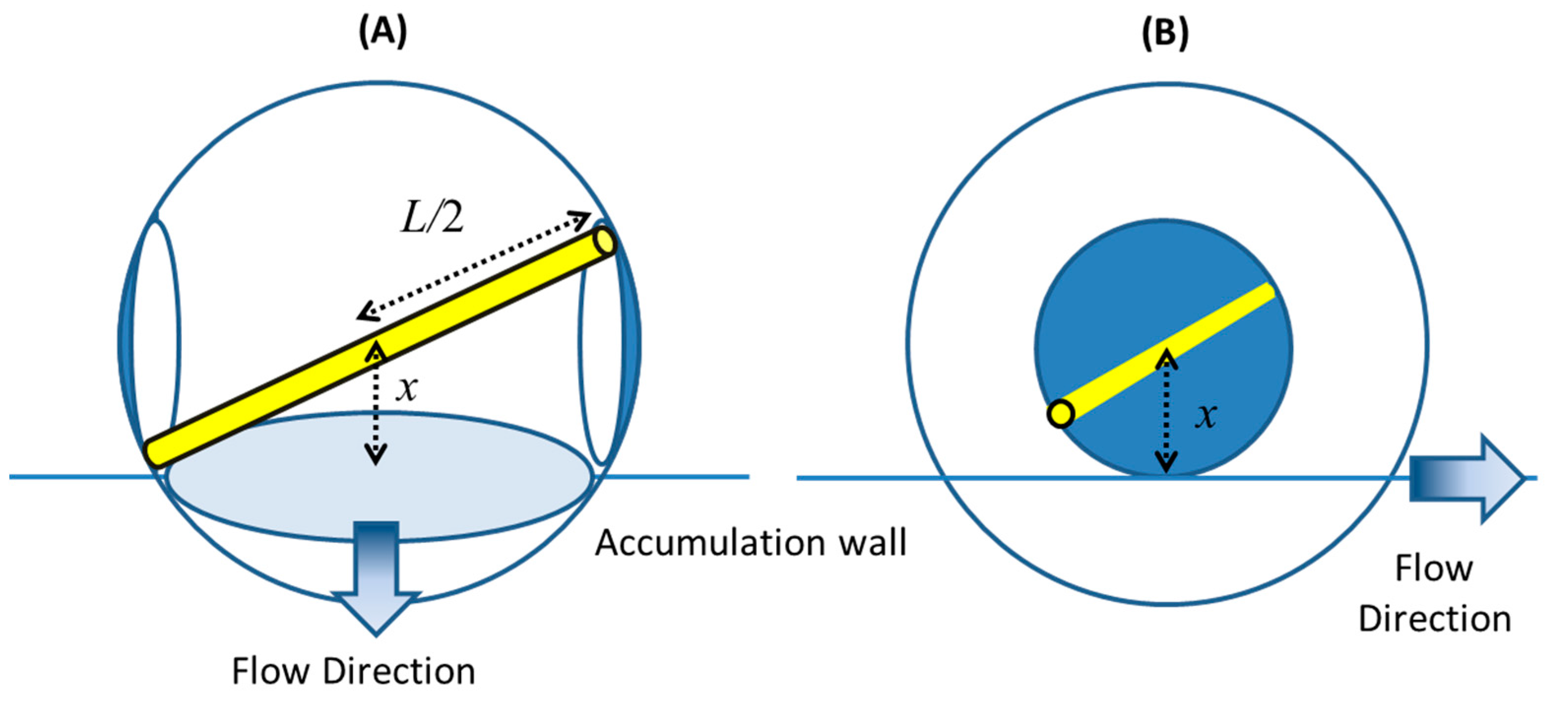
Figure 2. Schematic demonstration of the pole-vault rotation of a rod-like particle near a wall under a shear flow.

Figure 2. Schematic demonstration of the pole-vault rotation of a rod-like particle near a wall under a shear flow.

As shown in Figure 3, if the pole-vault rotation is considered, the allowed orientation distribution of a rod will be different from that shown for the original steric-entropic mode. The restricted area is where the rod tips can rotate like kayak paddling. The corresponding S(x) can be derived as the ratio of the rotation-allowed area to the spherical surface area in the previous section:

Figure 3. (A) A schematic demonstration of the restricted orientation configuration (shaded region on the sphere) of a rod with the pole-vault rotation with length L and its center-of-mass position at x. (B) the same demonstration in the z-direction view.

Figure 3. (A) A schematic demonstration of the restricted orientation configuration (shaded region on the sphere) of a rod with the pole-vault rotation with length L and its center-of-mass position at x. (B) the same demonstration in the z-direction view.

$$S\left(x\right)=1-\sqrt{1-{\left[\frac{2x}{L}\right]}^2}\equiv S_{\infty }\left(x\right)$$

(10)

Here, we define the original S(x) from equation (9) as S₀(x), which represents the correction for the allowable orientation distribution for pure Brownian rotation (Pe_r = 0). Note here that the form of (10) is coincidently identical to that of the original steric-entropic mode for a disk [5]. The newly derived S(x) in (10) is defined as S_∞(x), which is the correction for non-Brownian rotation (Pe_r = ∞). However, flow conditions for Brownian rods in FFF are typically neither Pe_r = 0 nor Pe_r = ∞. Therefore, the actual S(x) assuming a flow condition at a position x, Pe_r(x) using (6) and (7), must be obtained. We assume that S(x) is a linear combination of both S₀(x) and S_∞(x) according to Pe_r(x). Additionally, the contributions of S₀(x) and S_∞(x) to S(x) are assumed to be equal at Pe_r = 1 where the shear rate and Brownian rotation are equally affecting the rod orientation. This is valid as long as the flow regime is located in the Stokes region. Additionally, there is no need to derive the actual orientation distribution but rather the correction factor, which is related to the relative area of the allowable distribution. Therefore, considering the local flow condition, Pe_r(x), S(x) can be evaluated as follows:

$$S\left(x\right)=\left(1-0.5P{e}_r\right)S_0\left(x\right)+0.5P{e}_r{S}_{\infty }\left(x\right), \text{if} P{e}_r<1$$

(11)

$$S\left(x\right)=\frac{0.5}{P{e}_r}{S}_0\left(x\right)+\left(1-\frac{0.5}{P{e}_r}\right)S_{\infty }\left(x\right), \text{if} P{e}_r>1$$

(12)

Equation (11) or (12) is used to evaluate (4) to investigate the Ar-dependent elution behavior in terms of our new model. The expression for Pe_r(x) can be derived by using the derivative of (3) in x, (6) and (7):

$$P{e}_r\left(x\right)=\langle v\left(x\right)\rangle \left[\left(\frac{1}{w}\right)-\left(\frac{2x}{w^2}\right)\right]\frac{2\pi \mu L^3}{k_{B}T\ln \left(2Ar\right)}$$

(13)

2.4. Numerical Calculation

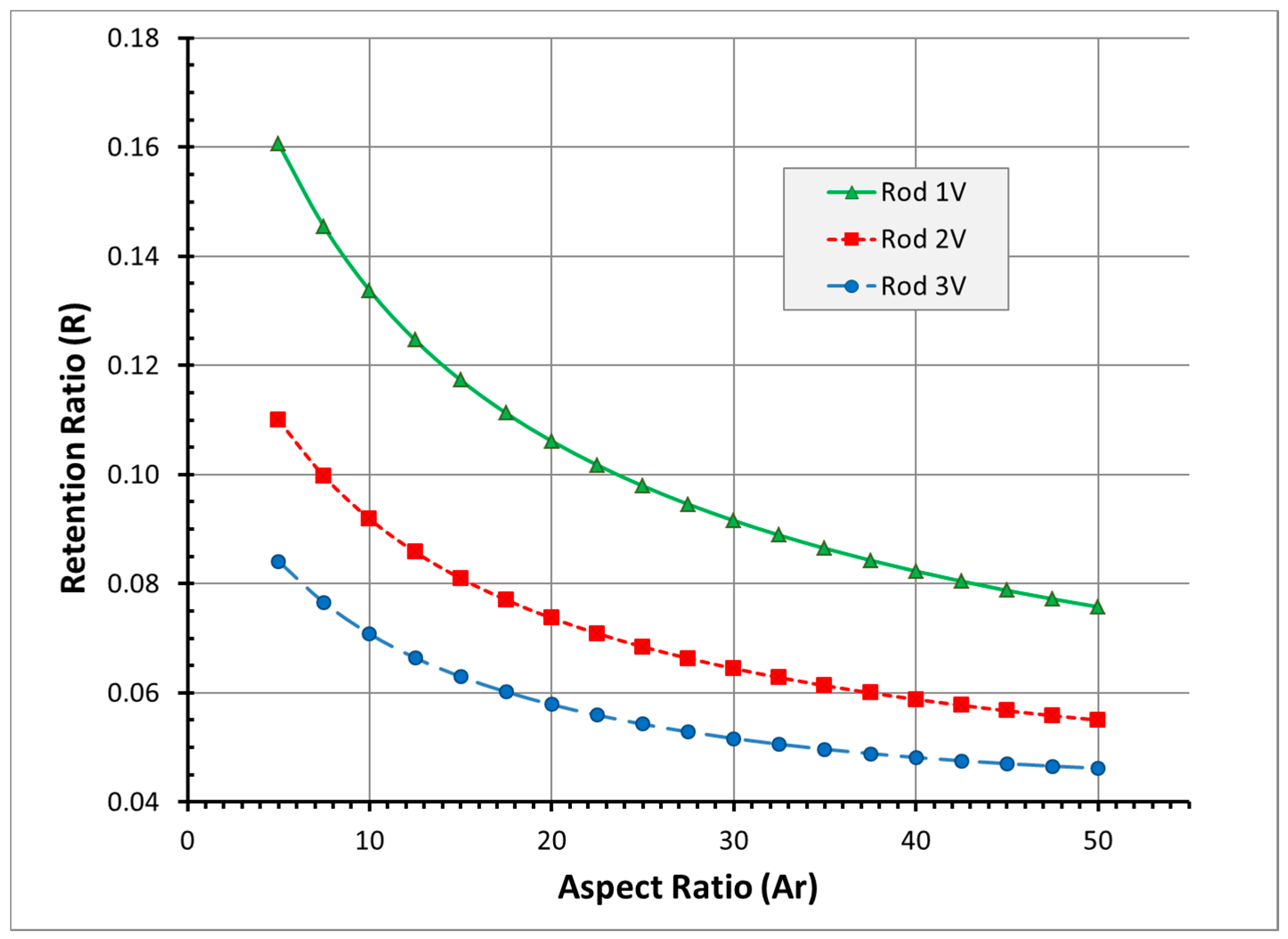
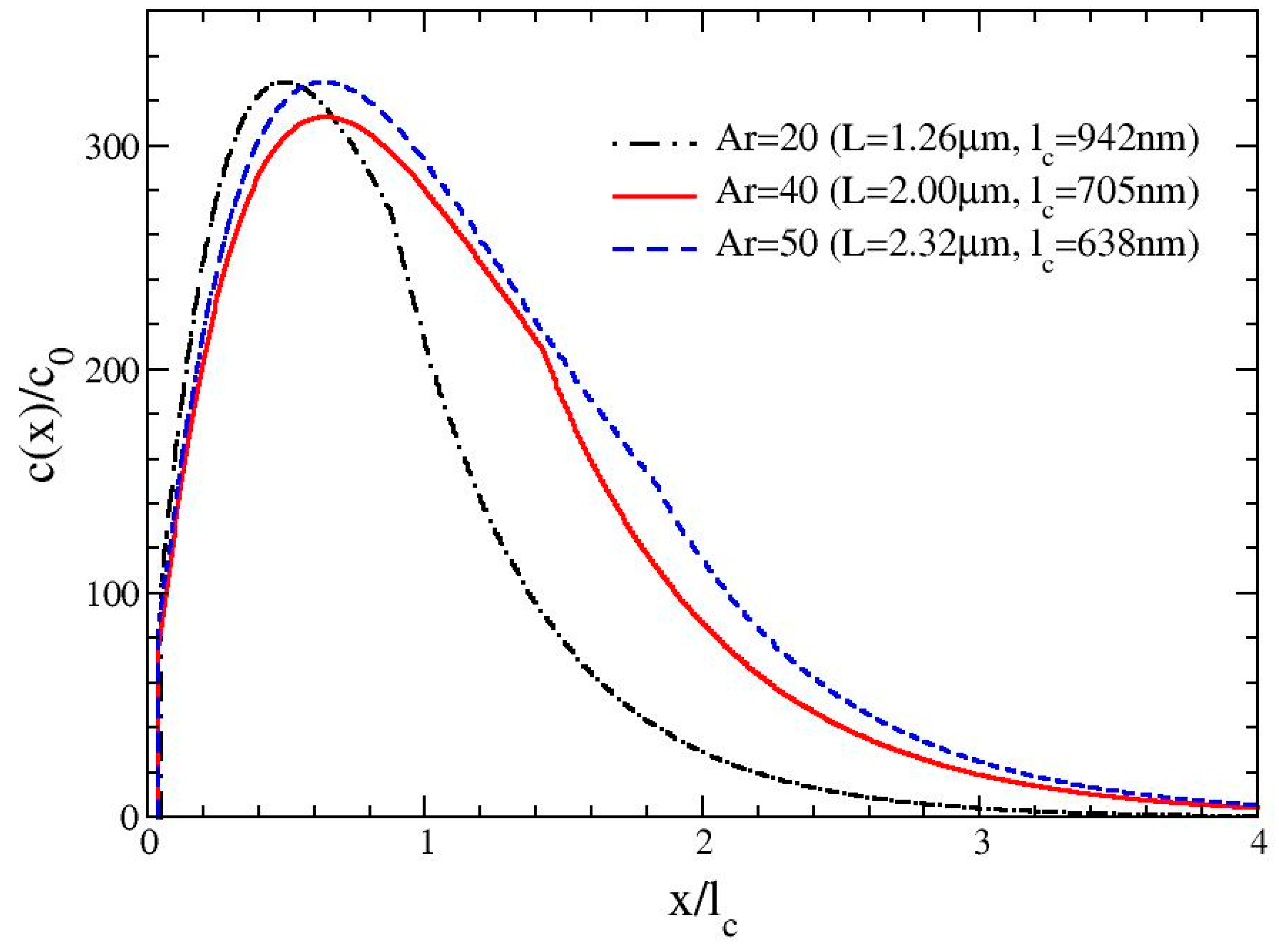
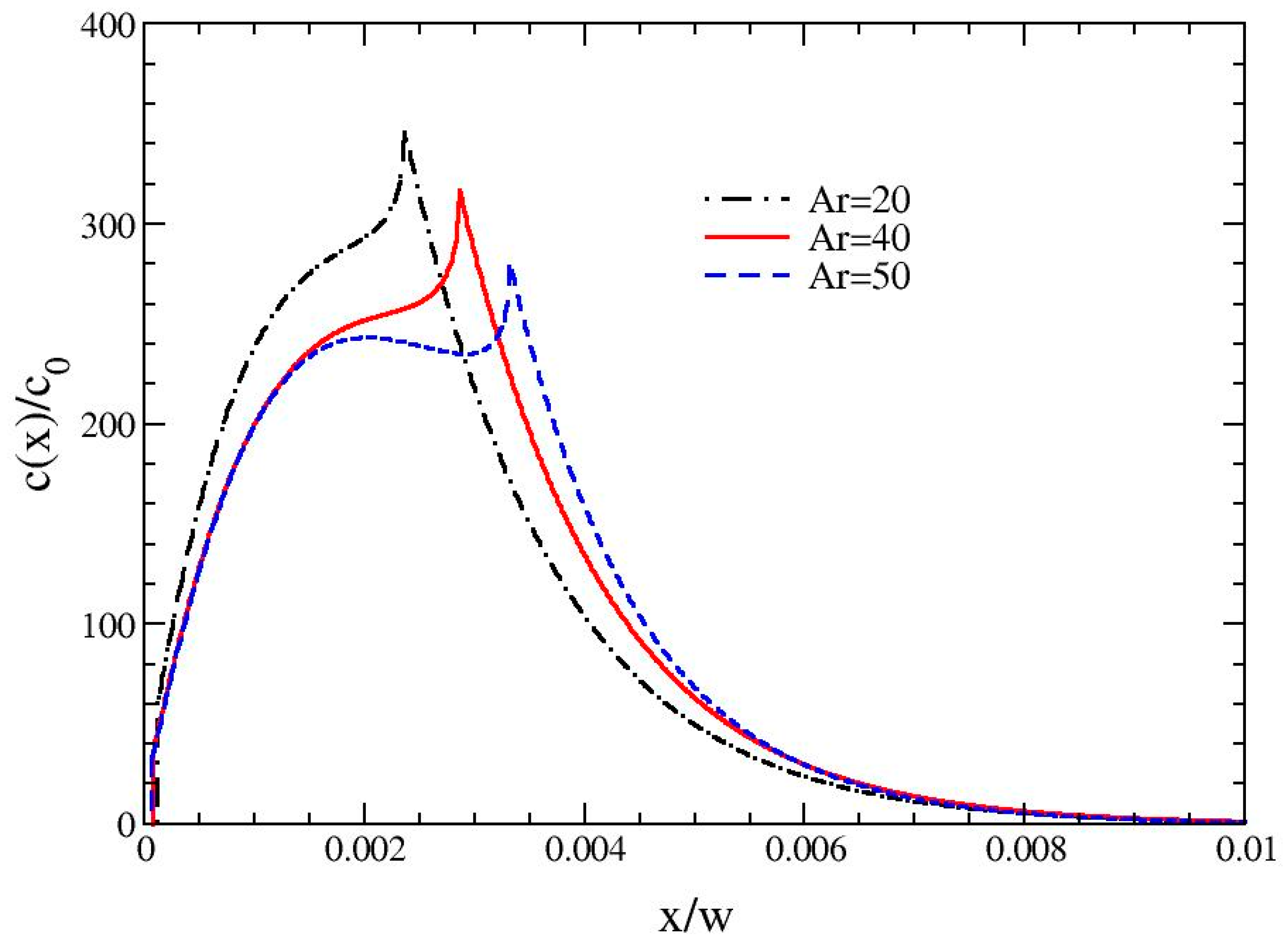
Equation (4) is evaluated for three different cases of S(x): S(x) = 1 where the steric-entropic mode is not considered, S(x) = S₀(x) where the original model of the steric-entropic mode is considered, and S(x) as in (11) or (12) with a new model considering the pole-vault rotation. The resulting c(x) from (4) is used to evaluate R using (2). The integrations in each calculation are performed numerically using the trapezoidal method with the integration steps less than 0.01d, which gives convergent results.

The geometries of rod-like particles for the investigation of the Ar-dependent elution are chosen as constant-volume rods: An arbitrary set of L and d of a cylindrical rod with Ar = 5 is chosen. The geometries of rods with higher Ar are generated on the basis of the same volume as that of a rod with Ar = 5 (increasing L and decreasing d to maintain the volume). The Ar-increment is made up to Ar = 50. Note here that the choice of the minimum Ar = 5 is because the model in this work was derived based on the slender-body model [12]. The extension of our model to rods with Ar < 5 will be performed as our future work. It is also worth noting that we replicated the methodology used for the constant-volume rods as described above to investigate the constant-diameter rods (i.e., increasing L for a constant d). The resulting trend was the same as that from the investigation on the constant-volume rods (data not shown).

Flow conditions of U_x and <v> are chosen so that most of the rods in the Ar range (5–50) should be under each desired mode: The normal mode condition corresponds to l_c > 0.5L and Pe_r(x = 0.5L) < 100, while the steric-entropic mode is for L > 2l_c > d and Pe_r(x = 0.5L) < 100. Note here that Pe_r < 100 has been chosen to avoid the hyper-layer mode [7]. In each analysis, three representative flow conditions were shown for demonstration. The solvent properties (density, viscosity, and temperature) are chosen as those of water at room temperature (ρ = 1000 kg/m³, μ = 0.001 Pa.s, T = 293 K).

3. Results and Discussion

3.1. Normal Mode

We investigated the Ar-dependence of separation behavior in the normal mode by evaluating R as a function of Ar using (2) and (4) with S(x) ≈ 1. Figure 4 shows the predicted trend for Ar versus R for particles with three different volumes under the same flow condition were predicted. The predicted results show that R decreases with increasing Ar (“Ar-reduced elution”) for particles with the same volume. This trend can be explained using (6): Although the term, ln(2Ar), in the denominator increases with increasing Ar, the increase of L³ in the numerator exceeds that in the denominator. Therefore, the subsequent increase of Pe_s results in the reduction of R with increasing Ar. Comparing the results of R among different volumes of particles, R decreases with increasing volume for the same Ar, which is expected by the classical FFF theory in the normal mode (slower elution time for larger volumes).

Although the correction of each D_⊥ by the local orientation effect [7] was included in (4), the Ar-enhanced elution was not predicted for the same volume rods in the normal mode. However, the Ar-enhanced elution in the normal mode can be found in a mixture of particles when the volumes of the rods are chosen so that they decrease with increasing Ar, as shown in Figure 4 (e.g., a particle mixture of rods with the volume of 3.93 × 10⁻²¹m³ and Ar = 20; 1.66 × 10⁻²¹m³ and Ar = 30; and 0.490 × 10⁻²¹m³ and Ar = 50).

Figure 4. Prediction of R as a function of Ar in the normal mode with S(x) ≈ 1 for the rods with three different volumes (Rod 1V: 4.90 × 10⁻²² m³, Rod 2V: 1.66 × 10⁻²¹ m³, Rod 3V: 3.93 × 10⁻²¹ m³) under a flow condition of <v> = 5 × 10⁻⁵ m/s and U_x = 4 × 10⁻⁷ m/s.

Figure 4. Prediction of R as a function of Ar in the normal mode with S(x) ≈ 1 for the rods with three different volumes (Rod 1V: 4.90 × 10⁻²² m³, Rod 2V: 1.66 × 10⁻²¹ m³, Rod 3V: 3.93 × 10⁻²¹ m³) under a flow condition of <v> = 5 × 10⁻⁵ m/s and U_x = 4 × 10⁻⁷ m/s.

3.2. Original Steric-Entropic Mode with Nonconstant Cloud Thickness

The effect of the original steric-entropic mode, derived in [5], on separation behavior was investigated by evaluating (2) using (4) with (9). For the constant-volume scenario, a volume of 3.93 × 10⁻²¹m³ (Ar = 5, L = 500 nm and d = 100 nm) was chosen. Three different flow conditions in the steric-entropic mode (L > 2l_c > d and Pe_r < 100) were chosen for the demonstration (summarized as Flow 1V, 2V, and 3V in Table 1). The results in Figure 5 show the Ar-reduced elution trend, which is different from both the experimental observation [9] and the prediction [5]. We also note here that we could not find the Ar-enhanced trend under any flow conditions in the steric-entropic mode (L > 2l_c > d and Pe_r < 100).

Table 1. Summary of the flow conditions used in the calculations for the steric-entropic mode investigation. The ranges for Pe_r and 2l_c/L are for rods in 5 ≤ Ar ≤ 50.

Flow Condition Name	Ux (×10−6 m/s)	<v> (×10−4 m/s)	Per	2lc/L	Steric-entropic mode range
Flow 1V	1.5	1.0	0.0241–1.20	3.45–0.367	Ar > 17.5
Flow 2V	2.0	2.0	0.0487–2.39	2.96–0.275	Ar > 15.0
Flow 3V	4.0	4.0	0.0722–3.59	1.48–0.138	Ar > 7.5

Table 1. Summary of the flow conditions used in the calculations for the steric-entropic mode investigation. The ranges for Pe_r and 2l_c/L are for rods in 5 ≤ Ar ≤ 50.

Flow Condition Name	Ux (×10−6 m/s)	<v> (×10−4 m/s)	Per	2lc/L	Steric-entropic mode range
Flow 1V	1.5	1.0	0.0241–1.20	3.45–0.367	Ar > 17.5
Flow 2V	2.0	2.0	0.0487–2.39	2.96–0.275	Ar > 15.0
Flow 3V	4.0	4.0	0.0722–3.59	1.48–0.138	Ar > 7.5

Figure 5. Prediction of R as a function of Ar in the original steric-entropic mode with S(x) = S₀(x) and nonconstant l_c for rods with a constant volume of 3.23 × 10⁻²¹ m³ under various flow conditions (see Table 1).

Figure 5. Prediction of R as a function of Ar in the original steric-entropic mode with S(x) = S₀(x) and nonconstant l_c for rods with a constant volume of 3.23 × 10⁻²¹ m³ under various flow conditions (see Table 1).

These trends can be explained by comparing c(x) for the rods of each Ar. We chose the case of Flow 2V for the demonstration. In Figure 6, each c(x) was evaluated for the rods with three different values of Ar (20, 40, and 50) and plotted as a function x/l_c, the distance from the wall relative to l_c (as in the original steric-entropic mode prediction). As Ar increases, c(x) is distributed farther away from the accumulation wall (x = 0). This trend is the same as the prediction by the original steric-entropic mode although the Ar-enhanced elution is not shown here. This can be explained by the released assumption of constant l_c: Since the values of l_c are changed, the actual distribution is different from what is shown as a function of x/l_c. This indicates that the results in Figure 6 should be plotted as a function of a different variable to properly display the trend. We re-scaled the results in Figure 6 with x/w and plotted them in Figure 7. Each c(x) appears to be similar to each other. However, if the x-positions of the maximum c(x) are compared, each distribution is squeezed towards the accumulation wall with increasing Ar, which results in the Ar-reduced trend predicted in Figure 5.

As indicated in the legend of Figure 6, the values of l_c are very small compared to w = 350 μm, which can be assumed to be constant in the original steric-entropic mode. Yet when comparing the values of the l_c of rods with different Ar under the same flow condition, the ratio between the l_c of the rods corresponds to the ratio of the D_⊥ of each individual rod. Furthermore, D_⊥ affects the c(x) in a wider x-range whereas the steric-entropic mode can only affect the c(x) in shorter x-ranges (very near the wall: x ~ 0.5L). In other words, although the steric-entropic term S(x) lifts the distribution c(x) away from the wall with increasing Ar, the values of l_c actually decrease due to the reduction of D_⊥. As a result, the overall c(x) is pushed down towards the wall (slower elution). Therefore, for the explanation of the Ar-enhanced elution using the steric-entropic mode, we propose an improved model in the next section.

Figure 6. Prediction of c(x) as a function of x/l_c, a distance from the bottom wall normalized with l_c, for rods with a volume of 3.23 × 10⁻²¹ m³ and different values of Ar in the original steric-entropic mode with S(x) = S₀(x) and nonconstant l_c under Flow 2V.

Figure 6. Prediction of c(x) as a function of x/l_c, a distance from the bottom wall normalized with l_c, for rods with a volume of 3.23 × 10⁻²¹ m³ and different values of Ar in the original steric-entropic mode with S(x) = S₀(x) and nonconstant l_c under Flow 2V.

Figure 7. Prediction of c(x) as a function of x/w, a distance from the bottom wall normalized with w, for rods with a volume of 3.23 × 10⁻²¹ m³ and different values of Ar in the original steric-entropic mode with S(x) = S₀(x) and nonconstant l_c under Flow 2V.

Figure 7. Prediction of c(x) as a function of x/w, a distance from the bottom wall normalized with w, for rods with a volume of 3.23 × 10⁻²¹ m³ and different values of Ar in the original steric-entropic mode with S(x) = S₀(x) and nonconstant l_c under Flow 2V.

3.3. Improved Steric-Entropic Mode

The effect of the improved steric-entropic mode, derived in Section 2.3, on the separation behavior was investigated by evaluating (2) using (4), (11) and (12). The geometries of rods and the flow conditions for this investigation were chosen as the same conditions used in the analysis for the original steric-entropic mode in Section 3.2. The results for the rods with different Ar and constant volume (under the same flow conditions as in Figure 5) are shown in Figure 8. For Flow 1V and 2V, R decreases with increasing Ar at lower values of Ar while the Ar-enhanced elution trend emerges at higher values of Ar; however, Flow 3V resulted in the Ar-enhanced elution trend only at a certain Ar range.

This Ar-enhanced elution trend can be explained by comparing different distributions of c(x) for the rods with various values of Ar in the Ar-enhanced elution range. Figure 9 shows the distributions of c(x) for the constant-volume rods with Ar = 20, 40 and 50. Although c(x) is plotted as a function of x/w (constant l_c assumption was not made), it is clearly shown that the distributions of c(x) are lifted away from the wall with increasing Ar. The Ar-enhanced elution trend predicted by the improved steric-entropic mode suggests that this model can be a starting model, which can be developed further to fully explain the experimentally observed Ar-enhanced elution [9]. More discussion on the flow and rod geometry conditions for the Ar-enhanced elution trend will be made in the next section.

Figure 8. Prediction of R as a function of Ar in the new steric-entropic mode with (11) and (12) and nonconstant l_c for rods with a constant volume of 3.23 × 10⁻²¹ m³ under various flow conditions (see Table 1).

Figure 8. Prediction of R as a function of Ar in the new steric-entropic mode with (11) and (12) and nonconstant l_c for rods with a constant volume of 3.23 × 10⁻²¹ m³ under various flow conditions (see Table 1).

Figure 9. Prediction of c(x) as a function of x/w, a distance from the bottom wall normalized with w, for rods with a constant volume of 3.23 × 10⁻²¹ m³ and different values of Ar in the new steric-entropic mode and nonconstant l_c under Flow 2V.

Figure 9. Prediction of c(x) as a function of x/w, a distance from the bottom wall normalized with w, for rods with a constant volume of 3.23 × 10⁻²¹ m³ and different values of Ar in the new steric-entropic mode and nonconstant l_c under Flow 2V.

3.4. Identification of the Conditions for the Ar-Enhanced Elution

The Ar-enhanced elution trend, predicted by our model for the improved steric-entropic mode, only happens under specific flow conditions. We analyzed the predicted results in Figure 6 and Figure 7 as an attempt to identify those flow conditions. We conjectured that the interplay between Pe_r and 2l_c/L controls the Ar-dependent elution: There is a transition between the rod-wall interactions by Brownian rotation and the pole-vault rotation around Pe_r = 1. Additionally, l_c/2L is related to the competition between U_x and D_⊥; it is expected that the Ar-enhanced elution trend happens when the pole-vault rotation lifts the rod distribution away from the wall under the conditions where U_x is not strong enough to push this lifted distribution down towards the wall again. Our analysis found that the Ar-enhanced elution trend happens when Pe_r is approximately between the range of 0.8–2 and 2l_c/L is approximately between the range of 0.6–0.3. These ranges can be interpreted as the condition when the rod-wall interaction transition (Pe_r = 1) happens under the l_c of approximately 0.25L (the steric-entropic mode is not overly suppressed by U_x).

3.5. Comparison with the Experimental Observation

Figure 10A shows the experimentally observed elution data of GNRs with Ar = 1.4, 3.1, 3.4 and 4.4 (L = 34 nm, 77 nm, 38 nm, and 44 nm, respectively) under a flow condition of U_x = 4 × 10⁻⁴ m/s and <v> = 4 × 10⁻⁴ m/s (converted from 8 mL/min and 0.5 mL/min considering the geometry of AF4 used in [9]). If those experimental conditions are used in the prediction of R using the new model, the results do not agree with the experimental data. The Ar-enhanced elution trend can be found for the rods with the same values of Ar in a different set of flow conditions and rod geometries, as shown in Figure 10B.

However, the values of R and the slope of R/Ar show a reduction in an order of magnitude. The flow condition for the Ar-enhanced elution (Pe_r ~ 1 and l_c ~ 0.25L), identified by our new model, does not correspond to the experimental data. Note here that our work focused on improving the original steric-entropic model to show the Ar-enhanced elution trend. We are currently working on further development of this model for the enhanced quantitative agreement with the experimental data. The current quantitative discrepancy between the new model’s prediction and the experimental data can be attributed to the following point: The superposition assumed in (11) and (12) may be applied differently. In that case, the flow conditions for the Ar-enhanced elution (identified as Pe_r ~ 1 and l_c ~ 0.25L) will be different. Our model is derived based on the constant <v> in Fl-FFF whereas <v> in AF4 channel changes in the axial direction. The effect of the axial position-dependent Pe_r is not known. Our model also should be extended for rods with Ar < 5 because the slender-body approximation [12] was used in the model derivation. Furthermore, the particle-wall interaction due to the surface charge effect [20] is also going to be considered. Brownian dynamics simulations as well as verification through experiments will be performed for the future development.

Figure 10. Retention ratios as a function of Ar: (A) Experimental data [9] of GNRs with Ar = 1.4, 3.1, 3.4 and 4.4 (L = 34 nm, 77 nm, 38 nm, and 44 nm, respectively) eluted under U_x = 4 × 10⁻⁴ m/s and <v> = 4 × 10⁻⁴ m/s in AF4 channel and (B) the new model prediction of the rods with Ar = 1.4, 3.1, 3.4 and 4.4 (L = 340 nm, 770 nm, 380 nm, and 440 nm, respectively) eluted under U_x = 1.2 × 10⁻⁵ m/s and <v> = 8 × 10⁻³ m/s in Fl-FFF.

Figure 10. Retention ratios as a function of Ar: (A) Experimental data [9] of GNRs with Ar = 1.4, 3.1, 3.4 and 4.4 (L = 34 nm, 77 nm, 38 nm, and 44 nm, respectively) eluted under U_x = 4 × 10⁻⁴ m/s and <v> = 4 × 10⁻⁴ m/s in AF4 channel and (B) the new model prediction of the rods with Ar = 1.4, 3.1, 3.4 and 4.4 (L = 340 nm, 770 nm, 380 nm, and 440 nm, respectively) eluted under U_x = 1.2 × 10⁻⁵ m/s and <v> = 8 × 10⁻³ m/s in Fl-FFF.

4. Conclusions

We have shown that our new model for the steric-entropic mode can be used to predict the Ar-enhanced elution trend. Our new model improved the mechanism for the steric-entropic mode [5] by means of incorporating the pole-vault rotation of rod-like particles. In the normal mode, we have shown that the Ar-enhanced elution can be possible for the case where the rods have a larger Ar and larger volume. Our investigation of the original steric-entropic mode showed that the Ar-enhanced elution trend is not shown when the constant l_c assumption is released. Predictions of the separation behaviors by our new model showed that the Ar-enhanced elution trend is possible for certain flow conditions: Transition in the rod-wall interaction mechanisms (Brownian rotation and pole-vault rotation) happens while l_c is about a quarter size of a rod length (Pe_r ~ 1 and l_c ~ 0.25L, based on the current model).

Although the new model can be viewed as a prototype to qualitatively show the Ar-enhanced trend, its quantitative agreement with the experimental data must be improved. The extension to low Ar rods, consideration of the surface charge effect, simulation of the actual AF4 channel, as well as confirmation by Brownian dynamics simulations and experiments are presently being performed.