Dynamic Analysis of a Particle Motion System
Abstract
:1. Introduction
2. Model
2.1. Symmetry and Dissipation
2.2. Existence and Uniqueness of the Solution
2.3. Continuous Dependence on Initial Conditions
2.4. Equilibrium and Stability
2.5. Hopf Bifurcation
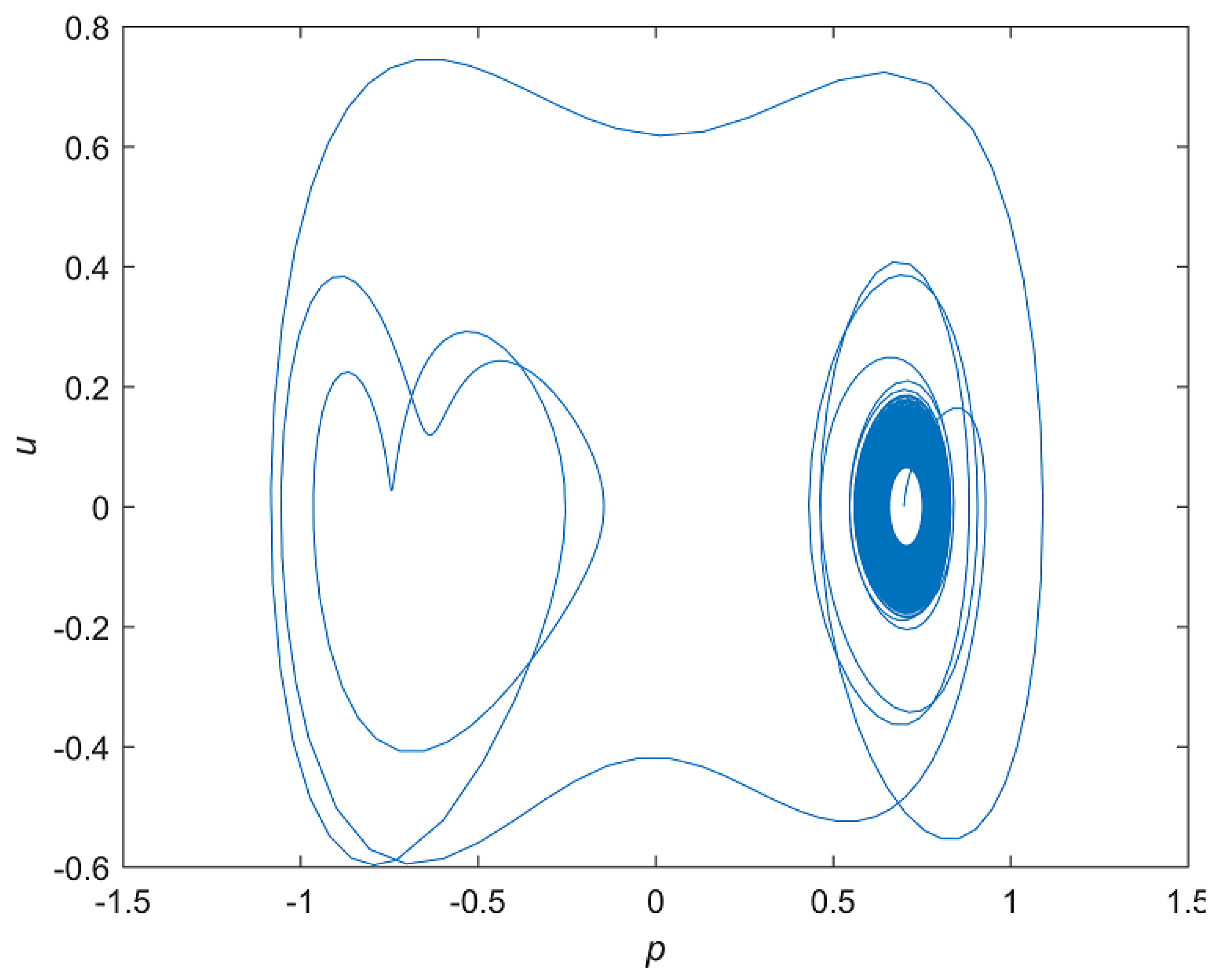
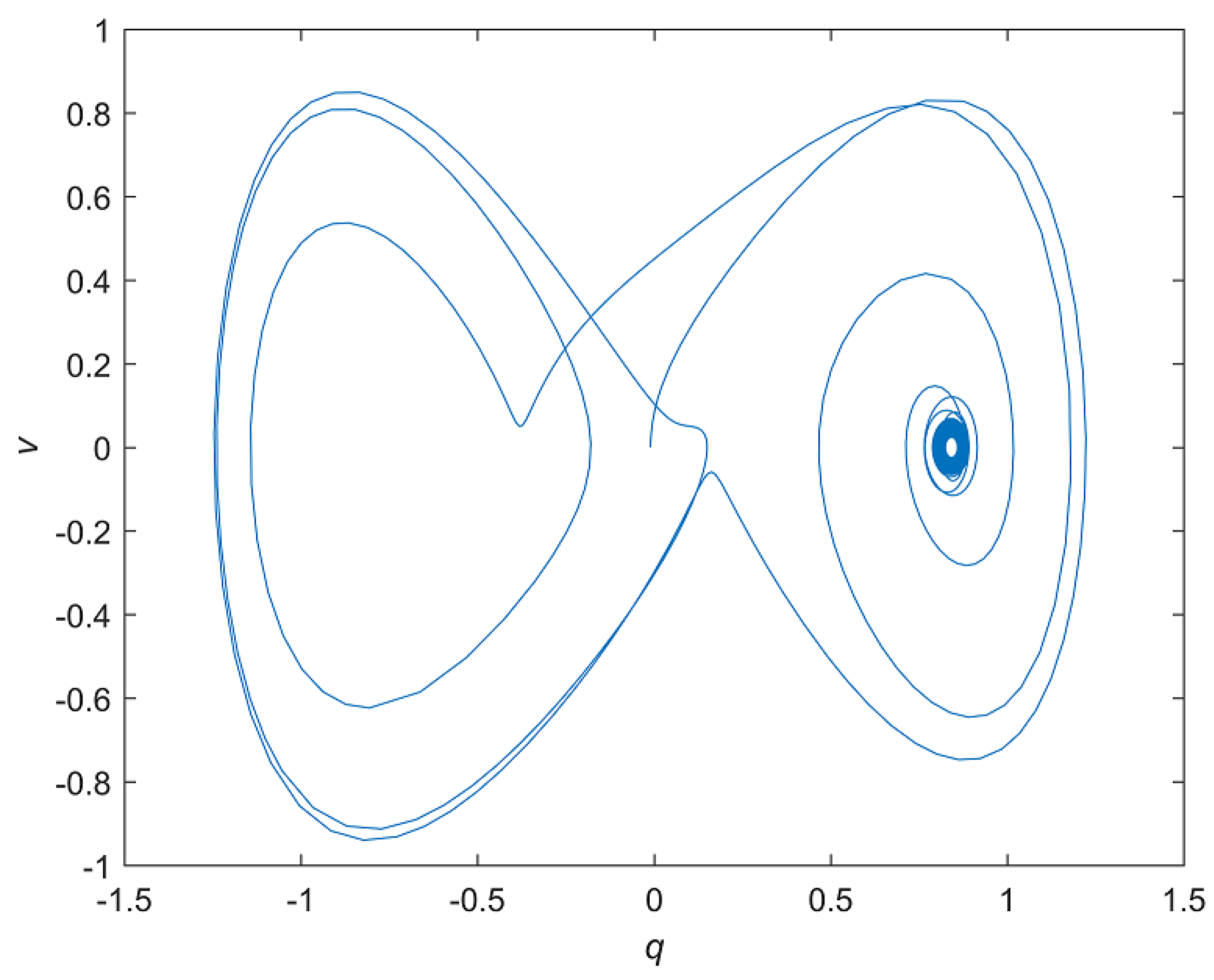
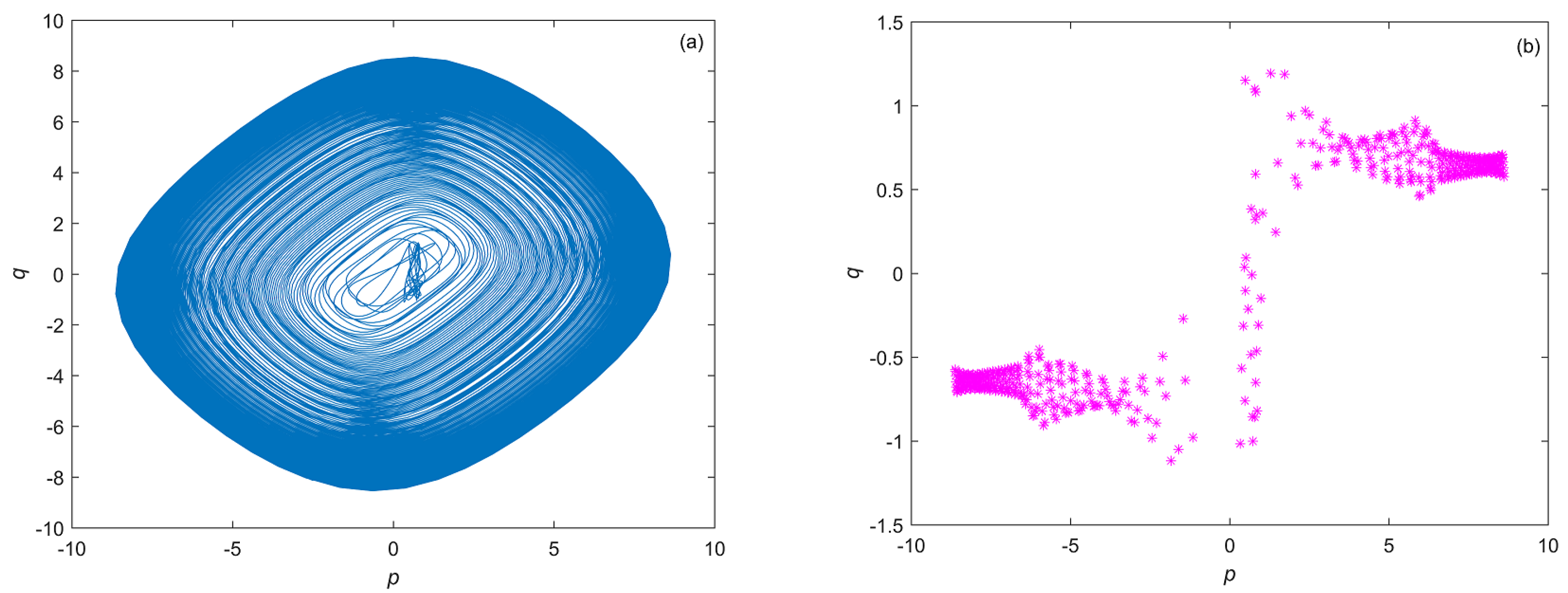
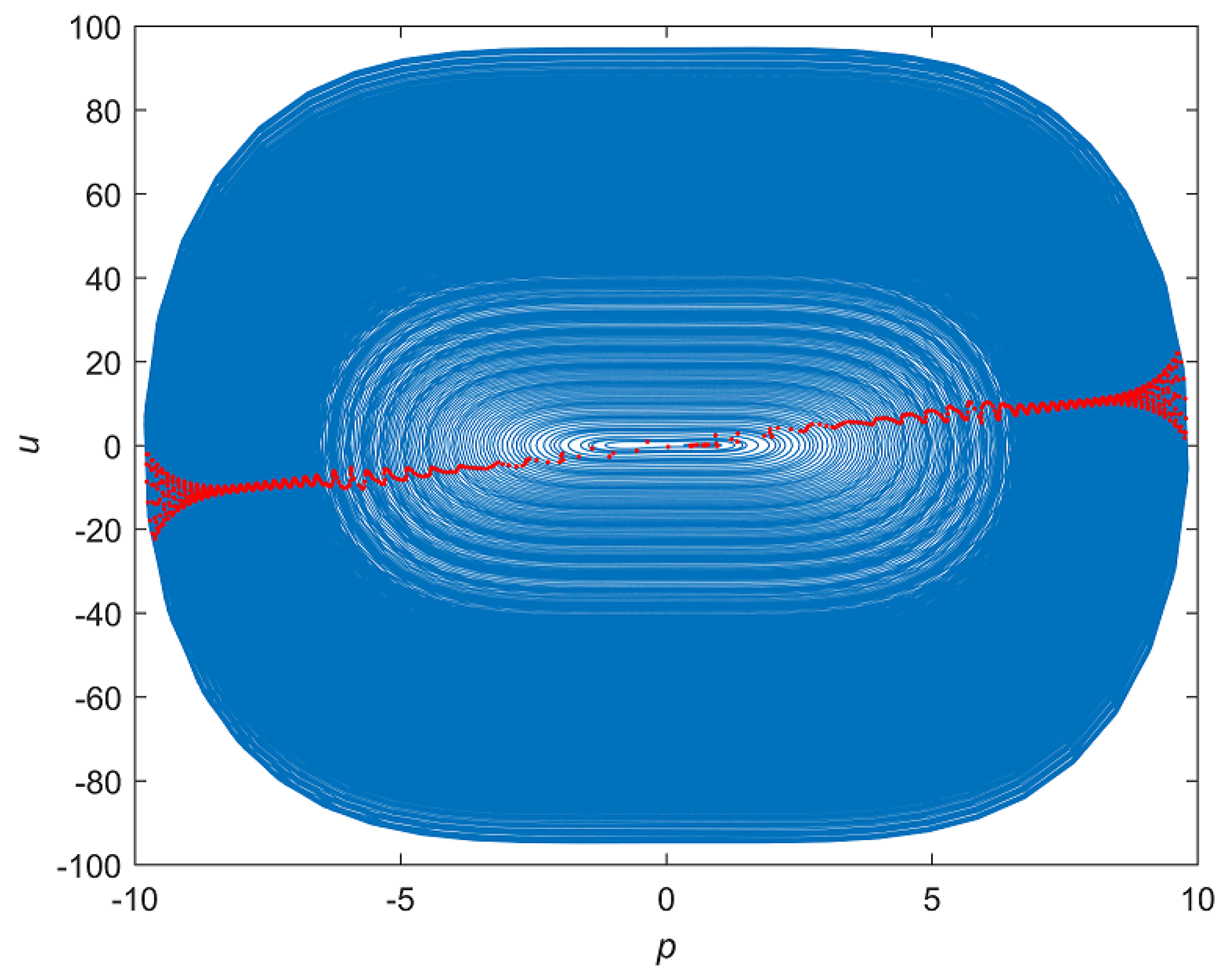
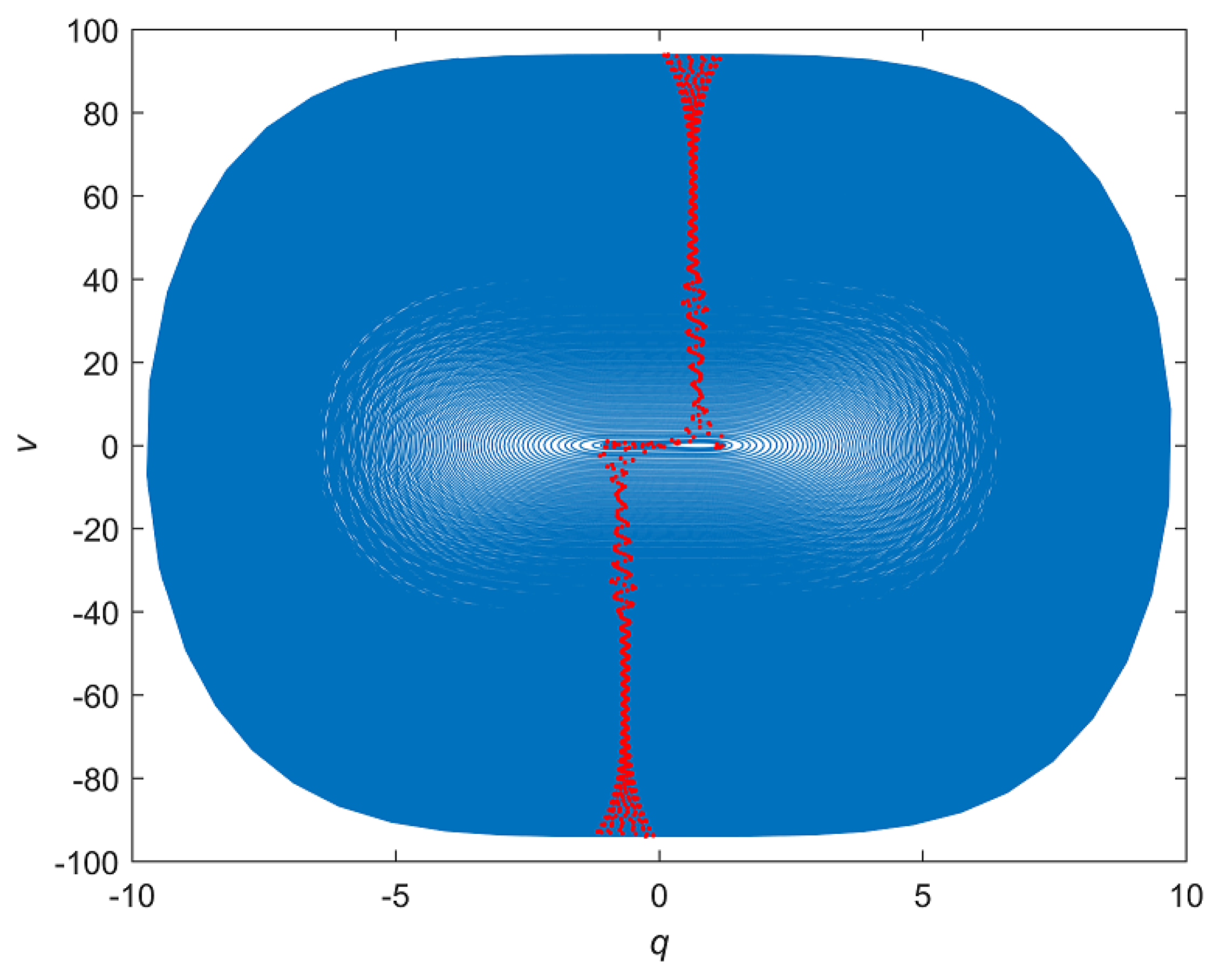
3. Simulation
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Abbott, N.L. Colloid Science Collides with Liquid Crystals. Science 2013, 342, 1326–1327. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; Davidson, R.C. Chaotic particle dynamics in free-electron lasers. Phys. Rev. A 1991, 43, 5541. [Google Scholar] [CrossRef] [PubMed]
- Hashimoto, K.; Tanahashi, N. Universality in chaos of particle motion near black hole horizon. Phys. Rev. D 2017, 95, 024007. [Google Scholar] [CrossRef] [Green Version]
- Sprott, J.C.; Xiong, A. Classifying and quantifying basins of attraction. Chaos 2015, 25, 22–30. [Google Scholar] [CrossRef] [PubMed]
- Boeing, G. Visual analysis of nonlinear dynamical systems: Chaos, fractals, self-similarity and the limits of prediction. System 2016, 4, 37–54. [Google Scholar] [CrossRef]
- Bradley, E.; Kantz, H. Nonlinear time-series analysis revisited. Chaos 2015, 25, 097610. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sander, E.; Yorke, J.A. The Many Facets of Chaos. Int. J. Bifurcat. Chaos 2015, 25, 1530011. [Google Scholar] [CrossRef]
- Yuan, F.; Wang, G.; Wang, X. Extreme multistability in a memristor-based multi-scroll hyperchaotic system. Chaos 2016, 26, 507–519. [Google Scholar] [CrossRef]
- Zhou, P.; Yang, F. Hyperchaos, chaos, and horseshoe in a 4D nonlinear system with an infinite number of equilibrium points. Nonlinear Dyn. 2013, 76, 473–480. [Google Scholar] [CrossRef]
- Liu, X.; Shen, X.S.; Zhang, H. Multi-scroll chaotic and hyperchaotic attractors generated from chen system. Int. J. Bifurcat. Chaos 2012, 22, 1250033. [Google Scholar] [CrossRef]
- Pine, D.J.; Gollub, J.P.; Brady, J.F.; Leshansky, A.M. Chaos and threshold for irreversibility in sheared suspensions. Nature 2005, 438, 997–1000. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Enkeleida, L.; Petia, M.V. Periodic and chaotic orbits of plane-confined micro-rotors in creeping flows. J. Nonlinear Sci. 2015, 25, 1111–1123. [Google Scholar]
- AlZahrani, A.M.; Frolov, V.P.; Shoom, A.A. Critical escape velocity for a charged particle moving around a weakly magnetized Schwarzschild black hole. Phys. Rev. D 2013, 87, 084043. [Google Scholar] [CrossRef]
- Kuwana, C.M.; Oliveiraz, J.A.; Leonel, E.D. A family of dissipative two-dimensional mappings: Chaotic, regular and steady state dynamics investigation. Phys. A 2014, 395, 458–465. [Google Scholar] [CrossRef]
- Oliveira, D.F.; Leonel, E.D. Parameter space for a dissipative Fermi-Ulam model. New J. Phys. 2011, 13, 123012. [Google Scholar] [CrossRef]
- Costa, D.R. A dissipative Fermi-Ulam model under two different kinds of dissipation. Commun. Nonlinear Sci. 2015, 22, 1263–1274. [Google Scholar] [CrossRef]
- Carr, J. Applications of Centre Manifold Theory; Springer: New York, NY, USA, 1981. [Google Scholar]
- Gaspard, P.; Briggs, M.E.; Francis, M.K.; Sengers, J.V.; Gammon, R.W.; Dorfman, J.R.; Calabrese, R.V. Experimental evidence for microscopic chaos. Nature 1998, 6696, 865–868. [Google Scholar] [CrossRef]
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining Lyapunov exponents from a time series. Physica D 1985, 16, 285–317. [Google Scholar] [CrossRef] [Green Version]
- Awrejcewicz, J.; Olejnik, P. Stick-slip dynamics of a two-degree-of-freedom system. Int. J. Bifurcat. Chaos 2013, 13, 843–861. [Google Scholar] [CrossRef]
- Li, J.; Wu, H.; Mei, F. Dynamic analysis for the hyperchaotic system with nonholonomic constraints. Nonlinear Dyn. 2017, 90, 2557–2569. [Google Scholar] [CrossRef]
- Chang, C.; Ge, Z. Complete identification of chaos of nonlinear nonholonomic systems. Nonlinear Dyn. 2010, 60, 551–559. [Google Scholar] [CrossRef]

| Equilibrium Points | Eigenvalues of the Jacobian Matrix | Equilibria Type |
|---|---|---|
| , , | saddle-focus point | |
| , , | saddle-focus point | |
| , , | saddle-focus point | |
| , , | saddle-focus point | |
| , , | saddle-focus point | |
| , | focus point | |
| , | focus point | |
| , | focus point | |
| , | focus point |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, N.; Li, J. Dynamic Analysis of a Particle Motion System. Mathematics 2019, 7, 7. https://doi.org/10.3390/math7010007
Cui N, Li J. Dynamic Analysis of a Particle Motion System. Mathematics. 2019; 7(1):7. https://doi.org/10.3390/math7010007
Chicago/Turabian StyleCui, Ning, and Junhong Li. 2019. "Dynamic Analysis of a Particle Motion System" Mathematics 7, no. 1: 7. https://doi.org/10.3390/math7010007




