Social Context and the Spread of HIV: An Evolutionary Game-Theoretic Investigation on the Impacts of Social Stigma on Epidemic Outcomes
Abstract
:1. Introduction
Related Literature
- Most fundamentally, the SIR model [13] provides a conceptual foundation for modeling the spread of disease. This model divides the population into the categories of susceptible (S), infected (I), and recovered (R) and also specifies two parameters that determine rates of disease transmission: the mixing or transmission coefficient (β) and per-infection rate of recovery (σ). 4
- Sources of information—either global or local—affect rates of disease transmission.
- The type of available information—either prevalence or belief based—influences rates of transmission, and belief-based information need not reflect actual disease prevalence.
- Human behavior affects disease transmission by influencing the S, I, R, β and/or σ terms in the SIR model.
- Analysts can fruitfully use game theory to model relevant decisions (e.g., whether or not to vaccinate).
- Behavioral traits related to disease transmission can, themselves, be transferred among individuals; hence such traits and their prevalence evolve over time.
- Local social network structure affects the transmission of information, behavioral traits, and, indeed, levels of infection across populations.
2. Models of Behavior and HIV Transmission
2.1. An Evolutionary Game-Theoretic Perspective
- Nature decides whether each player is an HIV carrier (HIV+), an event that occurs with probability p.
- Each player privately observes nature’s move and then either signals to their potential partner that he or she is HIV+ (S) or does not signal (NS). The latter choice could imply, honestly or not, an HIV− status.
- Neither player observes the other’s type, but each observes either S or NS. Each then either accepts a relationship with the other (A) or rejects the relationship (R).
- If and only if both choose A, a relationship ensues.
- Payoffs follow.

- HIV+ agents either signal or not, depending on whether they are RE or IR, but they always accept relationships.
- HIV− agents never signal, but depending on whether they are A- or C-types, they either always accept a relationship or do so only if they have not received an HIV+ signal.
| Phenotype (proportion) | HIV+ & REpq | HIV+ & IRp(1 − q) | HIV− & A(1 − p)z | HIV− & C(1 − p)(1 − z) |
|---|---|---|---|---|
| HIV+ & RE | L − Sc | L − Sc, L − Sa | L − Sc | −Sc, 0 * |
| pq | L − Sc | L − τ − Sa | ||
| HIV+ & IR | L − Sa | L − G, L − G | L − G, L − T | L − G, L − T |
| p(1 − q) | L − Sc | |||
| HIV− & A | L − τ − Sa | L − T, L − G | L, L | L, L |
| (1 − p)z | L − Sc | |||
| HIV− & C | 0, −Sc * | L − T, L − G | L, L | L, L |
| (1 − p)(1 − z) |
| ESS Outcome | Existence | Stability |
|---|---|---|
| RE is an ESS | (i) (1 − p)G(q) + pSa(z) > (1 − p)(1 − z)L + Sc(q), as q → 1 | a. (i) holds for all q or b. ∂Φ/∂q > 0: G’ > Sc’ |
| IR is an ESS | (ii) Sc(q) + (1 − p)(1 − z)L > G(q), as q → 0 | c. (ii) holds for all q or b. ∂Φ/∂q > 0: G’ > Sc’ |
| Polymorphic q* | (iii) (1 − pq*)G(q)+ pq*Sa(z) = (1 − p)(1 − z)L + Sc(q*), for any q < 1 | d. ∂Φ/∂q < 0: G’ < Sc’ |
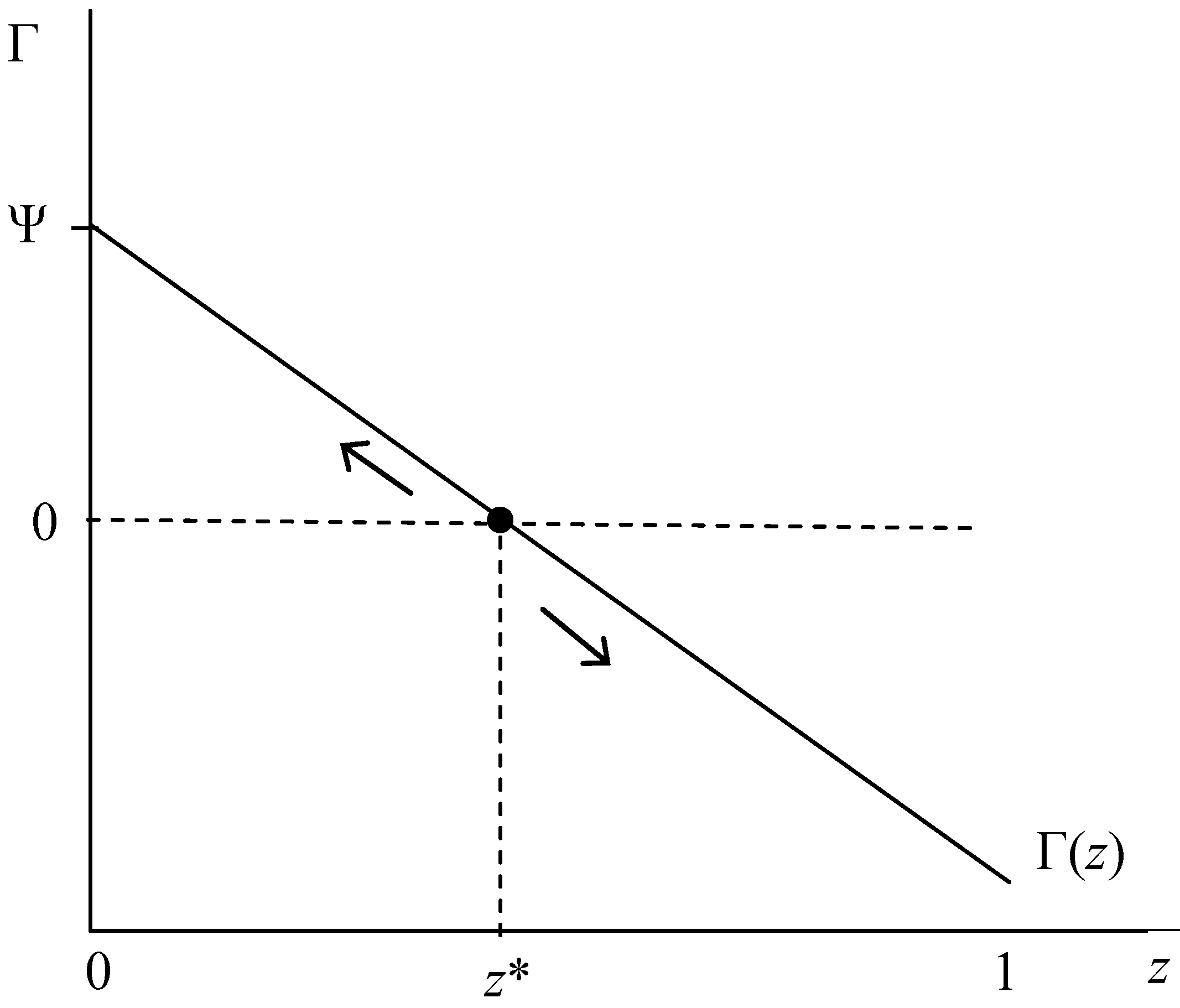
| A is an ESS | (iv) L > τ + Sa(z), as z → 1 | e. (iii) holds for all z or f. ∂Γ/∂z < 0: Sa’ < 0 |
| C is an ESS | (v) τ + Sa(z) > L, as z → 0 | g. (iii) holds for all z or f. ∂Γ/∂z < 0: Sa’ < 0 |
| Polymorphic z* | (vi) τ + Sa (z*)= L, for any z∈ [0,1] | h. ∂Γ/∂z > 0: Sa’ > 0 |
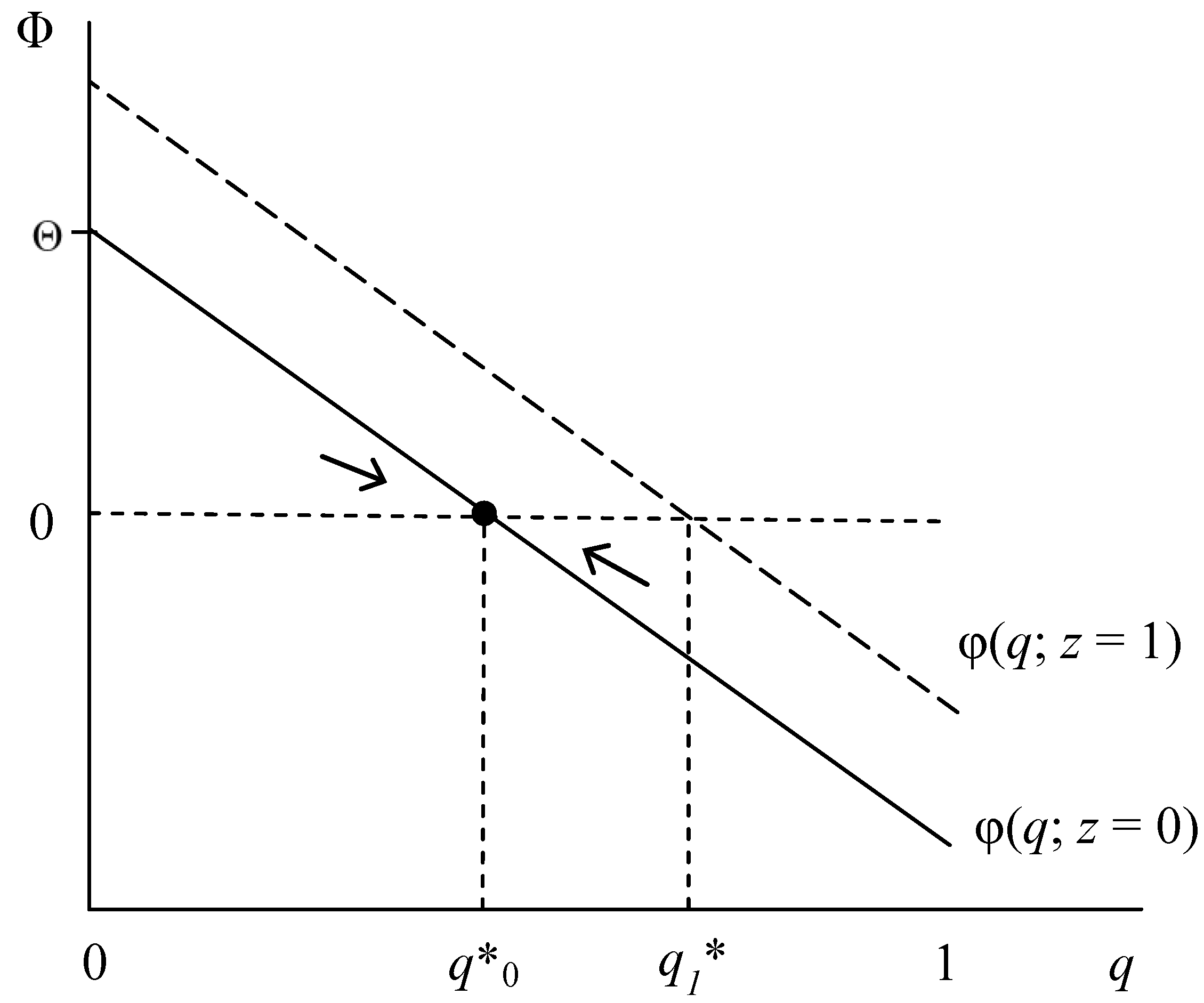
| A. RE vs. IR Fitness | |
|---|---|
| Partial Derivative | Statement, Φ and q* decrease (d) or increase (i) in: |
| (i) ∂Φ/∂Sc = −1 | Condition stigma (d) |
| (ii) ∂Φ/∂Sa = pq | Association stigma (i) |
| (iii) ∂Φ/∂L = −(1 − p)(1 − z) | Relationship utility (d) |
| (iv) ∂Φ/∂G = 1 − pq | Guilt (i) |
| (v) ∂Φ/∂z = (1 − p)L | The population proportion of A-types (i) |
| (vi) ∂Φ/∂p = (1 − z)L + qSa − qG | The population proportion of HIV+ agents (i) or (d); if (1 − z)L + qSa > qG, then (i). |
| B. A vs. C Fitness | |
| Partial Derivative | Statement, Γ and Ψ decrease (d) or increase (i) in: |
| (vii) ∂Γ/∂τ = 1 | Informed transmission (i) |
| (viii) ∂Γ/∂Sa = 1 | Association stigma (i) |
| (ix) ∂Γ/∂L = 1 | Relationship value (d) |
2.2. The SIR Model of Infection
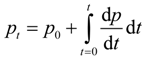
| Partial derivatives for Φ and Γ from Table 3 | Impacts on τ (via E) | Partial derivatives with respect to β |
|---|---|---|
| ∂Φ/∂Sc < 0 | ∂τ/∂Sc > 0 | (x) ∂β/∂Sc > 0 |
| ∂Φ/∂L < 0 and ∂Γ/∂L < 0 | -- | (xi) ∂β/∂L > 0 |
| ∂Φ/∂G > 0 | -- | (xii) ∂β/∂G < 0 |
| ∂Φ/∂Sa > 0 and ∂Γ/∂Sa > 0 | ∂τ/∂Sa > 0 | (xiii) ∂β/∂Sa indeterminate (see below) |
| ∂Φ/∂p > 0 (usually) | -- | (xiv) ∂β/∂p = (∂q/∂p)(∂β/∂q) < 0 |
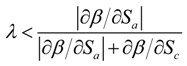
3. Conclusions
- Our discussion of evolutionary equilibria implies the following:
- Among the HIV+ population, the behavioral traits of honest and dishonest reporting of an HIV+ status (the RE and IR phenotypes) can both survive. More precisely, both phenotypes coexist in a polymorphic evolutionary equilibrium, as signified by a stable (or possibly oscillating) population ratio of REs (q*). Arguably, such mixes exist in most societies.
- Among the HIV− population, the behavioral traits of unconditional and conditional acceptance of relationships (the A and C phenotypes) can each be evolutionary stable strategies. Moreover, the accompanying evolutionary dynamics likely exhibit a positive-feedback dynamic whereby increased prevalence of phenotype A (C) above (below) critical mass tipping point (unstable internal equilibrium z*) enhances its own fitness. We interpret this result to imply two that predominance (rather than 100%) of either A- or C-types will accompany a q* equilibrium.
- The evolutionary model thus generates two stable evolutionary equilibrium combinations of phenotypes: a polymorphic mix q* of the RE and IR phenotypes among the HIV+ population, combined with either a predominantly A or predominantly C phenotype among the HIV− population.
- Concerning key influences on the nature of the evolutionary equilibria, we find:
- 4.
- The two types of social stigma—condition and association stigma—exert opposing direct influences on the fitness Φ of the RE phenotype. Whereas condition stigma compromises RE fitness, reducing equilibrium proportion q*, association stigma (Sa) enhances Φ and hence increases q*, ceteris paribus.
- 5.
- Fitness Φ and proportion q* also increase in guilt G and decrease in relationship value L.
- 6.
- and q* increase in society’s proportion z of A-types and, under specified conditions, also increase in disease prevalence p, potentially generating some negative-feedback with respect to disease prevalence.
- 7.
- C-type fitness Γ increases in Sa and decreases in L.
- Combining these findings with the SIR model, we find:
- 8.
- Condition stigma Sc unambiguously enhances disease transmission as represented by SIR mixing coefficient β and the rate di/dt. In this regard, Sc both reduces q* (from finding 4) and reduces acceptance of AIDS education (E), ultimately enhancing (informed) transmission rate τ.
- 9.
- Association stigma Sa, by contrast, can exert a negative impact on HIV transmission: whereas Sa enhances transmission by reducing E, Sa also increases q* and enhances Γ (as in findings 4 and 7).
- 10.
- Either evolutionary equilibrium (q*, A) or (q*, C) lends some stability to the SIR mixing parameter β.
- 11.
- The distinction between the (q*, A) and (q*, C) equilibria, has an ambiguous impact on β: On one hand, an all or predominantly A-type equilibrium leads to relatively high q*, tending to decrease β. On the other hand, as shown in Equation (13), β increases in z.
- 12.
- Finding 9 notwithstanding, the greater the share of condition stigma within a society’s overall social stigma, the greater the likelihood that overall social stigma enhances the SIR rate of HIV transmission.
Extensions
Acknowledgements
Authors Contribution
Conflicts of Interest
References
- A. Dixit, S. Skeath, and D.H. Reiley Jr. Games of Strategy, 3rd ed. New York, NY, USA: W.W. Norton, 2009. [Google Scholar]
- M. Smith. Evolutionary Genetics. Oxford, UK: Oxford University Press, 1989. [Google Scholar]
- H. Gintis. Game Theory Evolving, 2nd ed. Princeton, NJ, USA: Princeton University Press, 2009. [Google Scholar]
- W.H. Sandholm. Population Games and Evolutionary Dynamics. Princeton, NJ, USA: Princeton University Press, 2010. [Google Scholar]
- O. Williamson. The Economic Institutions of Capitalism. New York, NY, USA: Free Press, 1985. [Google Scholar]
- J. Stiglitz. “Information and the change in the paradigm in economics.” Amer. Econ. Rev. 92 (2002): 460–501. [Google Scholar] [CrossRef]
- E. Fehr, and U. Fischbacher. “Why social preferences matter—The impact of non-selfish motives on competition, cooperation and incentives.” Econ. J. 112 (2002): C1–C33. [Google Scholar] [CrossRef]
- S. Bowles. Microeconomics: Behavior, Institutions, and Evolution. Princeton, NJ, USA: Princeton University Press, 2004. [Google Scholar]
- S. Bowles, and S. Polanía-Reyes. “Economic incentives and social preferences: Substitutes or complements? ” J. Econ. Lit. 50 (2012): 1–57. [Google Scholar]
- W.D. Ferguson. Collective Action and Exchange: A Game-Theoretic Approach to Contemporary Political Economy. Stanford, CA, USA: Stanford University Press, 2013. [Google Scholar]
- T. Sandler. Collective Action: Theory and Applications. Ann Arbor, MI, USA: The University of Michigan Press, 1992. [Google Scholar]
- S. Funk, M. Salathé, and V.A.A. Jansen. “Modeling the influence of human behavior on the spread of infectious diseases: A review.” J. R. Soc. Interface 7 (2010): 1247–1256. [Google Scholar] [CrossRef]
- W.O. Kermack, and A.G. McKendrick. “A contribution to the mathematical theory of epidemics.” Proc. R. Soc. Lond. A 115 (1927): 700–721. [Google Scholar] [CrossRef]
- K.D. Schroeder, and F.G. Rojas. “A game theoretical analysis of sexually transmitted disease epidemics.” Ration. Soc. 14 (2002): 353–383. [Google Scholar] [CrossRef]
- R. Smith, K. Rossetto, and B.L. Peterson. “A meta-analysis of disclosure of one’s HIV-positive status, stigma and social support.” AIDS Care 20 (2008): 1266–1275. [Google Scholar] [CrossRef]
- R. King, D. Katuntu, J. Lifshay, L. Packel, R. Batamwita, S. Nakayiwa, B. Abang, F. Babirye, P. Lindkvist, E. Johansson, and et al. “Process and outcomes of HIV serostatus disclosure to sexual partners among people living with HIV in Uganda.” AIDS Behav. 12 (2008): 232–243. [Google Scholar] [CrossRef]
- S.C. Kalichman, M. DiMarco, J. Austin, W. Luke, and K. DiFonzo. “Stress, social support, and HIV-status disclosure to family and friends among HIV-positive men and women.” J. Behav. Med. 26 (2003): 315–332. [Google Scholar] [CrossRef]
- H. Liu, Z. Hu, X. Li, B. Stanton, S. Naar-King, and H. Yang. “Understanding interrelationships among HIV-related stigma, concern about HIV infection, and intent to disclose HIV serostatus: A pretest-posttest study in a rural area of eastern China.” AIDS Patient Care STDS 20 (2006): 133–142. [Google Scholar] [CrossRef]
- D.S. Wilson, and E.O. Wilson. “Rethinking the theoretical foundation of sociobiology.” Q. Rev. Biol. 82 (2008): 327–348. [Google Scholar] [CrossRef]
- R. Dawkins. The Selfish Gene, Thirtieth Anniversary Edition ed. Oxford, UK: Oxford University Press, 2006. [Google Scholar]
- J. Epstein. Generative Social Science: Studies in Agent-Based Computational Modeling. Princeton, NJ, USA: Princeton University Press, 2006. [Google Scholar]
- D. Dequech. “Institutions, social norms, and decision-theoretic norms.” J. Econ. Behav. Organ. 72 (2009): 70–78. [Google Scholar] [CrossRef]
- J. Elster. The Cement of Society. Cambridge, UK: Cambridge University Press, 1989. [Google Scholar]
- J. Elster. “Social norms and economic theory.” J. Econ. Perspect. 3 (1989): 99–117. [Google Scholar] [CrossRef]
- F. Mengel. “Matching Structure and the cultural transmission of social norms.” J Econ. Behav. Organ. 67 (2008): 608–623. [Google Scholar] [CrossRef]
- “The SIR Model for Spread of Disease.” Available online: https://www.math.duke.edu/education/ccp/materials/diffcalc/sir/sir1.html (accessed on 12 October 2013).
- W. Güth. “An evolutionary approach to explaining cooperative behavior by reciprocal incentives.” Int. J. Game Theory 24 (1995): 323–344. [Google Scholar] [CrossRef]
- S. Berninghaus, C. Korth, and S. Napel. “Reciprocity—An indirect evolutionary analysis.” J. Evol. Econ. 17 (2007): 579–603. [Google Scholar] [CrossRef]
- R. Shilts. And the Band Played On: Politics, People, and the AIDS Epidemic. New York, NY, USA: Saint Martin’s Press, 1987. [Google Scholar]
- M.O. Jackson. Social and Economic Networks. Princeton, NJ, USA: Princeton University Press, 2008. [Google Scholar]
- F. Vega-Redondo. Complex Social Network Analysis. Cambridge, UK: Cambridge University Press, 2007. [Google Scholar]
- 1For an intuitive undergraduate introduction to applied game theory, see Dixit, Skeath and Reiley [1].
- 7For Bowles, strategies (not individuals) are the “personae dramatis” of evolutionary game theory [8], p. 60.
- 8The dynamic emergence properties of evolutionary models present a new terrain for economic and social scientific analysis; see Epstein [21].
- 9The full stage game includes all such interactions between all possible pairs, where each agent in a pair may belong to one of four distinct combinations of phenotype, with associated probabilities. In Figure 1, Pat does not know Chris’s HIV− status and Chris will not signal (nor would an HIV− Pat; see payoffs); Pat will always accept a relationship if Chris agrees (Pat is an A-type; defined on page 178).
- 10Here Smeans signal HIV+ and NS can imply HIV−. By contrast, in many games, a better-informed party signals (honestly or not) the presence of some advantageous characteristic (e.g., high qualifications for a job). While the S and NS names could be reversed without affecting outcomes, we choose this terminology because it more accurately reflects stylized relationship dynamics.
- 11For simplicity, we combine AIDs education and access to protection into the variable E and hereafter refer to it as AIDs education.
- 12In a more complicated model, a C-type agent could base his probability of acceptance on the population infection rate p. Another variation could introduce a third behavioral phenotype at this stage: conformists, who do what they expect others to do.
- 13In terms of infection, they have nothing to lose. Implicitly we assume that for IR agents, L > Sa.
- 15Each member of these pairs is an evolutionary stable strategy (an ESS). A strategy is an ESS if, once it has attained significant predominance in a population (as in 99%), it cannot be successfully invaded by a new “mutant” strategy-because (in that region) the mutant receives lower fitness payoffs. Note that the ESS concept does not specify what would happen in cases with a substantial proportion of mutants (e.g., 30%).
- 16Our brief review of relevant empirical literature clearly suggests a mix of honest reporting and concealment.
- 17A more complete (and far more complicated) model would include full specification of differential replicator equations for all four phenotypes (specified over time) and would consider long-term implications of changes in population ratios z, q, and p on all four phenotypes. The conclusion mentions this possible extension.
- 18The basin of attraction around an all C-type equilibrium increases.
- 19We assume that this second-order effect does not outweigh the first-order effect shown in Table 3, (ii).
- 20We assume homogeneous mixing among agents (effectively no social network), hence parameter β characterizes all social interaction that affects disease transmission.
- 21This relation follows from the requirement that proportions s(t), i(t), and r(t) must always sum to 1; hence, the three time trends sum to 0. An intuitive explanation (with slightly different notation) appears at [26].
- 22A more complicated model could add immunization.
- 23It is easy to deduce influences on Equation (7) from our discussion of Equation (9).
- 24The probability of a HIV+ HIV− match between two partners is 2p(1 − p). There are N/2 possible matches in population of size N. Note that Equation (12) accounts for the probability of a rejected relationship in an RE/C-type match.
- 25∂β/∂Sa < 0 if and only if |(∂β/∂q)(∂q/∂Sa)zτ| + |(∂β/∂z)(∂z/∂Sa)qτ| > |(∂τ/∂z)(∂τ/∂Sa)qz|.
- 26Whether society settles on an equilibrium p will depend (ceteris paribus) on the relationship between birth and death rates-a topic beyond the scope of this paper.
- 27Preliminary analysis suggests that the more complex C-type would not alter key results of a polymorphic IR-RE equilibrium and positive feedback dynamics for A- and C-types. Adding an F-type as a fifth behavioral phenotype would complicate the model considerably, but a prior analysis suggested this addition did not significantly affect outcomes; but its inclusion could generate a negative-feedback dynamic for relationship acceptance, operating above a tipping-point level of p, where the A-type would lose relative fitness.
- 28For a discussion of agent-based models, see Epstein [21].
- 29For a dramatic example of how connectedness affected HIV transmission in its early history, see Shilts [29]. For an introduction to social network theory with an application to the SIR model, see Ferguson [10]; for detailed treatments of social network analysis see Jackson [30] and Vega-Redondo [31].
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Ferguson, W.D.; Nguyen, T.K. Social Context and the Spread of HIV: An Evolutionary Game-Theoretic Investigation on the Impacts of Social Stigma on Epidemic Outcomes. Economies 2014, 2, 171-192. https://doi.org/10.3390/economies2030171
Ferguson WD, Nguyen TK. Social Context and the Spread of HIV: An Evolutionary Game-Theoretic Investigation on the Impacts of Social Stigma on Epidemic Outcomes. Economies. 2014; 2(3):171-192. https://doi.org/10.3390/economies2030171
Chicago/Turabian StyleFerguson, William D., and Trang Kieu Nguyen. 2014. "Social Context and the Spread of HIV: An Evolutionary Game-Theoretic Investigation on the Impacts of Social Stigma on Epidemic Outcomes" Economies 2, no. 3: 171-192. https://doi.org/10.3390/economies2030171




