Encoding Two-Qubit Logical States and Quantum Operations Using the Energy States of a Physical System

Abstract

In this paper, we introduce a novel coding scheme, which allows single quantum systems to encode multi-qubit registers. This allows for more efficient use of resources and the economy in designing quantum systems. The scheme is based on the notion of encoding logical quantum states using the charge degree of freedom of the discrete energy spectrum that is formed by introducing impurities in a semiconductor material. We propose a mechanism of performing single qubit operations and controlled two-qubit operations, providing a mechanism for achieving these operations using appropriate pulses generated by Rabi oscillations. The above architecture is simulated using the Armonk single qubit quantum computer of IBM to encode two logical quantum states into the energy states of Armonk’s qubit and using custom pulses to perform one and two-qubit quantum operations.

1. Introduction

Quantum algorithms are known to outperform their classical counterparts in a variety of computational tasks [1,2,3]; various proposals have also been suggested for the physical implementation of quantum computers, while multiple implementations have also taken place [4,5]. Most of the proposed implementation techniques rely on the representation of the quantum logical unit of information, the qubit, to a degree of freedom of the underlying physical system. There are thus qubits that have energy eigenstates as basis states, qubits that have spin eigenstates as basis states and so on. Although a typical quantum computing architecture may refer to fundamental configurations of qubits and their interaction, resulting implementations will normally involve error correcting mechanisms to accommodate for the various sources of quantum error such as measurement error, decoherence and depolarization. While classically, it is straightforward to copy the state of a bit to multiple bits and use redundancy for error correction, the no-cloning theorem prohibits this approach for qubits. Instead, the codes used for qubits involve entanglement; the bit flip code and the Shor Code [6] are typical examples of quantum error correction codes. The need for error correction imposes the necessity of implementing an extra number of qubits to any implementation of a quantum computing architecture. The totality of the qubits used to both store and perform quantum error correction is typically referred to as the physical qubits of the system. In contrast, the logical amount of information encoded in the system is referred to as the logical qubits. Therefore, a system implementing the bit flip code that uses two extra qubits to perform error correction to a single state will have three physical qubits and one logical.

In this paper, we investigate a way to reduce the amount of error, and thus the need to correct extra physical qubits, by investigating the principles of quantum error correction and performing them to the domain of the architecture, i.e., the domain of the logical computation itself. Instead of using the eigenstates of two-state physical systems to encode single qubits, we allow more eigenstates to be used, thus encoding multiple qubits to the eigenstates of a single system. This transforms quantum operations involving multiple qubits, such as the CNOT, to quantum operations that are performed using the eigenstates of a single physical system. In this sense, entangled states at the logical level can be created by involving a single system at the physical level. Since a main source of error is the interactions between qubits, this process is expected to reduce the overall amount of error.

The paper is structured as follows: In Section 2, we give a brief overview on how, in principle, multiple quantum logical states can be mapped to single physical states with an example of how a CNOT gate can be implemented using a harmonic oscillator. We then build upon the main idea of the harmonic oscillator to propose a more robust schema of encoding information using the charge degree of freedom of impurity atoms embedded in semiconductor materials. Section 3 provides the core idea by presenting how the mapping model is implemented in charge qubits defined by donor electrons of impurity atoms embedded in a semiconductor structure. 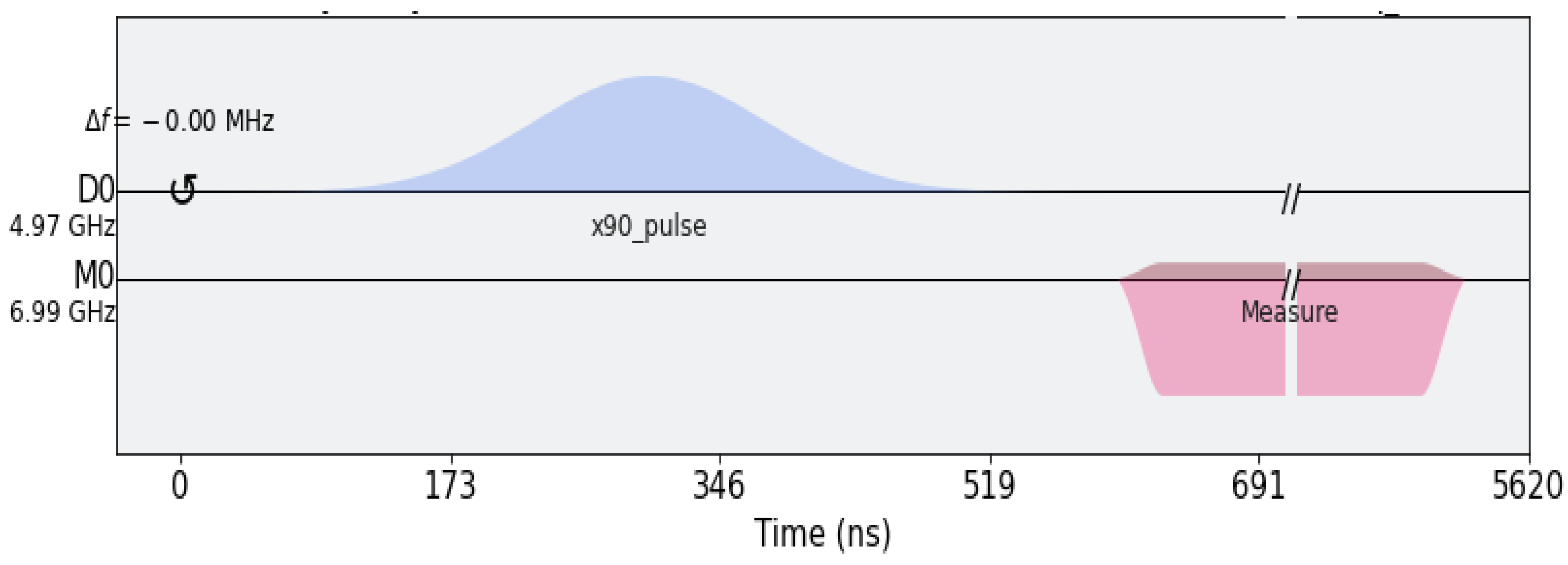The method by which single and two-qubit quantum gates are implemented in the model is also presented in Section 3. where, we also perform a simulation of the proposed architecture using the IBM Armonk single qubit computer [5]. Finally, Section 4 offers a discussion of the results of this work.

2. Materials and Methods

The idea of encoding multiple qubit states to a single physical state is not new. An example can be seen in the quantum oscillator case [7]. Though not a good candidate for the physical realization of quantum physical systems due to issues with scaling and equidistant energy separation, the quantum oscillator can be used to demonstrate the principle of mapping multiple qubit states to a single physical state.

Consider, for example, the following mapping:

$$\begin{gathered} {|00\rangle }_L\to |0\rangle \\ {|01\rangle }_L\to |2\rangle \\ {|10\rangle }_L\to \frac{\left(|4\rangle +|1\rangle \right)}{\sqrt{2}} \\ {|11\rangle }_L\to \frac{\left(|4\rangle -|1\rangle \right)}{\sqrt{2}} \end{gathered}$$

(1)

where subscript L corresponds to the logical quantum states. States on the right side, appearing without subscript, correspond to the energy levels of the quantum oscillator. The energy eigenstates of the quantum oscillator evolve with time as:

$$|n\rangle \to e^{-i\pi n\omega t}|n\rangle$$

(2)

Consequently, if we allow the system to evolve for time t equal to π/$\hslash \omega$ then the state changes according to:

$$|n\rangle \to {\left(-1\right)}^n|n\rangle$$

(3)

so that odd labeled physical states (in this case, the $|1\rangle$ state) change sign. Applying for the logical states appearing in the Equation (1) state $|10\rangle$, changes to $|11\rangle$ and vice versa, while the other two states remain unchanged, corresponds to the truth table of the quantum CNOT gate; considering the first qubit to be the control and the second one the target qubit.

Although the quantum harmonic oscillator architecture presented above is more of a theoretical schema, architectures that divert from the typical mapping of a single physical degree of freedom to a single qubit state have been developed. A hybrid approach, for example, that uses different mechanisms to encode different parts of a quantum computation has been implemented in [8], where the control qubit of a C-SWAP Gate was implemented using a photon’s polarization, whereas the SWAP part was implemented using four degrees of the photonic angular momentum. In general, the concept of hyperentanglement [9] allows the usage of multiple degrees of freedom of a single physical system to encode quantum information. The approach presented in this paper uses only one degree of freedom.

The typical spin systems used for quantum computing consist of two eigenstates sufficient for encoding a single qubit. For the purpose of the current work, we needed to map multi-qubit registers to eigenstates of single physical systems; therefore, charge qubits are a better candidate that allow for such encodings. Charge qubits are implemented using the energy charge of freedom of a quantum system. Typical efforts to construct an architecture based on charge qubits include the encoding of a qubit based on the presence of Cooper pairs [10] or encoding to the charge degree of freedom of electrons in semiconductor devices [11,12]. More recently, architectures that are based on neutral atoms have been proposed [13]. These architectures make use of laser beams targeted at an atom ensemble to cool them to temperatures of the order of mK; they then use pulses to excite the atoms and use the energy states as the computational basis.

Similar to the two-spin system is the archetypal model for spin qubits, in which a two-level atom can be used for prototyping quantum logic operations on a single qubit. Scaling a physical system to allow for operations on an arbitrary number of qubits is one of the biggest challenges of quantum computing. In the case of the two-level atom, the straightforward method of scaling the system by adding more energy levels becomes quickly inefficient, as the gap between higher levels becomes very narrow and, after a certain point, practically continuous. This is also the case for the harmonic oscillator state presented above.

This difficulty can be overcome by various methods such as those mentioned in the first paragraph; for the purposes of the current work, a semiconductor material with a pentavalent donor impurity contributing one extra donor electron is considered (Figure 1). Depending on the material and the doping substance, multiple energy eigenstates may be introduced in the semiconductor bandgap. For the purposes of the present treatment, it will be assumed that energy levels can be raised as desired by the appropriate placement of impurities in the semiconductor grid and that any degeneracies can be lifted by applying the appropriate external electric fields. It is further assumed that for the transitions of interest, the selection rules resulting from the symmetries of the material are always allowed and that energy levels may always be defined such that the energy differences between transition levels may always be matched by incoming electromagnetic pulses. All other energy levels are sufficiently detuned and thus not affected by the incoming pulse.

For the pair energy levels depicted in Figure 1, the following mapping between physical and quantum logical states is considered:

$$\begin{gathered} |00\rangle \to |1\rangle \\ |01\rangle \to |2\rangle \\ |10\rangle \to |3\rangle \\ |11\rangle \to |4\rangle \end{gathered}$$

(4)

Transitions between states will be analyzed for two cases, namely single qubit and two-qubit operations.

A typical method for a quantum state, to make transitions between energy eigenstates, is by making use of Rabi oscillations. The dynamics of Rabi oscillations have already been studied as candidates for encoding qubits and manipulating quantum information [14,15]; for the domain of semiconductors in particular, there are already results that demonstrate the feasibility of quantum control using spin qubits in GaAs quantum dots [16] and Si quantum dot systems [17]. Here we will give an overview on how the same approach can also be followed to manipulate the logical states, as these were defined in Equation (4).

Consider that an electric pulse is applied to the electron in Figure 1. It can be shown that under the rotating wave approximation [18], the state of the electron will evolve according to:

$$\left[{\dot{c}}_0\left(t\right) {\dot{c}}_1\left(t\right)\right]=\left[\frac{i{\mathsf{\Omega }}_R}{2}{e}^{-i\phi }{e}^{\mathsf{\Delta }t}{c}_0\left(t\right) \frac{i{\mathsf{\Omega }}_R}{2}{e}^{-i\phi }{e}^{\mathsf{\Delta }t}{c}_1\left(t\right)\right]$$

(5)

c_i is the amplitude of the ith state, Ω_R the Rabi frequency determined by the energy of the incident pulse and the electric dipole matrix and Δ = ν − ω the detuning, ν is the frequency of the incident pulse and ω = ω₂ − ω₁ is the frequency difference between the two states. An electric field that is near-resonant with the transition when applied for a finite time, can be used to perform an arbitrary rotation between the two states, the exact time being dependent on the detuning and Rabi frequency.

Consider the setup depicted in Figure 2, where ω_1→2 = ω_3→4 with ω_1→3 and ω_2→4 being sufficiently detuned that a pulse nearly resonant with ω_1→2 = ω_3→4 is applied. This pulse must be applied for sufficient time to perform any transition between states |1⟩ and |2⟩ if the electron is in one of these states, or between |3⟩ and |4⟩ if the electron is in one of those states. The mapping defined in Equation (4) corresponds to a single qubit operation on the second qubit. If a single qubit operation is required in the first qubit, the same argument may be followed for frequencies ω_1→2 = ω_3→4, which will allow the first qubit to be arbitrarily controlled.

Though the above setup will only work for frequencies that are pairwise degenerate, the technique may be slightly modified to accompany non-degenerate states, providing those transitions are allowed by the selection rules and that all frequencies are sufficiently detuned. The modification is implemented to perform two pulses in succession; the detuned pulse will not affect the electron, while the resonant pulse will perform the desired rotation.

For the two-qubit case, based on Equation (4), and considering the rightmost logical qubit to be the controlled qubit, the required transitions for the CNOT gate at the physical representation are:

$$\begin{gathered} |1\rangle \to |1\rangle \\ |2\rangle \to |2\rangle \\ |3\rangle \to |4\rangle \\ |4\rangle \to |3\rangle \end{gathered}$$

(6)

If ω_3→4 is sufficiently detuned from any other transition frequency, a π Rabi pulse with this resonance will perform the desired transition.

3. Results

To establish the validity of the approach, we exhibited the dynamics of the system using the IBM Armonk, a single qubit quantum computer developed by IBM that can be accessed via the Qiskit SDK [5]. For the purpose of this work, encoded four quantum states into the physical states of Armonk’s single qubit. Though Armonk provides its own set of single qubit gates, we drove it using custom-made pulses, making use of its higher energy states. The possibility of using higher energy levels of a transmon system has already been studied in [19], where the authors proved, by studying decoherence and decay times for π pulses used for consecutive excitation frequencies, that higher excited states could be used for computation.

In this work, for our proposed mapping, treated two separate cases: (a) Single qubit operations and (b) two-qubit operations

3.1. Single Qubit Operations

Single qubit operations involve the generation of pulses that, when applied to the system, alter only one of the qubits in the logical space. In a similar fashion, with the encoding of multiple qubit states in the charge degree of freedom of the electron of an impurity atom embedded in semiconductor material explained in Section 2, let us consider energy states $|0\rangle$, $|1\rangle$, $|2\rangle$, $|3\rangle$ of Armonk’s single qubit and follow a similar mapping, as in Equation (4):

$$\begin{gathered} {|00\rangle }_L\to {|0\rangle }_{Armonk} \\ {|01\rangle }_L\to {|1\rangle }_{Armonk} \\ {|10\rangle }_L\to {|2\rangle }_{Armonk} \\ {|11\rangle }_L\to {|3\rangle }_{Armonk} \end{gathered}$$

(7)

We investigated how we can create pulses that, when performed at the level of physical qubits, isolate qubits at the logical level. Taking the logical ground state ${|00\rangle }_L$ for example, creating a superposition of equal probabilities for the first qubit will take the state to $\frac{1}{\sqrt{2}}({|00\rangle }_L+{|01\rangle }_L)$, which, as can be seen by Equation (7), is equivalent to the physical state $\frac{1}{\sqrt{2}}({|0\rangle }_{Armonk}+{|1\rangle }_{Armonk})$. To drive this, we needed to create a pi/2 pulse between the ground and the first excited state of the physical qubit. This was achieved using IBM’s Quantum Experience Aer library [5]. Briefly, the steps followed were:

• Calibration of the qubit to derive the transition frequency.
• Derivation of the characteristics of the pi Rabi pulse.
• Confirmation of the Rabi pulse by applying it to the ground state of Armonk’s qubit.
• Clustering the samples of the measured results and an equivalent number of ground states to derive the mean values around the ground and first excited states.
• Based on the characteristics of the Rabi pulse derived in Step 3, define a pi/2 pulse with half the amplitude of the original Rabi pulse used to perform a full flip.
• Drive the Armonk’s qubit originally set to the ground state, with the pulse derived at Section 3.1 and measure the results.

Figure 3 and Figure 4 show a scatter plot with the results obtained by performing the above steps in Armonk’s qubit 1024 times. The two black dots correspond to the mean values of the ground and first excited states, as these were derived at Step 4 after calibrating the qubit. It can be seen that our results are roughly equally separated between the ground and first excited state, as was expected from the mappings discussed above.

Although the above discussion depicts the feasibility of isolating qubits at the logical level, for a general single qubit gate, the full truth table should be taken into account when constructing pulses. The truth table of the Hadamard Gate, for example, when considering both states of the logical qubit that does not take part in the computation, can be summarized as:

$$\begin{gathered} |00{\rangle }_L{H}_1\to |0\rangle \otimes \frac{1}{\sqrt{2}}{\left(|0\rangle +|1\rangle \right)}_L=\frac{1}{\sqrt{2}}{\left(|00\rangle +|01\rangle \right)}_L \to \frac{1}{\sqrt{2}}{\left(|0\rangle +|1\rangle \right)}_{Armonk} \\ |01{\rangle }_L{H}_1\to |0\rangle \otimes \frac{1}{\sqrt{2}}{\left(|0\rangle -|1\rangle \right)}_L=\frac{1}{\sqrt{2}}{\left(|00\rangle -|01\rangle \right)}_L \to \frac{1}{\sqrt{2}}{\left(|0\rangle -|1\rangle \right)}_{Armonk} \\ |10{\rangle }_L{H}_1\to |1\rangle \otimes \frac{1}{\sqrt{2}}{\left(|0\rangle +|1\rangle \right)}_L=\frac{1}{\sqrt{2}}{\left(|10\rangle +|11\rangle \right)}_L \to \frac{1}{\sqrt{2}}{\left(|2\rangle +|3\rangle \right)}_{Armonk} \\ |11{\rangle }_L{H}_1\to |1\rangle \otimes \frac{1}{\sqrt{2}}{\left(|0\rangle -|1\rangle \right)}_L=\frac{1}{\sqrt{2}}{\left(|10\rangle -|11\rangle \right)}_L \to \frac{1}{\sqrt{2}}{\left(|2\rangle -|3\rangle \right)}_{Armonk} \end{gathered}$$

(8)

Therefore, it is necessary to also consider the higher energy states when constructing a full Hadamard Gate. Following the same approach as before, we constructed a pi/2 pulse between Armonk’s higher energy states of $|2\rangle$ and $|3\rangle$. Section 3.2 discusses how to construct such pulses, as these are needed for the two-qubit operations with the mappings used. Assuming that the pulses used to drive transitions between $|0\rangle$ and $|1\rangle$, and between $|2\rangle$ and $|3\rangle$ are sufficiently detuned, as is the case for a correctly calibrated qubit, a combined pulse that consists of pi/2 pulses for each one of the transitions will be able to create superpositions of the first logical qubits, regardless of the state of the other qubit.

3.2. Two-Qubit Operations

Recalling the discussion in Section 3.1 and applying it to the Armonk qubit, the correspondence between logical and physical states for the CNOT Gate can be summarized as:

$$\begin{gathered} |0{\rangle }_{Armonk}\to |00{\rangle }_L CNOT\to |00{\rangle }_L\to |0{\rangle }_{Armonk} \\ |1{\rangle }_{Armonk}\to |01{\rangle }_L CNOT\to |01{\rangle }_L\to |1{\rangle }_{Armonk} \\ |2{\rangle }_{Armonk}\to |01{\rangle }_L CNOT\to |11{\rangle }_L\to |3{\rangle }_{Armonk} \\ |3{\rangle }_{Armonk}\to |11{\rangle }_L CNOT\to |10{\rangle }_L\to |2{\rangle }_{Armonk} \end{gathered}$$

(9)

It is thus sufficient to construct a pulse that performs a flip between states $|2\rangle$ and $|3\rangle$ of the Armonk’s qubit. Unfortunately, there is no direct way of exciting higher energy states from the ground state of Armonk’s qubit due to the limitations of maximum pulse power. To overcome this, we used the first excited state (which can be reached by applying a pi pulse to the ground state in a similar fashion as explained in Section 3.1) and then applied a sideband to this base pulse. We then gauged the qubit for a response and retrieved the candidate frequency for the 1→2 transition. After this, we can fully calibrated the other characteristics of the transition pulse (e.g., amplitude) following the same procedure as in Section 3.1. The definition of the 2→3 pulse followed the same rules; we excited the state from 0 to 1 and then to 2, after this, we applied another sideband to find the transition frequency of 2→3. Figure 5 depicts the definition of the sweeping pulse (main plus sideband) for the 1→2 transition. In contrast, Figure 6 depicts the measured signal for each of the test frequencies. For this particular experiment, the first two extrema, centered at around 2.63 GHz, were considered for constructing and testing the Rabi pulse for the transition.

It is to be noted that, as the level of the excited state grows, experiments may become less reliable and dependent upon the calibration status of the system. However, they can be used to depict that, in principle, higher-level energy states can be used to perform encodings involving multiple logical quantum states.

Concerning the error propagation, we can estimate that each transition required induces an error that is of the order of the error for the Pauli X Gate of the architecture. For the Armonk quantum computer, this is equal to 3.27 × 10⁻⁴ A single logical qubit operation requires two such pulses, whereas the controlled operation requires only one. Assuming accumulative error and no extra error correction between the steps of computation,

Table 1. Estimation of total number of Hadamard and CNOT Gates that can be performed on Armonk for the two-qubit case.

Total Circuit Depth	# of Hadamard Gates	# of CNOT Gates
300	0	300
157	157	0
228	76	152

. depicts the total number of gates supported to achieve a computation with an accumulated error of less than 10%. It should be noted as the scaling factor increases (more logical qubit states are encoded into distinct energy levels), operations will involve more pulses, thereby further decreasing the circuit depth.

4. Discussion

In this paper, we investigated the possibility of using multiple energy states to densely encode logical qubit states. We pointed out a possible physical system where this architecture can be implemented; this consists of a semiconductor device embedded with impurities. These systems are generally robust enough to introduce multiple energy bands, as these can be controlled by the number and types of impurities. We finally demonstrated the physical possibility of manipulating such states by encoding a two-qubit register into the first four energy states of IBM’s single qubit computer Armonk, and constructing specific pulses consistent with the logical truth tables of the quantum Hadamard and Controlled NOT gates. One interesting feature that was observed was the fact that for quantum gates that involve more than one qubit, the required physical manipulation was less complex than that required for the single qubit case. This behavior is to be expected, as altering the physical state of the underlying physical qubit may induce changes to multiple logical basis states. In principle, the more constraining the logical operation is (e.g., CNOT), the less manipulation of energy levels it will require.

Scaling the above schema to more dense coding is straightforward; however, the physical limitation may put an upper bound in the number of states encoded by a single physical system, with the exact bound being dependent on the underlying architecture. One limitation is the energy separation. Although we can, in theory, envisage introducing multiple controllable energy states for donor atoms, there is a limit where separating these states may become practically impossible. Another limitation is the number of pulses needed to perform quantum logical gates, which scales up as the number of logical quantum states that are encoded into the energy spectrum increases. For the case equal to two that was studied in the present work, we needed two pulses for single-qubit gates and one pulse for two-qubit gates; it is straightforward to see that for the mapping of a three logical state, we would need three pulses of a single-qubit gate, two pulses of a two-qubit case and we could perform a three-qubit case (e.g., Toffoli gate) with a single pulse. In general, the amount of single-system pulses grows linearly with the amount of qubits encoded. The extent to which our approach is efficient depends on the parameters of the underlying architecture. For example, for the transmon case, the Belem backend of IBM has an average error of an X gate equal to ~ 2.5 × 10⁻⁴, while that of the CNOT is ~1 × 10⁻⁴. The relaxation and dephasing times are equal to ~75 us and ~90 us respectively. Though these parameters are computed for the base case, where only the ground and first excited state are used and, therefore, need experimental re-evaluation for the case of higher excited states used in our work, it can be seen that in first-order, they hint that the number of single-qubit operations that can be performed before the error accumulated is comparable to that of the controlled case, is in the order of ~100.

It should be noted that even with systems specifically designed to accommodate higher energy levels into the computation, it cannot realistically be expected that a complete circuit that is of a size sufficient to perform useful computation can be performed in its entirety in the energy spectrum of a physical system. By separating qubits into logical groups, within which only single system pulses are needed, we expect that the overall number of controlled pulses will be significantly reduced. Nevertheless, physical coupling operations will still be required to perform logical controlled operations between qubits that belong to different groups. Future work will focus on handling these issues by introducing couplings between neighboring physical systems; proof of the concept is being developed using Belem, a 5-qubit backend provided by IBM, with the aim of using the results to expand the semiconductor model.