3.1. Niño 3 and Tskin
Three major El Niño events occurred during the 2001–2010 period: 2002–2003, 2006–2007, and 2009–2010, as evidenced by positive anomalies of Niño 3 indices (
Figure 2). Conversely, there were four La Niña events over the period. They were present for 2000–2001, 2005–2006, 2007–2008, and 2010–2011. Thus, even we only have 10 years of MODIS data, there was adequate information about SST anomalies, as there were a total of seven occurrences of either a El Niño or La Niña event during the timeframe.
Figure 2.
Plot of Niño 3 SST indices with respect to time for 2000–2010, calculated by computing Empirical Orthogonal Function (EOF) on Niño 3 SSTs. Data from Climate Prediction Center website [
55].
Figure 2.
Plot of Niño 3 SST indices with respect to time for 2000–2010, calculated by computing Empirical Orthogonal Function (EOF) on Niño 3 SSTs. Data from Climate Prediction Center website [
55].
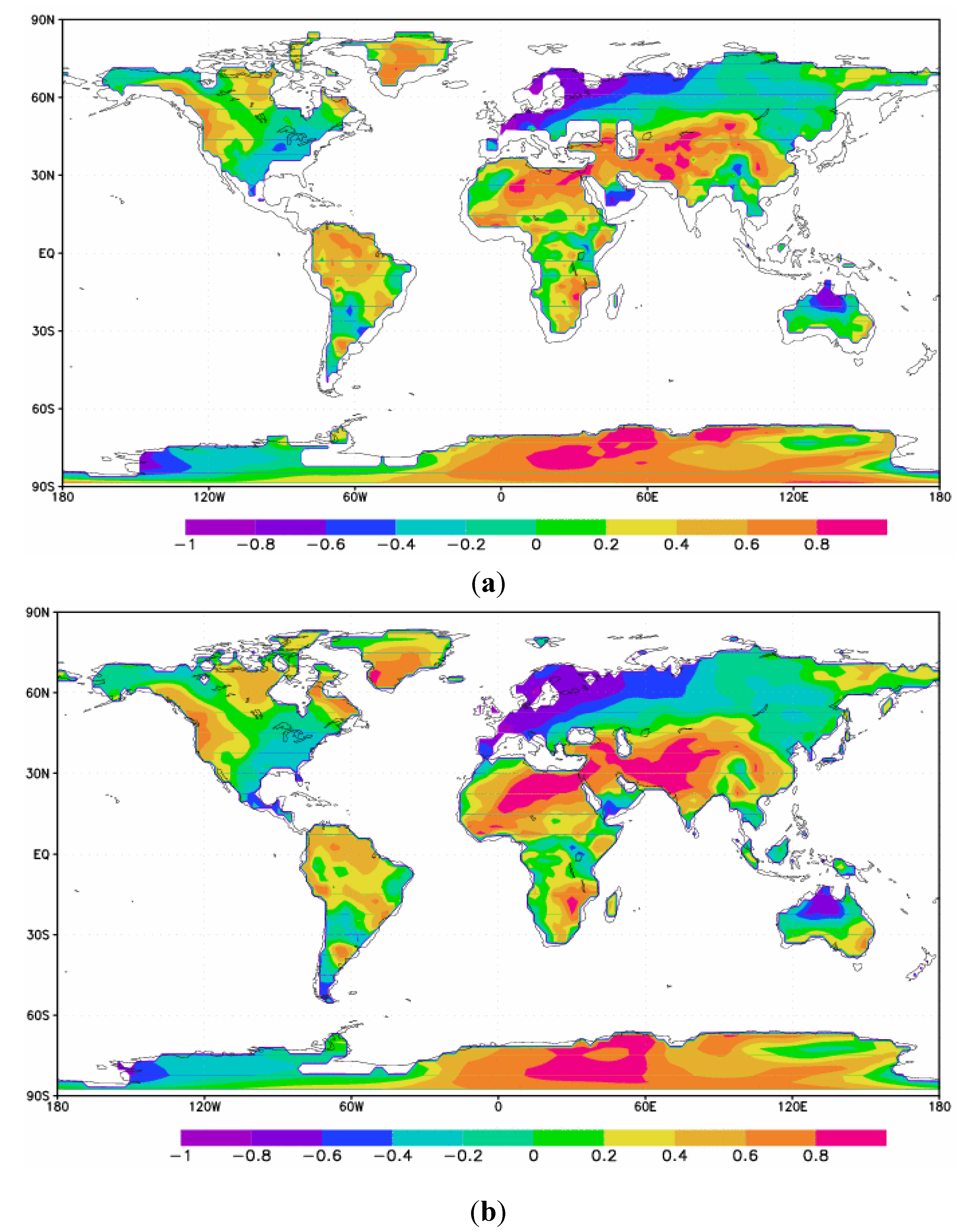
Correlation coefficients of Niño 3 and T
skin help to identify for which regions T
skin is sensitive to ENSO (
Figure 3(a)). Very high positive coefficients suggest that an increase in January T
skin from one year to the next tends to be associated with an increase in the Niño 3 value for the same month. On the contrary, strong negative correlation coefficients suggest that higher Niño 3 SST anomalies are associated with cooler T
skin values. The highest values (0.8–1) are found on the Russia/Kazahkstan border northeast of the Caspian Sea, in parts of interior Russia, and in areas along the northern edge of Antarctica. In particular, the maximum is 0.85, on the southwestern edge of the Caspian Sea. The strongest negative value (−0.82) is located in southwestern Africa at 20°S and 15°E. In North America, there are positive coefficients along the west coast of the USA extending into Canada and Alaska; this agrees with the finding of higher than average temperature anomalies along the West Coast, in Alaska, and over Southern Canada during an El Niño event [
41]. In addition, correlation coefficients of 0.2–0.8 are present over the Rocky Mountains. The Great Plains and Midwest have slightly to moderate negative correlation coefficients of 0 to −0.6. Strong negative correlation coefficients exist over northern Mexico (−0.4 to −1), indicating that warmer Niño 3 SST anomalies in January are associated with lower T
skin values, while the Southeastern USA generally has small negative correlations (0 to −0.4), although stronger in Florida (up to −0.6).
Figure 3.
(a) Correlation coefficients between January Niño 3 SST anomalies and January MODIS Daytime Tskin (0.05° × 0.05° resolution, regridded to 0.5° × 0.5°) over the period of 2001–2010; (b) Correlation coefficients between July Niño 3 SST anomalies and July MODIS Daytime Tskin (0.05° × 0.05° resolution, regridded to 0.5° × 0.5°) over the period of 2001–2010.
Figure 3.
(a) Correlation coefficients between January Niño 3 SST anomalies and January MODIS Daytime Tskin (0.05° × 0.05° resolution, regridded to 0.5° × 0.5°) over the period of 2001–2010; (b) Correlation coefficients between July Niño 3 SST anomalies and July MODIS Daytime Tskin (0.05° × 0.05° resolution, regridded to 0.5° × 0.5°) over the period of 2001–2010.
In Europe, there are strong negative correlation coefficients (−0.4 to −1) over the Northern Europe region including Denmark, Sweden, and Norway. Eurasia, on the other hand, has slight positive correlations across its interior (0 to 0.4), increasing to higher values in the far eastern portion (0.4 to 0.8). This agrees with the observation that higher Eastern Pacific SSTs are associated with warmer January temperatures in this region [
11].
Many of the very low values of less than −0.6 tend to be concentrated along or near the coast of continents as opposed to inland, including southeast Brazil, southern Chile, the southern edge of Saudi Arabia, the eastern tip of Africa, and other areas. A notable exception to this trend occurs in Australia, which has the strongest negative correlations in the interior of the continent.
Furthermore, three major areas have negative correlations over large valleys and flatlands with positive correlations over nearby mountains. In Australia, the central lowlands have negative correlations as low as −0.6 to −1, while the Great Dividing Range is associated with positive values. In the United States, the intermountain west generally has positive correlations of 0.2 to 0.8, but there are a few areas with values of 0 to 0.2, including the southern end of the Central Valley of California (between the coast ranges and Sierra Nevada), and the south end of the Puget Sound and Chehalis Valley in Washington (between the Olympic Mountains and Cascades). Finally, between 30°S and 60°S in South America, there are strong negative correlations along the coast west of the Andes, with positive correlations in some areas of these mountains. These findings raise an interesting question: Is there evidence that higher-than-normal Niño 3 SST anomalies in January are associated with cooler large scale valleys and flatlands worldwide? This could be an example of a local effect of ENSO.
By contrast, in July, Niño 3 SST anomalies and T
skin can have large differences (
Figure 3(b)) from the pattern in January. For example, correlation coefficients over the Norway/Sweden/Finland region are negative and between −0.2 to −1 in January, while for July, they are positive and between 0 and 0.8. In addition, values go from negative (0 to −0.6) to positive (0 to 0.8) over much of the eastern half of the United States, in particular the Gulf Coast and southern Plains. Furthermore, strong negative correlation coefficients in January over Mexico are now replaced with positive correlations in July. Finally, over the far eastern portion of Eurasia, there is a large shift from moderate to strong positive correlation coefficients in January (0.4 to 0.8) to highly negative coefficients in July (−0.6 to −1).
The strongest negative correlation coefficient value for July is −0.89, found at 45°N and 120°E. The area of negative values in this region generally ranges from −0.6 to −0.8. Large regions of positive correlations are present over an area extending from Northern Mexico to the Southern Great Plains, the southern portion of South America including Argentina and Chile, and Australia. The pixel with the highest positive correlation coefficient is located over the southern Sahara Desert, with a value of 0.89. The fore mentioned areas of positive correlations are in the subtropical vicinity of 30°N or 30°S. On the other hand, the two areas of strongest negative correlations are centered near 60°N.
In North America, areas of the USA along the west coast and southern Alaska have small to strong positive correlation coefficients (0.2 to 0.8), while most of the Northeast is covered by weakly negative correlations (0 to −0.4), although a few stronger spots are present (−0.4 to −0.6). Positive correlations cover most of Australia (0.2 to 0.8), with an area of negative values present over the southwestern corner (−0.2 to −0.6). Finally, patterns over Europe and Asia are quite variable, with differences as noted.
Lag correlations between January Niño 3 SST anomalies and July T
skin (
Figure 4(a)) show that key regions with negative correlation coefficients (−0.4 to −0.1) occur over South America in the vicinity of 30°S, a section of the Southern and Southeastern USA and extreme Northern Mexico, and a swath in the northern tropical latitudes of Africa. In particular, the strongest positive correlation is 0.90 over extreme eastern Siberia (65°N, 175°E); the strongest negative correlation is −0.83 (35°S, 75°W). In addition, strong positive correlations (>0.6) occur over the eastern end of Siberia, eastern Brazil, part of the Southwestern USA, South Africa, and an area near the Russia/China/Mongolia region.
Figure 4.
(a) Lag correlation coefficients between January Niño 3 SST anomalies and July MODIS Daytime Tskin (0.05° × 0.05° resolution, regridded to 0.5° × 0.5°) over the period of 2001–2010; (b) Lag correlation coefficients between July Niño 3 SST anomalies and January MODIS Daytime Tskin (0.05° × 0.05° resolution, regridded to 0.5° × 0.5°) over the period of 2001–2010.
Figure 4.
(a) Lag correlation coefficients between January Niño 3 SST anomalies and July MODIS Daytime Tskin (0.05° × 0.05° resolution, regridded to 0.5° × 0.5°) over the period of 2001–2010; (b) Lag correlation coefficients between July Niño 3 SST anomalies and January MODIS Daytime Tskin (0.05° × 0.05° resolution, regridded to 0.5° × 0.5°) over the period of 2001–2010.
Since T
skin represents the surface temperature of the land, it is very sensitive to vegetation type, as governed by the surface energy budget [
29]. A large difference occurs between the Southwest and Southeast USA, partly due to differences in land type and vegetation coverage. Specifically, high positive values occur over desert areas and mixed terrain, while flatter grasslands are present to the east, with negative values. This is a good example of the local mechanism affecting the impact of ENSO on T
skin. Since T
skin represents the surface temperature of the land, it is very sensitive to vegetation type, which can be seen from this example.
Comparing the non-lag correlations of July Niño 3 SST anomalies (
Figure 3(b)) to lag correlations for January and July (
Figure 4(a)) reveals a number of important differences: first, while the non-lag correlation has distinct strong negative correlation regions at 60°N latitude (90°W, 50°E, and 150°E longitude), the lag correlation has many regions of positive correlations at this latitude. In addition, at 30°N and 30°S, there is evidence of reversal as well, from positive (non-lag) to negative (lag). For example, the northern Mexico/Southern USA region at 100°W has strong positive correlations of 0.4 to 0.8 for non-lag July, but negative correlations of −0.4 to −0.8 when a lag is performed.
The plot of correlation coefficients between July Niño 3 anomalies and January T
skin (
Figure 4(b)) is important to examine, as it shows two critical features: first, it reveals the time interval between SST warming and the corresponding atmospheric response. Second, it may suggest how T
skin is impacted in Northern Hemisphere winter, which is when the effects of ENSO are most apparent, as mentioned in the literature [
39,
40].
The highest correlation is 0.95 over the Sahara Desert (15°N, 15°E), and the lowest is −0.93 in eastern Spain (40°N, 10°W). The most distinctive region is the large swath of positive values (0.8 to 0.95) over northern Africa, which suggests a very strong relationship between Niño 3 SST anomalies and Tskin over the region. Conversely, very strong negative correlation coefficients are present over western and central Europe, including Portugal, Spain, France, and Germany. This is an important finding, since there are still uncertainties about how exactly ENSO affects Europe.
Focusing over North America, high negative values occur over Florida and western Cuba (−0.6 to −1), which is consistent with the finding that El Niño conditions are usually associated with cooler winter conditions over the Gulf States [
35,
36]. Nevertheless, Eastern Cuba correlations are close to 0. In addition, there is a large swath of strong positive correlation coefficients (>0.6) extending southward from Alaska into British Columbia and the Northwestern USA, supporting the finding that an El Niño event usually produces warmer winters over the area [
35,
41,
42]. Furthermore, it appears that the Appalachian Mountains have stronger negative correlations than the surrounding areas of lower elevation.
To see which relationships are most meaningful, areas of statistical significance were plotted for the correlations between July Niño 3 SST anomalies and January T
skin (
Figure 5). As mentioned previously, to be statistically significant at a 95% confidence level, the correlation coefficient must be greater than or equal to 0.632, or less than or equal to −0.632. This is because there are 10 data points (n = 10) and thus the degrees of freedom is 8 (df = n − 2 = 10 − 2 = 8), and using a Pearson Product Moment Correlation table yields this correlation value for a 95% confidence level. When examining the areas of statistical significance, some major patterns can be seen. First, the aforementioned areas of negative correlations over western and central Europe are statistically significant at the 95% level, as is the belt of positive correlations extending from northern Africa into the Middle East. There are also areas of significance over the over the parts of the western USA and western Canada. In addition, an interesting wavelike pattern is seen over the southern Greenland, but the strong suggestion of cooling over Western Europe. This could be related to the jet stream patterns present for an El Niño, that is, a ridge over eastern Canada and southern Greenland, and a trough over Western Europe.
Figure 5.
Areas of 95% statistical significance for the lag correlation coefficients between July Niño 3 SST anomalies and January MODIS Daytime Tskin over the period of 2001–2010.
Figure 5.
Areas of 95% statistical significance for the lag correlation coefficients between July Niño 3 SST anomalies and January MODIS Daytime Tskin over the period of 2001–2010.
In order to see the relationship of Niño 3 SST anomalies and T
skin over a 12-month cycle, correlations were also done on a yearly scale. Specifically, temporal correlation coefficients were calculated between Niño 3 SST anomalies and T
skin for each year of the period. A comparison of correlations for individual years shows great variability, from highly negative to highly positive or vice versa. The SD of yearly correlation coefficients over the 2001–2010 timeframe was calculated to test the sensitivity of land regions (
Figure 6). Low SDs represent little change in yearly correlation values, while high SDs explain large variations in correlations. The highest SDs are 0.6–0.9, occurring over the eastern tip of South America in Brazil, much of the southern portion of Africa, and parts of western and northern Australia. Thus, the areas of high variability generally occur in the tropics between 30°N and 30°S, although mostly in the Southern Hemisphere.
The lowest SDs of 0.1–0.3 occur in equatorial and sub-tropical regions, including parts of northern South America, central Africa, and much of India. Most areas in the mid-latitudes in the Northern Hemisphere have values of 0.5–0.6. There is clearly more variability in the Southern Hemisphere.
Figure 6.
Standard deviations of yearly correlations for Niño 3 SST anomalies and MODIS Tskin over the period of 2001–2010.
Figure 6.
Standard deviations of yearly correlations for Niño 3 SST anomalies and MODIS Tskin over the period of 2001–2010.
3.2. Niño 3 and Tair vs. Tskin
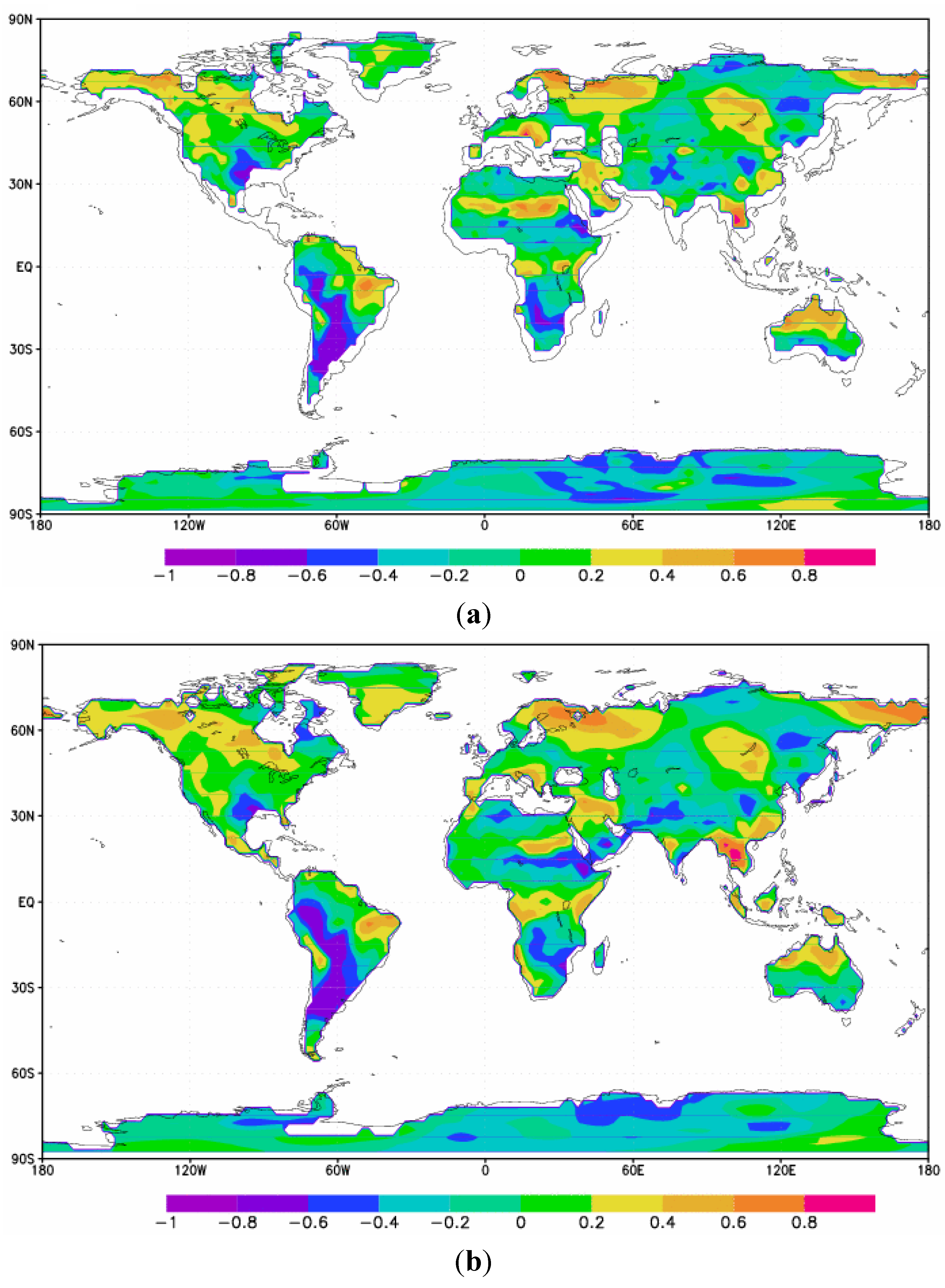
Comparing the lag correlation between January Niño 3 SST anomalies and July NCEP/NCAR T
skin (
Figure 7(a)), to that of MODIS, the patterns are similar, with differences over Africa and Australia. Notable similarities include the negative correlation regions over the South/Southeast USA and South America, and large areas of positive correlations over northwestern Europe and central and eastern Siberia, with high positive values over Eastern Brazil as well. However, the area of negative correlations in South America is much larger in latitudinal area for the NCEP/NCAR data, extending north to the equator, rather than 30°S for the MODIS data. Nevertheless, values are in the same range (−0.4 to −1). The point in eastern Brazil of highest values is shifted west slightly for the NCEP/NCAR data. The large positive region over Northwestern Europe and central and eastern Siberia appear very similar in both plots, both in area and detail. With the exception of the area of negative correlations over the South, most of North America varies between very slightly positive (0 to 0.4) to more strongly positive (0.4 to 0.8) using both sources. Despite the lower resolution of NCEP/NCAR, patterns are generally the same. Finally, there are a few small spots of negative correlations in Europe that agree in location and magnitude: one at about 70°N 90°E, one at 60°N 120°E, and another at 30°N 100°E.
Figure 7.
(a) NCEP/NCAR Reanalysis lag correlation coefficients between January Niño 3 SST anomalies and July NCEP/NCAR Tskin (192 × 94 grid points) over the period of 2001–2010; (b) NCEP/NCAR Reanalysis lag correlation coefficients between January Niño 3 SST anomalies and July NCEP/NCAR Tair (144 × 73 grid points) over the period of 2001–2010.
Figure 7.
(a) NCEP/NCAR Reanalysis lag correlation coefficients between January Niño 3 SST anomalies and July NCEP/NCAR Tskin (192 × 94 grid points) over the period of 2001–2010; (b) NCEP/NCAR Reanalysis lag correlation coefficients between January Niño 3 SST anomalies and July NCEP/NCAR Tair (144 × 73 grid points) over the period of 2001–2010.
Three major differences are observed: first, while the MODIS correlation shows values close to or at zero over Australia, the NCEP/NCAR plot has a distinct region of positive values at the northern end of this area (0.2–0.8), which is completely absent from the other source. Second, the region of strong positive correlation coefficients over Southern Africa from the MODIS data is not present in the NCEP/NCAR plot. Instead, a region of very high correlations is present just to the north. Finally, the belt of very strong negative correlations in Northern Africa from the MODIS data is replaced by a swath of the opposite sign.
A discussion of the correlation between July Niño 3 SST anomalies and January T
skin from NCEP/NCAR Reanalysis Data (
Figure 8(a)), along with its relationship to the same correlation done using MODIS data (
Figure 4(b)) now follows. The major patterns found are similar in both cases; nevertheless, there are some minor differences.
Figure 8.
(a) NCEP/NCAR Reanalysis lag correlation coefficients between July Niño 3 SST anomalies and January NCEP/NCAR Tskin (192 × 94 grid points) over the period of 2001–2010; (b) NCEP/NCAR Reanalysis lag correlation coefficients between July Niño 3 SST anomalies and January NCEP/NCAR Tair (144 × 73 grid points) over the period of 2001–2010.
Figure 8.
(a) NCEP/NCAR Reanalysis lag correlation coefficients between July Niño 3 SST anomalies and January NCEP/NCAR Tskin (192 × 94 grid points) over the period of 2001–2010; (b) NCEP/NCAR Reanalysis lag correlation coefficients between July Niño 3 SST anomalies and January NCEP/NCAR Tair (144 × 73 grid points) over the period of 2001–2010.
The major large scale patterns existing for both cases include the region of high positive correlations over the northwest USA extending into Alaska, and very strong negative correlations over northwestern Europe. However, the swath of very high correlations over the Sahara Desert is not quite as strong; only a couple small regions of values >0.8 are present, with values mostly from 0.4 to 0.8. In Australia, unlike the clear difference that was seen for the January/July correlation, the pattern for July/January is the same, with negative correlations in the northernmost areas of the continent, and slightly positive values over the Eastern Highlands.
The correlation between Niño 3 SST anomalies in January and T
air from the following July shows remarkably similar patterns to those found for T
skin (
Figure 7(b)). Focusing on the large distinctive patterns, the swath of negative correlations in South America appears similar in both size and magnitude, as do the three positive regions over Russia. The spot of negative values over the Southeastern USA is similar, and the general pattern of positive values extending from the northwest USA into Alaska is the same. One difference between the two different types of temperature is that the latitudinal band of positive correlations in Northern Africa around 30°N is not as strong when using T
air. Also, over Greenland, the T
skin analysis has most of the landmass covered in very weak positive correlation (0 to 0.2), while for T
air, it is slightly higher (mostly 0.2 to 0.4). Nonetheless, the overall range of values for this region is small, possibly due to snow and ice buildup, a local mechanism differences between T
air and T
skin.
A comparison of the correlations between July Niño 3 SST anomalies and January T
skin and T
air (
Figure 8(a,b)) from NCEP/NCAR Reanalysis data now follows. First, one important difference exists for the swath of positive values over northern Africa. The analysis done using MODIS T
skin shows a more significant region than NCEP/NCAR T
skin, but the plot using MODIS T
air agrees more with NCEP/NCAR T
skin. In general, most of the large patterns are similar, such as the regions of positive values over northern South America and the strong negative correlation coefficients over western and central Europe, as well as smaller areas.
An important feature present is the belt of strongest negative correlations (<−0.6) over northwestern and north-central Europe, and past research has shown a possible wintertime cooling over northern and central Europe for an ENSO event [
44].
3.3. Uncertainty Analysis
Three major sources of uncertainty remain in this study. The first is related to the satellite data inaccuracies in MODIS Tskin retrieval. The second is related to the statistical approach we specifically use. The third is the limits of the NCEP/NCAR Reanalysis Data.
First, several uncertainties exist for the retrieval of T
skin by MODIS. One source of error is cloud contamination [
50,
56]. Never will MODIS have the ability to measure T
skin under cloudy skies [
50].
The retrieval techniques for retrieving T
skin from satellite measurements for land applications have increased greatly in recent years
. MODIS uses thermal infrared bands to measure T
skin [
50]. It is retrieved from thermal emission at specific wavelengths in which the atmosphere is relatively transparent. However, even in the most transparent regions, atmospheric emissivity and attenuation are not negligible, thus requiring corrections [
29,
56]. The split-window algorithm is the primary algorithm used to generate the MODIS T
skin products [
57]. It was first suggested in the 1970’s [
58] as a way to measure T
skin by using two separate thermal channels
. However, this algorithm still has errors in T
skin because it is dependent on the infrared wavelength used for the measurement, spectral dependence of the emissivity, angle at which the measurement is made, state of the surface (roughness, surface type, moisture, vegetation cover,
etc.), and height of the instrument above the surface [
59]. Overall, there are several factors that can lead to errors for T
skin measurement.
T
skin is also dependent on land cover [
29]. For instance, a desert surface may heat up more rapidly during the day than a forest. Different land covers produce different emissivities. Hence, errors in emissivity can clearly produce errors in T
skin. Also, due to the high land surface heterogeneity, each pixel of the satellite generally contains more than one land type, but MODIS only calculates one T
skin value for this pixel [
50]. In general, emissivity is one of the largest uncertainty sources in SWT [
56]. T
skin will have an error of 0.7 °C per 1% emissivity uncertainty [
59,
60].
Instrument noise and variability are additional sources of error [
60]. Furthermore, the state of the atmosphere above (
i.e., atmospheric moisture distribution, amount, and geometrical distribution of cloud cover and aerosol) also affects the accuracy of T
skin measurement. Clearly, there are many sources of uncertainty that can lead to an incorrect T
skin. Consequently, a wide range of errors may occur when one tries to measure a single accurate T
skin measurement from space [
56].
Finally, all of the mentioned sources of uncertainty are not independent [
59]. For example, emissivity may vary with viewing angle, so an error in viewing angle could change the value of emissivity, further increasing error of T
skin.
Due to the limited duration of data, the statistical approach used leads to uncertainty. The Pearson Product-Moment Correlation Coefficient, used in this study, has three key assumptions associated with it [
61]: (1) the relationship between two variables is linear; (2) both variables constitute interval scales; and (3) both variables are normally distributed. If one or more of these assumptions are not satisfied, the correlation coefficient may not produce true unbiased relationships between two variables. A normal distribution assumes that half of the data population is below the mean and half is above the mean. In addition, outliers can greatly affect the value of the correlation [
62]. In a set of data with a clear linear relationship, one data point outside of the main range can greatly distort the strength of the relationship given by the correlation coefficient. It is important to keep all of these assumptions in mind when evaluating the results of this study. More years of data would help increase the degrees of freedom and lower the value of the correlation coefficient required for a level of 95% confidence. However, MODIS Terra data has only been available since 2001, and although 10 years of data includes multiple El Niño and La Niña events over the period, it may not be adequate for a serious Pearson Product-Moment analysis.
Finally, the third major area of uncertainty lies in the NCEP/NCAR Reanalysis data for T
air and T
skin. First, from 1998–2004, there was disagreement from sea ice analyses whether a certain location was either ocean or land, particularly in the Arctic region [
63]. This resulted in both T
air and T
skin being significantly higher than actual values over parts of the polar regions, potentially affecting the values of
r.
Second, the NCEP/NCAR Reanalysis data has a poor representation of clouds [
64]. Clouds have a large effect on the value of T
skin [
29]; for example, when a cloud passes over a region, a decrease in T
skin occurs, due to a decrease in absorbed downward shortwave radiation at the surface. Thus, this particular representation by NCEP/NCAR Reanalysis data could produce errors in T
skin.
In addition, soil moisture can cause cooler daytime temperatures through surface evaporation. However, the NCEP/NCAR Reanalysis data omits this important variable. Because of this, along with the poor depiction of clouds, the surface-heat budget has serious errors [
64]. Clouds and soil moisture are critical to the surface-heat budget for correct surface temperatures, and hence the reason for inaccuracies. Overall, interpretation of T
skin from NCEP/NCAR Reanalysis data is complex [
65].