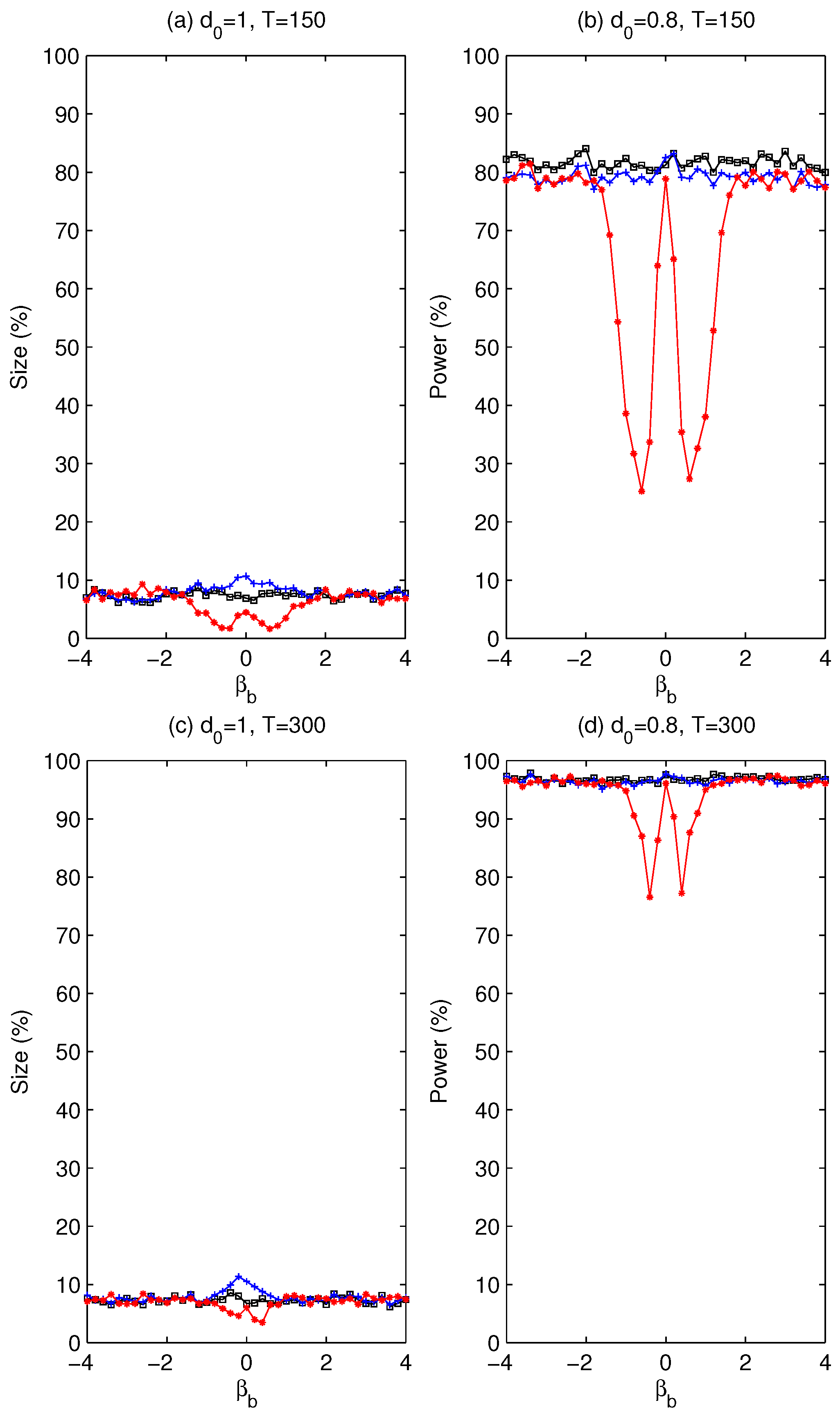
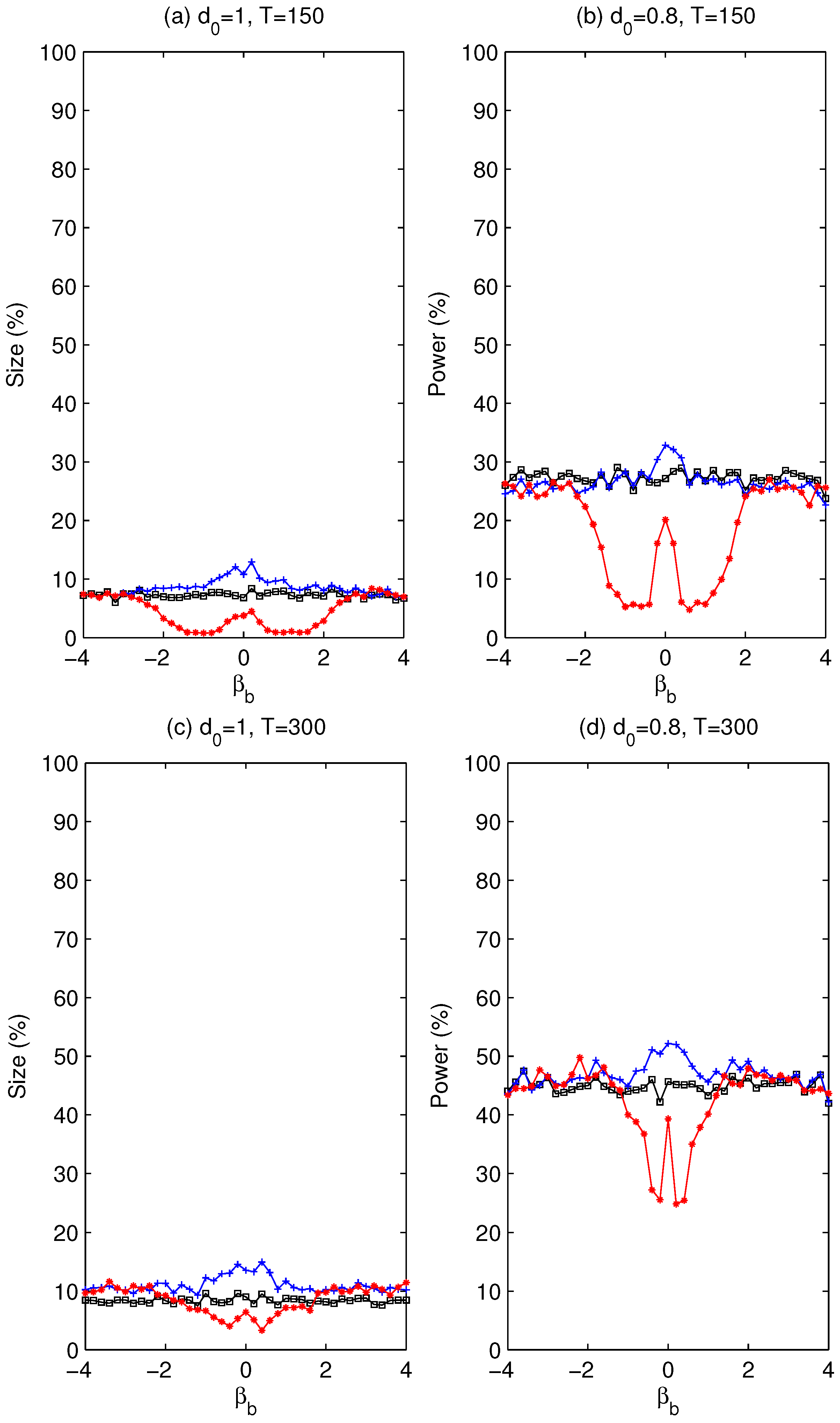
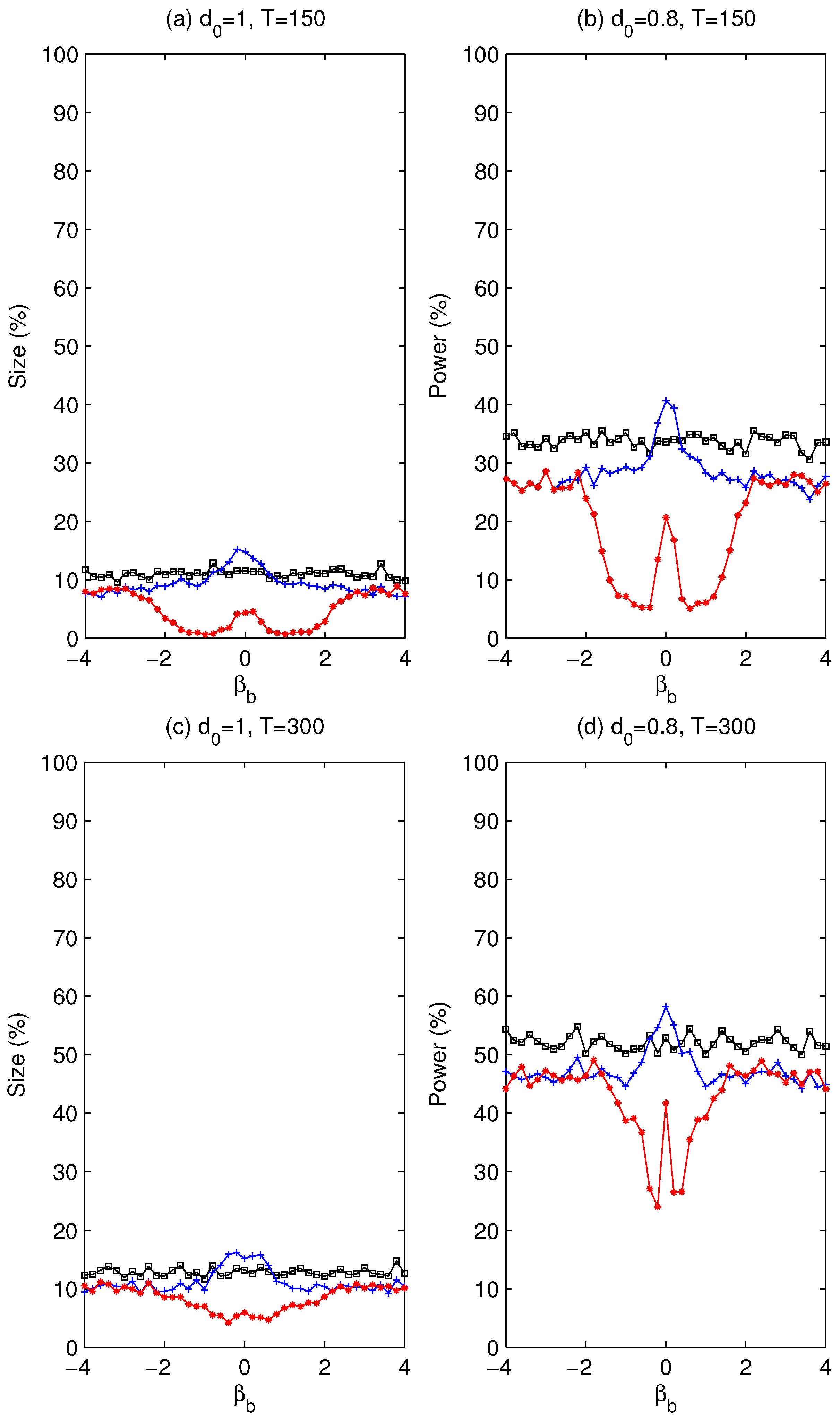
3.2. Slope and Intercept Change in Trending Series
We now introduce a deterministic time trend in the models. We follow the notation in Kim and Perron (2009) [
10] (henceforth KP) from which we will use some relevant results. The DGPs are specified as
Model A0: (Deterministic time trend without a structural change)
Model A2: (Joint broken trend)
where
is a dummy variable for a slope change in trend given by
Model A3: (Locally disjoint broken trend)
Following KP, we can rewrite Models A1–A3 as follows:
where
,
,
In matrix notation, the models defined previously can be specified as
, where
,
,
, and
.
Consider first Model A0, where no structural change is allowed. By taking first differences, we can rewrite (
5) as follows:
The ordinary least squares (OLS) estimate of
is
, which is consistent under both
and
.
3 We define
, the OLS residuals from the regression model (
8).
Theorem 2 (Linear Trend). Under Assumption 1, suppose that the process is generated under the null hypothesis of (
5).
Consider the Lagrange Multiplier test defined by:Under the null hypothesis , it holds that as , . In what follows, the aim is to devise Lagrange Multiplier tests allowing for a slope change in trend with or without a concurrent level shift. The following assumption is essential to that effect.
Assumption 2. and for some .
Assumption 2 ensures that there is a single slope change in trend, and that the pre- and post-break samples are not asymptotically negligible, which is a standard assumption needed to derive useful asymptotic results. Model A1 (level shift only) will be revisited later.
The break date can be estimated by using a global least-squares criterion:
where
is the matrix that projects on the range space of
; i.e.,
and
,
. Note that
is the same as
, except
is replaced with a generic break date
. Perron and Zhu (2005) [
8] (henceforth, PZ) established the consistency, rate of convergence, and limiting distribution of parameter estimates when the error is an
process. With
constructed using the estimate
, the OLS estimate of
ϕ is
, and the resulting sum of squared residuals is, for an estimated break fraction
(the subscript
s refers to the fact that we consider a static regression; a dynamic regression with lagged dependent variables will be considered later):
where
is the projection matrix associated with
. The rate of convergence of
for Models A2 and A3 is
with
errors (see Theorem 3 in PZ). Chang and Perron (2016) [
33] derived the consistency and rate of convergence of
when the noise component is a fractional process with the differencing parameter
. Specifically, for Models A2 and A3,
if
and
. With the consistent estimates
, we can construct the detrended process
, and the Lagrange Multiplier test statistic
is given by
The convergence rate of the estimate
is not fast enough to guarantee that
has the standard normal limit under
. KP faced a similar issue in dealing with unit root tests. They introduced a heuristic explanation of the issue involved, which we briefly review. Let
denote an estimate of the break fraction such that
for some
. The detrended series
is given by
where
and
are matrices stacking
and
, respectively, and the idempotent matrix
. It is obvious that
only if the true break date is used in
. In finite samples,
in general; thereby,
will not be zero. It turns out that a fast rate of convergence for the estimate of the break date is needed for the effect of
on the Lagrange Multiplier test to become negligible asymptotically. The following proposition provides a sufficient condition under which
under
.
Proposition 1. Suppose that the process is generated under the null hypothesis of Model A2 or A3, and that Assumptions 1 and 2 hold. Then, it holds that, as , if .
Proposition 1 implies that the estimate of the break fraction should converge at a rate faster than
. As shown above,
does not satisfy this condition. Hence, we need to consider alternative ways to accelerate the rate of convergence of the estimate of the break fraction. KP suggested two possible approaches. The first is based on minimizing the sum of squared residuals (SSR) of a dynamic regression model. This method is similar to that in Hatanaka and Yamada (1999) [
34]. The relevant dynamic regressions are specified as follows:
where
for
and 0 otherwise. Under the null hypothesis, we obtain an estimate of the break fraction
which has a faster rate of convergence, such that
for Models A2 and A3 (see Proposition 1 in KP). Let
denote the Lagrange Multiplier test statistic with
replacing
. It is worth noting that, as discussed by Hatanaka and Yamada (1999) [
34] and KP, the estimate
has a negative bias in finite samples, especially for Model A3. As we shall see, this will affect the finite sample properties of the tests.
The second approach is to use a trimmed data set using a window whose length depends on the sample size and which contains the estimated break date. The trimmed series then consists of the original one with the data points in the window excluded. KP showed that the rate of convergence of
can be increased with the trimmed data set. Suppose that the estimate of the break fraction satisfies
for some
, and the trimming window has length
with
,
, and
. With this specification, the length of the window is negligible in the limit compared to the sample size
T, but is still large enough to include the true break date asymptotically. Following KP’s suggestion, one proceeds as follows:
Remark 2. If the window contains either end of the data, then the process turns out to be Model A0 (no structural break), and the statistic in Theorem 2 should be applied to the trimmed data .
The trimmed process will satisfy the properties of Model A2 regardless of the specification of the original data , which implies that we can use a common limit distribution. The following proposition states the limiting distribution of the Lagrange Multiplier test based on the trimmed data, which is the same as would be obtained if the break date was known in Model A2.
Proposition 2. Suppose that the process is generated under the null hypothesis of Model A2 or A3, and that Assumptions 1 and 2 hold. Then, it holds that as , .
As shown in KP, under the null hypothesis of a unit root, the estimate of the break fraction converges in probability to the true break fraction at some rate greater than T. Hence, the sufficient condition in Proposition 1 is satisfied, so that the proof of Proposition 2 is trivial and omitted.
In concluding this section, we consider the case where there is a change in mean; that is, , as in Models A1 and A3. In Model A1, we assume that there is a level shift only; that is, and . Under the null hypothesis, a stochastic trend generated by the error process tends to dominate a level shift. Hence, we cannot estimate the break fraction consistently, because the magnitude of the level shift is asymptotically negligible. In finite samples, we can ignore the level shift if the magnitude of the break is small. Then, Model A1 can be treated as Model A0, and we can follow the testing procedure pertaining to Theorem 2. However, a loss of power is inevitable if a large change in mean is ignored.
On the other hand, the level shift can be specified as an increasing function of the sample size; i.e.,
for some
and
. As addressed in Harvey et al. (2001) [
35], PZ, and KP, this specification provides better approximations of the properties of the tests in finite samples when the level shifts are not very small. The models with
are labeled as Models A1b and A3b, respectively.
Proposition 3. Suppose that the process is generated under the null hypothesis of Model A1b or A3b. Then, diverges as .
Although the rate of convergence of the estimate of the break fraction is faster than in the case of a change in slope (see Proposition 7 in KP), Proposition 3 states that the LM tests cannot obtain the standard normal limiting distribution. Hence, the LM test
, using the critical values from the standard normal distribution, suffers from some liberal size distortions, even when
is large.
4 3.3. Using a Pre-Test for a Break in Slope
The results of Theorem 2 and Proposition 2 show that the limit distribution of the test is the same whether there is a break in slope introduced as a regressor or not, even when the DGP specifies that no break is present. Hence, unlike the case of testing for a unit root as in KP, theoretically there is no need to carry a pre-test to improve the power of the test. However, Chang and Perron (2016) [
33] considered Models A2 and A3 with fractionally integrated errors and showed that the so-called spurious break issue occurs with the order of fractional integration
. This extended the results on Nunes et al. (1995) [
36], who considered the unit root case. This means that under both the null and alternative hypotheses, if a break in slope is not present and one is allowed in the regression, the fitted model will with large probability suggests the presence of a break. This could have an effect on both the size and power of the test. On one hand, the slope change regressor may induce added liberal size distortions in finite samples because of the overfit. On the other hand, since when no break exists in the DGP it is a superfluous regressor, power maybe be reduced. Hence, it may be the case that in finite samples it is beneficial to use a pre-test for a change in slope and try to choose between models (
5) and (
7). Since a test for a change in mean will be inconsistent, there is no point in trying to distinguish between models (
5) and (
6) or between model (
4) and the corresponding one without the change in mean.
Iacone et al. (2013) [
37] suggested a sup-Wald type test (
) for Model A2. In particular, it is robust to any order of fractional integration
located in an interval
excluding the boundary case 0.5. More precisely, given their recommended choice for the bandwidth when constructing the local Whittle estimate of
, their test is consistent for values of
in the interval
, though we believe the proof can be modified to allow the interval
. It follows the generalized least squares approach to construct the test statistic for a structural change in trend by taking
-differences from the data. To make the test feasible, the fully extended local whittle (FELW) estimator
of Abadir (2007) [
38] is considered. While the FELW estimator is constructed under the null hypothesis of no structural change, Iacone et al. (2013) [
37] showed that it also satisfies the necessary condition for consistency, even with a local break in trend. Since the true break date is unknown a priori, the final statistic
uses the
sup functional of Andrews (1993) [
39] across all admissible break dates. This test is asymptotically size controlled for all
’s in the prescribed range. Using this pre-test, we can then define the alternative estimate of the break fraction
, where
τ is the critical value for the
test with a nominal size
. Given that
is a consistent test,
if
is a consistent estimate of
. If there is no break in the DGP, we can expect that
of the estimates
’s are nonzero. In order to obtain a consistent estimate of
under the null of no structural break, we assume that the critical value
τ is a function of the sample size
T. Since
with a local break, let
for
. This specification introduced in KP is useful because it does not have any effect on the consistency of the test
and does guarantee that
when no break is present. Hence, based on the consistency of
, it is recommended to use
if
and
if
. The LM test statistics with the pre-test are denoted by
,
, and
. Whether using a pre-test is beneficial will be assessed later via simulation experiments about the size and power of the tests.