iMASKO: A Genetic Algorithm Based Optimization Framework for Wireless Sensor Networks
Abstract
:1. Introduction
2. GA-Based Works on WSNs
2.1. Introduction of GA
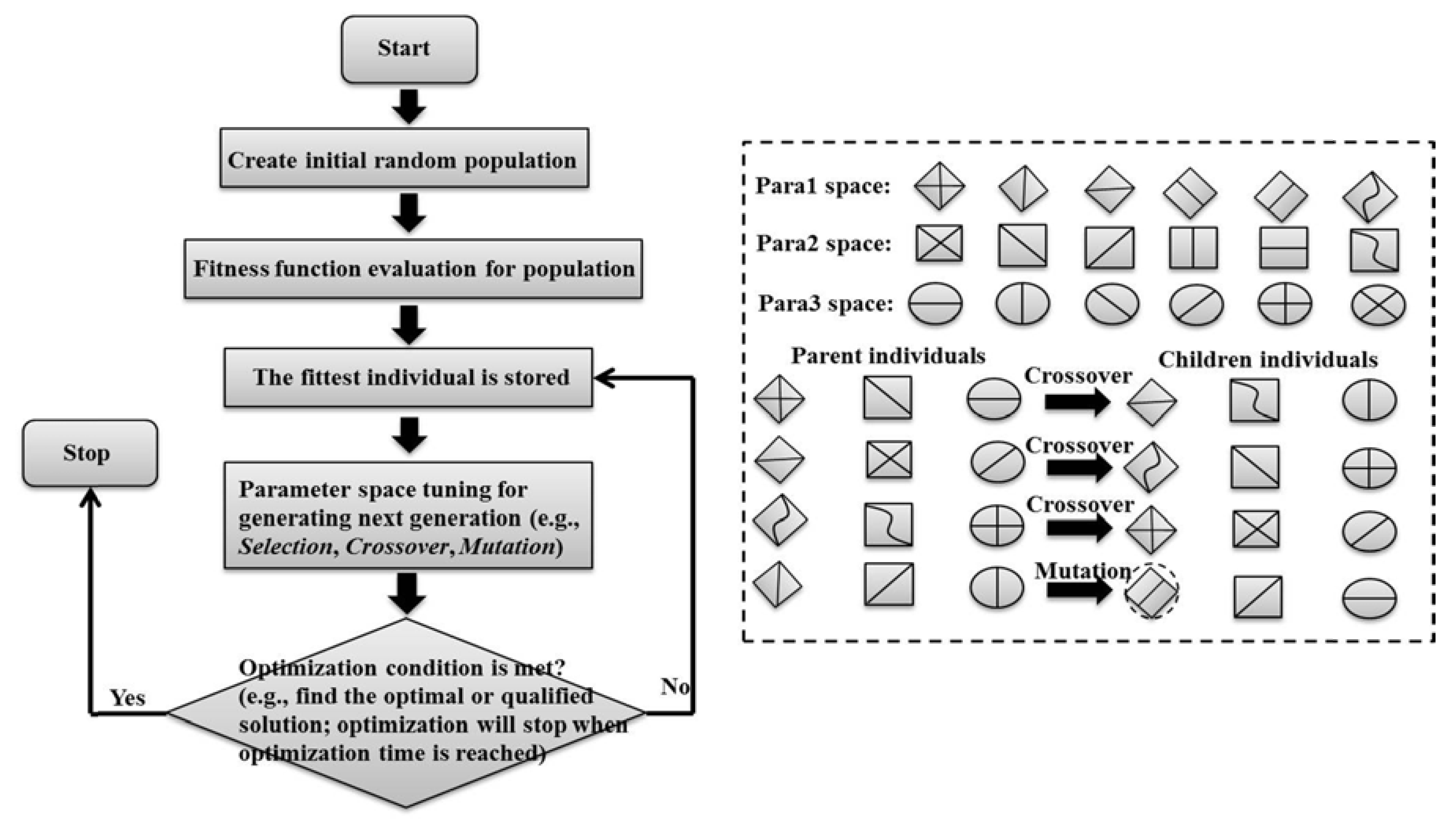
| Advantages of GAs |
|---|
| √ Parallelism, efficiency, reliability, easily modified for different problems |
| √ Large and wide solution space searching ability |
| √ Non-knowledge based optimization process |
| √ Use of fitness function for evaluation |
| √ Easy to discover global optimum, avoid trapping in local optima |
| √ Capable of multi-objective optimization and can return a suite of potential solutions |
| √ Good choice for large-scale/wide variety optimization problems |
2.2. GA-Based Optimization in WSNs
3. Motivation of Proposing the Optimization Framework
4. Design and Implementation of the Optimization Framework
4.1. Architecture of the Framework (iMASKO)
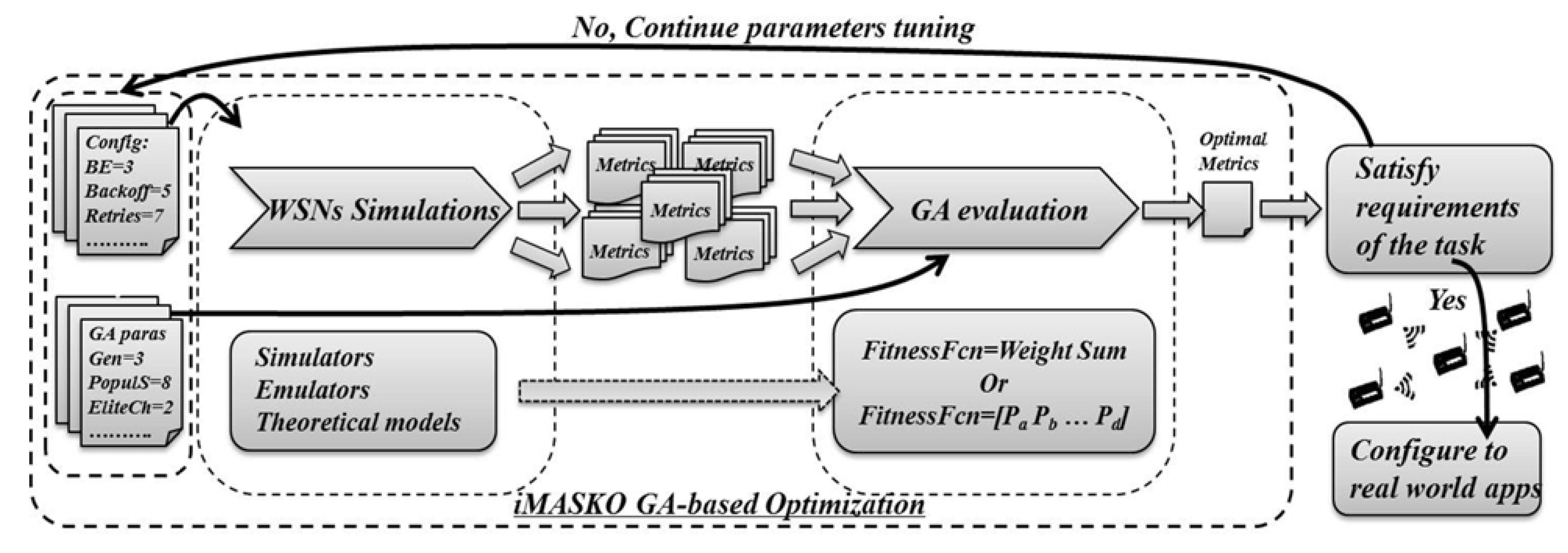
| iMASKO Optimization Process |
|---|
| Input initial solution: X, P ## X-parameters space, P-performance space |
| 1: assume that: Xbest ← X, Pbest ← P |
| ## Starting optimization until condition met |
| 2: while stop condition not met then do #condition (e.g., max generation exceeded) |
| 3: Xnext ← generate(X) #GA operations: selection, crossover, mutation |
| ## Evaluations are proceeded in parallel |
| 4: Pnext ← evaluate(Xnext) #evaluate results from SystemC simulations |
| 5: △cost ← compare(Pnext, P) #△cost = Pnext − P |
| 5: if△cost ≤ 0 |
| 6: X ← Xnext, P ← Pnext |
| 7: if (P ≤Pbest) |
| 8: Xbest ← X, Pbest ← P |
| 9: end if |
| 10: end if |
| 11: end while ## when condition is met |
| 12: return/output: Xbest, Pbest |
4.2. Performance Metrics
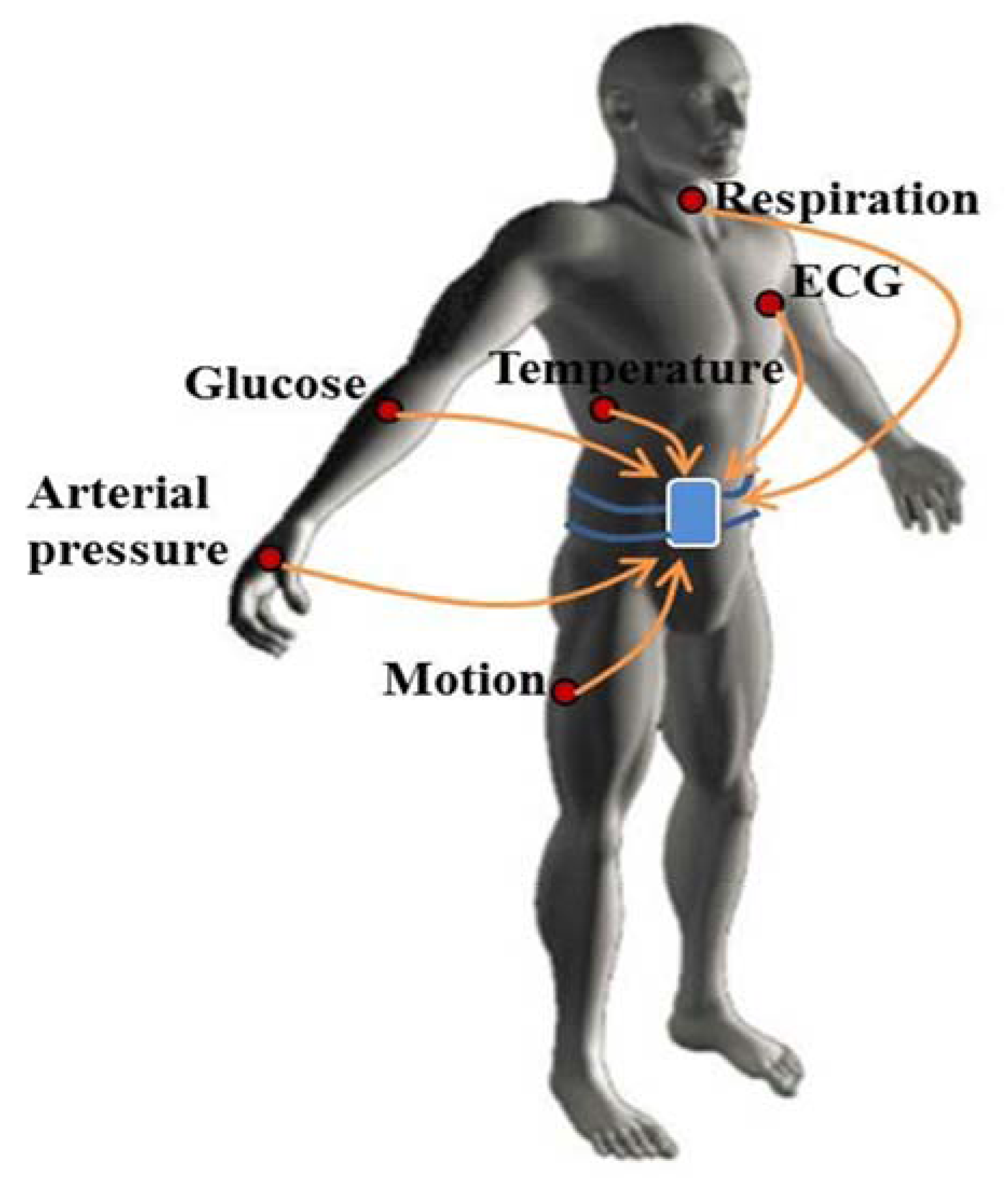
- Energy Consumption: in most application scenarios, the sensor network must run for a long period of time to fulfill the given task without human interference (e.g., for battery recharge), thus, energy saving has always been a significant concern for extending the lifetime of the sensor network/node. Otherwise, the network will not remain operational until the required task is completed. As the energy consumption of the microcontroller (μCEnergy) and transceiver (TraEnergy) are the most power consuming parts, most works focus on saving the energy from these two parts at both the hardware and software levels. In hardware, ultra low power devices are used, especially in medical/health-care applications [2,35,36]. In software, as mentioned in Section 1, various kinds of energy-efficient MAC protocols, duty-cycling based communication strategies and data aggregation routings are proposed and measured. All kinds of efforts are made to achieve an energy-aware sensor network, and according to different requirements, energy performance could be measured and expressed in many ways (e.g., power consumption-mW, µW, lifetime-days, months, years). A taxonomy of energy related performance metrics is summarized in [37].
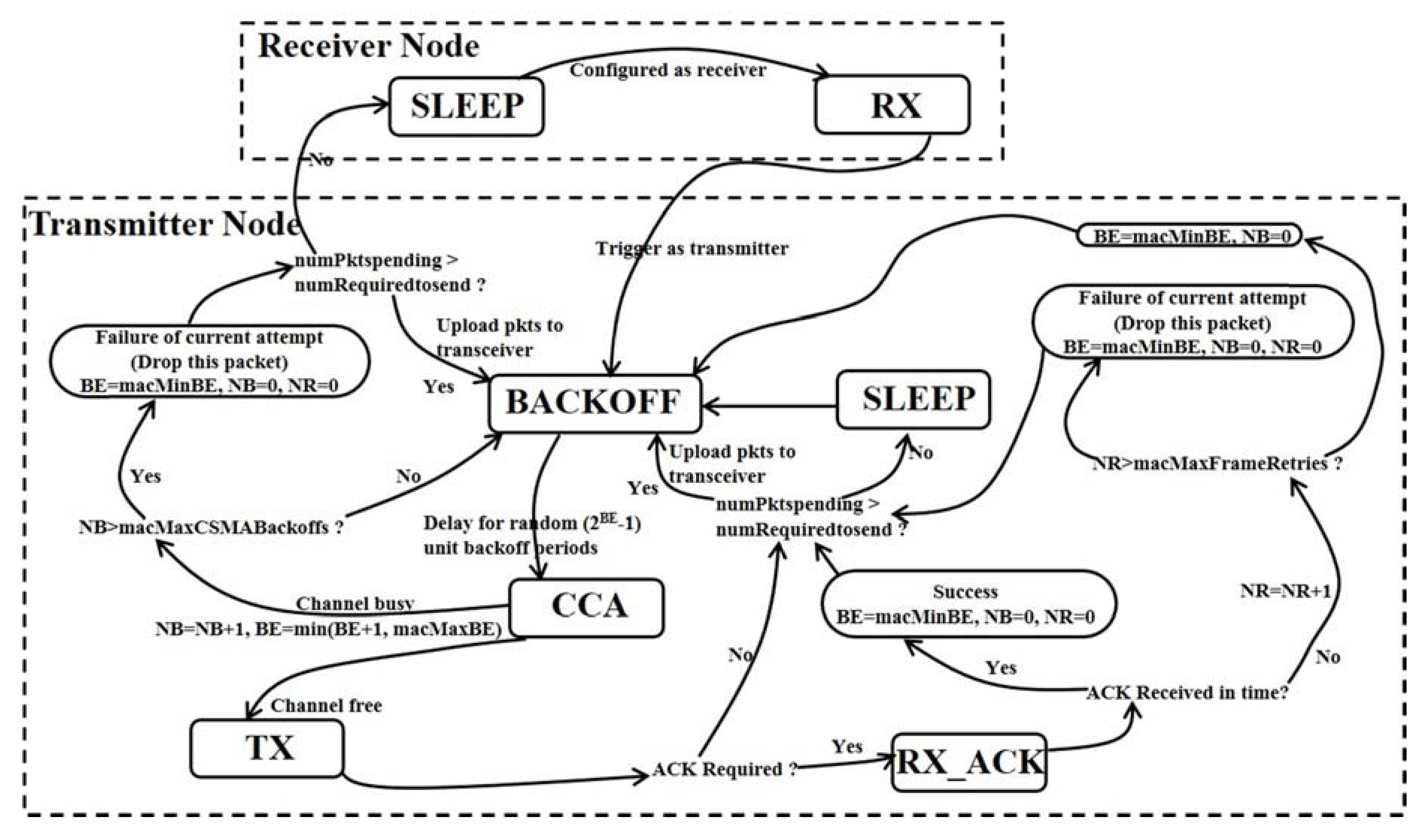
- Network Reliability: for this metric, packet loss probability (PktLossPro) or packet delivery rate (PDR) are often adopted as the evaluation standard. PDR here is defined as the ratio of the number of packets successfully received (successful receiving of ACK) to the total number of packets that are sensed for transmitting. PktLossPro is the probability that a packet sensed for sending will be dropped or fail to be transmitted (PktLossPro=1 − PDR). If a MAC layer algorithm is used, such as the unslotted/slotted CSMA/CA algorithm of IEEE 802.15.4, the packet loss can take place due to the packet drop in channel access failures (PktCAFs) and collision failures (PktCFs). PktCAFs denotes that a packet encounters (1 + macMaxCSMABackoffs) consecutive CCA failures, while PktCFs occurs when it suffers (1 + macMaxFrameBackoffs) times of collision failures, which take place during the packet transmission or transmission of the ACK frame. Besides, the loss of packet can also be caused by packet overflow (PktOverflw), which means that before starting to transmit the pending data packet (pending in MCU), a new data packet is sensed and replaces the pending packet. Therefore, evaluations can be made in detail with PktCAFs, PktCFs, and PktOverflw in addition to PktLossPro and PDR.
- Network Delay: packet latency is usually used to evaluate network delay. Packet latency can be divided into three sub-types: successful packet latency (SucPktLatency), all packet latency (AllPktLatency), and data packet latency (DataPktLatency). SucPktLatency is defined as the time interval between the instant at which the data packet is sensed and the instant at which is successfully transmitted by receiving its ACK frame. Compared to SucPktLatency, AllPktLatency takes both successful packet transmission and failure packet transmission (caused by PktCAFs or PktCFs) into consideration. DataPktLatency is calculated as the time interval from sensing the data packet to the receipt of this packet by the sink node (or coordinator).
4.3. Cost Function (Weighted Sum)
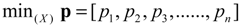
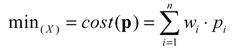
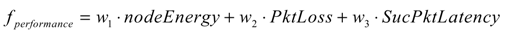

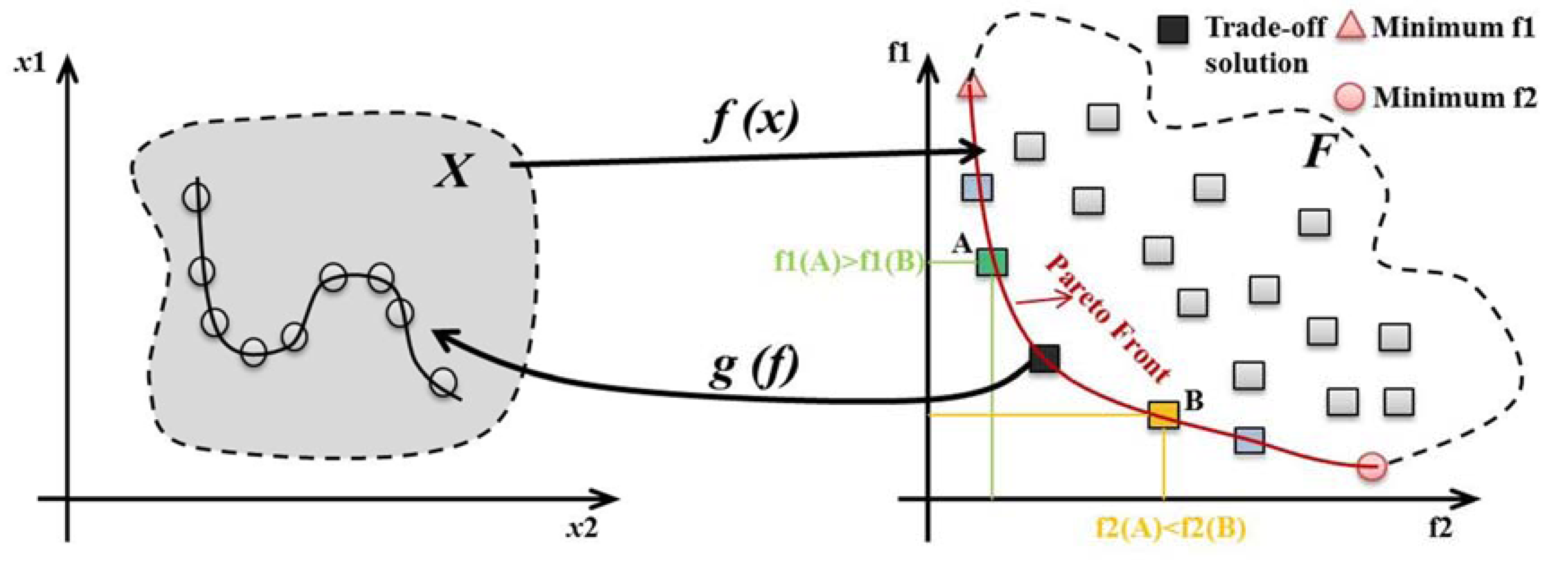
4.4. Multiobjective GA for Pareto-Front Optimization
 , F-solution space), which can be described as a solution f = [f1…fn] dominating
, F-solution space), which can be described as a solution f = [f1…fn] dominating  . This condition is true if each parameter of f is not greater than the corresponding parameter in f* and there is at least one parameter that is less, i.e.,
. This condition is true if each parameter of f is not greater than the corresponding parameter in f* and there is at least one parameter that is less, i.e.,  for each i and
for each i and  for some i. This is presented as
for some i. This is presented as  to mean f dominates f*, and the total description in mathematics can be given as follows:
to mean f dominates f*, and the total description in mathematics can be given as follows:
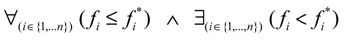

- Platform selection: this part is to load the mote platforms. Executable files of SystemC simulation are placed under the same folder, which contains several mote platforms implemented in our SystemC simulation environment (including iHop@Node [40], Telos [41], MICAz, MICA2). The option -n <platform> is adopted to select the specific mote platform for the optimization experiments. An example command line can be given as: > ./imasko -n Telos.
- Simulation parameters config: this part is used to set the corresponding parameters of SystemC simulation, such as sample rate, sample times, CSMA/CA algorithm, output power, receiver sensitivity, and independent simulation run times. The corresponding options in iMASKO for the above parameter settings are -sr <samplerate>, -st <simulationtimes>, -alg <algorithm>, -op <outputpwr>, -rs <sensitivity> and -r <runs>. Among the options, samplerate, simulationtimes, algorithm (0-unslotted, 1-slotted), outputpwr, sensitivity, and runs are all integers. An example command line would be: > ./imasko -sr 10 -st 100 -alg 0 -op 0 -rs -95 -r 50, which means that the sample rate is set as 10 Hz, the simulation runs for 100 ms, unslotted CSMA/CA is selected, output power is set as 0 dBm, receiver sensitivity is configured as −95 dBm and finally 50 independent simulations (different seeds) are required for average results. Default values will be used if the corresponding parameters are not set in the command line.
- GA config: GA related parameters are configured in this part. Parameter space under GA optimization can be configured by setting their upper and lower boundaries. In the experiment of this work, the options -lbminBE <minBElb>, -ubminBE <minBEub>, -lbmaxBE <maxBElb>, -ubmaxBE <maxBEub>, -lbBackoff <Backofflb>, -ubBackoff<Backoffub>, -lbRetries<Retrieslb> and -ubRetries<Retriesub> are used to specify the lower and upper bounds of the unslotted algorithm’s four parameters, which are macMinBE, macMaxBE, macMaxCSMABackoffs and macMaxFrameRetries. These boundary values are used to limit the parameter space range during the whole optimization process, and they can also be employed to initialize the PopInitRange parameter in GA at the very beginning of the optimization. In addition, other commonly used GA parameters are also configurable by command lines, the provided parameters include GA’s PopulationSize, Generations, CrossoverFraction, CreationFcn, SelectionFcn, MutationFcn, CrossoverFcn. The corresponding options in iMASKO are -ps <populationsize>, -g <generations>, -cf <crossoverfraction>, -creatf <@creationfunction>, -selectf <@selectionfunction>, -mutf <@mutationfunction>, and -crossf <@crossoverfunction>. Among these options, populationsize and generations are integers, crossoverfraction is a float number within the range 0 through 1. Finally, creationfunction, selectionfunction, mutationfunction, and crossoverfunction are the names of the functions which are provided by the GA library (e.g., @gacreationuniform, @selectionstochunif, @mutationgaussian, @crossoverscattered) or the user custom functions. Likewise, if the parameters are not set via the command line, default values will be used. An example command line can be: > ./imasko -ps 20 -g 100 -cf 0.8 -mutf @mutationgaussian.
- Seeds Generator: due to the quad-core CPUs of the server, each simulation actually consists of four parallel and independent (independent seeds) runs for average results, so the use of -s1 <seeds1>, -s2 <seeds2>, -s3 <seeds3> and -s4 <seeds5> (integers for seeds1, seeds2, seeds3, and seeds4) can specify different seeds for the four independent runs, and all the generated seeds can be stored and used in the optimization process to guarantee reproducibility of results
- Result Saving: the use of -save <filename> can save the final result file with the user defined file name and with any suffix. As an example: > ./imasko -save GAresults.log.
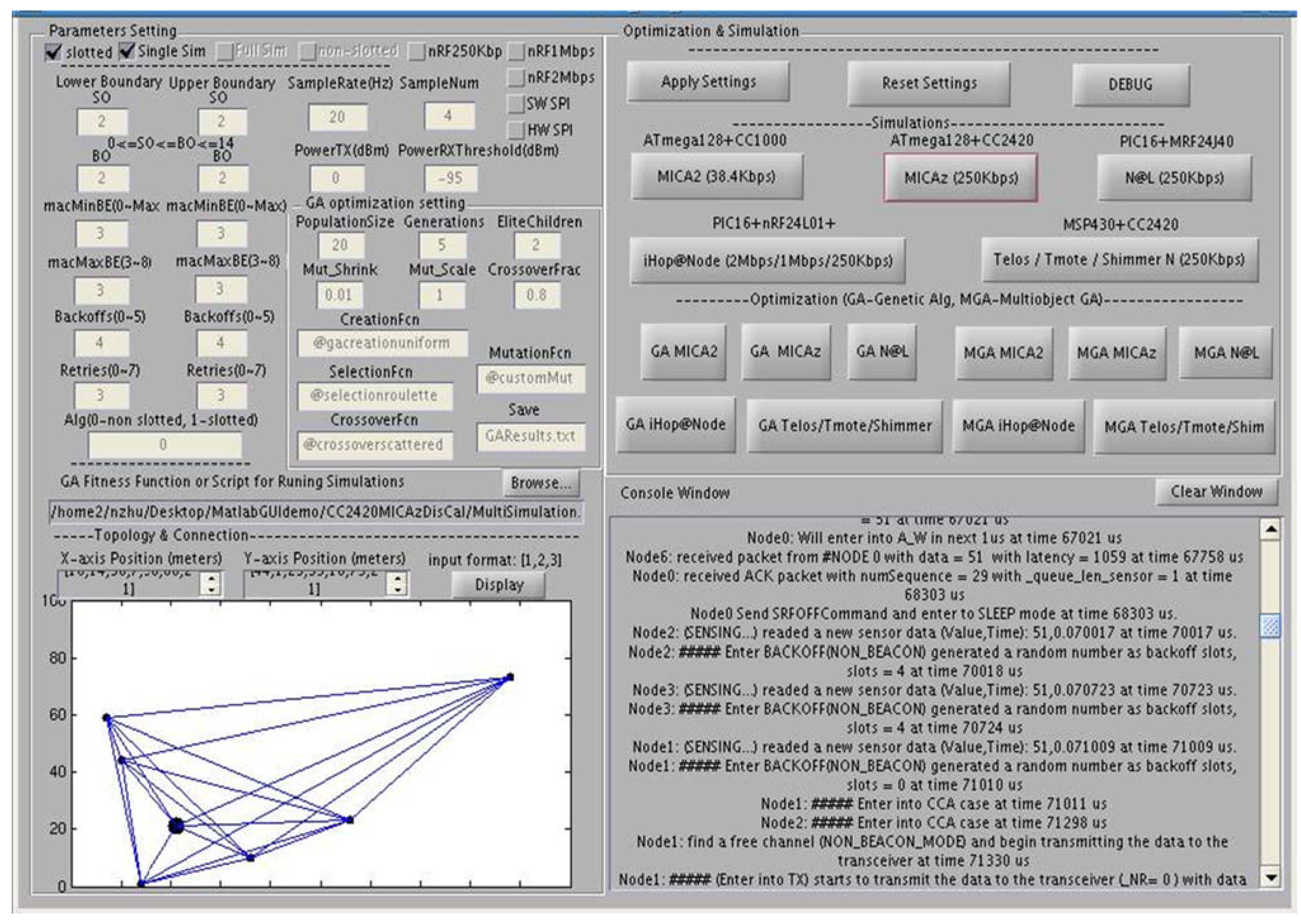
4.6. Generic Use of iMASKO
5. Experimental Results
5.1. Part I—Results of Weighted Sum Optimization
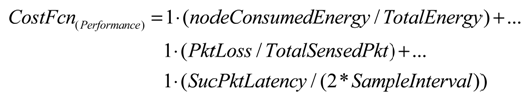
| Fixed macMaxBE | Parameter Combinations | Weight Sum Range | Simulation Time (min) |
|---|---|---|---|
| 3 | 192 | 0.504349 ~ 0.812070 | 34.397 |
| 4 | 240 | 0.498976 ~ 0.982988 | 43.622 |
| 5 | 288 | 0.497637 ~ 1.292583 | 53.144 |
| 6 | 336 | 0.507912 ~ 1.747466 | 61.901 |
| 7 | 384 | 0.507912 ~ 1.834899 | 69.886 |
| 8 | 432 | 0.507912 ~ 1.935943 | 76.702 |
| Total | 1,872 | 0.497637 ~ 1.935943 | 339 |
| Full Weighted Sum Range: 0.497637-----------------------------------------> 1.935943 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Area | 0.5% | 1% | 2% | 3% | 4% | 5% | 6% | 7% | 8% |
| Value | 0.5048 | 0.5120 | 0.5264 | 0.5408 | 0.5552 | 0.5696 | 0.5839 | 0.5983 | 0.6127 |
| Popul Size (Opt time) | The following statistics indicate the probabilities that optimization results fall within each specific area (Average optimization time for 5/10/20/30 are shown next to the population size) | ||||||||
| 5 (1.28 min) | 2% | 19% | 45% | 74% | 85% | 91% | 94% | 97% | 98% |
| 10 (2.74 min) | 3% | 35% | 72% | 94% | 100% | 100% | 100% | 100% | 100% |
| 20 (5.25 min) | 5% | 63% | 94% | 100% | 100% | 100% | 100% | 100% | 100% |
| 30 (8.00 min) | 7% | 76% | 99% | 100% | 100% | 100% | 100% | 100% | 100% |
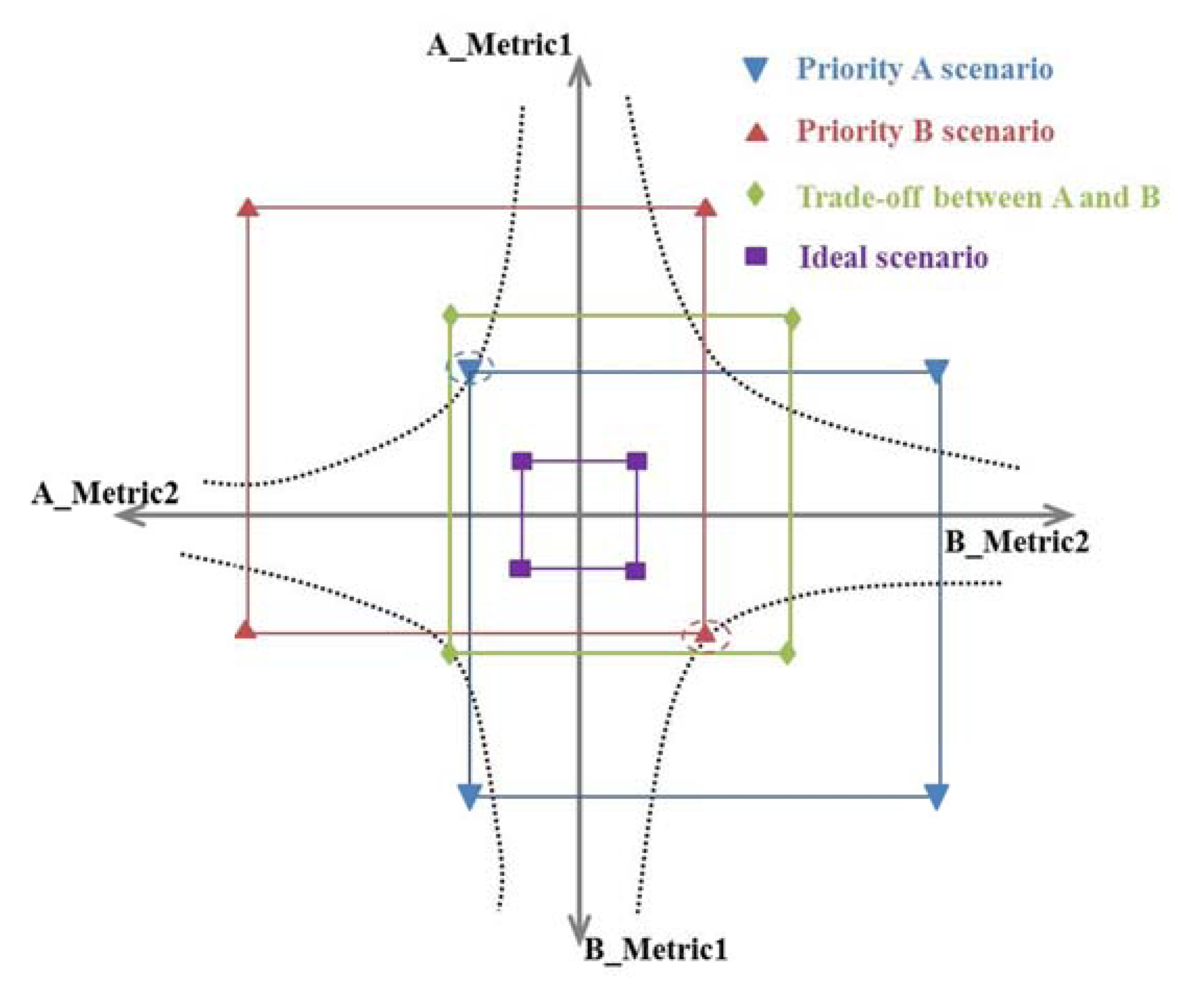
5.2. Part II—Results of Multi-Scenario and Multi-Objective Optimization
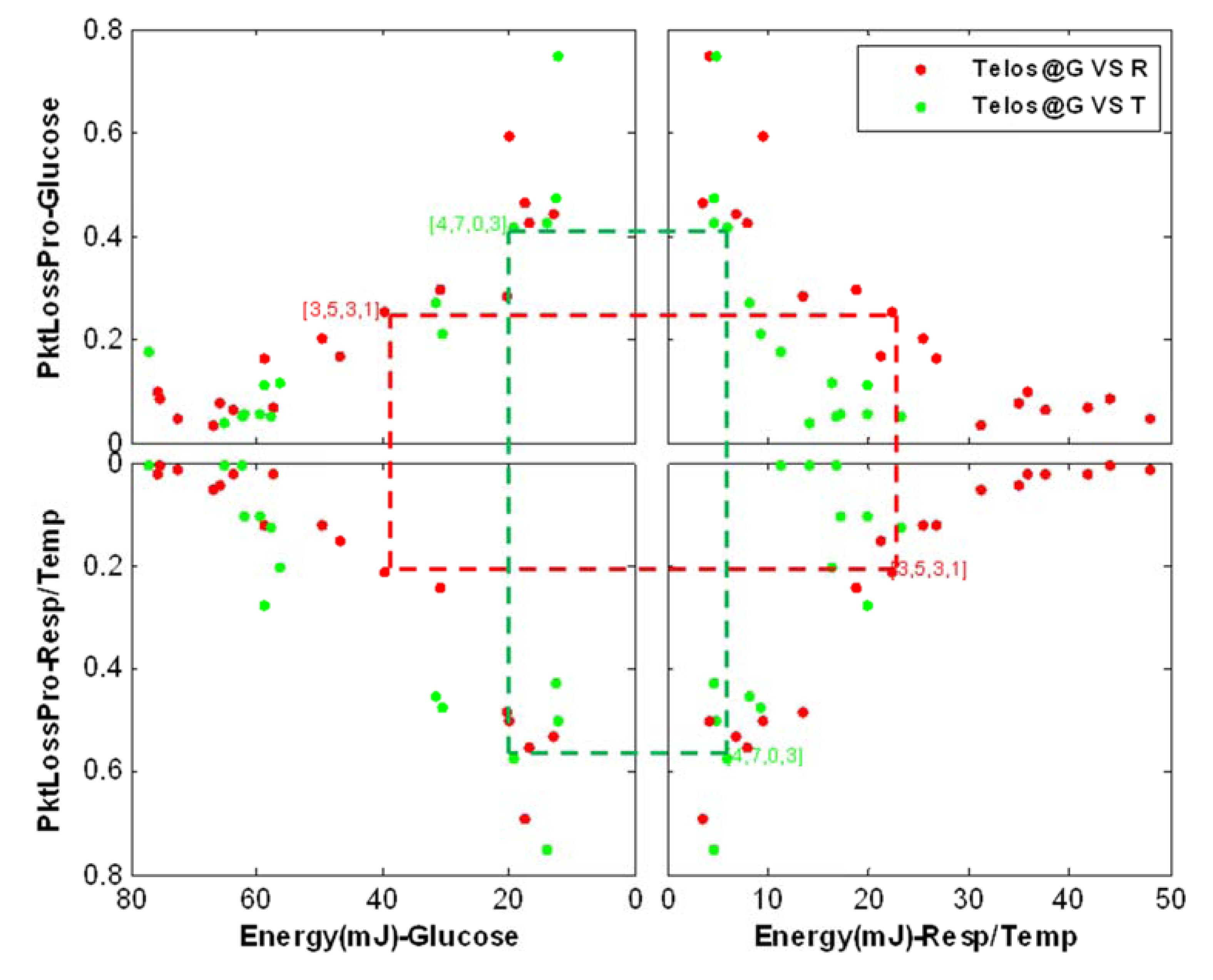
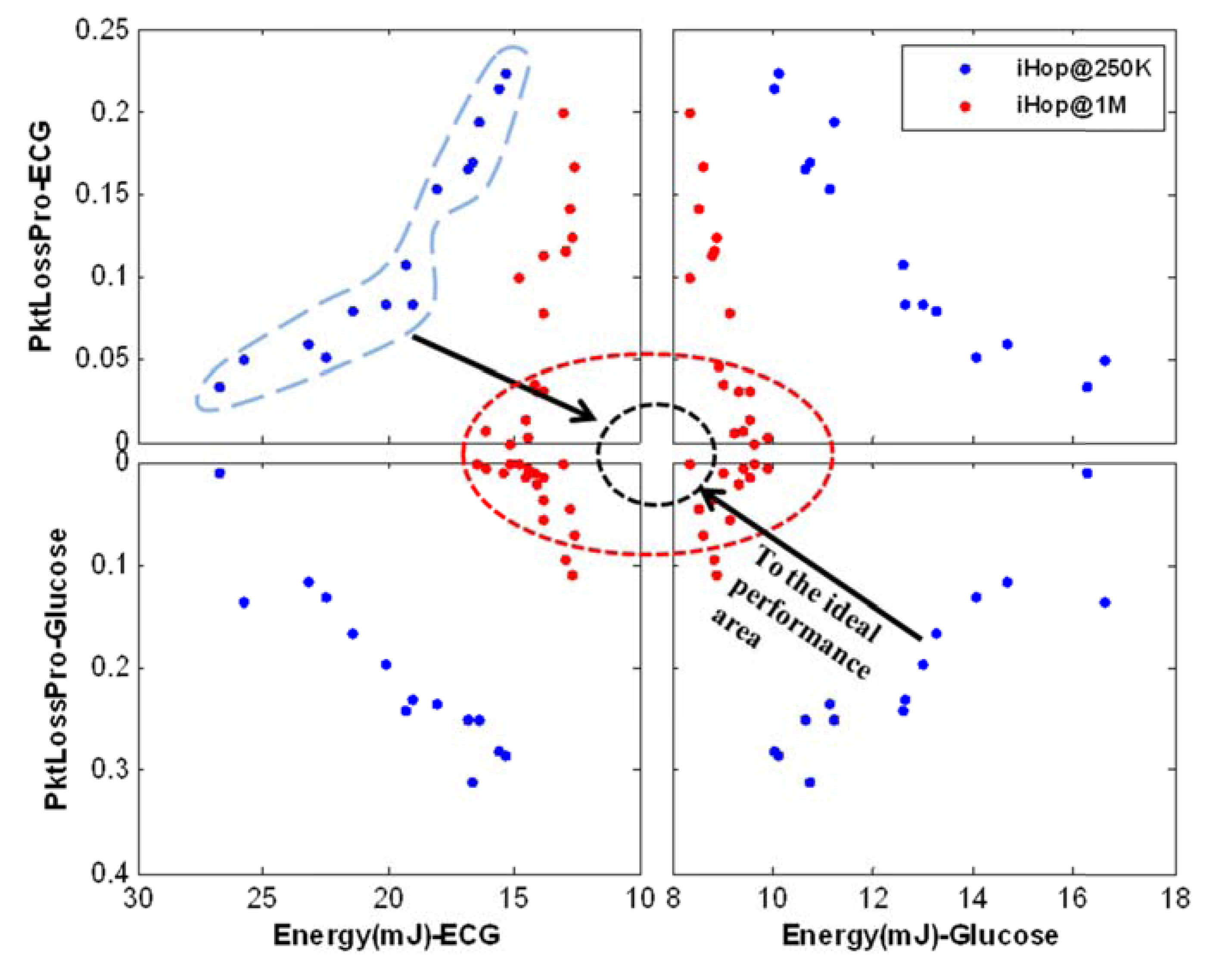
6. Conclusion and Future Work
Conflicts of Interest
References
- Zhu, N.H.; O’Connor, I. Performance Evaluations of Unslotted CSMA/CA Algorithm at High Data Rate WSNs Scenario. In Proceeding of the 9th IEEE International Wireless Communications and Mobile Computing Conference (IWCMC 2013), Cagliari, Italy, 1–5 July 2013; pp. 406–411.
- Mackensen, E.; Lai, M.; Wendt, T.M. Bluetooth Low Energy (BLE) based wireless sensors. IEEE Sens. 2012, 1–4. [Google Scholar]
- Zhang, J.Y.; Orlik, P.V.; Sahinoglu, Z.; Molisch, A.F.; Kinney, P. UWB systems for wireless sensor networks. Proc. IEEE 2009, 97, 313–331. [Google Scholar] [CrossRef]
- Buratti, C.; Conti, A.; Dardari, D.; Verdone, R. An overview on wireless sensor networks technology and evolution. Sensors 2009, 9, 6869–6896. [Google Scholar] [CrossRef]
- Castagnetti, A.; Pegatoquet, A.; Belleudy, C.; Auguin, M. A framework for modeling and simulating energy harvesting WSN nodes with efficient power management policies. EURASIP J. Embed. Sys. 2012, 8, 1–20. [Google Scholar]
- Sonavane, S.S.; Kumar, V.; Patil, B.P. MSP430 and nRF24L01 based wireless sensor network design with adaptive power control. ICGST CNIR J. 2009, 8, 11–15. [Google Scholar]
- Pouwelse, J.; Langendoen, K.; Sips, H. Dynamic Voltage Scaling on a Low-Power Microprocessor. In Proceeding of the 7th Annual International Conference on Mobile Computing and Networking, Rome, Italy, 16–21 July 2001; pp. 251–259.
- Benini, L.; Bogliolo, A.; de Micheli, G. A survey of design techniques for system-level dynamic power management. IEEE Trans. Large Scale Integr. Sys. 2000, 8, 299–316. [Google Scholar] [CrossRef]
- Ye, W.; Heidemann, J.; Estrin, D. Medium access control with coordinated adaptive sleeping for wireless sensor networks. IEEE/ACM Trans. Netw. 2004, 12, 493–506. [Google Scholar] [CrossRef]
- van Dam, T.; Langendoen, K. An Adaptive Energy-Efficient MAC Protocol for Wireless Sensor Networks. In Proceeding of the First ACM SenSys conference, Los Angeles, CA, USA, 5–7 November 2003; pp. 171–180.
- El-Hoiydi, A.; Decotignie, J.D.; Enz, C.; le Roux, E. WiseMAC: An Ultra Low Power MAC Protocol for the WiseNET Wireless Sensor Network. In Proceeding of the First ACM SenSys Conference (SenSys 2003), Los Angeles, CA, USA, 5–7 November 2003; pp. 302–303.
- Polastre, J.; Hill, J.; Culler, D. Versatile Low Power Media Access for Wireless Sensor Networks. In Proceeding of the 2nd ACM SenSys conference (SenSys 2004), Baltimore, MD, USA, 3–5 November 2004; pp. 95–107.
- Kimura, N.; Latifi, S. A Survey on Data Compression in Wireless Sensor Networks. In Proceeding of the International Conference on Information Technology: Coding and Computing (ITCC 2005), Las Vegas, NV, USA, 4–6 April 2005; pp. 8–13.
- Xiang, L.; Luo, J.; Vasilakos, A.V. Compressed Data Aggregation for Energy Efficient Wireless Sensor Networks. In Proceeding of IEEE Communications Society Conference on SensorMesh and Ad Hoc Communications and Networks (SECON 2011), Salt Lake City, UT, USA, 27–30 June 2011; pp. 46–54.
- Krishnamachari, B.; Estrin, D.; Wicker, S. The Impact of Data Aggregation in Wireless Sensor Networks. In Proceeding of 22nd International Conference on Distributed Computing Systems Workshops, Vienna, Austria, 2–5 July 2002; pp. 575–578.
- Chilamkurti, N.; Zeadally, S.; Vasilakos, A.; Sharma, V. Cross-layer support for energy efficient routing in wireless sensor networks. J. Sens. 2009. [Google Scholar]
- IEEE 802 Working Group, Part 15.4: Wireless Medium Access Control (MAC) and Physical Layer (PHY) Specifications for Low-Rate Wireless Personal Area Networks (LR-WPANs); IEEE Std 802.15.4-2006; 2006.
- He, Y.; Sun, J.; Ma, X.; Vasilakos, A.V.; Yuan, R.; Gong, W. Semi-random backoff: towards resource reservation for channel access in wireless LANS. IEEE/ACM Trans. Netw. 2003, 21, 204–217. [Google Scholar]
- The MathWorks Inc. Genetic Algorithm-Find Global Minima for Highly Nonlinear Problems. Available online: http://www.mathworks.cn/discovery/genetic-algorithm.html (accessed on 6 May 2013).
- Sivanandam, S.N.; Deepa, S.N. Genetic Algorithms. In Introduction to Genetic Algorithms; Springer: Berlin, Germany, 2007; Chapter 2; pp. 15–36. [Google Scholar]
- Sivanandam, S.N.; Deepa, S.N. Applications of Genetic Algorithm. In Introduction to Genetic Algorithms; Springer: Berlin, Germany, 2007; Chapter 10; pp. 317–402. [Google Scholar]
- Frantz, F.; Labrak, L.; O’Connor, I. 3D IC floorplanning: Automating optimization settings and exploring new thermal-aware management techniques. Microelectron. J. 2012, 43, 423–432. [Google Scholar] [CrossRef]
- Chipperfield, A.; Fleming, P.; Pohlheim, H.; Fonseca, C. Genetic algorithm toolbox user’s guide. Available online: http://crystalgate.shef.ac.uk/code/manual.pdf (accessed on 10 May 2013).
- Hussain, S.; Matin, A.W.; Islam, O. Genetic algorithm for hierarchical wireless sensor networks. J. Netw. 2007, 2, 87–97. [Google Scholar]
- Sudha, N.; Valarmathi, M.L.; Neyandar, T.C. Optimizing Energy in WSN Using Evolutionary Algorithm. In Proceeding of IJCA on International Conference on VLSICommunications and Instrumentation (ICVCI 2011), Kerala, India, 7–9 April 2011; pp. 26–29.
- Liu, J.; Ravishankar, C.V. LEACH-GA: Genetic algorithm-based energy-efficient adaptive clustering protocol for wireless sensor networks. Int. J. Mach. Learn. Comput. 2011, 1, 79–85. [Google Scholar]
- Yen, Y.S.; Chao, H.C.; Chang, R.S.; Vasilakos, A. Flooding-limited and multi-constrained QoS multicast routing based on the genetic algorithm for MANETs. Math. Comput. Model. 2011, 53, 2238–2250. [Google Scholar] [CrossRef]
- Ferentinos, K.P.; Tsiligiridis, T.A. Adaptive design optimization of wireless sensor networks using genetic algorithms. Comput. Netw. 2007, 51, 1031–1051. [Google Scholar] [CrossRef]
- Sengupta, S.; Das, S.; Nasir, M.D.; Panigrahi, B.K. Multi-objective node deployment in WSNs: In search of an optimal trade-off among coverage, lifetime, energy consumption, and connectivity. Eng. Appl. Arti. Intell. 2013, 26, 405–416. [Google Scholar] [CrossRef]
- Chaudhry, S.B.; Hung, V.C.; Guha, R.K.; Stanley, K.O. Pareto-based evolutionary computational approach for wireless sensor placement. Eng. Appl. Arti. Intell. 2011, 24, 409–425. [Google Scholar] [CrossRef]
- Sengupta, S.; Das, S.; Nasir, M.; Vasilakos, A.V.; Pedrycz, W. An evolutionary multiobjective sleep-scheduling scheme for differentiated coverage in wireless sensor networks. IEEE Trans. Sys. Man Cybern. Part C Appl. Rev. 2012, 42, 1093–1102. [Google Scholar] [CrossRef]
- Zhu, N.; Mieyeville, F.; Navarro, D.; Du, W.; O’Connor, I. Research on High Data Rate Wireless Sensor Networks. In Proceedings of 14ème Journées Nationales du Réseau Doctoral de Micro et Nanoélectronique (JNRDM 2011), Paris, France, 23–25 May 2011.
- Zhu, N.; O’Connor, I. Energy Performance of High Data Rate and Low Power Transceiver based Wireless Body Area Networks. In Proceeding of 2nd International Conference on Sensor Networks (SENSORNETS 2013), Barcelona, Spain, 19–21 Feburary 2013; pp. 141–144.
- Du, W.; Mieyeville, F.; Navarro, D.; O’Connor, I. IDEA1: A validated SystemC-based system-level design and simulation environment for wireless sensor networks. EURASIP J. Wirel. Commun. Netw. 2011, 143. [Google Scholar]
- Chen, Z.; Hu, C.; Liao, J.; Liu, S. Protocol Architecture for Wireless Body Area Network based on nRF24L01. In Proceeding of IEEE International Conference on Automation and Logistics (ICAL 2008), Qingdao, China, 1–3 September 2008; pp. 3050–3054.
- Weder, A. An Energy Model of the Ultra-Low-Power Transceiver nRF24L01 for Wireless Body Sensor Networks. In Proceeding of 2010 Second International Conference on Computational IntelligenceCommunication Systems and Networks (CICSyN 2010), Liverpool, UK, 28–30 July 2010; pp. 118–123.
- Wang, X.; Vasilakos, A.V.; Chen, M.; Liu, Y.; Kwon, T.T. A survey of green mobile networks: opportunities and challenges. Mob. Netw. Appl. 2012, 17, 4–20. [Google Scholar] [CrossRef]
- Bhatti, M.S.; Kapoor, D.; Kalia, R.K.; Reddy, A.S.; Thukral, A.K. RSM and ANN modeling for electrocoagulation of copper from simulated wastewater: Multi objective optimization using genetic algorithm approach. Desalination 2011, 274, 74–80. [Google Scholar] [CrossRef]
- Ferreira, F.F. Architectural Exploration Methods and Tools for Heterogeneous 3D-IC. Ph.D. Thesis, Ecole Centrale de Lyon, Lyon, France, 26 October 2012. [Google Scholar]
- Zhu, N.; O’Connor, I. Energy Measurements and Evaluations on High Data Rate and Ultra Low Power WSN Node. In Proceeding of IEEE International Conference on NetworkingSensing and Control (ICNSC 2013), Paris, France, 10–12 April 2013; pp. 232–236.
- Polastre, J.; Szewczyk, R.; Culler, D. Telos: Enabling Ultra-Low Power Wireless Research. In Proceeding of Fourth International Symposium on Information Processing in Sensor Networks (IPSN 2005), Los Angeles, CA, USA, 25–27 April 2005; pp. 364–369.
- Varga, A.; Hornig, R. An Overview of the OMNeT++ Simulation Environment. In Proceeding of the 1st International Conference on Simulation Tools and Techniques for Communications, Networks and Systems & Workshops (Simutools 2008), Marseille, France, 3–7 March 2008.
- Simon, G.; Völgyesi, P.; Maróti, M.; Lédeczi, A. Simulation-Based Optimization of Communication Protocols for Large-Scale Wireless Sensor Networks. In Proceeding of IEEE Aerospace Conference, Big Sky, MT, USA, 8–15 March 2003; pp. 3_1339–3_1346.
- Latré, B.; Braem, B.; Moerman, I.; Blondia, C.; Demeester, P. A Survey on wireless body area networks. Wireless Netw. 2011, 17, 1–18. [Google Scholar] [CrossRef]
- Chen, M.; Gonzalez, S.; Vasilakos, A.; Cao, H.; Leung, V.C.M. Body area networks: A survey. Mobile Netw. Appl. 2011, 16, 171–193. [Google Scholar] [CrossRef]
- Microchip Technology Inc. PIC16F87/88 Data Sheet. Available online: http://ww1.microchip.com/downloads/en/devicedoc/30487c.pdf (accessed on 8 Feburary 2013).
- Nordic Semiconductor Inc. nRF24L01+ Product Specification. Available online: http://www.nordicsemi.com/eng/content/download/2726/34069/file/nRF24L01P_Product_Specification_1_0.pdf (accessed on 2 April 2013).
- Microchip Technology Inc. Microchip MiWi™ Wireless Networking Protocol Stack. Available online: http://ww1.microchip.com/downloads/en/AppNotes/AN1066%20-%20MiWi%20App%20Note.pdf (accessed on 18 Feburary 2013).
- Xiao, Y.; Peng, M.; Gibson, J.; Xie, G.G.; Du, D.Z.; Vasilakos, A.V. Tight performance bounds of multihop fair access for mac protocols in wireless sensor networks and underwater sensor networks. IEEE Trans. Mob. Comput. 2012, 11, 1538–1554. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Zhu, N.; O'Connor, I. iMASKO: A Genetic Algorithm Based Optimization Framework for Wireless Sensor Networks. J. Sens. Actuator Netw. 2013, 2, 675-699. https://doi.org/10.3390/jsan2040675
Zhu N, O'Connor I. iMASKO: A Genetic Algorithm Based Optimization Framework for Wireless Sensor Networks. Journal of Sensor and Actuator Networks. 2013; 2(4):675-699. https://doi.org/10.3390/jsan2040675
Chicago/Turabian StyleZhu, Nanhao, and Ian O'Connor. 2013. "iMASKO: A Genetic Algorithm Based Optimization Framework for Wireless Sensor Networks" Journal of Sensor and Actuator Networks 2, no. 4: 675-699. https://doi.org/10.3390/jsan2040675




