Self-Affinity, Self-Similarity and Disturbance of Soil Seed Banks by Tillage
Abstract
:1. Introduction
2. Results and Discussion
2.1. General Characterization
| Species | Family | Biological type | Importance as weed |
|---|---|---|---|
| Amaranthus albus L. | Amaranthaceae | Therophyte | 2 |
| Amaranthus retroflexus L. | Amaranthaceae | Therophyte | 3 |
| Chenopodium album L. | Amaranthaceae | Therophyte | 3 |
| Senecio vulgaris L. | Asteraceae | Therophyte | 3 |
| Diplotaxis catholica (L.) DC. | Brassicaceae | Therophyte | 3 |
| Raphanus raphanistrum L. | Brassicaceae | Therophyte | 3 |
| Rapistrum rugosum (L.) All. | Brassicaceae | Therophyte | 2 |
| Sisymbrium irio L. | Brassicaceae | Therophyte | − |
| Cerastium glomeratum Thuill. | Caryophyllaceae | Therophyte | 2 |
| Silene gallica L. | Caryophyllaceae | Therophyte | 2 |
| Spergularia purpurea (Pers.) G. Don | Caryophyllaceae | Therophyte | 2 |
| Stellaria media (L.) Vill. | Caryophyllaceae | Therophyte | 3 |
| Trifolium glomeratum L. | Fabaceae | Therophyte | − |
| Juncus bufonius L. | Juncaceae | Therophyte | 1 |
| Plantago coronopus L. | Plantaginaceae | Therophyte or Hemicryptophyte | 2 |
| Cynodon dactylon (L.) Pers. | Poaceae | Hemicryptophyte | 3 |
| Paspalum dilatatum Poir. | Poaceae | Hemicryptophyte | − |
| Poa annua L. | Poaceae | Therophyte or Hemicryptophyte | 3 |
| Rumex acetosella L. | Polygonaceae | Hemicryptophyte | 1 |
| Reseda luteola L. | Resedaceae | Hemicryptophyte | 2 |
2.2. Seed-Size Distributions
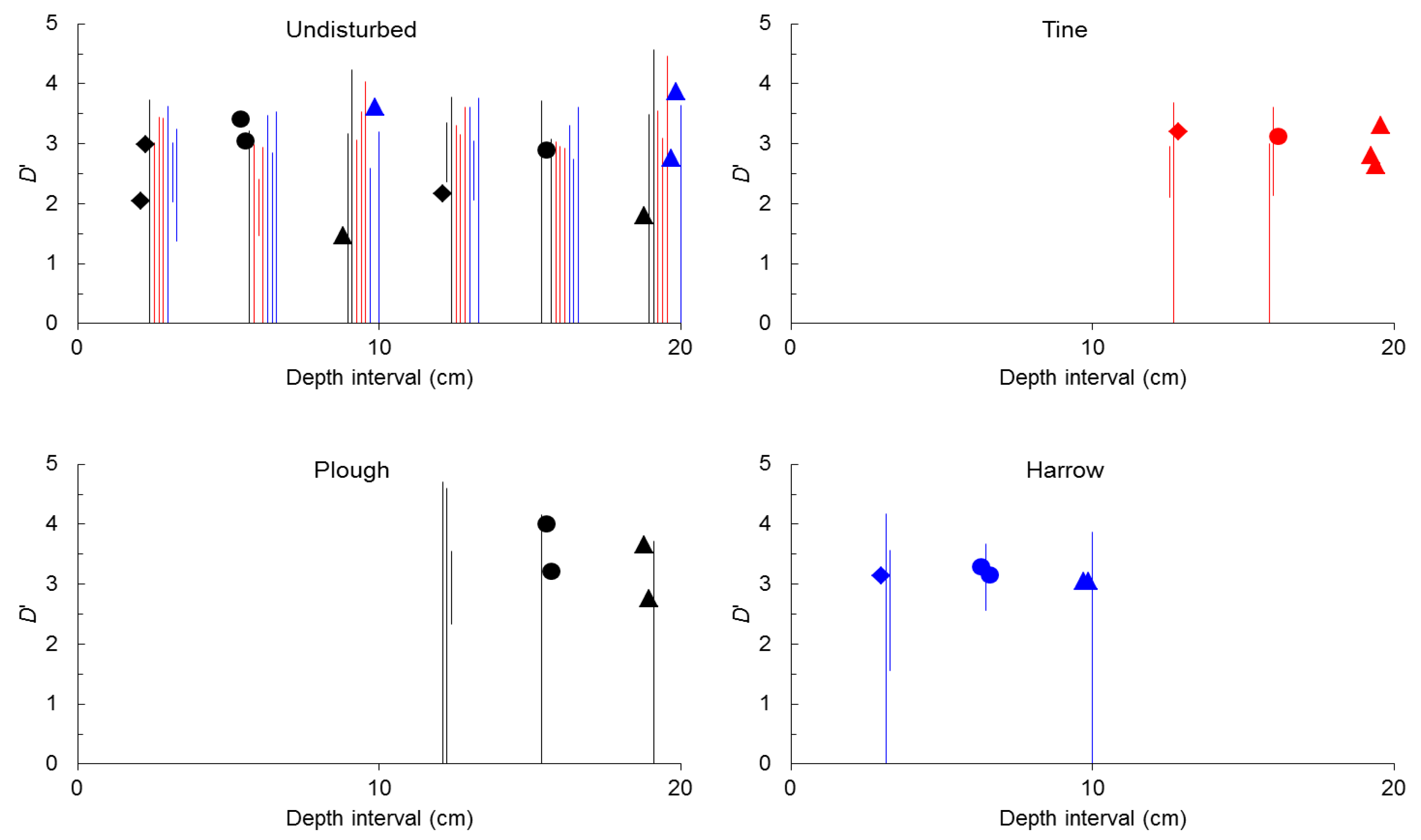
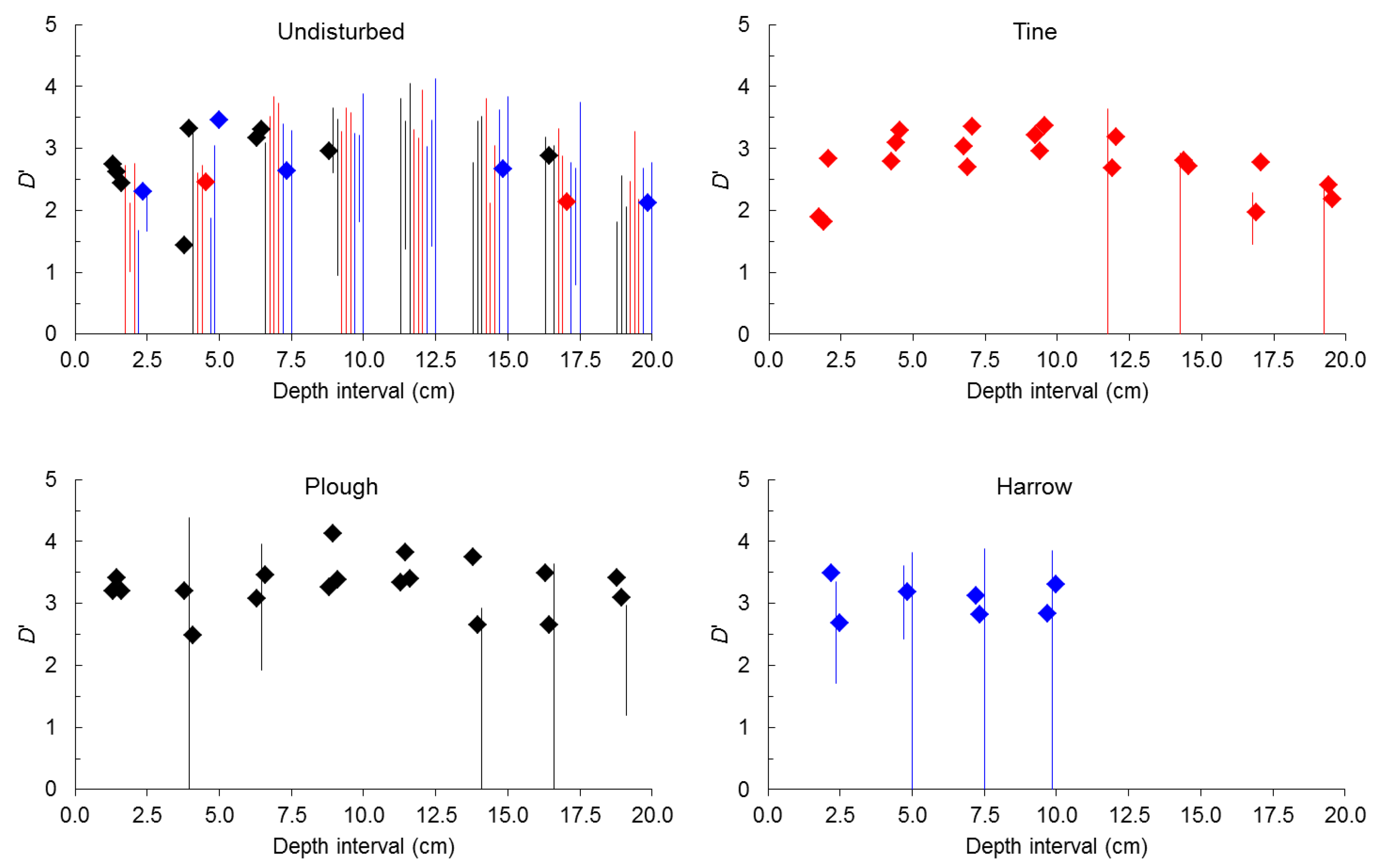


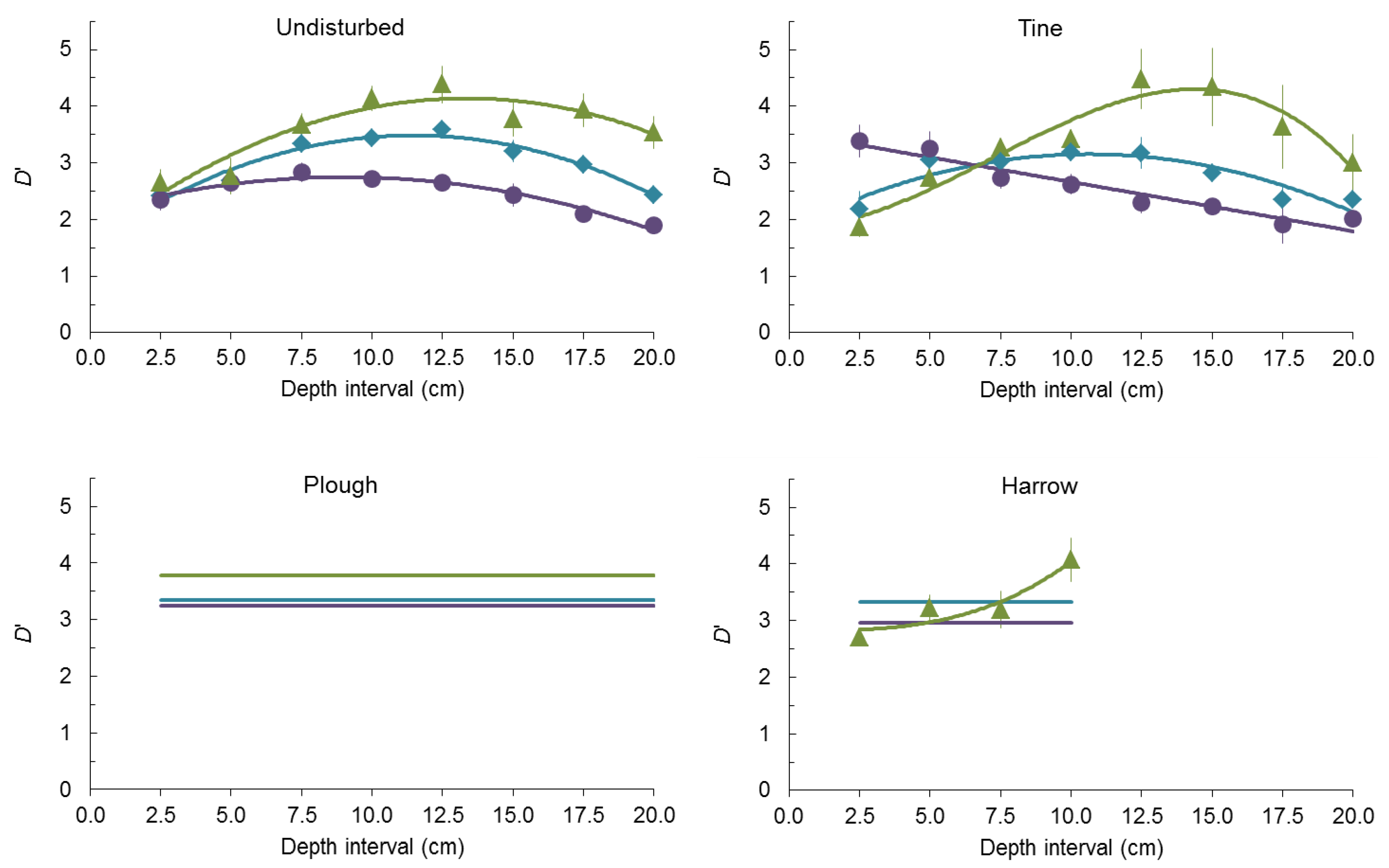

3. Experimental Section
3.1. Location, Soil Seed Bank Sampling and Tillage Experiment
3.2. Sample Processing
3.3. Modeling Seed-Size Distributions
3.3.1. Power Law
3.3.2. Statistical Analyses
4. Conclusions
Acknowledgments
Conflicts of Interest
References
- Levin, S.A. The problem of pattern and scale in ecology. Ecology 1992, 73, 1943–1967. [Google Scholar] [CrossRef]
- Lemly, J.M.; Cooper, D.J. Multiscale factors control community and species distribution in mountain peatlands. Botany 2011, 89, 689–713. [Google Scholar] [CrossRef]
- Harper, J.L. Population Biology of Plants; Academic Press: London, UK, 1977; p. 892. [Google Scholar]
- Harper, J.L.; Lovell, P.H.; Moore, K.G. The shapes and sizes of seeds. Annu. Rev. Ecol. Syst. 1970, 1, 327–356. [Google Scholar]
- Drabo, I.; Ladeinde, T.A.O.; Redden, R.; Smithson, J.B. Inheritance of seed size and number per pod in cowpeas (Vigna unguiculata L. Walp.). Field Crops Res. 1985, 11, 335–344. [Google Scholar]
- Salisbury, E.J. The Reproductive Capacity of Plants. Studies in Quantitative Biology; G. Bell and Sons: London, UK, 1942; p. 244. [Google Scholar]
- Leishman, M.R.; Wright, I.J.; Moles, A.T.; Westoby, M. The Evolutionary Ecology of Seed Size. In Seeds: The Ecology of Regeneration in Plant Communities, 2nd ed.; Fenner, M., Ed.; CABI Publishing: Wallingford, UK, 2000; pp. 31–57. [Google Scholar]
- Reader, R.J. Control of seedling emergence by ground cover and seed predation in relation to seed size for some old-field species. J. Ecol. 1993, 81, 169–175. [Google Scholar] [CrossRef]
- Milberg, P.; Andersson, L.; Thompson, K. Large-seeded species are less dependent on light for germination than small-seeded ones. Seed Sci. Res. 2000, 10, 99–74. [Google Scholar] [CrossRef]
- Thompson, K.; Band, S.R.; Hogdson, J.G. Seed size and shape predict persistence in soil. Funct. Ecol. 1993, 7, 236–241. [Google Scholar] [CrossRef]
- Bekker, R.M.; Bakker, J.P.; Grandin, U.; Kalamees, R.; Milberg, P.; Poschlod, P.; Thompson, K.; Willems, J.H. Seed size, shape and vertical distribution in the soil: Indicators of seed longevity. Funct. Ecol. 1998, 12, 834–842. [Google Scholar] [CrossRef]
- Ghersa, C.M.; Martínez-Ghersa, M.A. Ecological correlates of weed seed size and persistence in the soil under different tilling systems: Implications for weed management. Field Crops Res. 2000, 67, 141–148. [Google Scholar] [CrossRef]
- Peco, B.; Traba, J.; Levassor, C.; Sánchez, A.M.; Azcárate, F.M. Seed size, shape and persistence in dry Mediterranean grass and scrublands. Seed Sci. Res. 2003, 13, 87–95. [Google Scholar] [CrossRef]
- Baker, H.G. Seed weight in relation to environmental conditions in California. Ecology 1972, 53, 997–1010. [Google Scholar] [CrossRef]
- Leishman, M.R.; Westoby, M. Hypotheses on seed size: Tests using the semiarid flora of Western New South Wales, Australia. Am. Nat. 1994, 143, 890–906. [Google Scholar]
- Moles, A.T.; Ackerly, D.D.; Webb, C.O.; Tweddle, J.C.; Dickie, J.B.; Westoby, M. A brief history of seed size. Science 2005, 307, 576–580. [Google Scholar] [CrossRef]
- Salisbury, E. Seed size and mass in relation to environment. Proc. R. Soc. Lond. B Biol. Sci. 1974, 186, 83–88. [Google Scholar] [CrossRef]
- Primack, R.B. Relationships among flowers, fruits, and seeds. Annu. Rev. Ecol. Syst. 1987, 18, 409–430. [Google Scholar]
- Cerdà, A.; García-Fayos, P. The influence of seed size and shape on their removal by water erosion. Catena 2002, 48, 293–301. [Google Scholar] [CrossRef]
- Marañón, T.; Grubb, P.J. Physiological basis and ecological significance of the seed size and relative growth rate relationship in Mediterranean annuals. Funct. Ecol. 1993, 7, 591–599. [Google Scholar] [CrossRef]
- Leishman, M.R.; Westoby, M. The role of seed size in seedling establishment in dry soil conditions—Experimental evidence from semi-arid species. J. Ecol. 1994, 82, 249–258. [Google Scholar] [CrossRef]
- Quero, J.L.; Villar, R.; Marañón, T.; Zamora, R.; Poorter, L. Seed-mass effects in four Mediterranean Quercus species (Fagaceae) growing in contrasting light environments. Am. J. Bot. 2007, 94, 1795–1803. [Google Scholar] [CrossRef]
- Marañón, T.; Bartolome, J.W. Seed and seedling populations in two contrasted communities: Open grassland and oak (Quercus agrifolia) understory in California. Oecol. Plant. 1989, 10, 147–158. [Google Scholar]
- Guo, Q.; Brown, J.H.; Valone, T.J.; Kachman, S.D. Constraints of seed size on plant distribution and abundance. Ecology 2000, 81, 2149–2155. [Google Scholar] [CrossRef]
- Csontos, P.; Tamás, J.; Podani, J. Slope aspects affects the seed mass spectrum of grassland vegetation. Seed Sci. Res. 2004, 14, 349–385. [Google Scholar]
- Baker, H.G. Some Aspects of the Natural History of Seed Banks. In Ecology of Soil Seed Banks; Leck, M.L., Parker, V.T., Simpson, R.L., Eds.; Academic Press: San Diego, CA, USA, 1989; pp. 9–21. [Google Scholar]
- Díaz-Villa, M.D.; Marañon, T.; Arroyo, J.; Garrido, B. Soil seed bank and floristic diversity in a forest-grassland mosaic in southern Spain. J. Veg. Sci. 2003, 14, 701–709. [Google Scholar] [CrossRef] [Green Version]
- Templeton, A.R.; Levin, D.A. Evolutionary consequences of seed pools. Am. Nat. 1979, 114, 232–249. [Google Scholar]
- Mandák, B.; Zákravský, P.; Mahelka, V.; Plačková, I. Can soil seed banks serve as genetic memory? A study of three species with contrasting life history strategies. PLoS One 2012, 7, 1–12. [Google Scholar]
- Casco, H.; Dias, A.S.; Dias, L.S. Modeling size-number distributions of seeds for use in soil bank studies. J. Integr. Plant Biol. 2008, 50, 531–535. [Google Scholar] [CrossRef]
- Weibull, W. A statistical distribution function of wide applicability. J. Appl. Mech. 1951, 18, 293–297. [Google Scholar]
- Turcotte, D.L. Fractals and fragmentation. J. Geophys. Res. 1986, 91, 1921–1926. [Google Scholar] [CrossRef]
- Lord, J.; Westoby, M.; Leishman, M. Seed size and philogeny in six temperate floras: Constraints, niche conservatism, and adaptation. Am. Nat. 1995, 146, 349–364. [Google Scholar]
- Mandelbrot, B. How long is the coast of Britain? Statistical self-similarity and fractional dimension. Science 1967, 156, 636–638. [Google Scholar]
- Mandelbrot, B.B. The Fractal Geometry of Nature; Freeman: New York, NY, USA, 1983; p. 468. [Google Scholar]
- Stanley, H.E.; Meakin, P. Multifractal phenomena in physics and chemistry. Nature 1988, 335, 405–409. [Google Scholar] [CrossRef]
- Scheuring, I.; Riedl, R.H. Applications of multifractals to the analysis of vegetation pattern. J. Veg. Sci. 1994, 5, 489–496. [Google Scholar] [CrossRef]
- Burrough, P.A. Multiscale sources of spatial variation in soil. I. The application of fractal concepts to nested levels of soil variation. J. Soil Sci. 1983, 34, 577–597. [Google Scholar] [CrossRef]
- Casco, H.; Dias, L.S. Estimating seed mass and volume from linear dimensions of seeds. Seed Sci. Technol. 2008, 36, 230–236. [Google Scholar]
- Williams, G.H. Dictionary of Weeds of Western Europe; Elsevier: Amsterdam, The Netherlands, 1982; p. 320. [Google Scholar]
- Cavers, P.B.; Benoit, D.L. Seed Banks in Arable Land. In Ecology of Soil Seed Banks; Leck, M.L., Parker, V.T., Simpson, R.L., Eds.; Academic Press: San Diego, CA, USA, 1989; pp. 309–328. [Google Scholar]
- Van Esso, M.L.; Ghersa, C.M.; Soriano, A. Cultivation effects on the dynamics of a johnson grass seed population in the soil profile. Soil Tillage Res. 1986, 6, 325–335. [Google Scholar] [CrossRef]
- Walter, D.J.; Kenkel, N.C. Landscape complexity in space and time. Community Ecol. 2001, 2, 109–119. [Google Scholar] [CrossRef]
- Cousens, R.; Wallinga, J.; Shaw, M. Are the spatial patterns of weeds scale-invariant? Oikos 2004, 107, 251–264. [Google Scholar]
- Walter, D.J.; Kenkel, N.C. Fractal analysis of spatio-temporal dynamics in boreal forest landscapes. Abstr. Bot. 1998, 22, 13–28. [Google Scholar]
- Palmer, M.W. Fractal geometry: A tool for describing spatial patterns of plant communities. Vegetatio 1988, 75, 91–102. [Google Scholar] [CrossRef]
- Vedyushkin, M.A. Fractal properties of forest spatial structure. Vegetatio 1994, 113, 65–70. [Google Scholar] [CrossRef]
- Tyler, S.W.; Wheatcraft, S.W. Application of fractal mathematics to soil water retention estimation. Soil Sci. Soc. Am. J. 1989, 53, 987–996. [Google Scholar] [CrossRef]
- Wu, Q.; Borkovec, M.; Sticher, H. On particle-size distributions in soils. Soil Sci. Soc. Am. J. 1993, 57, 883–890. [Google Scholar] [CrossRef]
- Perfect, E.; Kay, B.D.; Ferguson, J.A.; Silva, A.P.; Denholm, K.A. Comparison of functions for characterizing the dry aggregate size distribution of tilled soil. Soil Tillage Res. 1993, 28, 123–139. [Google Scholar] [CrossRef]
- Thompson, K.; Bakker, J.P.; Bekker, R.M. The Soil Seed Banks of North West Europe: Methodology, Density and Longevity; Cambridge University Press: Cambridge, UK, 1997; p. 276. [Google Scholar]
- Malone, C.R. A rapid method for enumeration of viable seeds in soil. Weeds 1967, 15, 381–382. [Google Scholar] [CrossRef]
- Ball, D.A.; Miller, S.D. A comparison of techniques for estimation of arable soil seedbanks and their relationship to weed flora. Weed Res. 1989, 29, 365–373. [Google Scholar] [CrossRef]
- Roberts, H.A.; Ricketts, M.E. Quantitative relationships between the weed flora after cultivation and the seed population in the soil. Weed Res. 1979, 19, 269–275. [Google Scholar] [CrossRef]
- Vasconcellos, J.C. Sementes Estranhas do Trigo; Federação Nacional dos Produtores de Trigo: Lisboa, Portugal, 1968; p. 114. [Google Scholar]
- Delorit, R.J. An Illustrated Taxonomy Manual of Weed Seeds; Agronomy Publications: River Falls, WI, USA, 1970; p. 175. [Google Scholar]
- Villarias, J.L. Control de Malas Hierbas. I Atlas de Malas Hierbas, 2nd ed.; Mundi-Prensa: Madrid, Spain, 1979; p. 301. [Google Scholar]
- Delorit, R.J.; Gunn, C.R. Seeds of Continental United States Legumes (Fabaceae); Agronomy Publications: River Falls, WI, USA, 1986; p. 134. [Google Scholar]
- Elmore, C.D. Weed Identification Guide; Southern Weed Science Society: Champaign, IL, USA, 1985. [Google Scholar]
- The Plant List. Available online: http://www.theplantlist.org/ (accessed on 8 November 2012).
- Ury, H.K. A comparison of four procedures for multiple comparisons among means (pairwise contrasts) for arbitrary sample sizes. Technometrics 1976, 18, 89–97. [Google Scholar] [CrossRef]
- Sokal, R.R.; Rohlf, F.J. Biometry: The Principles and Practice of Statistics in Biological Research, 3rd ed.; Freeman: New York, NY, USA, 1995; p. 887. [Google Scholar]
- Box, G.E.P.; Cox, D.R. An analysis of transformations. J. R. Stat. Soc. B 1964, 26, 211–252. [Google Scholar]
- Draper, N.R.; Smith, H. Applied Regression Analysis, 3rd ed.; Wiley: New York, NY, USA, 1998; p. 706. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Dias, L.S. Self-Affinity, Self-Similarity and Disturbance of Soil Seed Banks by Tillage. Plants 2013, 2, 455-472. https://doi.org/10.3390/plants2030455
Dias LS. Self-Affinity, Self-Similarity and Disturbance of Soil Seed Banks by Tillage. Plants. 2013; 2(3):455-472. https://doi.org/10.3390/plants2030455
Chicago/Turabian StyleDias, Luís S. 2013. "Self-Affinity, Self-Similarity and Disturbance of Soil Seed Banks by Tillage" Plants 2, no. 3: 455-472. https://doi.org/10.3390/plants2030455





