Visual Analysis for Nowcasting of Multidimensional Lightning Data
Abstract
:1. Introduction
2. Methodological Framework—State of the Art
2.1. Lightning Data Detection and Position Accuracy
2.2. Thunderstorm and Lightning Cell Nowcasting
2.2.1. Cell Identification and Tracking
2.2.2. Cell Nowcasting
2.3. Explorative Visualization of Lightning Data
3. Lightning Points Test Dataset
| Date | Time | Latitude (°) | Longitude (°) | Altitude (km) |
|---|---|---|---|---|
| 20100722 | 17:45:35.9266801 | 49.0177 | 12.8592 | 9.7 |
| 20100722 | 18:13:12.8011952 | 50.4351 | 11.6775 | 0 |
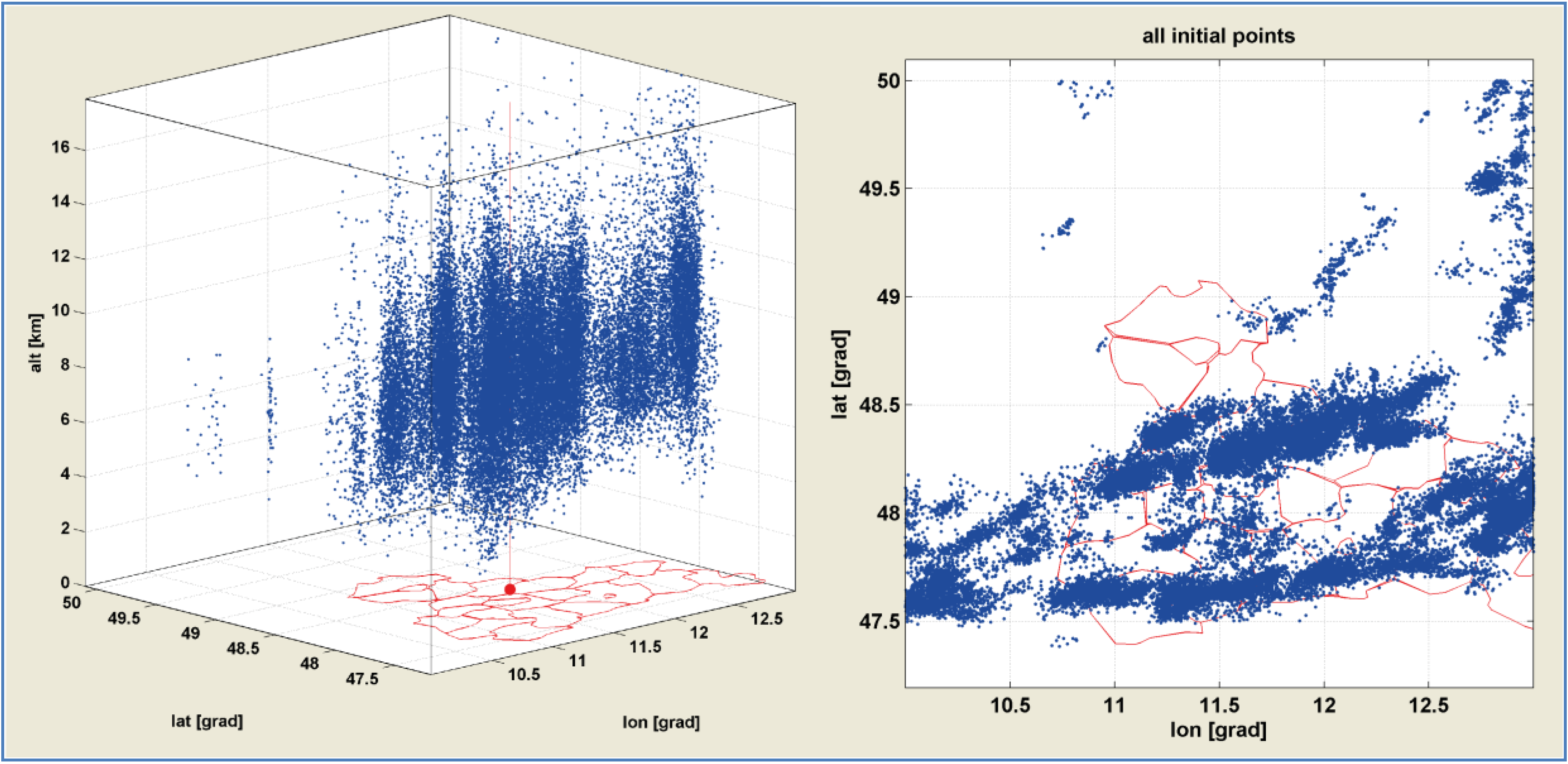
4. Development of an Interactive Tool for Lightning Data Analysis
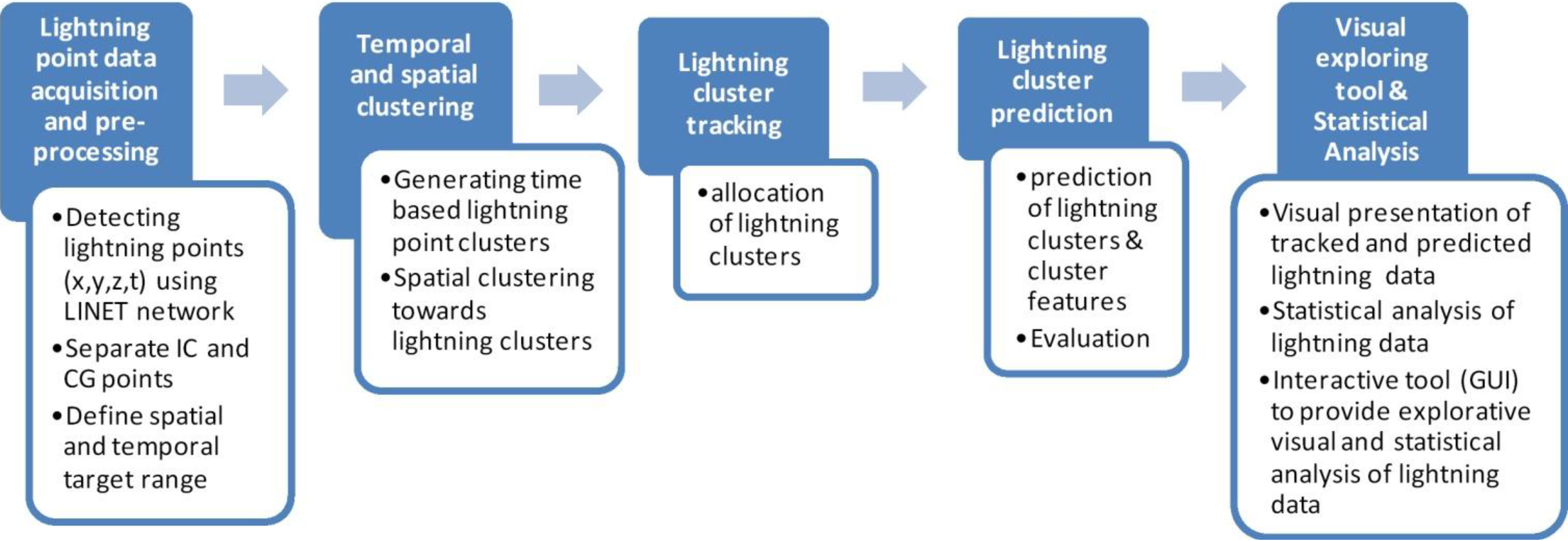
4.1. Workflow: Lightning Detection, Clustering, Tracking, Prediction, and Visualization
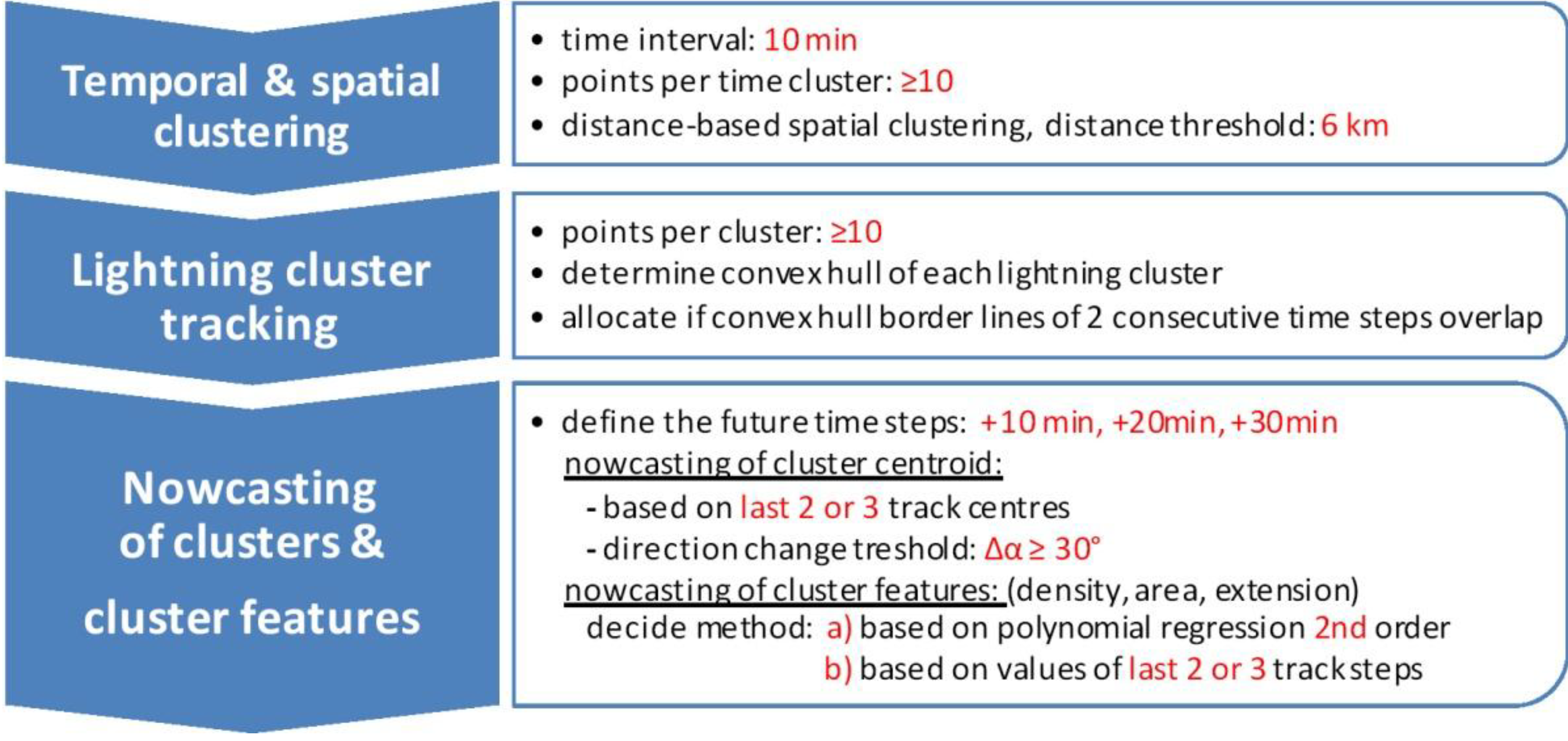
4.2. Lightning Cluster Identification and Tracking
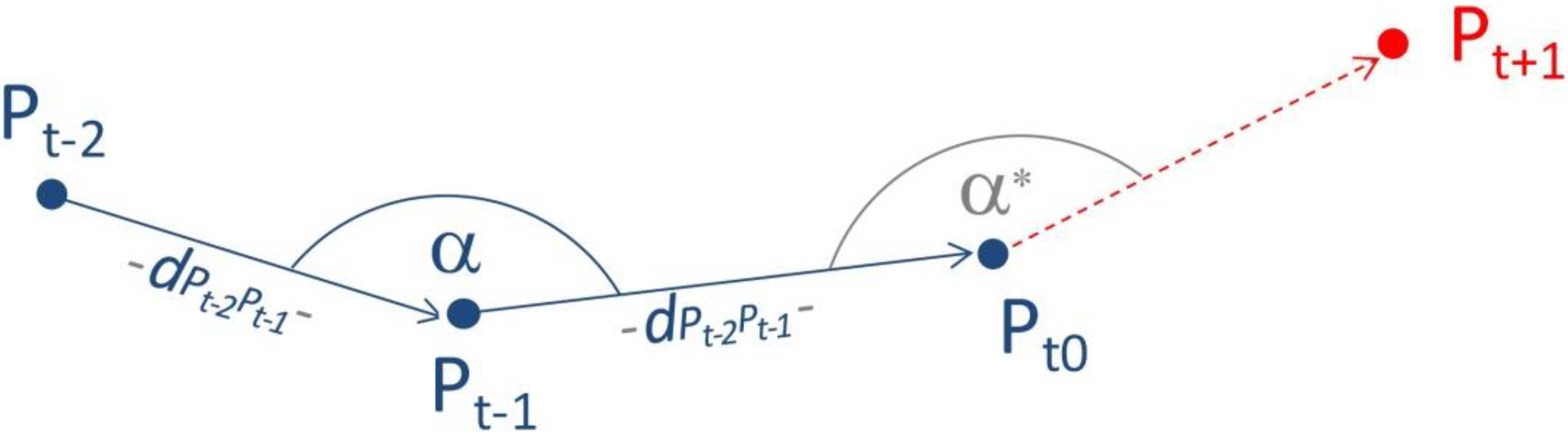
4.3. Lightning Nowcasting and Evaluation
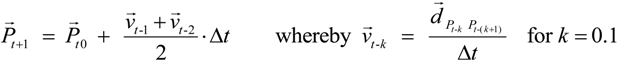
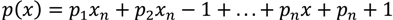
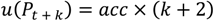
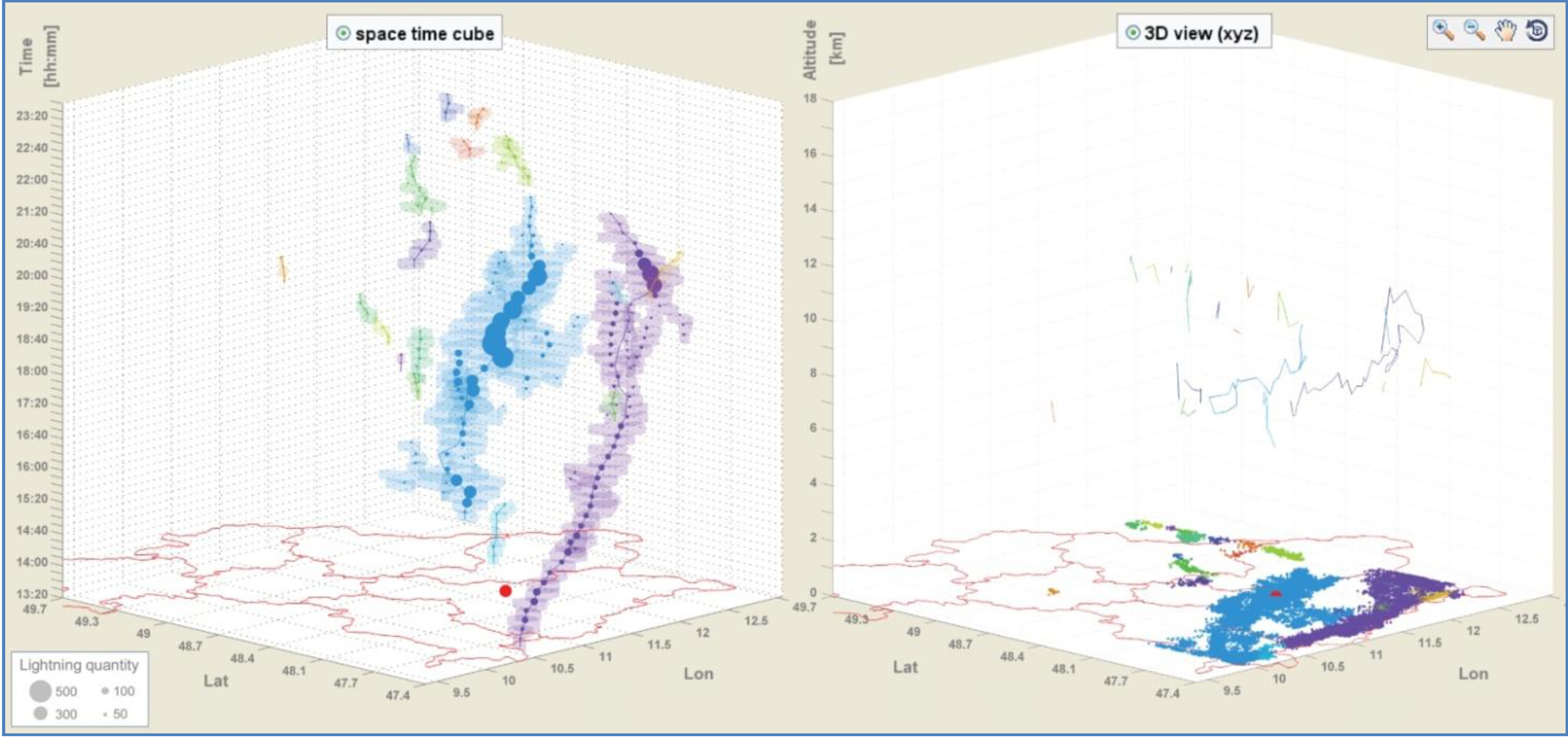
4.4. Interactive Visual and Statistical Analysis of Dynamic Lightning Cluster Features
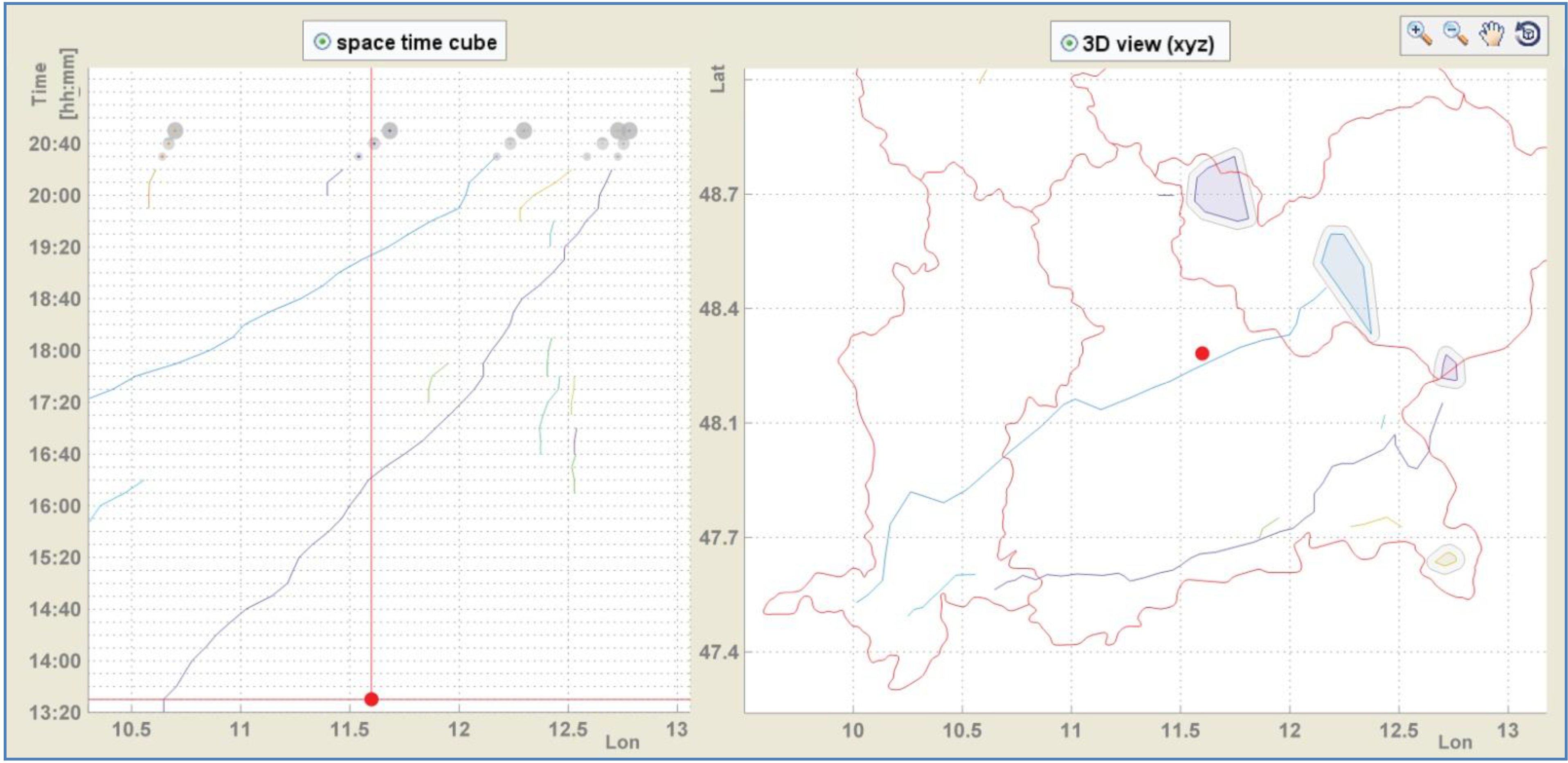
4.4.1. Lightning Graphic User Interface (GUI)
| 2D | 3D | STC | ||||
| visual presentation | cluster features | point cloud | ● | ● | ● | |
| centroid point | ● | ● | ● | |||
| extension | convex hull | ● | ● | ● | ||
| ellipse | ● | |||||
| ellipsoid | ● | |||||
| rectangle | ● | |||||
| cuboid | ● | |||||
| * uncertainty buffer | ● | ● | ● | |||
| track features | track line | ● | ● | ● | ||
| track lane | ● | ● | ● | |||
| * uncertainty buffer | ● | ● | ● | |||
| cluster features | track features | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| point cloud | centroid (incl. cluster density information) | convex hull surface | convex hull edges | ellipse/ellipsoid interior | ellipse/ellipsoid edges | rectangle/cuboid interior | rectangle/cuboid edges | * uncertainty buffer | track line | track lane edges | track lane interior | *uncertainty buffer | |
| Form | ● | ||||||||||||
| Color | ● | ● | ● | ● | ● | ● | ● | ● | ● | ● | ● | ||
| Texture | ● | ● | ● | ● | ● | ● | ● | ● | ● | ● | ● | ● | ● |
| Luminance | ● | ● | ● | ● | ● | ● | ● | ● | ● | ● | ● | ● | ● |
| Size | ● | ● | ● | ● | ● | ● | ● | ||||||
| Sharpness | ● | ● | ● | ● | ● | ● | |||||||
| Transparency | ● | ● | ● | ● | ● | ● | |||||||
| Saturation | ● | ● | ● | ● | ● | ● | ● | ● | ● | ● | ● | ● | ● |
- load in lightning point data (x,y,z,t)
- choose between 3D-view (x-y-z) and STC (x-y-t)
- choose/combine between different cluster and track feature visualizations, see Table 2
- enable nowcasting for the next 10, 20, 30, …, 60 min
- adapt graphic variables
- set limits for temporal and spatial range
- explore plotted data via zoom, pan, rotate, animate


4.4.2. Statistical Analysis of Dynamic Lightning Cluster Features
| statistical analysis | cluster features | point coordinates | |
| centroid coordinates | |||
| max/min of altitude | |||
| quantity/intensity, area, volume | |||
| spatial extension | |||
| velocity, acceleration | |||
| distance to last cluster centroid | |||
| uncertainty of nowcasted cluster centroids and cluster features | |||
| track features | length (distance) and duration | ||
| variations of cluster features (max, min) | |||
| track size | sum of clusters | ||
| sum of points | |||
| sum of area/volume | |||
5. Results and Discussion
5.1. Lightning Cluster Tracking and Nowcasting
5.2. Visual and Statistical Analysis Using a Lightning GUI

6. Conclusions and Outlook
Acknowledgments
Conflicts of Interest
References
- Generalisation of Geographic Information: Cartographic Modelling and Applications; Mackaness, W.A.; Ruas, A.; Sarjakoski, L.T. (Eds.) Elsevier: Amsterdam, The Netherlands, 2007; p. 386.
- Andrienko, G.; Andrienko, N.; Dykes, J.; Fabrikant, S.I.; Wachowicz, M. Geovisualization of dynamics, movement and change: Key issues and developing approaches in visualization research. Inf. Vis. 2008, 7, 173–180. [Google Scholar] [CrossRef]
- Keim, D.; Andrienko, G.; Fekete, J.-D.; Görg, C.; Kohlhammer, J.; Melançon, G. Visual Analytics: Definition, Process, and Challenges. In Information Visualization: Human-Centered Issues and Perspectives; Springer: Berlin, Germany, 2008. [Google Scholar]
- Turk, A. Designing Advanced GIS Visualisations Using Cognitive Ergonomics Theories, Models and Procedures. In Proceeding of the 16th International Cartographic Conference, Cologne, Germany, 3–9 May 1993.
- Krisp, J.M.; Peters, S.; Murphy, C.E.; Fan, H. Visual bandwidth selection for kernel density maps. Photogrammetrie Fernerkundung Geoinf. 2009, 2009, 445–454. [Google Scholar] [CrossRef]
- Krisp, J.M.; Peters, S. Visualizing Dynamic 3D Densities: A Lava-Lamp Approach. In Proceeding of the 13th AGILE International Conference on Geographic Information Science, Guimaraes, Portugal, 10–14 May 2010.
- risp, J.M.; Peters, S.; Burkert, F.; Butenuth, M. Visual Identification of Scattered Crowd Movement Patterns Using a Directed Kernel Density Estimation. In Proceedings of SPM2010 Mobile Tartu, Tartu, Estonia, 26–28 August 2010.
- Peters, S.; Krisp, J.M. Density Calculation for Moving Points. In Proceeding of the 13th AGILE International Conference on Geographic Information Science, Guimaraes, Portugal, 10–14 May 2010.
- Peters, S. Quadtree-and octree-based approach for point data selection in 2D or 3D. Ann. GIS 2013, 19, 37–44. [Google Scholar] [CrossRef]
- Krisp, J.M.; Peters, S. Directed kernel density estimation (DKDE) for time series visualization. Ann. GIS 2011, 17, 155–162. [Google Scholar] [CrossRef]
- Kraak, M.J. The Space-Time Cube Revisited from a Geovisualization Perspective. In Proceeding of the 21st International Cartographic Conference, Durban, South Africa, 10–16 August 2003; pp. 1988–1996.
- Andrienko, N.; Andrienko, G. Exploratory Analysis of Spatial and Temporal Data; Springer: Berlin, Germany, 2006. [Google Scholar]
- Andrienko, N.; Andrienko, G. A visual analytics framework for spatio-temporal analysis and modelling. Data Min. Knowl. Discov. 2012, 27, 55–83. [Google Scholar]
- Andrienko, G.; Andrienko, N.; Keim, D.; MacEachren, A.M.; Wrobel, S. Challenging problems of geospatial visual analytics. J. Vis. Lang. Comput. 2011, 22, 251–256. [Google Scholar] [CrossRef]
- Andrienko, G.; Andrienko, N.; Jankowski, P.; Keim, D.; Kraak, M.-J.; MacEachren, A.; Wrobel, S. Geovisual analytics for spatial decision support: Setting the research agenda. Int. J. Geogr. Inf. Sci. 2007, 21, 839–857. [Google Scholar] [CrossRef]
- Andrienko, G.; Andrienko, N.; Demsar, U.; Dransch, D.; Dykes, J.; Fabrikant, S.I.; Jern, M.; Kraak, M.-J.; Schumann, H.; Tominski, C. Space, time and visual analytics. Int. J. Geogr. Inf. Sci. 2010, 24, 1577–1600. [Google Scholar] [CrossRef]
- NVAC PNNL: Information Visualization and Visual Analytics. Available online: http://vis.pnnl.gov/ (accessed on 21 August 2013).
- VisMaster VisMaster»Visual Analytics—Mastering the Information Age. Available online: http://www.vismaster.eu/ (accessed on 21 August 2013).
- MOVE MOVE—WG 4: Visual Analytics for Movement and Cognitive Issues. Available online: http://www.move-cost.info/ (accessed on 21 August 2013).
- MacEachren, A.M.; Kraak, M.J. Research challenges in geovisualization. Cartogr. Geogr. Inf. Sci. 2001, 28, 3–12. [Google Scholar] [CrossRef]
- Virrantaus, K.; Fairbairn, D.; Kraak, M.-J. ICA research agenda on cartography and GI science. Cartogr. J. 2009, 46, 63–75. [Google Scholar] [CrossRef]
- Cook, K.; Grinstein, G.; Whiting, M.; Cooper, M.; Havig, P.; Liggett, K.; Nebesh, B.; Paul, C.L. VAST Challenge 2012: Visual Analytics for Big Data. In Proceedings of 2012 IEEE Conference on Visual Analytics Science and Technology (VAST), Seattle, WA, USA, 14–19 October 2012; pp. 251–255.
- Krisp, J.M.; Peters, S.; Polous, K.; Fan, H.; Meng, L. Getting in and out of a Taxi: Spatio-Temporal Hotspot Analysis for Floating Taxi Data in Shanghai. In Proceedings of Networks for Mobility 2012, Stuttgart, Germany, 27–28 September 2012.
- Kitagawa, N.; Brook, M.; Workman, E. Continuing currents in cloud-to-ground lightning discharges. J. Geophys. Res. 1962, 67, 637–647. [Google Scholar] [CrossRef]
- Betz, H.D.; Schmidt, K.; Oettinger, W.P. LINET—An International VLF/LF Lightning Detection Network in Europe. In Lightning: Principles, Instruments and Applications; Betz, H.D., Schumann, U., Laroche, P., Eds.; Springer: Holland, The Netherlands, 2009; pp. 115–140. [Google Scholar]
- Betz, H.D.; Schmidt, K.; Oettinger, W.P.; Montag, B. Cell-tracking with lightning data from LINET. Adv. Geosci. 2008, 17, 55–61. [Google Scholar] [CrossRef]
- Peters, S.; Meng, L.; Betz, H.D. Visual Analysis of Lightning Data Using Space-Time-Cube. In Proceeding of the 26th International Cartographic Conference (ICC), Dresden, Germany, 25–30 August 2013. in press.
- WMO Nowcasting. Available online: http://www.wmo.int/pages/prog/amp/pwsp/Nowcasting.htm (accessed on 21 August 2013).
- Galton, A. Dynamic collectives and their collective dynamics. Spat. Inf. Theory 2005, 3693, 300–315. [Google Scholar]
- Meyer, V. Thunderstorm Tracking and Monitoring on the Basis of Three-dimensional Lightning Data and Conventional and Polarimetric Radar Data. Ph.D. Thesis, Ludwig-Maximilians-Universität München, Munich, Germany, 2010. [Google Scholar]
- Li, L.; Schmid, W.; Joss, J. Nowcasting of motion and growth of precipitation with radar over a complex orography. J. Appl. Meteorol. 1995, 34, 1286–1300. [Google Scholar] [CrossRef]
- Johnson, J.; MacKeen, P.L.; Witt, A.; Mitchell, E.D.W.; Stumpf, G.J.; Eilts, M.D.; Thomas, K.W. The storm cell identification and tracking algorithm: An enhanced WSR-88D algorithm. Weather Forecast. 1998, 13, 263–276. [Google Scholar] [CrossRef]
- Rinehart, R.; Garvey, E. Three-dimensional storm motion detection by conventional weather radar. Nature 1978. [Google Scholar] [CrossRef]
- Zinner, T.; Mannstein, H.; Tafferner, A. Cb-TRAM: Tracking and monitoring severe convection from onset over rapid development to mature phase using multi-channel Meteosat-8 SEVIRI data. Meteorol. Atmos. Phys. 2008, 101, 191–210. [Google Scholar] [CrossRef]
- Dixon, M.; Wiener, G. TITAN: Thunderstorm identification, tracking, analysis, and nowcasting-A radar-based methodoloy. J. Atmos. Ocean. Technol. 1993, 10, 785–797. [Google Scholar] [CrossRef]
- Handwerker, J. Cell tracking with TRACE3D—A new algorithm. Atmos. Res. 2002, 61, 15–34. [Google Scholar] [CrossRef]
- Hering, A.; Morel, C.; Galli, G.; Sénési, S.; Ambrosetti, P.; Boscacci, M. Nowcasting Thunderstorms in the Alpine Region Using a Radar Based Adaptive Thresholding Scheme. In Proceedings of the Third ERAD Conference, Visby, Sweden, 6–10 September 2004; pp. 206–211.
- Steinacker, R.; Dorninger, M.; Wölfelmaier, F.; Krennert, T. Automatic tracking of convective cells and cell complexes from lightning and radar data. Meteorol. Atmos. Phys. 2000, 72, 101–110. [Google Scholar] [CrossRef]
- Bonelli, P.; Marcacci, P. Thunderstorm nowcasting by means of lightning and radar data: Algorithms and applications in northern Italy. Nat. Hazards Earth Syst. Sci. 2008, 8, 1187–1198. [Google Scholar] [CrossRef]
- Bolliger, M.; Binder, P.; Rossa, A. Tracking Cloud Patterns by Rapid Scan Imagery in the Alpine Region. In Proceedings of 10th AMS Conference on Moutain Meterology, Park City, UT, USA, 17–21 June 2002; Volume 12, pp. 73–80.
- Jain, A.K.; Dubes, R.C. Algorithms for Clustering Data; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 1988. [Google Scholar]
- Han, J.; Kamber, M. Data Mining: Concepts and Techniques; Morgan Kaufmann: San Francisco, CA, USA, 2006. [Google Scholar]
- Soul, K.; Archibald, E.; Hardaker, P.; Hounsell, A. Using the GANDOLF system as a tool to aid the forecasting of lightning strikes. Meteorol. Appl. 2002, 9, 229–238. [Google Scholar] [CrossRef]
- Yeung, L.H.; Lai, E.S.; Chiu, S.K. Lightning Initiation and Intensity Nowcasting Based on Isothermal Radar Reflectivity—A Conceptual Model. In Proceeding of the 33rd International Conference on Radar Meteorology, Cairns, QLD, Australia, 6–10 August 2007; pp. 6–10.
- Turdukulov, U.D.; Kraak, M.-J.; Blok, C.A. Designing a visual environment for exploration of time series of remote sensing data: In search for convective clouds. Comput. Graph. 2007, 31, 370–379. [Google Scholar] [CrossRef]
- Jain, A.K.; Murty, M.N.; Flynn, P.J. Data clustering: A review. ACM Comput. Surv. (CSUR) 1999, 31, 264–323. [Google Scholar] [CrossRef]
- Bertin, J. Semiology of Graphics: Diagrams, Networks, Maps; The University of Wisconsin Press: Madison, WI, USA, 1983. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Peters, S.; Meng, L. Visual Analysis for Nowcasting of Multidimensional Lightning Data. ISPRS Int. J. Geo-Inf. 2013, 2, 817-836. https://doi.org/10.3390/ijgi2030817
Peters S, Meng L. Visual Analysis for Nowcasting of Multidimensional Lightning Data. ISPRS International Journal of Geo-Information. 2013; 2(3):817-836. https://doi.org/10.3390/ijgi2030817
Chicago/Turabian StylePeters, Stefan, and Liqiu Meng. 2013. "Visual Analysis for Nowcasting of Multidimensional Lightning Data" ISPRS International Journal of Geo-Information 2, no. 3: 817-836. https://doi.org/10.3390/ijgi2030817




