HCTNav: A Path Planning Algorithm for Low-Cost Autonomous Robot Navigation in Indoor Environments
Abstract
:1. Introduction
2. Environment and System Model

3. The HCTNav Algorithm
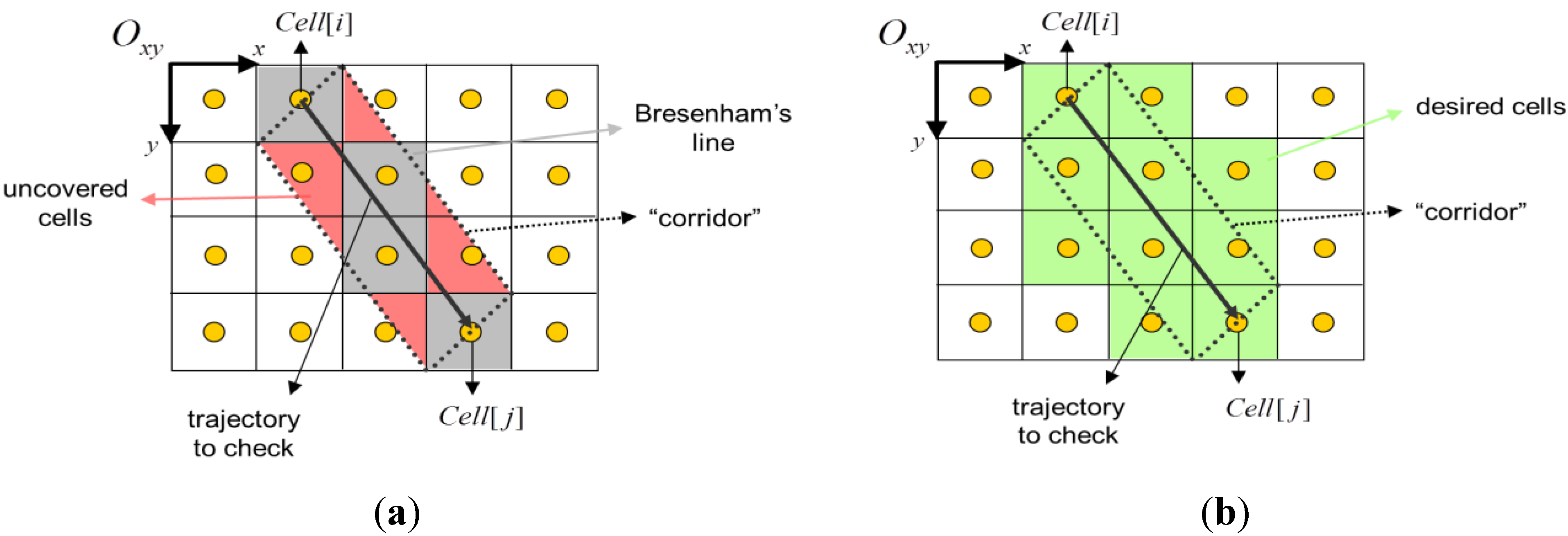
3.1. Obstacle Detection
- Internal B-lines: Using the 1st quadrant from Figure 3, the two B-lines from Cell [i] to Cell [j], changing the condition sign (see below).
- First-level external B-lines: Using the 1st quadrant from Figure 3, the two B-lines from Cellx+1 [i] to Celly−1 [j] and from Celly+1 [i] to Cellx−1 [j].
- Second-level external B-lines: Using the 1st quadrant from Figure 3, the two B-lines from Cellx+2 [i] to Celly−1 [j] and from Celly+1 [i] to Cellx−2 [j].


|
3.2. Choosing the Next Turning-Point
- Condition-1: obstacle contour tile;
- Condition-2: inbound and free tile;
- Condition-3: not visited and not marked as turning-point;
- Condition-4: obstacle-free trajectory (from current position).
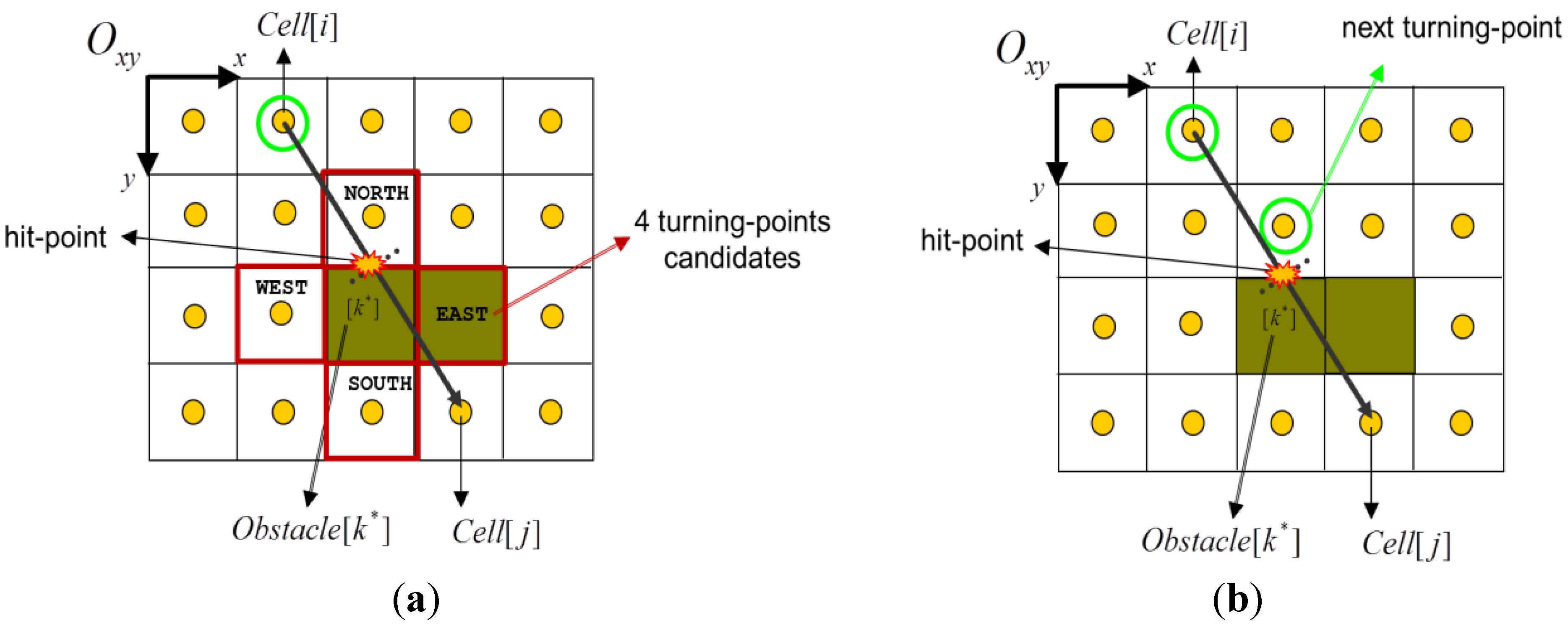
- 1)
- if no valid candidate is returned, then a dead-end is detected (no new edge is created);
- 2)
- if the new turning-point Node[c*] is different from the current position Node[i], then a new edge is assigned to the path-graph. The pointer Edge[c* ← i] is stored and its weight w is initialized with the straight distance between Cell [i] and Cell [c*] centers;
- 3)
- if the turning-point matches the current position then HCTNav proceeds to surround the obstacle (see next subsection).
|
3.3. Surrounding Current Obstacle
- Condition-3’: not the current position and not in the initial contour list.
|
3.4. Building the Final Path
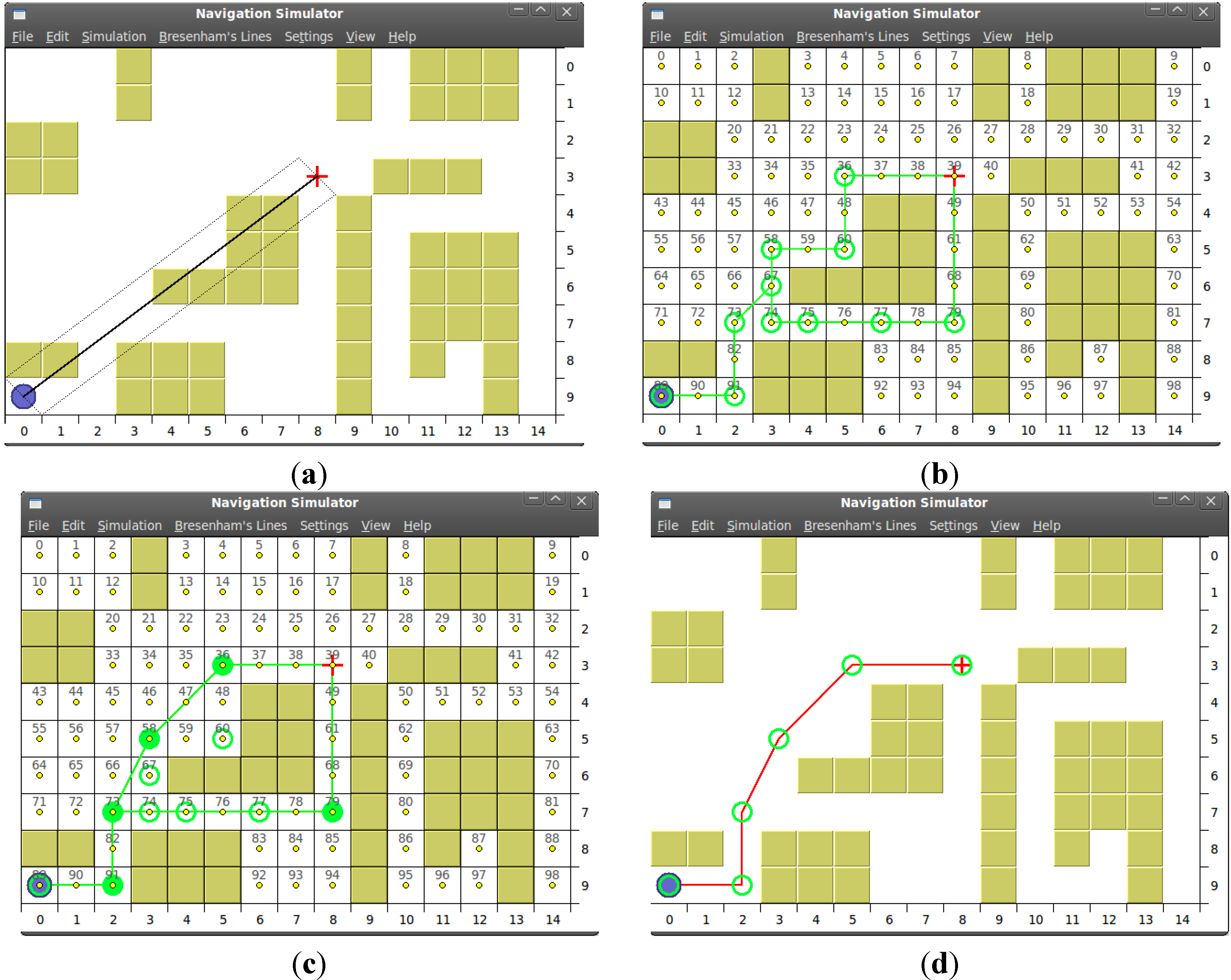
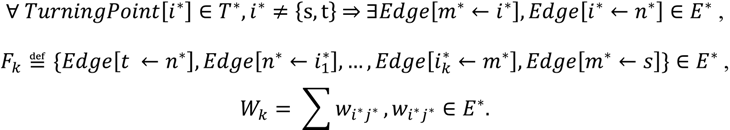
4. Experimental Section
4.1. Test-Bench
4.1.1. Algorithms Implementation
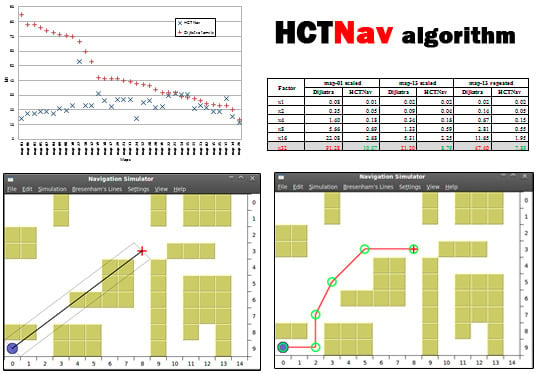
4.2. Simulation Results
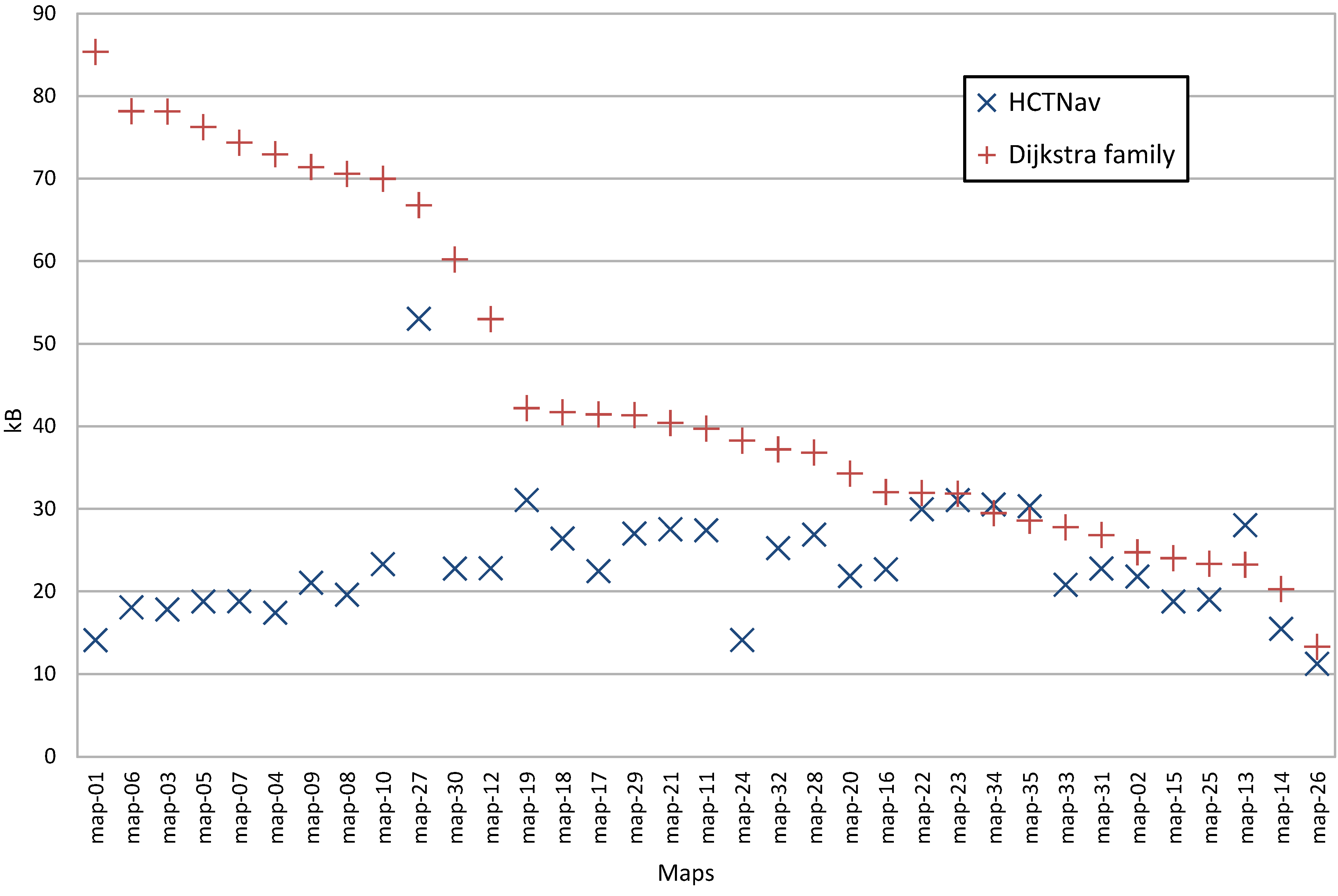
4.2.1. Dynamic Memory Usage
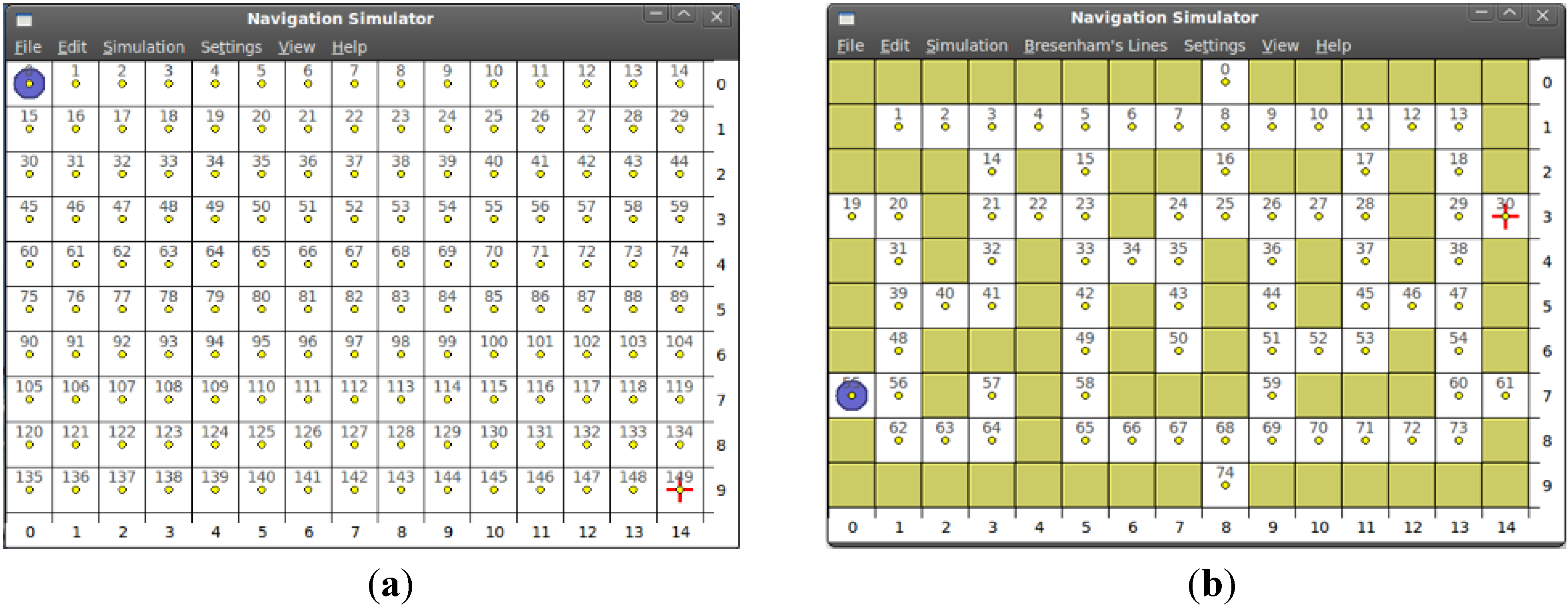
4.2.2. Scalability over Map Resizing
| Factor | map-01 Scaled | map-13 Scaled | map-13 Repeated | |||
|---|---|---|---|---|---|---|
| Dijkstra | HCTNav | Dijkstra | HCTNav | Dijkstra | HCTNav | |
| ×1 | 0.08 | 0.01 | 0.02 | 0.02 | 0.02 | 0.02 |
| ×2 | 0.35 | 0.05 | 0.09 | 0.04 | 0.14 | 0.05 |
| ×4 | 1.40 | 0.18 | 0.34 | 0.16 | 0.67 | 0.15 |
| ×8 | 5.66 | 0.69 | 1.33 | 0.59 | 2.81 | 0.55 |
| ×16 | 22.08 | 2.68 | 5.31 | 2.25 | 11.65 | 1.95 |
| ×32 | 91.28 | 10.07 | 21.20 | 8.79 | 47.40 | 7.89 |
4.2.3. Execution Time Impact
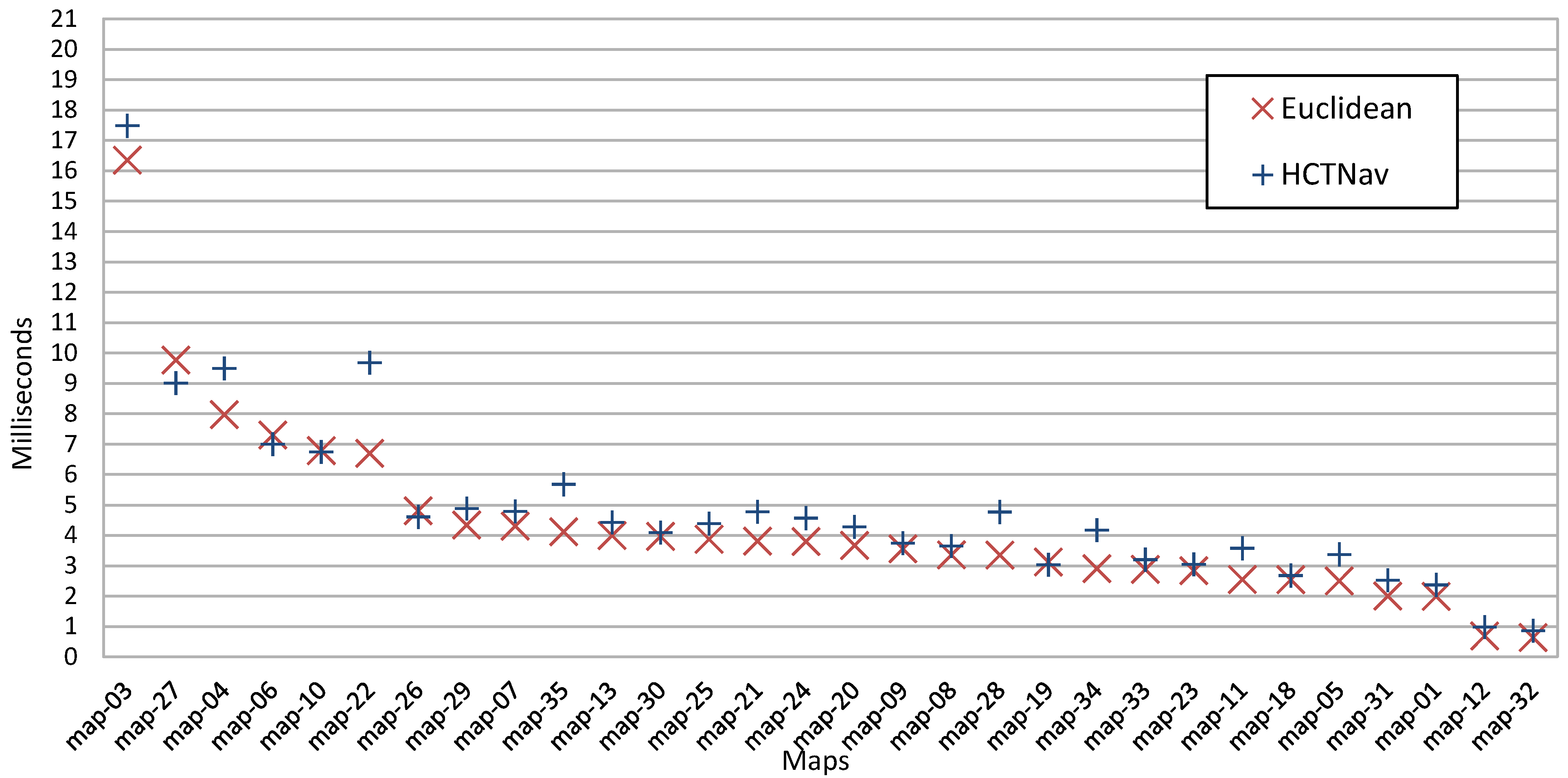
4.2.4. Path Length Comparison
| Map Name | Number of Possible Paths | Percentage of Different Paths | Difference Mean | Difference Variance |
|---|---|---|---|---|
| map-01 | 11175 | 0.00% | 0.00 | 0.0 |
| map-02 | 10712 | 0.00% | 0.00 | 0.0 |
| map-03 | 10153 | 3.20% | 0.19 | 0.6 |
| map-04 | 8911 | 4.72% | 0.25 | 0.9 |
| map-05 | 9870 | 7.50% | 0.22 | 0.8 |
| map-06 | 10153 | 6.30% | 0.27 | 0.1 |
| map-07 | 9591 | 5.18% | 0.30 | 0.9 |
| map-08 | 9045 | 4.61% | 0.28 | 0.1 |
| map-09 | 8911 | 6.06% | 0.30 | 0.1 |
| map-10 | 9045 | 12.66% | 0.30 | 0.1 |
| map-11 | 4371 | 22.24% | 0.25 | 0.1 |
| map-12 | 6441 | 6.27% | 0.29 | 0.6 |
| map-13 | 2485 | 9.46% | 0.29 | 0.05 |
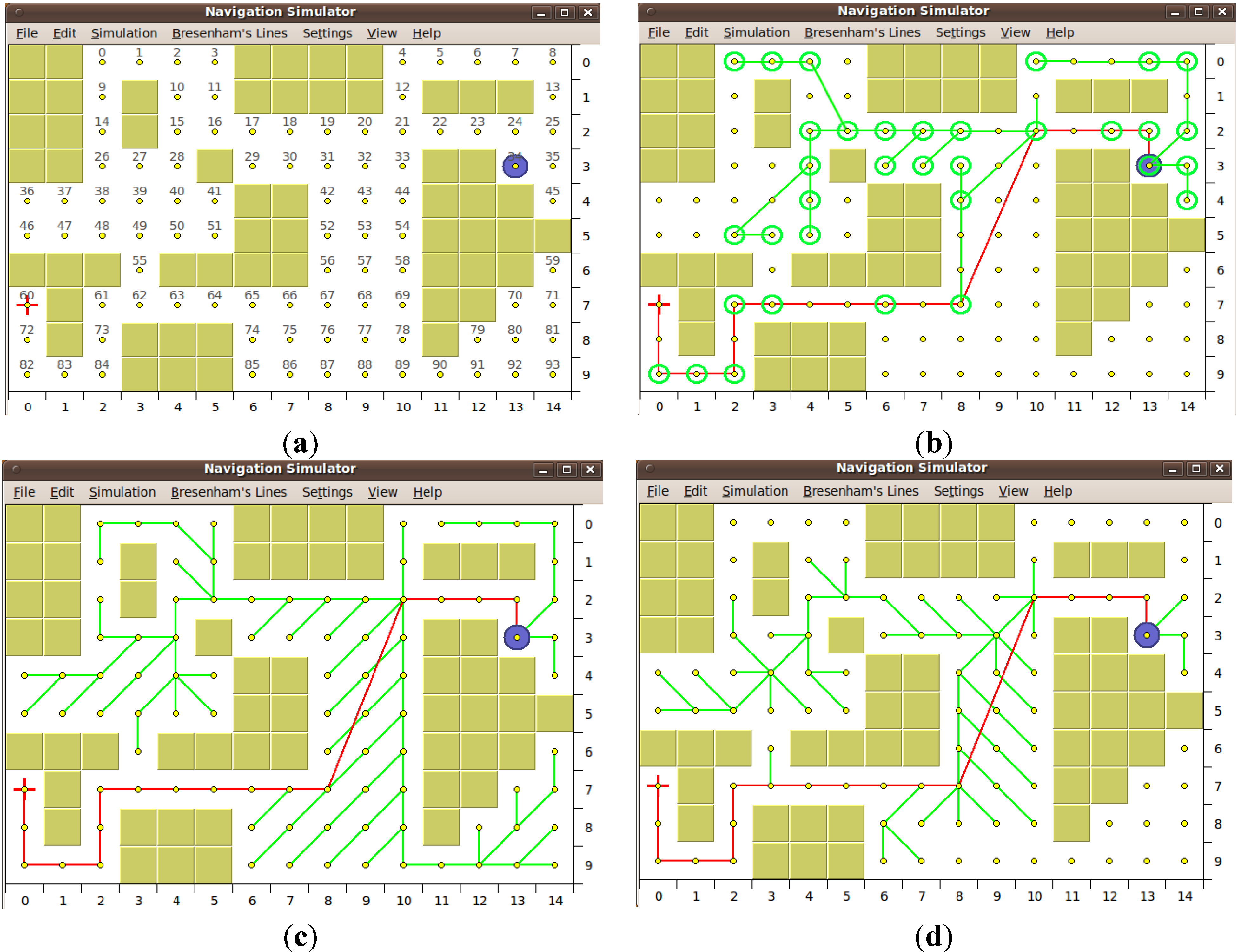
4.3. Qualitative Discussion
4.3.1 HCTNav vs. Dijkstra and A*
- HCTNav only requires a set of nodes representing the free cells in the binary map, whereas Dijkstra also needs to know all possible edges. This simplification reflects considerable memory saving during run-time, especially when the maps grow in cell number.
- Edges are composed during the execution and could span multiple nodes; instead, in the common Dijkstra family implementations, used for this comparison, only one-hop edges are evaluated and stored as a preprocessing of the map, due to the exploding cost of storing all the possible edges in the initial graph.
- In HCTNav we introduced an obstacle control strategy to find the intermediate transit nodes (turning-points) from which to begin to surround obstacles. Dijkstra simply does not consider obstructions as they are implicitly removed at the construction of the initial graph.
- The difference between the path lengths between the HCTNav and the Dijkstra is lower than a third of a cell. Considering that it is also a third of the size of the robot, it is not significant.
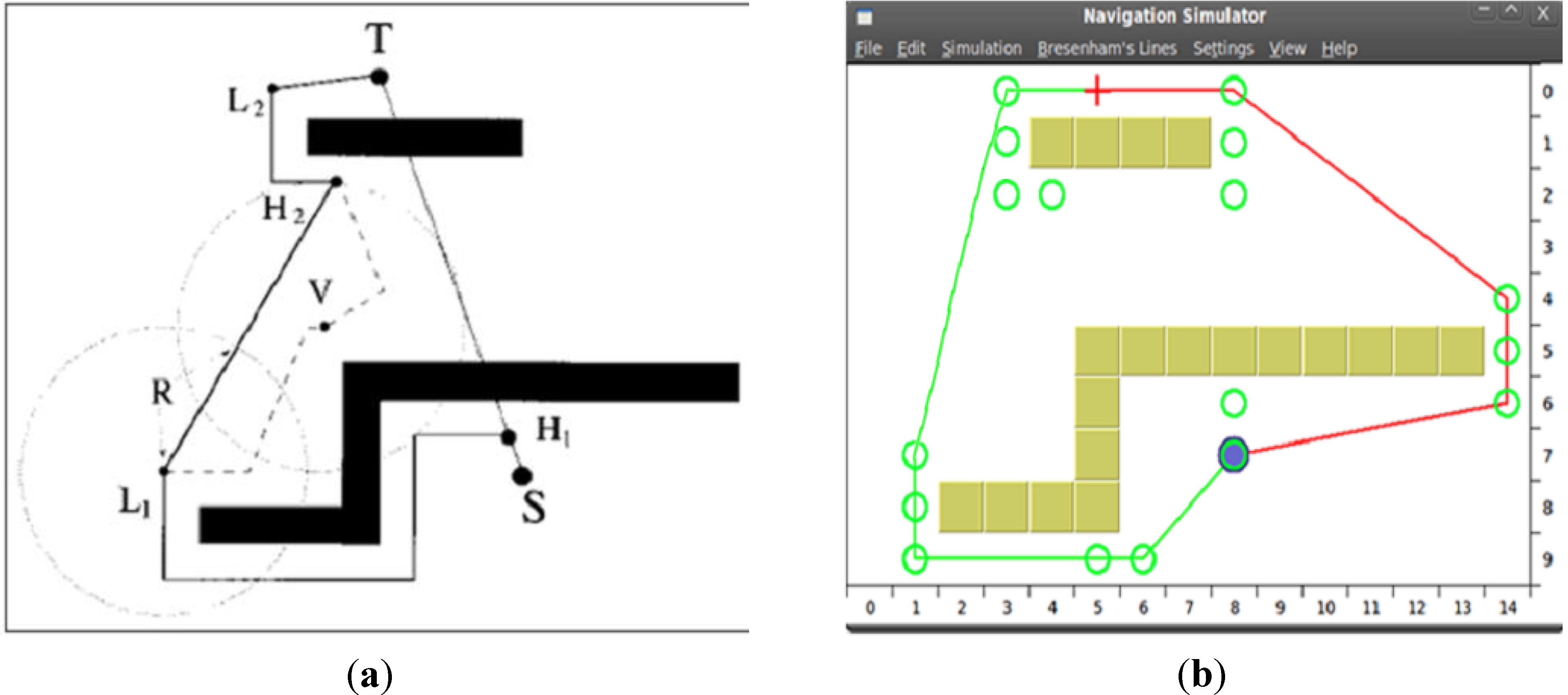
4.3.2. HCTNav vs. DistBug
5. Conclusions
Acknowledgements
Conflict of Interest
References
- Fu, L.; Sun, D.; Rilett, L.R. Heuristic shortest path algorithms for transportation applications: State of the art. Comput. Oper. Res. 2006, 33, 3324–3343. [Google Scholar] [CrossRef]
- Antich, J.; Ortiz, A.; Minguez, J. A Bug-Inspired Algorithm for Efficient Anytime Path Planning. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, St. Louis, MO, USA, 10–15 October 2009; pp. 5407–5413.
- Cormen, T.H.; Leiserson, C.E.; Rivest, R.L.; Stein, C. Dijkstra’s Algorithm. In Introduction to Algorithms, 2nd ed.; MIT Press: Cambridge, MA, USA, 2001; pp. 595–601. [Google Scholar]
- Idris, M.; Bakar, S.; Tamil, E.; Razak, Z.; Noor, N. High-Speed Shortest Path Co-Processor Design. In Proceedings of Third Asia International Conference on Modelling & Simulation, Bali, Indonesia, 25–29 May 2009; pp. 626–631.
- Cain, T. Practical Optimizations for A* Path Generation. In AI Game Programming Wisdom, 2nd ed.; Charles River Editors: Boston, MA, USA, 2003; pp. 146–152. [Google Scholar]
- Grant, K.; Mould, D. Combining Heuristic and Landmark Search for Path Planning. In Proceedings of the Confereunce on Futre Play: Research, Play, Share, Toronto, ON, Canada, 3–5 November 2008; pp. 9–16.
- Goto, T.; Kosaka, T.; Noborio, H. On the Heuristics of A* or A Algorithm in ITS and Robot Path Planning. In Proceedings of IEEE/RSJ International Conference on Intelligent Robot and Systems, Las Vegas, NV, USA, 27–31 October 2003; pp. 1159–1166.
- Bollobas, B. Modern Graph Theory; Springer: Heidelberg, Germany, 1998; pp. 252–259. [Google Scholar]
- Selamat, A.; Zolfpour-Arokhlo, M.; Hashim, S.Z. A Fast Path Planning Algorithm for Route Guidance System. In Proceedings of IEEE International Conference on Systems, Man and Cybernetics, Anchorage, AK, USA, 9–12 October 2011; pp. 2773–2778.
- Langerwisch, M.; Wagner, B. Dynamic Path Planning for Coordinated Motion of multiple Mobile Robots. In Proceedings of IEEE International Conference on Intelligent Transportation Systems, Washington, DC, USA, 5–7 October 2011; pp. 1989–1994.
- Zhou, J.; Lin, H. A Self-Localization and Path Planning Technique for Mobile Robot Navigation. In Proceedings of the Intelligent Control and Automation (WCICA), Taipei, China, 21–25 June 2011; pp. 694–699.
- Abdul-Jabbar, J.M.; Alwan, M.A.; Al-ebadi, M. A new hardware architecture for parallel shortest path searching processor based-on FPGA technology. Int. J. Electron. Comput. Sci. Eng. 2012, 1, 2572–2582. [Google Scholar]
- Jiang, Z.; Wu, J. On Achieving the Shortest-Path Routing in 2-D Meshes. In Proceedings of the Parallel and Distributed Processing Symposium, Long Beach, CA, USA, 26–30 March 2007; pp. 26–30.
- Lumelsky, V.J.; Stepanov, A. Path-planning strategies for a point mobile automaton moving amidst obstacles of arbitrary shape. Algorithmica 1987, 2, 403–430. [Google Scholar] [CrossRef]
- Lumelsky, V.J.; Skewis, T. Incorporating range sensing in the robot navigation function. IEEE Trans. Syst. Man Cybern. 1990, 2, 1058–1068. [Google Scholar] [CrossRef]
- Kamon, I.; Rivlin, E. Sensory-based motion planning with global proofs. IEEE Trans. Robot. Autom. 1997, 13, 814–822. [Google Scholar] [CrossRef]
- Knudson, M.; Tumer, K. Adaptive navigation for autonomous robots. Auton. Robots 2011, 59, 410–420. [Google Scholar] [CrossRef]
- Sharef, S.M.; Sa’id, W.K.; Khoshaba, F.S. A Rule-Based System for Trajectory Planning of an Indoor Mobile Robot. In Proceedings of the International Multi-Conference on Systems Signals and Devices, Amman, Jordan, 27–30 June 2010; pp. 1–7.
- Yu, N.; Ma, C. Mobile Robot Map Building Based on Cellular Automata. In Proceedings of the Pacific-Asia Conference on Circuits, Communications and System, Wuhan, China, 17–18 July 2011; pp. 1–4.
- Gonzalez-Arjona, D.; Sanchez, A.; de Castro, A.; Garrido, J. Occupancy-Grid Indoor Mapping Using FPGA-Based Mobile Robots. In Proceedings of the Conference on Design of Circuits and Integrated Systems, Albufeira, Portugal, 16–18 November 2011; pp. 345–350.
- Buckland, M. Programming Game AI by Example, 1st ed.; Wordware Publishing: Plano, TX, USA, 2005; pp. 193–248. [Google Scholar]
- Bresenham, J.E. Algorithm for computer control of a digital plotter. IBM Syst. J. 1965, 4, 25–30. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Pala, M.; Eraghi, N.O.; López-Colino, F.; Sanchez, A.; De Castro, A.; Garrido, J. HCTNav: A Path Planning Algorithm for Low-Cost Autonomous Robot Navigation in Indoor Environments. ISPRS Int. J. Geo-Inf. 2013, 2, 729-748. https://doi.org/10.3390/ijgi2030729
Pala M, Eraghi NO, López-Colino F, Sanchez A, De Castro A, Garrido J. HCTNav: A Path Planning Algorithm for Low-Cost Autonomous Robot Navigation in Indoor Environments. ISPRS International Journal of Geo-Information. 2013; 2(3):729-748. https://doi.org/10.3390/ijgi2030729
Chicago/Turabian StylePala, Marco, Nafiseh Osati Eraghi, Fernando López-Colino, Alberto Sanchez, Angel De Castro, and Javier Garrido. 2013. "HCTNav: A Path Planning Algorithm for Low-Cost Autonomous Robot Navigation in Indoor Environments" ISPRS International Journal of Geo-Information 2, no. 3: 729-748. https://doi.org/10.3390/ijgi2030729