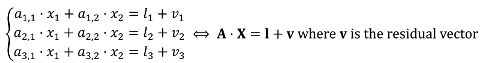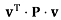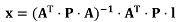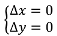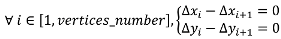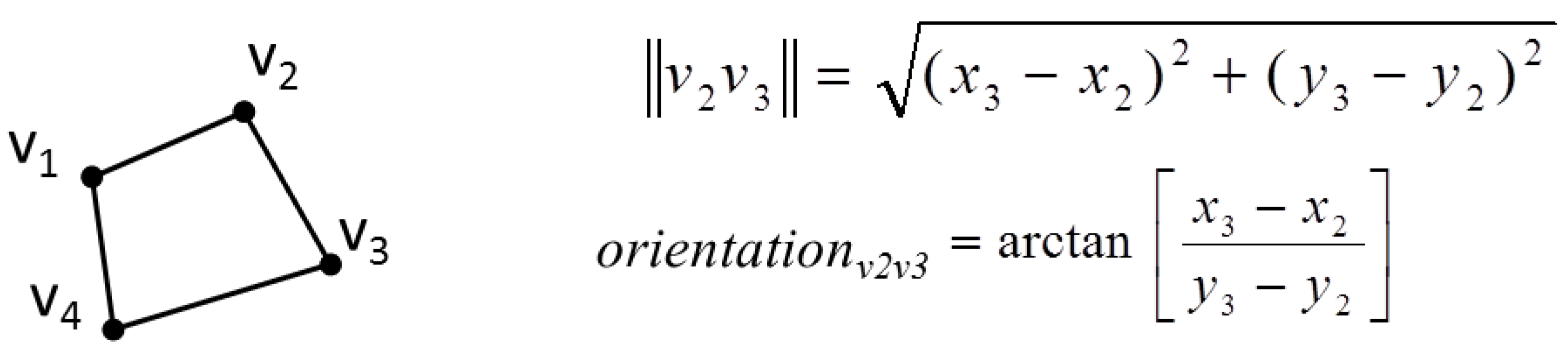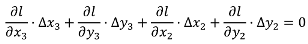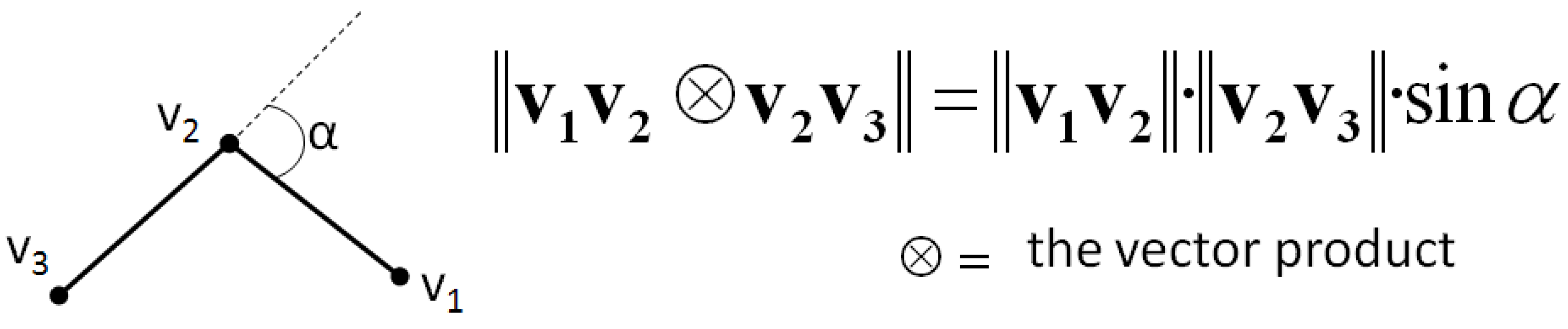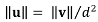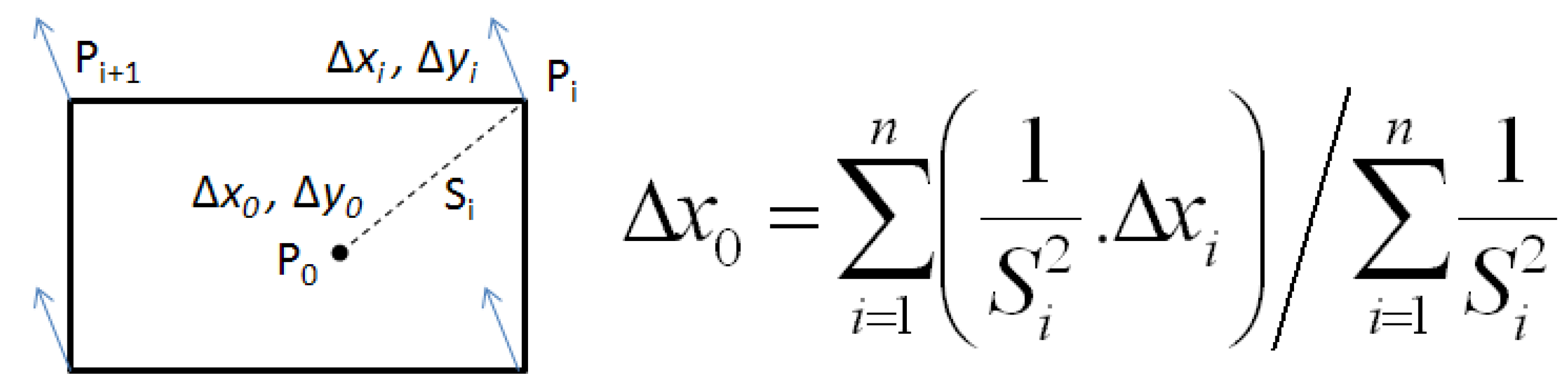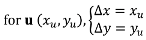The proposed shape preserving conflation framework is based on the least squares generalization model presented in the previous section. The next section describes its principles; then, constraints to maintain shape, to conflate data and to maintain data consistency are presented; finally, additional propagation mechanisms are proposed.
3.2.1. Principles
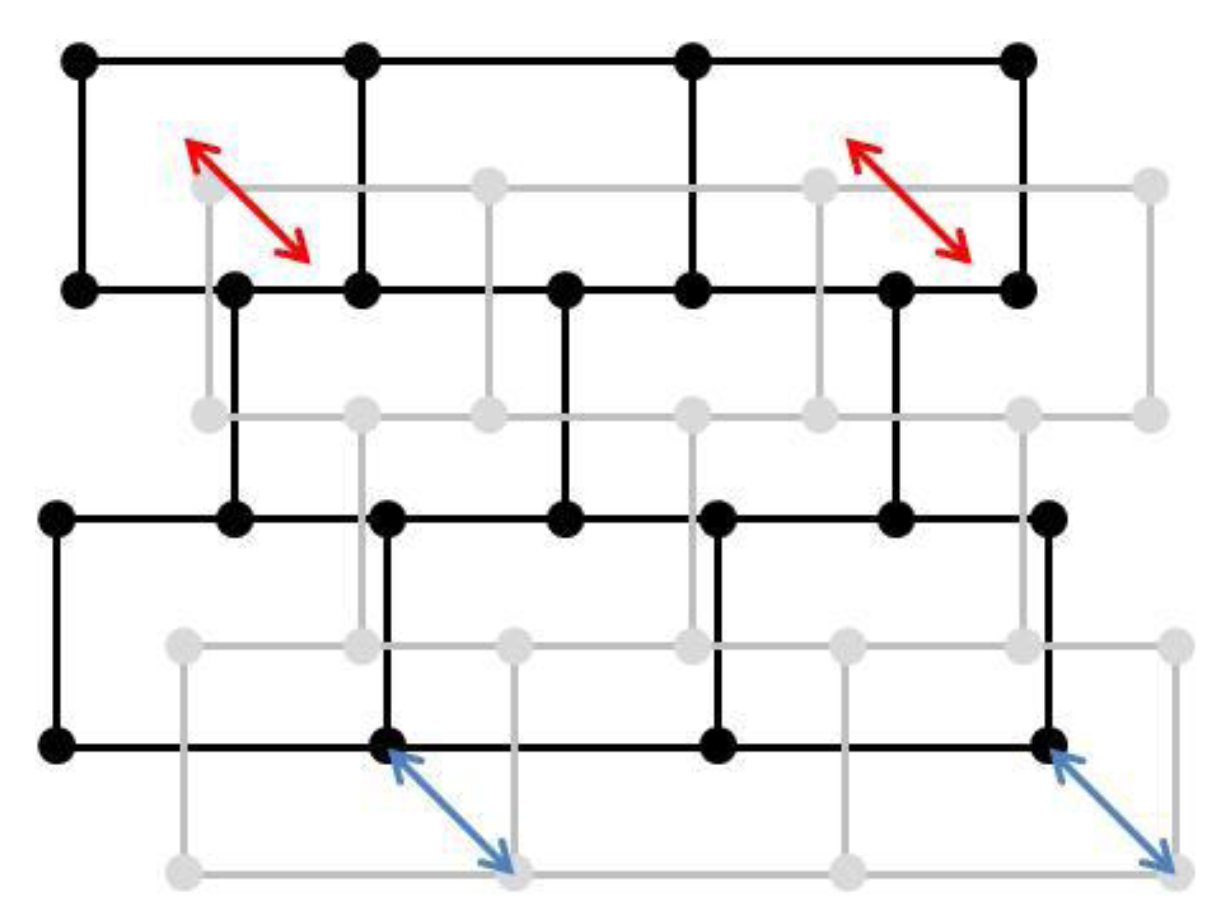
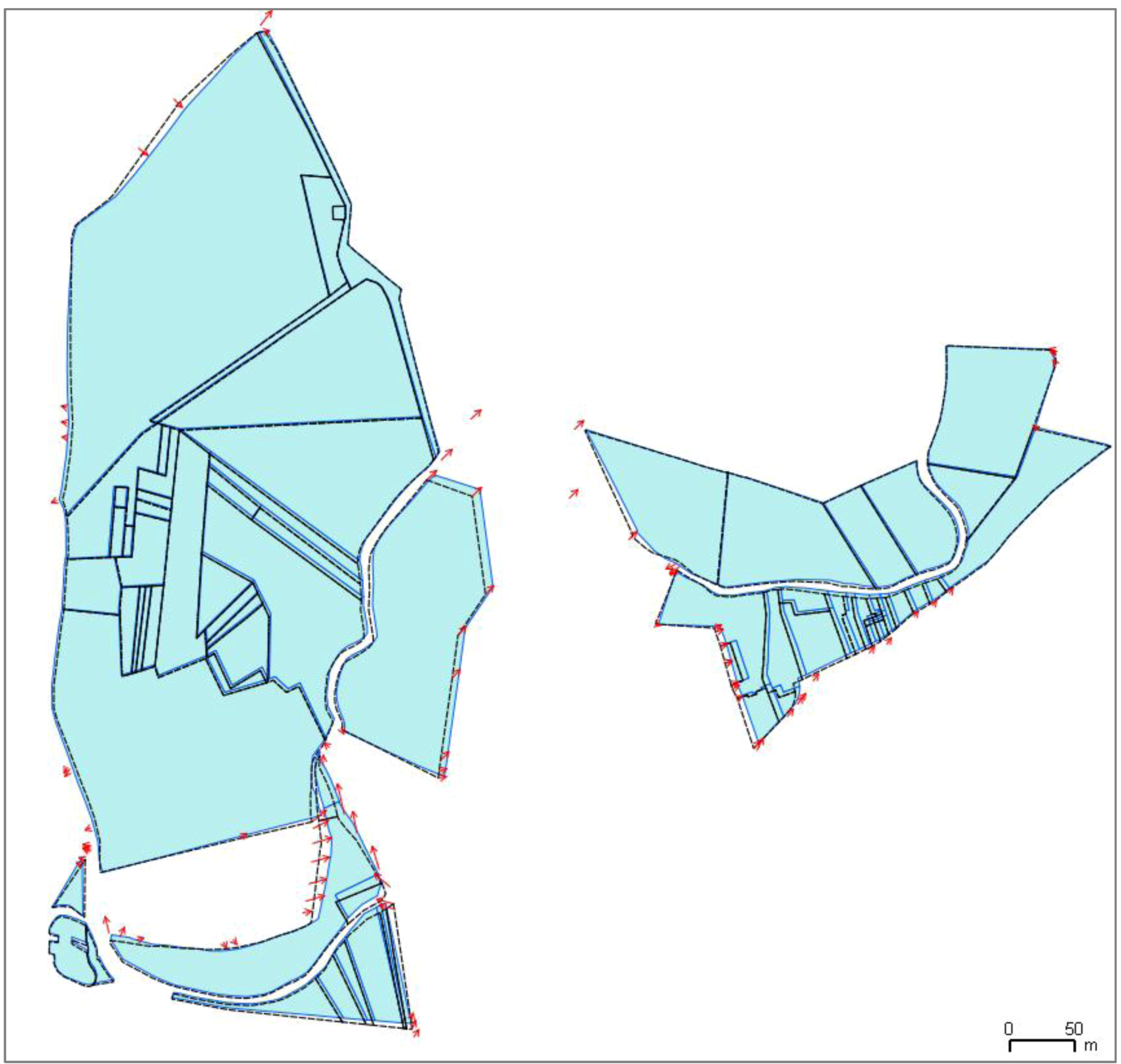
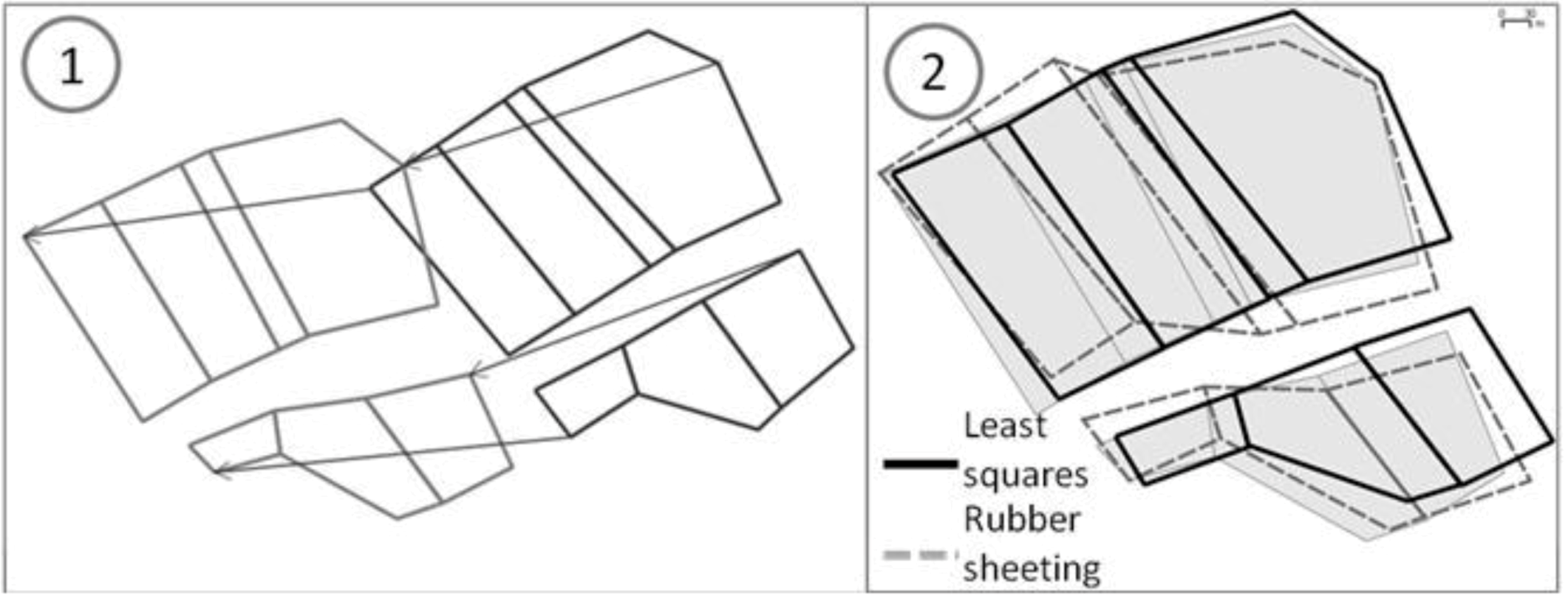
The proposed framework requires a major hypothesis on input data: the datasets to conflate have to be matched, at least minimally. A full feature-to-feature matching is not necessary (
Figure 4). The matching result may be either matched vertices or matched features, like in
Figure 4, but at least one feature or one vertex has to be matched. It is the only requirement for the matching: the framework is able to conflate dataset with one matching or with half of the features matched. Displacement vectors are extracted from the matching, which will guide the least squares conflation: the vectors are computed from points of the matched features belonging to the least precise dataset to points of the corresponding feature in the most precise dataset. If the matched features are structurally different (e.g., not the same level of detail and thus, a different number of vertices), it is not a problem as a displacement vector can be extracted from the centroid, for instance.
Figure 4.
Two sets of polygonal data to be conflated: two feature-to-feature matchings (red arrows) and two vertex-to-vertex matchings (blue arrows).
Figure 4.
Two sets of polygonal data to be conflated: two feature-to-feature matchings (red arrows) and two vertex-to-vertex matchings (blue arrows).
The principles of the least squares shape preserving conflation model takes the generalization model up. The unknowns in the linear equation system are the coordinate displacements ∆
x and ∆
y (including points that were not matched). The unknowns are not the difference between points before and after generalization anymore, but the difference before and after conflation. The equations are translations of constraints on the features to be conflated: a constraint on a feature is translated by one (or more) equation for every point of the feature geometry. Constraints introduced to conflate data are balanced by constraints to preserve the initial shape which leads to an over constrained linear system. As the main goal of the conflation model is to merge geometries, the constraints that control conflation are weighted more than the constraints that preserve shapes. Indeed, weight setting is a key task in this least squares framework [
25]. In order to avoid overloading the equation system, some features can be excluded from the least squares and be conflated thanks to propagation mechanisms derived from map generalization techniques [
26]. Finally, the shape preserving conflation model provides assessment of the deformations carried out to conflate data, derived from residual vector
v, which gives a direct value for the geometrical error estimation of Adams
et al. [
2].
3.2.2. Constraints to Preserve Shape
In order to preserve the shapes of the conflated objects, specific constraints can apply to them, depending on the feature type: for instance, stiffness constraints can apply to buildings or urban land use parcels and curvature constraints can apply to rivers or natural land use parcels. However, a constraint is common to all feature types to avoid over displacements that could lead to horizontal positioning errors: the initial position of the conflated features should be preserved. It corresponds to the movement constraint described by Harrie [
23] and it is translated into two simple equations:
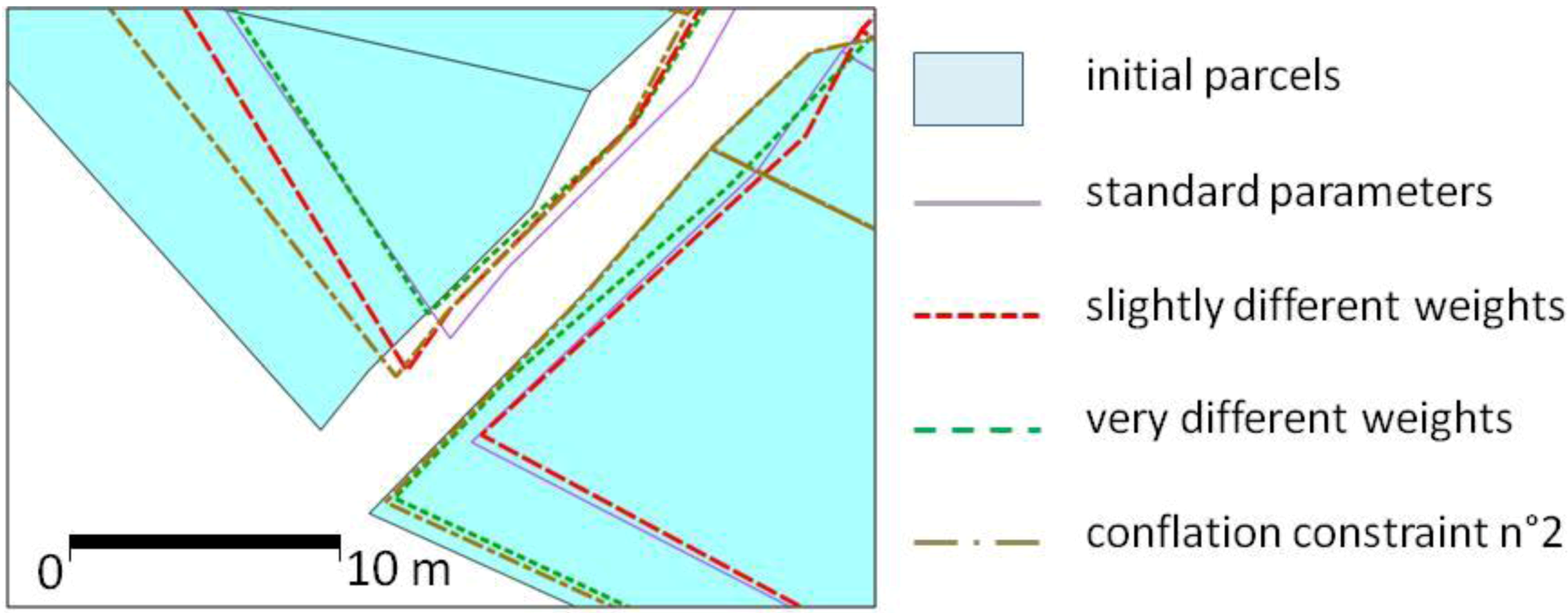
As it is a very restrictive constraint, it should be very slightly weighted to allow some movements in the least squares solutions. For instance, the weight put in the
P matrix lines corresponding to this constraint is 1 in our experiments while other constraints (e.g., the conflation constraint described in
Section 3.2.3) have a weight of 20.
In order to preserve the shape of features that should only be translated and/or rotated, the stiffness constraint from Harrie [
23] constrains the position of successive vertices (Equation (5)).
Alternative preserving constraints are possible for stiff objects that are allowed to be distorted a little more than with the stiffness constraint: a side orientation constraint and a segment length constraint [
24] (
Figure 5). Both equations are nonlinear but can be linearized by derivation, as the unknowns are here ∆x and ∆y. Thus, the preservation of length l of the segment |v2, v3| would be the linear Equation (6). The same linearization can be applied to the side orientation constraint.
Figure 5.
Nonlinear equations for segment length and orientation in a stiff feature.
Figure 5.
Nonlinear equations for segment length and orientation in a stiff feature.
The previous shape preservation constraints are mostly dedicated to stiff (or man-made) features like buildings, streets, or parcels. But considering features whose shape was crafted by nature like rivers, forests, mountain roads, or lakes, requires the definition of other constraints. We propose to use the curvature constraint introduced by Harrie [
23] that forces the preservation of the curvature between successive line segments. The problem of curvature preservation is transformed into a simpler problem, the preservation of the angle α between two successive line segments, which is linearized using the vector product definition (
Figure 6). The computation of the linear equation from the vector product is detailed by Harrie [
23].
Figure 6.
Expression of the curvature preservation constraint.
Figure 6.
Expression of the curvature preservation constraint.
3.2.3. Constraints to Conflate Data
To balance the constraints to maintain shape, it is necessary to introduce constraints that force conflation. We compute such constraints based on matches of features. Our least squares conflation framework requires these matches as input. Three kind of conflation constraints are proposed in the framework from very local action to propagation actions close to the rubber sheeting approach. For each one, the cases where it should be used are briefly discussed.
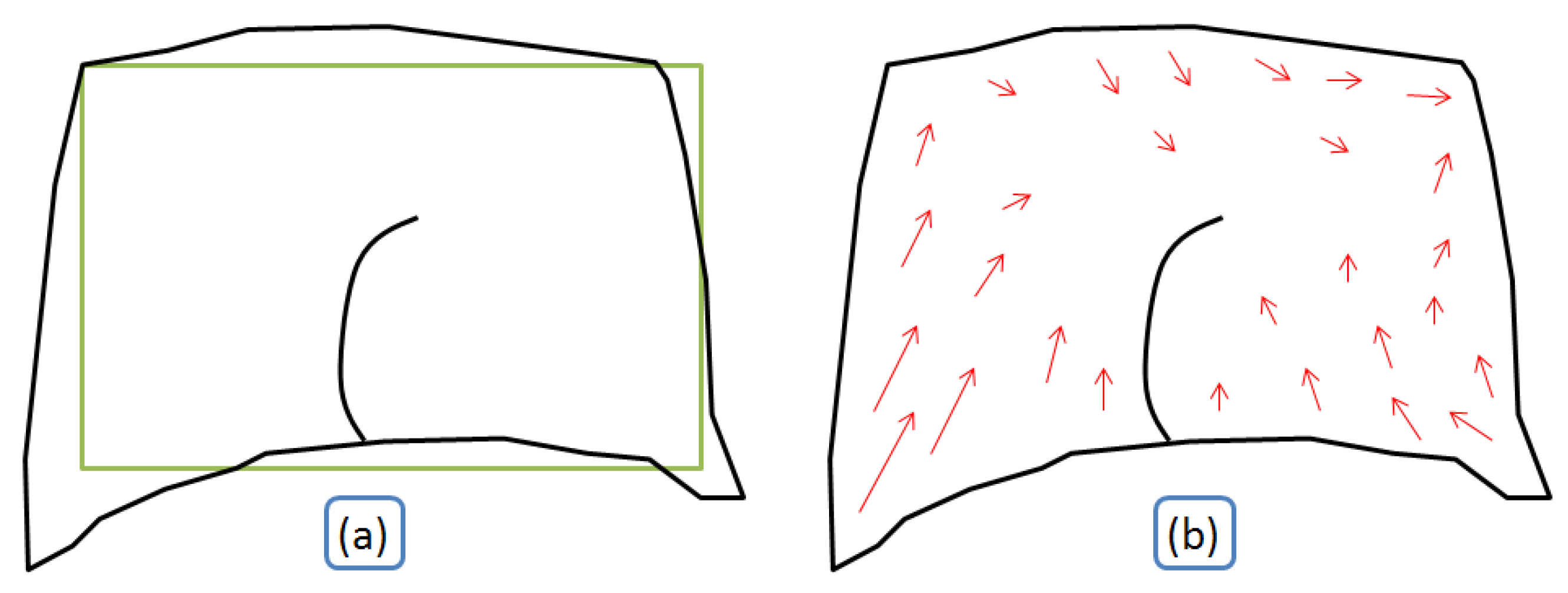
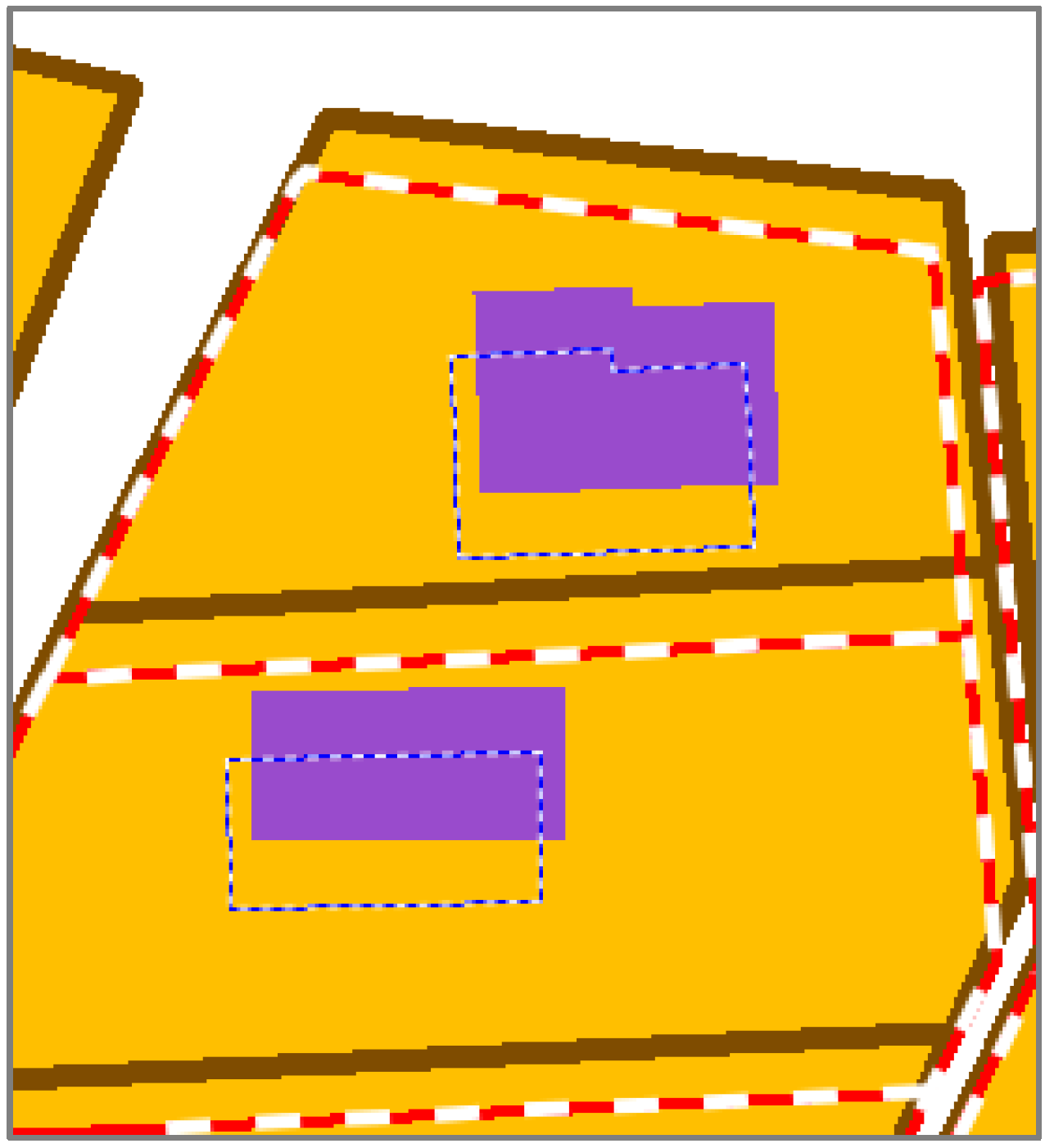
All constraints rely on the computing of displacement vectors from the features matched in the conflated datasets. For each matched feature, the feature matching is transformed into vertex matching: the vertices in the less detailed dataset are matched to vertices of the matched feature in the most detailed dataset (
Figure 7). Displacement vectors are computed for each matched vertex from the least detailed dataset to the most detailed one: the vectors represent the displacement the vertices should do, to conflate the geometries.
Figure 7.
Computing vector displacement from the partial matching of features (the textured features are matched).
Figure 7.
Computing vector displacement from the partial matching of features (the textured features are matched).
In the first two proposed constraints, only the features close to matched points (
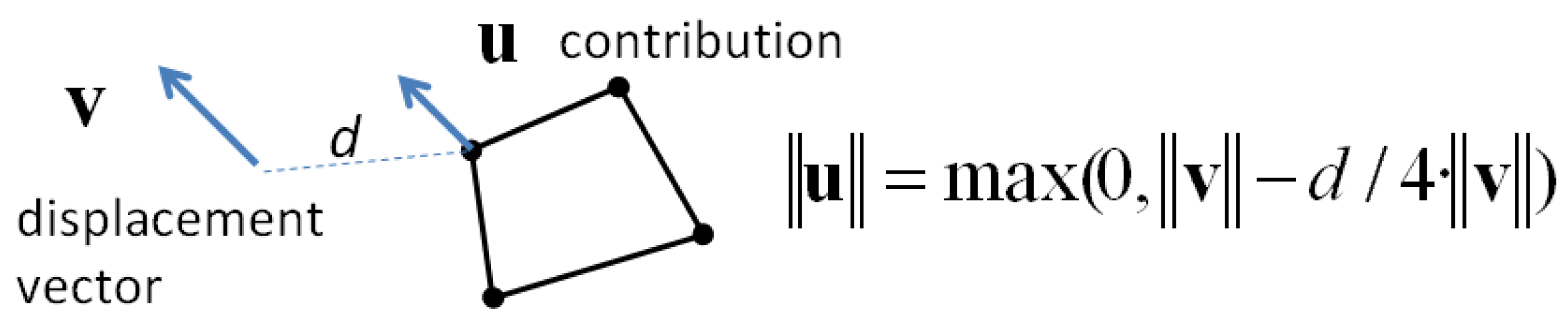
i.e., to displacement vectors) are constrained, the other features being conflated only by shape preservation and data consistency constraints. In the first constraint, the influence of displacement vectors is local: only the closest vertex of the close features, to a displacement vector, is constrained by this displacement vector. The search radius is proportional to the vector length (a “5 times length” threshold was used in our implementation). The vertex is constrained with the same direction as the vector but the length is absorbed proportionally to distance, with a factor (4 is proposed) that slows the absorption (
Figure 8). This constraint is sufficient when the positional shift between the conflated datasets is low and is effective when the number of previously matched features is low.
Figure 8.
Conflation constraint 1: contribution of the displacement vector to the closest vertex of close features.
Figure 8.
Conflation constraint 1: contribution of the displacement vector to the closest vertex of close features.
The second constraint is very similar to the first one as the constrained features and vertices are the same. The difference lies in the way the contribution norm is computed (Equation (7)), which absorbs more quickly the displacements. This constraint is preferred to the first one when the positional shift between datasets is large, as it avoids unexpected deformations.
The third constraint is inspired from the rubber sheeting conflation method and is applied on every vertex of every conflated feature. Every vector contributes in an inverse proportional way to the computation of the propagation in a given point (
Figure 9). This constraint is particularly effective in datasets where the positional shift between the datasets is large, as the big deformation is propagated and absorbed by a bigger number of features.
Figure 9.
Computation of the contribution of displacement vectors in a given point P0.
Figure 9.
Computation of the contribution of displacement vectors in a given point P0.
For the three constraints, the linear equations on the constrained points are very simple, for a vector
u that aggregates the displacement vectors contributions:
3.2.4. Constraints to Maintain Data Consistency
The previous sections propose constraints that allow a conflation that preserve the initial shape of geographic objects. But geographic objects are not isolated in a dataset and share relationship, particularly topological and proximity relations. Our least squares based conflation framework allows preserving these geographic relations thanks to dedicated constraints; three constraints are presented in this section. None is dedicated to topology preservation as topology preservation is inferred in our framework: when features share geometries, their common vertices are only taken into account once in the adjustment and when geometries are transformed by adjustment results, one vertex displacement modifies all features that share the vertex.
The first presented constraint preserves proximity relations between conflated features,
i.e., the inter-distance between conflated features does not greatly increase nor decrease. This constraint is inspired from the spatial conflicts constraints from Harrie and Sester [
23,
24] that ensure a minimal distance between feature symbols. The constraint relies on the computation of neighborhoods for every feature to identify the initial proximity relations. As in [
23,
24], the neighborhood computation is based on a constrained Delaunay triangulation [
27,
28] of the features vertices (and constrained by the features segments). The triangulation graph is pruned to identify real proximities (
Figure 10): edges inside features are dropped as well as too long edges (if features are too far, it is not a proximity relation!). Like Harrie’s method [
23], the remaining edges allow introducing two kinds of constraints: point-to-point constraints and point-to-segment constraints. When edges represent the shortest distance between two features (case 3 in
Figure 10), a segment length constraint (Equation (6)) is put on the extreme points of the edge (point-to-point distance). When the distance between two features separated by a triangle is less than the shortest edge between them (case 4 in
Figure 10), a point-to-segment constraint is introduced, which deals with the three nodes of the triangle. The distance to preserve is the distance between the single point and the middle of the two other points. This distance expressed with the coordinates of the three points is not linear [
23], so the derivative is used like in (Equation (6)) to get the linear equation that preserves this distance.
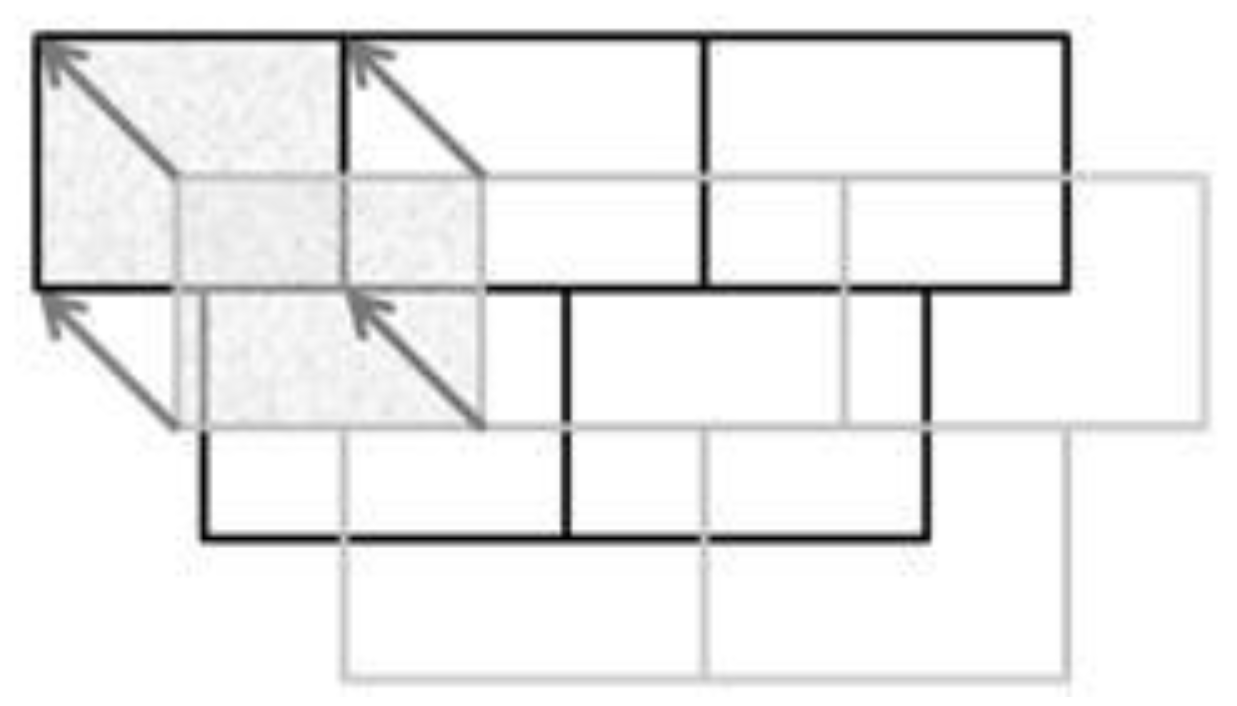
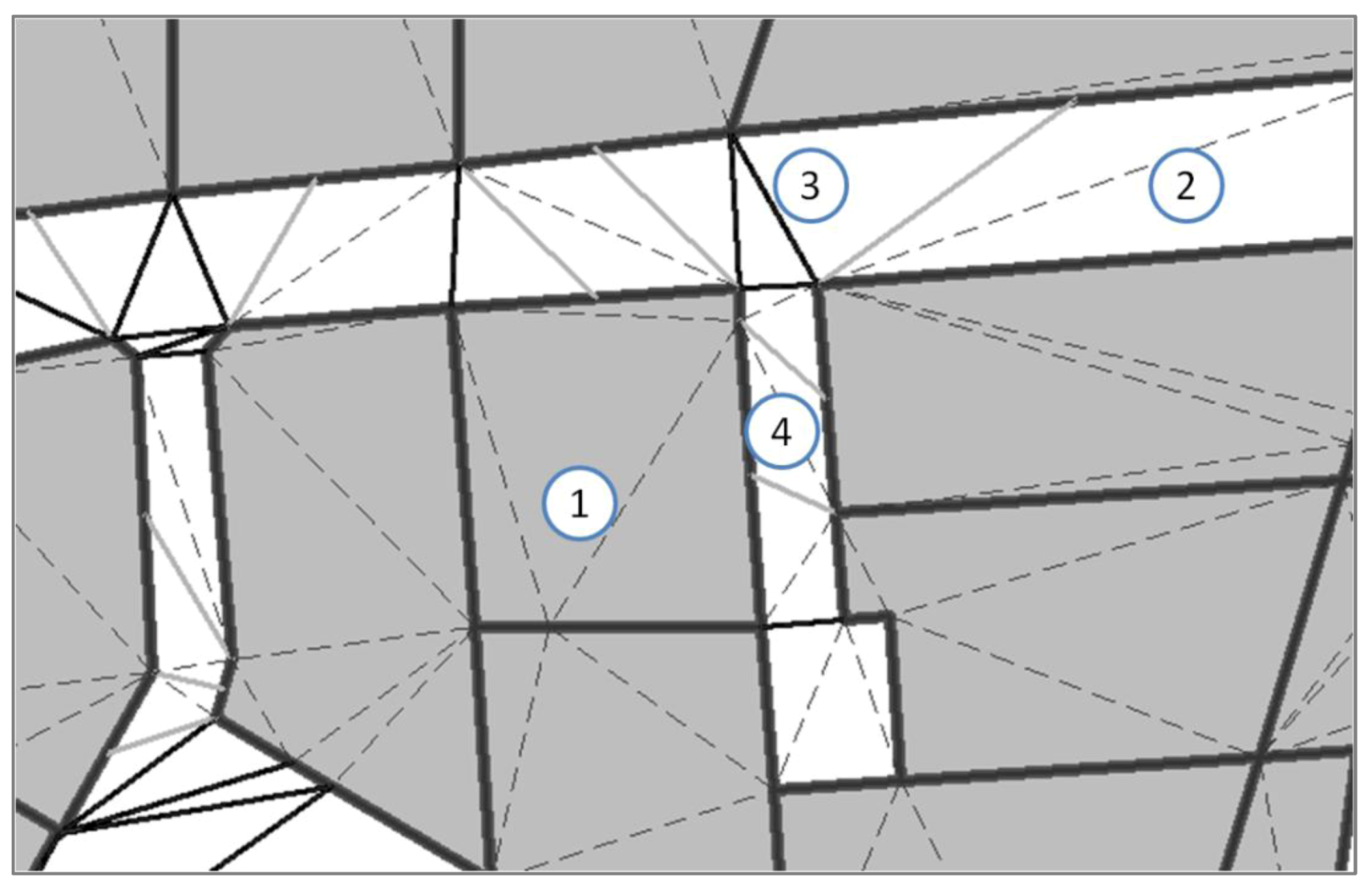
Figure 10.
Constrained Delaunay triangulation used to identify proximities: (1) dashed edges dropped because inside objects, (2) edge dropped as distance > threshold, (3) black edges used for point-to-point proximity, (4) grey edges used for point-to-segment proximity.
Figure 10.
Constrained Delaunay triangulation used to identify proximities: (1) dashed edges dropped because inside objects, (2) edge dropped as distance > threshold, (3) black edges used for point-to-point proximity, (4) grey edges used for point-to-segment proximity.
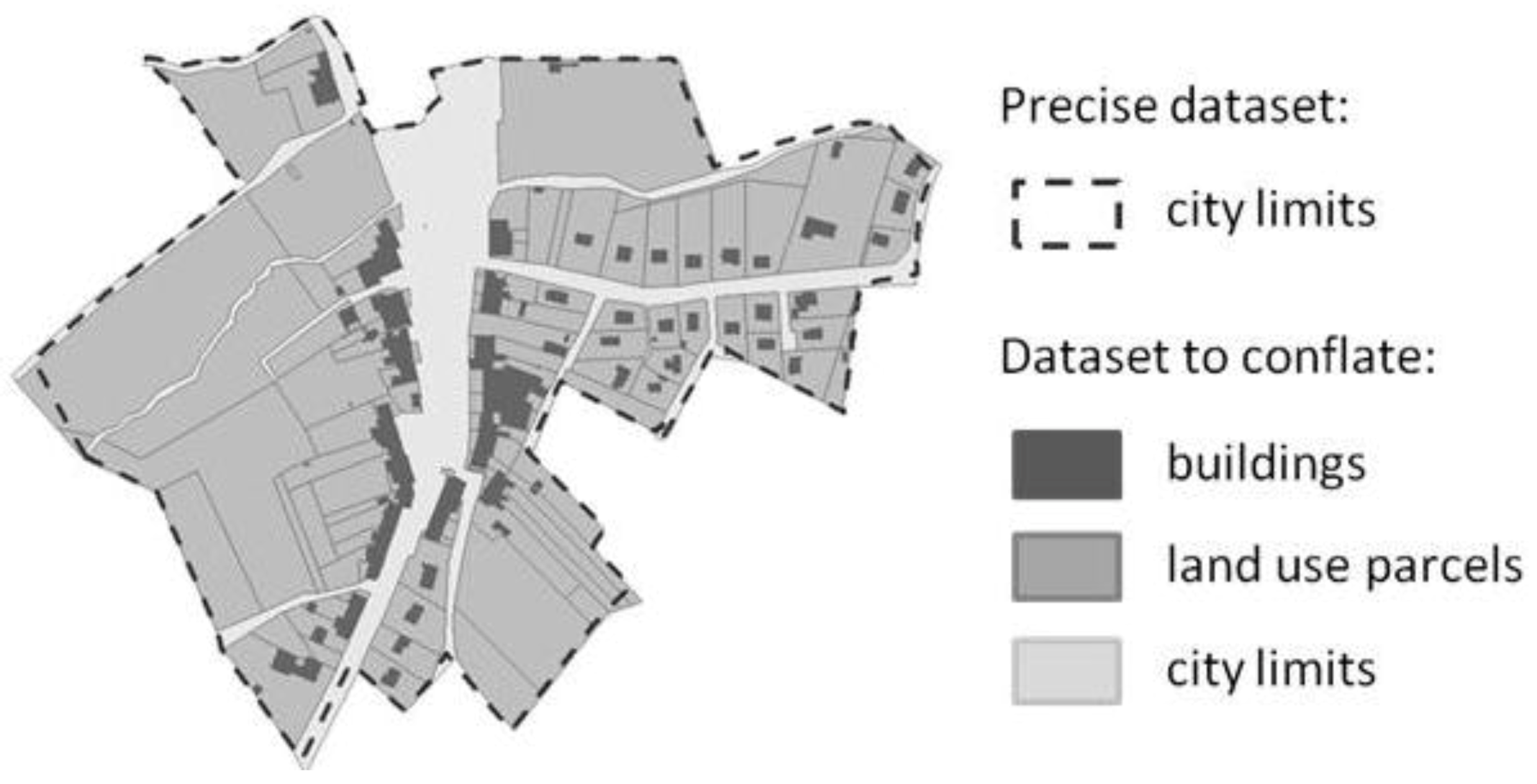
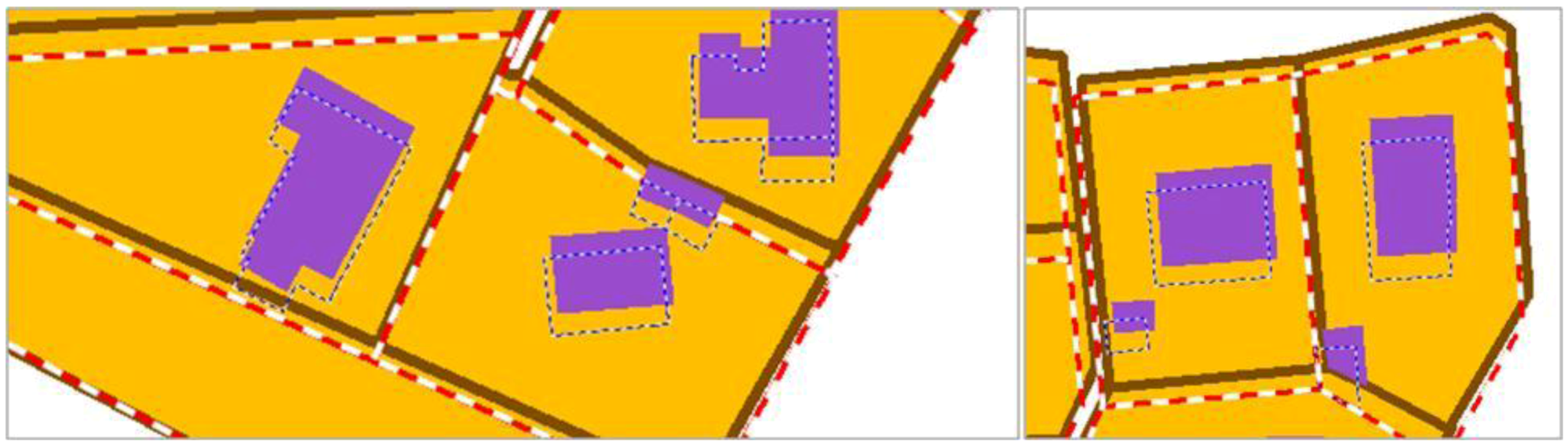
In order to preserve relations with features that are not part of conflation (for instance, additional features in the most detailed dataset), the same type of constraint can be adapted. The same neighborhood computation principle is used but equations are simpler in the derivative computation, as the vertices of the non-conflated features are fixed (the derivative of their coordinates is zero). In the test case presented in the results section, land use parcels are conflated with a more detailed dataset that contains precise city limits, in which the parcels are conflated and a road network with good positional accuracy. The proximity between parcels and roads is preserved so that parcels might not cross roads.
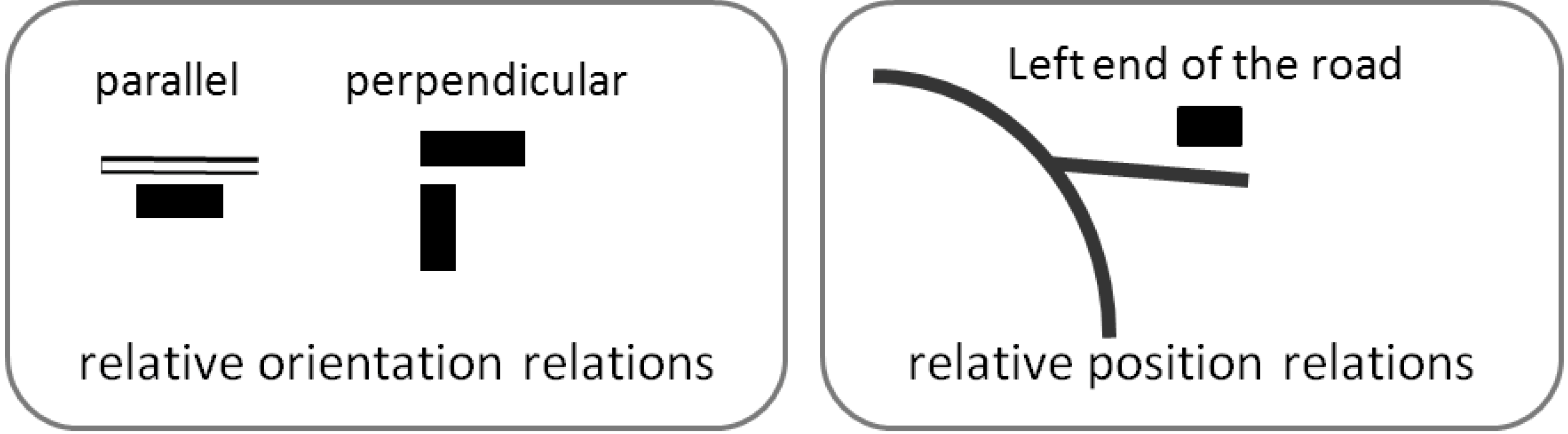
In addition to proximity relations, it may be important to preserve relative orientation relations (e.g., a building parallel to a road, buildings whose main orientation is perpendicular,
etc.) and relative position relations (e.g., a building is at the left end of dead end road) (
Figure 11). The proposed conflation framework contains constraints to preserve each of the three kinds of relations.
Figure 11.
Examples of relative orientation and position relations to preserve during conflation.
Figure 11.
Examples of relative orientation and position relations to preserve during conflation.
As with the proximity relations, these relations should first be identified in the initial data, and then the constraints are applied to the related features. The relative position relation is identified each time there is a proximity relation (identified by triangulation) between features that are prone to this kind of constraints (e.g., a dead end and a building). The identification of relative orientation relations is also based on proximities and relies on the measure of the general orientation of polygons [
29]: when the general orientations of two close features are either parallel or perpendicular, a constraint is added.
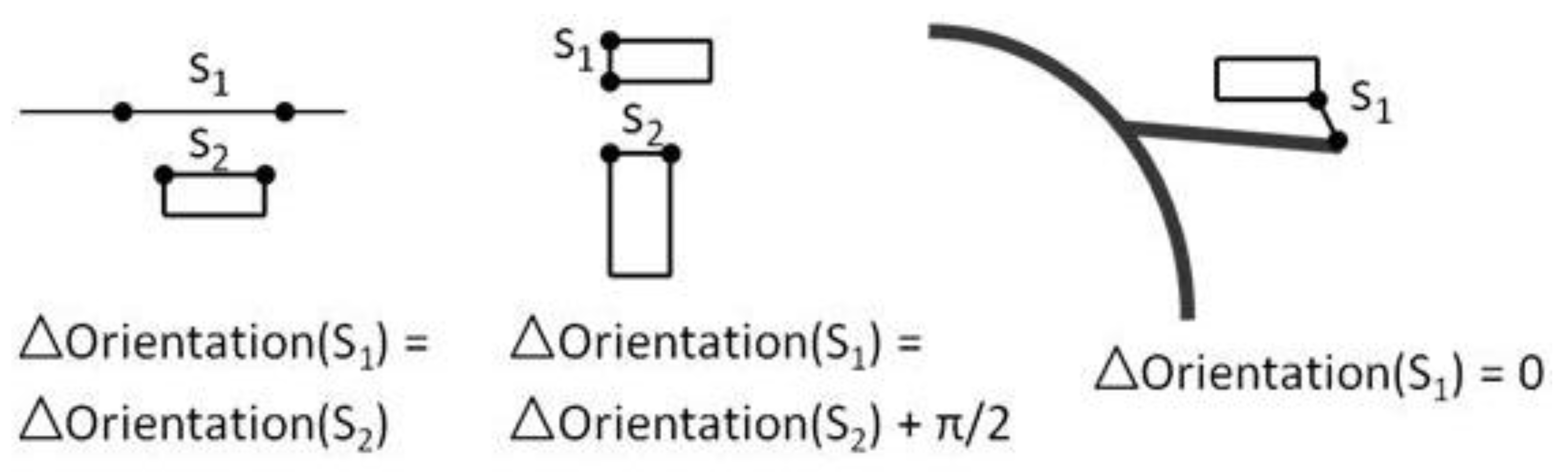
Figure 12 describes how both constraints are transformed into linear equations on feature vertices. The orientation of the chosen segments is computed as in
Figure 5 and linearized as in Equation (6).
Figure 12.
Constraint expression of the preservation of relative orientation and position relations.
Figure 12.
Constraint expression of the preservation of relative orientation and position relations.
3.2.5. Propagation of Additional Data
The experiments will show that the least squares conflation framework may generate very large equation systems that could slow computation down or even prevent the solution from being computed. In order to avoid too large systems, the framework allows excluding features from least squares conflation and applying to the excluded features propagation mechanisms from the least squares solution. Two kinds of mechanisms are proposed, one for features topologically connected to conflated features and one for features that are inside or near conflated features.
Both mechanisms rely on the computation of vectors from the least squares displacements. Every vector contributes in an inverse proportional way to the computation of the propagation in a given point (
Figure 9), like in the third conflation constraint, or like in the rubber sheeting processes.
In order to allow a propagation on additional features topologically connected to conflated features, which preserves the topological connection, the framework identifies the topological relationships before the conflation. Therefore, topological connection points are added to the geometry points that are constrained. This addition is automatically done in the implemented framework, benefiting from the GIS capabilities of the platform. Then, the least square solution on the connected points is applied to both features. The remaining points of the propagated features are displaced as in
Figure 9, considering only the vectors of the connected points (
Figure 13). If the connected points have quite different displacement vectors, the propagated feature may be distorted. Nevertheless, it is preferred to preserve topology rather than shape here, as preserving both is not possible. Added to that, if the least squares conflation does preserve shape, the case with quite different vectors on connected points will not occur.
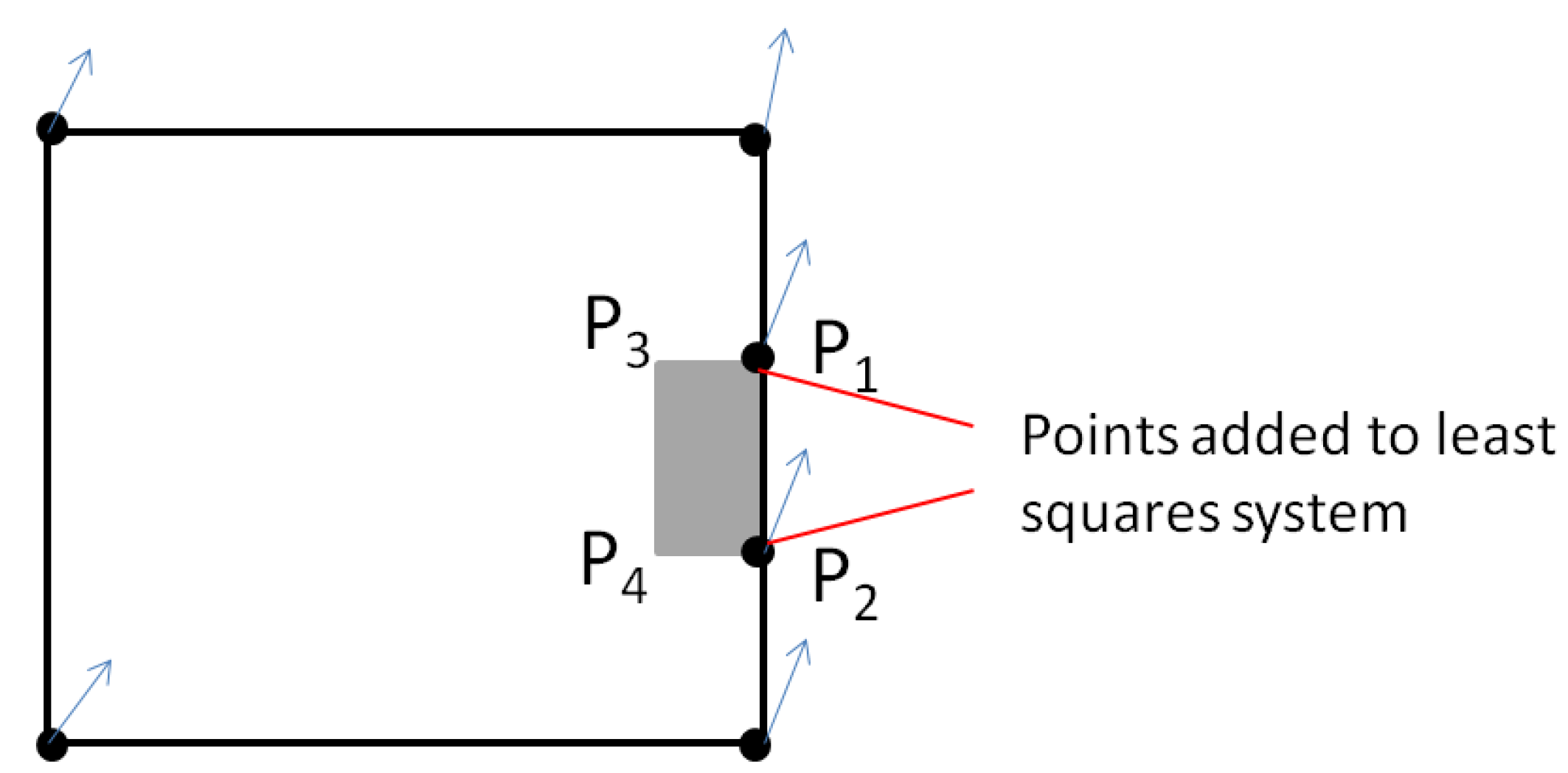
Figure 13.
Propagation for topologically connected objects: the connected points are added to the system and a propagated displacement is applied to the remaining points (P3 and P4).
Figure 13.
Propagation for topologically connected objects: the connected points are added to the system and a propagated displacement is applied to the remaining points (P3 and P4).
For the additional objects that are not topologically connected to features conflated by least squares (
i.e., features inside or near conflated features), a propagation is computed as in
Figure 9 on the centroid of the features. Then, the features are simply translated using the centroid propagation, preserving their initial shape.
The decision on which features to propagate and which features to adjust requires knowledge of the use case. Therefore, we leave this decision to the user. However, some general rules to choose can be enunciated:
Only unmatched features should be propagated.
Small features and rigid features like should be preferred for propagation as such features often need fewer distortions.
Features inside conflated features are good candidates for propagation, as it provides accurate propagation vectors.