Recent Trends in Lower-Limb Robotic Rehabilitation Orthosis: Control Scheme and Strategy for Pneumatic Muscle Actuated Gait Trainers
Abstract
:1. Introduction
2. Existing Lower-Limb Orthoses for Gait Rehabilitations and Evaluations
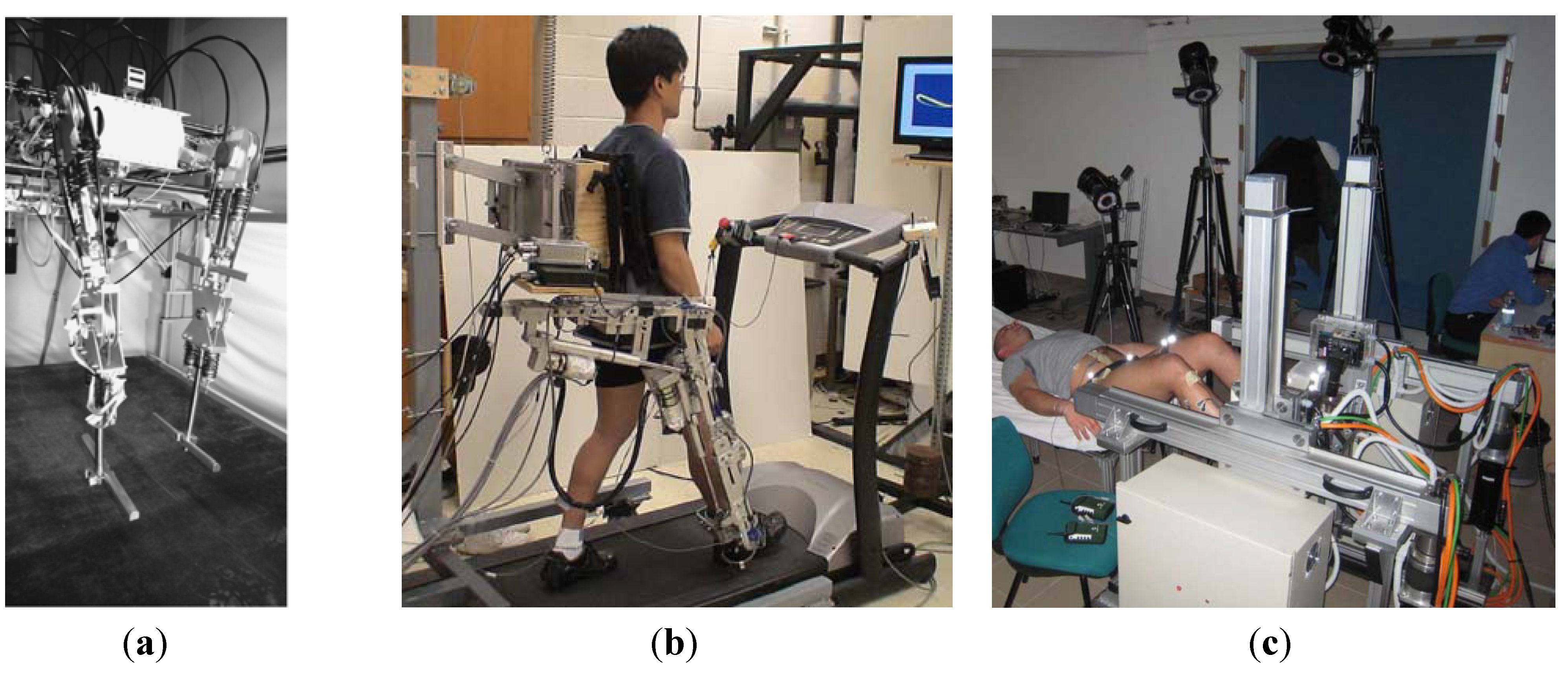
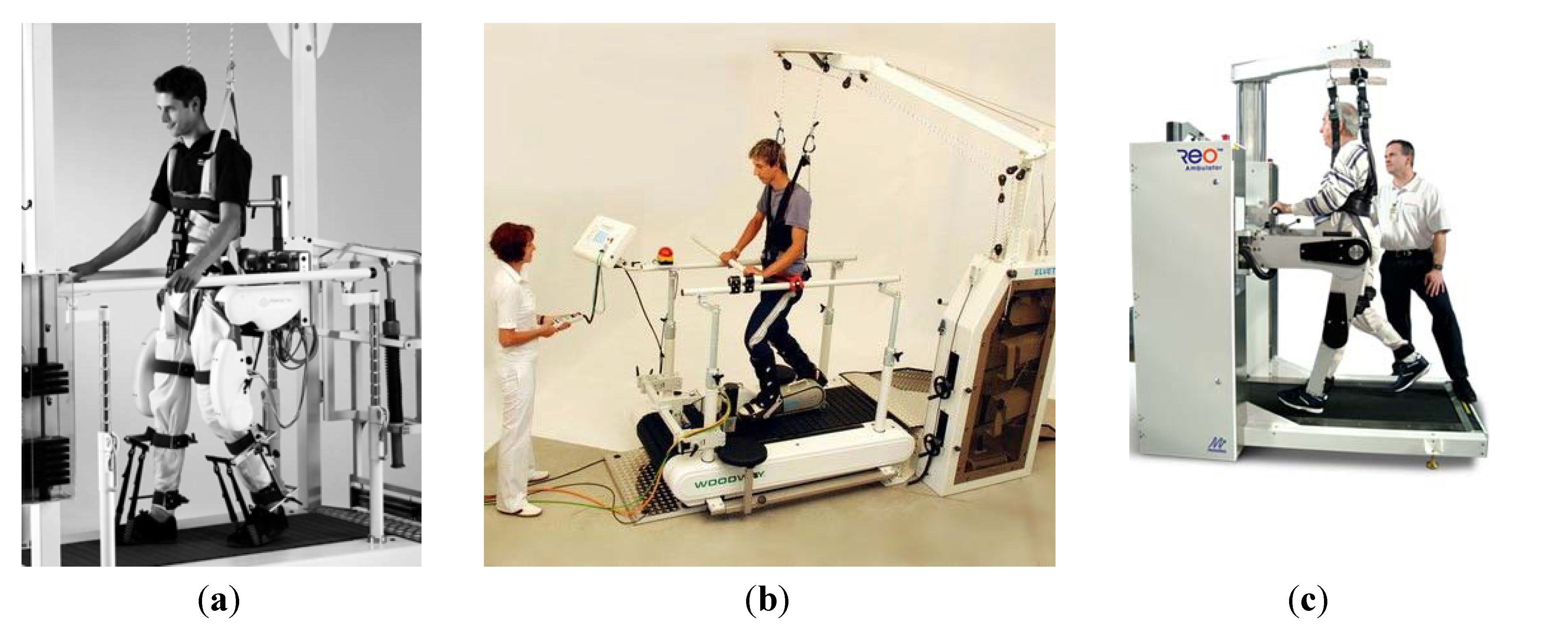
2.1. Motorized Lower-Limb Orthosis Systems for Rehabilitation
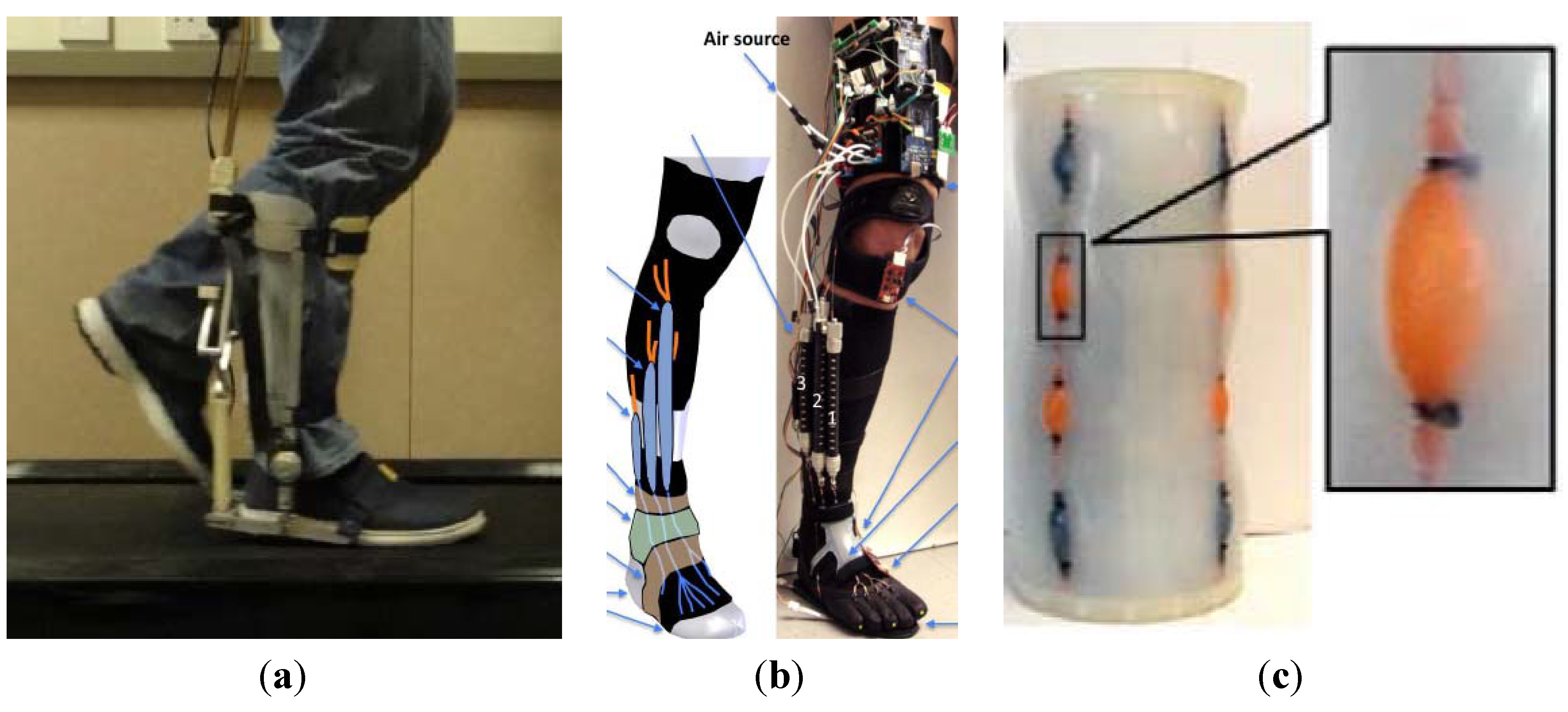
2.2. Attributes of Pneumatic Muscle Actuators (PMA)
2.3. Pneumatic Muscle Actuated Lower-Limb Rehabilitation Orthosis System




| Comparison of Existing Pneumatic Muscle Actuated Lower-Limb Rehabilitation Orthosis Systems | ||||||
|---|---|---|---|---|---|---|
| Orthosis System | Time Scale | Robotic System Types | Actuators | Antagonistic Actuators | Control System | References |
| Hip orthosis exoskeleton | 2004 | Hip orthoses | McKibben pneumatic muscle | Mono-articular for hip joint (flexion) | Position control using the potentiometers for activating the control valves | [31,32] |
| Robotic gait trainer (RGT) | 2006 | Foot orthoses | Lightweight spring over muscle (SOM) | Mono-articular for ankle joint (dorsiflexion) | Angular position control system | [33] |
| Ankle-foot orthosis (AFO) | 2006 | Foot orthoses | McKibben pneumatic muscle | Mono-articular for ankle joint (dorsiflexion and plantar-flexion) | Proportional myoelectric control using a PC-based controller | [34,35,36] |
| Powered lower-limb orthosis | 2006 | Treadmill gait trainers | Pneumatic muscle actuators (PMA) | Mono-articular for hip joint (flexion, extension, abduction and adduction), knee joint (flexion and extension) and ankle joint (dorsiflexion and plantar-flexion) | Intelligent embedded control mechanism (a three-level PID joint torque control scheme) | [37] |
| Robotic gait trainer in water (RGTW) | 2008 | Over-ground gait trainers with orthosis | McKibben pneumatic muscle | Mono-articular for hip joint (flexion and extension) and knee joint (flexion and extension) | Position control system | [38] |
| Powered ankle-foot exoskeleton | 2009 | Foot orthoses | Pneumatic artificial muscle (PAM) | Mono-articular for ankle joint (dorsiflexion and plantar-flexion) | Electromyography (EMG) control with feed-forward algorithm | [39,40,41,42] |
| Powered knee-ankle-foot orthosis (KAFO) | 2009 | Knee and foot orthoses | McKibben pneumatic muscle | Mono-articular for knee joint (flexion and extension) and ankle joint (dorsiflexion and plantar-flexion) | Physiological-inspired controller using electromyography | [43] |
| Continuous passive motion (CPM) | 2009 | Stationary gait and ankle trainers | Pneumatic artificial muscle (PAM) | _ | _ | [44] |
| Power-assist lower-limb orthosis | 2010 | Over-ground gait trainers (mobile) | McKibben pneumatic muscle | Mono-articular for knee joint (extension) | Inverse control and loop transfer recovery (LTR) feedback control | [45] |
| Active ankle-foot orthosis (AAFO) | 2011 | Foot orthoses | McKibben pneumatic muscle | Mono-articular for ankle joint (plantar-flexion) | Feedback control that utilizes a fuzzy logic gait phase detection system | [46] |
| Bio-inspired active soft orthotic device | 2011 | Foot orthoses | Pneumatic artificial muscle (PAM) | Mono-articular for ankle joint (dorsiflexion, inversion and eversion) | Feed-forward and feedback controllers | [47] |
| Active modular elastomer sleeve for soft wearable assistance robots | 2012 | Knee orthoses | Miniaturized McKibben pneumatic muscle | Mono-articular for knee joint (flexion and extension) | Through shape and rigidity control | [48] |
| Knee-ankle-foot orthosis (KAFO) | 2012 | Knee and foot orthoses | Pneumatic artificial muscle (PAM) | Mono-articular for hip joint (flexion and extension) and knee joint (flexion and extension) | _ | [49] |
| Orthosis for walking assistant | 2013 | Hip orthoses | Straight fiber pneumatic artificial muscle (PMA) | Mono-articular for hip joint (flexion) | Dual pneumatic control system (DPCS) with a pulse-width modulation (PWM) signal | [50] |
| Six degree of freedom robotic orthosis for gait rehabilitation | 2013 | Treadmill gait trainers | McKibben pneumatic muscle | Mono-articular for hip joint (flexion and extension) and knee joint (flexion and extension) | Adaptive impedance control using boundary-layer-augmented sliding mode control (BASMC) | [51,52] |
3. Control Scheme and Strategy
3.1. Pneumatic Muscle Actuators’ Control System
3.2. Co-Contraction of Antagonistic Muscle Control
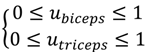
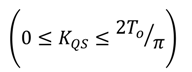
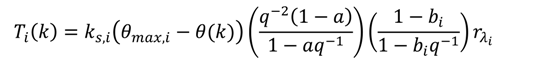
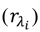 is the desired recruitment level, (q−1) is the backward shift operator, (q−2) is the delay of two sampling steps and (k) is the sampling index.
is the desired recruitment level, (q−1) is the backward shift operator, (q−2) is the delay of two sampling steps and (k) is the sampling index.
3.3. Simulation of the Co-Contraction Model for Antagonistic Muscles

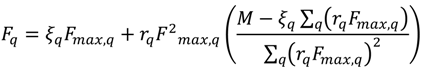
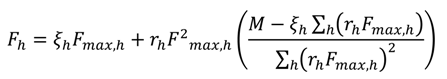
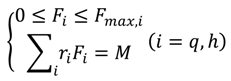
3.4. Co-Contraction Model for Antagonistic Actuators
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Wernig, A.; Muller, S.; Nanassy, A.; Cagol, E. Laufband therapy based on “rules of spinal locomotion” is effective in spinal cord injured persons. Eur. J. Neurosci. 1995, 7, 823–829. [Google Scholar] [CrossRef]
- Wernig, A.; Nanassy, A.; Muller, S. Maintenance of locomotor abilities following laufband (treadmill) therapy in para- and tetraplegic persons: Follow-up studies. Spinal Cord 1998, 36, 744–749. [Google Scholar]
- Dietz, V.; Muller, R.; Colombo, G. Locomotor activity in spinal man: Significance of afferent input from joint and load receptors. Brain 2002, 125, 2626–2634. [Google Scholar] [CrossRef]
- Dietz, V.; Harkema, S.J. Locomotor activity in spinal cord-injured persons. J. Appl. Physiol. 2004, 96, 1954–1960. [Google Scholar] [CrossRef]
- Díaz, I.; Gil, J.J.; Sánchez, E. Lower-limb robotic rehabilitation: Literature review and challenges. J. Robot. 2011, 2011, 759764:1–759764:11. [Google Scholar]
- Marchal-Crespo, L.; Reinkensmeyer, D.J. Review of control strategies for robotic movement training after neurologic injury. J. Neuro-Eng. Rehabil. 2009, 6, 20:1–20:15. [Google Scholar]
- Pennycott, A.; Wyss, D.; Vallery, H.; Klamroth-Marganska, V.; Riener, R. Towards more effective robotic gait training for stroke rehabilitation: A review. J. Neuro-Eng. Rehabil. 2012, 9, 1–13. [Google Scholar] [CrossRef]
- Dollar, A.M.; Herr, H. Lower extremity exoskeletons and active orthoses: Challenges and state-of-the-art. IEEE Transact. Robot. 2008, 24, 144–158. [Google Scholar] [CrossRef]
- Colombo, G.; Wirz, M.; Dietz, V. Driven gait orthosis for improvement of locomotor training in paraplegics patients. International Medical Society of Paraplegia. Spinal Cord 2001, 39, 252–255. [Google Scholar] [CrossRef]
- Jazernik, S.; Colombo, G.; Morari, M. Automatic gait pattern adaptation algorithms for rehabilitation with a 4-DOF robotic orthosis. IEEE Transact. Robot. Autom. 2004, 20, 574–582. [Google Scholar] [CrossRef]
- Lunenburger, L.; Colombo, G.; Riener, R. Biofeedback for robotic gait rehabilitation. J. Neuro-Eng. Rehabil. 2007, 4, 1:1–1:11. [Google Scholar] [CrossRef]
- Freivogel, S.; Schmalohr, D.; Mehrholz, J. Improved walking ability and reduced therapeutic stress with an electromechanical gait device. J. Rehabil. Med. 2009, 41, 734–739. [Google Scholar] [CrossRef]
- Fisher, S.; Lucas, L.; Thrasher, T.A. Robot-assisted gait training for patients with hemiparesis due to stroke. Top Stroke Rehabil. 2011, 18, 269–276. [Google Scholar] [CrossRef]
- West, R.G. Powered Gait Orthosis and Method of Utilizing SAME. U.S. Patent 6689075, 29 January 2004. [Google Scholar]
- Veneman, J.; Kruidhof, R.; Hekman, E.; Ekkelenkamp, R.; van Asseldonk, E.; van der Kooij, H. Design and evaluation of the LOPES exoskeleton robot for interactive gait rehabilitation. IEEE Trans. Neural Syst. Rehabil. Eng. 2007, 15, 379–386. [Google Scholar]
- Vallery, H.; Veneman, J.; van Asseldonk, E.; Ekkelenkamp, R.; Buss, M.; van der Kooij, H. Compliant actuation of rehabilitation robots. IEEE Robot. Autom. Mag. 2008, 15, 60–69. [Google Scholar]
- Banala, S.K.; Kim, S.H.; Agrawal, S.K.; Scholz, J.P. Robot assisted gait training with active leg exoskeleton (ALEX). IEEE Trans. Neural Syst. Rehabil. Eng. 2009, 17, 2–8. [Google Scholar] [CrossRef]
- Banala, S.K.; Agrawal, S.K.; Kim, S.H.; Scholz, J.P. Novel gait adaptation and neuromotor training results using an active leg exoskeleton. IEEE/ASME Trans. Mechatron. 2010, 15, 216–225. [Google Scholar] [CrossRef]
- Monaco, V.; Galardi, G.; Coscia, M.; Martelli, D.; Micera, S. Design and evaluation of NEUROBike: A neuro-rehabilitative platform for bedridden post-strike patients. IEEE Trans. Neural Syst. Rehabil. Eng. 2012, 20, 845–852. [Google Scholar]
- Taherifar, A.; Mousavi, M.; Rassaf, A.; Ghiasi, F.; Hadian, M.R. LOKOIRAN—A novel robot for rehabilitation of spinal cord injury sand stroke patients. In Proceedings of the RSI/ISM International Conference on Robotics and Mechatronics, Tehran, Iran, 12–14 February 2013.
- Pietrusinski, M.; Cajigas, I.; Severini, G.; Bonato, P.; Mavroidis, C. Robotic gait rehabilitation trainer. IEEE/ASME Trans. Mechatron. 2014, 19, 490–499. [Google Scholar] [CrossRef]
- Tondu, B.; Lopez, P. Modelling and control of McKibben artificial muscle robot actuators. IEEE Control Syst. Mag. 2000, 20, 15–38. [Google Scholar] [CrossRef]
- Caldwell, D.G.; Razak, A.; Goodwin, M. Braided artificial muscle actuators. In Proceedings of the IFAC, Southampton, UK, 18–21 April 1993; pp. 507–512.
- Caldwell, D.G.; Medrano-Cerda, G.A.; Goodwin, M. Characteristics and adaptive control of pneumatic muscle actuators for a robotic elbow. In Proceedings of the International Conference Robotics Automation, San Diego, CA, USA, 8–13 May 1994; Volume 4, pp. 3558–3563.
- Caldwell, D.G.; Medrano-Cerda, G.A.; Goodwin, M. Control of pneumatic muscle actuators. IEEE Control Syst. Mag. 1995, 15, 40–48. [Google Scholar] [CrossRef]
- Caldwell, D.G.; Tsagarakis, N.; Medrano-Cerda, G.A. Biomimetic actuators: Polymeric pseudo muscular actuators and pneumatic muscle actuators for biological emulation. Mechatronics 2000, 10, 499–530. [Google Scholar] [CrossRef]
- Davis, S.; Tsagarakis, N.; Canderle, J.; Caldwell, D.G. Enhanced modeling and performance in braided pneumatic muscle actuators. Int. J. Robot. Res. 2003, 22, 213–227. [Google Scholar] [CrossRef]
- Davis, S.; Caldwell, D.G. Braid effects on contractile range and friction modeling in pneumatic muscle actuators. Int. J. Robot. Res. 2006, 25, 359–369. [Google Scholar] [CrossRef]
- Chou, C.P.; Hannaford, B. Static and dynamic characteristics of McKibben pneumatic artificial muscles. In Proceedings of the IEEE International Conference Robotics Automation, San Diego, CA, USA, 8–13 May 1994; Volume 1, pp. 281–286.
- Chou, C.P.; Hannaford, B. Measurement and modeling of McKibben pneumatic artificial muscles. IEEE Trans. Robot. Autom. 1996, 12, 90–102. [Google Scholar] [CrossRef]
- Nascimento, B.G.; Vimieiro, C.B.; Nagem, D.A.; Pinotti, M. Hip orthosis powered by pneumatic artificial muscle: Voluntary activation in absence of myoelectrical signal. Artif. Organs 2008, 32, 317–322. [Google Scholar] [CrossRef]
- Vimieiro, C.B.S.; do Nascimento, B.G.; Nagem, D.A.P.; Pinotti, M. Development of a hip orthosis using pneumatic artificial muscles. In Proceeding of TMSi, São Paulo, Spain, 18–19 July 2005.
- Bharadwaj, K.; Sugar, T.G. Kinematics of a robotic gait trainer for stroke rehabilitation. In Proceedings of the IEEE International Conference on Robotics and Automation, Orlando, FL, USA, 15–19 May 2006.
- Ferris, D.P.; Gordon, K.E.; Sawicki, G.S.; Peethambaran, A. An improved powered ankle-foot orthosis using proportional myoelectric control. Gait Posture 2006, 23, 425–428. [Google Scholar] [CrossRef]
- Ferris, D.P.; Czerniecki, J.M.; Hannaford, B. An ankle-foot orthosis powered by artificial pneumatic muscles. J. Appl. Biomech. 2005, 21, 189–197. [Google Scholar]
- Gordon, K.E.; Sawicki, G.S.; Fessis, D.P. Mechanical performance of artificial pneumatic muscles to power an ankle-foot orthosis. J. Biomech. 2006, 39, 1832–1841. [Google Scholar] [CrossRef]
- Costa, N.; Bezdicek, M.; Brown, M.; Gray, J.O.; Caldwell, D.G. Joint motion control of a powered lower limb orthosis for rehabilitation. Int. J. Autom. Comput. 2006, 3, 271–281. [Google Scholar] [CrossRef]
- Miyoshi, T.; Hiramatsu, K.; Yamamoto, S.I.; Nakazawa, K.; Akai, M. Robotic gait trainer in water: Development of an underwater gait-training orthosis. Disabil. Rehabil. 2008, 30, 81–87. [Google Scholar] [CrossRef]
- Malcom, P.; Fiers, P.; Segers, V.; van Caekenberghe, I.; Lenoir, M.; de Clercq, D. Experimental study on the role of the ankle push off in the walk-to-run transition by means of a powered ankle-foot-exoskeleton. Gait Posture 2009, 30, 322–327. [Google Scholar] [CrossRef]
- Malcom, P.; Segers, V.; van Caekenberghe, I.; de Clercq, D. Experimental study of the influence of the m. tibialis anterior on the walk-to-run transition by means of a powered ankle-foot-exoskeleton. Gait Posture 2009, 29, 6–10. [Google Scholar] [CrossRef]
- Galle, S.; Malcom, P.; Derave, W.; de Clercq, D. Adaptation to walking with an exoskeleton that assists ankle extension. Gait Posture 2013, 38, 495–499. [Google Scholar] [CrossRef]
- Malcom, P.; Derave, W.; Galle, S.; de Clercq, D. A simple exoskeleton that assist plantarflexion can reduce the metabolic cost of human walking. PLoS One 2013, 8, 0056137. [Google Scholar]
- Sawicki, G.S.; Fessis, D.P. A pneumatically powered knee-ankle-foot orthosis (KAFO) with myoelectric activation and inhibition. J. Neuro-Eng. Rehabil. 2009, 6, 23:1–23:16. [Google Scholar]
- Deaconescu, T.T.; Deaconescu, A.I. Pneumatic muscle actuated equipment for continuous passive motion. IAENG Trans. Eng. Technol. 2009. [Google Scholar] [CrossRef]
- Yeh, T.J.; Wu, M.J.; Lu, T.J.; Wu, F.K.; Huang, C.R. Control of McKibben pneumatic muscles for a power-assist, lower-limb orthosis. Mechatronics 2010, 20, 686–697. [Google Scholar] [CrossRef]
- Carberry, J.; Hinchly, G.; Buckerfield, J.; Taylor, E.; Burton, T.; Madgwick, S.; Vaidyanathan, R. Parametric design of an active ankle foot orthosis with passive compliance. In Proceedings of the Computer-Based Medical System (CBMS), Bristol, UK, 27–30 June 2011.
- Park, Y.; Chen, B.; Young, D.; Stirling, L.; Wood, R.; Goldfield, E.; Nagpal, R. Bio-inspired Active Soft Orthotic Device for Ankle Foot Pathologies. In Proceedings of the International Conference on Robots and Systems (IROS), San Francisco, CA, USA, 25–30 September 2011.
- Park, Y.; Chen, B.; Majidi, C.; Wood, R.; Nagpal, R.; Goldfield, E. Active Modular Elastomer Sleeve for Soft Wearable Assistance Robots. In Proceedings of the IEEE International Conference on Robots and Systems (IROS), Vilamoura, Portugal, 7–12 October 2012.
- Teng, C.M.; Wong, Z.Y.; The, W.Y.; Chong, Y.Z. Design and development of inexpensive pneumatically-powered assisted knee-ankle-foot orthosis for gait rehabilitation-preliminary finding. In Proceedings of the International Conference on Biomedical Engineering (ICoBE), Penang, Malaysia, 27–28 February 2012.
- Kawamura, T.; Takanaka, K. Development of an orthosis for walking assistance using pneumatic artificial muscle-a quantitative assessment of the effect of assistance. In Proceedings of the International Conference on Rehabilitation Robotics, Seattle, WA, USA, 24–26 June 2013.
- Hussain, S.; Xie, S.Q.; Jamwal, P.K. Adaptive impedance control of a robotic orthosis for gait rehabilitation. IEEE Trans. Cybern. 2013, 43, 1025–1034. [Google Scholar] [CrossRef]
- Hussain, S.; Xie, S.Q.; Jamwal, P.K. Robust nonlinear control of an intrinsically compliant robotic gait training orthosis. IEEE Trans. Syst. Man Cybern.: Syst. 2013, 43, 655–665. [Google Scholar] [CrossRef]
- Caldwell, D.G.; Medrano-Cerda, G.A.; Goodwin, M.J. Braided pneumatic actuator control of a multi jointed manipulator. In Proceedings of the International Conference on System, Man and Cybernetics, Le Touquet, France, 17–20 October 1993.
- Caldwell, D.G.; Medrano-Cerda, G.A.; Goodwin, M. Characteristics and adaptive control of pneumatic muscle actuators for a robotic elbow. In Proceedings of the International Conference on Robotics and Automation, San Diego, CA, USA, 8–13 May 1994.
- Caldwell, D.G.; Medrano-Cerda, G.A.; Goodwin, M. Control of a pneumatic muscle actuators. IEEE Trans. Control Syst. 1995, 15, 40–48. [Google Scholar] [CrossRef]
- Medrano-Cerda, G.A.; Bowler, C.J.; Caldwell, D.G. Adaptive position control of antagonistic pneumatic muscle actuators. In Proceedings of the International Conference on Intelligent Robots and Systems, Pittsburgh, PA, USA, 5–9 August 1995; Volume 1, pp. 378–383.
- Hamerlain, M. An anthropomorphic robot arm driven by artificial muscles using a variable structure control. In Proceedings of the International Conference on Intelligent Robots and Systems, Pittsburgh, PA, USA, 5–9 August1995; Volume 1, pp. 550–555.
- Iskarous, M.; Kawamura, K. Intelligent control using a neuro-fuzzy network. In Proceedings of the International Conference on Intelligent Robots and Systems, Pittsburgh, PA, USA, 5–9 August 1995; Volume 3, pp. 350–355.
- Van der Smagt, P.; Groen, F.; Schulten, K. Analysis and control of a rubbertuator arm. Biol. Cybern. 1996, 75, 433–440. [Google Scholar] [CrossRef]
- Cai, D.; Yamaura, H. A robust controller for manipulator driven by artificial muscle actuator. In Proceedings of the IEEE International Conference on Control Applications, Dearborn, MI, USA, 15–18 September 1996.
- Bowler, C.J.; Caldwell, D.G.; Medrano-Cerda, G.A. Pneumatic muscle actuators: Musculature for an anthropomorphic robot arm. IEEE Colloq. Actuator Technol. 1996, 8, 1–6. [Google Scholar]
- Repperger, D.W.; Johnson, K.R.; Phillips, C.A. Nonlinear feedback controller design of a pneumatic muscle actuator system. In Proceedings of the American Control Conference, San Diego, CA, USA, 2–4 June 1999.
- Carbonell, P.; Jiang, Z.P.; Repperger, D.W. Nonlinear control of a pneumatic muscle actuator: Backstepping vs. Sliding-mode. In Proceedings of the IEEE International Conference on Control Applications, Mexico City, Mexico, 5–7 September 2001.
- Carbonell, P.; Jiang, Z.P.; Repperger, D.W. A fuzzy backstepping controller for a pneumatic muscle actuator system. In Proceedings of the IEEE International Symposium on Intelligent Control, Mexico City, Mexico, 5–7 September 2001; pp. 353–358.
- Folgheraiter, M.; Gini, G.; Perkowski, M.; Pivtoraiko, M. Adaptive reflex control for an artificial hand. In Proceedings of the SYROCO, Wrocław, Poland, 1–3 September 2003.
- Balasubramanian, K.; Rattan, K.S. Feedforward control of a non-linear pneumatic muscle system using fuzzy logic. In Proceedings of the IEEE International Conference on Fuzzy Systems, St. Louis, MO, USA, 25–28 May 2003; Volume 1, pp. 272–277.
- Ahn, K.K.; Thanh, T.C. Improvement of the control performance of pneumatic artificial muscle manipulators using an intelligent switching control method. KSME Int. J. 2004, 18, 1388–1400. [Google Scholar]
- Ahn, K.K.; Thanh, T.C. Nonlinear PID control to improve the control performance of the pneumatic artificial muscle manipulator using neural network. J. Mech. Sci. Technol. 2005, 19, 106–116. [Google Scholar] [CrossRef]
- Aschemann, H.; Schindele, D. Sliding-mode control of a high-speed linear axis driven by pneumatic muscle actuators. IEEE Trans. Ind. Electron. 2008, 55, 3855–3864. [Google Scholar] [CrossRef]
- Cho, S.H. Trajectory tracking control of a pneumatic c-y table using neural network based PID control. Int. J. Precis. Eng. Manuf. 2009, 10, 37–44. [Google Scholar] [CrossRef]
- Xing, K.; Huang, J.; Wang, Y.; Wu, J.; Xu, Q.; He, J. Tracking control of pneumatic artificial muscle actuators based on sliding mode and non-linear disturbance observer. IET Control Theory Appl. 2010, 10, 2058–2070. [Google Scholar]
- Hogan, N. Adaptive control of mechanical impedance by coactivation of antagonist muscles. IEEE Trans. Autom. Control 1984, 29, 681–690. [Google Scholar] [CrossRef]
- Murray, W.R. Modelling elbow equilibrium in the presence of co-contraction. In Proceedings of the Bioengineering Conference, Durham, NH, USA, 10–11 March 1988; pp. 190–193.
- Murray, W.R.; Hogan, N. Co-contraction of antagonist muscles: Prediction and observation. In Proceedings of the Joint Dynamics and ControlIEEE International Conference on Engineering in Medicine and Biology Society (EMBS), New Orleans, LA, USA, 4–7 November 1988; Voluem 4, pp. 1926–1927.
- Migliore, S.A.; Brown, E.A.; de Weerth, S.P. Novel nonlinear elastic actuators for passively controlling robotic joint compliance. Trans. ASME 2007, 129, 406–412. [Google Scholar] [CrossRef]
- Schepelmann, A.; Taylor, M.D.; Geyer, H. Development of a testbed for robotic neuromuscular controllers. In Robotics: Science and Systems VIII; University of Sydney: Sydney, Australia, 2013. [Google Scholar]
- Laffranchi, M.; Tsagarakis, N.G.; Cannella, F.; Caldwell, D.G. Antagonistic and series elastic actuators: A comparative analysis on the energy consumption. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, St. Louis, MO, USA, 10–15 October 2009.
- Klauer, C.; Raisch, J.; Schauer, T. Advanced control strategies for neuro-prosthetic systems. In Proceedings of the Technically Assisted Rehabilitation (TAR), Berlin, Germany, 14–15 March 2013.
- Mitrovic, D.; Klanke, S.; Osu, R.; Kawato, M.; Vijayakumar, S. A computational model of limb impedance control based on principles of internal model uncertainty. PLoS One 2010. [Google Scholar] [CrossRef]
- Dierick, F.; Domicent, C.; Detrembleur, C. Relationship between antagonistic leg muscles co-contraction and body centre of gravity mechanics in different level gait disorders. J. Electromyogr.Kinesiol. 2002, 12, 59–66. [Google Scholar] [CrossRef]
- Milner, T.E.; Cloutier, C. The effect of antagonist muscle co-contraction on damping of the wrist joint during voluntary movement. In Proceedings of the IEEE 17th Annual Conference on Engineering in Medicine and Biology Society, Montreal, Canada, 20–23 September 1995; Volume 2, pp. 1247–1248.
- Hollerbach, K.; Ramos, C.F.; Kazerooni, H. Destabilizing effects of muscular co-contraction in human-machine interaction. In Proceedings of the American Control Conference, San Francisco, CA, USA, 2–4 June 1993.
- Fu, C.; Wang, R. The influence of co-contraction to the arm impedance during free planar movement. In Proceedings of the International Conference on Bioinformatics and Biomedical Engineering (ICBBE), Beijing, China, 11–13 June 2009; pp. 1–3.
- Lynch, C.L.; Sayenko, D.; Popovic, M.R. Co-contraction of antagonist muscles during knee extension against gravity: Insights for functional electrical simulation control design. In Proceedings of the IEEE International Conference on Engineering in Medicine and Biology Society (EMBS), San Diego, California, USA, 28 August–1 September 2012.
- Odhner, L.; Asada, H. Equilibrium point control of artificial muscles using recruitment of many motor units. In Proceedings of the IEEE/RAS International Conference on Biomedical Robotics and Biomechatronics, Scottsdale, AZ, USA, 19–22 October 2008.
- Missenard, O.; Mottet, D.; Perrey, S. The role of cocontraction in the impairment of movement accuracy with fatigue. Exp. Brain Res. 2008, 185, 151–156. [Google Scholar] [CrossRef]
- Klauer, C.; Raisch, J.; Schauer, T. Nonlinear joint-angle feedback control of electrically simulated and λ-controlled antagonistic muscle pairs. In Proceedings of the European Control Conference (ECC), Zurich, Switzerland, 17–19 July 2013.
- Spagnol, P.; Klauer, C.; Previdi, F.; Raisch, J.; Schauer, T. Modelling and online-identification of electrically stimulated antagonistic muscles for horizontal shoulder abduction and adduction. In Proceedings of the European Control Conference (ECC), Zurich, Switzerland, 17–19 July 2013.
- Ferris, D.P.; Lewis, C.L. Robotic lower limb exoskeletons using proportional myoelectric control. In Proceedings of the IEEE International Conference on Engineering in Medicine and Biology Society (EMBS), Minneapolis, MN, USA, 2–6 September 2009.
- Mankala, K.K.; Banala, S.K.; Agrawal, S.K. Passive swing assistive exoskeletons for motor-incomplete spinal cord injury patients. In Proceedings of the IEEE International Conference on Robotics and Automation, Roma, Italy, 10–14 April 2007.
- Kumamoto, M.; Oshima, T.; Fujukawa, T. Control properties of a two-joint link mechanism equipped with mono- and bi-articular actuators. In Proceedings of the IEEE International Workshop on Robot and Human Interactive Communication, Osaka, Japan, 27–29 September 2000.
- Shimizu, S.; Momose, N.; Oshima, T.; Koyanagi, K. Development of robot leg which provided with the bi-articular actuator for training techniques of rehabilitation. In Proceedings of the IEEE International Symposium on Robot and Human Interactive Communication, Toyama, Japan, 27 September–2 October 2009.
- Salvucci, V.; Oh, S.; Hori, Y. Infinity norm approach for precise force control of manipulators driven by bi-articular actuators. In Proceedings of the Annual Conference on IEEE Industrial Electronics Society, Glendale, AZ, USA, 7–10 November 2010; pp. 1908–1913.
- Salvucci, V.; Oh, S.; Hori, Y.; Kimura, Y. Disturbance rejection improvement in non-redundant robot arms using bi-articular actuators. In Proceedings of the Industrial Electronics (ISIE), Gdańsk, Poland, 27–30 June 2011; pp. 2159–2164.
- Salvucci, V.; Kimura, Y.; Oh, Y.; Hori, Y. Experimental verification of infinity norm approach for force maximization of manipulators driven by bi-articular actuators. In Proceedings of the American Control Conference on O’Farrell Street, San Francisco, CA, USA, 29 June–1 July 2011.
- Selen, L.P.J.; Beek, P.J.; van Dieen, J.H. Can co-activation reduce kinematics variability? A simulation study. Biol. Cybern. 2005, 93, 373–381. [Google Scholar] [CrossRef]
- Durfee, W.K. Task-based methods for evaluating electrically stimulated antagonist muscle controllers. IEEE Trans. Biomed. Eng. 1989, 36, 309–321. [Google Scholar] [CrossRef]
- Mohammed, S.; Fraisse, P.; Guiraud, D.; Poignet, P.; el Makssoud, H. Towards a co-contraction muscle control strategy for paraplegics. In Proceedings of the 44th IEEE Conference on Decision and Control, Seville, Spain, 12–15 December 2005; pp. 7428–7433.
- Mohammed, S.; Poignet, P.; Fraisse, P.; Guiraud, D. Optimal stimulation patterns for knee joint movement restoration during co-contraction of antagonist muscles. In Proceedings of the International Conference on Biomedical Robotics and Biomechatronics, Tokyo, Japan, 26–29 September 2010; pp. 678–692.
- Heitmann, S.; Ferns, N.; Breakspear, M. Muscle co-contraction modulates damping and joint stability in a three-link biomechanical limb. Front. Neurorobot. 2012, 5, 5:1–5:14. [Google Scholar]
- Kawai, H.; Murao, T.; Sato, R.; Fujita, M. Passivity-based control for 2DOF robot manipulators with antagonistic bi-articular muscles. In Proceedings of the IEEE International Conference on Control Applications (CCA), Denver, CO, USA, 28–30 September 2011; pp. 1451–1456.
- Kawai, K.S.H.; Murao, T.; Fujita, M. Open-loop control for 2DOF robot manipulators with antagonistic bi-articular muscles. In Proceedings of the IEEE International Conference on Control Applications (CCA), Dubrovnik, Croatia, 3–5 October 2012; pp. 1346–1351.
- Kawai, Y.; Kawai, H.; Fujita, M. RISE control for 2DOF human lower limb with antagonistic bi-articular muscles. In Proceedings of the IEEE International Conference on Control Applications (CCA), Hyderabad, India, 28–30 August 2013; pp. 109–114.
- Kawai, Y.; Downey, R.J.; Kawai, H.; Dixon, W.E. Co-Contraction of Antagonist Bi-Articular Muscles for Tracking Control of Human Limb. Available online: http://wwwr.kanazawa-it.ac.jp/kawai/research/2013/CDC13KaDoKaDi.pdf (accessed on 12 March 2014).
- Kawai, Y. A Design of Co-Contraction Level of Antagonist Muscles with Muscle Contraction Dynamics for Tracking Control of Human Limb. Available online: http://k-lab.e.ishikawa-nct.ac.jp/paper/2013/SICE13_0447_FI.pdf (accessed on 12 March 2014).
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Dzahir, M.A.M.; Yamamoto, S.-i. Recent Trends in Lower-Limb Robotic Rehabilitation Orthosis: Control Scheme and Strategy for Pneumatic Muscle Actuated Gait Trainers. Robotics 2014, 3, 120-148. https://doi.org/10.3390/robotics3020120
Dzahir MAM, Yamamoto S-i. Recent Trends in Lower-Limb Robotic Rehabilitation Orthosis: Control Scheme and Strategy for Pneumatic Muscle Actuated Gait Trainers. Robotics. 2014; 3(2):120-148. https://doi.org/10.3390/robotics3020120
Chicago/Turabian StyleDzahir, Mohd Azuwan Mat, and Shin-ichiroh Yamamoto. 2014. "Recent Trends in Lower-Limb Robotic Rehabilitation Orthosis: Control Scheme and Strategy for Pneumatic Muscle Actuated Gait Trainers" Robotics 3, no. 2: 120-148. https://doi.org/10.3390/robotics3020120
APA StyleDzahir, M. A. M., & Yamamoto, S.-i. (2014). Recent Trends in Lower-Limb Robotic Rehabilitation Orthosis: Control Scheme and Strategy for Pneumatic Muscle Actuated Gait Trainers. Robotics, 3(2), 120-148. https://doi.org/10.3390/robotics3020120