Self-Assembly of Human Serum Albumin: A Simplex Phenomenon
Abstract
:1. Introduction
2. Results
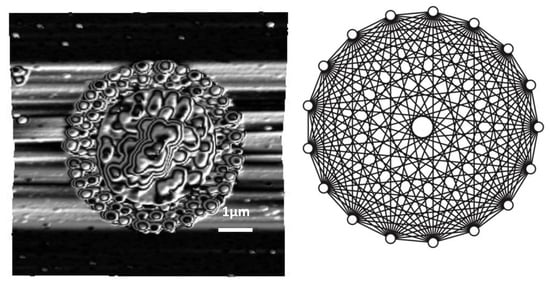
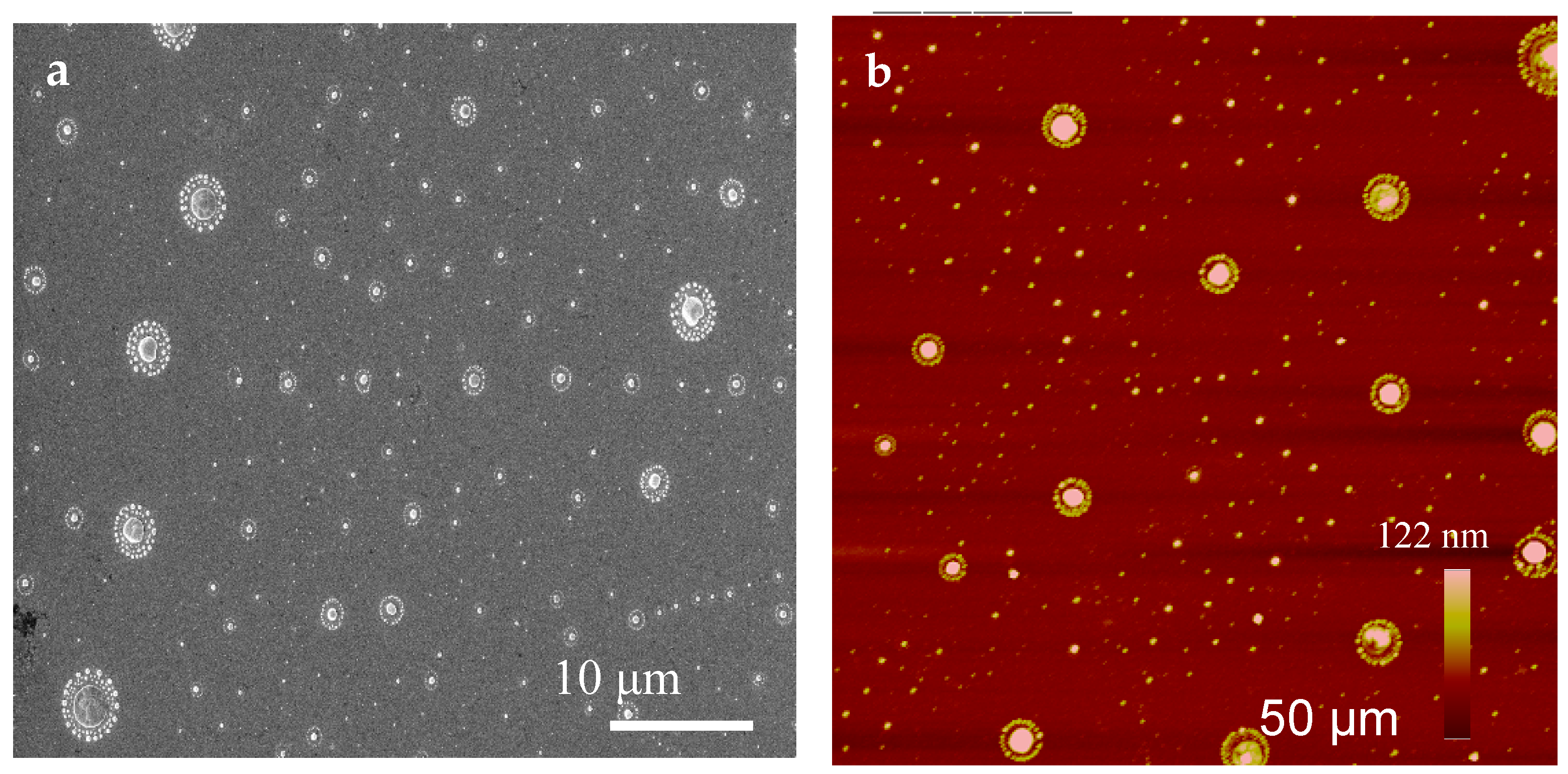
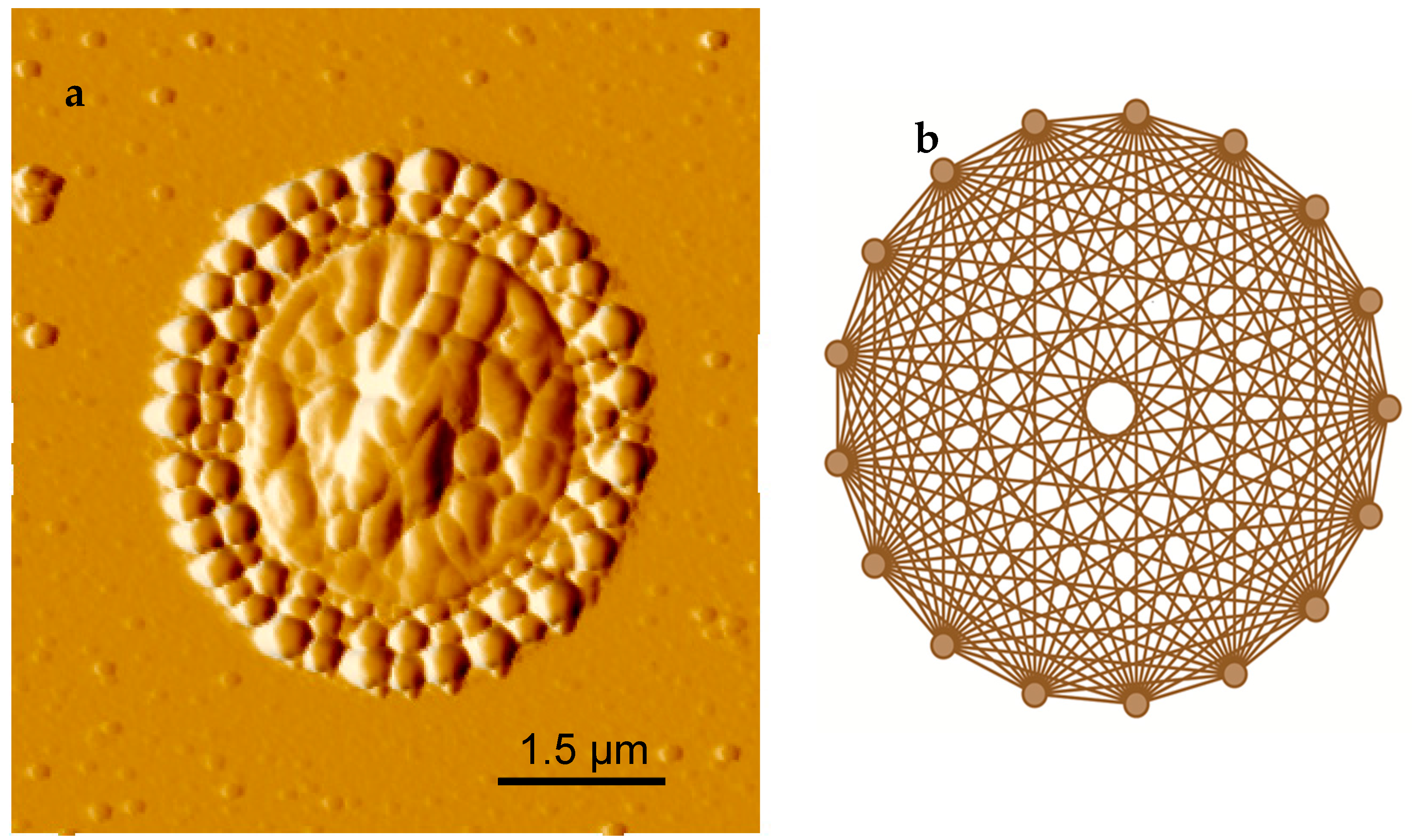
2.1. Experimental Results
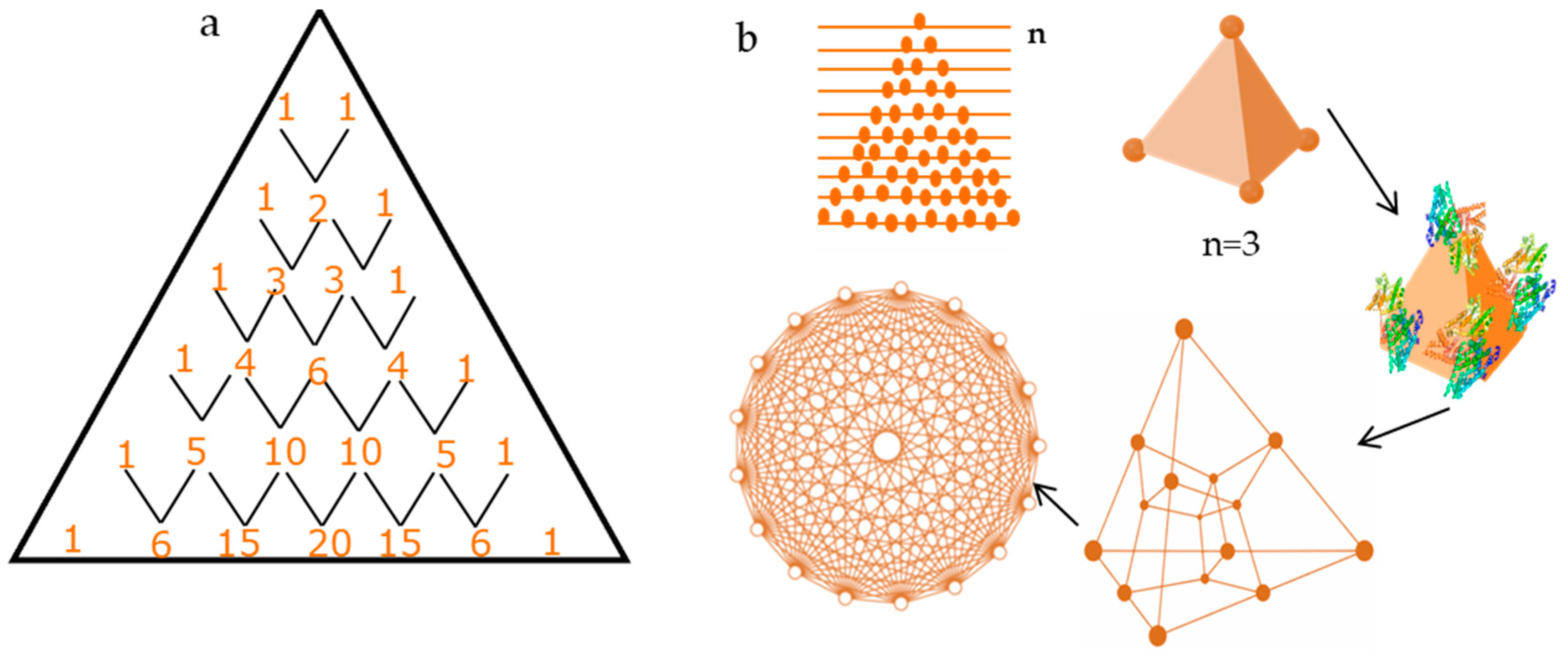
2.2. Pattern Similarity to Geometric n-Simplex
2.3. Thermodynamics of Pattern Formation
2.4. Chemical Kinetics of Pattern Formation
3. Discussion
4. Materials and Methods
4.1. Materials
4.2. HSA Pattern Generation
4.3. Atomic Force Microscopy
4.4. Scanning Electron Microscopy
4.5. Dynamic Light Scattering
4.6. Circular Dichroism Spectropolarimetery
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Gates, B.D.; Xu, Q.B.; Stewart, M.; Ryan, D.; Willson, C.G.; Whitesides, G.M. New approaches to nanofabrication: Molding, printing, and other techniques. Chem. Rev. 2005, 105, 1171–1196. [Google Scholar] [CrossRef] [PubMed]
- Love, J.C.; Estroff, L.A.; Kriebel, J.K.; Nuzzo, R.G.; Whitesides, G.M. Self-assembled monolayers of thiolates on metals as a form of nanotechnology. Chem. Rev. 2005, 105, 1103–1169. [Google Scholar] [CrossRef] [PubMed]
- Otero, R.; Gallego, J.M.; Vázquez de Parga, A.L.; Martín, N.; Miranda, R. Molecular self-assembly at solid surfaces. Adv. Mater. 2011, 23, 5148–5176. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Huang, W.; Liu, J.; Zhu, X.; Yan, D. Self-assembly of hyperbranched polymers and its biomedical applications. Adv. Mater. 2010, 22, 4567–4590. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.-L.; Keith, M.B.; Oradian-Odak, J.; James, J.D. In situ AFM study amelogenin assembly and disassembly dynamics on charged surfaces provides insigt on matrix protein self-assembly. J. Am. Chem. Soc. 2011, 133, 17406–17413. [Google Scholar] [CrossRef] [PubMed]
- Agheli, H.; Malmstrem, J.; Larson, E.M.; Textor, M.; Sutherland, D.S. Large area protein nanopatterning for biological applications. Nano Lett. 2006, 6, 1165–1171. [Google Scholar] [CrossRef] [PubMed]
- De Santis, E.; Ryadnov, M.G. Peptide self-assembly for nanomaterials: The new kid on the block. Chem. Soc. Rev. 2015, 44, 8288–8300. [Google Scholar] [CrossRef] [PubMed]
- Matsuurua, K. Rational design of self-assembled proteins and peptides for nano and microsized archietectures. RSC Adv. 2014, 4, 2942–2953. [Google Scholar] [CrossRef]
- Luo, Q.; Hou, C.; Bai, Y.; Wang, R.; Liu, J. Protein assembly: Versatile approaches to construct highly ordered nanostructures. Chem Rev. 2016, 116, 13571–13632. [Google Scholar] [CrossRef] [PubMed]
- Tien, J.; Terfort, A.; Whitesides, G.M. Microfabrication through Electrostatic Self-Assembly. Langmuir 1997, 13, 5349–5355. [Google Scholar] [CrossRef]
- Stauth, S.A.; Parviz, B.A. Self-Assembled Single-Crystal Silicon Circuits on Plastic. Proc. Natl. Acad. Sci. USA 2006, 103, 13922–13927. [Google Scholar] [CrossRef] [PubMed]
- Grzybowski, B.A.; Stone, H.A.; Whitesides, G.M. Dynamic Self-Assembly of Magnetized, Millimetre-Sized Objects Rotating at a Liquid Air Interface. Nature 2000, 405, 1033–1036. [Google Scholar] [PubMed]
- Hong, S.W.; Huh, J.; Gu, X.; Lee, D.G.; Jo, W.H.; Park, S.; Xu, T.; Russel, T.P. Unidirectionally aligned line patterns driven by entropic effects on faceted surfaces. Proc. Natl. Acad. Sci. USA 2012, 109, 1402–1406. [Google Scholar] [CrossRef] [PubMed]
- Plass, R.; Last, J.A.; Bartelt, N.C.; Kellogg, G.L. Nanostructures: Self-assembled domain patterns. Nature 2001, 412, 875. [Google Scholar] [CrossRef] [PubMed]
- Bandopadhyay, A.; Pati, R.; Sahu, S.; Peper, F.; Fujita, D. Massively parallel computing on an organic molecular layer. Nat. Phys. 2010, 6, 369–375. [Google Scholar] [CrossRef]
- Cheng, S.; Aggarwal, A.; Stevens, M.J. Self-assembly of artificial microtubules. Soft Matter 2012, 8, 5666–5678. [Google Scholar] [CrossRef]
- Chang, H.Y.; Lin, Y.L.; Sheng, Y.J. Multilayered Polymersome Formed by Amphiphilic Asymmetric Macromolecular Brushes. Macromolecules 2012, 45, 4778–4789. [Google Scholar] [CrossRef]
- Venkatachalam, D.K.; Fletcher, N.H.; Sood, D.K.; Elliman, R.G. Self-assembled nanoparticle spirals from two-dimensional compositional banding in thin films. Appl. Phys. Lett. 2009, 94, 213110. [Google Scholar] [CrossRef]
- Adams, M.; Dogic, Z.; Keller, S.L.; Fraden, S. Entropically Driven Microphase Transitions in Mixtures of Colloidal Rods and Spheres. Nature 1998, 393, 349–352. [Google Scholar]
- Solokolov, I.; Yang, H.; Ozin, G.A.; Kresge, C.T. Radial Patterns in Mesoporous Silica. Adv. Mater. 1999, 11, 636–642. [Google Scholar] [CrossRef]
- Thakur, G.; Prashanthi, K.; Thundat, T. Directed self-assembly of proteins into discrete radial patterns. Sci. Rep. 2013, 3, 1923. [Google Scholar] [CrossRef] [PubMed]
- Thakur, G.; Prashanthi, K.; Thundat, T. Self-assembly of Proteins into three-dimensional structures using bioconjugation. Mater. Res. Soc. Proc. 2014, 1663, 1–8. [Google Scholar] [CrossRef]
- Hilton, P.; Pedersen, J. Looking into Pascal’s triangle: Combinatorics, arithmetic, and geometry. Math. Mag. 1987, 60, 305–316. [Google Scholar] [CrossRef]
- Putz, J.F. The Pascal polytope: An extension of Pascal’s triangle to N dimensions. Coll. Math. J. 1986, 17, 144–155. [Google Scholar] [CrossRef]
- Alberto, P.; Rocha, N.H.; Vicente, L.N. Pattern search methods for user-provided points: Application to molecular geometry problems. SIOPT 2004, 14, 1216–1236. [Google Scholar] [CrossRef]
- Thompson, D.W. On Growth and Form, 3rd ed.; Cambridge University Press: Cambridge, UK, 2014; pp. 88–265. ISBN 978-1-107-67256-7. [Google Scholar]
- Le, H.; Small, C.G. Multidimensional scaling of simplex shapes. Pattern Recognit. 1999, 32, 1601–1613. [Google Scholar] [CrossRef]
- Kuriyan, J.; Konforti, B.; Wemmer, D. The Molecules of Life: Physical and Chemical Principles; Garland Science: New York, NY, USA, 2013; pp. 238–367. ISBN 978-0-8153-4188-8. [Google Scholar]
- Atkins, P.W.; De Paula, J. Atkins’ Physical Chemistry, 9th ed.; Oxford University Press: New York, NY, USA, 2010; pp. 604–648. ISBN 978-0-19-969740-3. [Google Scholar]
- Hakala, R.W. A new derivation of Boltzman distribution law. J. Chem. Educ. 1961, 38, 33. [Google Scholar] [CrossRef]
- Rialdi, G.; Battistel, E. Thermodynamics of proteins in unusual environments. Biophys. Chem. 2007, 126, 65–69. [Google Scholar] [CrossRef] [PubMed]
- Friedman, E.; Grubbs, W.T. The Boltzmann distribution and Pascal’s triangle. Chem. Educ. 2003, 8, 116–121. [Google Scholar]
- Lee, C.F. Self-assembly of protein amyloids: A competition between amorphous and ordered aggregation. Phys. Rev. E 2009, 80, 031922. [Google Scholar] [CrossRef] [PubMed]
- Kiselev, M.A.; Gryzunov, I.A.; Dobretsov, G.E.; Komarova, M.N. Size of human serum albumin in solution. Biofizika 2001, 46, 423–427. [Google Scholar] [PubMed]
- Epstein, I.R.; Pojman, J.A. An Introduction to Nonlinear Chemical Dynamics; Oxford University Press: New York, NY, USA, 1998; pp. 109–299. ISBN 0-19-509670-3. [Google Scholar]
- Andronov, A.A.; Vitt, A.A.; Khaikin, S.E. Theory of Oscillators; Pregamon: New York, NY, USA, 1966; pp. 209–350. ISBN 978-1-4831-6724-4. [Google Scholar]
- Scott, S.K. Chemical Chaos; Clarendon Press: Oxford, UK, 1994; pp. 1–70. ISBN 0-19-855658-6. [Google Scholar]
- Dell’Orco, D. Fast prediction of thermodynamics and kinetics of protein–protein recognition from structures: From molecular design to system biology. Mol. Biosyst. 2009, 5, 323–334. [Google Scholar] [CrossRef] [PubMed]
- Barnes, G.T.; Gentle, I.R. Interfacial Science: An Introduction, 2nd ed.; Oxford University Press: New York, NY, USA, 2011; pp. 242–253. ISBN 978-019-957118-5. [Google Scholar]
- Sharp, K.A.; Honig, B. Calculating total electrostatic energies with the non-linear Poisson-Boltzmann equation. J. Phys. Chem. 1990, 94, 7684–7692. [Google Scholar] [CrossRef]
- Fogolari, F.; Brigo, A.; Molinari, H. The Poisson–Boltzmann equation for biomolecular electrostatics: A tool for structural biology. J. Mol. Recognit. 2002, 15, 377–392. [Google Scholar] [CrossRef] [PubMed]
- Levine, S. The Free Energy of the Double Layer of a Colloidal Particle. Proc. Phys. Soc. 1951, 64, 781. [Google Scholar] [CrossRef]
- Baxter, R.J. Exactly Solved Models in Statistical Mechanics; Academic Press Inc.: London, UK, 2007; pp. 8–42. ISBN 10-0486-46721-4. [Google Scholar]

© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thakur, G.; Prashanthi, K.; Jiang, K.; Thundat, T. Self-Assembly of Human Serum Albumin: A Simplex Phenomenon. Biomolecules 2017, 7, 69. https://doi.org/10.3390/biom7030069
Thakur G, Prashanthi K, Jiang K, Thundat T. Self-Assembly of Human Serum Albumin: A Simplex Phenomenon. Biomolecules. 2017; 7(3):69. https://doi.org/10.3390/biom7030069
Chicago/Turabian StyleThakur, Garima, Kovur Prashanthi, Keren Jiang, and Thomas Thundat. 2017. "Self-Assembly of Human Serum Albumin: A Simplex Phenomenon" Biomolecules 7, no. 3: 69. https://doi.org/10.3390/biom7030069
APA StyleThakur, G., Prashanthi, K., Jiang, K., & Thundat, T. (2017). Self-Assembly of Human Serum Albumin: A Simplex Phenomenon. Biomolecules, 7(3), 69. https://doi.org/10.3390/biom7030069