Calculations of Resonance Parameters for the Doubly Excited ¹P° States in Ps⁻ Using Exponentially Correlated Wave Functions

Abstract

Recent observations on resonance states of the positronium negative ion (Ps⁻) in the laboratory created huge interest in terms of the calculation of the resonance parameters of the simple three-lepton system. We calculate the resonance parameters for the doubly excited ¹P° states in Ps⁻ using correlated exponential wave functions based on the complex-coordinate rotation method. The resonance energies and widths for the ¹P° Feshbach resonance states in Ps⁻ below the N = 2, 3, 4, 5 Ps thresholds are reported. The ¹P° shape resonance above the N = 2, 4 Ps thresholds are also reported. Our predications are in agreement with the available results. Few Feshbach resonance parameters below the N = 4 and 5 Ps thresholds have been reported in the literature. Our predictions will provide useful information for future resonance experiments in Ps⁻.

1. Introduction

The study of doubly excited resonance states (DERS) in Ps⁻ has found significant relevance since the experimental observations of Michishio et al. [1] for a ¹P° shape resonance in Ps⁻ near the N = 2 positronium (Ps) threshold. The DERS that appear from the closed channel and open channel segments of the scattering wave functions are commonly known, respectively, as Feshbach resonances (or closed channel resonances) and shape resonances (or open channel resonances). The present work aims to report on both the ¹P° shape and Feshbach resonances in Ps⁻.

To introduce this system, it would be of interest to recall its historical development from its existence and stability. The existence of the Ps⁻ was predicted by Wheeler in 1946 [2], and its ground state energy—the only stable state—was first reported by Hylleraas in 1946 [3]. Mills first reported the observation of the Ps⁻ in the laboratory [4]. He also reported the decay rate of this elusive ion [5]. Since then, a great number of theoretical studies and several experimental observations have been devoted to exploring the basic properties of this simplest bound three-lepton $(e^{-},e^{+},e^{-})$ system, and such a system was investigated as an interesting triatomic (XYX) molecule [6]. The molecular spectra of the Ps⁻ exhibiting the rotational and vibrational spectra are presented with illustrations in previous articles [6,7]. Theoretical predictions and experimental determinations for the Ps⁻ have been highlighted in recent papers [8,9,10,11,12,13,14,15,16].

The DERS in Ps⁻ were first reported by Ho [17]. He calculated the S-wave resonance parameters (RP) of this ion. After this pioneering work [17] on the resonance states in Ps⁻, a great number of theoretical calculations on resonance states in Ps⁻ below the N = 2 Ps threshold have been reported in the literature, including the ¹P° Feshbach [7,18,19,20,21,22] and shape [7,12,22,23] resonance states. Until now, many of these studies used different sophisticated methods or techniques or approaches, such as the technique of direct solution of the three-body scattering problem [24], the stabilization method (SM) [11,21,25,26], the complex-coordinate rotation method (CRM) [11,12,13,25,26], the technique of adiabatic molecular approximation [6], the Kohn variational method [27], the adiabatic treatment in hyperspherical coordinates (ATHC) [18,28,29], and the hyperspherical close-coupling approach (HCCA) [22,30,31,32].

First, we will briefly summarize previous works studying the doubly-excited ¹P° resonance states, as these DERS are of our present interest. The ¹P° Feshbach resonances in Ps⁻ below the N = 2 Ps threshold have been studied by Botero [18] using the ATHC, and by Bhatia and Ho [19], using the CRM with Hylleraas-type wave functions (HW). Ho and Bhatia [20] studied the doubly excited ¹P° Feshbach resonance states below the N = 3, 4, 5, 6 Ps thresholds using the HW based on the CRM. The ¹P° shape resonances in the Ps⁻ above the N = 2, 4 and 6 threshold have also been reported by Ho and Bhatia [23], using the HW and utilizing the CRM. Igarashi et al. [22] reported the ¹P° Feshbach resonances near the N = 2, 3, 4 Ps thresholds and shape resonance associated with the N = 2 Ps threshold in the framework of HCCA. We have reported the ¹P° Feshbach resonance parameter [21] below the N = 2 Ps threshold based on the SM and the ¹P° shape resonance parameters [12] above the N = 3 Ps threshold based on the CRM using the exponentially correlated wave functions (ECW). In the present work, we calculate the ¹P° Feshbach RP in Ps⁻ below the N = 2, 3, 4, 5 thresholds and the shape RP in Ps⁻ above the N = 2 and 4 thresholds by using the ECW and the CRM. Throughout this paper, the RP are meant for resonance energies and total widths, and atomic units (a.u.) are used unless stated otherwise.

2. Theory

The Hamiltonian (in atomic units) for the proposed $(e^{-},e^{+},e^{-})$ system can be written as

$$H=T+V,$$

(1)

$$T=-\frac{1}{2}{\displaystyle \sum _{i=1}^3{\nabla }_i^2},$$

(2)

$$V={\displaystyle \sum _{\begin{array}{l}i,j=1\\ i<j\end{array}}^3\frac{q_i{q}_j}{r_{ij}}},$$

(3)

where $q_1$, $q_2$, and $q_3$ indicate the charges of two electrons 1, 2 and the positron, respectively and $r_{ij}$ is the relative distance between the particle i and j.

As stated in the previous section, the ¹P° state ECW can be proposed in the following form by introducing an overall scaling parameter $\omega$ and a permutation operator ${\widehat{P}}_{12}$ for two electrons:

$$\mathsf{\Psi }(\omega )={\displaystyle \sum _{\begin{array}{c}i=1\\ l_1+l_2=L\end{array}}^{N_B}{C}_i{\phi }_i}(\omega ),$$

(4)

$${\phi }_i(\omega )=(1+{\widehat{P}}_{12}){\displaystyle \sum _{\begin{array}{c}i=1\\ l_1+l_2=L\end{array}}^{N_B}{C}_i\exp [(-{\alpha }_i{r}_{13}-{\beta }_i{r}_{23}-{\gamma }_i{r}_{21})\omega ]{\mathbf{Y}}_{LM}^{l_1,l_2}({\mathbf{r}}_{13},{\mathbf{r}}_{23})}$$

(5a)

A well-known form of the bipolar harmonics ${\mathbf{Y}}_{LM}^{l_1,l_2}(r_1,r_2)$:

$${\mathbf{Y}}_{LM}^{l_1,l_2}(r_{13},r_{23})=r_{13}^{l_1}{r}_{23}^{l_2}{\displaystyle \sum _{m_1,m_2}\left(\begin{array}{ccc}{l}_1& l_2& L\\ m_1& m_2& -M\end{array}\right)Y_{l_1{m}_1}({\widehat{r}}_{13})Y_{l_1{m}_2}({\widehat{r}}_{23})},$$

(5b)

where $N_B$ is the number of basis terms. The nonlinear variational parameters ${\alpha }_i,{\beta }_i,{\gamma }_i$ in the ECW (4) are generated by the proper choice of a quasi-random process of the following form

$$Z_i=\left[\frac{1}{2}k(k+1)\sqrt{p_Z}\right](R_{2,Z}-R_{1,Z})+R_{1,Z},$$

(6)

$\left[z\right]$ assumes the fractional part of $z$, the real intervals $\left[R_{1,Z},{\mathrm{R}}_{2,Z}\right]$ $(Z=\alpha ,\beta ,\gamma )$ require optimization to obtain the appropriate values of $R_{1,Z}$ and $R_{2,Z}$. $p_Z$ stands for a prime number and it takes the numbers 2, 3, and 5 for $Z=\alpha$ $Z=\beta$ and $Z=\gamma$, respectively.

To set the present DERS calculations using the CRM [33], the radial coordinates are transformed following a dilation rule comprising of the so-called rotational angle $\theta$.

$$r\to r\exp (i\theta ),$$

(7)

and the form of the transformed Hamiltonian:

$$H(\theta )\to \left(-\frac{1}{2}{\displaystyle \sum _{i=1}^3{\nabla }_i^2}\right)\exp (-2i\theta )+\left({\displaystyle \sum _{\begin{array}{l}i,j=1\\ i<j\end{array}}^3\frac{q_i{q}_j}{r_{ij}}}\right)\exp (-i\theta ),$$

(8)

In the case of nonorthogonal basis functions, the overlap and Hamiltonian matrices take the form

$$N_{nm}(\omega )=\langle {\phi }_n(\omega )|{\phi }_m(\omega )\rangle$$

(9)

and

$$H_{nm}(\theta ,\omega )=\langle {\phi }_n(\omega )|H(\theta )|{\phi }_m(\omega )\rangle$$

(10)

The complex characteristic values can be obtained by solving the equation

$${\displaystyle \sum _n{\displaystyle \sum _m{C}_{nm}}}[H_{nm}(\theta ,\omega )-E(\theta ,\omega )N_{nm}(\omega )]=0$$

(11)

Resonance poles can be located by observing the complex energy $E(\theta ,\omega )$ for various values of $\theta$ and $\omega$. The complex resonance energy is given by

$$E_{res}=E_r-\frac{i\mathsf{\Gamma }}{2}$$

(12)

where $E_r$ is the resonance energy, and $\mathsf{\Gamma }$ is the width. The RP are identified by locating stabilized roots with respect to the variation of the scaling parameter $\omega$ in the ECW for optimum choice of the nonlinear variational parameters ${\alpha }_i,{\beta }_i,{\gamma }_i$, and of the rotational angle $\theta$.

3. Results and Discussions

To extract RP (resonance positions and widths), we calculate the complex-energy eigen values $E(\theta ,\omega )$ for different values of $\theta$ and $\omega$ by diagonalizing the transformed Hamiltonian matrix. For the present problem, the parameters $\theta$ and $\omega$ are varied respectively from 0.00 to 0.60 with mesh size 0.02 and from 0.1 to 0.6 with mesh size 0.001. Exploiting the computational technique, we extract the ¹P° resonance states associated with the N = 2, 3, 4, 5 Ps threshold. Figure 1 depicts the rotational paths near the pole for the ¹P° (1) Feshbach resonance (FR) in the Ps⁻ lying below the Ps (N = 2) threshold in the energy plane (EP) for five different values of the scaling parameter ω using 900-term ECW. In this figure $\theta$ = 0.20 (002) 0.40 means the $\theta$ assumes the value from 0.2 to 0.4 with mesh size 0.02. Similarly, Figure 2, Figure 3, Figure 4 and Figure 5 shows respectively the rotational paths near the poles for the ¹P° (2) Feshbach resonance below the N = 2 Ps threshold, for the ¹P° (4) FR below the N = 3 Ps threshold, for the ¹P° (5) Feshbach resonance below the N = 5 Ps threshold, and for the ¹P° (7) FR below the N = 5 Ps threshold. From Figure 1, we can determine the RP $(E_r,\mathsf{\Gamma }/2)$ as (−0.063155862 ± 2 × 10⁻⁹, 0.459 × 10⁻⁶ ± 1 × 10⁻⁹) a.u. In a similar way, from Figure 2, Figure 3, Figure 4 and Figure 5, we can estimate the RP $(E_r,\mathsf{\Gamma }/2)$ respectively as (−0.06254245 ± 4 × 10⁻⁸, 0.11 × 10⁻⁶ ± 3 × 10⁻⁸), (−0.0281013 ± 1 × 10⁻⁶, 0.169 × 10⁻⁴ ± 2 × 10⁻⁶), (−0.010580 ± 3 × 10⁻⁶, 0.16 × 10⁻⁴ ± 3 × 10⁻⁶), and (−0.010384 ± 3 × 10⁻⁶, 0.19 × 10⁻⁴ ± 3 × 10⁻⁶). All the results obtained from the present calculations are summarized in

Table 1. The ¹P° Feshbach and shape RPs (in a.u.) in Ps⁻ associated with the N = 2, 3, 4, 5 Ps thresholds. The numbers in the parentheses denote the uncertainty in the last digit.

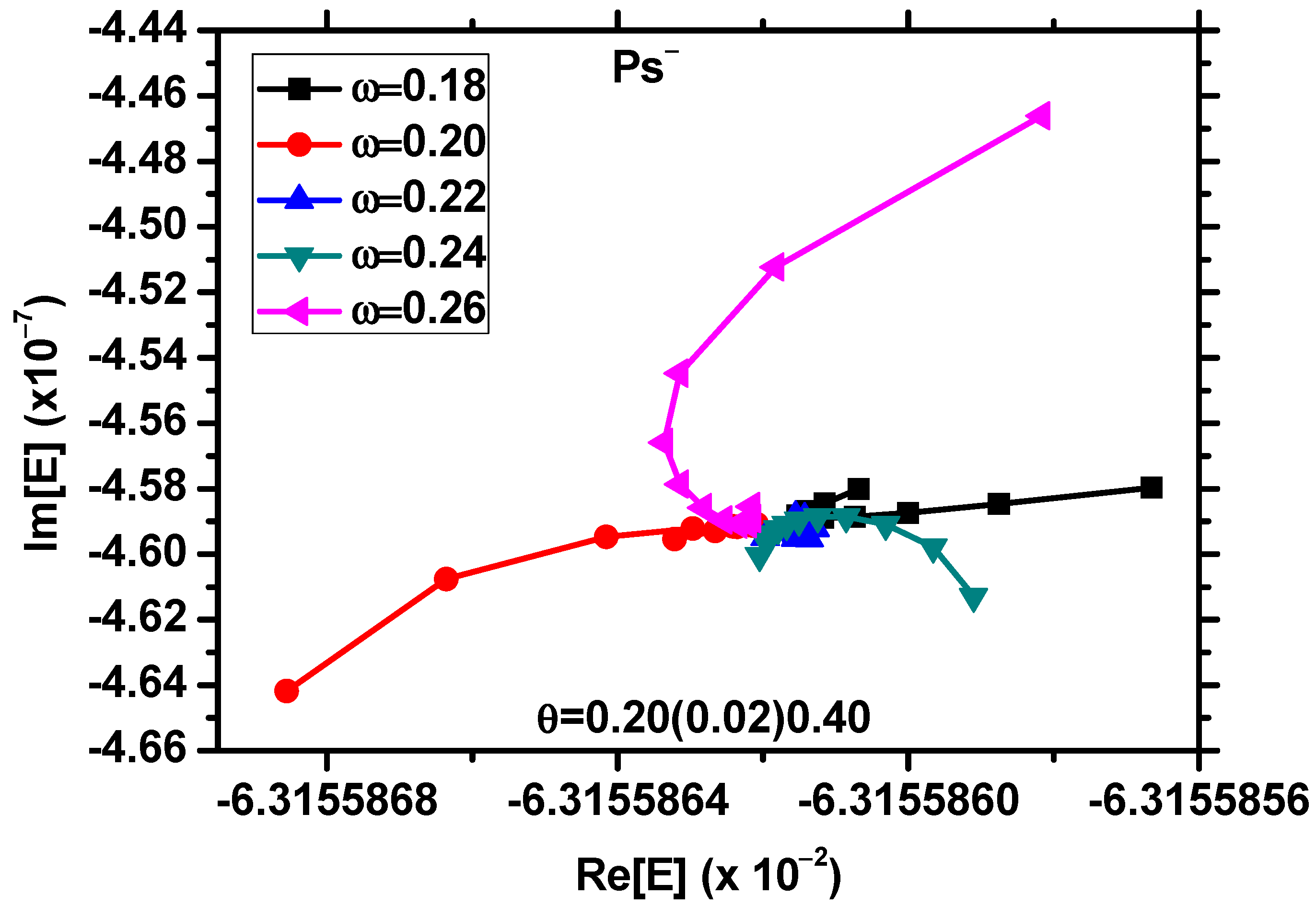
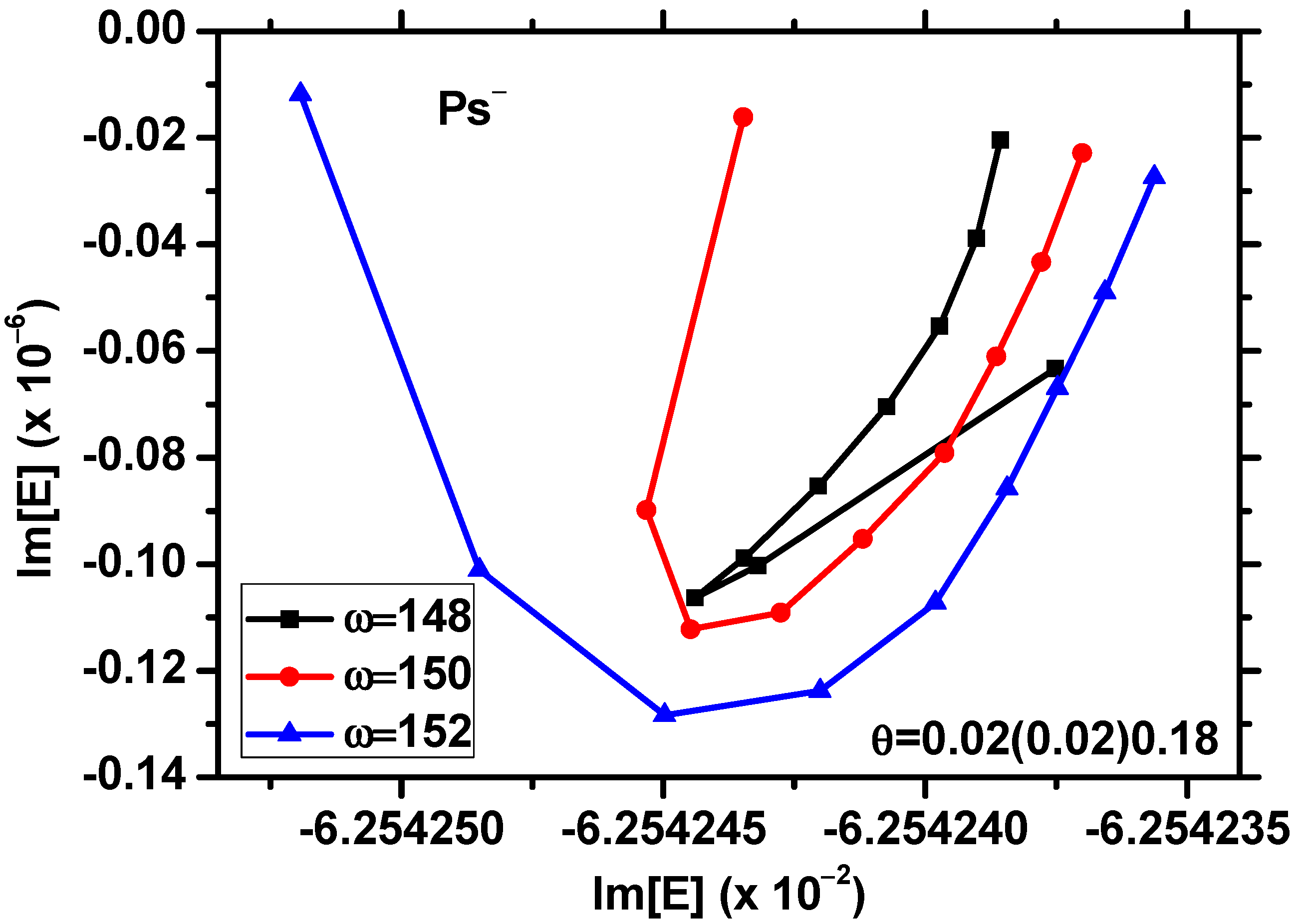
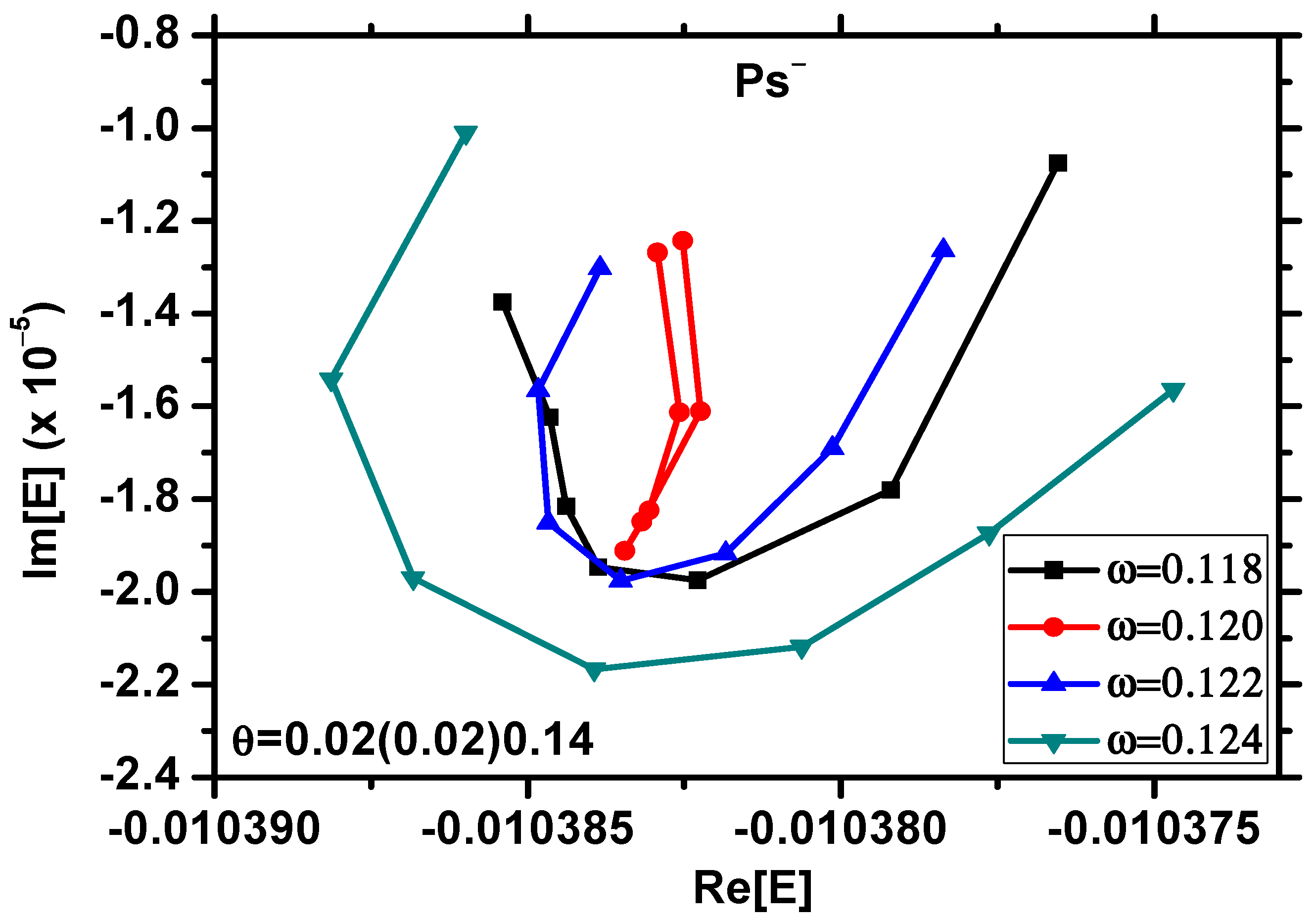
	Present Calculations		Other Calculations
	${\mathit{E}}_{\mathit{r}}$	$\frac{\mathsf{\Gamma }}{2}$	${\mathit{E}}_{\mathit{r}}$	$\frac{\mathsf{\Gamma }}{2}$	Reference
N = 2: Eth = −0.0625
1P° (1)	−0.063155862(2)	0.459(1) × 10−6	−0.0631553(1.5) −0.0631559 −0.063155 −0.0625087	0.5(1.5) × 10−6 0.4435 × 10−6 0.41 × 10−6	a b c d
1P° (2)	−0.06254244(4)	0.11(3) × 10−6	−0.062543	0.125 × 10−6	c
1P° (shape)	−0.06218(2)	0.00020(2)	−0.06217(1.5)	0.000225(1.5)	e
			−0.062158	0.00032	c
N = 3: Eth = −0.0277777777778
1P° (1)	−0.03162236(2)	0.0001103(2)	−0.03162235(0.5)	0.0001103(0.5)	a
			−0.031621	0.00011	c
1P° (2)	−0.02921495(2)	0.75(2) × 10−6	−0.02921495(0.5)	0.75(0.5) × 10−6	a
			−0.029212	0.75 × 10−6	c
1P° (3)	−0.0281276(1)	0.33(3) × 10−6	−0.028125	0.30 × 10−6	c
1P° (4)	−0.0281013(1)	0.169(2) × 10−4	−0.028099	0.165 × 10−4	c
1P° (5)	−0.027863(1)	0.2(1) × 10−6	−0.027864	0.435 × 10−7	c
1P° (6)	−0.027809(2)	0.28(3) × 10−5	−0.027811	0.175 × 10−5	c
1P° (shape)	−0.0255(2)	0.0021(2)			f
N = 4: Eth = −0.015625
1P° (1)	−0.01889032(1)	0.0000154	−0.01889035(0.5)	0.0000154(0.5)	g
			−0.018890385(1)	0.000015395	h
			−0.018863	0.000016	c
1P° (2)	−0.01704109(1)	0.8(2) × 10−6	−0.01704125(0.5)	0.65 × 10−6	g
			−0.017031	0.55 × 10−6	c
1P° (3)	−0.016536(2)	0.10(2) × 10−4	−0.0165385(0.5)	0.098(0.5) × 10−4	g
			−0.016480	0.1 × 10−4
1P° (4)	−0.016163(1)	0.2(1) × 10−5	−0.016161(2.5)	0.235(2.5) × 10−5	g
			−0.016139	0.21 × 10−6	c
1P° (5)	−0.015882(2)	0.20(2) × 10−4	−0.015880 (2.5)	0.085(2.5) × 10−4	g
			−0.015855	0.32 × 10−5	c
1P° (6)	−0.015802(1)	0.10(1) × 10−5	−0.0158025(1)	0.125(1) × 10−5	g
			−0.015819	0.65 × 10−7	c
1P° (7)	−0.01566(2)	0.035(3) × 10−5
1P° (shape)	−0.01548(1)	0.000022(2)	−0.0154875(0.5)	0.000015(0.5)	e
			−0.0154775(1.5)	0.0000305	h
N = 5: Eth = −0.01
1P° (1)	−0.012463(2)	0.16(2) × 10−4	−0.0124625(0.5)	0.1525(5) × 10−4	g
			−0.01246295	0.1525 × 10−4	h
1P° (2)	−0.011216(1)	0.2(1) × 10−5	−0.0112155(2.5)	0.135 × 10−5	g
1P° (3)	−0.01104(1)	0.22(1) × 10−4	−0.01104375(0.5)	0.1575(0.5) × 10−4	g
1P° (4)	−0.01083(2)	0.70(2) × 10−4	−0.010830(0.5)	0.68(0.5) × 10−4	g
			−0.01083009(1.5)	0.68045 × 10−4	h
1P° (5)	−0.010580(3)	0.16(3) × 10−4
1P° (6)	−0.01048(1)	0.2(1) × 10−4
1P° (7)	−0.010384(3)	0.19(3) × 10−4
1P° (8)	−0.01022(1)	0.7(1) × 10−4

a: Bhatia and Ho [19], b: Kar and Ho [21], c: Igarashi et al. [22], d: Botero [18], e: Ho and Bhatia [23], f: Kar and Ho [12], g: Ho and Bhatia [20], h: Ivanov and Ho [7].

and

Table 2. The ¹P° Feshbach and shape RP (in eV) in Ps⁻ associated with the N = 2, 3, 4, 5 Ps thresholds. The resonance positions are measured from the ground state of the Ps⁻ ion.

	Present Calculations
	${\mathit{E}}_{\mathit{r}}\left(\mathbf{eV}\right)$	$\mathsf{\Gamma }$ (meV)
	N = 2
1P° (1)	5.4109623645	0.024980052
1P° (2)	5.4276543	0.0060
1P° (shape)	5.43752	10.88456
	5.437(1) a	10(2) a
	N = 3
1P° (1)	6.26903263	6.002832
1P° (2)	6.33454159	0.0408
1P° (3)	6.36412989	0.01796
1P° (4)	6.36484555	0.9198
1P° (5)	6.37133002	0.0109
1P° (6)	6.372799	0.1524
1P° (shape)	6.4356 b	114.29 b
	N = 4
1P° (1)	6.61548907	0.83811
1P° (2)	6.66580918	0.0436
1P° (3)	6.6795534	0.544
1P° (4)	6.6897032	0.108
1P° (5)	6.6973496	1.088
1P° (6)	6.6995265	0.0544
1P° (7)	6.70339	1.9048
1P° (shape)	6.70829	1.198
	N = 5
1P° (1)	6.790385	0.0870
1P° (2)	6.824318	0.108
1P° (3)	6.829107	1.20
1P° (4)	6.834822	3.810
1P° (5)	6.841624	0.870
1P° (6)	6.844346	1.08
1P° (7)	6.846958	1.034
1P° (8)	6.85142	3.80

^a Experiment (Ref. [1]), ^b Our recent work (Ref. [12]).

.

In Table 1, we present the ¹P° Feshbach resonance energies and widths (in a.u.) in Ps⁻ below the N = 2, 3, 4, 5 Ps thresholds. The ¹P° (7) FR below the N = 4 Ps threshold and the ¹P° (5), ¹P° (6), ¹P° (7), ¹P° (8) Feshbach resonances below the N = 5 Ps threshold are reported for the first time in the literature, to the best of our knowledge. In this table, we also present the ¹P° shape resonances obtained from the resent calculations above the N = 2 and 4 Ps thresholds. The ¹P° shape RP above the N = 3 threshold are taken from our recent work [12] and are presented in this table for completeness. In Table 1, we have also included the available results from the other calculations [18,19,20,21,22,23]. Table 1 shows that our predications of RP using the ECW are in agreement with the results of Bhatia et al. [19] and Ho et al. [20,23] using HW and the CRM. The ¹P° intrashell resonance states are also in agreement with those obtained by Ivanov and Ho [7] using CI-type basis functions and the CRM. Table 1 also shows that our resonance energies and widths are fairly comparable with the reported results of Igarashi et al. [22], except for the resonance widths of the ¹P° (4), ¹P° (5), ¹P° (6) resonance states below the N = 4 Ps threshold. The numbers in the table inside parentheses denote the uncertainty in the last digit. But our listed results in this table from the works of Ho and collaborators [7,19,20,23] are converted from Rydberg units to atomic units, and so the uncertainty in the last digit exhibits a value with fractional part. The discrepancy in resonance widths is probably due to the technique used or due to interference of higher lying states in HCCA calculations. The discrepancy with other calculations in terms of precision is probably due to the use of different computational tools in different calculations. Though only a few results are presented as new in this paper, all of the results shown in Table 1 were obtained using different wave functions.

Our estimated FR energy and width below the Ps (N = 2) threshold are also in good accord with our previous work using the 600-term CEW and the stabilization method [21]. In Table 2, we present our calculated resonance energies for the doubly excited ¹P° states using the ECW and the CRM in electron volts (eV). To express our present results from a.u. to eV, we measure the resonance energy from the ground state of the Ps⁻ (−0.2620050702325 a.u. [34]). The corresponding resonance widths obtained from this calculation are presented in meV. To convert a.u. to eV, we use the relation 1 a.u. = 27.21138501195 [35]. Table 2 shows that the ¹P° shape resonance above the N = 2 Ps threshold obtained from the present calculation is in good agreement with the recent experimental observation [1]. We have examined convergence of our calculations with the increasing number of terms in ECW. We have also studied the stability of our works with different choices of nonlinear variational parameters. Our estimated resonance parameters are convergent and stable up to the quoted digits in Table 1.

4. Conclusions

In this work, we have calculated the resonance parameters for the doubly excited ¹P° states in Ps⁻ using correlated exponential wave functions in the framework of the complex-coordinate rotation method. The resonance energies and widths for the ¹P° resonance states in Ps⁻ below the N = 2, 3, 4, 5 Ps thresholds are reported. The ¹P° shape resonance above the N = 2, 4 Ps thresholds are also reported. Few resonance states have been identified for the first time in the literature. The resonance energies and widths obtained from this work, using different wave functions as compared with those used in earlier investigations, are in agreement with the available data. With the recent experimental observation of the ¹P° shape resonance states in the positronium ions, it is hoped that our investigations for the doubly excited ¹P° resonance states will provide useful information for future resonance experiments in Ps⁻.