Quasar Black Hole Mass Estimates from High-Ionization Lines: Breaking a Taboo?
Abstract
:1. Introduction: Statement of the Problem
2. Importance of Black Hole Mass Determination
3. Virial Black Hole Mass Estimates
Caveats
4. The Rehabilitating Power of Eigenvector 1
5. Virial Broadening Estimators along the Quasar MS
5.1. LILs: H and MgII2800
5.2. LIL VBE at High L
- substitution of the BC in place of the full H profile. This method requires a multicomponent maximum likelihood fitting, and is fairly reliable for Population A (even for extreme Population A) and Population B spectral types where the VBC is creating a profile inflection;
- symmetrization of the profile: FWHM FWHM−2 c(1/2);
- correction based on spectral type. In practice, this means to correct H for Population B sources by a factor as reported in Table 1.
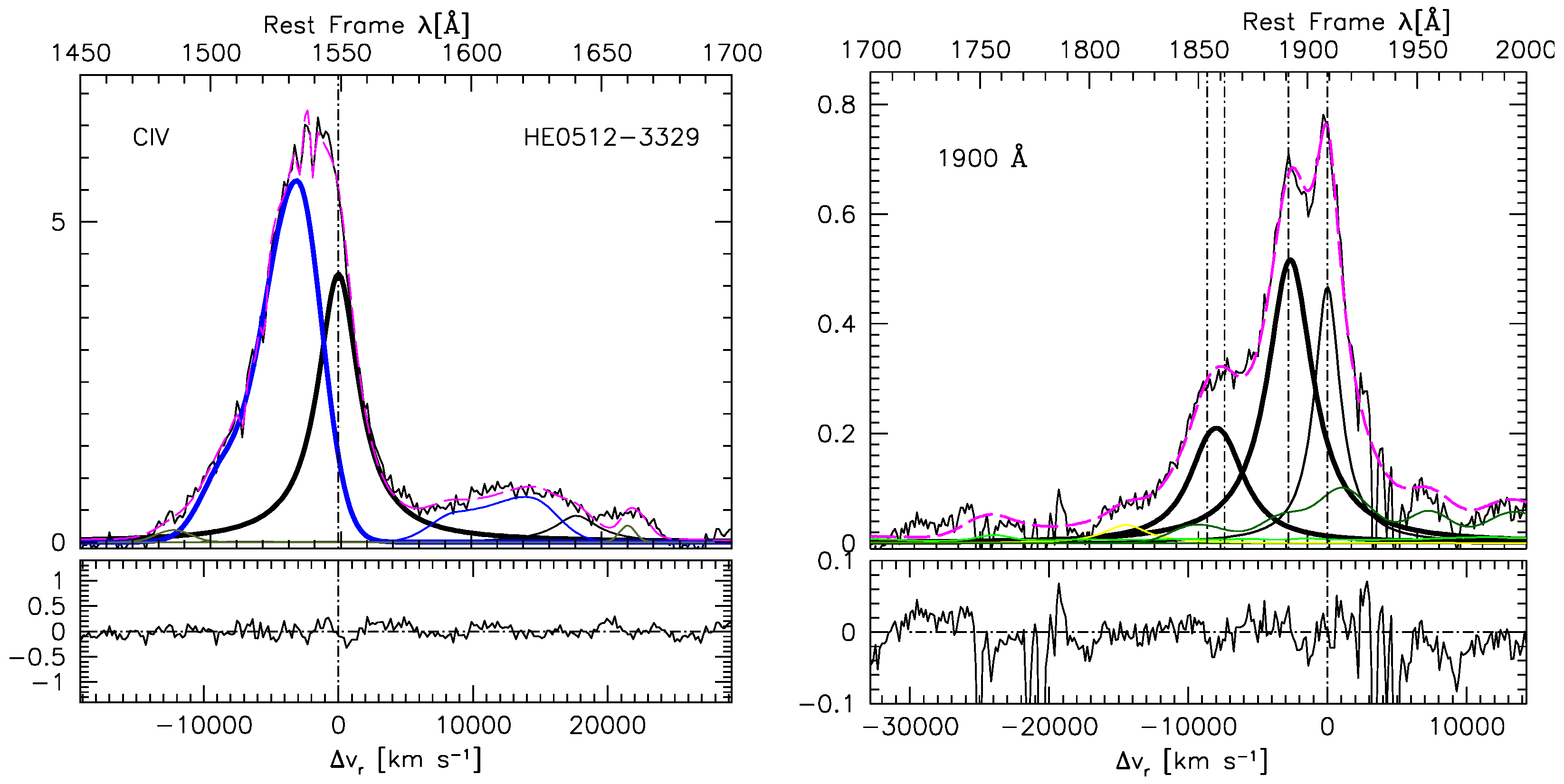
5.3. CIV
5.4. A CIV1549 VBE
5.5. Intermediate Ionization Lines (IILs)
6. Photoionization Masses
7. Conclusions
- Low-ionization lines (H, MgII 2800) provide reliable virial broadening estimators by applying corrections to the observed line width. The corrections depend on the spectral type along the E1 MS, but they are relatively small (less than 30%), and work up to the highest L of quasars.
- The HIL CIV1549 is not immediately providing a reliable virial broadening estimator. The profile is broadened by an excess emission on its blue side. The shift amplitude depends on both and L. Large shifts are observed in Population A, with Eddington ratio above a critical .
- It is possible to apply corrections to the observed CIV broadening, but they remain cumbersome even for Population A. Population B sources at low Eddington ratio require a different correction (still ill-defined by the analysis of Marziani et al. [45] as Population B sources are most affected by the Eddington ratio bias mentioned in Section 5.3).
- Preliminary results on the 1900 blend indicate that the IILs lines could provide a better choice than CIV; IIL FWHM measurements appear intrinsically more robust than those of CIV since they do not require corrections based on shift measurement with respect to rest frame. However, more data are needed to assess their reliability.
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| BC | Broad component |
| BLR | Broad line region |
| E1 | Eigenvector 1 |
| HE | Hamburg-ESO |
| HIL | High ionization line |
| IIL | Intermediate ionization line |
| IP | Ionization potential |
| ISAAC | Infrared Spectrometer and Array Camera |
| LIL | Low ionization line |
| FWHM | Full width half maximum |
| FWHM | Full width zero intensity |
| MS | Main sequence |
| NLSy1 | Narrow-line Seyfert 1 |
| SDSS | Sloan digital sky survey |
| VBE | Virial broadening estimator |
References
- Berk, D.E.V.; Richards, G.T.; Bauer, A.; Strauss, M.A.; Schneider, D.P.; Heckman, T.M.; York, D.G.; Hall, P.B.; Fan, X.; Knapp, G.R.; et al. Composite Quasar Spectra from the Sloan Digital Sky Survey. Astron. J. 2001, 122, 549–564. [Google Scholar] [CrossRef]
- Burbidge, G.R.; Burbidge, E.M. Quasi-Stellar Objects; Freeman: San Francisco, CA, USA, 1967. [Google Scholar]
- Marziani, P.; Sulentic, J.W. Quasar Outflows in the 4D Eigenvector 1 Context. Astron. Rev. 2012, 7, 33–57. [Google Scholar] [CrossRef]
- Marziani, P.; Sulentic, J.W. Estimating black hole masses in quasars using broad optical and UV emission lines. New Astron. Rev. 2012, 56, 49–63. [Google Scholar] [CrossRef]
- Shen, Y. The mass of quasars. Bull. Astron. Soc. India 2013, 41, 61–115. [Google Scholar]
- Sulentic, J.W.; Bachev, R.; Marziani, P.; Negrete, C.A.; Dultzin, D. Civλ1549 as an Eigenvector 1 Parameter for Active Galactic Nuclei. Astrophys. J. 2007, 666, 757–777. [Google Scholar] [CrossRef]
- Netzer, H.; Lira, P.; Trakhtenbrot, B.; Shemmer, O.; Cury, I. Black Hole Mass and Growth Rate at High Redshift. Astrophys. J. 2007, 671, 1256–1263. [Google Scholar] [CrossRef]
- Mejía-Restrepo, J.E.; Trakhtenbrot, B.; Lira, P.; Netzer, H.; Capellupo, D.M. Active galactic nuclei at z ∼ 1.5: II. Black Hole Mass estimation by means of broad emission lines. Mon. Not. R. Astron. Soc. 2016, 460, 187–211. [Google Scholar] [CrossRef]
- Brotherton, M.S.; Runnoe, J.C.; Shang, Z.; DiPompeo, M.A. Bias in C IV-based quasar black hole mass scaling relationships from reverberation mapped samples. Mon. Not. R. Astron. Soc. 2015, 451, 1290–1298. [Google Scholar] [CrossRef]
- Brotherton, M.S.; Runnoe, J.C.; Shang, Z.; Varju, M. Further Rehabilitating CIV-based Black Hole Mass Estimates in Quasars. In Proceedings of the 228th American Astronomical Society Meeting, San Diego, CA, USA, 12–16 June 2016; Abstracts. p. 400.05. [Google Scholar]
- Marziani, P.; Sulentic, J.W.; Stirpe, G.M.; Zamfir, S.; Calvani, M. VLT/ISAAC spectra of the Hβ region in intermediate-redshift quasars. III. Hβ broad-line profile analysis and inferences about BLR structure. Astron. Astrophys. 2009, 495, 83–112. [Google Scholar] [CrossRef]
- Marziani, P.; Sulentic, J.W.; Plauchu-Frayn, I.; del Olmo, A. Low-Ionization Outflows in High Eddington Ratio Quasars. Astrophys. J. 2013, 764, 150. [Google Scholar] [CrossRef]
- Marziani, P.; Sulentic, J.W.; Plauchu-Frayn, I.; del Olmo, A. Is Mg II 2800 a Reliable Virial Broadening Estimator for Quasars? Astron. Astrophys. 2013, 555, A89. [Google Scholar] [CrossRef]
- Sulentic, J.W.; del Olmo, A.; Marziani, P.; Martínez-Carballo, M.A.; D’Onofrio, M.; Dultzin, D.; Perea, J.; Martínez-Aldama, M.L.; Negrete, C.A.; Stirpe, G.M.; et al. What does Civλ1549 tell us about the physical driver of the Eigenvector Quasar Sequence? arXiv, 2017; arXiv:1708.03187. [Google Scholar]
- Fabian, A.C. Observational Evidence of Active Galactic Nuclei Feedback. Annu. Rev. Astron. Astrophys. 2012, 50, 455–489. [Google Scholar] [CrossRef]
- Kormendy, J.; Ho, L.C. Coevolution (Or Not) of Supermassive Black Holes and Host Galaxies. Annu. Rev. Astron. Astroph. 2013, 51, 511–653. [Google Scholar] [CrossRef]
- King, A.; Pounds, K. Powerful Outflows and Feedback from Active Galactic Nuclei. Annu. Rev. Astron. Astroph. 2015, 53, 115–154. [Google Scholar] [CrossRef]
- Ferland, G.J.; Hu, C.; Wang, J.; Baldwin, J.A.; Porter, R.L.; van Hoof, P.A.M.; Williams, R.J.R. Implications of Infalling Fe II-Emitting Clouds in Active Galactic Nuclei: Anisotropic Properties. Astrophys. J. Lett. 2009, 707, L82–L86. [Google Scholar] [CrossRef]
- Marziani, P.; Carballo, M.A.M.; Sulentic, J.W.; Del Olmo, A.; Stirpe, G.M.; Dultzin, D. The most powerful quasar outflows as revealed by the Civ λ1549 resonance line. Astrophys. Space Sci. 2016, 361, 29. [Google Scholar] [CrossRef]
- Smith, A.; Bromm, V.; Loeb, A. The first supermassive black holes. arXiv, 2017; arXiv:1703.03083. [Google Scholar] [CrossRef]
- Trakhtenbrot, B.; Urry, C.M.; Civano, F.; Rosario, D.J.; Elvis, M.; Schawinski, K.; Suh, H.; Bongiorno, A.; Simmons, B.D. An over-massive black hole in a typical star-forming galaxy, 2 billion years after the Big Bang. Science 2015, 349, 168–171. [Google Scholar] [CrossRef] [PubMed]
- Denney, K.D.; Pogge, R.W.; Assef, R.J.; Kochanek, C.S.; Peterson, B.M.; Vestergaard, M. C IV Line-width Anomalies: The Perils of Low Signal-to-noise Spectra. Astrophys. J. 2013, 775, 60. [Google Scholar] [CrossRef]
- Peterson, B.M.; Wandel, A. Keplerian Motion of Broad-Line Region Gas as Evidence for Supermassive Black Holes in Active Galactic Nuclei. Astrophys. J. Lett. 1999, 521, L95–L98. [Google Scholar] [CrossRef]
- Kaspi, S.; Smith, P.S.; Netzer, H.; Maoz, D.; Jannuzi, B.T.; Giveon, U. Reverberation Measurements for 17 Quasars and the Size-Mass-Luminosity Relations in Active Galactic Nuclei. Astrophys. J. 2000, 533, 631–649. [Google Scholar] [CrossRef]
- Kaspi, S.; Brandt, W.N.; Maoz, D.; Netzer, H.; Schneider, D.P.; Shemmer, O. Reverberation Mapping of High-Luminosity Quasars: First Results. Astrophys. J. 2007, 659, 997–1007. [Google Scholar] [CrossRef]
- Bentz, M.C.; Peterson, B.M.; Pogge, R.W.; Vestergaard, M. The Black Hole Mass-Bulge Luminosity Relationship for Active Galactic Nuclei From Reverberation Mapping and Hubble Space Telescope Imaging. Astrophys. J. Lett. 2009, 694, L166–L170. [Google Scholar] [CrossRef]
- Du, P.; Lu, K.X.; Hu, C.; Qiu, J.; Li, Y.R.; Huang, Y.K.; Wang, F.; Bai, J.M.; Bian, W.H.; Yuan, Y.F.; et al. Supermassive Black Holes with High Accretion Rates in Active Galactic Nuclei. VI. Velocity-resolved Reverberation Mapping of the Hβ Line. Astrophys. J. 2016, 820, 27. [Google Scholar] [CrossRef]
- Bentz, M.C.; Peterson, B.M.; Pogge, R.W.; Vestergaard, M.; Onken, C.A. The Radius-Luminosity Relationship for Active Galactic Nuclei: The Effect of Host-Galaxy Starlight on Luminosity Measurements. Astrophys. J. 2006, 644, 133–142. [Google Scholar] [CrossRef]
- Vestergaard, M.; Peterson, B.M. Determining Central Black Hole Masses in Distant Active Galaxies and Quasars. II. Improved Optical and UV Scaling Relationships. Astrophys. J. 2006, 641, 689–709. [Google Scholar] [CrossRef]
- Trakhtenbrot, B.; Netzer, H. Black hole growth to z = 2 − I. Improved virial methods for measuring MBH and L/LEdd. Mon. Not. R. Astron. Soc. 2012, 427, 3081–3102. [Google Scholar] [CrossRef]
- Shen, Y.; Liu, X. Comparing Single-epoch Virial Black Hole Mass Estimators for Luminous Quasars. Astrophys. J. 2012, 753, 125. [Google Scholar] [CrossRef]
- Park, D.; Woo, J.H.; Denney, K.D.; Shin, J. Calibrating C-IV-based Black Hole Mass Estimators. Astrophys. J. 2013, 770, 87. [Google Scholar] [CrossRef]
- Shen, Y.; Brandt, W.N.; Richards, G.T.; Denney, K.D.; Greene, J.E.; Grier, C.J.; Ho, L.C.; Peterson, B.M.; Petitjean, P.; Schneider, D.P.; et al. The Sloan Digital Sky Survey Reverberation Mapping Project: Velocity Shifts of Quasar Emission Lines. Astrophys. J. 2016, 831, 7. [Google Scholar] [CrossRef]
- Elvis, M.; Wilkes, B.J.; McDowell, J.C.; Green, R.F.; Bechtold, J.; Willner, S.P.; Oey, M.S.; Polomski, E.; Cutri, R. Atlas of quasar energy distributions. Astrophys. J. Suppl. Ser. 1994, 95, 1–68. [Google Scholar] [CrossRef]
- Richards, G.T.; Lacy, M.; Storrie-Lombardi, L.J.; Hall, P.B.; Gallagher, S.C.; Hines, D.C.; Fan, X.; Papovich, C.; Berk, D.E.V.; Trammell, G.B.; et al. Spectral Energy Distributions and Multiwavelength Selection of Type 1 Quasars. Astrophys. J. Suppl. Ser. 2006, 166, 470–497. [Google Scholar] [CrossRef]
- Runnoe, J.C.; Shang, Z.; Brotherton, M.S. The orientation dependence of quasar spectral energy distributions. Mon. Not. R. Astron. Soc. 2013, 435, 3251–3261. [Google Scholar] [CrossRef]
- Horne, K. AGN STORM collaboration. Echo Mapping of the Broad Emission-Line Region in NGC 5548. Zenodo 2017. [Google Scholar] [CrossRef]
- Pei, L.; Fausnaugh, M.M.; Barth, A.J.; Peterson, B.M.; Bentz, M.C.; De Rosa, G.; Denney, K.D.; Goad, M.R.; Kochanek, C.S.; Korista, K.T.; et al. Space Telescope and Optical Reverberation Mapping Project. V. Optical Spectroscopic Campaign and Emission-line Analysis for NGC 5548. Astrophys. J. 2017, 837, 131. [Google Scholar] [CrossRef]
- Fausnaugh, M.M.; Denney, K.D.; Barth, A.J.; Bentz, M.C.; Bottorff, M.C.; Carini, M.T.; Croxall, K.V.; De Rosa, G.; Goad, M.R.; Horne, K.; et al. Space Telescope and Optical Reverberation Mapping Project. III. Optical Continuum Emission and Broadband Time Delays in NGC 5548. Astrophys. J. 2016, 821, 56. [Google Scholar] [CrossRef]
- Bon, E.; Marziani, P.; Bon, N. Periodic optical variability of AGN. In Proceedings of the IAU Symposium 324: New Frontiers in Black Hole Astrophysics, Ljubljana, Slovenia, 12–16 September 2016; pp. 176–179. [Google Scholar]
- Bon, E.; Jovanović, P.; Marziani, P.; Shapovalova, A.I.; Bon, N.; Borka Jovanović, V.; Borka, D.; Sulentic, J.; Popović, L.Č. The First Spectroscopically Resolved Sub-parsec Orbit of a Supermassive Binary Black Hole. Astrophys. J. 2012, 759, 118. [Google Scholar] [CrossRef]
- Graham, M.J.; Djorgovski, S.G.; Stern, D.; Drake, A.J.; Mahabal, A.A.; Donalek, C.; Glikman, E.; Larson, S.; Christensen, E. A systematic search for close supermassive black hole binaries in the Catalina Real-time Transient Survey. Mon. Not. R. Astron. Soc. 2015, 453, 1562–1576. [Google Scholar] [CrossRef]
- Bon, E.; Zucker, S.; Netzer, H.; Marziani, P.; Bon, N.; Jovanović, P.; Shapovalova, A.I.; Komossa, S.; Gaskell, C.M.; Popović, L.Č.; et al. Evidence for Periodicity in 43 year-long Monitoring of NGC 5548. Astrophys. J. Suppl. Ser. 2016, 225, 29. [Google Scholar] [CrossRef]
- Charisi, M.; Bartos, I.; Haiman, Z.; Price-Whelan, A.M.; Graham, M.J.; Bellm, E.C.; Laher, R.R.; Márka, S. A population of short-period variable quasars from PTF as supermassive black hole binary candidates. Mon. Not. R. Astron. Soc. 2016, 463, 2145–2171. [Google Scholar] [CrossRef]
- Marziani, P.; Bon, E.; Bon, N.; Dultzin, D.; Del Olmo, A.; D’Onofrio, M. 2017; in preparation.
- Li, Y.R.; Wang, J.M.; Ho, L.C.; Lu, K.X.; Qiu, J.; Du, P.; Hu, C.; Huang, Y.K.; Zhang, Z.X.; Wang, K.; et al. Spectroscopic Indication of a Centi-parsec Supermassive Black Hole Binary in the Galactic Center of NGC 5548. Astrophys. J. 2016, 822, 4. [Google Scholar] [CrossRef]
- Croom, S.M. Do quasar broad-line velocity widths add any information to virial black hole mass estimates? arXiv, 2011; arXiv:1105.4391. [Google Scholar] [CrossRef]
- Woo, J.H.; Treu, T.; Barth, A.J.; Wright, S.A.; Walsh, J.L.; Bentz, M.C.; Martini, P.; Bennert, V.N.; Canalizo, G.; Filippenko, A.V.; et al. The Lick AGN Monitoring Project: The MBH-σ* Relation for Reverberation-mapped Active Galaxies. Astrophys. J. 2010, 716, 269–280. [Google Scholar] [CrossRef]
- Gültekin, K.; Richstone, D.O.; Gebhardt, K.; Lauer, T.R.; Tremaine, S.; Aller, M.C.; Bender, R.; Dressler, A.; Faber, S.M.; Filippenko, A.V.; et al. The M-σ and M-L Relations in Galactic Bulges, and Determinations of Their Intrinsic Scatter. Astrophys. J. 2009, 698, 198–221. [Google Scholar] [CrossRef]
- Onken, C.A.; Ferrarese, L.; Merritt, D.; Peterson, B.M.; Pogge, R.W.; Vestergaard, M.; Wandel, A. Supermassive Black Holes in Active Galactic Nuclei. II. Calibration of the Black Hole Mass-Velocity Dispersion Relationship for Active Galactic Nuclei. Astrophys. J. 2004, 615, 645–651. [Google Scholar] [CrossRef]
- Ferrarese, L.; Merritt, D. A Fundamental Relation between Supermassive Black Holes and Their Host Galaxies. Astrophys. J. Lett. 2000, 539, L9–L12. [Google Scholar] [CrossRef]
- Graham, A.W.; Onken, C.A.; Athanassoula, E.; Combes, F. An expanded Mbh-σ diagram, and a new calibration of active galactic nuclei masses. Mon. Not. R. Astron. Soc. 2011, 412, 2211–2228. [Google Scholar] [CrossRef]
- Collin, S.; Kawaguchi, T.; Peterson, B.M.; Vestergaard, M. Systematic effects in measurement of black hole masses by emission-line reverberation of active galactic nuclei: Eddington ratio and inclination. Astron. Astrophys. 2006, 456, 75–90. [Google Scholar] [CrossRef]
- Sulentic, J.W.; Marziani, P.; Zwitter, T.; Dultzin-Hacyan, D.; Calvani, M. The Demise of the Classical Broad-Line Region in the Luminous Quasar PG 1416-129. Astrophys. J. Lett. 2000, 545, L15–L18. [Google Scholar] [CrossRef]
- Sulentic, J.; Marziani, P.; Zamfir, S. The Case for Two Quasar Populations. Open Astron. 2011, 20, 427–434. [Google Scholar] [CrossRef]
- Fraix-Burnet, D.; Marziani, P.; D’Onofrio, M.; Dultzin, D. The Phylogeny of Quasars and the Ontogeny of Their Central Black Holes. Front. Astron. Space Sci. 2017, 4, 1. [Google Scholar] [CrossRef]
- Boroson, T.A.; Green, R.F. The emission-line properties of low-redshift quasi-stellar objects. Astrophys. J. Suppl. Ser. 1992, 80, 109–135. [Google Scholar] [CrossRef]
- Dultzin-Hacyan, D.; Sulentic, J.; Marziani, P.; Calvani, M.; Moles, M. A Correlation Analysis for Emission Lines in 52 AGN. In IAU Colloquium 159: Emission Lines in Active Galaxies: New Methods and Techniques; Peterson, B.M., Cheng, F.Z., Wilson, A.S., Eds.; Astronomical Society of the Pacific Conference Series; The Astronomical Society of the Pacific: San Francisco, CA, USA, 1997; Volume 113, p. 262. [Google Scholar]
- Shang, Z.; Wills, B.J.; Robinson, E.L.; Wills, D.; Laor, A.; Xie, B.; Yuan, J. The Baldwin Effect and Black Hole Accretion: A Spectral Principal Component Analysis of a Complete Quasar Sample. Astrophys. J. 2003, 586, 52–71. [Google Scholar] [CrossRef]
- Kruczek, N.E.; Richards, G.T.; Gallagher, S.C.; Deo, R.P.; Hall, P.B.; Hewett, P.C.; Leighly, K.M.; Krawczyk, C.M.; Proga, D. C IV Emission and the Ultraviolet through X-Ray Spectral Energy Distribution of Radio-quiet Quasars. Astron. J. 2011, 142, 130. [Google Scholar] [CrossRef]
- Tang, B.; Shang, Z.; Gu, Q.; Brotherton, M.S.; Runnoe, J.C. The Optical and Ultraviolet Emission-line Properties of Bright Quasars with Detailed Spectral Energy Distributions. Astrophys. J. Suppl. Ser. 2012, 201, 38. [Google Scholar] [CrossRef]
- Kuraszkiewicz, J.; Wilkes, B.J.; Schmidt, G.; Smith, P.S.; Cutri, R.; Czerny, B. Principal Component Analysis of the Spectral Energy Distribution and Emission Line Properties of Red 2MASS Active Galactic Nuclei. Astrophys. J. 2009, 692, 1180–1189. [Google Scholar] [CrossRef]
- Mao, Y.F.; Wang, J.; Wei, J.Y. Extending the Eigenvector 1 space to the optical variability of quasars. Res. Astron. Astrophys. 2009, 9, 529–537. [Google Scholar] [CrossRef]
- Grupe, D. A Complete Sample of Soft X-ray-selected AGNs. II. Statistical Analysis. Astron. J. 2004, 127, 1799–1810. [Google Scholar] [CrossRef]
- Wang, J.; Wei, J.Y.; He, X.T. A Sample of IRAS Infrared-selected Seyfert 1.5 Galaxies: Infrared Color α(60, 25)-dominated Eigenvector 1. Astrophys. J. 2006, 638, 106–119. [Google Scholar] [CrossRef]
- Richards, G.T.; Kruczek, N.E.; Gallagher, S.C.; Hall, P.B.; Hewett, P.C.; Leighly, K.M.; Deo, R.P.; Kratzer, R.M.; Shen, Y. Unification of Luminous Type 1 Quasars through C IV Emission. Astron. J. 2011, 141, 167. [Google Scholar] [CrossRef]
- Yip, C.W.; Connolly, A.J.; Berk, D.E.V.; Ma, Z.; Frieman, J.A.; SubbaRao, M.; Szalay, A.S.; Richards, G.T.; Hall, P.B.; Schneider, D.P.; et al. Spectral Classification of Quasars in the Sloan Digital Sky Survey: Eigenspectra, Redshift, and Luminosity Effects. Astron. J. 2004, 128, 2603–2630. [Google Scholar] [CrossRef]
- Shen, Y.; Ho, L.C. The diversity of quasars unified by accretion and orientation. Nature 2014, 513, 210–213. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Shen, Y. Dissecting the Quasar Main Sequence: Insight from Host Galaxy Properties. Astrophys. J. Lett. 2015, 804, L15. [Google Scholar] [CrossRef]
- Sulentic, J.W.; Marziani, P.; Zamanov, R.; Bachev, R.; Calvani, M.; Dultzin-Hacyan, D. Average Quasar Spectra in the Context of Eigenvector 1. Astrophys. J. Lett. 2002, 566, L71–L75. [Google Scholar] [CrossRef]
- Marziani, P.; Sulentic, J.W.; Zwitter, T.; Dultzin-Hacyan, D.; Calvani, M. Searching for the Physical Drivers of the Eigenvector 1 Correlation Space. Astrophys. J. 2001, 558, 553–560. [Google Scholar] [CrossRef]
- Sulentic, J.W.; Marziani, P.; Dultzin-Hacyan, D. Phenomenology of Broad Emission Lines in Active Galactic Nuclei. Annu. Rev. Astron. Astrophys. 2000, 38, 521–571. [Google Scholar] [CrossRef]
- Abramowicz, M.A.; Straub, O. Accretion discs. Scholarpedia 2014, 9, 2408. [Google Scholar] [CrossRef]
- Bon, N.; Bon, E.; Marziani, P.; Jovanović, P. Gravitational redshift of emission lines in the AGN spectra. Astrophys. Space Sci. 2015, 360, 41. [Google Scholar] [CrossRef]
- Wang, J.; Dong, X.; Wang, T.; Ho, L.C.; Yuan, W.; Wang, H.; Zhang, K.; Zhang, S.; Zhou, H. Estimating Black Hole Masses in Active Galactic Nuclei Using the Mg II λ2800 Emission Line. Astrophys. J. 2009, 707, 1334–1346. [Google Scholar] [CrossRef]
- Negrete, C.A.; Dultzin, D.; Marziani, P.; Sulentic, J.W. Reverberation and Photoionization Estimates of the Broad-line Region Radius in Low-z Quasars. Astrophys. J. 2013, 771, 31. [Google Scholar] [CrossRef]
- Zamfir, S.; Sulentic, J.W.; Marziani, P.; Dultzin, D. Detailed characterization of Hβ emission line profile in low-z SDSS quasars. Mon. Not. R. Astron. Soc. 2010, 403, 1759–1786. [Google Scholar] [CrossRef]
- Leighly, K.M. ASCA (and HST) observations of NLS1s. New Astron. Rev. 2000, 44, 395–402. [Google Scholar] [CrossRef]
- Bachev, R.; Marziani, P.; Sulentic, J.W.; Zamanov, R.; Calvani, M.; Dultzin-Hacyan, D. Average Ultraviolet Quasar Spectra in the Context of Eigenvector 1: A Baldwin Effect Governed by the Eddington Ratio? Astrophys. J. 2004, 617, 171–183. [Google Scholar] [CrossRef]
- Marziani, P.; Sulentic, J.W.; Negrete, C.A.; Dultzin, D.; Zamfir, S.; Bachev, R. Broad-line region physical conditions along the quasar eigenvector 1 sequence. Mon. Not. R. Astron. Soc. 2010, 409, 1033–1048. [Google Scholar] [CrossRef]
- Denney, K.D.; Vestergaard, M.; Watson, D.; Davis, T. Using Quasars as Standard Candles for Studying Dark Energy. In Proceedings of the American Astronomical Society Meeting, Austin, TX, USA, 8–12 January 2012; Abstracts. Volume 219, p. 440.20. [Google Scholar]
- Marziani, P.; Sulentic, J.W.; Zamanov, R.; Calvani, M.; Dultzin-Hacyan, D.; Bachev, R.; Zwitter, T. An Optical Spectroscopic Atlas of Low-Redshift Active Galactic Nuclei. Astrophys. J. Suppl. Ser. 2003, 145, 199–211. [Google Scholar] [CrossRef]
- Coatman, L.; Hewett, P.C.; Banerji, M.; Richards, G.T.; Hennawi, J.F.; Prochaska, J.X. Correcting C IV-based virial black hole masses. Mon. Not. R. Astron. Soc. 2017, 465, 2120–2142. [Google Scholar] [CrossRef]
- Sulentic, J.W.; Martínez-Carballo, M.A.; Marziani, P.; del Olmo, A.; Stirpe, G.M.; Zamfir, S.; Plauchu-Frayn, I. 3C 57 as an Atypical Radio-Loud Quasar: Implications for the Radio-Loud/Radio-Quiet Dichotomy. Mon. Not. R. Astron. Soc. 2015, 450, 1916–1925. [Google Scholar] [CrossRef]
- Saito, Y.; Imanishi, M.; Minowa, Y.; Morokuma, T.; Kawaguchi, T.; Sameshima, H.; Minezaki, T.; Oi, N.; Nagao, T.; Kawatatu, N.; et al. Near-infrared spectroscopy of quasars at z ∼ 3 and estimates of their supermassive black hole masses. Publ. Astron. Soc. Jpn. 2016, 68. [Google Scholar] [CrossRef]
- Coatman, L.; Hewett, P.C.; Banerji, M.; Richards, G.T. C IV emission-line properties and systematic trends in quasar black hole mass estimates. Mon. Not. R. Astron. Soc. 2016, 461, 647–665. [Google Scholar] [CrossRef]
- Negrete, A.; Dultzin, D.; Marziani, P.; Sulentic, J. BLR Physical Conditions in Extreme Population A Quasars: A Method to Estimate Central Black Hole Mass at High Redshift. Astrophys. J. 2012, 757, 62. [Google Scholar] [CrossRef]
- Negrete, C.A.; Dultzin, D.; Marziani, P.; Sulentic, J.W. A New Method to Obtain the Broad Line Region Size of High Redshift Quasars. Astrophys. J. 2014, 794, 95. [Google Scholar] [CrossRef]
| 1. | The following analysis pertains only type 1 quasars showing broad (FWHM km s) emission in permitted lines. |
| 2. | This happens also for MgII, but with much lower blueward displacements (few hundreds vs. few thousands km s). |

© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marziani, P.; Olmo, A.D.; Martínez-Aldama, M.L.; Dultzin, D.; Negrete, A.; Bon, E.; Bon, N.; D’Onofrio, M. Quasar Black Hole Mass Estimates from High-Ionization Lines: Breaking a Taboo? Atoms 2017, 5, 33. https://doi.org/10.3390/atoms5030033
Marziani P, Olmo AD, Martínez-Aldama ML, Dultzin D, Negrete A, Bon E, Bon N, D’Onofrio M. Quasar Black Hole Mass Estimates from High-Ionization Lines: Breaking a Taboo? Atoms. 2017; 5(3):33. https://doi.org/10.3390/atoms5030033
Chicago/Turabian StyleMarziani, Paola, Ascensión Del Olmo, Mary Loli Martínez-Aldama, Deborah Dultzin, Alenka Negrete, Edi Bon, Natasa Bon, and Mauro D’Onofrio. 2017. "Quasar Black Hole Mass Estimates from High-Ionization Lines: Breaking a Taboo?" Atoms 5, no. 3: 33. https://doi.org/10.3390/atoms5030033
APA StyleMarziani, P., Olmo, A. D., Martínez-Aldama, M. L., Dultzin, D., Negrete, A., Bon, E., Bon, N., & D’Onofrio, M. (2017). Quasar Black Hole Mass Estimates from High-Ionization Lines: Breaking a Taboo? Atoms, 5(3), 33. https://doi.org/10.3390/atoms5030033








