Stark Broadening from Impact Theory to Simulations
Abstract
:1. Introduction
2. Impact Broadening
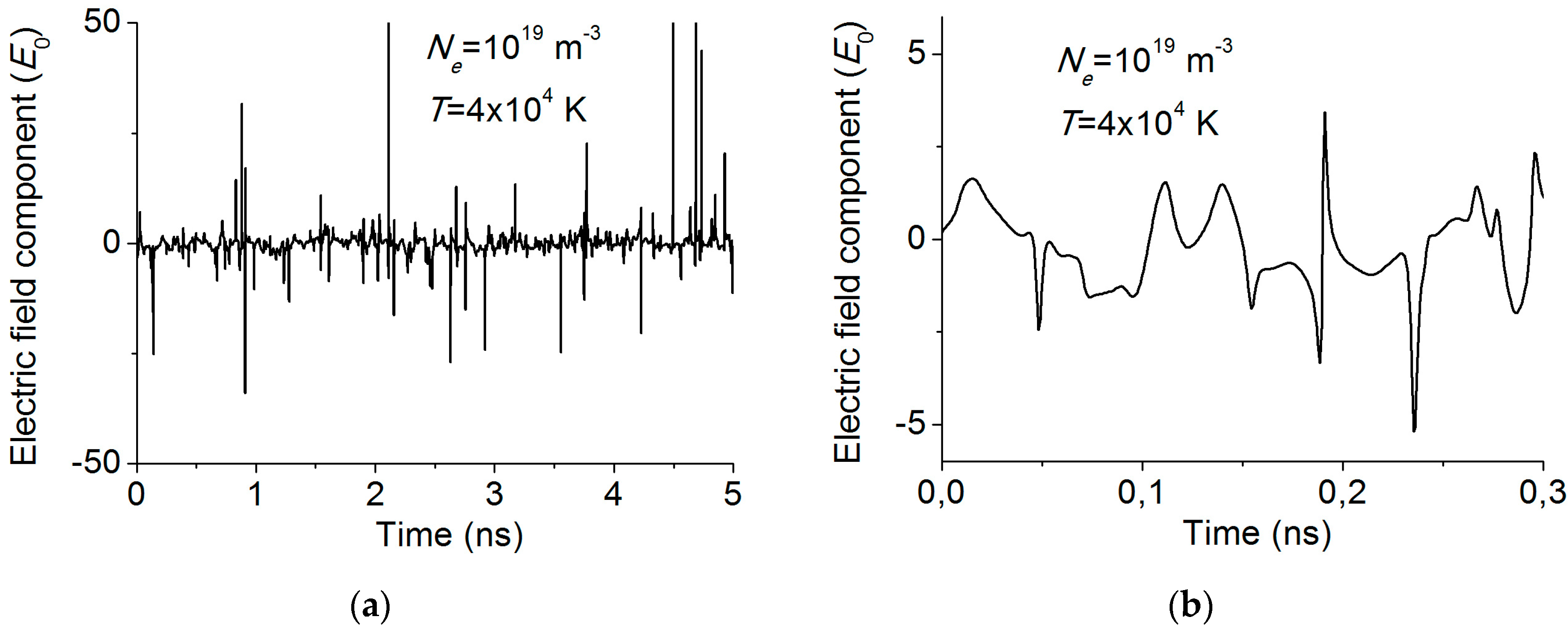
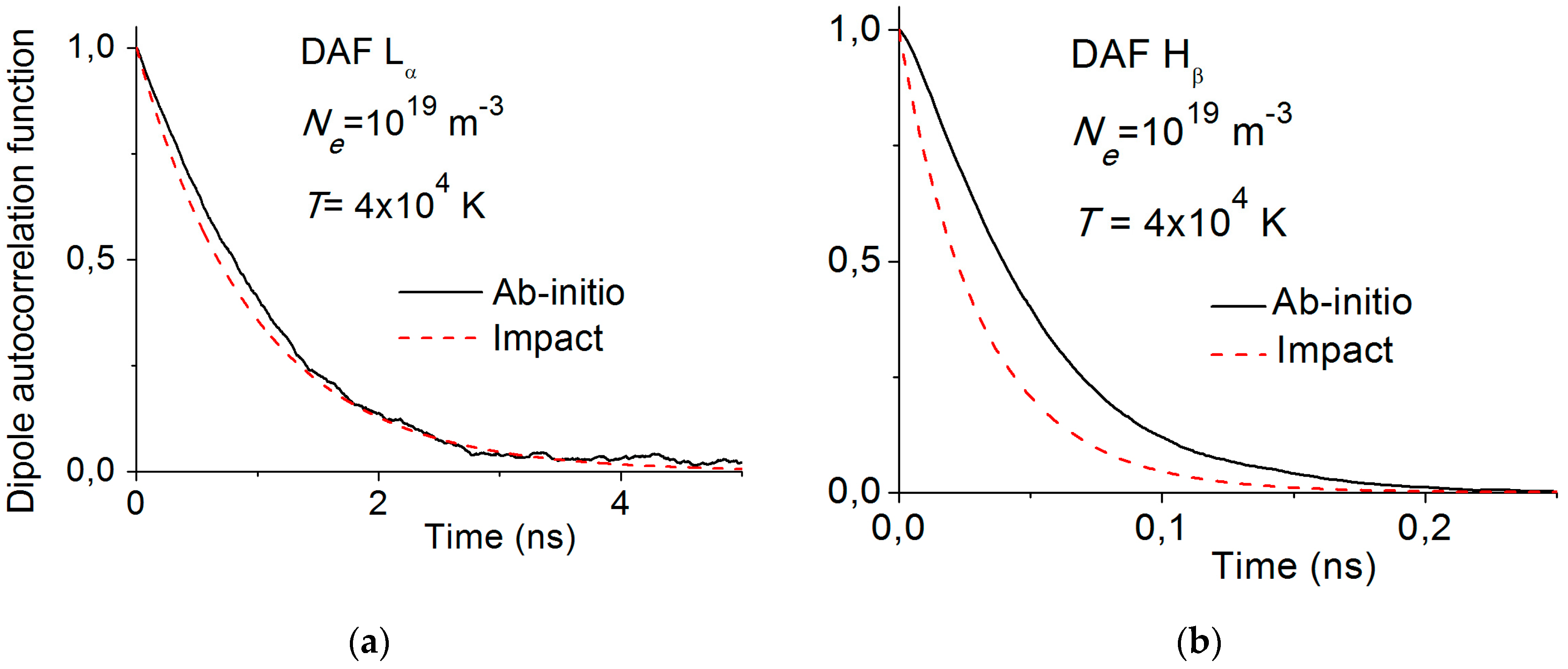
3. Simulations of Impact Theory and Ion Dynamics
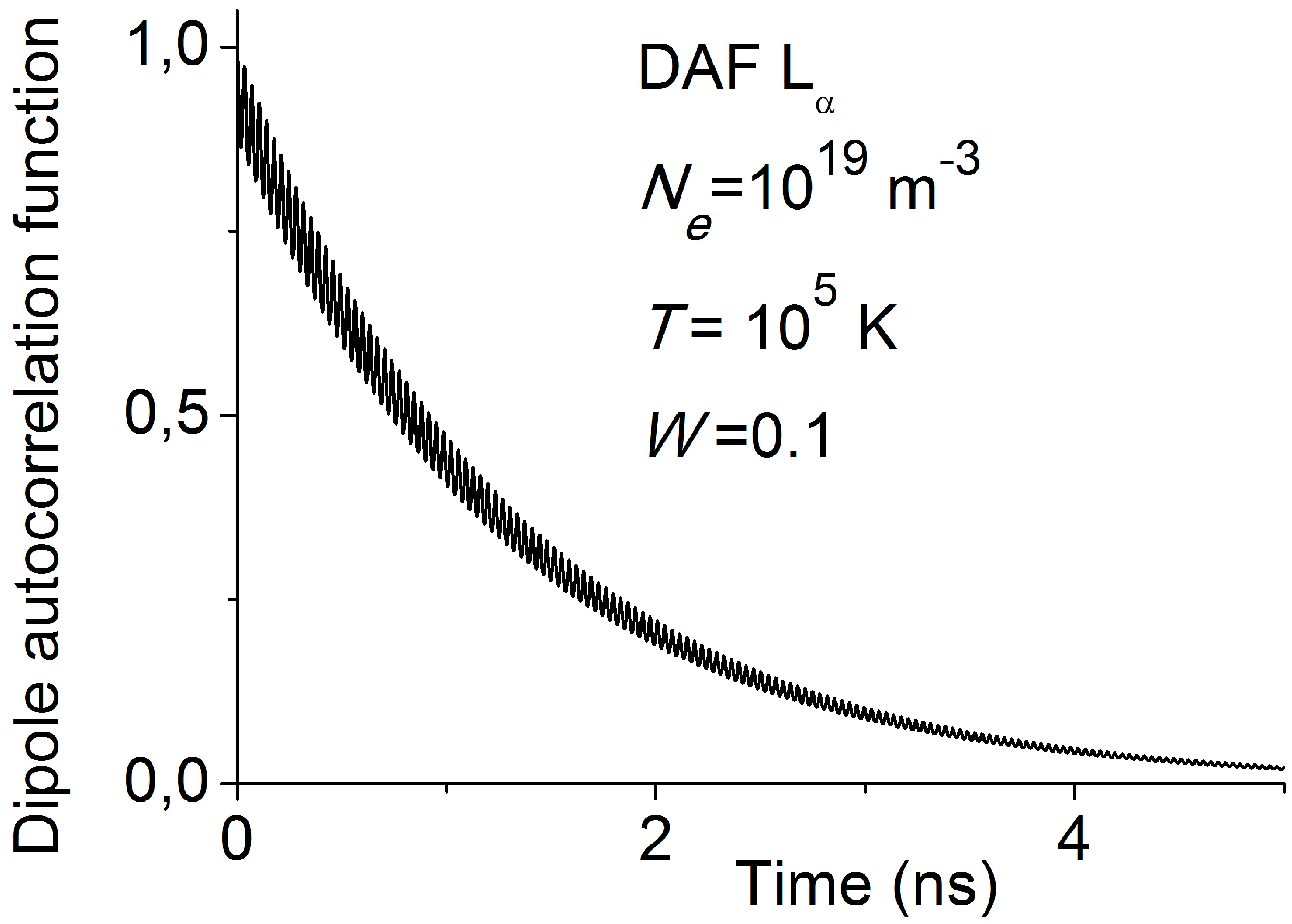
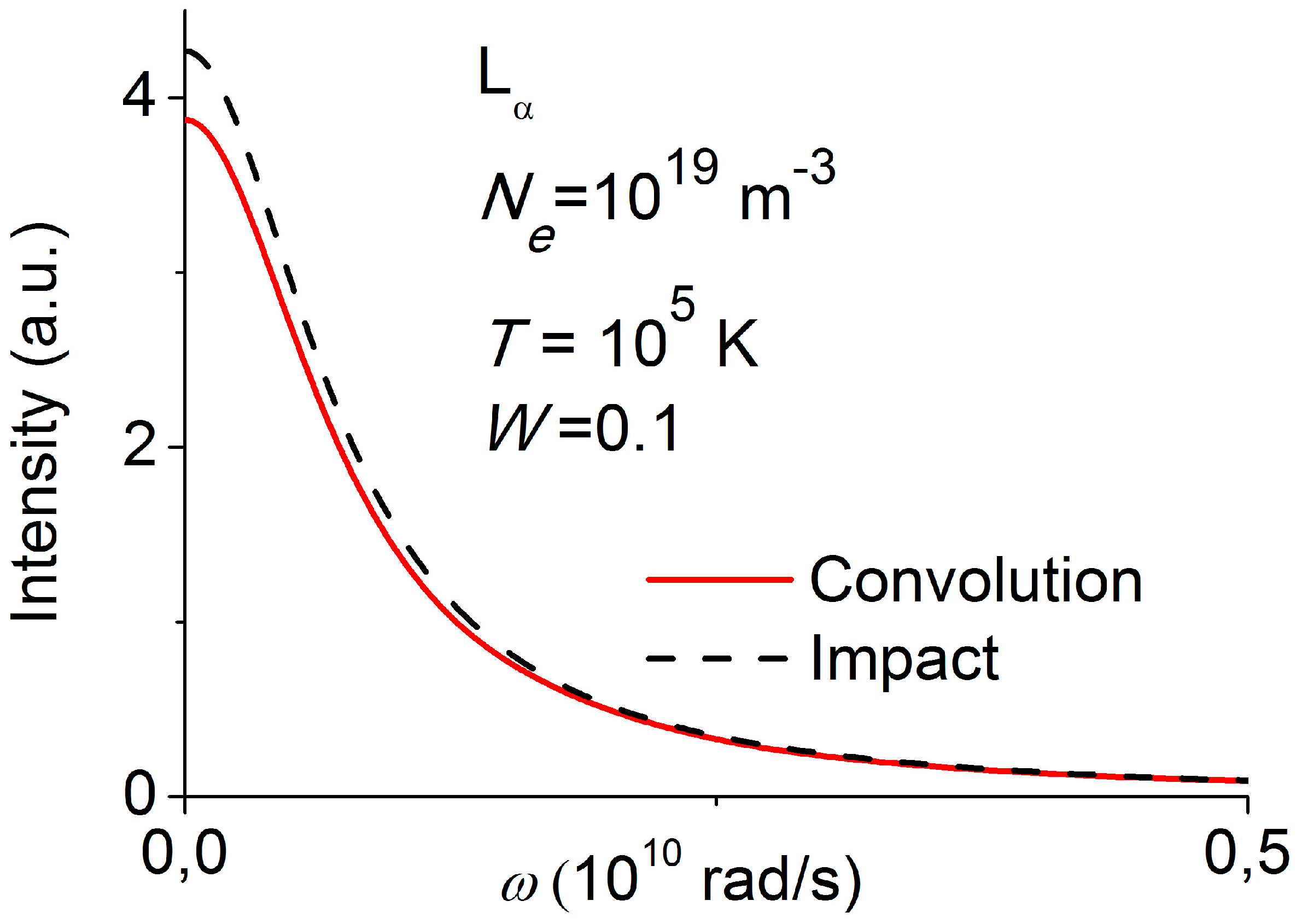
4. Effect of Plasma Waves
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Dimitrijević, M.S.; Konjević, N. Stark widths of doubly- and triply-ionized atom lines. J. Quant. Spectrosc. Radiat. Transf. 1980, 24, 451–459. [Google Scholar] [CrossRef]
- Baranger, M. General Impact Theory of Pressure Broadening. Phys. Rev. 1958, 112, 855–865. [Google Scholar] [CrossRef]
- McMahon, J.M.; Morales, M.A.; Pierleoni, C.; Ceperley, D.M. The properties of hydrogen and helium under extreme conditions. Rev. Mod. Phys. 2012, 84, 1607–1653. [Google Scholar] [CrossRef]
- Barnes, K.S.; Peach, G. The shape and shift of the resonance line of Ca+ perturbed by electron collisions. J. Phys. B 1970, 3, 350–362. [Google Scholar] [CrossRef]
- Bely, O.; Griem, H.R. Quantum-mechanical calculation for the electron-impact broadening of the resonance line of singly ionized magnesium. Phys. Rev. A 1970, 1, 97–105. [Google Scholar] [CrossRef]
- Elabidi, H.; Ben Nessib, N.; Sahal-Bréchot, S. Quantum-mechanical calculations of the electron-impact broadening of spectral lines for intermediate coupling. J. Phys. B 2004, 37, 63–71. [Google Scholar] [CrossRef]
- Elabidi, H.; Sahal-Bréchot, S.; Dimitrijević, M.S. Quantum Stark broadening of Ar XV lines. Strong collision and quadrupolar potential contributions. Adv. Space Res. 2014, 54, 1184–1189. [Google Scholar] [CrossRef]
- Griem, H.R. Semi-empirical formulas for the electron-impact widths and shifts of isolated ion lines in plasmas. Phys. Rev. 1968, 165, 258–266. [Google Scholar] [CrossRef]
- Van Regemorter, H. Rate of collisionnal excitation in stellar atmospheres. Astrophys. J. 1962, 136, 906–915. [Google Scholar] [CrossRef]
- Griem, H.R.; Kolb, A.C.; Shen, K.Y. Stark broadening of hydrogen lines in a plasma. Phys. Rev. 1959, 116, 4–16. [Google Scholar] [CrossRef]
- Sahal-Bréchot, S.; Dimitrijević, M.S.; Ben Nessib, N. Widths and shifts of isolated lines of neutral and ionized atoms perturbed by collisions with electrons and ions: An outline of the semiclassical perturbation (SCP) method and of the approximations used for the calculations. Atoms 2014, 2, 225–252. [Google Scholar] [CrossRef]
- Sahal-Bréchot, S.; Dimitrijević, M.S.; Moreau, N. STARK-B Database; LERMA, Observatory of Paris, France and Astronomical Observatory: Belgrade, Serbia, 2014; Available online: http://stark-b.obspm.fr (accessed on 12 August 2017).
- Griem, H.R. Principles of Plasma Spectroscopy; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Alexiou, S.; Lee, R.W. Semiclassical calculations of line broadening in plasmas: Comparison with quantal results. J. Quant. Spectrosc. Radiat. Transf. 2006, 99, 10–20. [Google Scholar] [CrossRef]
- Elabidi, H.; Sahal-Bréchot, S.; Ben Nessib, N. Quantum Stark broadening of the 3s-3p spectral lines in Li-like ions; Z-scaling and comparison with semi-classical perturbation theory. Eur. Phys. J. D 2009, 54, 51–64. [Google Scholar] [CrossRef]
- Wiese, W.L.; Kelleher, D.E.; Paquette, D.R. Detailed study of the Stark broadening of Balmer lines in a high density plasma. Phys. Rev. A 1972, 6, 1132–1153. [Google Scholar] [CrossRef]
- Voslamber, D. Unified model for Stark broadening. Z. Naturforsch. 1969, 24, 1458–1472. [Google Scholar]
- Smith, E.W.; Cooper, J.; Vidal, C.R. Unified classical-path treatment of Stark broadening in plasmas. Phys. Rev. 1969, 185, 140–151. [Google Scholar] [CrossRef]
- Grützmacher, K.; Wende, B. Discrepancies between the Stark–broadening theories of hydrogen and measurements of Lyman-α Stark profiles in a dense equilibrium plasma. Phys. Rev. A 1977, 16, 243–246. [Google Scholar] [CrossRef]
- Stamm, R.; Voslamber, D. On the role of ion dynamics in the Stark broadening of hydrogen lines. J. Quant. Spectrosc. Radiat. Transf. 1979, 22, 599–609. [Google Scholar] [CrossRef]
- Stamm, R.; Smith, E.W.; Talin, B. Study of hydrogen Stark profiles by means of computer simulation. Phys. Rev. A 1984, 30, 2039–2046. [Google Scholar] [CrossRef]
- Stamm, R.; Talin, B.; Pollock, E.L.; Iglesias, C.A. Ion-dynamics effects on the line shapes of hydrogenic emitters in plasmas. Phys. Rev. A 1986, 34, 4144–4152. [Google Scholar] [CrossRef]
- Rosato, J.; Capes, H.; Stamm, R. Ideal Coulomb plasma approximation in line shapes models: Problematic issues. Atoms 2014, 2, 253–258. [Google Scholar] [CrossRef] [Green Version]
- Vesely, F. Computational Physics, an Introduction; Plenum Press: New York, NY, USA, 1994. [Google Scholar]
- Brissaud, A.; Frisch, U. Theory of Stark broadening-II exact line profile with model microfield. J. Quant. Spectrosc. Radiat. Transf. 1971, 11, 1767–1783. [Google Scholar] [CrossRef]
- Stehlé, C. Stark broadening of hydrogen Lyman and Balmer in the conditions of stellar envelopes. Astron. Astrophys. Suppl. Ser. 1994, 104, 509–527. [Google Scholar]
- Talin, B.; Calisti, A.; Godbert, L.; Stamm, R.; Lee, R.W.; Klein, L. Frequency-fluctuation model for line-shape calculations in plasma spectroscopy. Phys. Rev. A 1995, 51, 1918–1928. [Google Scholar] [CrossRef] [PubMed]
- Spectral Line Shapes in Plasmas (SLSP) Code Comparison Workshop. Available online: http://plasma-gate.weizmann.ac.il/slsp/ (accessed on 20 July 2017).
- Moslem, W.M.; Shukla, P.K.; Eliasson, B. Surface plasma rogue waves. EPL 2011, 96, 25002. [Google Scholar] [CrossRef]
- Ahmed, S.M.; Metwally, M.S.; El-Hafeez, S.A.; Moslem, W.M. On the generation of rogue waves in dusty plasmas due to modulation instability of nonlinear Schrödinger equation. Appl. Math Inf. Sci. 2016, 10, 317–323. [Google Scholar] [CrossRef]
- Mc Kerr, M.; Kourakis, I.; Haas, F. Freak waves and electrostatic wavepacket modulation in a quantum electron–positron–ion plasma. Plasma Phys. Control. Fusion 2014, 56, 035007. [Google Scholar] [CrossRef]
- Erkintalo, M.; Genty, G.; Dudley, J.M. Rogue-wave-like characteristics in femtosecond supercontinuum generation. Opt. Lett. 2009, 34, 2468–2470. [Google Scholar] [CrossRef] [PubMed]
- Bludov, Y.V.; Konotop, V.V.; Akhmediev, N. Matter rogue waves. Phys. Rev. A 2009, 80, 033610. [Google Scholar] [CrossRef]
- Zakharov, V.E. Collapse of Langmuir waves. Sov. Phys. JETP 1972, 35, 908–914. [Google Scholar]
- Robinson, P.A. Nonlinear wave collapse and strong turbulence. Rev. Mod. Phys. 1997, 69, 507–573. [Google Scholar] [CrossRef]
- Bailung, H.; Sharma, S.K.; Nakamura, Y. Observation of Peregrine solitons in a multicomponent plasma with negative ions. Phys. Rev. Lett. 2011, 107, 255005. [Google Scholar] [CrossRef] [PubMed]
- Hannachi, I.; Stamm, R.; Rosato, J.; Marandet, Y. Effect of nonlinear wave collapse on line shapes in a plasma. EPL 2016, 114, 23002. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stamm, R.; Hannachi, I.; Meireni, M.; Godbert-Mouret, L.; Koubiti, M.; Marandet, Y.; Rosato, J.; Dimitrijević, M.S.; Simić, Z. Stark Broadening from Impact Theory to Simulations. Atoms 2017, 5, 32. https://doi.org/10.3390/atoms5030032
Stamm R, Hannachi I, Meireni M, Godbert-Mouret L, Koubiti M, Marandet Y, Rosato J, Dimitrijević MS, Simić Z. Stark Broadening from Impact Theory to Simulations. Atoms. 2017; 5(3):32. https://doi.org/10.3390/atoms5030032
Chicago/Turabian StyleStamm, Roland, Ibtissem Hannachi, Mutia Meireni, Laurence Godbert-Mouret, Mohammed Koubiti, Yannick Marandet, Joël Rosato, Milan S. Dimitrijević, and Zoran Simić. 2017. "Stark Broadening from Impact Theory to Simulations" Atoms 5, no. 3: 32. https://doi.org/10.3390/atoms5030032






