Radiative and Collisional Molecular Data and Virtual Laboratory Astrophysics
Abstract
1. Introduction
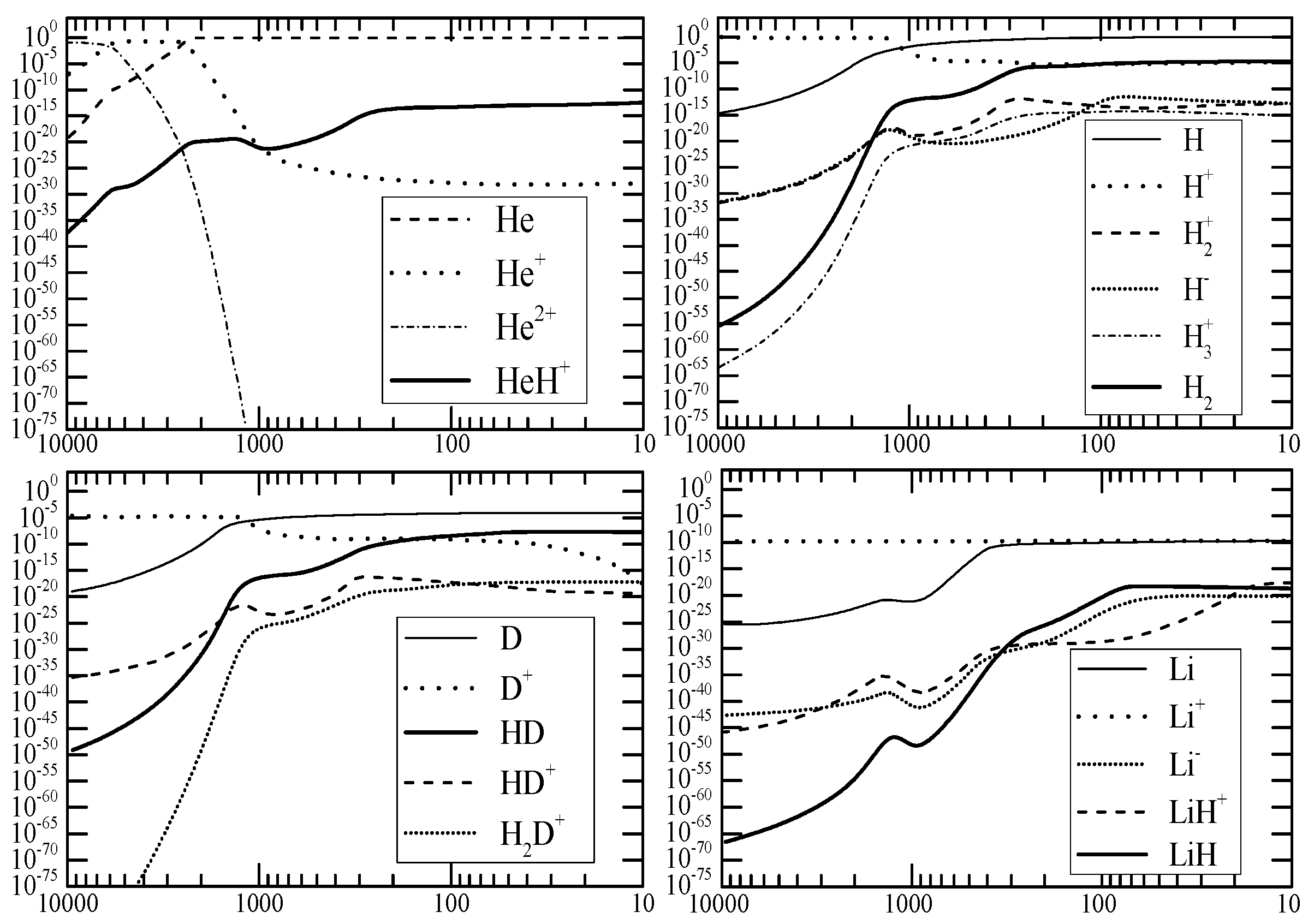
The Base Astrophysical Targets
2. MolD
2.1. Database Description
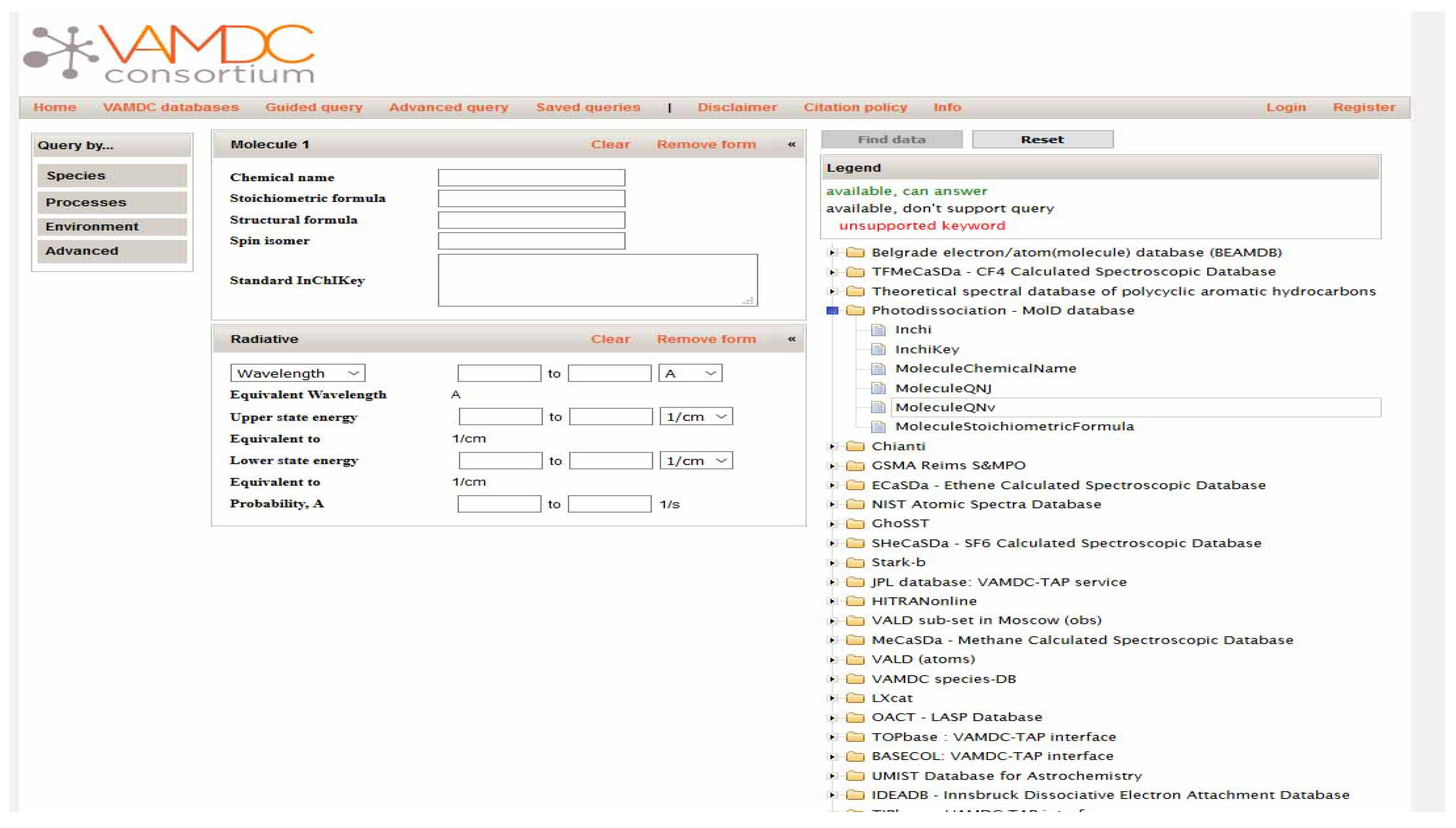
2.2. Accessing MolD Data
- Via MolD homepage (http://servo.aob.rs/mold). There is an AJAX-enabled (Asynchronous JavaScript and XML) web form for data querying as well as calculating and plotting average thermal cross sections along available wavelengths for a given temperatiure.
- Via VAMDC portal (http://portal.vamdc.eu), where one can pose a distributed query to 30 databases across the European scientific institutes.
- Via standalone applications which support VAMDC-TAP (Table Access Protoco) for data access and tranformation to VAMDC-XSAMS.
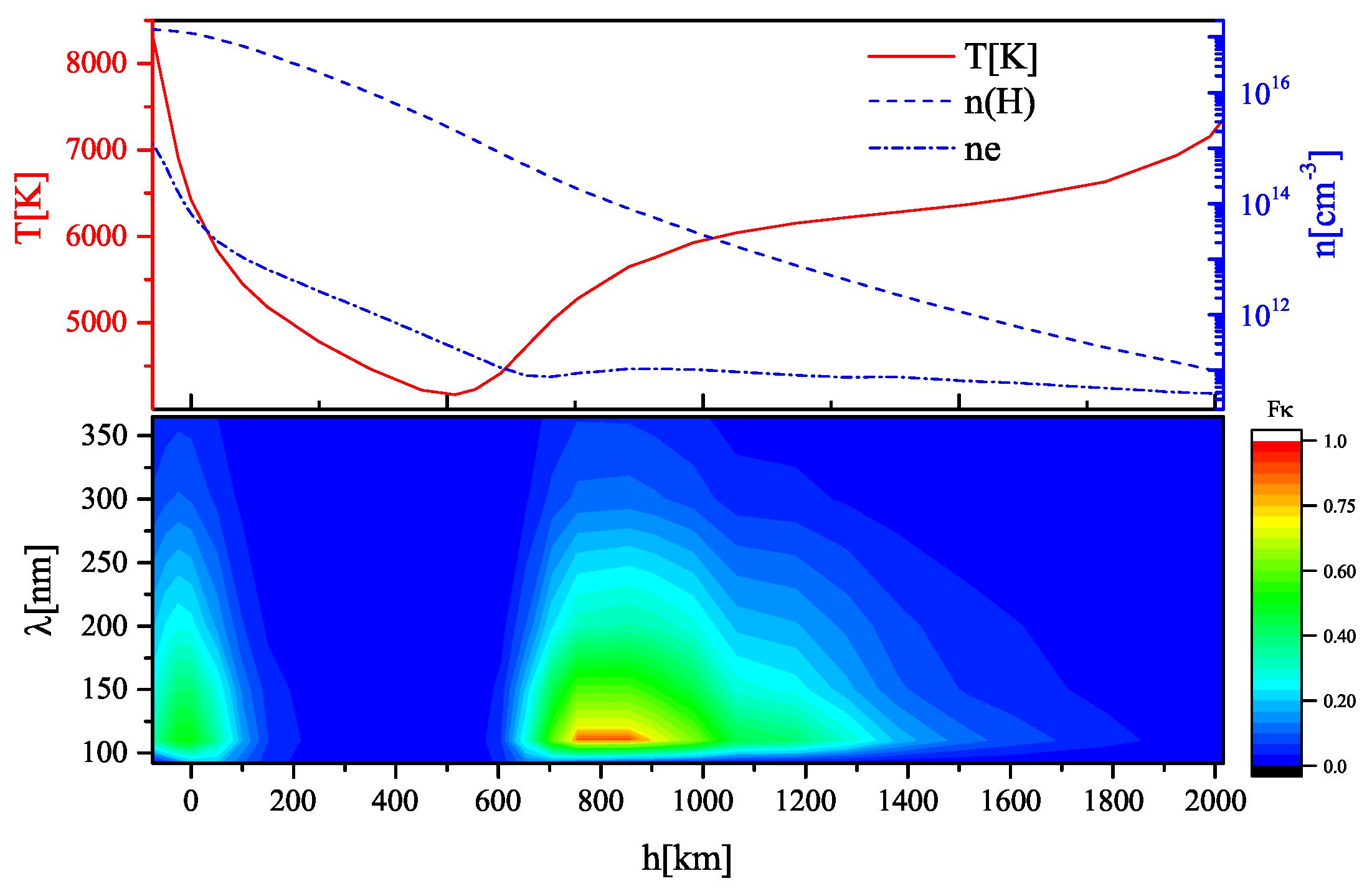
2.3. Example: H Molecular Ion
3. Future Developments and Concluding Remarks
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Marinković, B.P.; Vujčić, V.; Sushko, G.; Vudragović, D.; Marinković, D.B.; Đorđević, S.; Ivanović, S.; Nešić, M.; Jevremović, D.; Solov’yov, A.V.; et al. Development of collisional data base for elementary processes of electron scattering by atoms and molecules. Nucl. Instr. Meth. Phys. Res. B 2015, 354, 90–95. [Google Scholar] [CrossRef]
- Dubernet, M.L.; Antony, B.; Ba, Y.A.; Babikov, Y.L.; Bartschat, K.; Boudon, V.; Braams, B.; Chung, H.K.; Daniel, F.; Delahaye, F.; et al. The virtual atomic and molecular data centre (VAMDC) consortium. J. Phys. B 2016, 49, 074003. [Google Scholar] [CrossRef]
- Marinković, B.P.; Jevremović, D.; Srećković, V.A.; Vujčić, V.; Ignjatović, L.M.; Dimitrijević, M.S.; Mason, N.J. BEAMDB and MolD—Databases for atomic and molecular collisional and radiative processes: Belgrade nodes of VAMDC. Eur. Phys. J. D 2017, 71, 158. [Google Scholar] [CrossRef]
- Christensen-Dalsgaard, J.; Dappen, W.; Ajukov, S.; Anderson, E.; Antia, H.; Basu, S.; Baturin, V.; Berthomieu, G.; Chaboyer, B.; Chitre, S.; et al. The current state of solar modeling. Science 1996, 272, 1286. [Google Scholar] [CrossRef] [PubMed]
- Fontenla, J.; Curdt, W.; Haberreiter, M.; Harder, J.; Tian, H. Semiempirical models of the solar atmosphere. III. Set of non-LTE models for far-ultraviolet/extreme-ultraviolet irradiance computation. Astrophys. J. 2009, 707, 482. [Google Scholar] [CrossRef]
- Hauschildt, P.; Baron, E. Cool stellar atmospheres with PHOENIX. Mem. Soc. Astron. Ital. Suppl. 2005, 7, 140. [Google Scholar]
- Hauschildt, P.H.; Baron, E. A 3D radiative transfer framework-VI. PHOENIX/3D example applications. Astron. Astrophys. 2010, 509, A36. [Google Scholar] [CrossRef]
- Husser, T.O.; Wende-von Berg, S.; Dreizler, S.; Homeier, D.; Reiners, A.; Barman, T.; Hauschildt, P.H. A new extensive library of PHOENIX stellar atmospheres and synthetic spectra. Astron. Astrophys. 2013, 553, A6. [Google Scholar] [CrossRef]
- Augustovičová, L.; Špirko, V.; Kraemer, W.; Soldán, P. Radiative association of revisited. Astron. Astrophys. 2013, 553, A42. [Google Scholar] [CrossRef]
- Koester, D. Model atmospheres for DB white dwarfs. Astron. Astrophys. Suppl. Ser. 1980, 39, 401–409. [Google Scholar]
- Coppola, C.M.; Galli, D.; Palla, F.; Longo, S.; Chluba, J. Non-thermal photons and H2 formation in the early Universe. Mon. Not. R. Astron. Soc. 2013, 434, 114–122. [Google Scholar] [CrossRef]
- Klyucharev, A.; Bezuglov, N.; Matveev, A.; Mihajlov, A.; Ignjatović, L.M.; Dimitrijević, M. Rate coefficients for the chemi-ionization processes in sodium-and other alkali-metal geocosmical plasmas. New Astron. Rev. 2007, 51, 547–562. [Google Scholar] [CrossRef]
- Sugimura, K.; Coppola, C.M.; Omukai, K.; Galli, D.; Palla, F. Role of the channel in the primordial star formation under strong radiation field and the critical intensity for the supermassive star formation. Mon. Not. R. Astron. Soc. 2015, 456, 270–277. [Google Scholar] [CrossRef]
- Mihajlov, A.; Ignjatovic, L.M.; Sakan, N.; Dimitrijevic, M. The influence of -photo-dissociation and (H + H+)-radiative collisions on the solar atmosphere opacity in UV and VUV regions. Astron. Astrophys. 2007, 469, 749–754. [Google Scholar] [CrossRef]
- Ignjatović, L.M.; Mihajlov, A.; Srećković, V.; Dimitrijević, M. Absorption non-symmetric ion-atom processes in helium-rich white dwarf atmospheres. Mon. Not. R. Astron. Soc. 2014, 439, 2342–2350. [Google Scholar] [CrossRef]
- Srećković, V.; Mihajlov, A.; Ignjatović, L.M.; Dimitrijević, M. Ion-atom radiative processes in the solar atmosphere: Quiet Sun and sunspots. Adv. Space Res. 2014, 54, 1264–1271. [Google Scholar] [CrossRef]
- Babb, J.F. State resolved data for radiative association of H and H+ and for Photodissociation of . Astrophys. J. Suppl. Ser. 2015, 216, 21. [Google Scholar] [CrossRef]
- Heays, A.; Bosman, A.; van Dishoeck, E. Photodissociation and photoionisation of atoms and molecules of astrophysical interest. Astron. Astrophys. 2017, 602, A105. [Google Scholar] [CrossRef]
- Mihajlov, A.; Ignjatović, L.M.; Srećković, V.; Dimitrijević, M.; Metropoulos, A. The non-symmetric ion-atom radiative processes in the stellar atmospheres. Mon. Not. R. Astron. Soc. 2013, 431, 589–599. [Google Scholar] [CrossRef]
- Ignjatović, L.M.; Mihajlov, A.; Srećković, V.; Dimitrijević, M. The ion-atom absorption processes as one of the factors of the influence on the sunspot opacity. Mon. Not. R. Astron. Soc. 2014, 441, 1504–1512. [Google Scholar] [CrossRef]
- Puy, D.; Dubrovich, V.; Lipovka, A.; Talbi, D.; Vonlanthen, P. Molecular fluorine chemistry in the early Universe. Astron. Astrophys. 2007, 476, 685–689. [Google Scholar] [CrossRef]
- Vujčič, V.; Jevremović, D.; Mihajlov, A.; Ignjatović, L.M.; Srećković, V.; Dimitrijević, M.; Malović, M. MOL-D: A Collisional Database and Web Service within the Virtual Atomic and Molecular Data Center. J. Astrophys. Astron. 2015, 36, 693–703. [Google Scholar] [CrossRef]
- Forcier, J.; Bissex, P.; Chun, W.J. Python Web Development with Django; Addison-Wesley Professional: Indianapolis, IN, USA, 2008. [Google Scholar]
- Widenius, M.; Axmark, D. MySQL Reference Manual: Documentation from the Source; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2002. [Google Scholar]
- Ignjatović, L.M.; Mihajlov, A.; Sakan, N.; Dimitrijević, M.; Metropoulos, A. The total and relative contribution of the relevant absorption processes to the opacity of DB white dwarf atmospheres in the UV and VUV regions. Mon. Not. R. Astron. Soc. 2009, 396, 2201–2210. [Google Scholar] [CrossRef]
| 1. | |
| 2. | |
| 3. | |
| 4. |

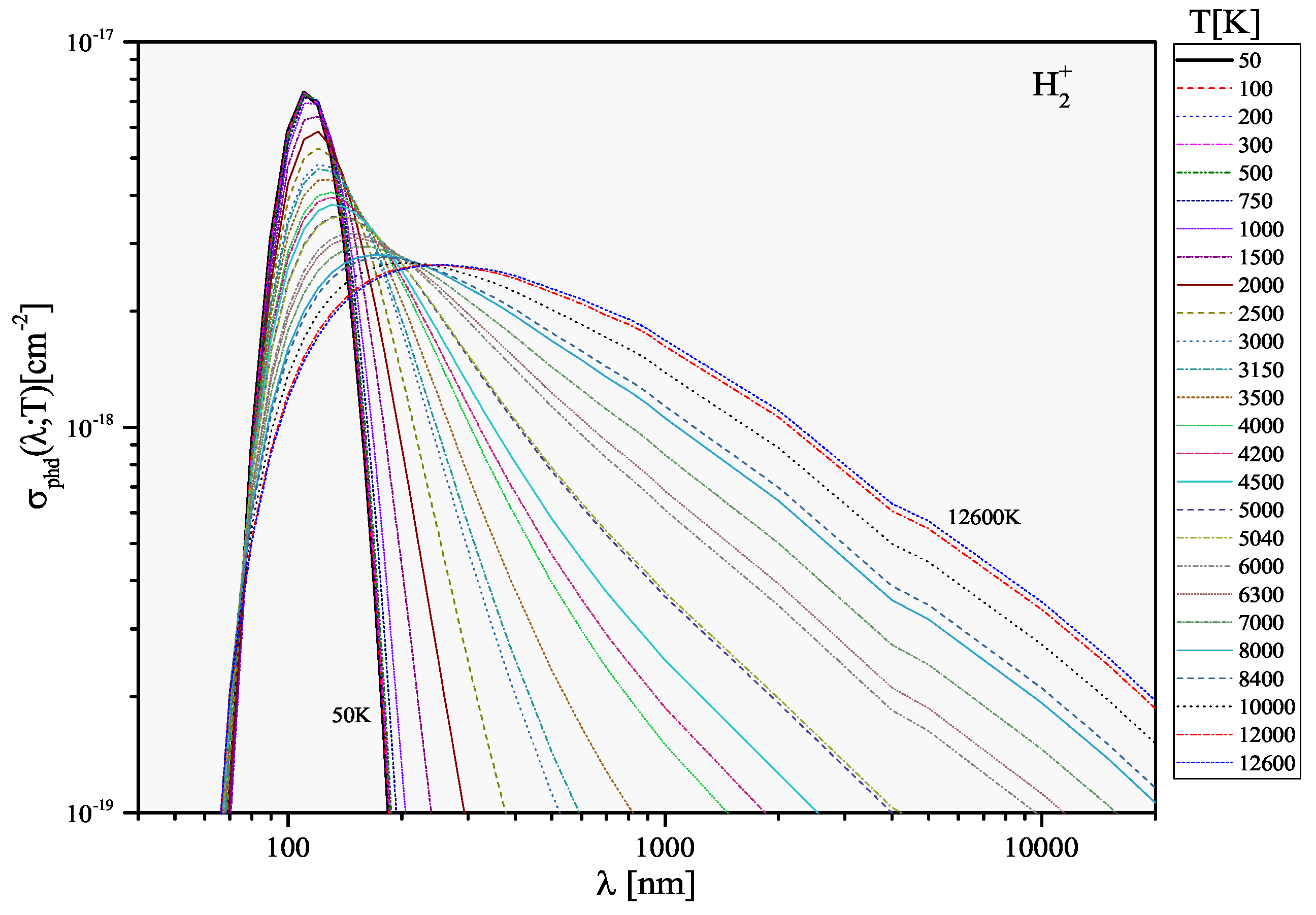
| (nm) | 3000 K | 4000 K | 5000 K | 6000 K | 7000 K | 8000 K | 9000 K | 10,000 K |
|---|---|---|---|---|---|---|---|---|
| 90 | 3.50E−37 | 2.62E−38 | 5.50E−39 | 1.93E−39 | 9.04E−40 | 5.07E−40 | 3.20E−40 | 2.20E−40 |
| 91 | 3.75E−37 | 2.78E−38 | 5.80E−39 | 2.03E−39 | 9.47E−40 | 5.30E−40 | 3.34E−40 | 2.29E−40 |
| 92 | 3.99E−37 | 2.94E−38 | 6.10E−39 | 2.12E−39 | 9.90E−40 | 5.53E−40 | 3.48E−40 | 2.39E−40 |
| 93 | 4.23E−37 | 3.10E−38 | 6.40E−39 | 2.22E−39 | 1.03E−39 | 5.76E−40 | 3.62E−40 | 2.48E−40 |
| 94 | 4.47E−37 | 3.25E−38 | 6.69E−39 | 2.31E−39 | 1.07E−39 | 5.98E−40 | 3.76E−40 | 2.57E−40 |
| 95 | 4.71E−37 | 3.41E−38 | 6.98E−39 | 2.41E−39 | 1.12E−39 | 6.20E−40 | 3.89E−40 | 2.66E−40 |
| 96 | 4.95E−37 | 3.56E−38 | 7.27E−39 | 2.50E−39 | 1.16E−39 | 6.42E−40 | 4.03E−40 | 2.75E−40 |
| 97 | 5.18E−37 | 3.70E−38 | 7.54E−39 | 2.59E−39 | 1.20E−39 | 6.63E−40 | 4.16E−40 | 2.84E−40 |
| 98 | 5.40E−37 | 3.85E−38 | 7.82E−39 | 2.68E−39 | 1.24E−39 | 6.85E−40 | 4.29E−40 | 2.92E−40 |
| 99 | 5.62E−37 | 3.99E−38 | 8.08E−39 | 2.76E−39 | 1.27E−39 | 7.05E−40 | 4.41E−40 | 3.01E−40 |
| 100 | 5.82E−37 | 4.12E−38 | 8.34E−39 | 2.85E−39 | 1.31E−39 | 7.26E−40 | 4.54E−40 | 3.09E−40 |
| 101 | 6.03E−37 | 4.25E−38 | 8.59E−39 | 2.93E−39 | 1.35E−39 | 7.46E−40 | 4.66E−40 | 3.17E−40 |
| 102 | 6.22E−37 | 4.38E−38 | 8.83E−39 | 3.01E−39 | 1.38E−39 | 7.65E−40 | 4.78E−40 | 3.26E−40 |
| 103 | 6.40E−37 | 4.50E−38 | 9.06E−39 | 3.09E−39 | 1.42E−39 | 7.84E−40 | 4.90E−40 | 3.34E−40 |
| 104 | 6.58E−37 | 4.62E−38 | 9.29E−39 | 3.16E−39 | 1.45E−39 | 8.03E−40 | 5.02E−40 | 3.41E−40 |
| 105 | 6.74E−37 | 4.73E−38 | 9.51E−39 | 3.24E−39 | 1.49E−39 | 8.21E−40 | 5.13E−40 | 3.49E−40 |
| 106 | 6.90E−37 | 4.83E−38 | 9.72E−39 | 3.31E−39 | 1.52E−39 | 8.39E−40 | 5.24E−40 | 3.57E−40 |
| 107 | 7.04E−37 | 4.93E−38 | 9.92E−39 | 3.38E−39 | 1.55E−39 | 8.57E−40 | 5.35E−40 | 3.64E−40 |
| 108 | 7.18E−37 | 5.03E−38 | 1.01E−38 | 3.44E−39 | 1.58E−39 | 8.74E−40 | 5.46E−40 | 3.72E−40 |
| 109 | 7.30E−37 | 5.11E−38 | 1.03E−38 | 3.51E−39 | 1.61E−39 | 8.90E−40 | 5.56E−40 | 3.79E−40 |
| 110 | 7.41E−37 | 5.20E−38 | 1.05E−38 | 3.57E−39 | 1.64E−39 | 9.06E−40 | 5.67E−40 | 3.86E−40 |
| 111 | 7.52E−37 | 5.28E−38 | 1.06E−38 | 3.62E−39 | 1.67E−39 | 9.22E−40 | 5.77E−40 | 3.93E−40 |
| 112 | 7.61E−37 | 5.35E−38 | 1.08E−38 | 3.68E−39 | 1.69E−39 | 9.37E−40 | 5.86E−40 | 3.99E−40 |
| 113 | 7.69E−37 | 5.42E−38 | 1.09E−38 | 3.73E−39 | 1.72E−39 | 9.52E−40 | 5.96E−40 | 4.06E−40 |
| 114 | 7.77E−37 | 5.48E−38 | 1.11E−38 | 3.79E−39 | 1.74E−39 | 9.66E−40 | 6.05E−40 | 4.12E−40 |
| 115 | 7.83E−37 | 5.54E−38 | 1.12E−38 | 3.83E−39 | 1.77E−39 | 9.80E−40 | 6.14E−40 | 4.18E−40 |
| 116 | 7.89E−37 | 5.59E−38 | 1.13E−38 | 3.88E−39 | 1.79E−39 | 9.93E−40 | 6.22E−40 | 4.24E−40 |
| 117 | 7.93E−37 | 5.63E−38 | 1.15E−38 | 3.93E−39 | 1.81E−39 | 1.01E−39 | 6.31E−40 | 4.30E−40 |
| 118 | 7.97E−37 | 5.68E−38 | 1.16E−38 | 3.97E−39 | 1.83E−39 | 1.02E−39 | 6.39E−40 | 4.36E−40 |
| 119 | 8.00E−37 | 5.71E−38 | 1.17E−38 | 4.01E−39 | 1.85E−39 | 1.03E−39 | 6.46E−40 | 4.42E−40 |
| 120 | 8.02E−37 | 5.75E−38 | 1.18E−38 | 4.05E−39 | 1.87E−39 | 1.04E−39 | 6.54E−40 | 4.47E−40 |
| 121 | 8.03E−37 | 5.78E−38 | 1.18E−38 | 4.08E−39 | 1.89E−39 | 1.05E−39 | 6.62E−40 | 4.52E−40 |
| 122 | 8.04E−37 | 5.80E−38 | 1.19E−38 | 4.12E−39 | 1.91E−39 | 1.06E−39 | 6.69E−40 | 4.57E−40 |
| 123 | 8.04E−37 | 5.82E−38 | 1.20E−38 | 4.15E−39 | 1.93E−39 | 1.07E−39 | 6.76E−40 | 4.62E−40 |
| 124 | 8.03E−37 | 5.84E−38 | 1.21E−38 | 4.18E−39 | 1.94E−39 | 1.08E−39 | 6.83E−40 | 4.67E−40 |
| 125 | 8.01E−37 | 5.85E−38 | 1.21E−38 | 4.21E−39 | 1.96E−39 | 1.09E−39 | 6.89E−40 | 4.72E−40 |
| 126 | 7.99E−37 | 5.86E−38 | 1.22E−38 | 4.23E−39 | 1.97E−39 | 1.10E−39 | 6.96E−40 | 4.77E−40 |
| 127 | 7.97E−37 | 5.87E−38 | 1.22E−38 | 4.26E−39 | 1.99E−39 | 1.11E−39 | 7.02E−40 | 4.81E−40 |
| 128 | 7.94E−37 | 5.87E−38 | 1.23E−38 | 4.28E−39 | 2.00E−39 | 1.12E−39 | 7.08E−40 | 4.86E−40 |
| 129 | 7.90E−37 | 5.87E−38 | 1.23E−38 | 4.30E−39 | 2.01E−39 | 1.13E−39 | 7.14E−40 | 4.90E−40 |
| 130 | 7.86E−37 | 5.87E−38 | 1.23E−38 | 4.32E−39 | 2.03E−39 | 1.14E−39 | 7.19E−40 | 4.94E−40 |
| 131 | 7.81E−37 | 5.86E−38 | 1.24E−38 | 4.34E−39 | 2.04E−39 | 1.15E−39 | 7.25E−40 | 4.98E−40 |
| 132 | 7.76E−37 | 5.86E−38 | 1.24E−38 | 4.36E−39 | 2.05E−39 | 1.15E−39 | 7.30E−40 | 5.02E−40 |
| 133 | 7.70E−37 | 5.84E−38 | 1.24E−38 | 4.37E−39 | 2.06E−39 | 1.16E−39 | 7.35E−40 | 5.06E−40 |
| 134 | 7.65E−37 | 5.83E−38 | 1.24E−38 | 4.39E−39 | 2.07E−39 | 1.17E−39 | 7.40E−40 | 5.10E−40 |
| 135 | 7.58E−37 | 5.82E−38 | 1.24E−38 | 4.40E−39 | 2.08E−39 | 1.17E−39 | 7.45E−40 | 5.13E−40 |
| 136 | 7.52E−37 | 5.80E−38 | 1.24E−38 | 4.41E−39 | 2.09E−39 | 1.18E−39 | 7.49E−40 | 5.17E−40 |
| 137 | 7.45E−37 | 5.78E−38 | 1.24E−38 | 4.42E−39 | 2.09E−39 | 1.19E−39 | 7.54E−40 | 5.20E−40 |
| 138 | 7.38E−37 | 5.76E−38 | 1.24E−38 | 4.43E−39 | 2.10E−39 | 1.19E−39 | 7.58E−40 | 5.24E−40 |
| 139 | 7.31E−37 | 5.73E−38 | 1.24E−38 | 4.43E−39 | 2.11E−39 | 1.20E−39 | 7.62E−40 | 5.27E−40 |
| 140 | 7.24E−37 | 5.71E−38 | 1.24E−38 | 4.44E−39 | 2.12E−39 | 1.20E−39 | 7.66E−40 | 5.30E−40 |
| 141 | 7.16E−37 | 5.68E−38 | 1.24E−38 | 4.45E−39 | 2.12E−39 | 1.21E−39 | 7.70E−40 | 5.33E−40 |
| 142 | 7.08E−37 | 5.65E−38 | 1.24E−38 | 4.45E−39 | 2.13E−39 | 1.21E−39 | 7.74E−40 | 5.36E−40 |
| 143 | 7.00E−37 | 5.62E−38 | 1.23E−38 | 4.45E−39 | 2.13E−39 | 1.22E−39 | 7.77E−40 | 5.39E−40 |
| 144 | 6.92E−37 | 5.59E−38 | 1.23E−38 | 4.46E−39 | 2.14E−39 | 1.22E−39 | 7.80E−40 | 5.41E−40 |
| 145 | 6.84E−37 | 5.56E−38 | 1.23E−38 | 4.46E−39 | 2.14E−39 | 1.22E−39 | 7.84E−40 | 5.44E−40 |
| 146 | 6.76E−37 | 5.52E−38 | 1.23E−38 | 4.46E−39 | 2.15E−39 | 1.23E−39 | 7.87E−40 | 5.46E−40 |
| 147 | 6.68E−37 | 5.49E−38 | 1.22E−38 | 4.46E−39 | 2.15E−39 | 1.23E−39 | 7.90E−40 | 5.49E−40 |
| 148 | 6.59E−37 | 5.45E−38 | 1.22E−38 | 4.46E−39 | 2.15E−39 | 1.23E−39 | 7.93E−40 | 5.51E−40 |
| 149 | 6.51E−37 | 5.42E−38 | 1.22E−38 | 4.45E−39 | 2.15E−39 | 1.24E−39 | 7.95E−40 | 5.54E−40 |
| 150 | 6.42E−37 | 5.38E−38 | 1.21E−38 | 4.45E−39 | 2.16E−39 | 1.24E−39 | 7.98E−40 | 5.56E−40 |
| 151 | 6.34E−37 | 5.34E−38 | 1.21E−38 | 4.45E−39 | 2.16E−39 | 1.24E−39 | 8.01E−40 | 5.58E−40 |
| 152 | 6.25E−37 | 5.30E−38 | 1.20E−38 | 4.44E−39 | 2.16E−39 | 1.25E−39 | 8.03E−40 | 5.60E−40 |
| 153 | 6.17E−37 | 5.26E−38 | 1.20E−38 | 4.44E−39 | 2.16E−39 | 1.25E−39 | 8.05E−40 | 5.62E−40 |
| 154 | 6.08E−37 | 5.22E−38 | 1.20E−38 | 4.43E−39 | 2.16E−39 | 1.25E−39 | 8.08E−40 | 5.64E−40 |
| 155 | 6.00E−37 | 5.18E−38 | 1.19E−38 | 4.43E−39 | 2.16E−39 | 1.25E−39 | 8.10E−40 | 5.66E−40 |
| 156 | 5.91E−37 | 5.14E−38 | 1.19E−38 | 4.42E−39 | 2.17E−39 | 1.25E−39 | 8.12E−40 | 5.68E−40 |
| 157 | 5.83E−37 | 5.10E−38 | 1.18E−38 | 4.42E−39 | 2.17E−39 | 1.26E−39 | 8.14E−40 | 5.70E−40 |
| 158 | 5.74E−37 | 5.06E−38 | 1.18E−38 | 4.41E−39 | 2.17E−39 | 1.26E−39 | 8.16E−40 | 5.72E−40 |
| 159 | 5.66E−37 | 5.02E−38 | 1.17E−38 | 4.40E−39 | 2.17E−39 | 1.26E−39 | 8.18E−40 | 5.73E−40 |
| 160 | 5.58E−37 | 4.98E−38 | 1.17E−38 | 4.39E−39 | 2.17E−39 | 1.26E−39 | 8.19E−40 | 5.75E−40 |
| 162 | 5.41E−37 | 4.90E−38 | 1.16E−38 | 4.37E−39 | 2.16E−39 | 1.26E−39 | 8.22E−40 | 5.78E−40 |
| 163 | 5.33E−37 | 4.85E−38 | 1.15E−38 | 4.36E−39 | 2.16E−39 | 1.26E−39 | 8.24E−40 | 5.79E−40 |
| 164 | 5.25E−37 | 4.81E−38 | 1.14E−38 | 4.35E−39 | 2.16E−39 | 1.27E−39 | 8.25E−40 | 5.81E−40 |
| 165 | 5.17E−37 | 4.77E−38 | 1.14E−38 | 4.34E−39 | 2.16E−39 | 1.27E−39 | 8.27E−40 | 5.82E−40 |
| 166 | 5.09E−37 | 4.73E−38 | 1.13E−38 | 4.33E−39 | 2.16E−39 | 1.27E−39 | 8.28E−40 | 5.83E−40 |
| 167 | 5.02E−37 | 4.68E−38 | 1.13E−38 | 4.32E−39 | 2.16E−39 | 1.27E−39 | 8.29E−40 | 5.85E−40 |
| 168 | 4.94E−37 | 4.64E−38 | 1.12E−38 | 4.31E−39 | 2.16E−39 | 1.27E−39 | 8.30E−40 | 5.86E−40 |
| 169 | 4.86E−37 | 4.60E−38 | 1.12E−38 | 4.30E−39 | 2.15E−39 | 1.27E−39 | 8.31E−40 | 5.87E−40 |
| 170 | 4.79E−37 | 4.56E−38 | 1.11E−38 | 4.29E−39 | 2.15E−39 | 1.27E−39 | 8.32E−40 | 5.88E−40 |
| 171 | 4.71E−37 | 4.52E−38 | 1.10E−38 | 4.27E−39 | 2.15E−39 | 1.27E−39 | 8.33E−40 | 5.89E−40 |
| 172 | 4.64E−37 | 4.48E−38 | 1.10E−38 | 4.26E−39 | 2.15E−39 | 1.27E−39 | 8.34E−40 | 5.90E−40 |
| 173 | 4.57E−37 | 4.43E−38 | 1.09E−38 | 4.25E−39 | 2.14E−39 | 1.27E−39 | 8.34E−40 | 5.91E−40 |
| 174 | 4.50E−37 | 4.39E−38 | 1.09E−38 | 4.24E−39 | 2.14E−39 | 1.27E−39 | 8.35E−40 | 5.92E−40 |
| 175 | 4.43E−37 | 4.35E−38 | 1.08E−38 | 4.22E−39 | 2.14E−39 | 1.27E−39 | 8.36E−40 | 5.93E−40 |
| 176 | 4.36E−37 | 4.31E−38 | 1.07E−38 | 4.21E−39 | 2.13E−39 | 1.27E−39 | 8.36E−40 | 5.94E−40 |
| 177 | 4.29E−37 | 4.27E−38 | 1.07E−38 | 4.20E−39 | 2.13E−39 | 1.27E−39 | 8.37E−40 | 5.94E−40 |
| 178 | 4.22E−37 | 4.23E−38 | 1.06E−38 | 4.18E−39 | 2.13E−39 | 1.27E−39 | 8.37E−40 | 5.95E−40 |
| 179 | 4.15E−37 | 4.19E−38 | 1.06E−38 | 4.17E−39 | 2.12E−39 | 1.27E−39 | 8.38E−40 | 5.96E−40 |
| 180 | 4.09E−37 | 4.15E−38 | 1.05E−38 | 4.16E−39 | 2.12E−39 | 1.27E−39 | 8.38E−40 | 5.96E−40 |
| 181 | 4.02E−37 | 4.11E−38 | 1.04E−38 | 4.14E−39 | 2.12E−39 | 1.27E−39 | 8.38E−40 | 5.97E−40 |
| 182 | 3.96E−37 | 4.07E−38 | 1.04E−38 | 4.13E−39 | 2.11E−39 | 1.26E−39 | 8.39E−40 | 5.98E−40 |
| 183 | 3.90E−37 | 4.03E−38 | 1.03E−38 | 4.11E−39 | 2.11E−39 | 1.26E−39 | 8.39E−40 | 5.98E−40 |
| 184 | 3.84E−37 | 4.00E−38 | 1.03E−38 | 4.10E−39 | 2.11E−39 | 1.26E−39 | 8.39E−40 | 5.99E−40 |
| 185 | 3.78E−37 | 3.96E−38 | 1.02E−38 | 4.09E−39 | 2.10E−39 | 1.26E−39 | 8.39E−40 | 5.99E−40 |
| 186 | 3.72E−37 | 3.92E−38 | 1.01E−38 | 4.07E−39 | 2.10E−39 | 1.26E−39 | 8.39E−40 | 6.00E−40 |
| 187 | 3.66E−37 | 3.88E−38 | 1.01E−38 | 4.06E−39 | 2.09E−39 | 1.26E−39 | 8.39E−40 | 6.00E−40 |
| 188 | 3.60E−37 | 3.84E−38 | 1.00E−38 | 4.04E−39 | 2.09E−39 | 1.26E−39 | 8.40E−40 | 6.01E−40 |
| 189 | 3.54E−37 | 3.81E−38 | 9.95E−39 | 4.03E−39 | 2.09E−39 | 1.26E−39 | 8.40E−40 | 6.01E−40 |
| 190 | 3.49E−37 | 3.77E−38 | 9.89E−39 | 4.01E−39 | 2.08E−39 | 1.26E−39 | 8.40E−40 | 6.02E−40 |
| 191 | 3.43E−37 | 3.73E−38 | 9.83E−39 | 4.00E−39 | 2.08E−39 | 1.26E−39 | 8.39E−40 | 6.02E−40 |
| 192 | 3.38E−37 | 3.70E−38 | 9.77E−39 | 3.98E−39 | 2.07E−39 | 1.26E−39 | 8.39E−40 | 6.02E−40 |
| 193 | 3.33E−37 | 3.66E−38 | 9.71E−39 | 3.97E−39 | 2.07E−39 | 1.25E−39 | 8.39E−40 | 6.03E−40 |
| 194 | 3.27E−37 | 3.63E−38 | 9.65E−39 | 3.95E−39 | 2.06E−39 | 1.25E−39 | 8.39E−40 | 6.03E−40 |
| 195 | 3.22E−37 | 3.59E−38 | 9.59E−39 | 3.94E−39 | 2.06E−39 | 1.25E−39 | 8.39E−40 | 6.03E−40 |
| 196 | 3.17E−37 | 3.56E−38 | 9.54E−39 | 3.92E−39 | 2.06E−39 | 1.25E−39 | 8.39E−40 | 6.03E−40 |
| 197 | 3.12E−37 | 3.52E−38 | 9.48E−39 | 3.91E−39 | 2.05E−39 | 1.25E−39 | 8.38E−40 | 6.04E−40 |
| 198 | 3.08E−37 | 3.49E−38 | 9.42E−39 | 3.89E−39 | 2.05E−39 | 1.25E−39 | 8.38E−40 | 6.04E−40 |
| 199 | 3.03E−37 | 3.46E−38 | 9.36E−39 | 3.88E−39 | 2.04E−39 | 1.25E−39 | 8.38E−40 | 6.04E−40 |
| 200 | 2.98E−37 | 3.42E−38 | 9.31E−39 | 3.86E−39 | 2.04E−39 | 1.24E−39 | 8.38E−40 | 6.04E−40 |
| 205 | 2.76E−37 | 3.26E−38 | 9.03E−39 | 3.79E−39 | 2.01E−39 | 1.24E−39 | 8.35E−40 | 6.04E−40 |
| 210 | 2.56E−37 | 3.11E−38 | 8.75E−39 | 3.71E−39 | 1.99E−39 | 1.23E−39 | 8.33E−40 | 6.04E−40 |
| 215 | 2.37E−37 | 2.97E−38 | 8.49E−39 | 3.64E−39 | 1.96E−39 | 1.22E−39 | 8.29E−40 | 6.03E−40 |
| 220 | 2.20E−37 | 2.83E−38 | 8.24E−39 | 3.57E−39 | 1.94E−39 | 1.21E−39 | 8.25E−40 | 6.02E−40 |
| 225 | 2.04E−37 | 2.71E−38 | 7.99E−39 | 3.50E−39 | 1.91E−39 | 1.20E−39 | 8.21E−40 | 6.01E−40 |
| 230 | 1.90E−37 | 2.59E−38 | 7.76E−39 | 3.43E−39 | 1.89E−39 | 1.19E−39 | 8.17E−40 | 5.99E−40 |
| 235 | 1.77E−37 | 2.48E−38 | 7.53E−39 | 3.36E−39 | 1.86E−39 | 1.18E−39 | 8.13E−40 | 5.98E−40 |
| 240 | 1.66E−37 | 2.37E−38 | 7.32E−39 | 3.30E−39 | 1.84E−39 | 1.17E−39 | 8.08E−40 | 5.96E−40 |
| 245 | 1.55E−37 | 2.27E−38 | 7.11E−39 | 3.23E−39 | 1.81E−39 | 1.16E−39 | 8.04E−40 | 5.94E−40 |
| 250 | 1.45E−37 | 2.18E−38 | 6.92E−39 | 3.17E−39 | 1.79E−39 | 1.15E−39 | 7.99E−40 | 5.92E−40 |
| 255 | 1.36E−37 | 2.09E−38 | 6.73E−39 | 3.11E−39 | 1.76E−39 | 1.13E−39 | 7.94E−40 | 5.90E−40 |
| 260 | 1.27E−37 | 2.01E−38 | 6.54E−39 | 3.05E−39 | 1.74E−39 | 1.12E−39 | 7.89E−40 | 5.87E−40 |
| 265 | 1.20E−37 | 1.93E−38 | 6.37E−39 | 2.99E−39 | 1.72E−39 | 1.11E−39 | 7.83E−40 | 5.84E−40 |
| 270 | 1.12E−37 | 1.85E−38 | 6.20E−39 | 2.94E−39 | 1.69E−39 | 1.10E−39 | 7.78E−40 | 5.82E−40 |
| 275 | 1.06E−37 | 1.78E−38 | 6.04E−39 | 2.89E−39 | 1.67E−39 | 1.09E−39 | 7.72E−40 | 5.79E−40 |
| 280 | 9.99E−38 | 1.72E−38 | 5.89E−39 | 2.83E−39 | 1.65E−39 | 1.08E−39 | 7.67E−40 | 5.76E−40 |
| 285 | 9.43E−38 | 1.66E−38 | 5.74E−39 | 2.78E−39 | 1.63E−39 | 1.07E−39 | 7.62E−40 | 5.73E−40 |
| 290 | 8.92E−38 | 1.60E−38 | 5.60E−39 | 2.73E−39 | 1.61E−39 | 1.06E−39 | 7.56E−40 | 5.70E−40 |
| 295 | 8.45E−38 | 1.54E−38 | 5.47E−39 | 2.69E−39 | 1.59E−39 | 1.05E−39 | 7.51E−40 | 5.67E−40 |
| 300 | 8.00E−38 | 1.49E−38 | 5.34E−39 | 2.64E−39 | 1.57E−39 | 1.04E−39 | 7.46E−40 | 5.64E−40 |
| 305 | 7.60E−38 | 1.44E−38 | 5.22E−39 | 2.60E−39 | 1.55E−39 | 1.03E−39 | 7.41E−40 | 5.61E−40 |
| 310 | 7.22E−38 | 1.39E−38 | 5.10E−39 | 2.56E−39 | 1.53E−39 | 1.02E−39 | 7.36E−40 | 5.59E−40 |
| 315 | 6.86E−38 | 1.35E−38 | 4.99E−39 | 2.52E−39 | 1.51E−39 | 1.01E−39 | 7.32E−40 | 5.56E−40 |
| 320 | 6.53E−38 | 1.31E−38 | 4.88E−39 | 2.48E−39 | 1.49E−39 | 1.01E−39 | 7.27E−40 | 5.53E−40 |
| 325 | 6.23E−38 | 1.27E−38 | 4.78E−39 | 2.44E−39 | 1.48E−39 | 9.96E−40 | 7.22E−40 | 5.51E−40 |
| 330 | 5.94E−38 | 1.23E−38 | 4.68E−39 | 2.40E−39 | 1.46E−39 | 9.88E−40 | 7.17E−40 | 5.48E−40 |
| 335 | 5.67E−38 | 1.19E−38 | 4.58E−39 | 2.37E−39 | 1.44E−39 | 9.79E−40 | 7.13E−40 | 5.45E−40 |
| 340 | 5.42E−38 | 1.16E−38 | 4.49E−39 | 2.33E−39 | 1.43E−39 | 9.71E−40 | 7.08E−40 | 5.43E−40 |
| 345 | 5.19E−38 | 1.13E−38 | 4.40E−39 | 2.30E−39 | 1.41E−39 | 9.63E−40 | 7.04E−40 | 5.40E−40 |
| 350 | 4.97E−38 | 1.09E−38 | 4.31E−39 | 2.26E−39 | 1.40E−39 | 9.55E−40 | 6.99E−40 | 5.37E−40 |
| 355 | 4.76E−38 | 1.06E−38 | 4.23E−39 | 2.23E−39 | 1.38E−39 | 9.47E−40 | 6.95E−40 | 5.35E−40 |
| 360 | 4.57E−38 | 1.04E−38 | 4.15E−39 | 2.20E−39 | 1.37E−39 | 9.39E−40 | 6.90E−40 | 5.32E−40 |
| 365 | 4.38E−38 | 1.01E−38 | 4.07E−39 | 2.17E−39 | 1.35E−39 | 9.32E−40 | 6.86E−40 | 5.29E−40 |
| 370 | 4.21E−38 | 9.82E−39 | 4.00E−39 | 2.14E−39 | 1.34E−39 | 9.24E−40 | 6.81E−40 | 5.26E−40 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Srećković, V.A.; Ignjatović, L.M.; Jevremović, D.; Vujčić, V.; Dimitrijević, M.S. Radiative and Collisional Molecular Data and Virtual Laboratory Astrophysics. Atoms 2017, 5, 31. https://doi.org/10.3390/atoms5030031
Srećković VA, Ignjatović LM, Jevremović D, Vujčić V, Dimitrijević MS. Radiative and Collisional Molecular Data and Virtual Laboratory Astrophysics. Atoms. 2017; 5(3):31. https://doi.org/10.3390/atoms5030031
Chicago/Turabian StyleSrećković, Vladimir A., Ljubinko M. Ignjatović, Darko Jevremović, Veljko Vujčić, and Milan S. Dimitrijević. 2017. "Radiative and Collisional Molecular Data and Virtual Laboratory Astrophysics" Atoms 5, no. 3: 31. https://doi.org/10.3390/atoms5030031
APA StyleSrećković, V. A., Ignjatović, L. M., Jevremović, D., Vujčić, V., & Dimitrijević, M. S. (2017). Radiative and Collisional Molecular Data and Virtual Laboratory Astrophysics. Atoms, 5(3), 31. https://doi.org/10.3390/atoms5030031








