Identification and Plasma Diagnostics Study of Extreme Ultraviolet Transitions in Highly Charged Yttrium
Abstract
:1. Introduction
2. Experiment
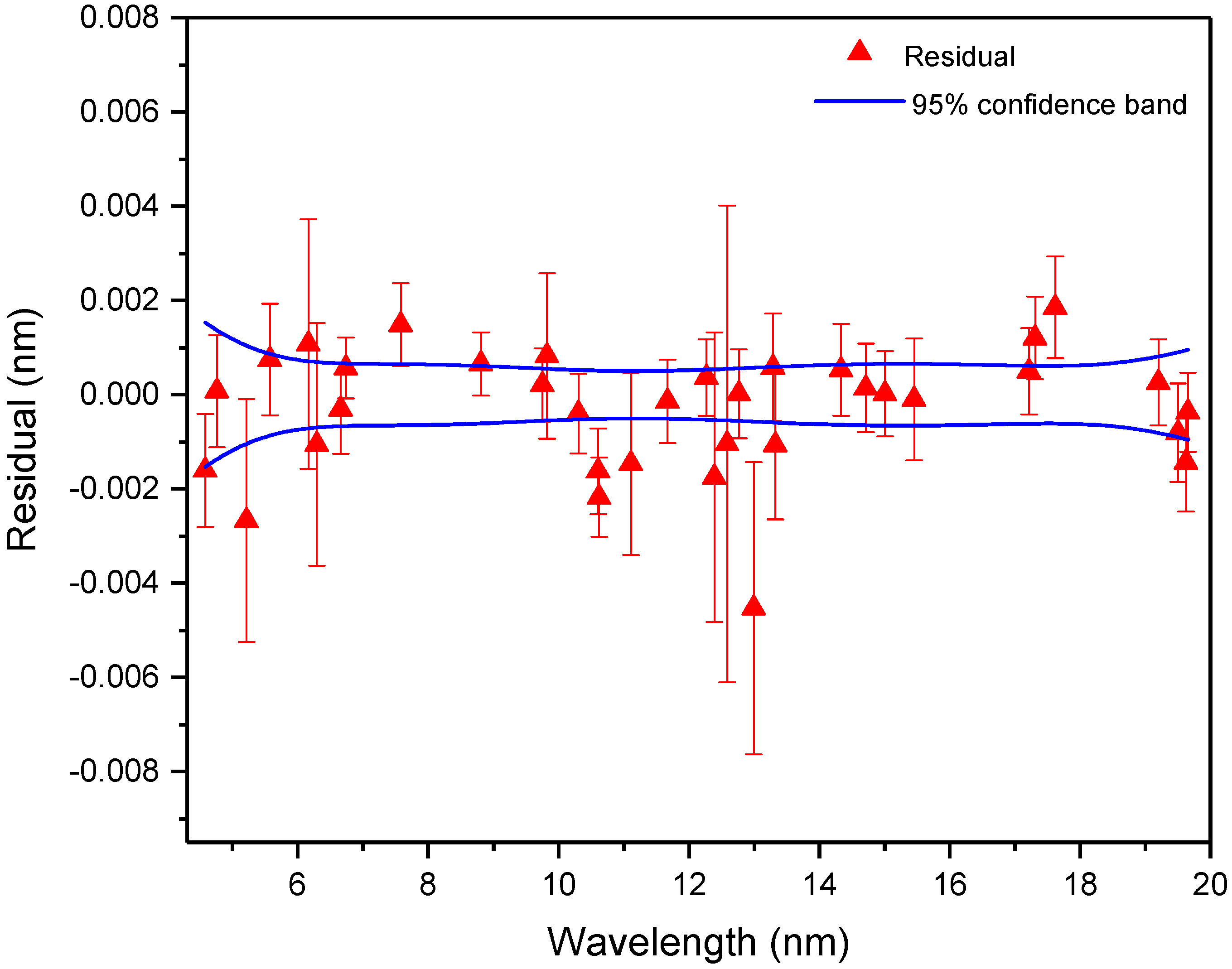
3. Wavelength Calibration
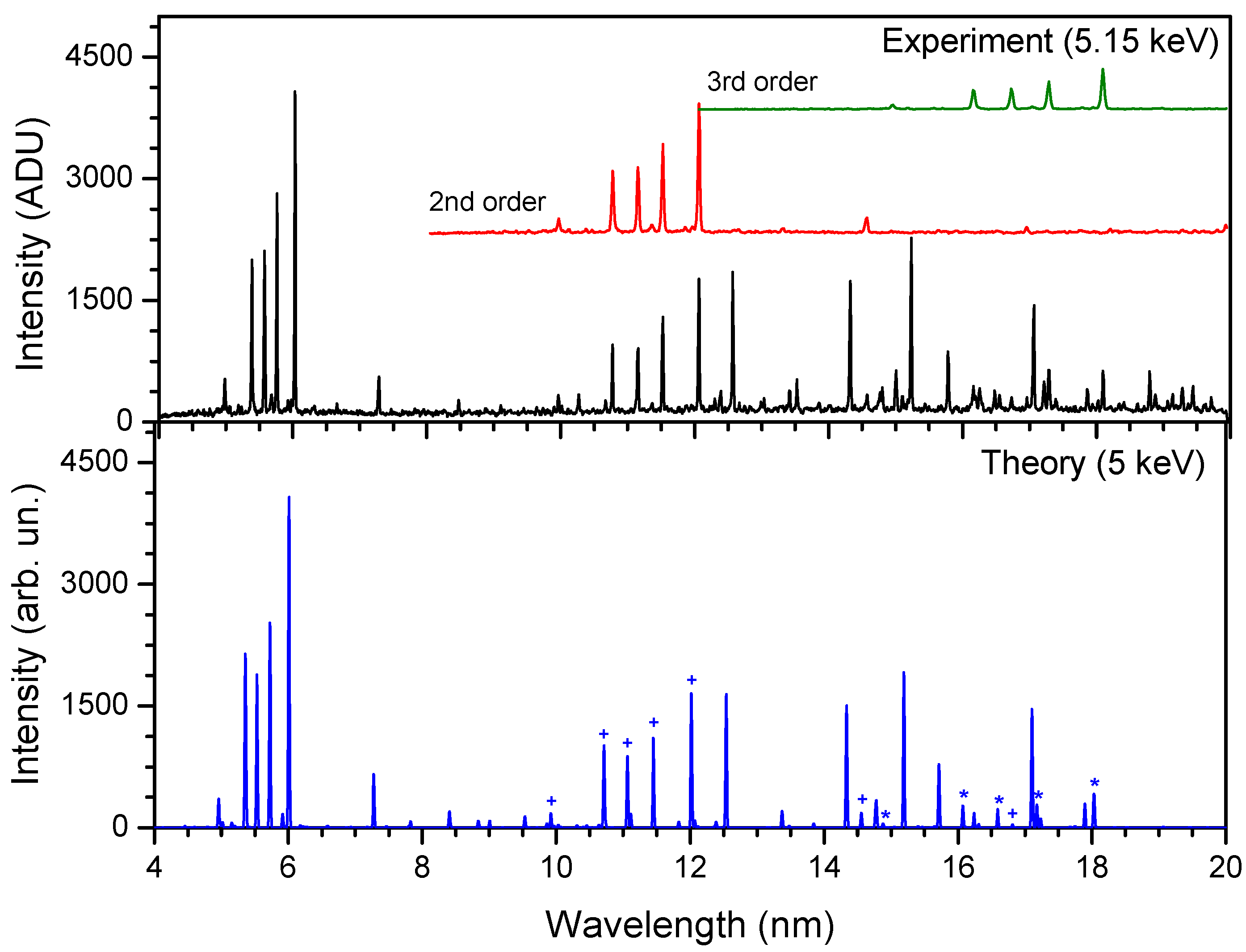
4. Theoretical Modeling
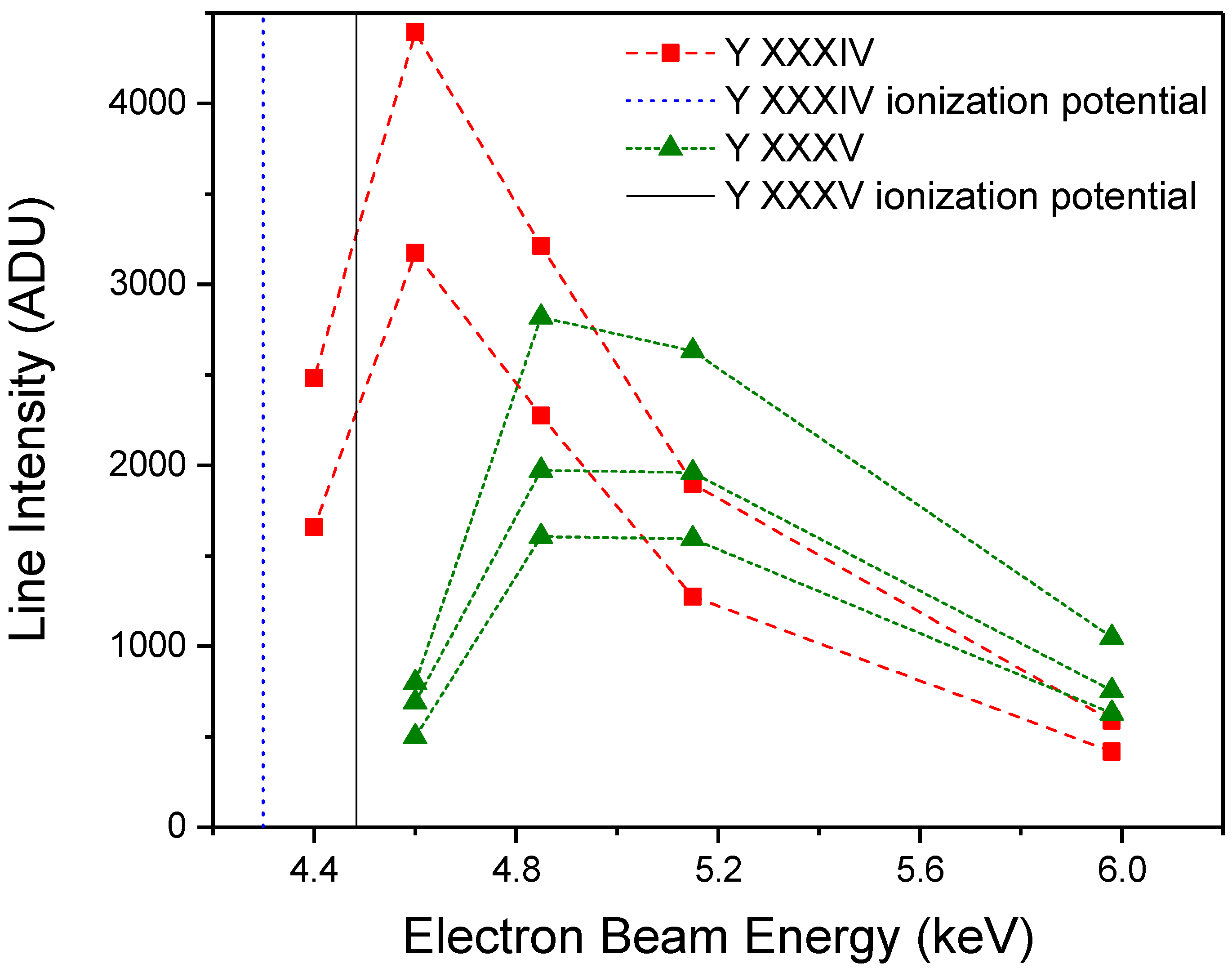
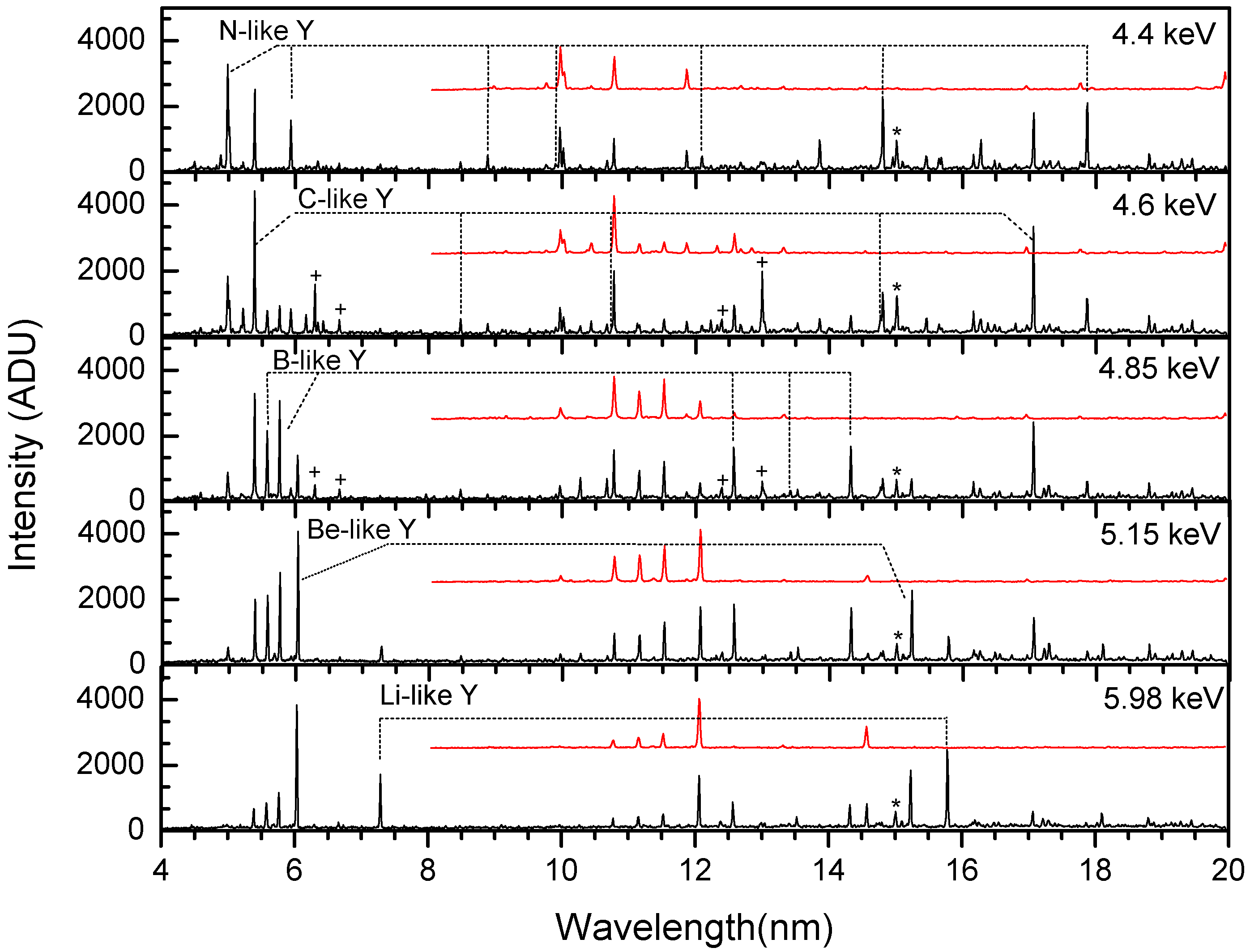
5. Line Identification
6. Results and Discussions
7. Diagnostically Important M1 Transitions
8. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Sapirstein, J.; Cheng, K.T. Tests of Quantum Electrodynamics with EBIT. Can. J. Phys. 2008, 86, 25–31. [Google Scholar] [CrossRef]
- Fahy, K.; Sokell, E.; O’Sullivan, G.; Aguilar, A.; Pomeroy, J.M.; Tan, J.N.; Gillaspy, J.D. Extreme-Ultraviolet Spectroscopy of Highly Charged Xenon Ions Created Using an Electron-Beam Ion Trap. Phys. Rev. A 2007, 75, 032520. [Google Scholar] [CrossRef]
- Podpaly, Y.A.; Gillaspy, J.D.; Reader, J.; Ralchenko, Y. EUV Measurements of Kr XXI–Kr XXXIV and the Effect of a Magnetic-Dipole Line on Allowed Transitions. J. Phys. B At. Mol. Opt. Phys. 2014, 47, 095702. [Google Scholar] [CrossRef]
- Podpaly, Y.A.; Gillaspy, J.D.; Reader, J.; Ralchenko, Y. Measurements and Identifications of Extreme Ultraviolet Spectra of Highly-Charged Sm and Er. J. Phys. B At. Mol. Opt. Phys. 2015, 48, 025002. [Google Scholar] [CrossRef]
- Reader, J.; Gillaspy, J.D.; Osin, D.; Ralchenko, Y. Extreme Ultraviolet Spectra and Analysis of Δn = 0 Transitions in Highly Charged Barium. J. Phys. B At. Mol. Opt. Phys. 2014, 47, 145003. [Google Scholar] [CrossRef]
- Gillaspy, J.D.; Draganić, I.N.; Ralchenko, Y.; Reader, J.; Tan, J.N.; Pomeroy, J.M.; Brewer, S.M. Measurement of the D-Line Doublet in High-Z Highly Charged Sodiumlike Ions. Phys. Rev. A 2009, 80, 010501. [Google Scholar] [CrossRef]
- Gillaspy, J.D.; Osin, D.; Ralchenko, Y.; Reader, J.; Blundell, S.A. Transition Energies of the D lines in Na-like ions. Phys. Rev. A 2013, 87, 062503. [Google Scholar] [CrossRef]
- Kilbane, D.; O’Sullivan, G.; Podpaly, Y.A.; Gillaspy, J.D.; Reader, J.; Ralchenko, Y. EUV Spectra of Rb-like to Ni-like Dysprosium Ions in an Electron Beam Ion Trap. Eur. Phys. J. D 2014, 68, 222. [Google Scholar] [CrossRef]
- Kilbane, D.; O’Sullivan, G.; Gillaspy, J.D.; Ralchenko, Y.; Reader, J. EUV Spectra of Rb-like to Cu-like Gadolinium Ions in an Electron-Beam Ion Trap. Phys. Rev. A 2012, 86, 042503. [Google Scholar] [CrossRef]
- Kilbane, D.; Gillaspy, J.D.; Ralchenko, Y.; Reader, J.; O’Sullivan, G. Extreme Ultraviolet Spectra from N-Shell Ions of Gd, Dy and W. Phys. Scr. 2013, T156, 014012. [Google Scholar] [CrossRef]
- Osin, D.; Reader, J.; Gillaspy, J.D.; Ralchenko, Y. Extreme Ultraviolet Spectra of Highly Charged Xenon Observed with an Electron Beam Ion Trap. J. Phys. B At. Mol. Opt. Phys. 2012, 45, 245001. [Google Scholar] [CrossRef]
- Osin, D.; Gillaspy, J.D.; Reader, J.; Ralchenko, Y. EUV Magnetic-Dipole Lines from Highly-Charged High-Z Ions with an Open 3D Shell. Eur. Phys. J. D 2012, 66, 286. [Google Scholar] [CrossRef]
- Ralchenko, Y.; Reader, J.; Pomeroy, J.M.; Tan, J.N.; Gillaspy, J.D. Spectra of W39+–W47+ in the 12–20 nm Region Observed with an EBIT Light Source. J. Phys. B At. Mol. Opt. Phys. 2007, 40, 3861–3875. [Google Scholar] [CrossRef]
- Ralchenko, Y.; Draganic, I.N.; Tan, J.N.; Gillaspy, J.D.; Pomeroy, J.M.; Reader, J.; Feldman, U.; Holland, G.E. EUV Spectra of Highly-Charged Ions W54+–W63+ Relevant to ITER Diagnostics. J. Phys. B At. Mol. Opt. Phys. 2008, 41, 021003. [Google Scholar] [CrossRef]
- Sugar, J.; Kaufman, V.; Indelicato, P.; Rowan, W.L. Analysis of Magnesiumlike Spectra from Cu XVIII to Mo XXXI. J. Opt. Soc. Am. B 1989, 6, 1437–1443. [Google Scholar] [CrossRef]
- Reader, J.; Kaufman, V.; Sugar, J.; Ekberg, J.O.; Feldman, U.; Brown, C.M.; Seely, J.F.; Rowan, W.L. 3s–3p, 3p–3d, and 3d–4f Transitions of Sodiumlike Ions. J. Opt. Soc. Am. B 1987, 4, 1821–1828. [Google Scholar]
- Jupén, C.; Denne, B.; Martinson, I. Transitions in Al-like, Mg-like and Na-like Kr and Mo, Observed in the JET Tokamak. Phys. Scr. 1990, 41, 669–674. [Google Scholar] [CrossRef]
- Hinnov, E. Highly Ionized Atoms in Tokamak Discharges. Phys. Rev. A 1976, 14, 1533–1541. [Google Scholar] [CrossRef]
- Hinnov, E.; Boody, F.; Cohen, S.; Feldman, U.; Hosea, J.; Sato, K.; Schwob, J.L.; Suckewer, S.; Wouters, A. Spectrum Lines of Highly Ionized, Zinc, Germanium, Zirconium, Molybdenum, and Silver Injected into Princeton Large Torus and Tokamak Fusion Test Reactor Tokamak Discharges. J. Opt. Soc. Am. B 1986, 3, 1288–1294. [Google Scholar] [CrossRef]
- Suckewer, S.; Hinnov, E.; Cohen, S.; Finkenthal, M.; Sato, K. Identification of Magnetic Dipole Lines above 2000 Å in Several Highly Ionized Mo and Zr Ions on the PLT Tokamak. Phys. Rev. A 1982, 26, 1161–1163. [Google Scholar] [CrossRef]
- Ekberg, J.O.; Feldman, U.; Seely, J.F.; Brown, C.M. Transitions and Energy Levels in Mg-like Ge XXI–Zr XXIX Observed in Laser-Produced Linear Plasmas. Phys. Scr. 1989, 40, 643–651. [Google Scholar] [CrossRef]
- Nilsen, J.; Beiersdorfer, P.; Widmann, K.; Decaux, V.; Elliott, S.R. Energies of Neon-like n = 4 to n = 2 Resonance Lines. Phys. Scr. 1996, 54, 183–187. [Google Scholar] [CrossRef]
- Fischer, C.F. Multiconfiguration Hartree-Fock Breit-Pauli Results for 2p1/2–2p3/2 Transitions in the Boron Sequence. J. Phys. B At. Mol. Phys. 1983, 16, 157–165. [Google Scholar] [CrossRef]
- Denne, B.; Magyar, G.; Jacquinot, J. Berylliumlike Mo XXXIX and Lithiumlike Mo XL Observed in the Joint European Torus Tokamak. Phys. Rev. A 1989, 40, 3702–3705. [Google Scholar] [CrossRef]
- Myrnäs, R.; Jupén, C.; Miecznik, G.; Martinson, I.; Denne-Hinnov, B. Transitions in Boronlike Ni XXIV, Ge XXVIII, Kr XXXII and Mo XXXVIII and Fluorinelike Zr XXXII and Mo XXXIV, Observed in the JET Tokamak. Phys. Scr. 1994, 49, 429–435. [Google Scholar] [CrossRef]
- Feldman, U.; Ekberg, J.O.; Seely, J.F.; Brown, C.M.; Kania, D.R.; MacGowan, B.J.; Keane, C.J.; Behring, W.E. Transitions of the Type 2s–2p in Highly Charged Flourinelike and Oxygenlike Mo, Cd, In, and Sn. J. Opt. Soc. Am. B 1991, 8, 531–537. [Google Scholar] [CrossRef]
- Curtis, L.J.; Ramanujam, P.S. Isoelectronic Wavelength Predictions for Magnetic-Dipole, Electric-Quadrupole, and Intercombination Transitions in the Mg Sequence. J. Opt. Soc. Am. 1983, 73, 979–984. [Google Scholar] [CrossRef]
- Ekberg, J.O.; Feldman, U.; Seely, J.F.; Brown, C.M.; MacGowan, B.J.; Kania, D.R.; Keane, C.J. Analysis of Magnesiumlike Spectra from Mo XXXI to Cs XLIV. Phys. Scr. 1991, 43, 19–32. [Google Scholar] [CrossRef]
- Seely, J.F.; Wagner, R.A. QED Contributions to the 3s–3p Transitions in Highly Charged Na-like Ions. Phys. Rev. A 1990, 41, 5246–5249. [Google Scholar] [CrossRef] [PubMed]
- Sugar, J.; Kaufman, V.; Rowan, W.L. Aluminiumlike Spectra of Copper Through Molybdenum. J. Opt. Soc. Am. B 1988, 5, 2183–2189. [Google Scholar] [CrossRef]
- Zhao, G.; Magain, P. Abundances of Neutron Capture Elements in Metal-Poor Dwarfs I. Yttrium and Zirconium. Astron. Astrophys. 1991, 244, 425–432. [Google Scholar]
- Redfors, A.; Cowley, C.R. Elemental Abundances of Yttrium and Zirconium in the Mercury-Manganese Stars ϕ Herculis, κ Cancri and ι Coronae Borealis. Astron. Astrophys. 1993, 271, 273–275. [Google Scholar]
- Kessler, T.; Moore, I.D.; Kudryavtsev, Y.; Peräjärvi, K.; Popov, A.; Ronkanen, P.; Sonoda, T.; Tordoff, B.; Wendt, K.D.A.; Äystö, J. Off-line Studies of the Laser Ionization of Yttrium at the IGISOL Facility. Nucl. Instrum. Methods Phys. Res. Sect. B 2008, 266, 681–700. [Google Scholar] [CrossRef]
- Wahlgren, G.M.; Carpenter, K.G.; Norris, R.P. Heavy Elements and Cool Stars. AIP Conf. Proc. Astron. 2008. [Google Scholar] [CrossRef]
- Osterbrock, D.E. Astrophysics of Gaseous Nebulae; W. H. Freeman & Co Ltd.: San Francisco, CA, USA, 1974. [Google Scholar]
- Denne, B.; Hinnov, E. Spectral Lines of Highly-Ionized Atoms for the Diagnostics of Fusion Plasmas. Phys. Scr. 1987, 35, 811–818. [Google Scholar] [CrossRef]
- Reader, J. 2s22p5–2s2p6 Transitions in the Flourinelike Ions Sr29+ and Y30+. Phys. Rev. A 1982, 26, 501–503. [Google Scholar] [CrossRef]
- Aggarwal, K.M.; Keenan, F.P. Radiative Rates for E1, E2, M1, and M2 Transitions in F-like ions with 37 ≤ Z ≤ 53. At. Data Nucl. Data Tables 2016, 109–110, 205–338. [Google Scholar] [CrossRef]
- Jönsson, P.; Alkauskas, A.; Gaigalas, G. Energies and E1, M1, E2 Transition Rates for States of the 2s22p5 and 2s2p6 Configurations in Fluorine-like Ions Between Si VI and W LXVI. At. Data Nucl. Data Tables 2013, 99, 431–446. [Google Scholar] [CrossRef]
- Khatri, I.; Goyal, A.; Aggarwal, S.; Singh, A.K.; Mohan, M. Extreme Ultraviolet and Soft X-ray Spectral Lines in Rb XXIX. Chin. Phys. B 2016, 25, 033201. [Google Scholar] [CrossRef]
- Alexander, E.; Even-Zohar, M.; Fraenkel, B.S.; Goldsmith, S. Classification of Transitions in the EUV Spectra of Y IX–XIII, Zr X–XIV, Nb XI–XV, and Mo XII–XVI. J. Opt. Soc. Am. 1971, 61, 508–514. [Google Scholar] [CrossRef]
- Ekberg, J.O.; Jupén, C.; Brown, C.M.; Feldman, U.; Seely, J.F. Classification of Resonance Transitions in Ge XIX, Se XXI, Sr XXV, Y XXVI and Zr XXVll. Phys. Scr. 1992, 46, 120–126. [Google Scholar] [CrossRef]
- Ekberg, J.O.; Redfors, A.; Brown, C.M.; Feldman, U.; Seely, J.F. Transitions and Energy Levels in Al-like Ge XX, Se XXII, Sr XXVI, Y XXVII and Zr XXVIII. Phys. Scr. 1991, 44, 539–547. [Google Scholar] [CrossRef]
- Reader, J. 3s2–3s3p and 3s3p–3s3d Transitions in Magnesiumlike Ions from Sr26+ to Rh33+. J. Opt. Soc. Am. 1983, 73, 796–799. [Google Scholar] [CrossRef]
- Reader, J.; Ekberg, J.O.; Feldman, U.; Brown, C.M.; Seely, J.F. Spectra and Energy Levels of Sodiumlike Ions from Y28+ to Sn39+. J. Opt. Soc. Am. B 1990, 7, 1176–1181. [Google Scholar] [CrossRef]
- Ateqad, N.; Chaghtai, M.S.Z.; Rahimullah, K. Addition to the Analysis of Y VII, VIII and Mo X. J. Phys. B At. Mol. Phys. 1984, 17, 4617–4622. [Google Scholar] [CrossRef]
- Litzén, U.; Hansson, A. Additions to the Spectra and Energy Levels of the Zinc-like Ions Y X–Cd XIX. Phys. Scr. 1989, 40, 468–471. [Google Scholar] [CrossRef]
- Nilsson, A.E.; Johansson, S.; Kurucz, R.L. The Spectrum of Singly Ionized Yttrium, Y II. Phys. Scr. 1991, 44, 226–257. [Google Scholar] [CrossRef]
- Epstein, G.L.; Reader, J. Spectrum and Energy Levels of Triply Ionized Yttrium (Y IV). J. Opt. Soc. Am. 1982, 72, 476–492. [Google Scholar] [CrossRef]
- Reader, J.; Acquista, N. Spectrum and Energy Levels of Ten-Times Ionized Yttrium (Y XI). J. Opt. Soc. Am. 1979, 69, 1285–1288. [Google Scholar] [CrossRef]
- Gillaspy, J.D. First Results from the EBIT at NIST. Phys. Scr. 1997, T71, 99. [Google Scholar] [CrossRef]
- Gillaspy, J.D.; Aglitskiy, Y.; Bell, E.W.; Brown, C.M.; Chandler, C.T.; Deslattes, R.D.; Feldman, U.; Hudson, L.T.; Laming, J.M.; Meyer, E.S.; et al. Overview of the Electron Beam Ion Trap Program at NIST. Phys. Scr. 1995, T59, 392–395. [Google Scholar] [CrossRef]
- Gillaspy, J.D. Testing QED in Sodium-like Gold and Xenon: Using Atomic Spectroscopy and an EBIT to Probe the Quantum Vacuum. J. Instrum. 2010, 5, C10005. [Google Scholar] [CrossRef]
- Gillaspy, J.D. Precision Spectroscopy of Trapped Highly Charged Heavy Elements: Pushing the Limits of Theory and Experiment. Phys. Scr. 2014, 89, 114004. [Google Scholar] [CrossRef]
- Sapirstein, J.; Cheng, K.T. S-Matrix Calculations of Energy Levels of Sodiumlike Ions. Phys. Rev. A 2015, 91, 062508. [Google Scholar] [CrossRef]
- Griem, H.R. Principles of Plasma Spectroscopy; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Ralchenko, Y.; Gillaspy, J.D.; Reader, J.; Osin, D.; Curry, J.J.; Podpaly, Y.A. Magnetic-Dipole Lines in 3dn Ions of High-Z Elements: Identification, Diagnostic Potential and Dielectronic Resonances. Phys. Scr. 2013, T156, 014082. [Google Scholar] [CrossRef]
- Ralchenko, Y.; Draganić, I.N.; Osin, D.; Gillaspy, J.D.; Reader, J. Spectroscopy of Diagnostically Important Magnetic-Dipole Lines in Highly Charged 3dn Ions of Tungsten. Phys. Rev. A 2011, 83, 032517. [Google Scholar] [CrossRef]
- Ralchenko, Yu. Density Dependence of the Forbidden Lines in Ni-like Tungsten. J. Phys. B At. Mol. Opt. Phys. 2007, 40, F175–F180. [Google Scholar] [CrossRef]
- Blagojević, B.; Le Bigot, E.-O.; Fahy, K.; Aguilar, A.; Makonyi, K.; Takács, E.; Tan, J.N.; Pomeory, J.M.; Burnett, J.H.; Gillaspy, J.D.; et al. A High Efficiency Ultrahigh Vacuum Compatible Flat Field Spectrometer for Extreme Ultraviolet Wavelengths. Rev. Sci. Instrum. 2005, 76, 083102. [Google Scholar] [CrossRef]
- Holland, G.E.; Boyer, C.N.; Seely, J.F.; Tan, J.N.; Pomeroy, J.M.; Gillaspy, J.D. Low Jitter Metal Vapor Vacuum Arc Ion Source for Electron Beam Ion Trap Injections. Rev. Sci. Instrum. 2005, 76, 073304. [Google Scholar] [CrossRef]
- Gillaspy, J.D. Highly Charged Ions. J. Phys. B At. Mol. Opt. Phys. 2001, 34, R93–R130. [Google Scholar] [CrossRef]
- Kramida, A.; Brown, C.M.; Feldman, U.; Reader, J. Extension and New Level Optimization of the Ne IV Spectrum. Phys. Scr. 2012, 85, 025303. [Google Scholar] [CrossRef]
- Ralchenko, Y.; Kramida, A.; Reader, J.; The NIST ASD Team. NIST Atomic Spectra Database (Version 5), 2011. Available online: http://physics.nist.gov/asd (accessed on 15 January 2017).
- Hughes, I.G.; Hase, T.P.A. Measurements and Their Uncertainties; Oxford University Press: Oxford, UK, 2010. [Google Scholar]
- Ralchenko, Y.; Maron, Y. Accelerated Recombination Due to Resonant Deexcitation of Metastable States. J. Quant. Spectosc. Radiat. Transf. 2001, 71, 609–621. [Google Scholar] [CrossRef]
- Gu, M.F. The Flexible Atomic Code. Can. J. Phys. 2008, 86, 675–689. [Google Scholar] [CrossRef]
- Safronova, U.I.; Cowan, T.E.; Safronova, M.S. Relativistic Many-Body Calculations of Electric-Dipole Lifetimes, Transition Rates and Oscillator Strengths for 2l−1–3l′ States in Ne-like Ions. J. Phys. B At. Mol. Opt. Phys. 2005, 38, 2741–2763. [Google Scholar] [CrossRef]
- Kim, Y.-K.; Baik, D.H.; Indelicato, P.; Desclaux, J.P. Resonance Transition Energies of Li-, Na-, and Cu-like Ions. Phys. Rev. A 1991, 44, 148–166. [Google Scholar] [CrossRef] [PubMed]
- Kozhedub, Y.S.; Volotka, A.V.; Artemyev, A.N.; Glazov, D.A.; Plunien, G.; Shabaev, V.M.; Tupitsyn, I.I.; Stöhlker, T. Relativistic Recoil, Electron-Correlation, and QED Effects on the 2pj–2s Transition Energies in Li-like Ions. Phys. Rev. A 2010, 81, 042513. [Google Scholar] [CrossRef]
- Blundell, S.A. Calculations of the Screened Self-Energy and Vacuum Polarization in Li-like, Na-like, and Cu-like Ions. Phys. Rev. A 1993, 47, 1790–1803. [Google Scholar] [CrossRef] [PubMed]
- Sapirstein, J.; Cheng, K.T. S-Matrix Calculations of Energy Levels of the Lithium Isoelectronic Sequence. Phys. Rev. A 2011, 83, 012504. [Google Scholar] [CrossRef]
- Seely, J.F. QED Contributions to the 2p–2s Transitions in Highly Charged Li-like Ions. Phys. Rev. A 1989, 39, 3682–3685. [Google Scholar] [CrossRef]
- Verdebout, S.; Nazé, C.; Jönsson, P.; Rynkun, P.; Godefroid, M.; Gaigalas, G. Hyperfine Structures and Landé gJ- Factors for n = 2 States in Beryllium-, Boron-, Carbon-, and Nitrogen-like Ions from Relativisitc Configuration Interaction Calculations. At. Data Nucl. Data Tables 2014, 100, 1111–1155. [Google Scholar] [CrossRef]
- Huang, K.-N.; Kim, Y.-K.; Cheng, K.T.; Desclaux, J.P. Correlation and Relativistic Effects in Spin-Orbit Splitting. Phys. Rev. Lett. 1982, 48, 1245. [Google Scholar] [CrossRef]
- Liu, H.; Jiang, G.; Hu, F.; Wang, C.-K.; Wang, Z.-B.; Yang, J.-M. Intercombination Transitions of the Carbon-like Isoelectronic Sequence. Chin. Phys. B 2013, 22, 073202. [Google Scholar] [CrossRef]
- Behring, W.E.; Brown, C.M.; Feldman, U.; Seely, J.F.; Reader, J.; Richardson, M.C. Transitions of the Type 2s–2p in Oxygenlike Y, Zr, and Nb. J. Opt. Soc. Am. B 1986, 3, 1113–1115. [Google Scholar] [CrossRef]
- Edlén, B. The 2p Interval of 2s22p5 and 2s22p. Opt. Pura Apl. 1977, 10, 123–129. [Google Scholar]
- Kaufman, V.; Sugar, J. Forbidden Lines in ns2npk Ground Configurations and nsnp Excited Configurations of Beryllium through Molybdenum Atoms and Ions. J. Phys. Chem. Ref. Data 1986, 15, 321–426. [Google Scholar] [CrossRef]
- Curtis, L.J.; Ramanujam, P.S. Ground-State Fine Sturcture for the B and F Isoelectronic Sequence Using the Extended Regular Doublet Law. Phys. Rev. A 1982, 26, 3672–3675. [Google Scholar] [CrossRef]
- Nilsen, J.; Scofield, J.H. Wavelengths of Neon-like 3p → 3s X-ray Laser Transitions. Phys. Scr. 1994, 49, 588–591. [Google Scholar] [CrossRef]
- Shimkaveg, G.M.; Carter, M.R.; Walling, R.S.; Ticehurst, J.M.; Mrowka, S.; Trebes, J.E.; MacGowan, B.J.; Dasilva, L.B.; Matthews, D.L.; London, R.A.; et al. X-ray Laser Coherence Experiments in Neon-like Yttrium. In Proceedings of the International Conference on Lasers ’91, San Diego, CA, USA, 9–13 December 1992; pp. 84–92. [Google Scholar]
- Matthews, D.L.; Hagelstein, P.L.; Rosen, M.D.; Eckart, M.J.; Ceglio, N.M.; Hazi, A.U.; Medecki, H.; Macgowan, B.J.; Trebes, J.E.; Whitten, B.L.; et al. Demonstration of a Soft X-Ray Amplifier. Phys. Rev. Lett. 1985, 54, 110. [Google Scholar] [CrossRef] [PubMed]
- Cogordan, J.A.; Lunell, S. Energies of 2p53s, 3p, and 3d Levels of Neon-like Ions from Relativistic MCDF Calculations, 20 ≤ Z ≤ 54. Phys. Scr. 1985, 33, 406–411. [Google Scholar] [CrossRef]
- Biersdorfer, P.; Obst, M.; Safronova, U.I. Radiative Decay Probabilities of the (2s223s1/2)J=0 Level in Neonlike Ions. Phys. Rev. A 2011, 83, 012514. [Google Scholar] [CrossRef]
- Fontes, C.J.; Zhang, H.L. Relativistic Distorted-Wave Collision Strengths for Δn = 0 Transitions in the 67 Li-like, F-like and Na-like Ions with 26 ≤ Z ≤ 92. At. Data Nucl. Data Tables 2017, 113, 293–315. [Google Scholar] [CrossRef]
- Santana, J.A. Relativistic MR-MP Energy Levels: Low-Lying States in the Mg Isoelectronic Sequence. At. Data Nucl. Data Tables 2016, 111–112, 87–186. [Google Scholar] [CrossRef]
- Safronova, U.I.; Jonson, W.R.; Berry, H.G. Excitation Energies and Transition Rates in Magensiumlike Ions. Phys. Rev. A 2000, 61, 052503. [Google Scholar] [CrossRef]
- Beiersdorfer, P. Precision Energy-Level Measurements and QED of Highly Charged Ions. Can. J. Phys. 2009, 87, 9–14. [Google Scholar] [CrossRef]
- Andersson, M.; Grumer, J.; Brage, T.; Zou, Y.-M.; Hutton, R. Analysis of the Competition Between Forbidden and Hyperfine-Induced Transitions in Ne-like Ions. Phys. Rev. A 2016, 93, 032506. [Google Scholar] [CrossRef]
- Beiersdorfer, P.; von Goeler, S.; Bitter, M.; Thorn, D.B. Measurement of the 3D → 2p Resonance to Intercombination Line-Intensity Ratio in Neonlike Fe XVII, Ge XXIII, and Se XXV. Phys. Rev. A 2001, 64, 032705. [Google Scholar] [CrossRef]
- Mauche, C.W.; Liedahl, D.A.; Fournier, K.B. First Application of the Fe XVII I(17.10 Å)/I(17.05 Å) Line Ratio to Constrain the Plasma Density of a Cosmic X-Ray Source. Astrophys. J. 2001, 560, 992–996. [Google Scholar] [CrossRef]
- Tallents, G.J. The Physics of Soft X-ray Lasers Pumped by Electron Collisions in Laser Plasmas. J. Phys. D 2003, 36, R259–R276. [Google Scholar] [CrossRef]


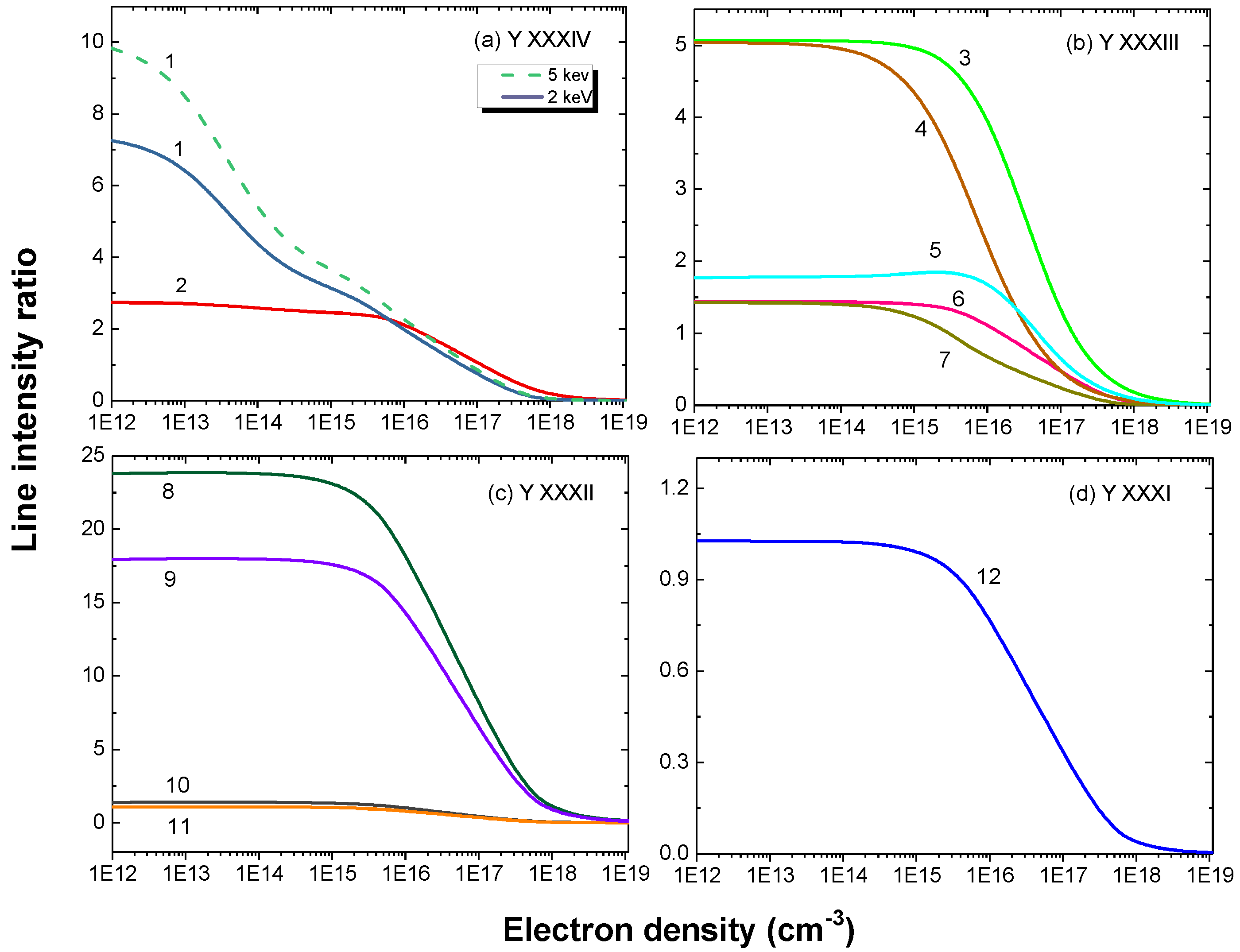
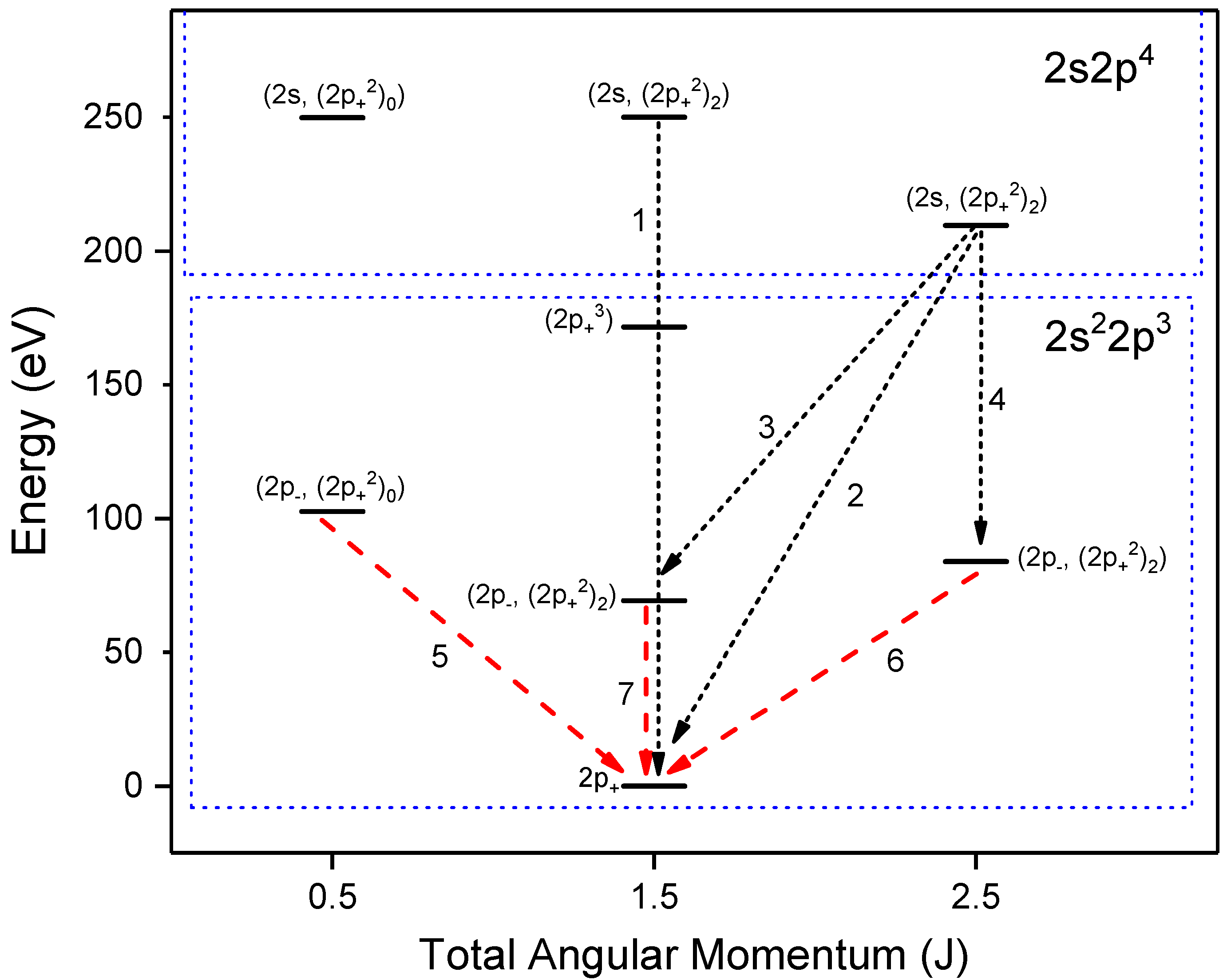
| Ion Charge | Seq. | Type | Lower Level | Upper Level | Experimental Wavelength (nm) | Theoretical Wavelength (nm) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| No. | Config. | Term | No. | Config. | Term | This Work | Previous Work | This Work | Previous Work | |||
| 36 | Li | E1 | 1 | 2 | 7.2771 | 7.2893 [69] | ||||||
| 7.2887(1) [70] | ||||||||||||
| 7.2892 [71] | ||||||||||||
| 7.2890(1) [72] | ||||||||||||
| 7.2888 [73] | ||||||||||||
| 36 | Li | E1 | 1 | 3 | 15.7139 | 15.7878 [69] | ||||||
| 15.7868(5) [70] | ||||||||||||
| 15.7865 [71] | ||||||||||||
| 15.7874(4) [72] | ||||||||||||
| 15.7867 [73] | ||||||||||||
| 35 | Be | E1 | 1 | 6 | 6.0322(5) | 6.0098 | 6.0337(20) [24] | |||||
| 6.0283 [74] | ||||||||||||
| 35 | Be | E1 | 1 | 3 | 15.2336(7) | 15.1907 | 15.2345(20) [24] | |||||
| 15.2302 [74] | ||||||||||||
| 34 | B | E1 | 1 | 7 | (, | 5.5768(6) | 5.5310 | 5.5771 [25] | ||||
| 34 | B | E1 | 1 | 6 | (, | 5.7623(6) | 5.7254 | 5.7629 [25] | ||||
| 34 | B | E1 | 1 | 3 | 12.5693(6) | 12.5372 | ||||||
| 34 | B | E1 | 2 | 5 | (, | 13.4185(8) | 13.3700 | |||||
| 34 | B | M1 | 1 | 2 | 14.3234(5) | 14.3363 | 14.321 [75] | |||||
| 14.322 [25] | ||||||||||||
| 33 | C | E1 | 1 | 7 | 5.3878(5) | 5.3571 | ||||||
| 33 | C | E1 | 3 | 7 | 8.4792(19) | 8.4071 | ||||||
| 33 | C | E1 | 2 | 5 | 11.1236(9) | 11.1132 | ||||||
| 33 | C | M1 | 1 | 3 | 14.7700(10) | 14.7668 | ||||||
| 33 | C | M1 | 1 | 2 | 17.0632(7) | 17.1036 | 17.0625 [76] | |||||
| 17.0558 [76] | ||||||||||||
| 32 | N | E1 | 1 | 8 | 4.9858(6) | 4.9593 | ||||||
| 32 | N | E1 | 1 | 6 | 5.9329(4) | 5.9151 | ||||||
| 32 | N | E1 | 2 | 6 | 8.8822(7) | 8.8358 | ||||||
| 32 | N | E1 | 3 | 6 | 9.9054(10) | 9.8612 | ||||||
| 32 | N | M1 | 1 | 4 | 12.0926(6) | 12.0717 | ||||||
| 32 | N | M1 | 1 | 3 | 14.8036(5) | 14.7819 | ||||||
| 32 | N | M1 | 1 | 2 | 17.8665(6) | 17.8947 | ||||||
| 31 | O | E1 | 1 | 7 | 4.4854(8) | 4.4857(15) [77] | 4.4567 | |||||
| 31 | O | E1 | 2 | 7 | 4.8871(12) | 4.8882(15) [77] | 4.8569 | |||||
| 31 | O | E1 | 1 | 6 | 5.0103(5) | 5.0085(15) [77] | 4.9828 | |||||
| 31 | O | E1 | 3 | 6 | 7.2352(8) | 7.2356(15) [77] | 7.1754 | |||||
| 31 | O | E1 | 4 | 6 | 7.8430(8) | 7.7848 | ||||||
| 31 | O | M1 | 1 | 4 | 13.8581(6) | 13.8442 | 13.89(2) [77] | |||||
| 31 | O | M1 | 1 | 3 | 16.2725(9) | 16.307 | 16.28(2) [77] | |||||
| 31 | O | E1 | 16 | 32 | 19.4383(8) | 19.4639 | ||||||
| 30 | F | E1 | 1 | 3 | 4.4500(7) | 4.4496(15) [37] | 4.417 | 4.4083 [26] | ||||
| 4.4486 [26] | ||||||||||||
| 4.4492 [39] | ||||||||||||
| 30 | F | E1 | 2 | 3 | 6.2115(14) | 6.2107(15) [37] | 6.1454 | 6.1299 [26] | ||||
| 6.2109 [26] | ||||||||||||
| 30 | F | M1 | 1 | 2 | 15.6801(11) | 15.7043 | 15.681(12) [37] | |||||
| 15.654(5) [78] | ||||||||||||
| 15.678 [26] | ||||||||||||
| 15.678(12) [79] | ||||||||||||
| 15.71 [38] | ||||||||||||
| 15.6826 [39] | ||||||||||||
| 15.685 [80] | ||||||||||||
| 29 | Ne | E1 | 3 | 20 | 7.8983(8) | 7.9003 | 7.914 [81] | |||||
| 29 | Ne | E1 | 3 | 11 | 12.5743(7) | 12.5696 | 12.576 [81] | |||||
| 29 | Ne | E1 | 12 | 24 | 12.9238(8) | 12.9267 | ||||||
| 29 | Ne | E1 | 5 | 15 | 13.0471(8) | 13.0550 | ||||||
| 29 | Ne | E1 | 2 | 10 | 14.8480(7) | 14.8389 | ||||||
| 29 | Ne | E1 | 10 | 22 | 15.3559(10) | 15.3587 | ||||||
| 29 | Ne | E1 | 19 | 26 | 15.3945(10) | 15.3972 | ||||||
| 29 | Ne | E1 | 18 | 25 | 15.4387(10) | 15.4444 | ||||||
| 29 | Ne | E1 | 3 | 10 | 15.4902(18) | 15.497(15) [82] | 15.4882 | 15.503 [81] | ||||
| 15.50 [83] | 15.50 [84] | |||||||||||
| 29 | Ne | E1 | 9 | 20 | 15.5024(8) | 15.4904 | 15.498 [81] | |||||
| 29 | Ne | E1 | 6 | 17 | 15.6711(10) | 15.6769 | ||||||
| 29 | Ne | E1 | 9 | 19 | 15.7208(7) | 15.714(15) [82] | 15.7085 | [81] | ||||
| 15.71 [83] | 15.71 [84] | |||||||||||
| 29 | Ne | E1 | 2 | 6 | 15.8537(7) | 15.8455 | ||||||
| 29 | Ne | M1 | 3 | 8 | 16.4817(7) | 16.4843 | ||||||
| 29 | Ne | E1 | 3 | 7 | 16.5411(8) | 16.537(15) [82] | 16.5488 | 16.542 [81] | ||||
| 16.463 [85] | ||||||||||||
| 16.484 [85] | ||||||||||||
| 28 | Na | E1 | 2 | 4 | 12.0979(8) | 12.098(20) [16] | 12.1353 | 12.09248 [86] | ||||
| 12.0993(7) [45] | ||||||||||||
| 28 | Na | E1 | 3 | 5 | 14.1938(7) | 14.1938(6) [16] | 14.2458 | 14.1873 [86] | ||||
| 14.1959(7) [45] | ||||||||||||
| 28 | Na | E1 | 1 | 3 | 15.1037(5) | 15.1035(10) [16] | 15.0542 | 15.1038 [55] | ||||
| 15.10402(40) [7] | ||||||||||||
| 15.1033 [29] | ||||||||||||
| 15.1038(7) [45] | ||||||||||||
| 15.0658 [86] | ||||||||||||
| 28 | Na | E1 | 1 | 2 | 19.6212(7) | [16] | 19.5175 | 19.6199 [55] | ||||
| 19.6209(7) [7] | ||||||||||||
| 19.6219 [29] | ||||||||||||
| 19.6213(7) [45] | ||||||||||||
| 27 | Mg | E1 | 5 | 14 | 12.8333(9) | 12.8352(10) [21] | 12.7875 | |||||
| 12.8349(5) [15] | ||||||||||||
| 12.8301(15) [44] | ||||||||||||
| 27 | Mg | E1 | 1 | 5 | 13.5276(5) | 13.5279(10) [21] | 13.4437 | 13.5276 [87] | ||||
| 13.5283(5) [15] | 13.5213 [88] | |||||||||||
| 13.5216(15) [44] | ||||||||||||
| 27 | Mg | E1 | 3 | 3s3p | 7 | 14.5650(20) | 14.5603(10) [21] | 14.528 | ||||
| 26 | Al | E1 | 1 | 10 | 10.9388(15) | 10.9391(20) [30] | 10.8578 | |||||
| 10.9413(10) [43] | ||||||||||||
| 26 | Al | E1 | 2 | 11 | 11.9072(12) | 11.9131(20) [30] | 11.8248 | |||||
| 11.9110(10) [43] | ||||||||||||
| 26 | Al | E1 | 2 | 10 | 12.9717(11) | 12.9729(20) [30] | 12.852 | |||||
| 12.9745(10) [43] | ||||||||||||
| 26 | Al | E1 | 1 | 8 | 13.0401(8) | 13.0416(20) [30] | 12.9265 | |||||
| 13.0417(10) [43] | ||||||||||||
| 26 | Al | E1 | 1 | 6 | 14.4883(8) | 14.4914(20) [30] | 14.4675 | |||||
| 14.4910(10) [43] | ||||||||||||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Silwal, R.; Takacs, E.; Dreiling, J.M.; Gillaspy, J.D.; Ralchenko, Y. Identification and Plasma Diagnostics Study of Extreme Ultraviolet Transitions in Highly Charged Yttrium. Atoms 2017, 5, 30. https://doi.org/10.3390/atoms5030030
Silwal R, Takacs E, Dreiling JM, Gillaspy JD, Ralchenko Y. Identification and Plasma Diagnostics Study of Extreme Ultraviolet Transitions in Highly Charged Yttrium. Atoms. 2017; 5(3):30. https://doi.org/10.3390/atoms5030030
Chicago/Turabian StyleSilwal, Roshani, Endre Takacs, Joan M. Dreiling, John D. Gillaspy, and Yuri Ralchenko. 2017. "Identification and Plasma Diagnostics Study of Extreme Ultraviolet Transitions in Highly Charged Yttrium" Atoms 5, no. 3: 30. https://doi.org/10.3390/atoms5030030






