Stark Widths of Ar II Spectral Lines in the Atmospheres of Subdwarf B Stars
Abstract
:1. Introduction
2. The Impact Semiclassical Perturbation Method
3. Stark Widths
- A = uncertainties within 15%
- B+ = uncertainties within 23%
- B = uncertainties within 30%
- C+ = uncertainties within 40%
- C = uncertainties within 50%
- D = uncertainties larger than 50%
4. Stark Broadening Effect in sdB Stars
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Werner, K.; Rauch, T.; Kruk, J.W. Far-UV spectroscopy of two extremely hot, helium-rich white dwarfs. Astron. Astrophys. 2017, 601. [Google Scholar] [CrossRef]
- Werner, K.; Rauch, T.; Kruk, J.W. Discovery of photospheric argon in very hot central stars of planetary nebulae and white dwarfs. Astron. Astrophys. 2007, 466, 317–322. [Google Scholar] [CrossRef]
- Rauch, T.; Ziegler, M.; Werner, K.; Kruk, J.W.; Oliveira, C.M.; Van de Putte, D.; Mignani, R.P.; Kerber, F. High-resolution FUSE and HST ultraviolet spectroscopy of the white dwarf central star of Sh 2-216. Astron. Astrophys. 2007, 470, 317–329. [Google Scholar] [CrossRef]
- Blanchette, J.-P.; Chayer, P.; Wesemael, F.; Fontaine, G.; Fontaine, M.; Dupuis, J.; Kruk, J.W.; Green, E.M.T. FUSE Determination of Abundances in Long-Period Pulsating V1093 Her (PG 1716 + 426) Stars. Astrophys. J. 2008, 678, 1329–1341. [Google Scholar] [CrossRef]
- O’Toole, S.J.; Heber, U.T. Abundance studies of sdB stars using UV echelle HST/STIS spectroscopy. Astron. Astrophys. 2006, 452, 579–590. [Google Scholar] [CrossRef]
- Heber, U.; Edelmann, H. Atmospheric Parameters and Abundances of sdB Stars. Astrophys. Space Sci. 2004, 291, 341–349. [Google Scholar] [CrossRef]
- Keenan, F.P.; Bates, B.; Dufton, P.L.; Holmgren, D.E.; Gilheany, S. The determination of element abundances in the solar neighborhood from B-type stellar spectra. I–Argon. Astrophys. J. 1990, 348, 322–327. [Google Scholar] [CrossRef]
- Kupfer, T.; Przybilla, N.; Heber, U.; Jeffery, C.S.; Behara, N.T.; Butler, K. Quantitative spectroscopy of extreme helium stars Model atmospheres and a non-LTE abundance analysis of BD + 10o2179. Mon. Not. R. Astron. Soc. 2017, 471, 877–890. [Google Scholar] [CrossRef]
- Popović, L.Č.; Simić, S.; Milovanović, N.; Dimitrijević, M.S. Stark Broadening Effect in Stellar Atmospheres: Nd II Lines. Astrophys. J. Suppl. Ser. 2001, 135, 109–114. [Google Scholar] [CrossRef]
- Simić, Z.; Dimitrijević, M.S.; Milovanović, N.; Sahal-Bréchot, S. Stark broadening of Cd I spectral lines. Astron. Astrophys. 2005, 441, 391–393. [Google Scholar] [CrossRef]
- Hamdi, R.; Ben Nessib, N.; Milovanović, N.; Popović, L.Č.; Dimitrijević, M.S.; Sahal-Bréchot, S. Atomic data and electron-impact broadening effect in DO white dwarf atmospheres: SiVI. Mon. Not. R. Astron. Soc. 2008, 387, 871–882. [Google Scholar] [CrossRef]
- Dimitrijević, M.S.; Simić, Z.; Kovačević, A.; Valjarević, A.; Sahal-Bréchot, S. Stark broadening of Xe VIII spectral lines. Mon. Not. R. Astron. Soc. 2015, 454, 1736–1741. [Google Scholar] [CrossRef]
- Hamdi, R.; Ben Nessib, N.; Sahal-Bréchot, S.; Dimitrijević, M.S. Stark widths of Ar III spectral lines in the atmospheres of subdwarf B stars. Adv. Space Res. 2014, 54, 1223–1230. [Google Scholar] [CrossRef]
- Sahal-Bréchot, S. Impact Theory of the Broadening and Shift of Spectral Lines due to Electrons and Ions in a Plasma. Astron. Astrophys. 1969, 1, 91–123. [Google Scholar]
- Sahal-Bréchot, S. Impact Theory of the Broadening and Shift of Spectral Lines due to Electrons and Ions in a Plasma (Continued). Astron. Astrophys. 1969, 2, 322–354. [Google Scholar]
- Cowan, R.D. The Theory of Atomic Structure and Spectra; Los Alamos Series in Basic and Applied Sciences; University of California Press: Berkeley, CA, USA, 1981; ISBN 9780520038219. [Google Scholar]
- Hamdi, R.; Ben Nessib, N.; Dimitrijević, M.S.; Sahal-Bréchot, S. Stark broadening of Pb IV spectral lines. Mon. Not. R. Astron. Soc. 2013, 431, 1039–1047. [Google Scholar] [CrossRef]
- Djeniže, S.; Malešević, M.; Srećković, A.; Milosavljević, M.; Purić, J. Stark broadening and shift of singly-ionized argon spectral lines in higher multiplets. J. Quant. Spectrosc. Radiat. Transf. 1989, 42, 429–435. [Google Scholar] [CrossRef]
- Dzierzega, K.; Musiol, K. Stark broadening and shift for Ar II lines. J. Quant. Spectrosc. Radiat. Transf. 1994, 52, 747–754. [Google Scholar] [CrossRef]
- Pellerin, S.; Musiol, K.; Chapelle, J. Measurement of atomic parameters of singly ionized argon lines. III. Stark broadening parameters. J. Quant. Spectrosc. Radiat. Transf. 1997, 57, 377–393. [Google Scholar] [CrossRef]
- Aparicio, J.A.; Gigosos, M.A.; González, V.R.; Pérez, C.; de la Rosa, M.I.; Mar, S. Measurement of Stark broadening and shift of singly ionized Ar lines. J. Phys. B 1998, 31, 1029–1048. [Google Scholar] [CrossRef]
- Iglesias, E.J.; Ghosh, J.; Elton, R.C.; Griem, H.R. Spectral-line width measurements in Ar II from a laser-heated gas-puff plasma. J. Quant. Spectrosc. Radiat. Transf. 2006, 98, 101–106. [Google Scholar] [CrossRef]
- Djurović, S.; Belmonte, M.T.; Peláez, R.J.; Aparicio, J.A.; Mar, S. Stark parameter measurement of Ar II UV spectral lines. Mon. Not. R. Astron. Soc. 2013, 433, 1082–1093. [Google Scholar] [CrossRef]
- Konjević, N.; Lesage, A.; Fuhr, J.R.; Wiese, W.L. Experimental Stark Widths and Shifts for Spectral Lines of Neutral and Ionized Atoms (A Critical Review of Selected Data for the Period 1989 Through 2000). J. Phys. Chem. Ref. Data 2002, 31, 819–927. [Google Scholar] [CrossRef]
- Kramida, A.; Ralchenko, Y.; Reader, J.; NIST ASD Team. NIST Atomic Spectra Database (ver. 5.1); National Institute of Standards and Technology: Gaithersburg, MD, USA, 2013. Available online: http://physics.nist.gov/asd (accessed on 9 March 2014).
- Ohl, R.G.; Chayer, P.; Moos, H.W. Photospheric Metals in the Far Ultraviolet Spectroscopic Explorer Spectrum of the Subdwarf B Star PG 0749+658. Astrophys. J. Lett. 2000, 538, L95–L98. [Google Scholar] [CrossRef]
- Jeffery, C.S.; Woolf, V.M.; Pollacco, D.L. Time-resolved spectral analysis of the pulsating helium star V652 Her. Astron. Astrophys. 2001, 376, 497–517. [Google Scholar] [CrossRef]
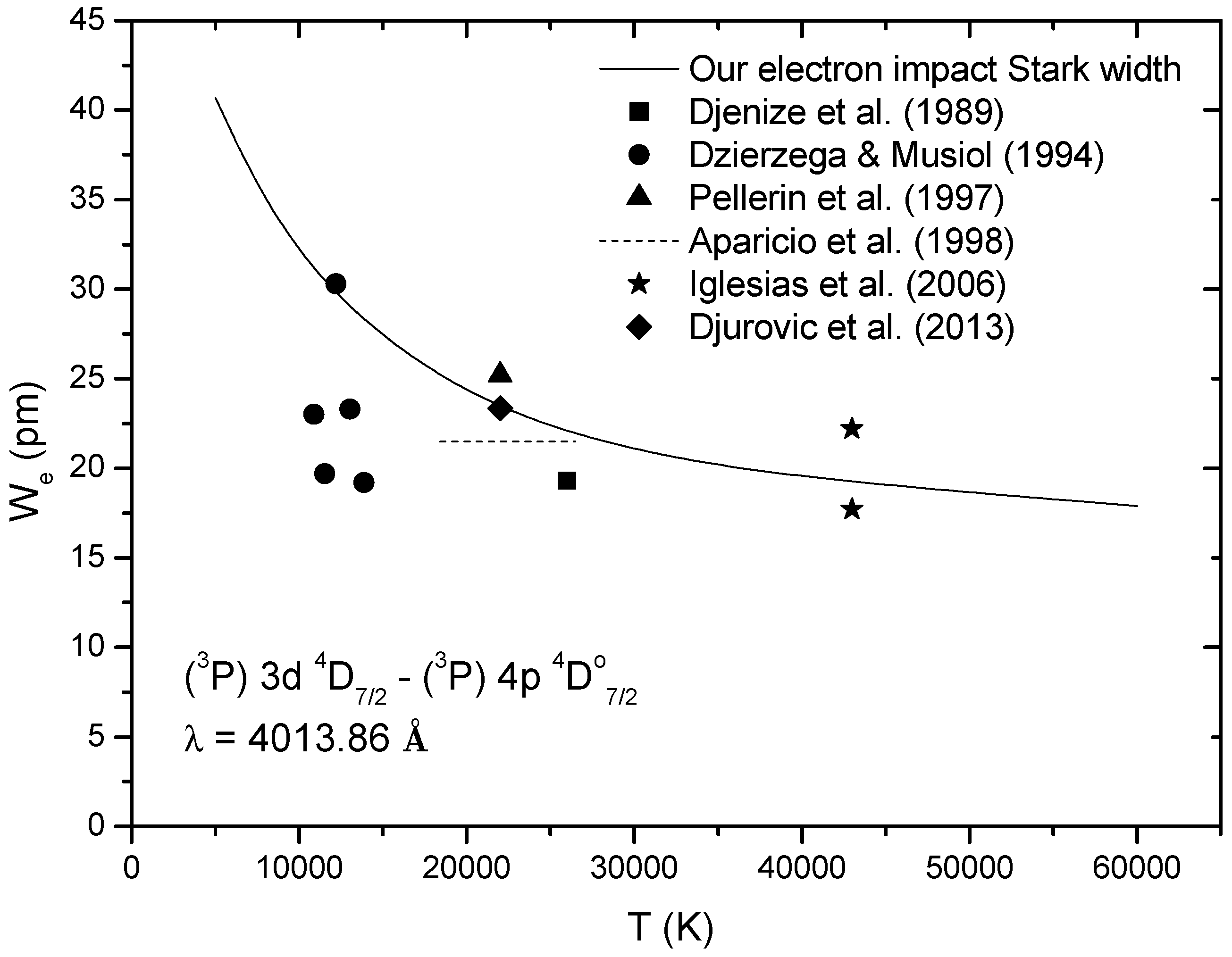
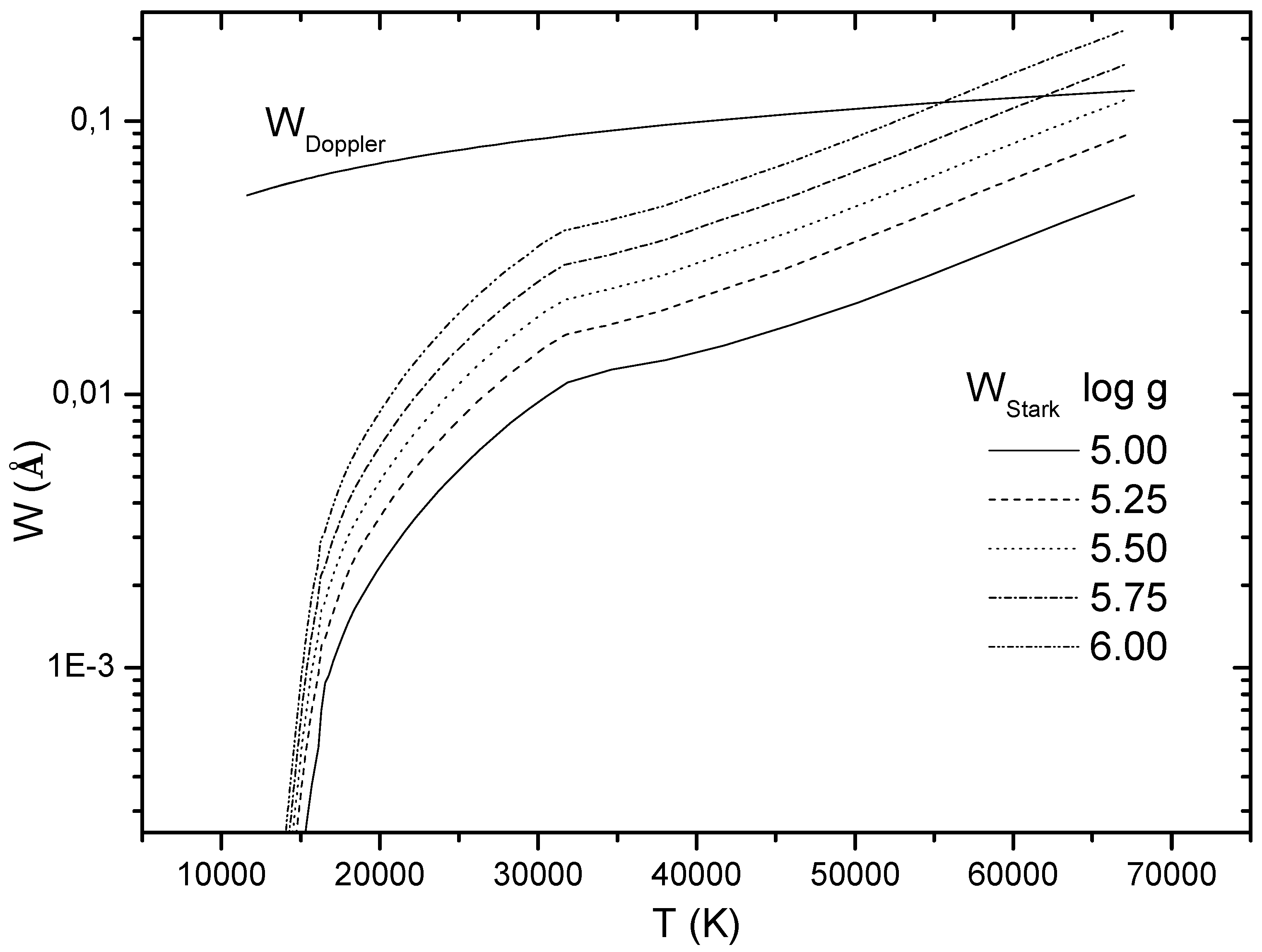
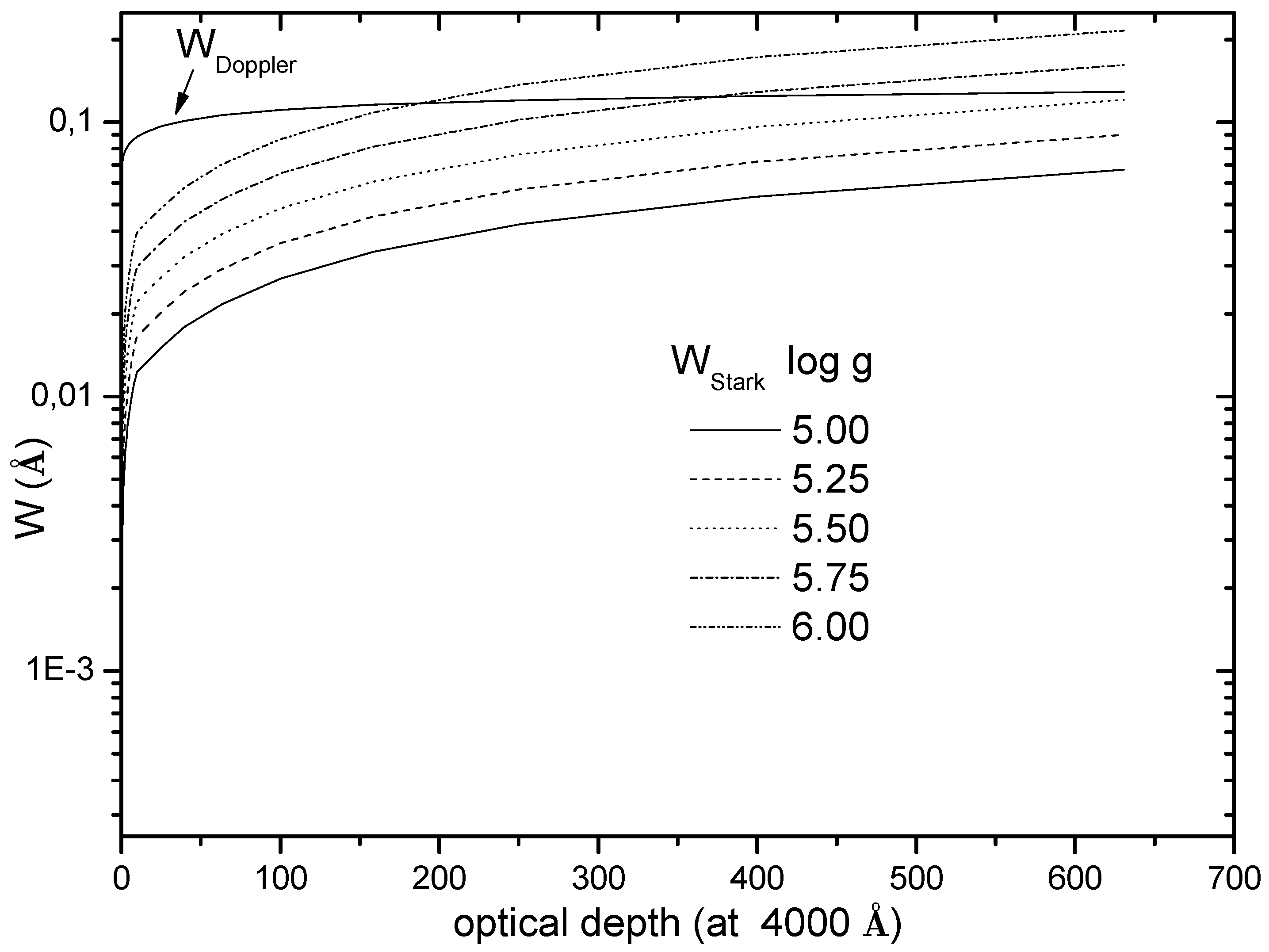
| Transition Array | Transition | (Å) | T (10 K) | N( cm) | W | W (pm) | W (pm) | W/W | Acc. | Ref. |
|---|---|---|---|---|---|---|---|---|---|---|
| (P) 3d– (P) 4p | D–P | 4400.99 | 22.0 | 1.00 | 34.3 | 25.2 | 3.78 | 1.18 | B | [20] |
| D–P | 4371.33 | 22.0 | 1.00 | 32.4 | 25.0 | 3.77 | 1.13 | B | [20] | |
| D–P | 4431.00 | 22.0 | 1.00 | 28.6 | 25.3 | 3.84 | 0.98 | B | [20] | |
| 18.4–26.5 | 1.00 | 31.3 | 26.8–24.0 | 3.71–3.93 | 1.02–1.12 | B | [21] | |||
| D–P | 4400.10 | 22.0 | 1.00 | 30.7 | 25.1 | 3.82 | 1.06 | B | [20] | |
| D–P | 4352.20 | 22.0 | 1.00 | 35.0 | 24.9 | 3.78 | 1.22 | B | [20] | |
| D–P | 4460.56 | 22.0 | 1.00 | 26.6 | 25.4 | 3.89 | 0.91 | B | [20] | |
| 18.4–26.5 | 1.00 | 36.8 | 27.0–24.1 | 3.78–4.00 | 1.19–1.31 | B | [21] | |||
| D–P | 4420.91 | 22.0 | 1.00 | 24.4 | 25.6 | 3.65 | 0.83 | B | [20] | |
| 18.4–26.5 | 1.00 | 33.8 | 27.2–24.3 | 3.76–3.97 | 1.09–1.20 | C+ | [21] | |||
| D–D | 4013.86 | 26.0 | 1.76 | 34.0 | 38.3 | 6.04 | 0.77 | B | [18] | |
| 10.88 | 2.03 | 46.7 | 60.4 | 5.89 | 0.70 | B+ | [19] | |||
| 11.52 | 1.79 | 35.3 | 52.1 | 5.29 | 0.62 | B+ | [19] | |||
| 12.20 | 0.74 | 22.4 | 21.0 | 2.04 | 0.96 | B+ | [19] | |||
| 13.03 | 1.10 | 25.6 | 30.5 | 3.37 | 0.76 | B+ | [19] | |||
| 13.88 | 1.39 | 26.7 | 37.6 | 4.29 | 0.64 | B+ | [19] | |||
| 22.0 | 1.00 | 25.2 | 23.0 | 3.36 | 0.96 | B | [20] | |||
| 18.4–26.5 | 1.00 | 21.5 | 24.4–21.6 | 3.26–3.45 | 0.77–0.86 | B+ | [21] | |||
| 43.0 | 4.50 | 100 | 85.7 | 16.2 | 0.98 | B | [22] | |||
| 43.0 | 7.20 | 160 | 137 | 25.9 | 0.98 | B | [22] | |||
| 43.0 | 9.00 | 160 | 171 | 32.3 | 0.79 | B | [22] | |||
| 22.0 | 1.00 | 23.34 | 23.0 | 3.36 | 0.86 | B | [23] | |||
| D–D | 3968.36 | 22.0 | 1.00 | 23.6 | 22.6 | 3.33 | 0.91 | B | [20] | |
| 18.4–26.5 | 1.00 | 29.4 | 24.0–21.4 | 3.24–3.43 | 1.08–1.18 | B+ | [21] | |||
| 43.0 | 4.50 | 80 | 84.8 | 16.1 | 0.79 | B | [22] | |||
| 43.0 | 7.20 | 100 | 136 | 25.7 | 0.62 | B | [22] | |||
| 43.0 | 9.00 | 160 | 169 | 32.1 | 0.80 | B | [22] | |||
| D–D | 3914.77 | 22.0 | 1.00 | 20.7 | 21.7 | 3.30 | 0.83 | B | [20] | |
| 18.4–26.5 | 1.00 | 20.9 | 23.1–20.6 | 3.20-3.40 | 0.79–0.87 | B+ | [21] | |||
| 22.0 | 1.00 | 18.39 | 21.7 | 3.30 | 0.74 | B | [23] | |||
| D–D | 3944.27 | 22.0 | 1.00 | 22.0 | 22.5 | 3.29 | 0.85 | B | [20] | |
| 18.4–26.5 | 1.00 | 24.0 | 23.8–21.2 | 3.19–3.38 | 0.90–0.98 | B+ | [21] | |||
| 22.0 | 1.00 | 23.25 | 22.5 | 3.29 | 0.90 | A | [23] | |||
| D–D | 3875.26 | 22.0 | 1.00 | 19.2 | 22.0 | 3.26 | 0.76 | B | [20] | |
| 18.4–26.5 | 1.00 | 27.5 | 23.4–20.6 | 3.17–3.36 | 1.04–1.15 | B+ | [21] | |||
| 22.0 | 1.00 | 17.62 | 22.0 | 3.26 | 0.70 | B | [23] | |||
| D–D | 4038.80 | 22.0 | 1.00 | 24.1 | 23.2 | 3.41 | 0.91 | B | [20] | |
| 18.4–26.5 | 1.00 | 29.9 | 24.6-21.9 | 3.31–3.51 | 1.07–1.18 | B | [21] | |||
| 22.0 | 1.00 | 24.05 | 23.2 | 3.41 | 0.90 | C | [23] | |||
| D–D | 3992.05 | 22.0 | 1.00 | 21.9 | 22.9 | 3.38 | 0.83 | B | [20] | |
| 18.4–26.5 | 1.00 | 32.4 | 24.3–21.7 | 3.27–3.47 | 1.18-1.29 | B+ | [21] | |||
| D–D | 3931.24 | 22.0 | 1.00 | 19.1 | 21.9 | 3.33 | 0.76 | B | [20] | |
| D–D | 3786.38 | 22.0 | 1.00 | 20.3 | 22.4 | 3.17 | 0.79 | B | [20] | |
| 18.4–26.5 | 1.00 | 23.7 | 23.8–21.3 | 3.08–3.27 | 0.88–0.96 | B+ | [21] | |||
| 22.0 | 1.00 | 23.49 | 22.4 | 3.17 | 0.92 | A | [23] | |||
| D–D | 3808.57 | 22.0 | 1.00 | 18.7 | 22.8 | 3.19 | 0.72 | B | [20] | |
| 22.0 | 1.00 | 22.53 | 22.8 | 3.19 | 0.87 | C | [23] | |||
| D–S | 3499.48 | 22.0 | 1.00 | 29.03 | 17.5 | 2.90 | 1.42 | C | [23] | |
| F–D | 6243.12 | 18.4–26.5 | 1.00 | 60.3 | 68.7–61.4 | 8.64–9.14 | 0.78–0.85 | B+ | [21] | |
| F–D | 6138.66 | 18.4–26.5 | 1.00 | 58.6 | 67.0–59.6 | 8.57–9.07 | 0.78–0.85 | B+ | [21] | |
| F–D | 6399.21 | 18.4–26.5 | 1.00 | 49.5 | 72.4–64.6 | 9.07–9.59 | 0.61–0.68 | B+ | [21] | |
| P–D | 6808.53 | 22.0 | 1.00 | 75.3 | 77.1 | 10.9 | 0.86 | B | [20] | |
| P–P | 6861.27 | 18.4–26.5 | 1.00 | 62.6 | 74.9–67.1 | 11.4–12.02 | 0.73–0.80 | B+ | [21] | |
| P–P | 6666.36 | 18.4–26.5 | 1.00 | 62.4 | 70.3–62.8 | 10.7–11.3 | 0.77–0.84 | B+ | [21] | |
| P–P | 6437.60 | 18.4–26.5 | 1.00 | 65.0 | 65.6–58.6 | 9.98–10.5 | 0.86–0.94 | B+ | [21] | |
| P–S | 6483.08 | 18.4–26.5 | 1.00 | 65.2 | 71.1–64.2 | 10.35–10.9 | 0.80-0.87 | B+ | [21] | |
| P–S | 6103.54 | 22.0 | 1.00 | 65.3 | 59.2 | 9.36 | 0.95 | B | [20] | |
| 18.4–26.5 | 1.00 | 61.3 | 62.6–56.3 | 9.14–9.65 | 0.85–0.93 | B+ | [21] | |||
| P–S | 7380.43 | 18.4–26.5 | 1.00 | 76.7 | 87.6–76.1 | 13.2–13.9 | 0.76–0.85 | B+ | [21] | |
| P–S | 7233.54 | 22.0 | 1.00 | 61.9 | 83.2 | 13.0 | 0.64 | C+ | [20] | |
| F–D | 6756.55 | 18.4–26.5 | 1.00 | 62.8 | 73.5–65.5 | 9.89–10.5 | 0.75–0.83 | B+ | [21] | |
| F - D | 6863.54 | 18.4–26.5 | 1.00 | 55.4 | 76.5–68.1 | 9.98–10.56 | 0.64–0.70 | A | [21] | |
| F–D | 6684.29 | 18.4–26.5 | 1.00 | 61.6 | 72.5–64.6 | 9.50–10.1 | 0.75–0.82 | B+ | [21] | |
| F–D | 6886.61 | 18.4–26.5 | 1.00 | 69.5 | 76.2–67.2 | 9.88–10.5 | 0.81-0.89 | A | [21] | |
| F–D | 6643.70 | 18.4–26.5 | 1.00 | 71.8 | 72.3–64.0 | 9.20–9.70 | 0.88–0.97 | B+ | [21] |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hamdi, R.; Ben Nessib, N.; Sahal Bréchot, S.; Dimitrijević, M.S. Stark Widths of Ar II Spectral Lines in the Atmospheres of Subdwarf B Stars. Atoms 2017, 5, 26. https://doi.org/10.3390/atoms5030026
Hamdi R, Ben Nessib N, Sahal Bréchot S, Dimitrijević MS. Stark Widths of Ar II Spectral Lines in the Atmospheres of Subdwarf B Stars. Atoms. 2017; 5(3):26. https://doi.org/10.3390/atoms5030026
Chicago/Turabian StyleHamdi, Rafik, Nabil Ben Nessib, Sylvie Sahal Bréchot, and Milan S. Dimitrijević. 2017. "Stark Widths of Ar II Spectral Lines in the Atmospheres of Subdwarf B Stars" Atoms 5, no. 3: 26. https://doi.org/10.3390/atoms5030026









