Detailed Opacity Calculations for Astrophysical Applications
Abstract
:1. Introduction
1.1. Radiative Opacity
2. Interpretation of Experiments
3. Stellar Envelopes
3.1. κ Mechanism
- The inward motion of a layer of the star tends to compress the layer and increase the density ρ.
- The layer becomes more opaque, the flux from the deeper layers gets stuck in the high opacity (κ) region.
- This heat increase causes a build-up of pressure that pushes the layer back out again.
- The layer expands, cools and becomes more transparent to radiation.
- Energy and pressure beneath the layer diminish.
- The layer falls inward and the cycle repeats.
3.2. Comparisons of Rosseland Means
4. The Boundary of the Radiative/Convective Zones of the Sun
- macroscopic processes in the radiative zone are not taken into account in the energetic balance of the Sun.
- the radiative transfer calculations are not accurate, either as concerns the Rosseland mean value that could be underestimated or in the treatment of the radiative acceleration which limits the gravitational settling and could lead to incorrect internal abundances. The radiative acceleration of species k reads
- iron, which contributes to the total opacity (including hydrogen and helium) at a level of 20% in most of the radiative zone because it is always partially ionized;
- oxygen, which becomes partially ionized at 0.6 R and plays a major role at the basis of the convective zone. The increase of its opacity contribution triggers the convection;
- silicon, which contributes about 10% at temperatures below 10 MK.
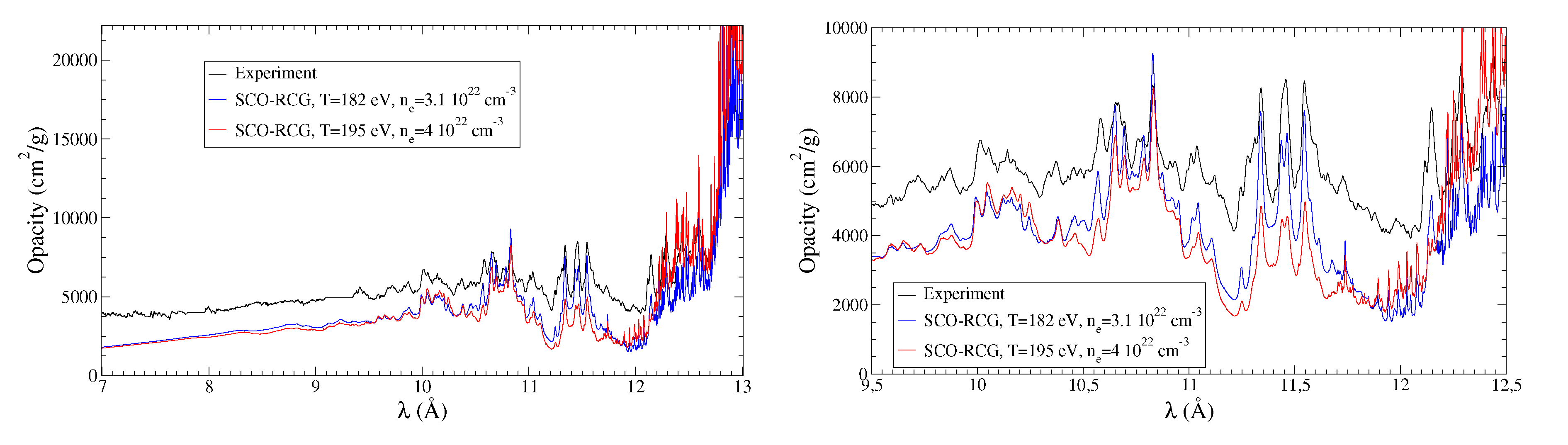
5. Attempts to Understand the Enigmatic Photo-Absorption Experiment on Iron Performed by Bailey et al. at Sandia National Laboratory
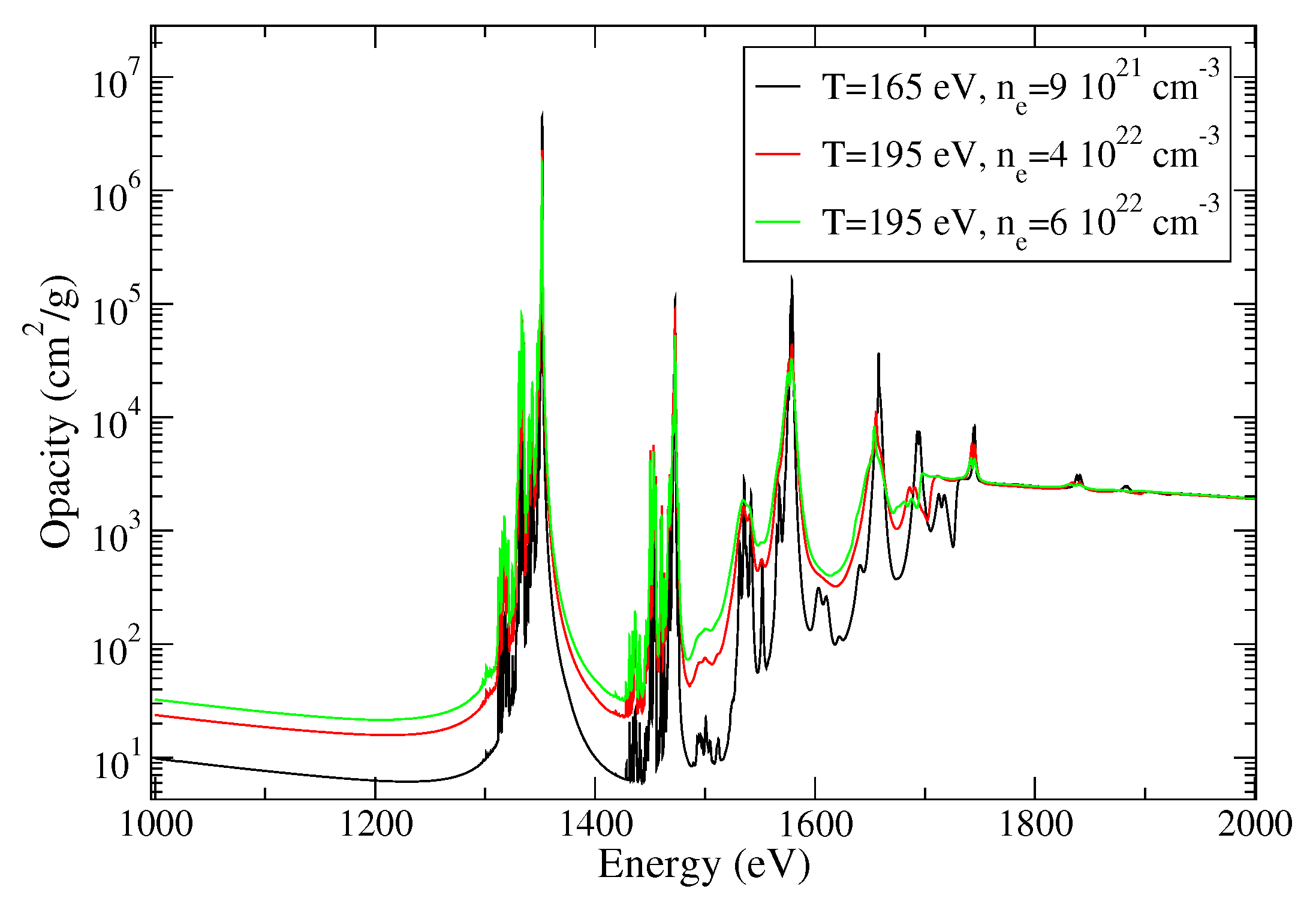
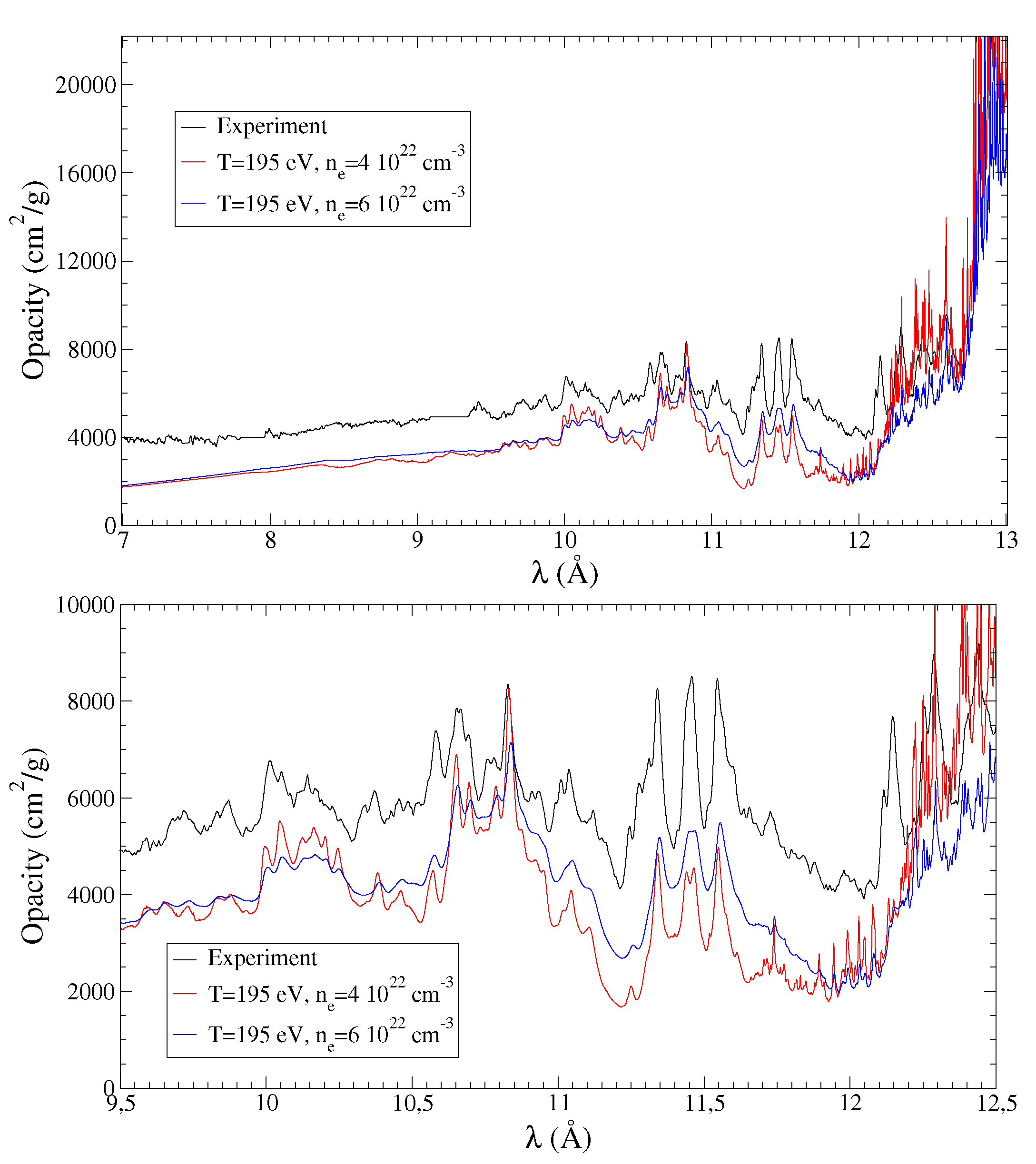
5.1. Effect of Density and Temperature
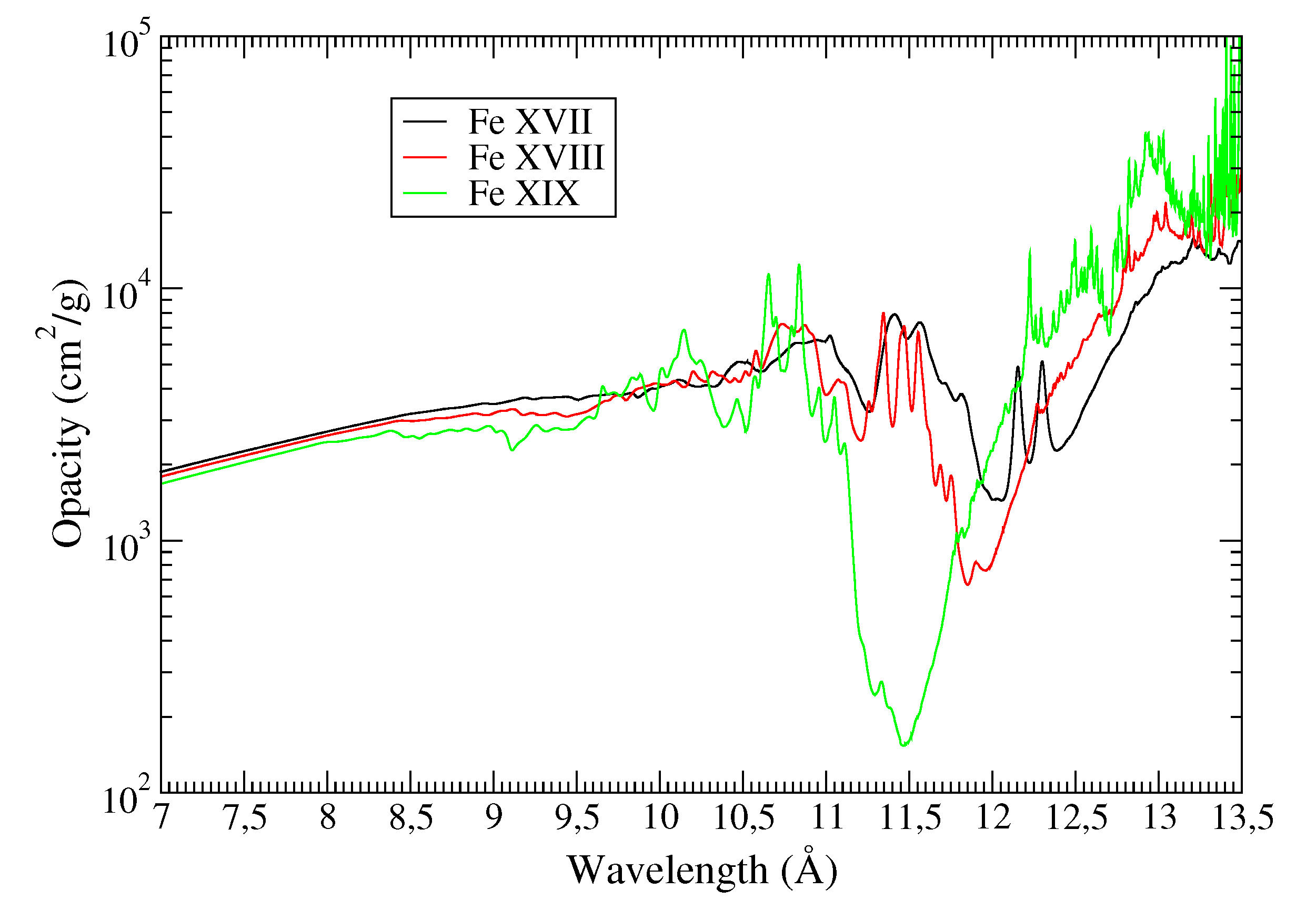
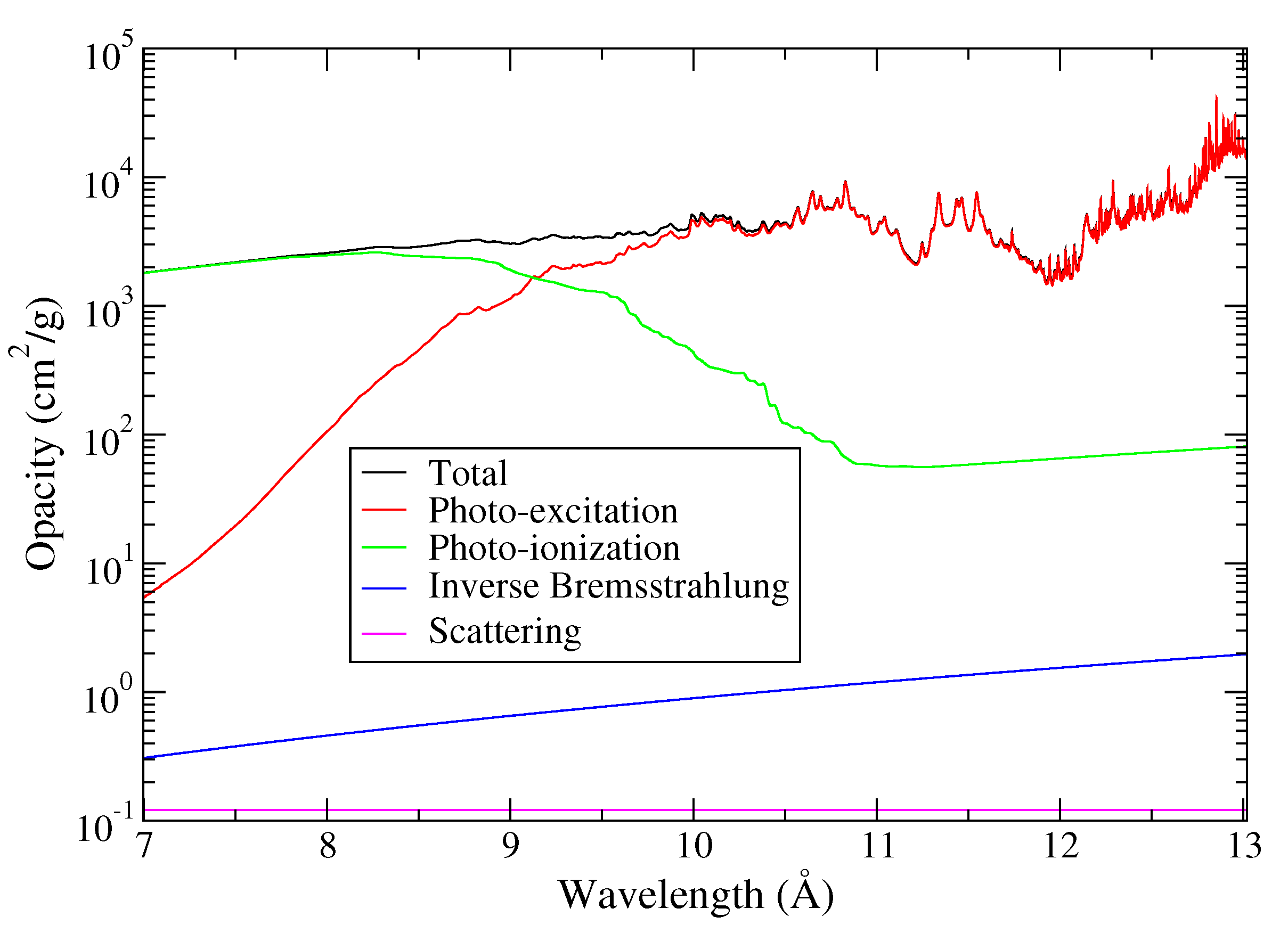
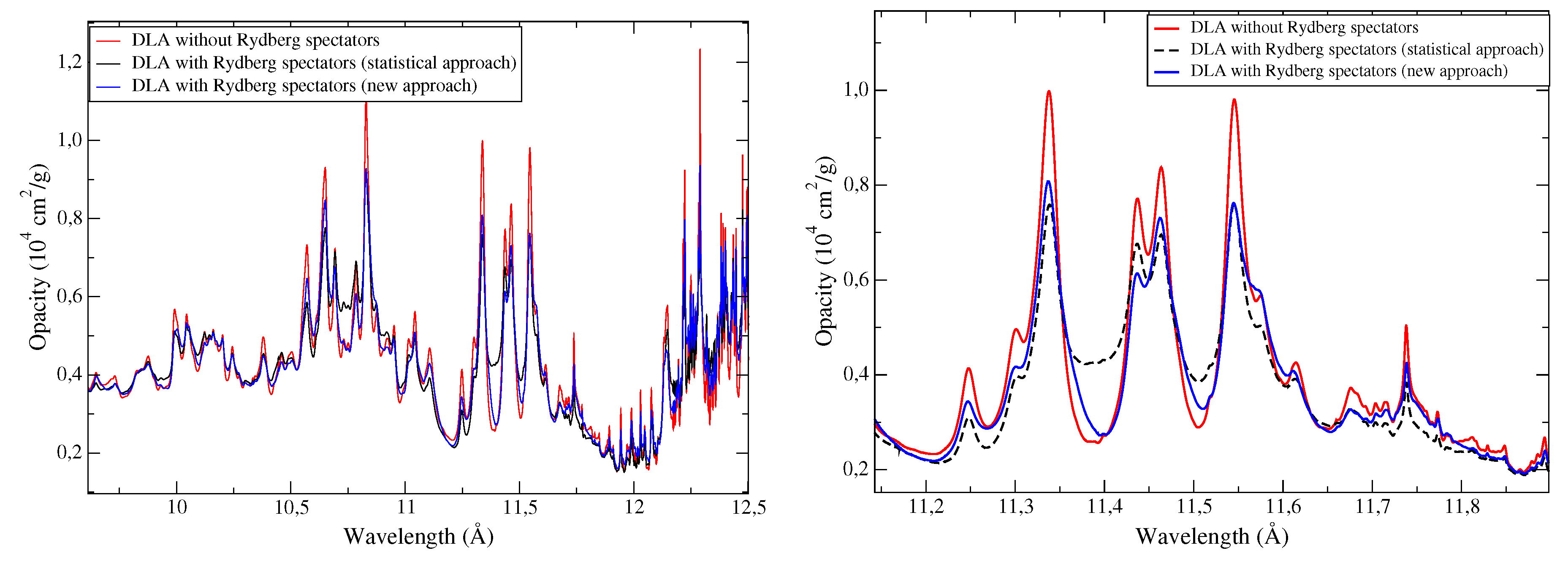
5.2. Effect of Highly Excited States
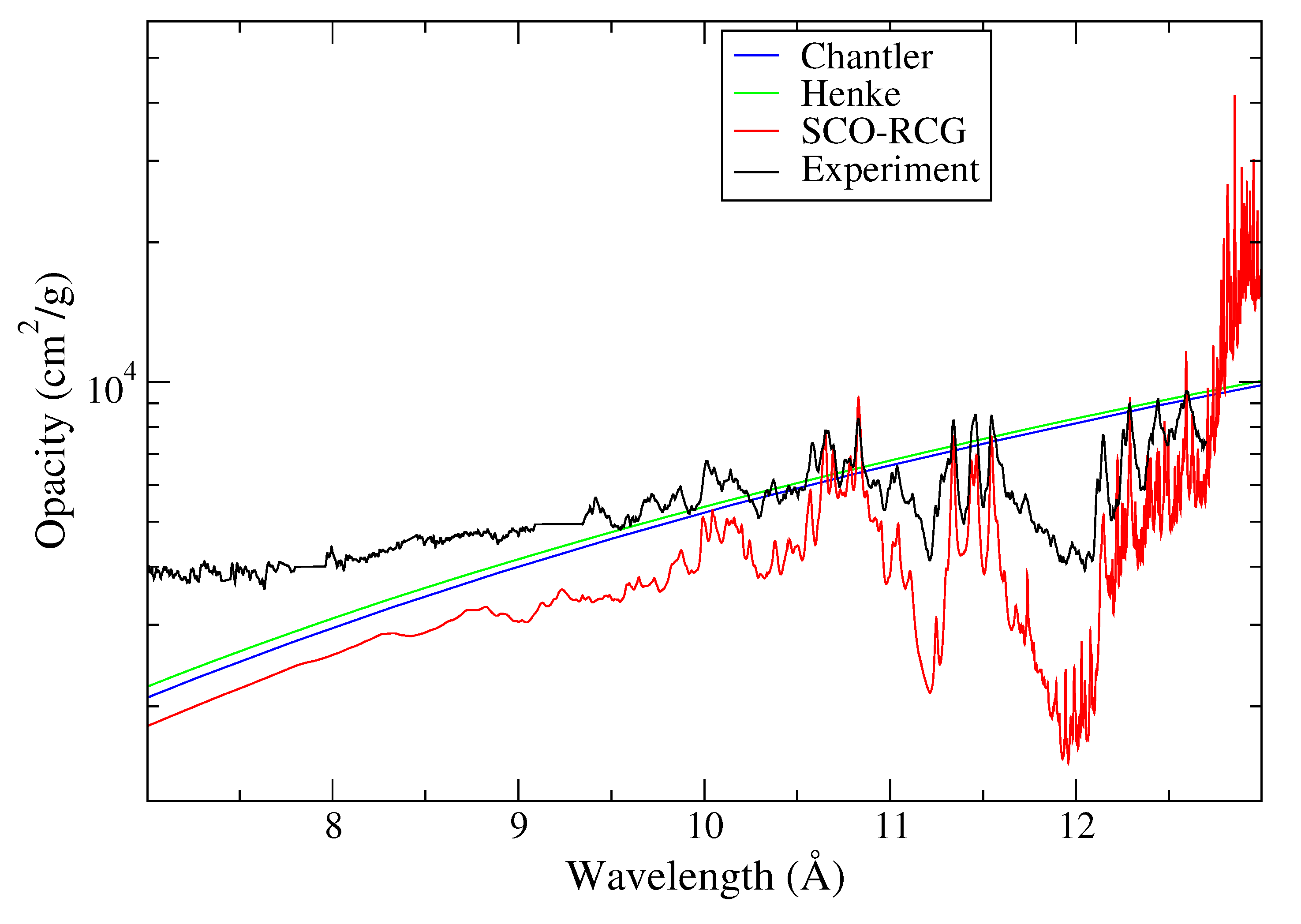
5.3. Comparison to Cold Opacity
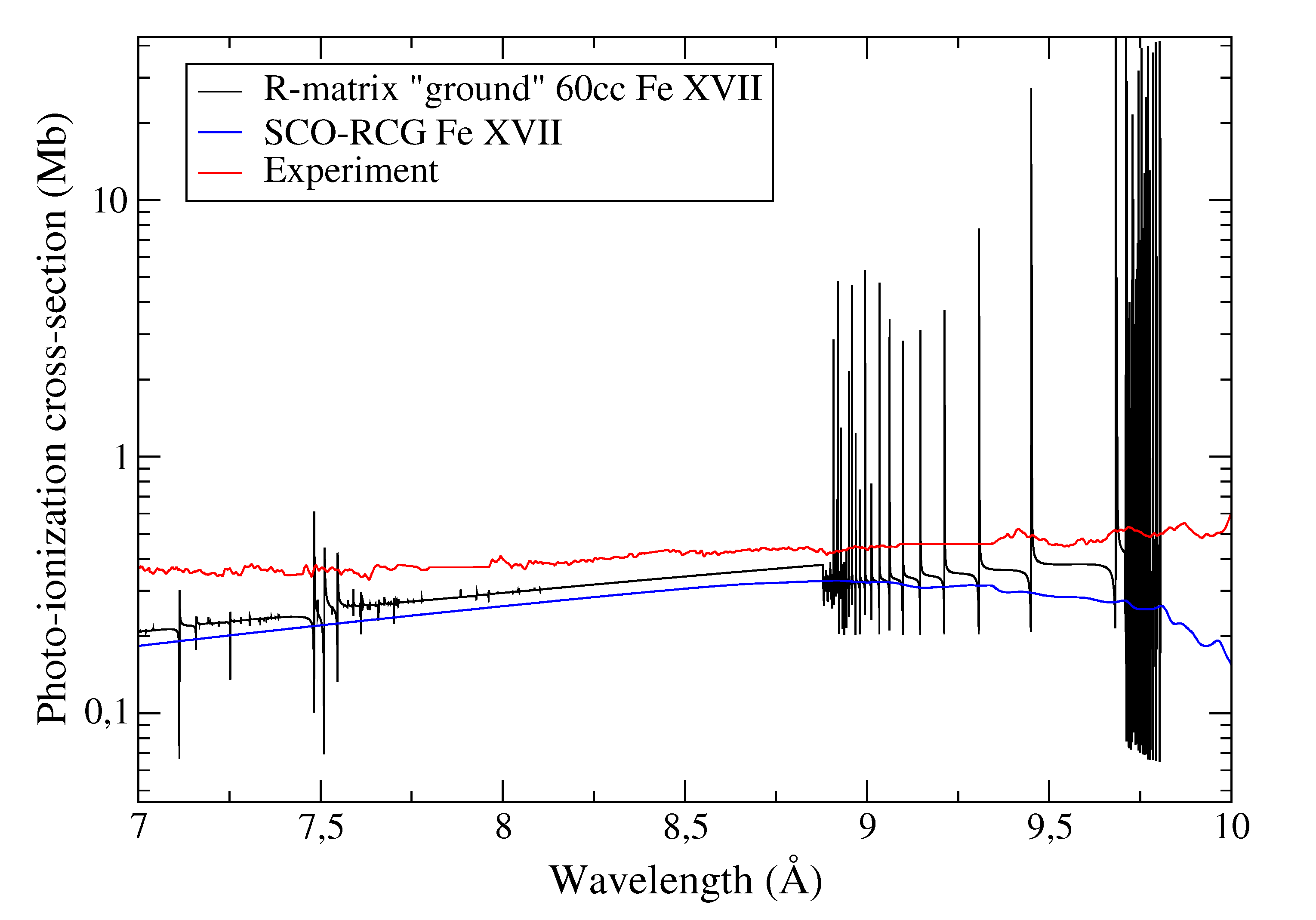
5.4. R-Matrix Photo-Ionization
5.5. Autoionization
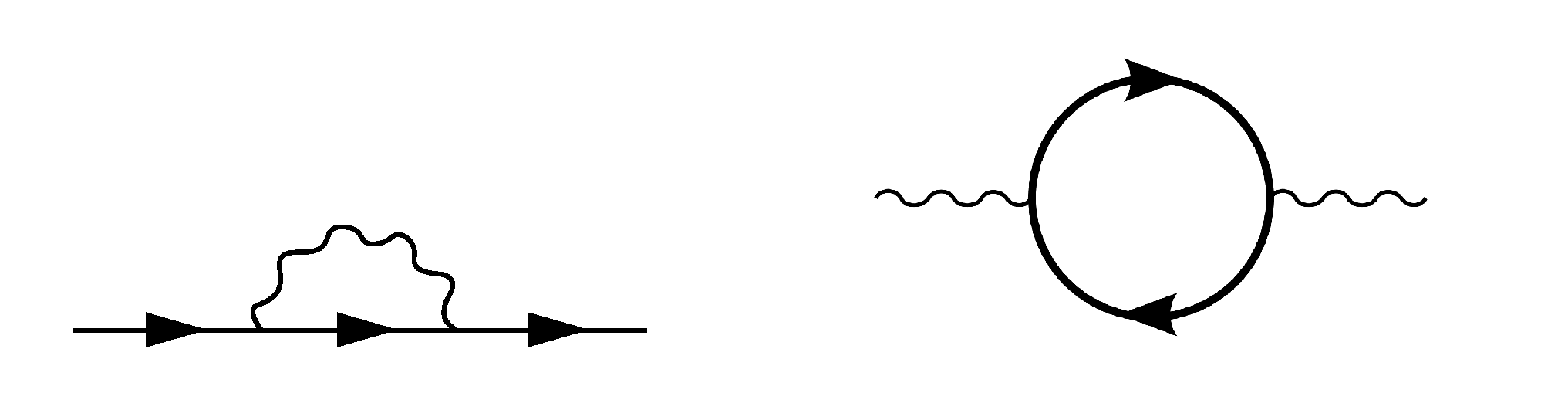
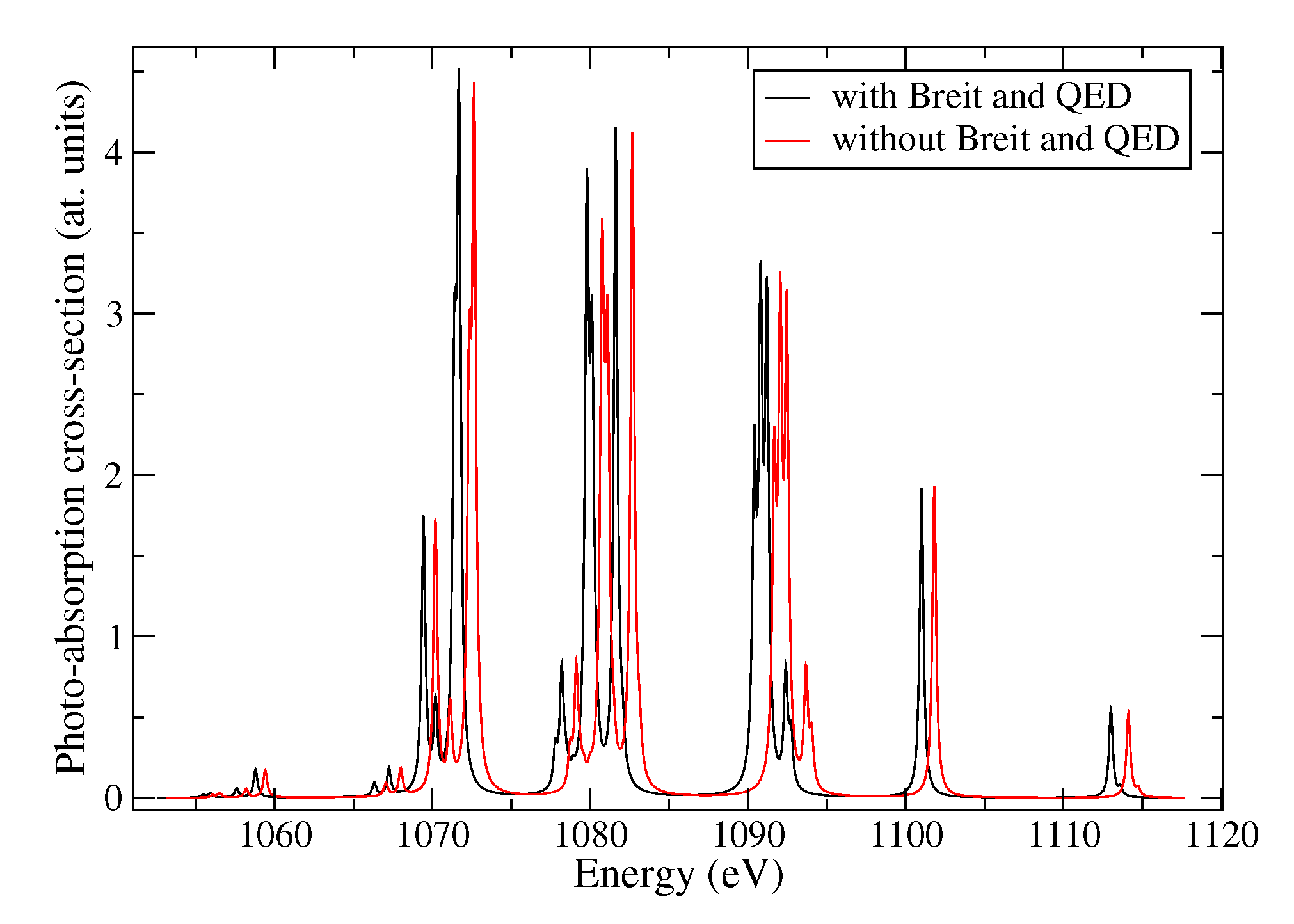
5.6. Breit Interaction and QED Corrections
6. Diagnostic Utility of the 3C/3D Line Ratio in Fe XVII: Another Issue about Iron...
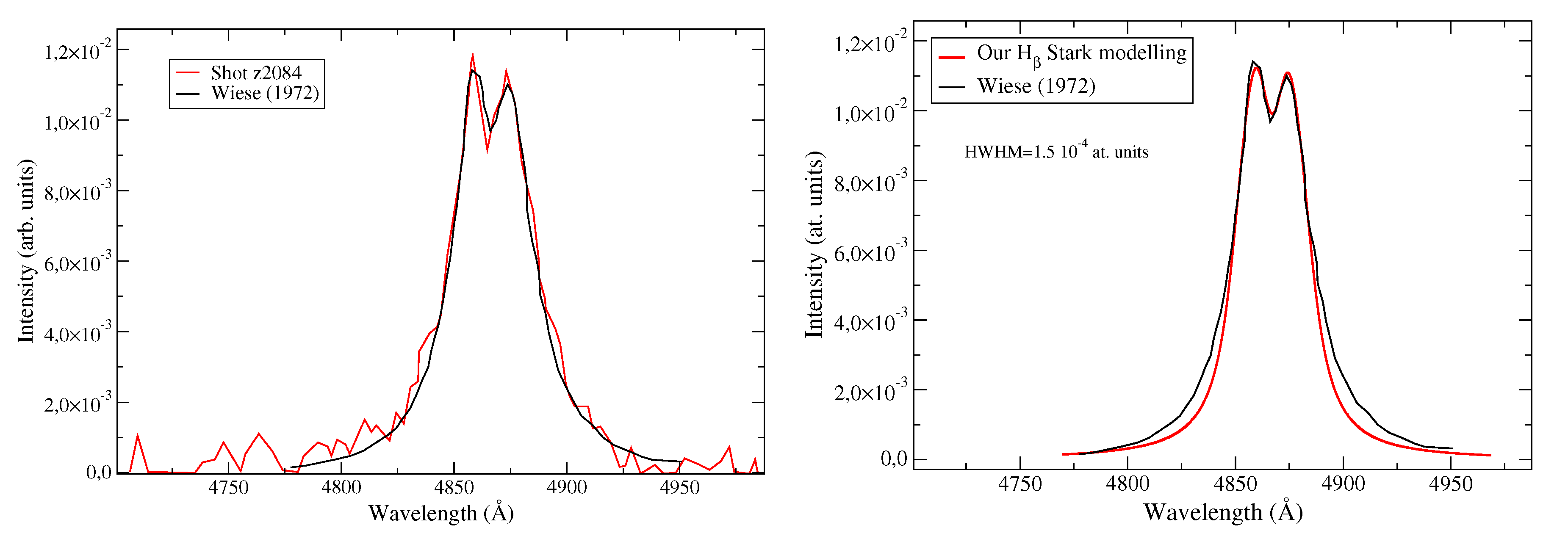
7. Stark Broadening, White Dwarfs and Balmer Lines
8. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Schlattl, H.; Weiss, A.; Raffelt, G. Helioseismological constraint on solar axion emission. Astropart. Phys. 1999, 10, 353–359. [Google Scholar] [CrossRef]
- Vinyoles, N.; Serenelli, A.; Villante, F.L.; Basu, S.; Redondo, J.; Isern, J. New axion and hidden photon constraints from a solar data global fit. J. Cosm. Astropart. Phys. 2015, 15, 1–27. [Google Scholar] [CrossRef]
- Simon, N.R. A plea for reexamining heavy element opacities in stars. Astrophys. J. 1982, 260, L87–L90. [Google Scholar] [CrossRef]
- Da Silva, S.B.; MacGowan, B.J.; Kania, D.R.; Back, C.A.; Hsieh, E.; Doyas, R.; Iglesias, C.A.; Rogers, F.J.; Lee, R.W. Absorption measurements demonstrating the importance of Δn=0 transitions in the opacity of iron. Phys. Rev. Lett. 1992, 69, 438–441. [Google Scholar] [CrossRef] [PubMed]
- Balona, L.A.; Dziembowski, W.A.; Pamyatnykh, A.A. The structure of the instability strip and mode identification for β Cep stars in three young open clusters. MNRAS 1997, 289, 25–36. [Google Scholar] [CrossRef]
- Eddington, A.S. Theories of Cepheid variation. Observatory 1926, 49, 88. [Google Scholar]
- Eddington, A.S. The Internal Composition of Stars; Cambridge University Press: Cambridge, UK, 1926. [Google Scholar]
- Asplund, M.; Grevesse, N.; Sauval, A.; Scott, P. The chemical composition of the Sun. A & A 2009, 47, 481–522. [Google Scholar]
- Bailey, J.E.; Rochau, G.A.; Hanse, S.B.; Nash, T.J.; Nielsen, D.S.; Lake, P.W.; Iglesias, C.A.; Mancini, R.C.; MacFarlane, J.J.; Golovkin, I.; et al. Experimental Investigation of Iron Plasma Opacity Models. AIP Conf. Proc. 2009, 1161, 40. [Google Scholar]
- Bailey, J.E.; Nagayama, T.; Loisel, G.P.; Rochau, G.A.; Blancard, C.; Colgan, J.; Cossé, P.; Faussurier, G.; Fontes, C.J.; Gilleron, F.; et al. A higher-than-predicted measurement of iron opacity at solar interior temperatures. Nature 2015, 517, 56–59. [Google Scholar] [CrossRef] [PubMed]
- Paerels, F.B.S.; Kahn, S.M. High-resolution X-ray spectroscopy with Chandra and XMM-Newton. Annu. Rev. Astron. Astrophys. 2003, 41, 291–342. [Google Scholar] [CrossRef]
- Wiese, W.L.; Kelleher, D.E.; Paquette, D.R. Detailed study of the Stark broadening of Balmer lines in a high-density plasma. Phys. Rev. A 1972, 6, 1132–1153. [Google Scholar] [CrossRef]
- Spiegel, E.A.; Zahn, J.-P. The solar tachocline. A & A 1992, 265, 106–114. [Google Scholar]
- Mayer, H. Methods of Opacity Calculations; Los Alamos Scientific Laboratory Report. LA 647; Los Alamos Scientific Laboratory: Los Alamos, NM, USA, 1947. [Google Scholar]
- Pain, J.-C.; Gilleron, F.; Porcherot, Q.; Blenski, T. The hybrid detailed/statistical opacity code SCO-RCG: New developments and applications. AIP Conf. Proc. 2017, 1811, 190010. [Google Scholar]
- Porcherot, Q.; Pain, J.-C.; Gilleron, F.; Blenski, T. A consistent approach for mixed detailed and statistical calculation of opacities in hot plasmas. High Energy Density Phys. 2011, 7, 234–239. [Google Scholar] [CrossRef]
- Pain, J.-C.; Gilleron, F. Accounting for highly excited states in detailed opacity calculations. High Energy Density Phys. 2015, 15, 30–45. [Google Scholar] [CrossRef]
- Pain, J.-C.; Gilleron, F.; Blenski, T. Detailed computation of hot-plasma atomic spectra. Laser Part. Beams 2015, 33, 201–210. [Google Scholar] [CrossRef]
- Blenski, T.; Grimaldi, A.; Perrot, F. A superconfiguration code based on the local density approximation. J. Quant. Spectrosc. Radiat. Transfer 2000, 65, 91–100. [Google Scholar] [CrossRef]
- Cowan, R.D. The Theory of Atomic Structure and Spectra; University of California Press: Berkeley, CA, USA, 1981. [Google Scholar]
- Perrot, F.; Blenski, T. Electronic structure and statistical mechanics of ionic configurations in hot plasmas. J. Phys. IV France 2000, 10, 474–480. [Google Scholar] [CrossRef]
- Bauche-Arnoult, C.; Bauche, J.; Klapisch, M. Variance of the distributions of energy levels and of the transition arrays in atomic spectra. Phys. Rev. A 1979, 20, 2424–2439. [Google Scholar] [CrossRef]
- Bauche-Arnoult, C.; Bauche, J.; Klapisch, M. Variance of the distributions of energy levels and of the transition arrays in atomic spectra. II. Configurations with more than two open subshells. Phys. Rev. A 1982, 25, 2641–2646. [Google Scholar] [CrossRef]
- Bauche-Arnoult, C.; Bauche, J.; Klapisch, M. Variance of the distributions of energy levels and of the transition arrays in atomic spectra. III. Case of spin-orbit-split arrays. Phys. Rev. A 1985, 31, 2248–2259. [Google Scholar] [CrossRef]
- Bar Shalom, A.; Oreg, J.; Goldstein, W.J.; Shvarts, D.; Zigler, A. Super-transition-arrays: A model for the spectral analysis of hot, dense plasma. Phys. Rev. A 1989, 40, 3183–3193. [Google Scholar] [CrossRef]
- Kurzweil, Y.; Hazak, G. Summation of the spectra of all partially resolved transition arrays in a supertransition array. Phys. Rev. A 2016, 94, 053210. [Google Scholar] [CrossRef] [PubMed]
- Davidson, S.J.; Foster, J.M.; Smith, C.C.; Warburton, K.A.; Rose, S.J. Investigation of the opacity of hot, dense aluminum in the region of its K edge. Appl. Phys. Lett. 1988, 52, 847–849. [Google Scholar] [CrossRef]
- Winhart, G.; Eidmann, K.; Iglesias, C.A.; Bar-shalom, A.; Mínguez, E.; Rose, S.J. XUV opacity measurements and comparison with models. J. Quant. Spectrosc. Radiat. Transfer 1995, 54, 437–446. [Google Scholar] [CrossRef]
- Winhart, G.; Eidmann, K.; Iglesias, C.A.; Bar-shalom, A. Measurements of extreme uv opacities of hot dense Al, Fe and Ho. Phys. Rev. E 1996, 53, R1332–R1335. [Google Scholar] [CrossRef]
- Dozières, M.; Thais, F.; Bastiani-Ceccotti, S.; Blenski, T.; Fariaut, J.; Fölsner, W.; Gilleron, F.; Khaghani, D.; Pain, J.-C.; Reverdin, C.; et al. X-ray opacity measurements in mid-Z dense plasmas with a new target design. High Energy Density Phys. 2015, 17, 231–239. [Google Scholar] [CrossRef]
- Bailey, J.E.; Arnault, P.; Blenski, T.; Dejonghe, G.; Peyrusse, O.; MacFarlane, J.J.; Mancini, R.C.; Cuneo, M.E.; Nielsen, D.S.; Rochau, G.A. Opacity measurements of tamped NaBr samples heated by z-pinch X-rays. J. Quant. Spectrosc. Radiat. Transf. 2003, 81, 31–45. [Google Scholar] [CrossRef]
- Bailey, J.E.; Chandler, G.A.; Cohen, D.; Cuneo, M.E.; Foord, M.E.; Heeter, R.F.; Jobe, D.; Lake, P.W.; MacFarlane, J.J.; Nash, T.J.; et al. Radiation science using Z-pinch X-rays. Phys. Plasmas 2002, 9, 2186–2194. [Google Scholar] [CrossRef]
- Bailey, J.E.; Rochau, G.A.; Iglesias, C.A.; Abdallah, J., Jr.; MacFarlane, J.J.; Golovkin, I.; Wang, P.; Mancini, R.C.; Lake, P.W.; Moore, T.C.; et al. Iron-Plasma Transmission Measurements at Temperatures Above 150 eV. Phys. Rev. Lett. 2007, 99, 265002. [Google Scholar] [CrossRef] [PubMed]
- Dervieux, V.; Loupias, B.; Baton, S.; Lecherbourg, L.; Glize, K.; Rousseaux, C.; Reverdin, C.; Gremillet, L.; Blancard, C.; Silvert, V.; et al. Characterization of near-LTE, high-temperature and high-density aluminum plasmas produced by ultra-high intensity lasers. High Energy Density Phys. 2015, 16, 12–17. [Google Scholar] [CrossRef]
- Michel, E.; Baglin, A.; Auvergne, M.; Catala, C.; Samadi, R.; Baudin, F.; Apourchaux, T.; Barban, C.; Weiss, W.W.; Berthomieu, G.; et al. CoRoT Measures Solar-Like Oscillations and Granulation in Stars Hotter than the Sun. Science 2008, 322, 558–560. [Google Scholar] [CrossRef] [PubMed]
- Turck-Chièze, S.; Delahaye, F.; Gilles, D.; Loisel, G.; Piau, L. On plasma radiative properties in stellar conditions. High Energy Density Phys. 2009, 5, 132–138. [Google Scholar] [CrossRef]
- Shapley, H. On the Nature and Cause of Cepheid Variation. Astrophys. J. 1914, 40, 448–465. [Google Scholar] [CrossRef]
- Eddington, A.S. Stars, Gaseous, On the pulsations of a gaseous star. MNRAS 1918, 79, 2–22. [Google Scholar] [CrossRef]
- Fontes, C.J.; Fryer, C.L.; Hungerford, A.L.; Hakel, P.; Colgan, J.; Kilcrease, D.P.; Sherill, M.E. Relativistic opacities for astrophysical applications. High Energy Density Phys. 2015, 16, 53–59. [Google Scholar] [CrossRef]
- Colgan, J.; Kilcrease, D.P.; Magee, N.H.; Sherrill, M.E.; Abdallah, J., Jr.; Hakel, P.; Fontes, C.J.; Guzik, J.A.; Mussack, K.A. A new generation of Los Alamos opacity tables. Astrophys. J. 2016, 817, 116–125. [Google Scholar] [CrossRef]
- Turck-Chièze, S.; Le Pennec, M.; Ducret, J.E.; Colgan, J.; Kilcrease, D.P.; Fontes, C.J.; Magee, N.; Gilleron, F.; Pain, J.C. Detailed opacity comparison for an improved stellar modeling of the envelopes of massive stars. Astrophys. J. 2016, 823, 78–92. [Google Scholar] [CrossRef]
- Seaton, M.J. Atomic Data for opacity calculations. I. General description. J. Phys. B 1987, 20, 6363–6378. [Google Scholar] [CrossRef]
- The Opacity Project Team. The Opacity Project, Vol. 1 (1995); Institute of Physics Publishing: Bristol, UK, 1996; Volume 2. [Google Scholar]
- TOPbase. Available online: http://cdsweb.u-strasbg.fr/topbase/topbase.html (accessed on 19 May 2017).
- OPServer. Available online: http://opacities.osc.edu (accessed on 19 May 2017).
- Iglesias, C.A.; Rogers, F.J. Updated OPAL opacities. Astrophys. J. 1996, 464, 943–953. [Google Scholar] [CrossRef]
- Daszynska-Daszkiewicz, J.; Walczak, P. Complex asteroseismology of the β Cep/slowly pulsating B-type pulsator ν Eridani: Constraints on opacities. MNRAS 2010, 403, 496–504. [Google Scholar] [CrossRef]
- Salmon, S.; Montalbán, J.; Morel, T.; Miglio, A.; Dupret, M.A.; Noels, A. Testing the effects of opacity and the chemical mixture on the excitation of pulsations in B stars of the Magellanic clouds. MNRAS 2012, 422, 3460–3474. [Google Scholar] [CrossRef]
- Iglesias, C.A. Iron-group opacities for B-stars. MNRAS 2015, 450, 2–9. [Google Scholar] [CrossRef]
- Moravveji, E. The impact of enhanced iron opacity on massive star pulsations: updated instability strip. MNRAS 2015, 455, L67–L71. [Google Scholar]
- Paxton, B.; Marchant, P.; Schwab, J.; Bauer, E.B.; Bildsten, L.; Cantiello, M.; Dessart, L.; Farmer, R.; Hu, H.; Langer, N.; et al. Modules for Experiments in Stellar Astrophysics (MESA): Binaries, Pulsations, and Explosions. Astrophys. J. 2015, 220, 15–58. [Google Scholar] [CrossRef]
- Langer, N.; Kudritzki, R.P. The spectroscopic Hertzsprung-Russell diagram. A & A 2014, 564, A52–A59. [Google Scholar]
- Asplund, M.; Grevesse, N.; Sauval, J. Cosmic Abundances as Records of Stellar Evolution and Nucleosynthesis. ASP Conf. Ser. 2005, 336, 25–38. [Google Scholar]
- Yang, W. Solar models with new low metal abundances. Astrophys. J. 2016, 821, 108–117. [Google Scholar] [CrossRef]
- Turck-Chièze, S.; Nghiem, P.; Couvidat, S.; Turcotte, S. Solar Internal Composition and Nuclear Reaction Rates in the Light of Helioseismology. Sol. Phys. 2001, 200, 323–342. [Google Scholar] [CrossRef]
- Turck-Chièze, S.; Couvidat, S.; Kosovichev, A.G.; Gabriel, A.H.; Berthomieu, G.; Brun, A.S.; Christensen-Dalsgaard, J.; Garciá, R.A.; Gough, D.O.; Provost, J.; et al. Solar neutrino emission deduced from a seismic model. Astrophys. J. 2001, 555, L69–L73. [Google Scholar] [CrossRef]
- Antia, H.M.; Basu, S. Determining solar abundances using heliosismology. Astrophys. J. 2006, 644, 1292–1298. [Google Scholar] [CrossRef]
- Guzik, J.A. Problems for the standard solar model arising from the new solar mixture. Mem. Soc. Astron. Ital. 2008, 79, 481–489. [Google Scholar]
- Serenelli, A.M.; Basu, S.; Ferguson, J.W.; Asplund, M. New solar composition: the problem with solar models revisited. Astrophys. J. 2009, 705, L123–L127. [Google Scholar] [CrossRef]
- Turck-Chièze, S.; Couvidat, S. Solar neutrinos, helioseismology and the solar internal dynamics. Rep. Prog. Phys. 2011, 74, 086901. [Google Scholar] [CrossRef]
- Basu, S.; Antia, M.H. Helioseismology and solar abundances. Phys. Rep. 2008, 457, 217–284. [Google Scholar] [CrossRef]
- Mussack, K.; Däppen, W. Dynamic screening correction for solar p − p reaction rates. Astrophys. J. 2011, 729, 96–101. [Google Scholar] [CrossRef]
- Fraser, G.W.; Read, A.M.; Sembay, S.; Carter, J.A.; Schyns, E. Potential solar axion signatures in X-ray observations with the XMM-Newton observatory. Mon. Not. R. Astron. Soc. 2014, 445, 2146–2168. [Google Scholar] [CrossRef]
- Redondo, J. Solar axion flux from the axion-electron coupling. J. Cosmol. Astropart. Phys. 2013, 12, 008. [Google Scholar] [CrossRef]
- Xiong, G.; Yang, J.; Zhang, J.; Hu, Z.; Zhao, Y.; Qing, B.; Yang, G.; Wei, M.; Yi, R.; Song, T.; et al. Opacity measurement and theoretical investigation of hot silicon plasma. Astrophys. J. 2016, 816, 36–46. [Google Scholar] [CrossRef]
- Savin, D.W.; Brickhouse, N.S.; Cowan, J.J.; Drake, R.P.; Federman, S.R.; Ferland, G.J.; Frank, A; Gudipati, M.S.; Haxton, W.C.; Herbst, E.; et al. The impact of recent advances in laboratory astrophysics on our understanding of the cosmos. Rep. Prog. Phys. 2012, 036901, 1–36. [Google Scholar] [CrossRef] [PubMed]
- Wei, H.G.; Shi, J.R.; Zhao, Z.Y.; Dong, Q.-L.; Li, Y.-T.; Wang, S.-J.; Zhang, J.; Liang, Z.; Zhang, J.-Y.; Wen, T.-S.; et al. Opacity studies of silicon in radiatively heated plasma. Astrophys. J. 2008, 683, 577–583. [Google Scholar] [CrossRef]
- Nagayama, T.; Bailey, J.E.; Mancini, R.C.; Iglesias, C.A.; Hansen, S.B.; Blancard, C.; Chung, H.K.; Colgan, J.; Cossé, P.; Faussurier, G.; et al. Model uncertainties of local-thermodynamic-equilibrium K-shell spectroscopy. High Energy Density Phys. 2016, 20, 17–22. [Google Scholar] [CrossRef]
- Iglesias, C.A.; Sonnad, V. Partially resolved transition array model for atomic spectra. High Energy Density Phys. 2012, 8, 154–160. [Google Scholar] [CrossRef]
- Iglesias, C.A. Partially resolved transition array model in intermediate coupling. High Energy Density Phys. 2012, 8, 260–265. [Google Scholar] [CrossRef]
- Wilson, B.G.; Iglesias, C.; Chen, M.H. Partially resolved super transition array method. High Energy Density Phys. 2015, 14, 67–73. [Google Scholar] [CrossRef]
- Henke, B.L.; Gullikson, E.M.; Davis, J.C. X-Ray Interactions: Photoabsorption, Scattering, Transmission, and Reflection at E = 50–30,000 eV, Z = 1–92. At. Data Nucl. Data Tables 1993, 54, 181–342. [Google Scholar] [CrossRef]
- Chantler, C.T. Theoretical form factor: attenuation and scattering tabulation for Z = 1–92 from E = 1–10 eV to E = 0.4–1.0 Mev. J. Phys. Chem. Ref. Data 1995, 24, 71–643. [Google Scholar] [CrossRef]
- Iglesias, C.A. Enigmatic photon absorption in plasmas near solar interior conditions. High Energy Density Phys. 2015, 15, 4–7. [Google Scholar] [CrossRef]
- Nahar, S.N.; Pradhan, A.K. Large Enhancement in High-Energy Photoionization of Fe XVII and Missing Continuum Plasma Opacity. Phys. Rev. Lett. 2016, 116, 235003. [Google Scholar] [CrossRef] [PubMed]
- Nahar, S.N.; Pradhan, A.K.; Chen, G.-X.; Eissner, W. Highly excited core resonances in photoionization of Fe XVII: Implications for plasma opacities. Phys. Rev. A 2011, 83, 053417. [Google Scholar] [CrossRef]
- Iglesias, C.A.; Hansen, S.B.; Blancard, C.; Colgan, J.; Cossé, P.; Faussurier, G.; Fontes, C.J.; Gilleron, F.; Kilcrease, D.P.; Pain, J.-C.; et al. Fe XVII opacity at solar interior conditions. Astrophys. J. 2017, in press. [Google Scholar] [CrossRef]
- Blancard, C.; Colgan, J.; Cossé, P.; Faussurier, G.; Fontes, C.J.; Gilleron, F.; Golovkin, I.; Hansen, S.B.; Iglesias, C.A.; Kilcrease, D.P.; et al. Comment on “Large Enhancement in High-Energy Photoionization of Fe XVII and Missing Continuum Plasma Opacity”. Phys. Rev. Lett. 2016, 117, 249501. [Google Scholar] [CrossRef] [PubMed]
- Thomas, W. Über die Zahl der Dispersionelektronen, die einem stationären Zustande zugeordnet sind. Naturwissenschaften 1925, 13, 627. [Google Scholar] [CrossRef]
- Kuhn, W. Über die Gesamtstärke der von einem Zustande ausgehenden Absorptionslinien. Z. Phys. 1925, 33, 408–412. [Google Scholar] [CrossRef]
- Nahar, S.N.; Pradhan, A.K. Reply to Comment on “Large Enhancement in High-Energy Photoionization of Fe XVII and Missing Continuum Plasma Opacity”. Phys. Rev. Lett. 2016, 117, 249502. [Google Scholar] [CrossRef] [PubMed]
- Blancard, C.; Cossé, P.; Faussurier, G. Solar mixture opacity calculations using detailed configuration and level accounting treatments. Astrophys. J. 2012, 745, 10–16. [Google Scholar] [CrossRef]
- Mondet, G.; Blancard, C.; Cossé, P.; Faussurier, G. Opacity Calculations for Solar Mixtures. Astrophys. J. Suppl. Ser. 2015, 220, 2–8. [Google Scholar] [CrossRef]
- Le Pennec, M.; Turck-Chièze, S.; Salmon, S.; Blancard, C.; Cossé, P.; Faussurier, G.; Mondet, G. First new solar models with OPAS opacity tables. Astrophys. J. 2015, 813, L42–L47. [Google Scholar] [CrossRef]
- Hansen, S.B.; Bauche, J.; Bauche-Arnoult, C.; Gu, M.F. Hybrid atomic models for spectroscopic plasma diagnostics. High Energy Density Phys. 2007, 3, 109–114. [Google Scholar] [CrossRef]
- Iglesias, C.A.; Chen, M.H.; Sonnad, V.; Wilson, B.G. A new detailed term accounting opacity code for mid-Z elements: TOPAZ. J. Quant. Spectrosc. Radiat. Transf. 2003, 81, 227–236. [Google Scholar] [CrossRef]
- Iglesias, C.A.; Chen, M.H.; Isaacs, W.A.; Sonnad, V.; Wilson, B.G. A New Detailed Term Accounting Opacity Code: TOPAZ. AIP Conf. Proc. 2004, 730, 161–167. [Google Scholar]
- Sampson, D.H.; Zhang, H.L.; Fontes, C.J. A fully relativistic approach for calculating atomic data for highly charged ions. Phys. Rep. 2009, 477, 111–214. [Google Scholar] [CrossRef]
- Gao, C.; Zeng, J. Validity of analytical formulas for autoionization and dielectronic capture rates used in collisional-radiative codes. Phys. Rev. A 2010, 82, 062515. [Google Scholar] [CrossRef]
- Bruneau, J. MCDF calculation of argon Auger process. J. Phys. B At. Mol. Phys. 1983, 16, 4135–4151. [Google Scholar] [CrossRef]
- Bruneau, J. Correlation and relaxation effects in ns2 − nsnp transitions. J. Phys. B At. Mol. Phys. 1984, 17, 3009–3028. [Google Scholar] [CrossRef]
- Gu, M.F. The flexible atomic code. Can. J. Phys. 2008, 86, 675–689. [Google Scholar] [CrossRef]
- Hansen, S.B. Balancing Detail and Completeness in Collisional-Radiative Models. In Modern Methods in collisional-Radiative Modeling of Plasmas; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Grant, I.P. Gauge invariance and relativistic radiative transitions. J. Phys. B Atom. Mol. Phys. 1974, 7, 1458–1475. [Google Scholar] [CrossRef]
- Grant, I.P. Relativistic Quantum Theory of Atoms and Molecules: Theory and Computation; Springer Series on Atomic, Optical, and Plasma Physics; Springer: New York, NY, USA, 2007. [Google Scholar]
- Uehling, E.A. Polarization effects in the positron theory. Phys. Rev. 1935, 48, 55–63. [Google Scholar] [CrossRef]
- Frolov, A.M.; Wardlaw, D.M. Analytical formula for the Uehling potential. Eur. Phys. J. B 2012, 85, 348–351. [Google Scholar] [CrossRef]
- Mohr, P.J. Numerical evaluation of the 1s1/2 state radiative level shift. Ann. Phys. 1974, 88, 52–87. [Google Scholar] [CrossRef]
- Erickson, G.W. Energy levels of one-electron atoms. J. Phys. Chem. Data 1977, 6, 831–839. [Google Scholar] [CrossRef]
- Mohr, P.J. Lamb shift in a strong Coulomb potential. Phys. Rev. Lett. 1975, 34, 105–120. [Google Scholar] [CrossRef]
- Mohr, P.J. Self energy of the n = 2 state in a strong Coulomb field. Phys. Rev. A 1982, 26, 2338–2354. [Google Scholar] [CrossRef]
- Curtis, L.J. Explicit functional approximations for the Z dependence of self-energy radiative corrections in hydrogen-like atoms. J. Phys. B 1985, 18, L651–L656. [Google Scholar] [CrossRef]
- Le Bigot, E.O.; Indelicato, P.; Mohr, P.J. QED self-energy contribution to highly excited atomic states. Phys. Rev. A 2001, 64, 052508. [Google Scholar] [CrossRef]
- Welton, T.A. Some observable effects of the quantum-mechanical fluctuations of the electromagnetic field. Phys. Rev. 1948, 74, 1157–1167. [Google Scholar] [CrossRef]
- Pain, J.-C.; Gilleron, F.; Comet, M.; Gilles, D. K-shell spectroscopy in hot plasmas: Stark effect, Breit interaction and QED corrections. AIP Conf. Proc. 2017, 1811, 040004. [Google Scholar]
- Slater, J.C. Quantum Theory of Molecules and Solids; McGraw-Hill Inc.: New York, NY, USA, 1974. [Google Scholar]
- Fournier, K.B.; Hansen, S.B. Resolution of the long-standing overprediction of the resonance to intercombination line-intensity ratio in mid-Z neonlike ions. Phys. Rev. A 2005, 71, 012717. [Google Scholar] [CrossRef]
- Bernitt, S.; Brown, G.V.; Rudolph, J.K.; Steinbrügge, R.; Graf, A.; Leutenegger, M.; Epp, S.W.; Eberle, S.; Kubiçek, K.; Mäckel, V.; et al. An unexpectedly low oscillator strength as the origin of the Fe XVII emission problem. Nature 2012, 492, 225–228. [Google Scholar] [CrossRef] [PubMed]
- Loch, S.D.; Ballance, C.P.; Li, Y.; Fogle, M.; Fontes, C.J. Non-equilibrium modeling of the Fe XVII 3C/3D line ratio in an intense X-ray free-electron laser excited plasma. Astrophys. J. 2015, 801, L13–L16. [Google Scholar] [CrossRef]
- Gabriel, A.H. Dielectronic Satellite Spectra for Highly-Charged Helium-Like Ion Lines. MNRAS 1972, 160, 99–119. [Google Scholar] [CrossRef]
- Swartz, D.A.; Sulkanen, M.E. Helium-like iron line temperature diagnostics in clusters of galaxies. Astrophys. J. 1993, 417, 487–493. [Google Scholar] [CrossRef]
- Dimitrijević, M.S.; Simić, Z.; Kovacˇević, A.; Valjarević, A.; Sahal-Bréchot, S. Stark broadening of Xe viii spectral lines. Mon. Not. R. Astron. Soc. 2015, 454, 1736–1741. [Google Scholar] [CrossRef]
- Tremblay, P.-E.; Bergeron, P. Spectroscopic analysis of DA white dwarfs: Stark broadening of hydrogen lines including nonideal effects. Astrophys. J. 2009, 696, 1755–1770. [Google Scholar] [CrossRef]
- Falcon, R.E.; Rochau, G.A.; Bailey, J.E.; Ellis, J.L.; Carlson, A.L.; Gomez, T.A.; Montgomery, M.H.; Winget, D.E.; Chen, E.Y.; Gomez, M.R.; et al. An experimental platform for creating white dwarf photospheres in the laboratory. High Energy Density Phys. 2013, 9, 82–90. [Google Scholar] [CrossRef]
- Montgomery, M.H.; Falcon, R.E.; Rochau, G.A.; Bailey, J.E.; Gomez, T.A.; Carlson, B.D.E.; Nagayama, T.; Stein, M.; Winget, D.E. An experimental platform for creating white dwarf photospheres in the laboratory: Preliminary results. High Energy Density Phys. 2015, 17, 168–174. [Google Scholar] [CrossRef]
- Pain, J.-C.; Gilleron, F.; Gilles, D. Stark effect modeling in the detailed opacity code SCO-RCG. J. Phys. Conf. Ser. 2016, 717, 012074. [Google Scholar] [CrossRef]
- Dufour, P.; Liebert, J.; Fontaine, G.; Behara, N. Rare White dwarf stars with carbon armospheres. Nature 2007, 450, 522–524. [Google Scholar] [CrossRef] [PubMed]
- Kepler, S.O.; Koester, D.; Ourique, G. A white dwarf with an oxygen atmosphere. Science 2009, 352, 67–70. [Google Scholar] [CrossRef] [PubMed]
- Gilleron, F.; Pain, J.-C. The ZEST (ZEeman-STark) Line-Shape Code. In Proceedings of the 4th Workshop on Spectral Line Shapes in Plasmas in Baden (Austria), Vienna, Austria, 20–24 March 2017.
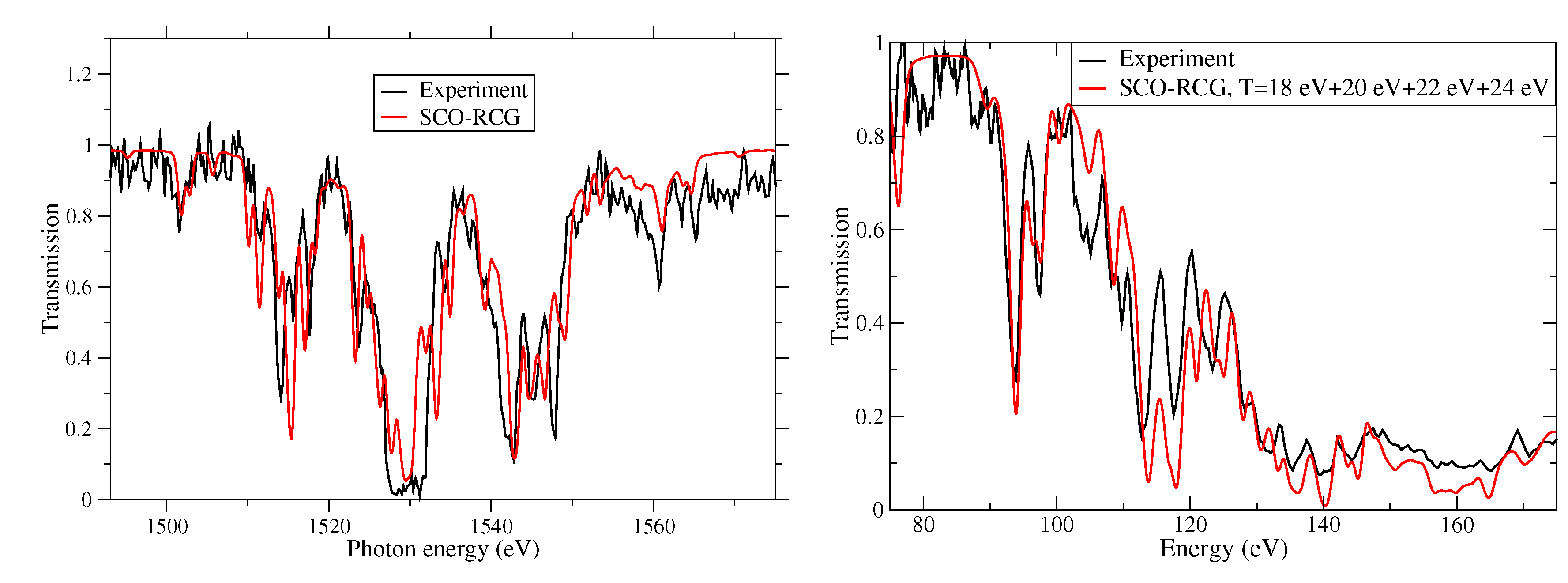
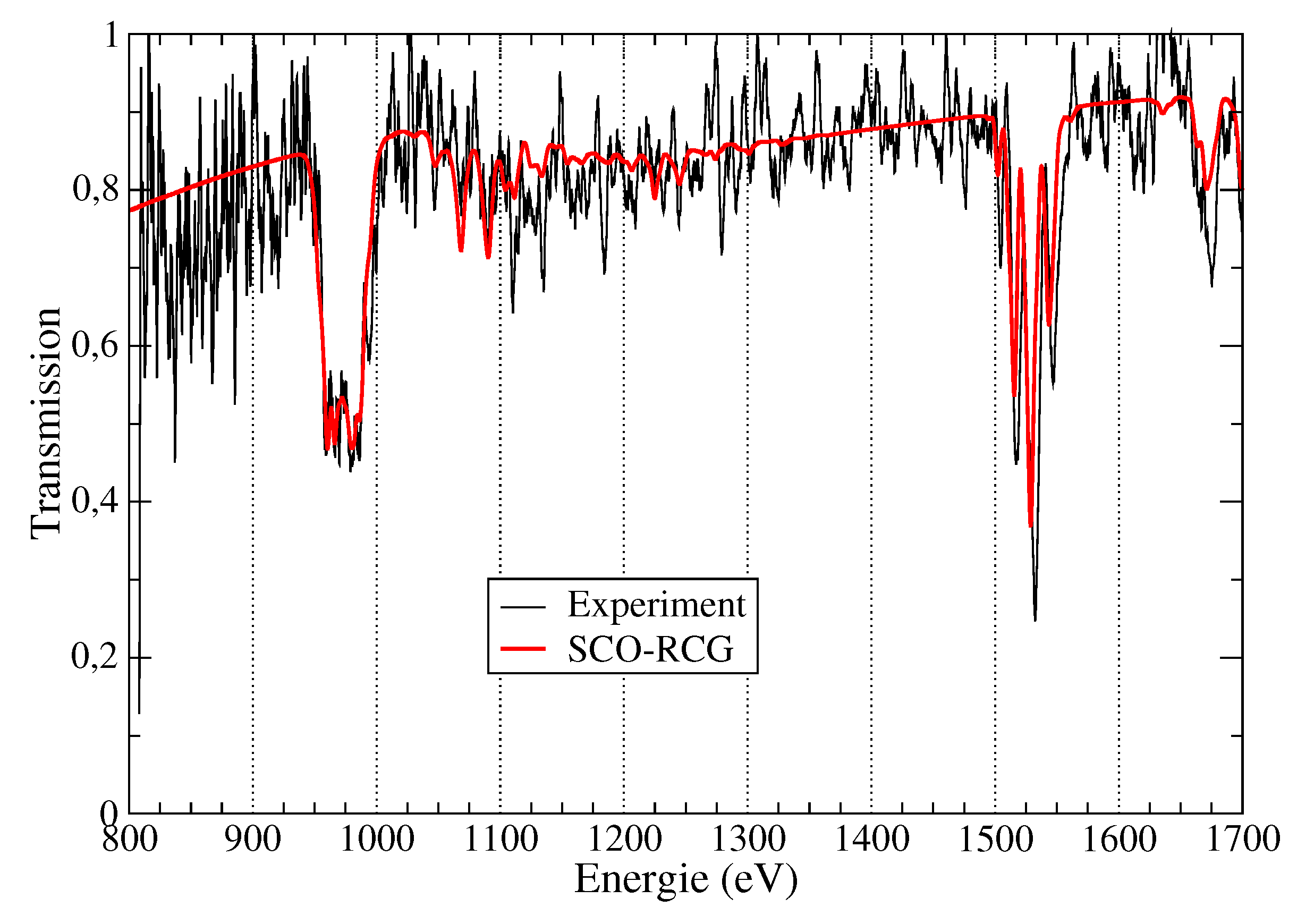
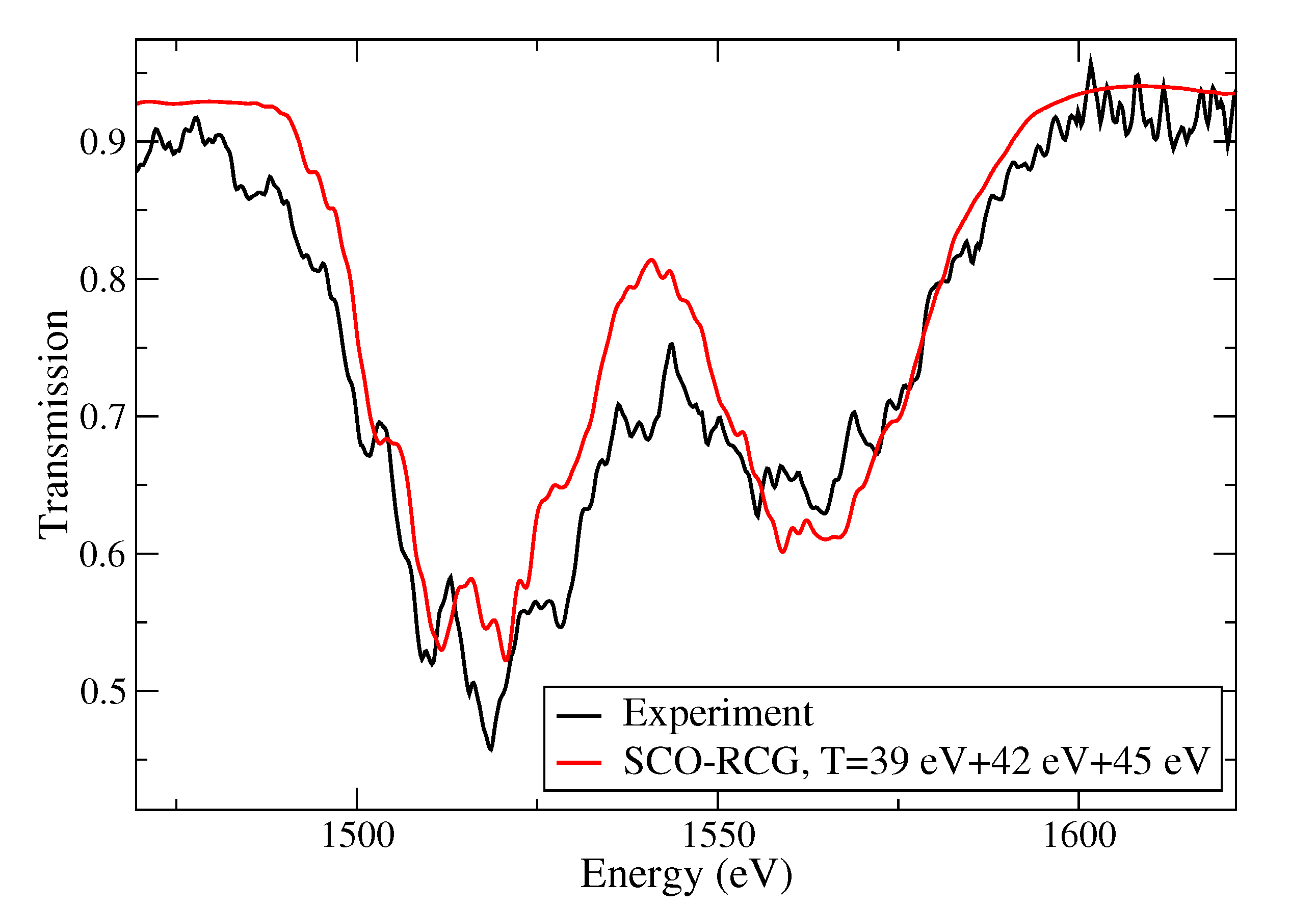

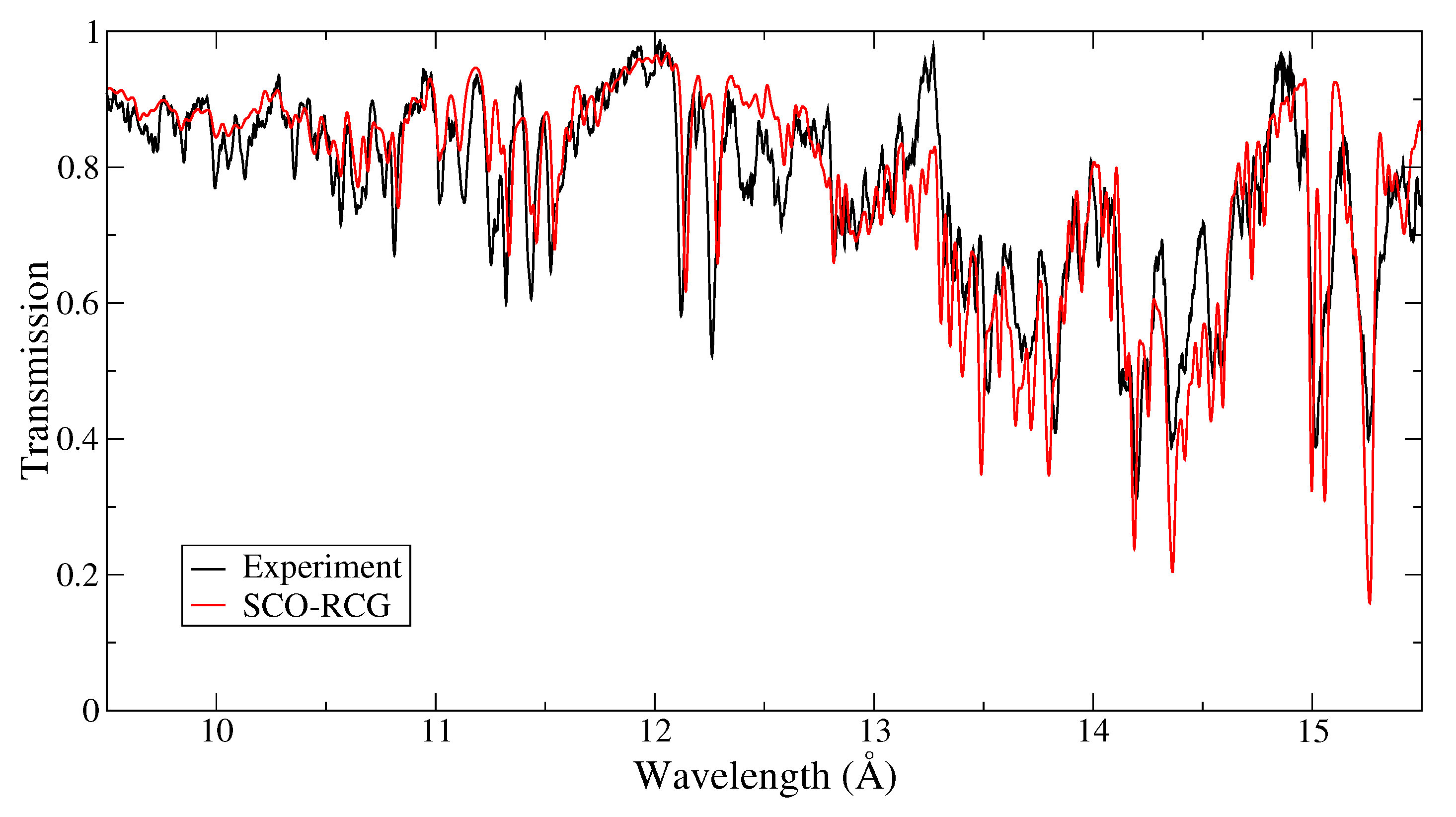
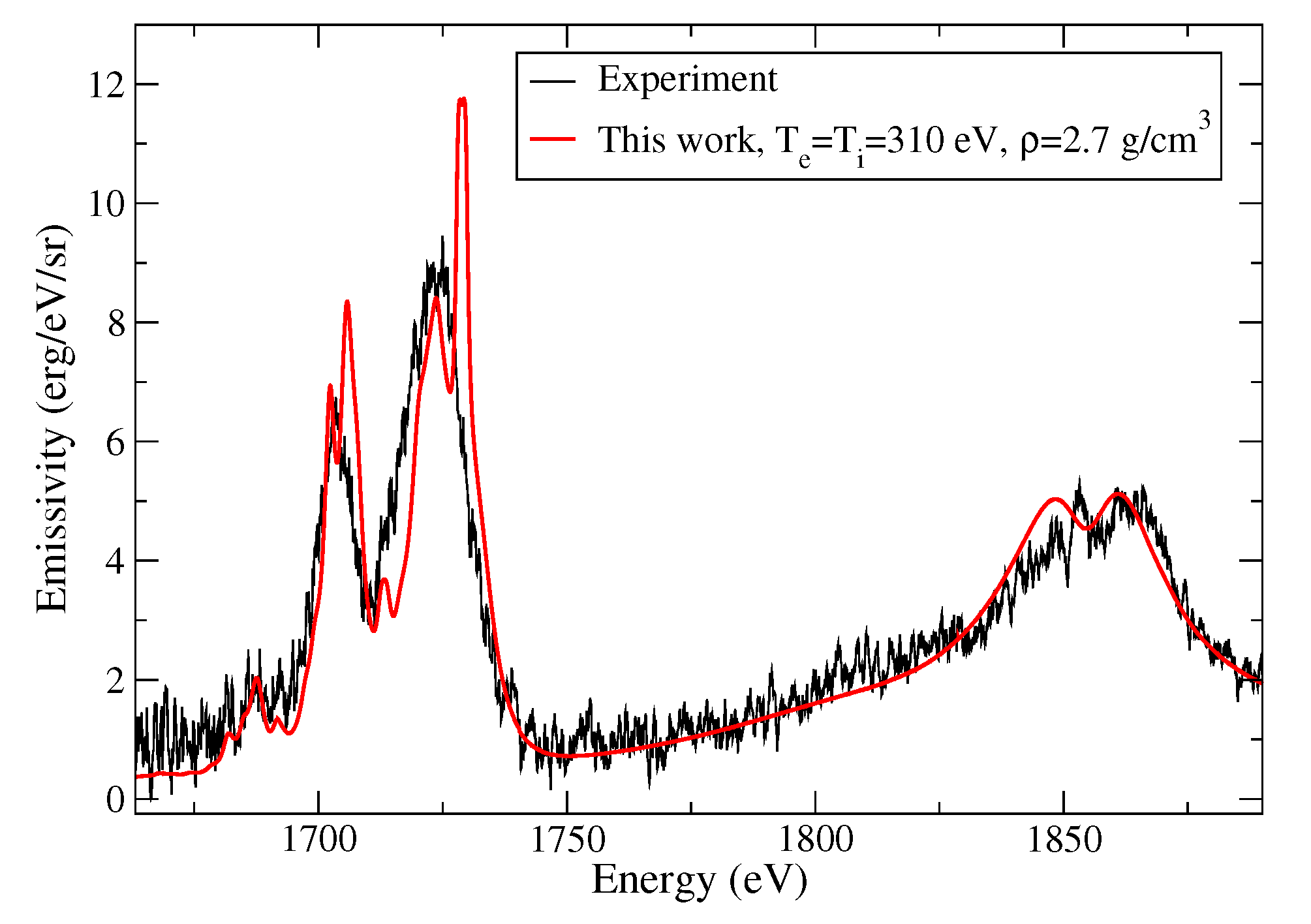
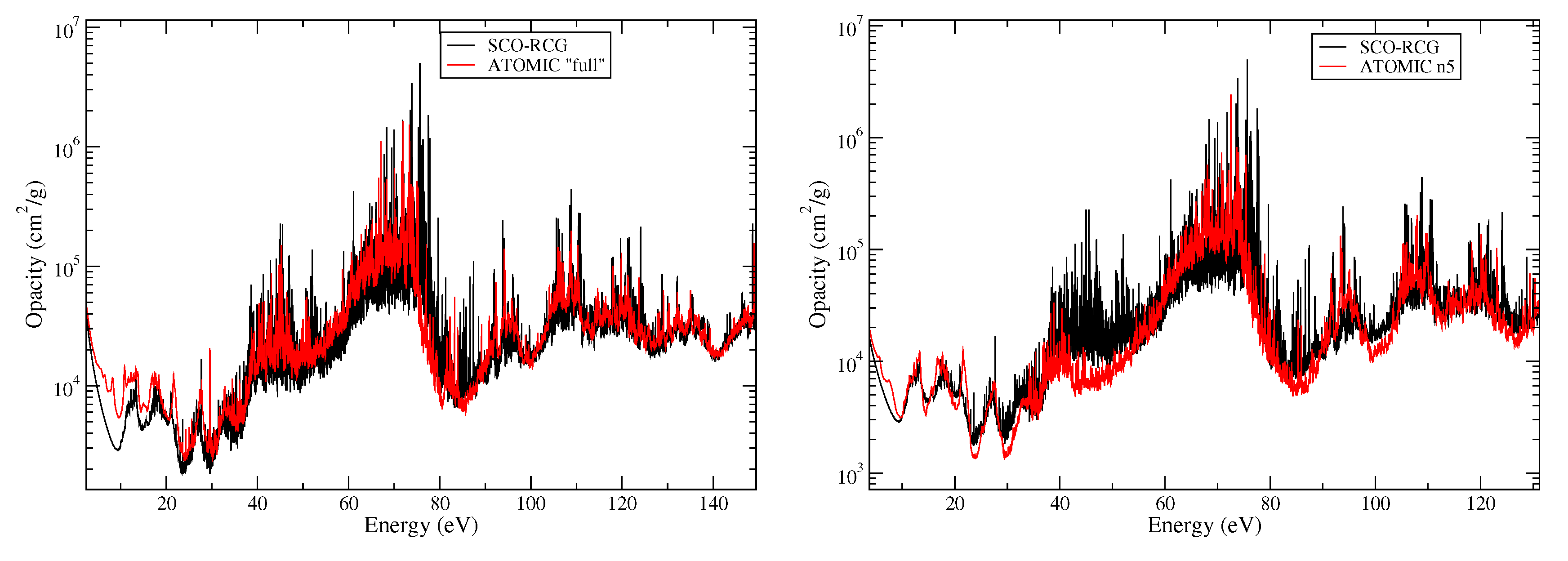
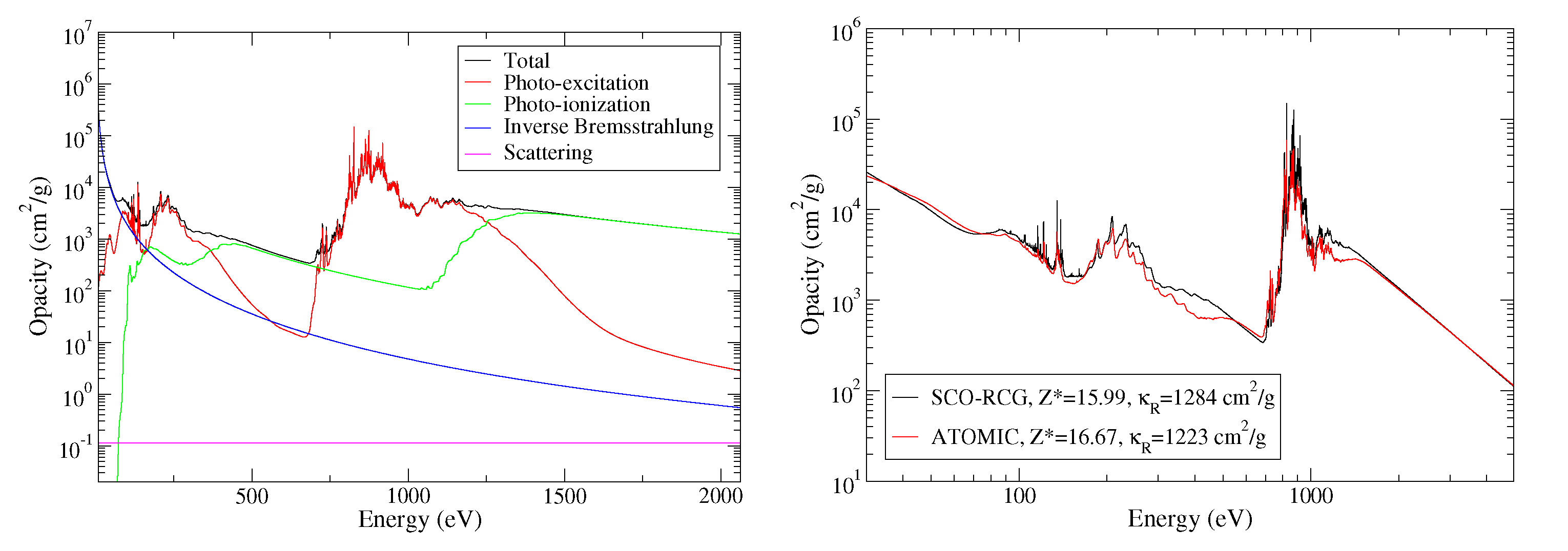
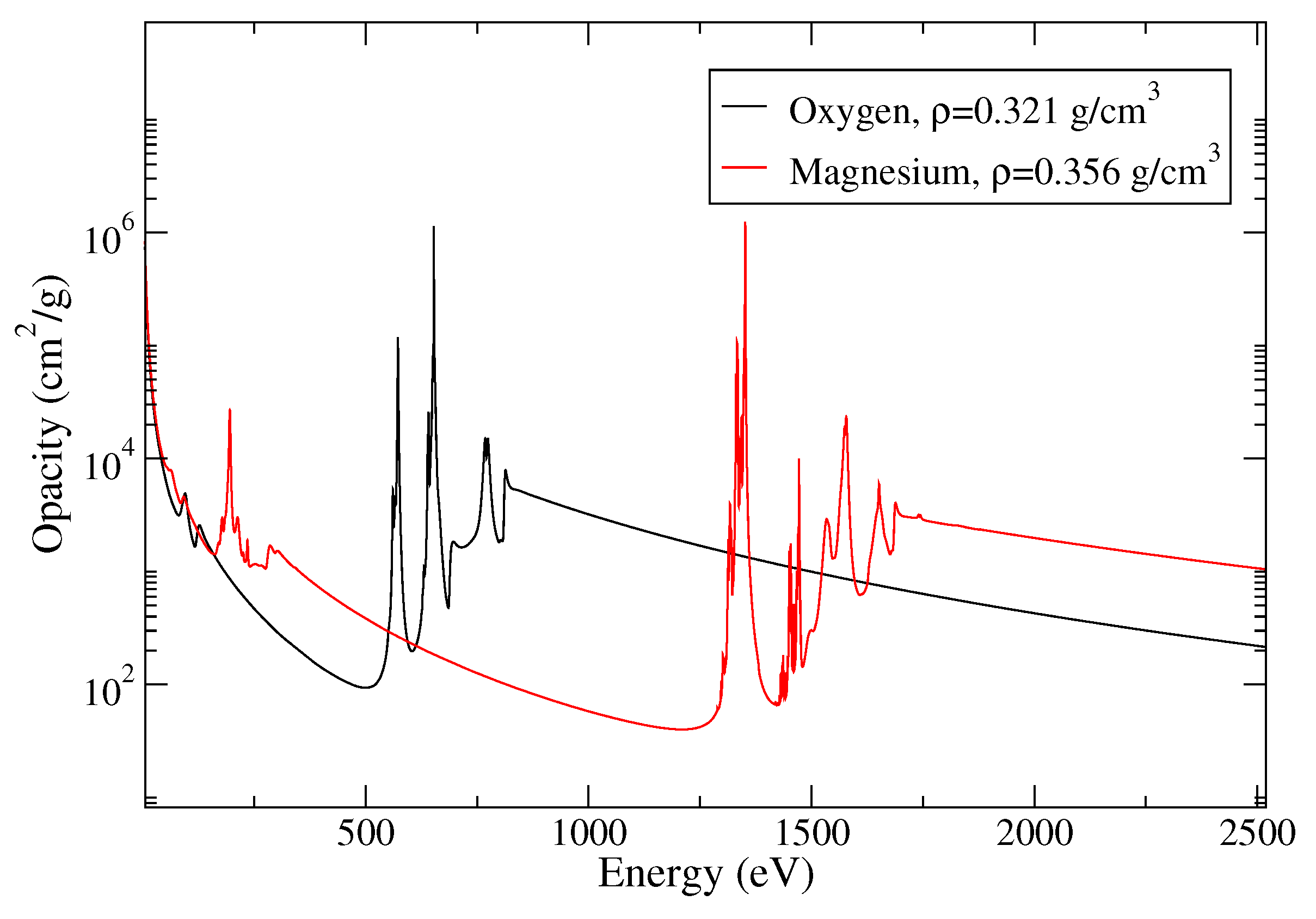
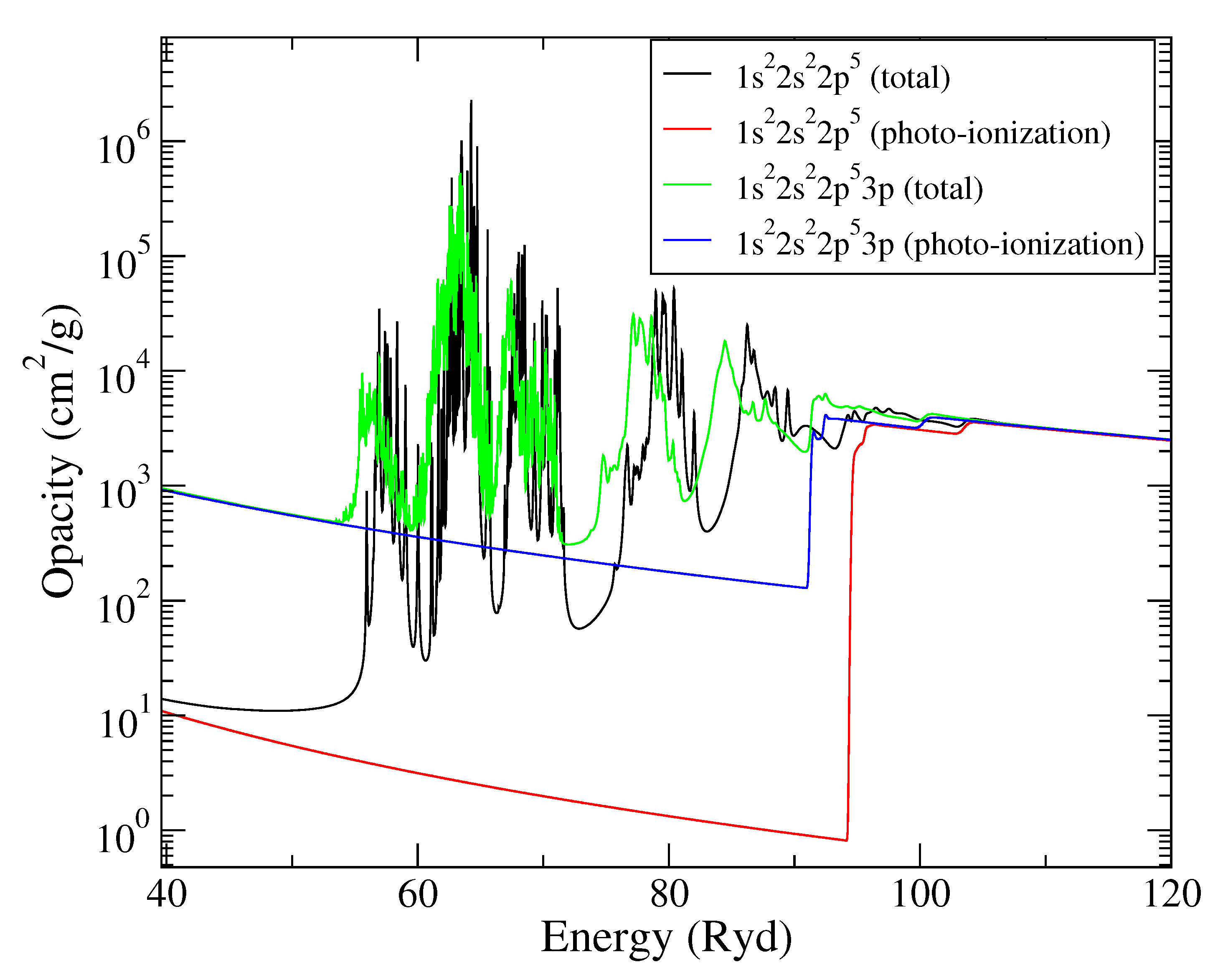
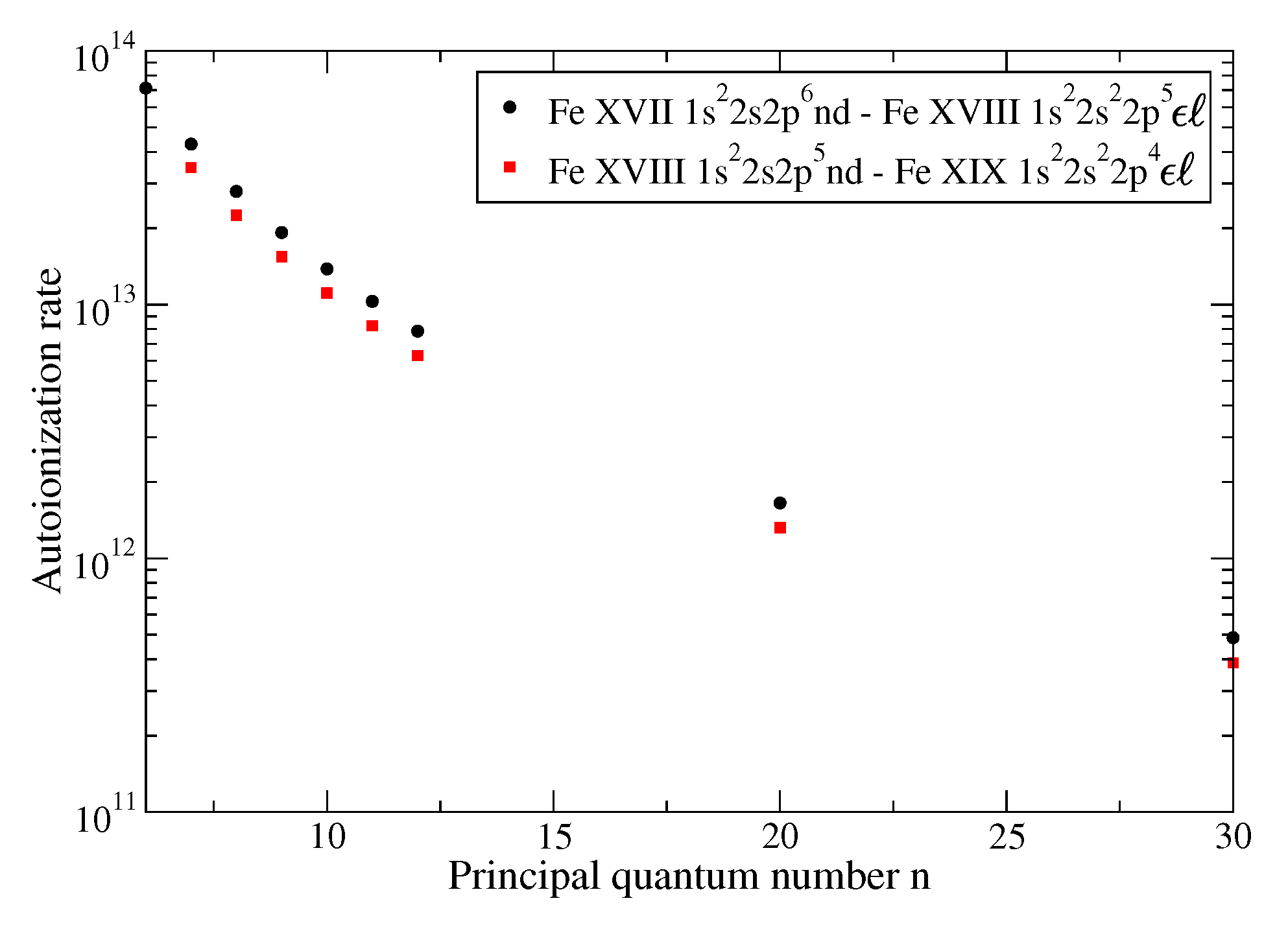
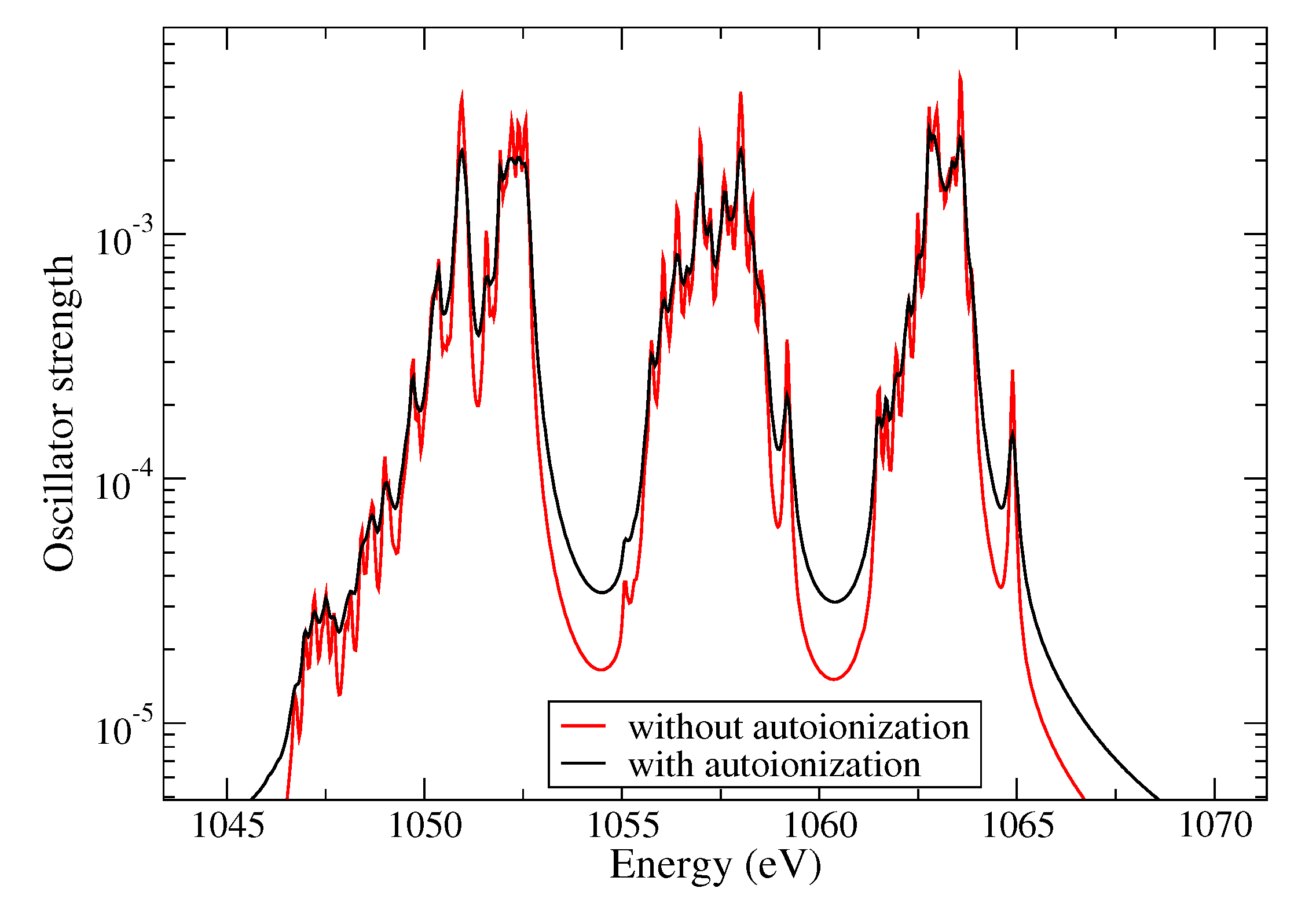
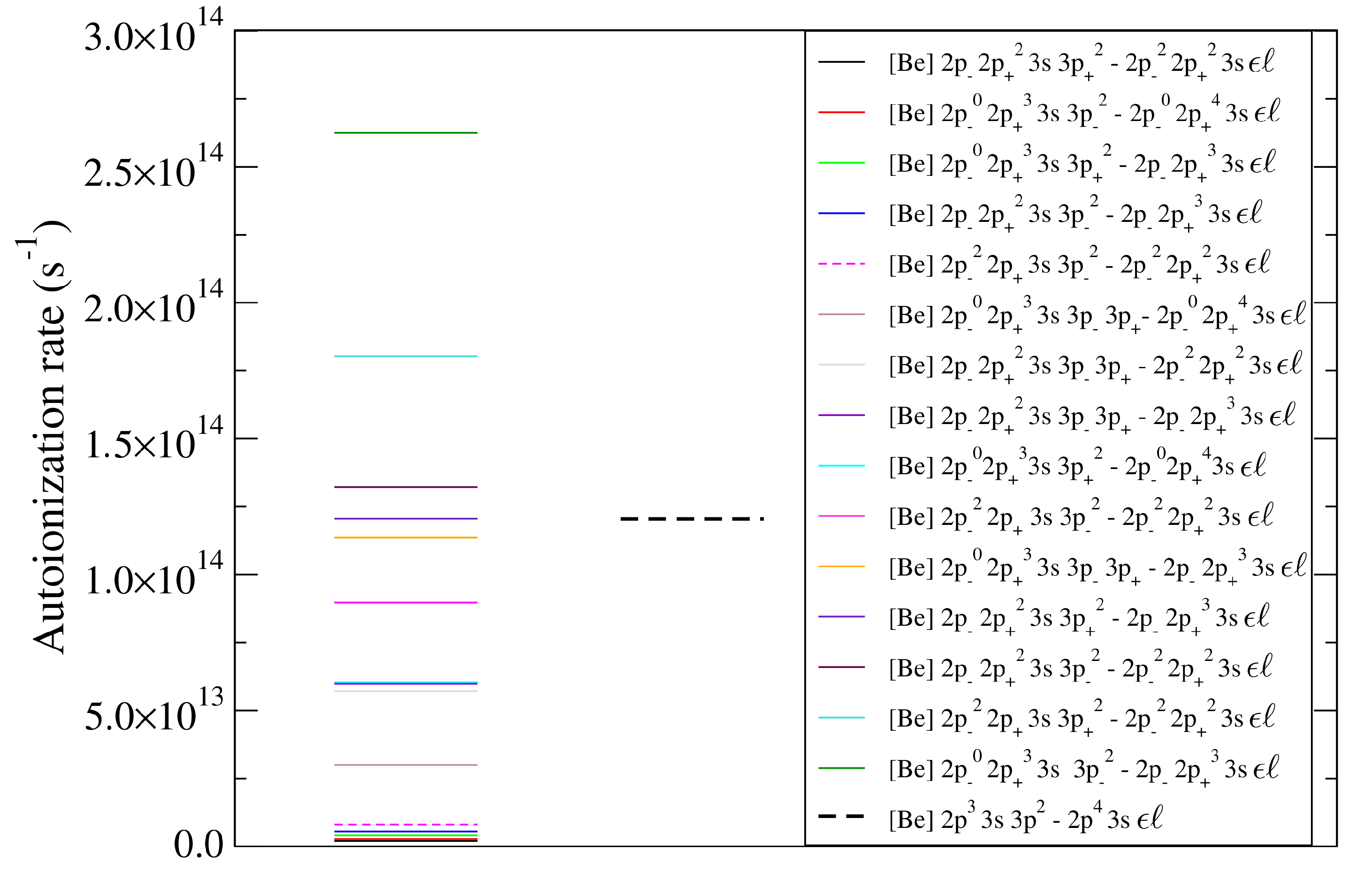
| T (K) | (cm) | ρ (g/cm) | OP (cm/g) | ATOMIC “Full” (cm/g) | SCO-RCG (cm/g) |
|---|---|---|---|---|---|
| 125,800 | 10 | 1.35 × 10 | 25 | 64 | 63 |
| 177,827 | 3.16 × 10 | 3.44 × 10 | 358 | 683 | 674 |
| 199,473 | 10 | 9.52 × 10 | 354 | 487 | 500 |
| 251,190 | 10 | 8.85 × 10 | 1270 | 1359 | 1313 |
| 295,553 | 3.16 × 10 | 2.44 × 10 | 232 | 232 | 122 |
| T (eV) | ρ (g/cm) | ATOMIC Full (cm/g) | ATOMIC n5 (cm/g) | SCO-RCG (cm/g) |
|---|---|---|---|---|
| 21 | 2 × 10 | 19,266 | 14,361 | 17,853 |
| 22 | 2 × 10 | 19,613 | 14,910 | 18,435 |
| 23 | 2 × 10 | 19,508 | 15,205 | 18,510 |
| 25 | 2 × 10 | 18,384 | 15,094 | 17,550 |
| Solar Radius Fraction () | T (eV) | (cm) |
|---|---|---|
| 0.5 | 340 | 8 × 10 |
| 0.6 | 270 | 2.5 × 10 |
| 0.7 | 200 | 10 |
| Source | Relative to Experiment |
|---|---|
| OP [42,43] | 0.59 |
| R-matrix [75,76] | 0.51 |
| ATOMIC [39,40] | 0.60 |
| OPAS [82,83,84] | 0.70 |
| SCO-RCG [17] | 0.64 |
| SCRAM [85] | 0.77 |
| TOPAZ [86,87] | 0.62 |
| Cold [72] | 0.75 |
| Autoionization Process | MCDF Configurations | FAC Configurations |
|---|---|---|
| – | 7.146 × 10 | 7.194 ×10 |
| – | 1.291 × 10 | 1.374 × 10 |
| – | 1.166 × 10 | 1.221 × 10 |
| – | 2.110 × 10 | 2.214 × 10 |
| – | 1.894 × 10 | 2.033 × 10 |
| – | 7.316 × 10 | 6.621 × 10 |
| – | 7.594 × 10 | 8.156 × 10 |
| – | 1.106 × 10 | 1.204 × 10 |
| – | 6.691 × 10 | 7.484 × 10 |
| Transition | Energy (eV) | Oscillator Strength | Oscillator Strength |
|---|---|---|---|
| 3C | 811.86 | 1.820727 × 10 | 1.853965 × 10 |
| 3D | 826.55 | 8.297194 × 10 | 8.432271 × 10 |
| Ratio r | 4.557 | 4.548 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pain, J.-C.; Gilleron, F.; Comet, M. Detailed Opacity Calculations for Astrophysical Applications. Atoms 2017, 5, 22. https://doi.org/10.3390/atoms5020022
Pain J-C, Gilleron F, Comet M. Detailed Opacity Calculations for Astrophysical Applications. Atoms. 2017; 5(2):22. https://doi.org/10.3390/atoms5020022
Chicago/Turabian StylePain, Jean-Christophe, Franck Gilleron, and Maxime Comet. 2017. "Detailed Opacity Calculations for Astrophysical Applications" Atoms 5, no. 2: 22. https://doi.org/10.3390/atoms5020022







