On Functional Module Detection in Metabolic Networks
Abstract
:1. Introduction
2. Complexity Definitions of Algorithms and Problem Classification
3. Network Diagrams: Hypergraphs and Bipartite Graphs
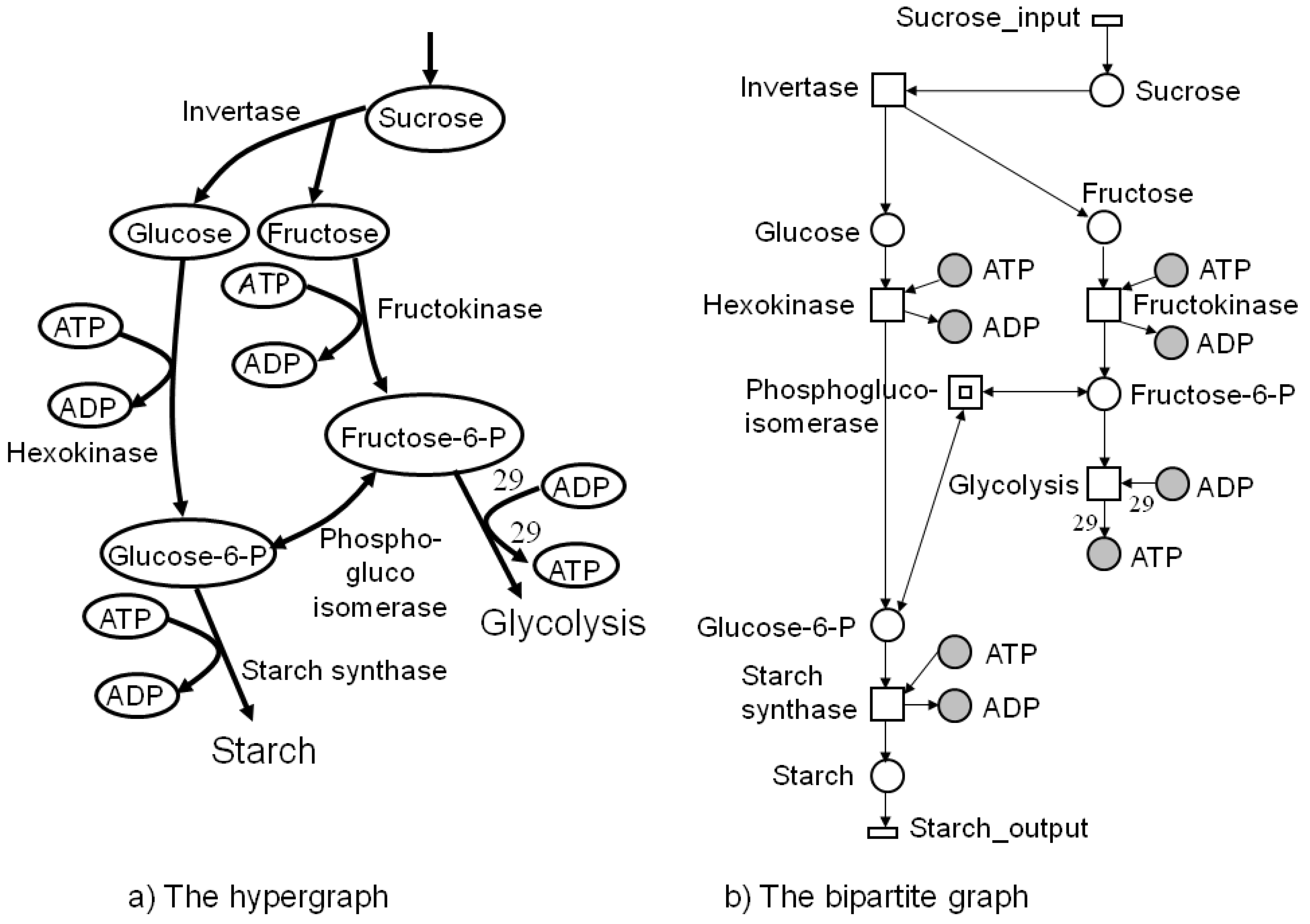
4. Petri Nets
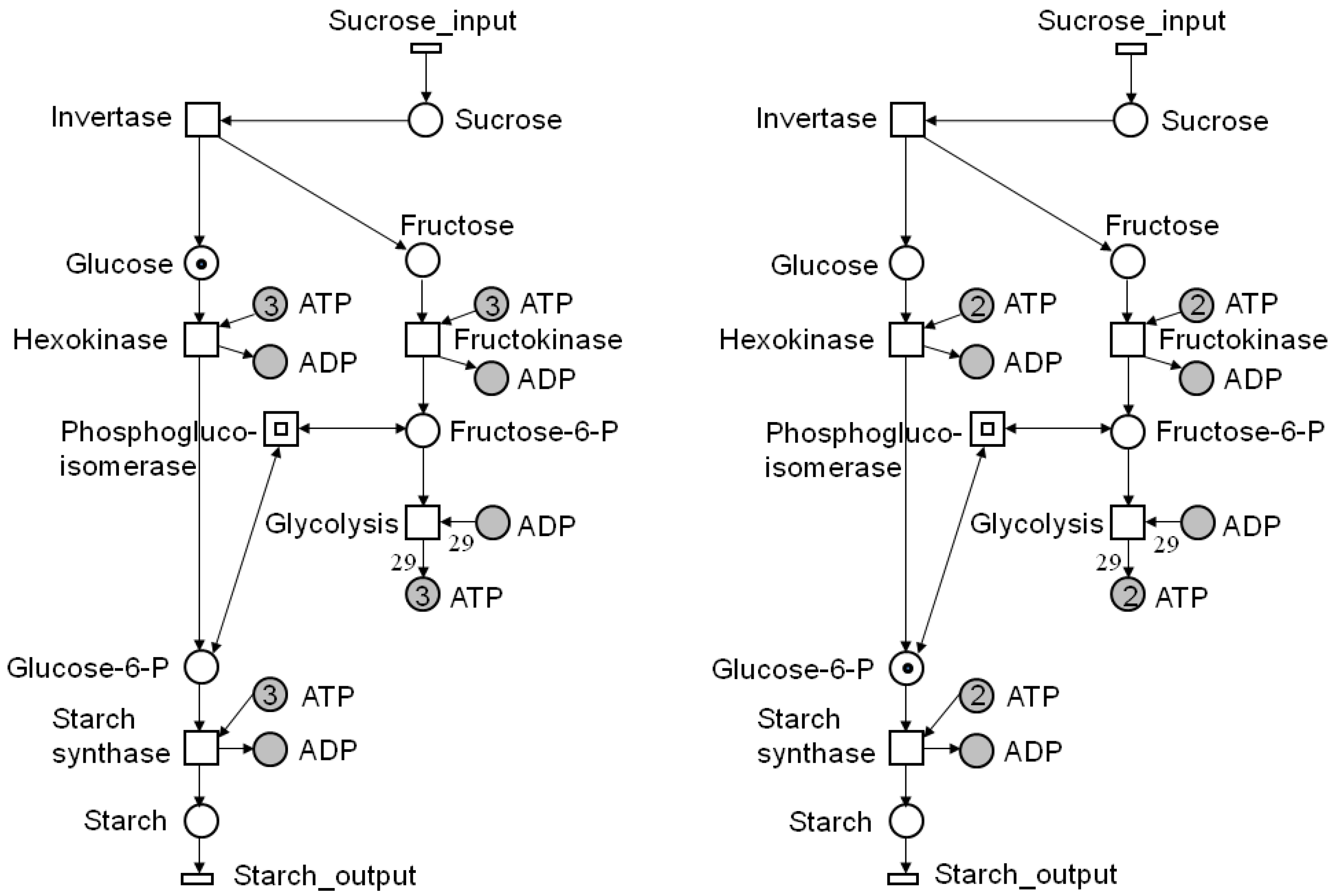
4.1. Reachability Analysis
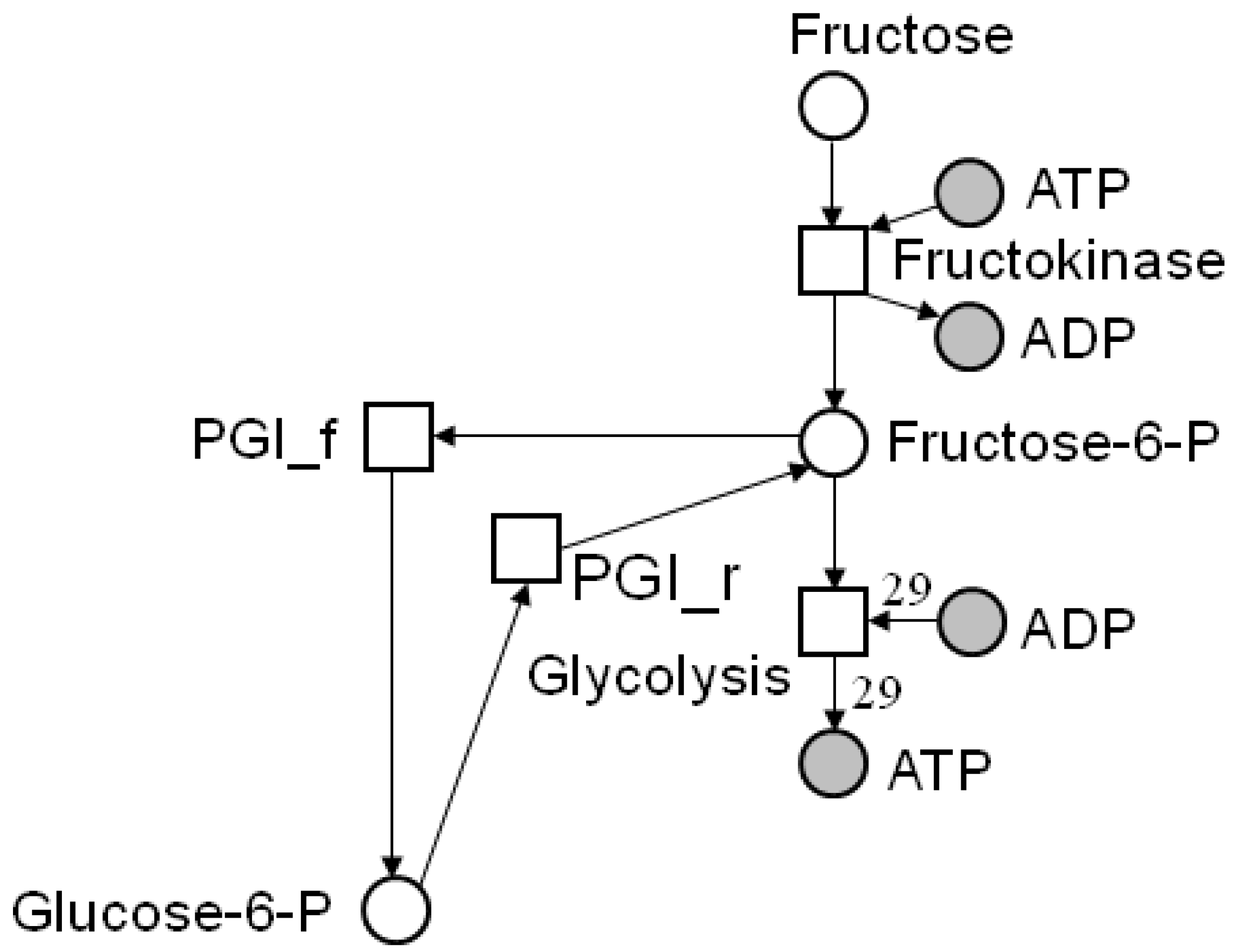
4.2. Incidence Matrix and Stoichiometric Matrix
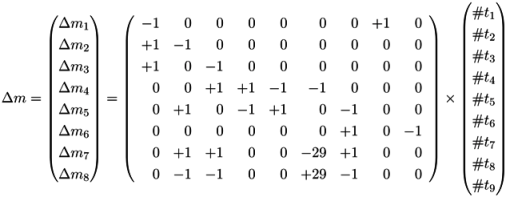
| C | t1: Inver-tase | t2: Hexo-kinase | t3: Fructo-kinase | t4: Phospho-glucosio-merase_f | t5: Phospho-glucosio-merase_b | t6: Glyco-lysis | t7: Starch synthase | t8: Sucrose input | t9: Starch output |
|---|---|---|---|---|---|---|---|---|---|
| p1: Sucrose | −1 | 0 | 0 | 0 | 0 | 0 | 0 | +1 | 0 |
| p2: Glucose | +1 | −1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| p3: Fructose | +1 | 0 | −1 | 0 | 0 | 0 | 0 | 0 | 0 |
| p4: F6P | 0 | 0 | +1 | +1 | −1 | −1 | 0 | 0 | 0 |
| p5: G6P | 0 | +1 | 0 | −1 | +1 | 0 | −1 | 0 | 0 |
| p6: Starch | 0 | 0 | 0 | 0 | 0 | 0 | +1 | 0 | −1 |
| p7: ADP | 0 | +1 | +1 | 0 | 0 | −29 | +1 | 0 | 0 |
| p8: ATP | 0 | −1 | −1 | 0 | 0 | +29 | −1 | 0 | 0 |

4.3. Invariants
4.4. Fourier-Motzkin Elimination Method








4.5. The CTI Property
4.5.1. The CTI Question
4.6. Geometric Point of View
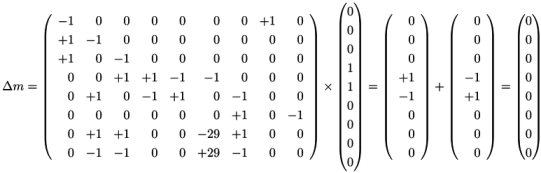
 , of all solutions of Equation (6) is a pointed convex cone. A network is CTI if and only if the effect of firing of all reactions can be compensated. Firing of all reactions in our example network in Figure 1 results in the following changes of metabolites:
, of all solutions of Equation (6) is a pointed convex cone. A network is CTI if and only if the effect of firing of all reactions can be compensated. Firing of all reactions in our example network in Figure 1 results in the following changes of metabolites:


5. Network Decomposition into Functional Modules
5.1. Steady-State Modules
5.1.1. Support Vector-Based Methods
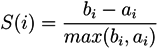
5.1.2. A Parikh Vector-Based Method
5.2. Communities As Non-Steady-State Modules
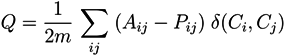
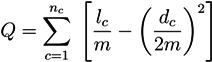
5.2.1. Q-Modularity
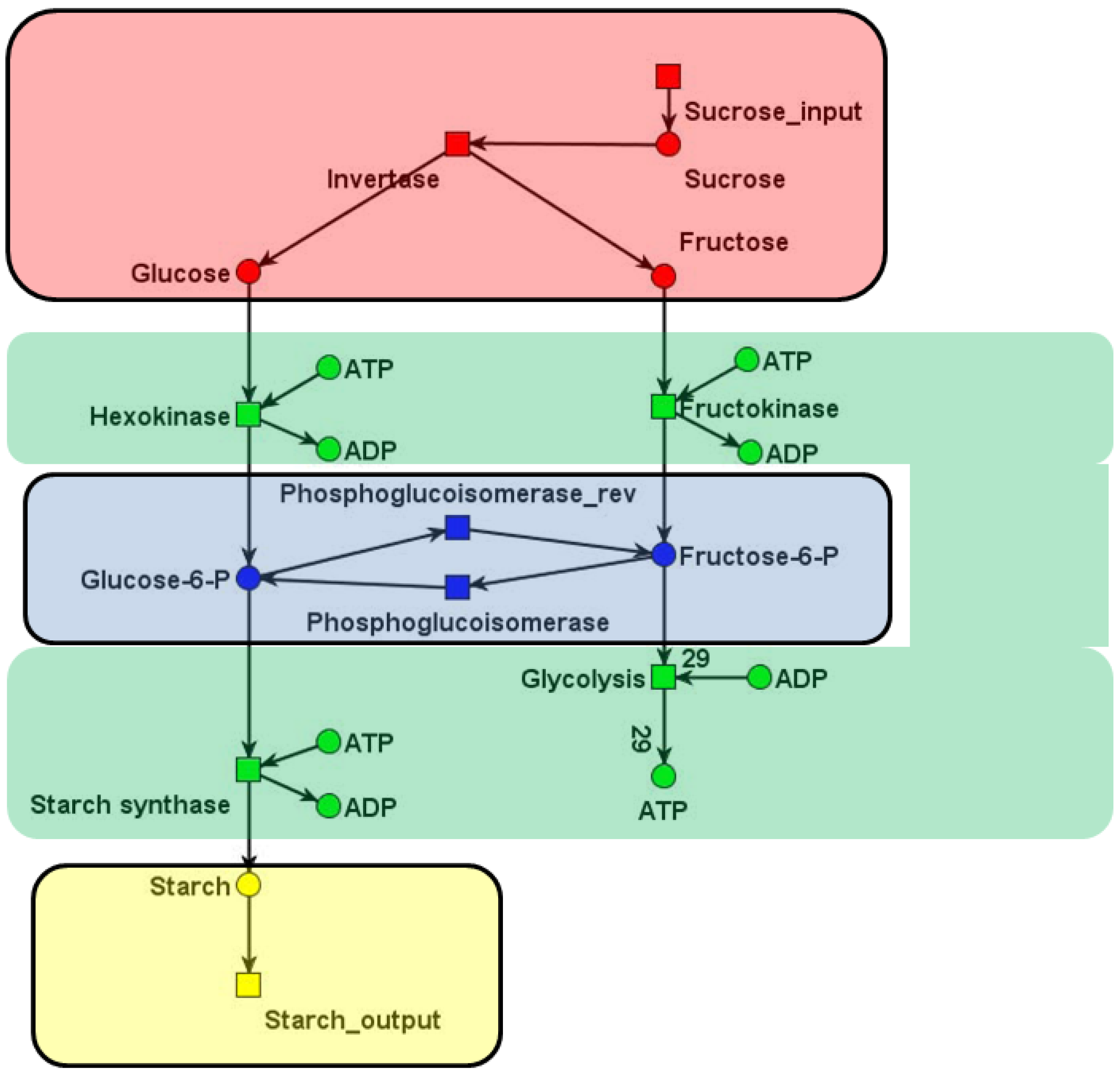
6. Application to Network Reduction and Verification

7. Summary and Conclusions
Conflict of Interest
References
- Ravasz, E.; Somera, A.L.; Mongru, D.A.; Oltvai, Z.N.; Barabási, A.L. Hierarchical organization of modularity in metabolic networks. Science 2002, 297, 1551–1555. [Google Scholar] [CrossRef]
- Jeong, H.; Tombor, B.; Albert, R.; Oltvai, Z.N.; Barabási, A.L. The large-scale organization of metabolic networks. Nature 2000, 407, 651–654. [Google Scholar] [CrossRef]
- Hao, D.; Ren, C.; Li, C. Revisiting the variation of clustering coefficient of biological networks suggests new modular structure. BMC Syst. Biol. 2012, 6, 34. [Google Scholar] [CrossRef]
- Reichardt, J.; Bornholdt, S. Detecting fuzzy community structures in complex networks with a potts model. Phys. Rev. Lett. 2004, 93, 218701. [Google Scholar] [CrossRef]
- Scott, J. Social network analysis. Sociology 1988, 22, 109–127. [Google Scholar] [CrossRef]
- Baldwin, C.Y. Where do transactions come from? Modularity, transactions, and the boundaries of firms. Ind. Corp. Chang. 2008, 17, 155–195. [Google Scholar] [CrossRef]
- Adomavicius, G.; Tuzhilin, A. Toward the next generation of recommender systems: A survey of the state-of-the-art and possible extensions. IEEE Trans. Knowl. Data Eng. 2005, 17, 734–749. [Google Scholar] [CrossRef]
- Su, X.; Khoshgoftaar, T.M. A survey of collaborative filtering techniques. Adv. Artif. Intell. 2009, 2009, 421425:1–421425:19. [Google Scholar]
- Zhou, M.; Venkatesh, K. Modeling, Simulation, and Control of Flexible Manufacturing Systems: A Petri Net Approach. In Intelligent Control and Intelligent Automation; World Scientific Publishing Company: Danvers, USA, 1999; Volume 6. [Google Scholar]
- Billington, J.; Diaz, M.; Rozenberg, G. Application of Petri Nets to Communication Networks; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 1999; Volume 1605. [Google Scholar]
- Kernighan, B.; Lin, S. An efficient heuristic procedure for partitioning graphs. Bell Syst. Tech. J. 1970, 49, 291–307. [Google Scholar] [CrossRef]
- Newman, M.E.J.; Girvan, M. Finding and evaluating community structure in networks. Phys. Rev. E 2004, 69 (2 Pt 2), 026113. [Google Scholar] [CrossRef]
- Fortunato, S. Community detection in graphs. Phys. Rep. 2010, 486, 75–174. [Google Scholar] [CrossRef]
- Heide, H.; Bleier, L.; Steger, M.; Ackermann, J.; Dröse, J.; Schwamb, B.; Zörnig, M.; Reichert, A.; Koch, I.; Wittig, I.; Brandt, U. Complexome profiling identifies TMEM126B as a component of the mitochondrial complex I assembly (MCIA) complex. Cell Metab. 2012, 16, 538–549. [Google Scholar] [CrossRef]
- Guillaume, J.L.; Latapy, M. Bipartite structure of all complex networks. Inf. Process. Lett. 2004, 90, 215–221. [Google Scholar] [CrossRef]
- Koch, I.; Reisig, W.; Schreiber, F. Modeling in Systems Biology: The Petri Net Approach; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Zaitsev, D. Decomposition of Petri nets. Cybern. Syst. Anal. 2004, 40, 739–746. [Google Scholar] [CrossRef]
- Zeng, Q. A polynomial-time decomposition algorithm for petri nets based on indexes of transitions. Inf. Technol. J. 2011, 10, 856–862. [Google Scholar] [CrossRef]
- Berthelot, G. Checking Properties of Nets using Transformations. In Advances in Petri Nets 1985; Rozenberg, G., Ed.; Springer: Berlin/Heidelberg, Germany, 1986; Volume 222, Lecture Notes in Computer Science; pp. 19–40. [Google Scholar]
- Berthelot, G. Transformations and Decompositions of Nets. In Petri Nets: Central Models and Their Properties; Brauer, W., Reisig, W., Rozenberg, G., Eds.; Springer: Berlin/Heidelberg, Germany, 1987; Volume 254, Lecture Notes in Computer Science; pp. 359–376. [Google Scholar]
- Murata, T. Petri Nets: Properties, Analysis and Applications. In Proceedings of the IEEE, April 1989; Volume 77, pp. 541–580.
- Starke, P. Analyse von Petri-Netz-Modellen; B.G. Teubner: Stuttgart, Germany, 1990. [Google Scholar]
- Knuth, D. Fundamental Algorithms, 3 ed.; The Art of Computer Programming; Addison-Wesley: Boston, MA, USA, 1997; Volume 1. [Google Scholar]
- Cormen, T.; Leiserson, C.; Rivest, R.; Stein, C. Introduction to Algorithms; The MIT Press: Cambridge, MS, USA, 2001. [Google Scholar]
- Garey, M.; Johnson, D. Computers and Intractability: A Guide to the Theory of NP-Completness; A series of books in the mathematical science; W.H. Freeman and Company: New York, NY, USA, 1979. [Google Scholar]
- Klee, V.; Minty, G. How good is the simplex algorithm? Inequalities 1972, III, 159–175. [Google Scholar]
- Zadeh, N. A bad network problem for the simplex method and other minimum cost flow algorithms. Math. Progr. 1973, 5, 255–266. [Google Scholar] [CrossRef]
- Adleman, L. Molecular computation of solutions to combinatorial problems. Science 1994, 266, 1021–1024. [Google Scholar]
- Lipton, R. DNA solution of hard computational problems. Science 1995, 268, 542–545. [Google Scholar]
- Shor, P.W. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. Soc. Ind. Appl. Math. Rev. 1999, 41, 303–332. [Google Scholar]
- Paun, G. Membrane Computing. In Fundamentals of Computation Theory; Lingas, A., Nilsson, B., Eds.; Springer: Berlin/Heidelberg, Germany, 2003; Volume 2751, Lecture Notes in Computer Science; pp. 177–220. [Google Scholar]
- Kanehisa, M.; Goto, S. KEGG: Kyoto encyclopedia of genes and genomes. Nucleic Acids Res. 2000, 28, 27–30. [Google Scholar] [CrossRef]
- Petri, C. Communication with automata. Ph.D. Thesis 63, Institut für Instrumentelle Mathematik, Bonn, Germany, 1962. [Google Scholar]
- Bryant, R. Binary Decision Diagrams and Beyond: Enabling Technologies for Formal Verification. In Proceedings International Conference on Computer Aided Design, San Jose, CA, USA, 5–9 November 1995; IEEE Computer Society Press: New York, NY, USA, 1995; pp. 236–245. [Google Scholar]
- Parikh, R. On context-free languages. J. Assoc. Comput. Mach. 1966, 13, 570–581. [Google Scholar] [CrossRef]
- Fourier, J. Solution d’une question particuliére du calcul des inègalitès. In Oeuvres 1826, II, 317–328. [Google Scholar]
- Colom, J.; Silva, M. Convex geometry and semiflows in P/T nets. A comparative study of algorithms for computation of minimal p-semiflows. Lect. Notes Comput. Sci. 1991, 483, 78–112. [Google Scholar]
- Esparza, J. Decidability and complexity of Petri net problems—An introduction. Lect. Notes Comput. Sci. 1998, 1491, 374–428. [Google Scholar] [CrossRef]
- Schuster, S.; Hilgetag, C. On elementary flux modes in biochemical reaction systems at steady state. J. Biol. Syst. 1994, 2, 165–182. [Google Scholar] [CrossRef]
- Wagner, C. Nullspace approach to determine the elementary modes of chemical reaction systems. J. Phys. Chem. B 2004, 108, 2425–2431. [Google Scholar] [CrossRef]
- Terzer, M.; Stelling, J. Large-scale computation of elementary flux modes with bit pattern trees. Bioinformatics 2008, 24, 2229–2235. [Google Scholar] [CrossRef]
- Jevremovic, D.; Boley, D.; Sosa, C. Divide-and-Conquer Approach to the Parallel Computation of Elementary Flux Modes in Metabolic Networks. In Proceedings of the IEEE International Symposium on Parallel & Distributed Processing, Busan, Korea, 26–28 May 2011; pp. 497–506.
- Lipton, R. The reachability problem requires exponential space; Technical report 63; Department of Computer Science, Yale University: New Haven, CT, USA, 1976. [Google Scholar]
- Schuster, S.; Pfeiffer, T.; Moldenhauer, F.; Koch, I.; Dandekar, T. Exploring the pathway structure of metabolism: Decomposition into subnetworks and application to Mycoplasma pneumoniae. Bioinformatics 2002, 18, 352–361. [Google Scholar]
- Farkas, J. Theorie der einfachen Ungleichungen. J. für Die Reine Angew. Math. 1902, 124, 1–27. [Google Scholar]
- Ackermann, J.; Einloft, J.; Nöthen, J.; Koch, I. Reduction techniques for network validation in systems biology. J. Theor. Biol. 2012, 315, 71–80. [Google Scholar] [CrossRef]
- Koch, I.; Junker, B.; Monika Heiner, M. Application of Petri net theory for modelling and validation of the sucrose breakdown pathway in the potato tuber. Bioinformatics 2005, 21, 1219–1226. [Google Scholar] [CrossRef]
- Liao, J.C.; Hou, S.Y.; Chao, Y.P. Pathway analysis, engineering and physiological considerations for redirecting central metabolism. Biotechnol. Bioeng. 1996, 52, 129–140. [Google Scholar] [CrossRef]
- Schuster, S.; Dandekar, T.; Fell, D.A. Detection of elementary flux modes in biochemical networks: A promising tool for pathway analysis and metabolic engineering. Trends Biotechnolol. 1999, 17, 53–60. [Google Scholar] [CrossRef]
- Fischer, E.; Sauer, U. A novel metabolic cycle catalyzes glucose oxidation and anaplerosis in hungry Escherichia coli. J. Biol. Chem. 2003, 278, 46446–46451. [Google Scholar] [CrossRef]
- Klamt, S.; Gilles, E.D. Minimal cut sets in biochemical reaction networks. Bioinformatics 2004, 20, 226–234. [Google Scholar] [CrossRef]
- Ballerstein, K.; von Kamp, A.; Klamt, S.; Haus, U.U. Minimal cut sets in a metabolic network are elementary modes in a dual network. Bioinformatics 2012, 28, 381–387. [Google Scholar] [CrossRef]
- Sackmann, A.; Formanowicz, D.; Formanowicz, P.; Koch, I.; Błażewicz, J. An analysis of the Petri net based model of the human body iron homeostasis process. Comput. Biol. Chem. 2007, 31, 1–10. [Google Scholar] [CrossRef]
- Grafahrend-Belau, E.; Schreiber, F.; Heiner, M.; Sackmann, A.; Junker, B.; Grunwald, S.; Speer, A.; Winder, K.; Ina Koch, I. Modularisation of biochemical networks through hierarchical cluster analysis of T-invariants of biochemical Petri nets. BMC Bioinforma. 2008, 9. [Google Scholar] [CrossRef]
- Bortfeldt, R.; Schuster, S.; Koch, I. Exhaustive analysis of the modular structure of the spliceosomal assembly network: A Petri net approach. In Silico Biol. 2010, 10, 0007. [Google Scholar]
- Sackmann, A. Modelling and Simulation of signaltransduction pathways of Saccharomyces crerevisiae based on Petri net theory. Diploma Thesis, Ernst Moritz Arndt-University Greifswald, Greifswald, Germany, 2005. [Google Scholar]
- Sackmann, A.; Heiner, M.; Koch, I. Application of Petri net based analysis techniques to signal transduction pathways. BMC Bioinforma. 2006, 7, 482. [Google Scholar] [CrossRef]
- Grafahrend-Belau, E. Classification of T-invariants in biochemical Petri nets based on different cluster analysis techniques. Master’s Thesis, Technnical University of Applied Sciences Berlin, Berlin, Germany, 2006. [Google Scholar]
- Backhaus, K.; Erichson, B.; Plinke, W.; Weiber, R. Multivariate Analysis Methods. An Application-oriented Introduction, 10th ed.; Springer: Berlin, Germany, 2003. (in German) [Google Scholar]
- Steinhausen, D.; Langer, K. Cluster Analysis. An Introduction to Methods for Automatic Classification; (in German). De Gruyter: Berlin, Germany, 1977. [Google Scholar]
- Durbin, R.; Eddy, S.; Krogh, A.; Mitchison, G. Biological Sequence Analysis-Probabilistic Models of Proteins and Nucleic Acids; Cambridge University Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Handl, J.; Knowles, J.; Kell, D.B. Computational cluster validation in post-genomic data analysis. Bioinformatics 2005, 21, 3201–3212. [Google Scholar] [CrossRef]
- Rousseeuw, P.J. Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef]
- Grunwald, S.; Speer, A.; Ackermann, J.; Koch, I. Petri net modelling of gene regulation of the Duchenne muscular dystrophy. BioSystems 2008, 92, 189–205. [Google Scholar]
- Pérès, S.; Beurton-Aimar, M.; Mazat, J.P. Pathway classification of TCA cycle. IEE Proc. Syst. Biol. 2006, 5, 369–371. [Google Scholar]
- Kaleta, C.; de Figueiredo, L.; Schuster, S. Can the whole be less than the sum of its parts? Pathway analysis in genome-scale metabolic networks using elementary flux patterns. Genome Res. 2009, 19, 1872–1883. [Google Scholar] [CrossRef]
- Pfeiffer, T.; Sánchez-Valdenebro, I.; Nuño, J.; Montero, F.; Schuster, S. METATOOL: For studying metabolic networks. Bioinformatics 1999, 15, 251–257. [Google Scholar] [CrossRef]
- Kholodenko, B.; Schuster, S.; Rohwer, J.; Cascante, M.; Westerhoff, H. Composite control of cell function:Metabolic pathways behaving as single control units. FEBS Lett. 1995, 368, 1–4. [Google Scholar] [CrossRef]
- Rohwer, J.; Schuster, S.; Westerhoff, H. How to recognize monofunctional units in a metabolic system. J. Theor. Biol. 1996, 179, 213–228. [Google Scholar] [CrossRef]
- Schlegel, J. Network validation and application of Q-modularity to bipartite, directed graphs, in particular Petri nets. Beachelor’s Thesis, Johann Wolfgang Goethe-University Frankfurt am Main, Frankfurt am Main, Germany, 2012. [Google Scholar]
- Li, C.; Donizelli, M.; Rodriguez, N.; Dharuri, H.; Endler, L.; Chelliah, V.; Li, L.; He, E.; Henry, A.; Stefan, M.I.; Snoep, J.L.; Hucka, M.; Le Novère, N.; Laibe, C. BioModels database: An enhanced, curated and annotated resource for published quantitative kinetic models. BMC Syst. Biol. 2010, 4, 92. [Google Scholar] [CrossRef]
- Gagneur, J.; Klamt, S. Computation of elementary modes: A unifying framework and the new binary approach. BMC Bioinforma. 2004, 5, 175. [Google Scholar] [CrossRef] [Green Version]
- Einloft, J.; Ackermann, J.; Nöthen, J.; Koch, I. MonaLisa-visualization and analysis of functional modules in biochemical networks. Bioinformatics 2013, 29, 1469–1470. [Google Scholar] [CrossRef]
- Murray, J. Mathematical Biology; Springer: Berlin/Heidelberg, Germany, 2002; Volume 2. [Google Scholar]
- Deuflhard, P.; Bornemann, F. Scientific Computing with Ordinary Differential Equations; Springer: Berlin/Heidelberg, Germany, 2002; Volume 42. [Google Scholar]
- Haken, H. Synergetics: An introduction; Springer: Berlin/Heidelberg, Germany, 1983; Volume 1. [Google Scholar]
- Gardiner, C.W. Handbook of Stochastic Methods; Springer: Berlin/Heidelberg, Germany, 1985; Volume 3. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Koch, I.; Ackermann, J. On Functional Module Detection in Metabolic Networks. Metabolites 2013, 3, 673-700. https://doi.org/10.3390/metabo3030673
Koch I, Ackermann J. On Functional Module Detection in Metabolic Networks. Metabolites. 2013; 3(3):673-700. https://doi.org/10.3390/metabo3030673
Chicago/Turabian StyleKoch, Ina, and Jörg Ackermann. 2013. "On Functional Module Detection in Metabolic Networks" Metabolites 3, no. 3: 673-700. https://doi.org/10.3390/metabo3030673




