Error Propagation Analysis for Quantitative Intracellular Metabolomics
Abstract
:Abbreviation
| Input variable | Symbol |
|---|---|
| Cell dry weight | cCDW |
| Cell dry weight specific biovolume | vCDW |
| Volume-specific biovolume | vbrs |
| Bioreactor sample volume | Vbrs |
| Cytosolic volume | Vcyt |
| Volume of the extraction reagent | Vexc |
| Total extraction volume | Vexc |
| Residual quenching volume after cell separation | Vres |
| Volume of the quenching reagent | Vque |
| Metabolite concentration of the standard | cstd |
| Metabolite concentration in the extract | cexc |
| Cytosolic metabolite concentration | ccyt |
| Metabolite concentration in the quenching supernatant | cqsn |
| Metabolite concentration in the culture broth | ccub |
| Leakage concentration | clea |
| Peak area quotient of respective sample type | 𝜐[…] |
| 12C peak area of respective sample type | η12C,[…] |
| 13C peak area of respective sample type | η13C,[…] |
1. Introduction
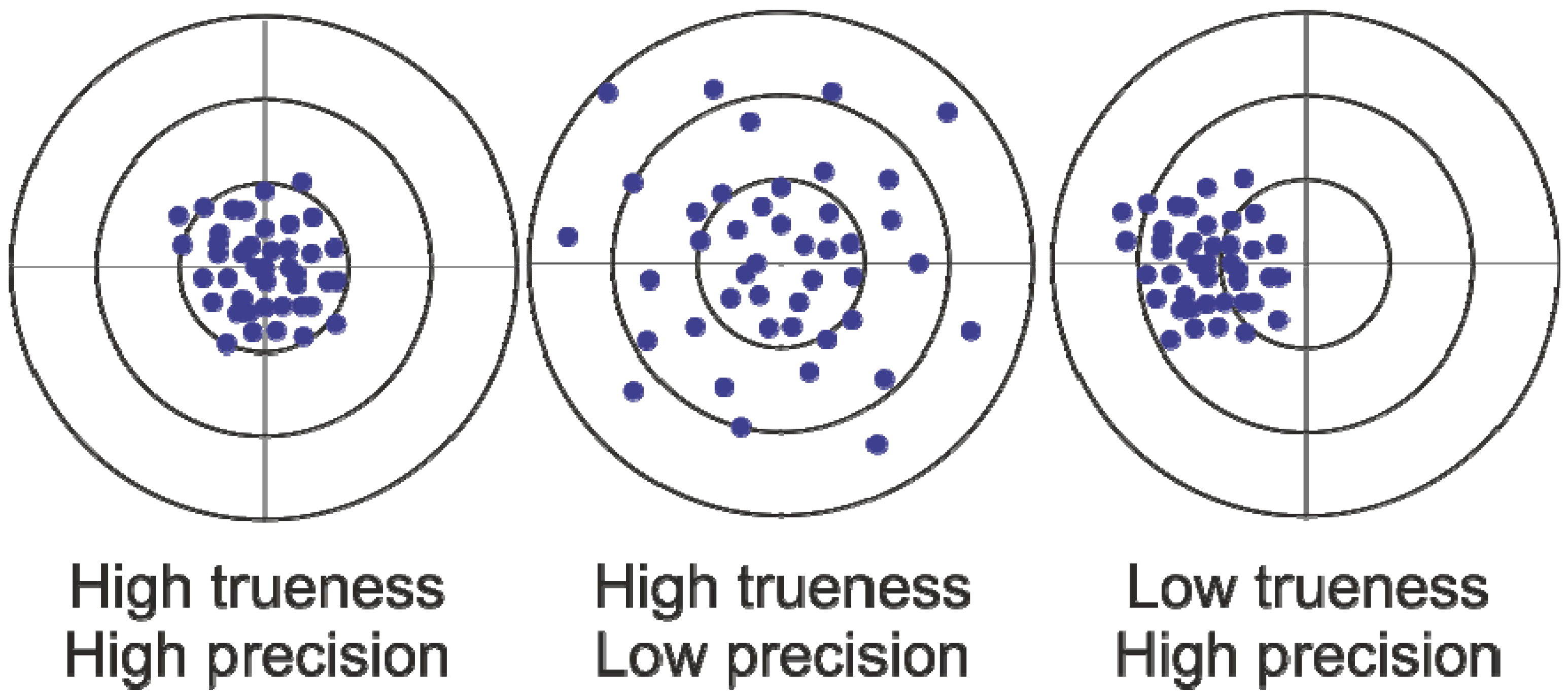
2. Results and Discussion
2.1. Sample Processing for Quantitative Intracellular Metabolomics
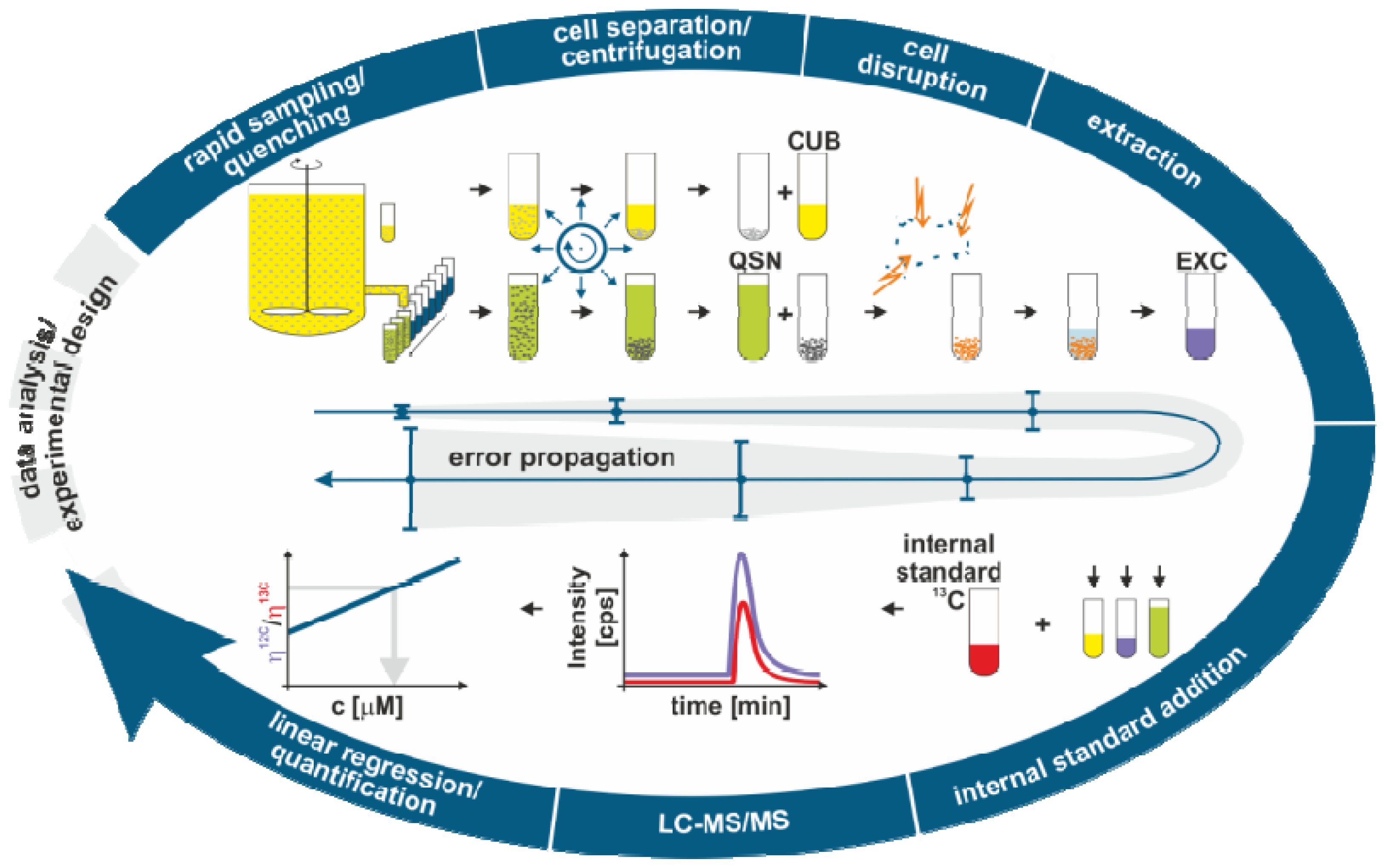
2.1.1. Biomass Determination
- appropriate volume for the metabolome sample,
- reference value for the resulting intracellular metabolite concentrations.
2.1.2. Metabolome Sampling
- exact withdrawal of the pre-defined sample volume,
- no time delay between sampling and inactivation of metabolism (quenching),
- no sample contamination.
2.1.3. Quenching
- fast inactivation of the cell’s metabolism in a state which is as close as possible to the in vivo state during cultivation,
- correction of metabolite loss as a result of leakage.
2.1.4. Cell Separation
- fast separation to minimize the dwell time of cells in the quenching solution,
- complete separation with minimal physical energy input.
2.1.5. Cell Disruption and Extraction
- complete cell disruption,
- extraction of the complete amount of all metabolites of interest,
- no degradation or chemical modification of metabolites,
- compatibility of all solvents with subsequent analytical techniques.
2.1.6. Analysis
- high sensitivity and selectivity,
- wide linear dynamic range and broad analytical spectrum,
- quantification via available standards.
2.2. Modeling the Metabolome Sample Processing
2.2.1. Estimation of Extract Concentrations
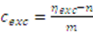
2.2.2. Estimation of Cytosolic Concentrations
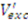 is then estimated from the cytosolic volume Vcyt of disrupted cells and the volume of the extraction reagent Vexc defined a priori:
is then estimated from the cytosolic volume Vcyt of disrupted cells and the volume of the extraction reagent Vexc defined a priori: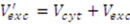
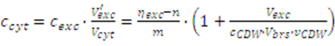
2.3. Correction for Systematic Errors
- independent of the actual experiment, e.g., the pre-defined sample volume Vbrs (cf. Equation (3)): in this case, the bias from a certain set-point value can be determined in a separate experiment (Table 1),
- dependent on the actual experiment, e.g., the final intracellular concentration ccyt (cf. Equation (5)): hence, for bias correction, additional measurements or internal standards are needed.
2.3.1. Matrix Effects
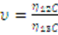
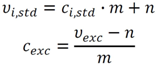
2.3.2. Measurement of Biovolume
2.3.3. Incomplete Cell Separation
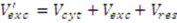
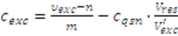
2.3.4. Metabolite Leakage
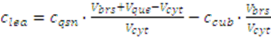
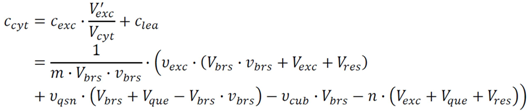
2.4. Application Example
2.4.1. Linearity Check
- 17 metabolites can be further processed without any restriction.
- For five metabolites, the upper linear measurement range is violated and further sample dilution is necessary.
- In the case of 22 metabolites, the lower linear measurement range is violated, indicating that the respective datasets cannot be further processed.
2.4.2. Effect of Bias Correction
- For 15 of the 17 metabolites, the use of the internal standard (IDMS) leads to an increase of the intracellular metabolite concentration.
- As expected, the actual measurement of the specific biovolume (vbrs) leads to a smaller total cytosolic volume and, hence, results in an increase of the intracellular metabolite concentration.
- Interestingly, for nearly all metabolites, the consideration of the residual quenching volume after cell separation (Vres) leads to only small changes in the intracellular concentration values. This can be easily explained by the opposing effect of metabolite dilution and carryover, as discussed previously in connection with Equation 9 and 10.
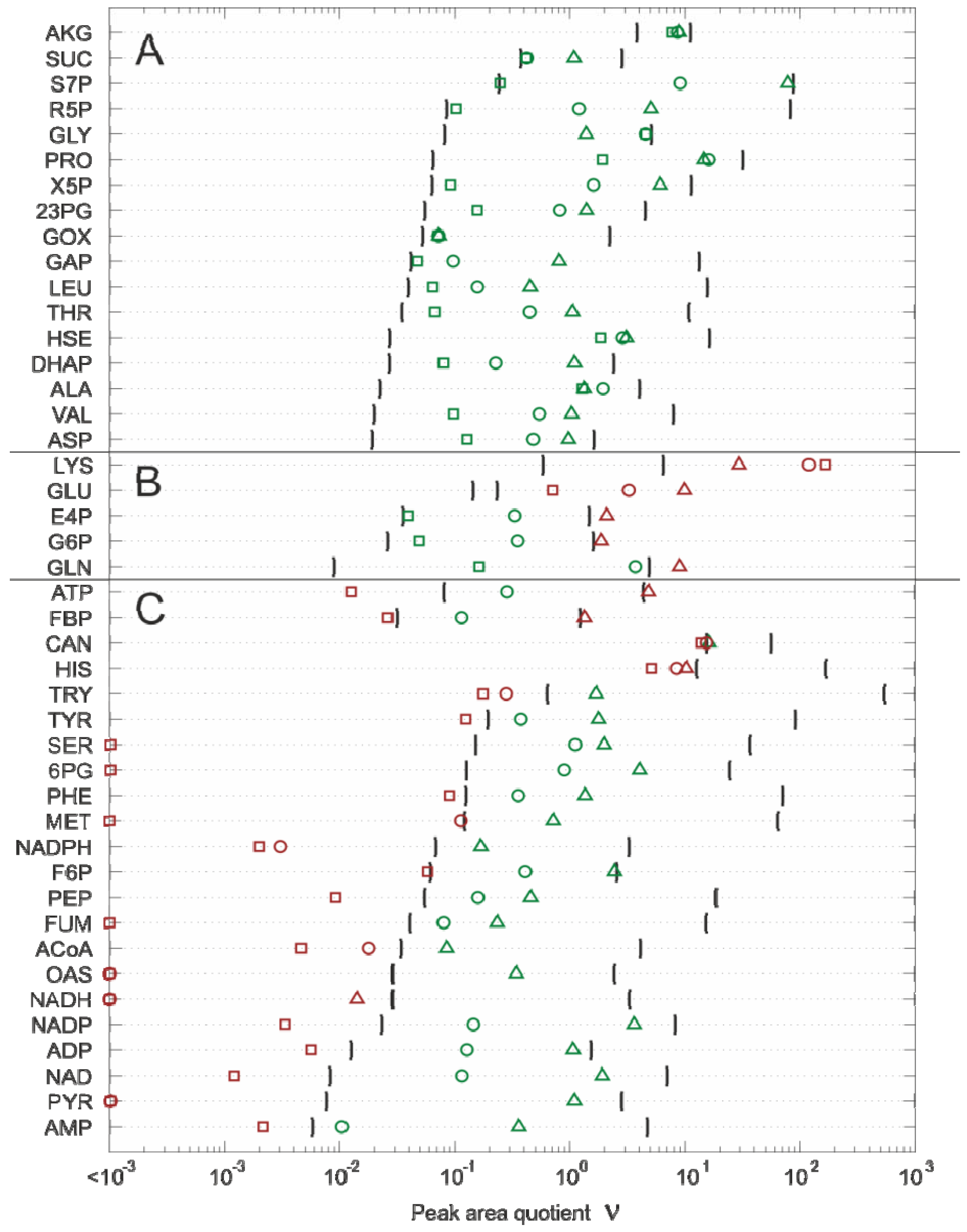
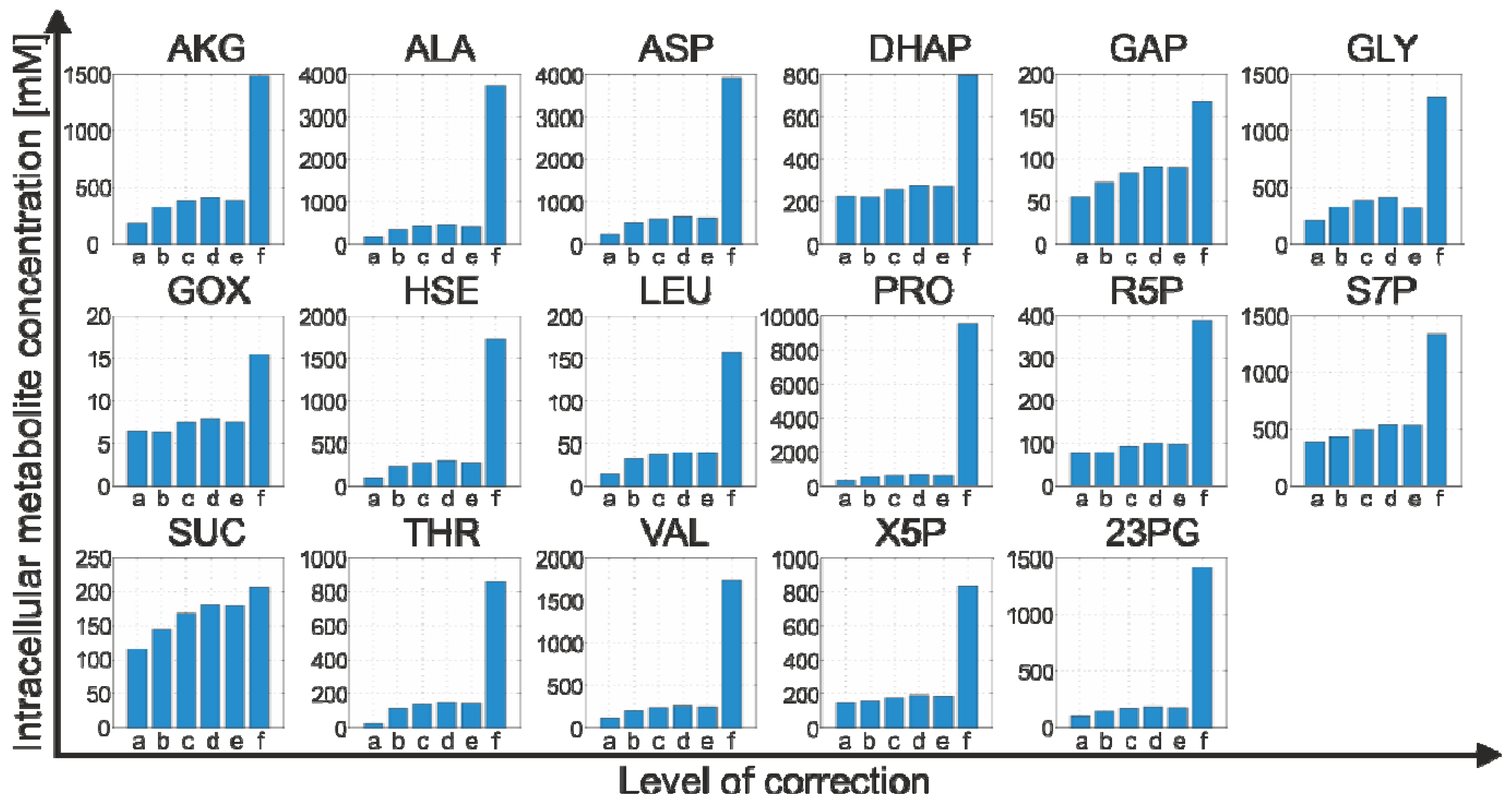
2.4.3. Propagation of Random Errors
| Input variable | Set point | Measurement value | Bias | Variance | Std. deviation [%] |
|---|---|---|---|---|---|
| cCDW [g L−1] | - | 3.95 | - | 0.03 | 4.38 |
| vCDW [µL mg−1] | - | 1.93a | - | 0.93 | 49.97 |
| vbrs [µL mL−1] | - | 5.205 | n.d.b | 0.01 | 1.92 |
| Vbrs [µL] | 5000 | 4782 | 218 | 1463.83 | 0.80 |
| Vexc [µL] | 1350 | 1372.275 | 22.275 | 303.74 | 1.27 |
| Vres [µL] | - | 100.61 | n.d. | 367.49 | 19.05 |
| Vque [µL] | 15000 | 15472.5 | 472.5 | 14565.11 | 0.78 |
| η12C,std_0.25 [counts] | - | 4.29E+06 | n.d. | 2.79E+10 | 3.89 |
| η12C,std_1 [counts] | - | 6.94E+06 | n.d. | 1.85E+11 | 6.20 |
| η12C,std_5 [counts] | - | 1.64E+07 | n.d. | 5.26E+11 | 4.42 |
| η13C,std_0.25 [counts] | - | 6.63E+06 | n.d. | 4.20E+09 | 0.98 |
| η13C,std_1 [counts] | - | 6.24E+06 | n.d. | 1.66E+10 | 2.06 |
| η13C,std_5 [counts] | - | 6.18E+06 | n.d. | 9.88E+09 | 1.61 |
| Metabolite | Intracellular metabolite concentration [µM] | |
|---|---|---|
| Reference model (Equation 5) | Refined model (Equation 12) | |
| GAP | 55.59 | 168.21 ± 8.67 |
| DHAP | 225.09 | 795.63 ± 40.97 |
| 23PG | 96.16 | 1415.56 ± 72.80 |
| R5P | 77.10 | 388.75 ± 16.48 |
| X5P | 143.75 | 827.88 ± 36.65 |
| S7P | 386.17 | 1340.28 ± 53.80 |
| AKG | 188.87 | 1485.31 ± 451.76 |
| SUC | 115.68 | 205.45 ± 69.68 |
| GOX | 6.48 | 15.38 ± 13.82 |
| GLY | 214.61 | 1292.55 ± 967.92 |
| ALA | 172.11 | 3722.25 ± 394.67 |
| VAL | 113.07 | 1742.05 ± 91.80 |
| ASP | 234.97 | 3903.36 ± 213.42 |
| HSE | 94.60 | 1721.95 ± 167.81 |
| THR | 25.37 | 862.88 ± 41.37 |
| LEU | 14.50 | 157.39 ± 9.10 |
| PRO | 322.62 | 9532.64 ± 497.28 |
2.4.4. Sensitivity Analysis
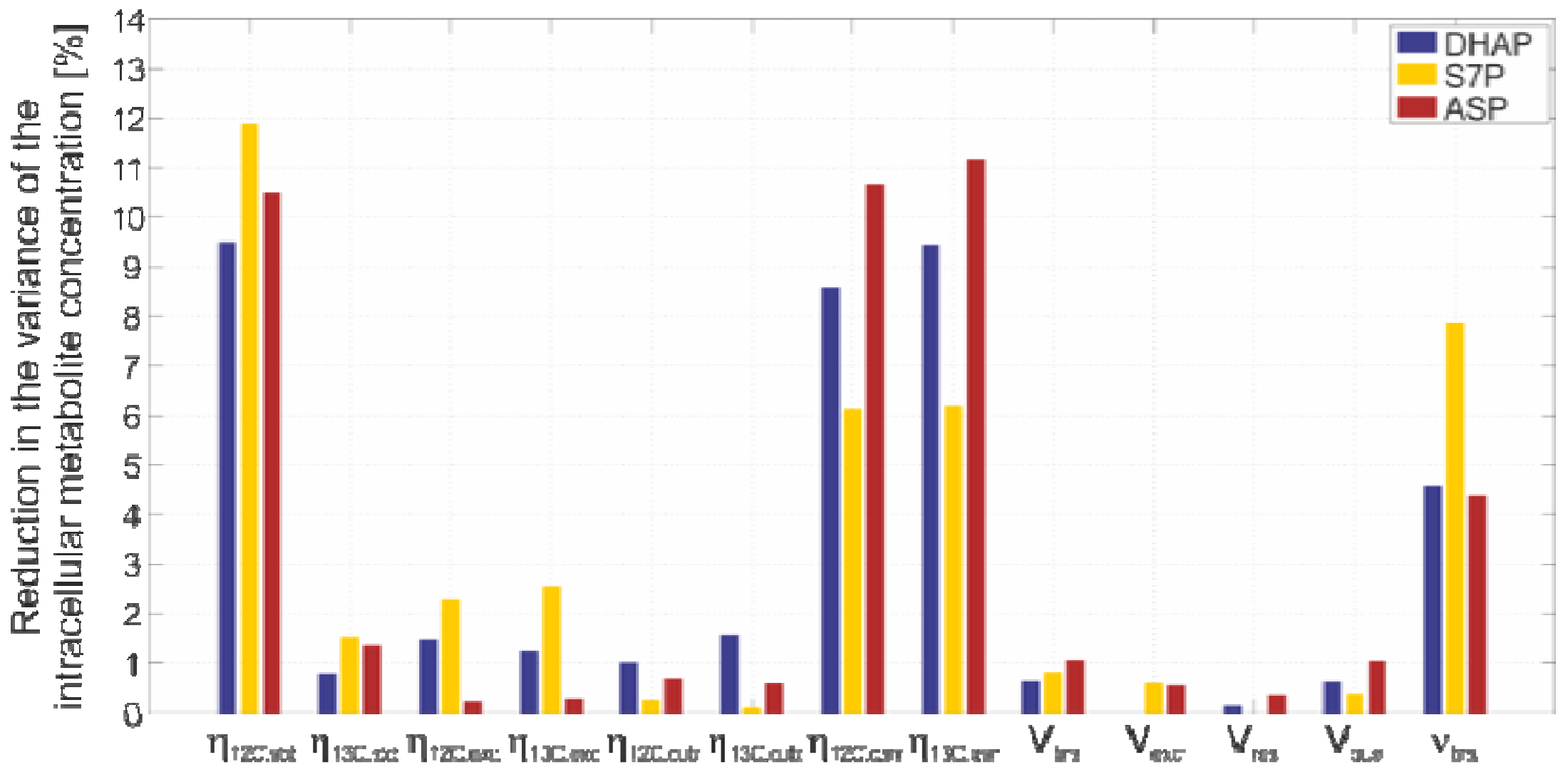
3. Experimental Section
3.1. Strain and Media
3.2. Cultivation Conditions
3.3. Sampling and Sample Processing
3.4. Offline Analysis
3.5. Metabolome Analysis
3.6. Estimation of Systematic and Random Errors
4. Conclusions
Acknowledgments
Conflict of Interest
References
- Buescher, J.M.; Liebermeister, W.; Jules, M.; Uhr, M.; Muntel, J.; Botella, E.; Hessling, B.; Kleijn, R.J.; Le Chat, L.; Lecointe, F.; et al. Global network reorganization during dynamic adaptations of Bacillus subtilis metabolism. Science 2012, 335, 1099–1103. [Google Scholar]
- Wiechert, W.; Noack, S. Mechanistic pathway modeling for industrial biotechnology: challenging but worthwhile. Curr. Opin. Biotechnol. 2011, 22, 604–610. [Google Scholar] [CrossRef]
- Oldiges, M.; Lutz, S.; Pflug, S.; Schroer, K.; Stein, N.; Wiendahl, C. Metabolomics: current state and evolving methodologies and tools. Appl. Microbiol. Biotechnol. 2007, 76, 495–511. [Google Scholar] [CrossRef]
- Villas-Boas, S.G.; Hojer-Pedersen, J.; Akesson, M.; Smedsgaard, J.; Nielsen, J. Global metabolite analysis of yeast: evaluation of sample preparation methods. Yeast 2005, 22, 1155–1169. [Google Scholar] [CrossRef]
- Harris, C.M.; Todd, R.W.; Bungard, S.J.; Lovitt, R.W.; Morris, J.G.; Kell, D.B. Dielectric permittivity of microbial suspensions at radio frequencies: a novel method for the real-time estimation of microbial biomass. Enzyme Microb. Technol. 1987, 9, 181–186. [Google Scholar] [CrossRef]
- Buziol, S.; Bashir, I.; Baumeister, A.; Claassen, W.; Noisommit-Rizzi, N.; Mailinger, W.; Reuss, M. New bioreactor-coupled rapid stopped-flow sampling technique for measurements of metabolite dynamics on a subsecond time scale. Biotechnol. Bioeng. 2002, 80, 632–636. [Google Scholar] [CrossRef]
- Bolten, C.J.; Kiefer, P.; Letisse, F.; Portais, J.C.; Wittmann, C. Sampling for metabolome analysis of microorganisms. Anal. Chem. 2007, 79, 3843–3849. [Google Scholar]
- Schädel, F.; Franco-Lara, E. Rapid sampling devices for metabolic engineering applications. Appl. Microbiol. Biotechnol. 2009, 83, 199–208. [Google Scholar] [CrossRef]
- Van Gulik, W.M.; Canelas, A.B.; Taymaz-Nikerel, H.; Douma, R.D.; de Jonge, L.P.; Heijnen, J.J. Fast sampling of the cellular metabolome. Methods Mol. Bio. 2012, 881, 279–306. [Google Scholar] [CrossRef]
- Taymaz-Nikerel, H.; de Mey, M.; Ras, C.; ten Pierick, A.; Seifar, R.M.; van Dam, J.C.; Heijnen, J.J.; van Gulik, W.M. Development and application of a differential method for reliable metabolome analysis in Escherichia coli. Anal. Biochem. 2009, 386, 9–19. [Google Scholar]
- Winder, C.L.; Dunn, W.B.; Schuler, S.; Broadhurst, D.; Jarvis, R.; Stephens, G.M.; Goodacre, R. Global metabolic profiling of Escherichia coli cultures: an evaluation of methods for quenching and extraction of intracellular metabolites. Anal. Chem. 2008, 80, 2939–2948. [Google Scholar] [CrossRef]
- Faijes, M.; Mars, A.E.; Smid, E.J. Comparison of quenching and extraction methodologies for metabolome analysis of Lactobacillus plantarum. Microb. Cell Fact. 2007, 6, 27. [Google Scholar] [CrossRef]
- Link, H.; Anselment, B.; Weuster-Botz, D. Leakage of adenylates during cold methanol/ glycerol quenching of Escherichia coli. Metabolomics 2008, 4, 240–247. [Google Scholar] [CrossRef]
- Paczia, N.; Nielgen, A.; Lehmann, T.; Gätgens, J.; Wiechert, W.; Noack, S. Extensive Exometabolome Analysis Reveals Extended Overflow Metabolism in Various Microorganisms. Microb. Cell Fact. 2012. [Google Scholar]
- Maharjan, R.P.; Ferenci, T. Global metabolite analysis: the influence of extraction methodology on metabolome profiles of Escherichia coli. Anal. biochem. 2003, 313, 145–154. [Google Scholar]
- Shin, M.H.; Lee, D.Y.; Liu, K.-H.; Fiehn, O.; Kim, K.H. Evaluation of sampling and extraction methodologies for the global metabolic profiling of Saccharophagus degradans. Anal. Chem. 2010, 82, 6660–6666. [Google Scholar]
- Baidoo, E.E.K.; Benke, P.I.; Keasling, J.D. Mass spectrometry-based microbial metabolomics. Methods Mol. biol. 2012, 881, 215–278. [Google Scholar] [CrossRef]
- Jessome, L.L.; Volmer, D.A. Ion Suppression: A Major Concern in Mass Spectrometry. LCGC 2006, 24, 498–510. [Google Scholar]
- Gans, P. Data Fitting in the Chemical Sciences; John Wiley & Sons: Chichester, UK, 1992. [Google Scholar]
- Wu, L.; Mashego, M.R.; van Dam, J.C.; Proell, A.M.; Vinke, J.L.; Ras, C.; van Winden, W.A.; van Gulik, W.M.; Heijnen, J.J. Quantitative analysis of the microbial metabolome by isotope dilution mass spectrometry using uniformLy 13C-labeled cell extracts as internal standards. Anal. Biochem. 2005, 336, 164–171. [Google Scholar] [CrossRef]
- Liang, H.R.; Foltz, R.L.; Meng, M.; Bennett, P. Ionization enhancement in atmospheric pressure chemical ionization and suppression in electrospray ionization between target drugs and stable-isotope-labeled internal standards in quantitative liquid chromatography/tandem mass spectrometry. Rapid Commun. Mass Spectrom. 2003, 17, 2815–2821. [Google Scholar]
- Efron, B. Bootstrap Methods: Another Look at the Jackknife. Ann. Statist. 1979, 7, 1–26. [Google Scholar] [CrossRef]
- Ronsch, H.; Kramer, R.; Morbach, S. Impact of osmotic stress on volume regulation, cytoplasmic solute composition and lysine production in Corynebacterium glutamicum MH20–22B. J. Biotechnol. 2003, 104, 87–97. [Google Scholar]
- Van Ooyen, J.; Noack, S.; Bott, M.; Reth, A.; Eggeling, L. Improved L-lysine production with Corynebacterium glutamicum and systemic insight into citrate synthase flux and activity. Biotechnol. Bioeng. 2012, 109, 2070–2081. [Google Scholar] [CrossRef]
- Keilhauer, C.; Eggeling, L.; Sahm, H. Isoleucine synthesis in Corynebacterium glutamicum: molecular analysis of the ilvB-ilvN-ilvC operon. J. Bacteriol. 1993, 175, 5595–5603. [Google Scholar]
- Luo, B.; Groenke, K.; Takors, R.; Wandrey, C.; Oldiges, M. Simultaneous determination of multiple intracellular metabolites in glycolysis, pentose phosphate pathway and tricarboxylic acid cycle by liquid chromatography-mass spectrometry. J. Chromatogr. A 2007, 1147, 153–164. [Google Scholar]
- Thiele, B.; Fullner, K.; Stein, N.; Oldiges, M.; Kuhn, A.J.; Hofmann, D. Analysis of amino acids without derivatization in barley extracts by LC-MS-MS. Anal. Bioanal. Chem. 2008, 391, 2663–2672. [Google Scholar] [CrossRef]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Tillack, J.; Paczia, N.; Nöh, K.; Wiechert, W.; Noack, S. Error Propagation Analysis for Quantitative Intracellular Metabolomics. Metabolites 2012, 2, 1012-1030. https://doi.org/10.3390/metabo2041012
Tillack J, Paczia N, Nöh K, Wiechert W, Noack S. Error Propagation Analysis for Quantitative Intracellular Metabolomics. Metabolites. 2012; 2(4):1012-1030. https://doi.org/10.3390/metabo2041012
Chicago/Turabian StyleTillack, Jana, Nicole Paczia, Katharina Nöh, Wolfgang Wiechert, and Stephan Noack. 2012. "Error Propagation Analysis for Quantitative Intracellular Metabolomics" Metabolites 2, no. 4: 1012-1030. https://doi.org/10.3390/metabo2041012
APA StyleTillack, J., Paczia, N., Nöh, K., Wiechert, W., & Noack, S. (2012). Error Propagation Analysis for Quantitative Intracellular Metabolomics. Metabolites, 2(4), 1012-1030. https://doi.org/10.3390/metabo2041012




