A Topological Characterization of Medium-Dependent Essential Metabolic Reactions
Abstract
:1. Introduction
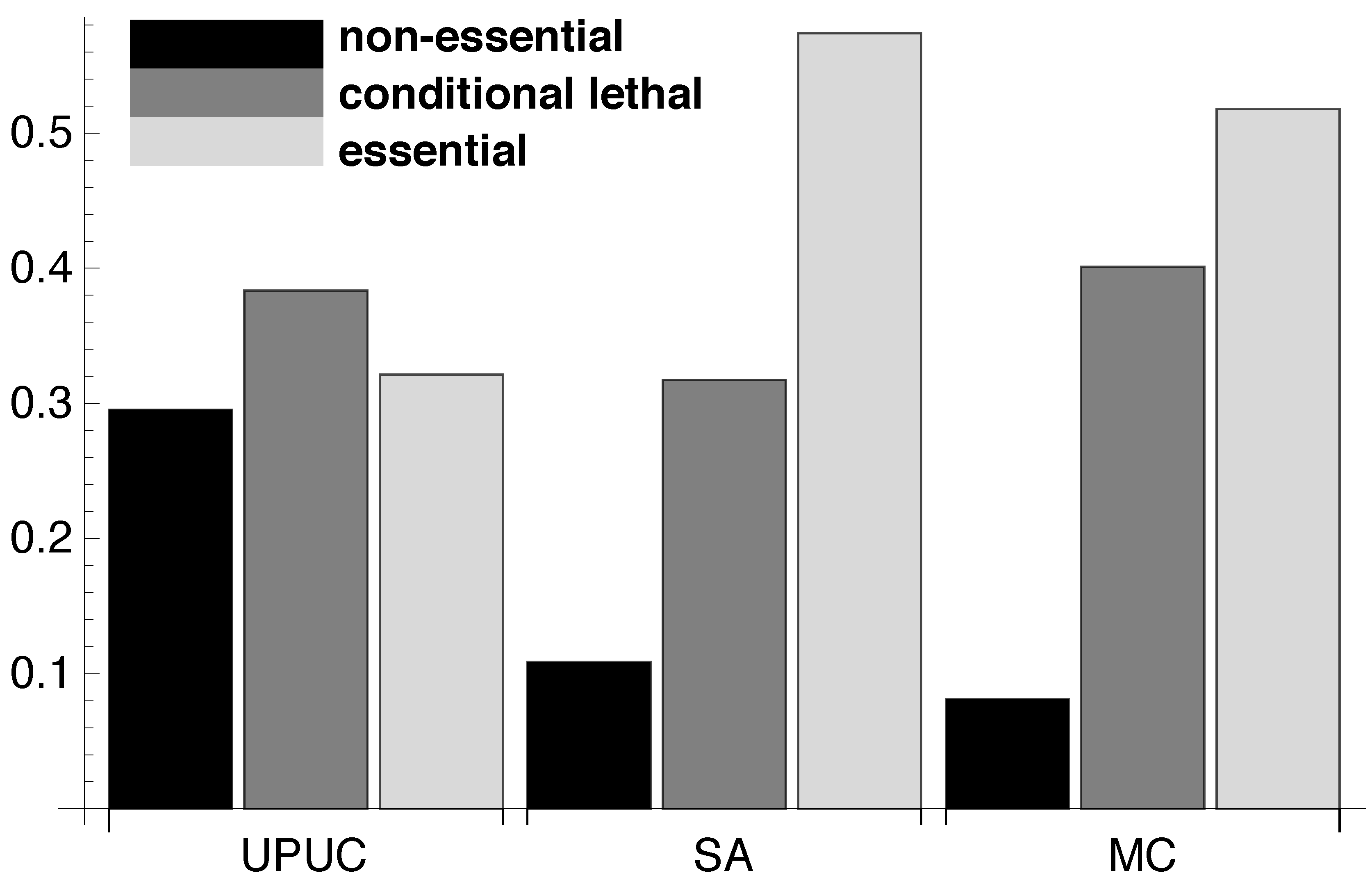
| Reactions | UPUC | SA | MC | No category | |
|---|---|---|---|---|---|
| Overall/Cytosol | 1284/707 | 296/193 | 238/230 | 231/197 | 820/375 |
| Non-essential (Overall/Cytosol) | 789/402 | 137/57 | 27/25 | 25/16 | 608/312 |
| Conditional lethal (Overall/Cytosol) | 326/162 | 90/74 | 73/73 | 85/79 | 198/55 |
| Essential (Overall/Cytosol) | 169/143 | 69/62 | 138/132 | 121/102 | 14/8 |
2. Results
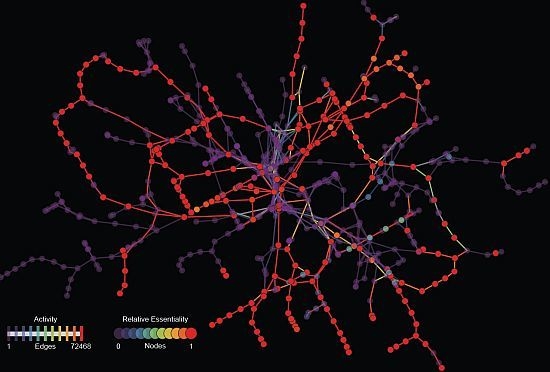
2.1. Relative Essentiality Analysis
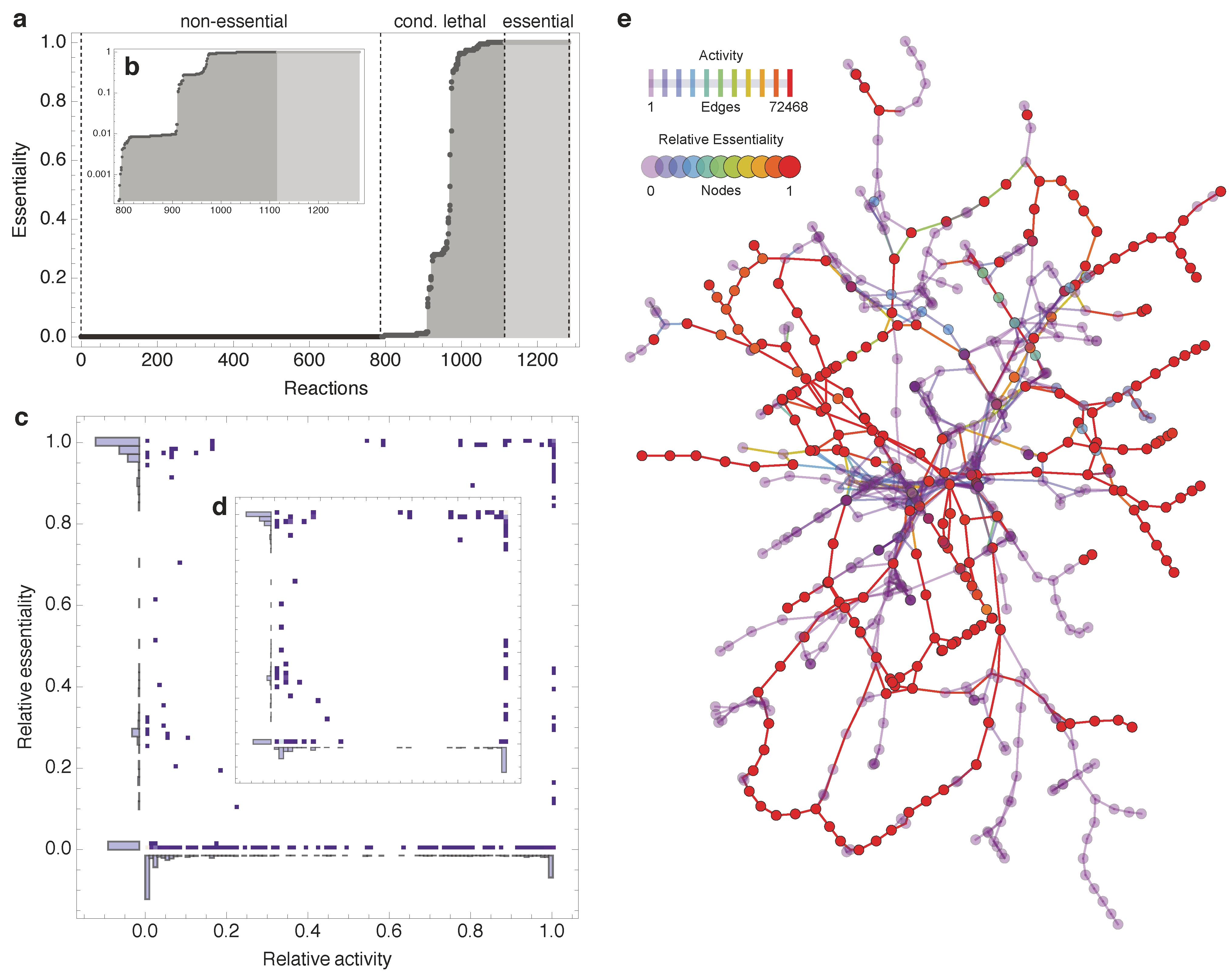
2.2. Topological Categories as Markers of Essential Reactions


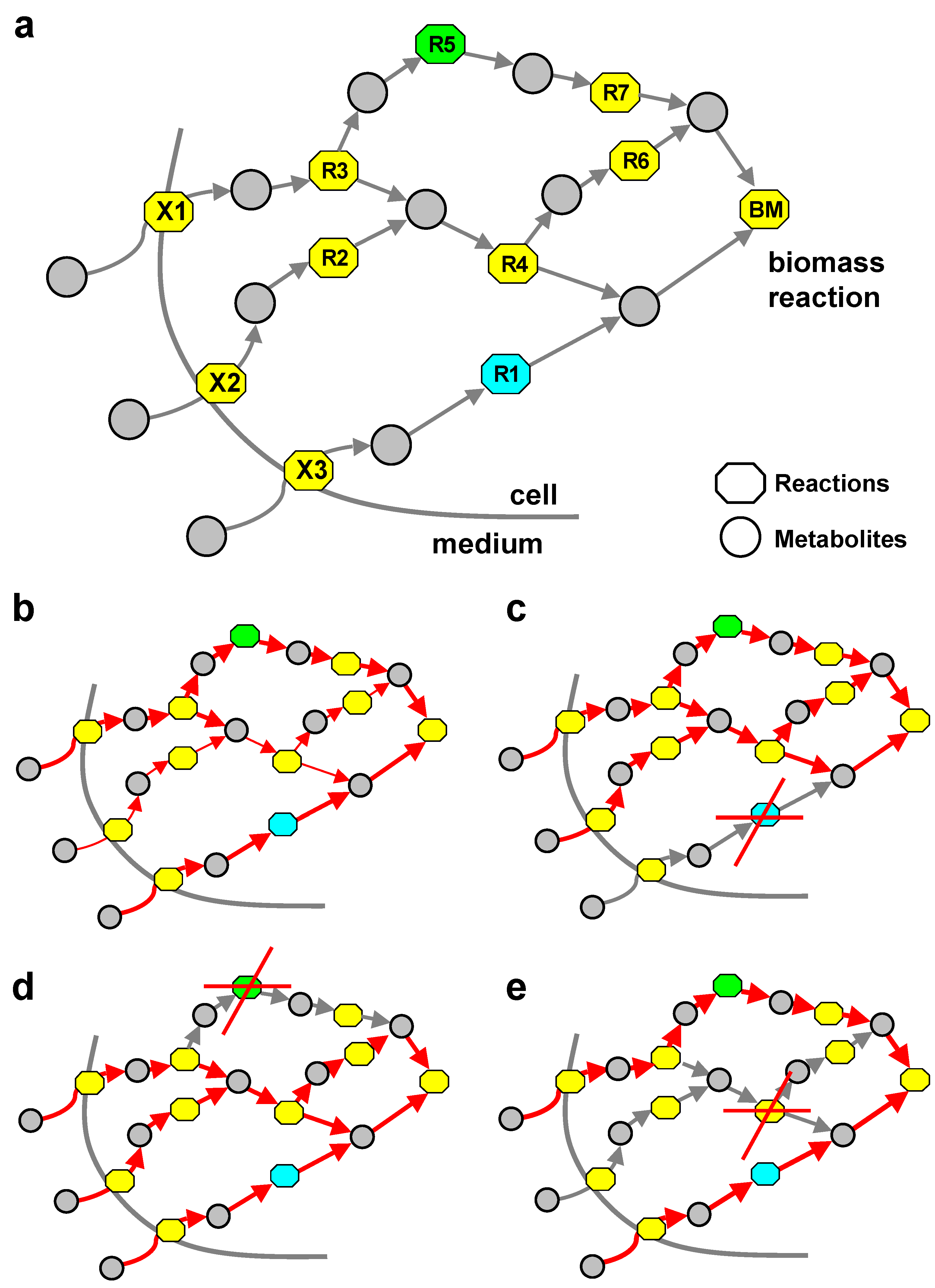
2.3. Distribution of Essentiality Classes Across Three-Node Subgraphs
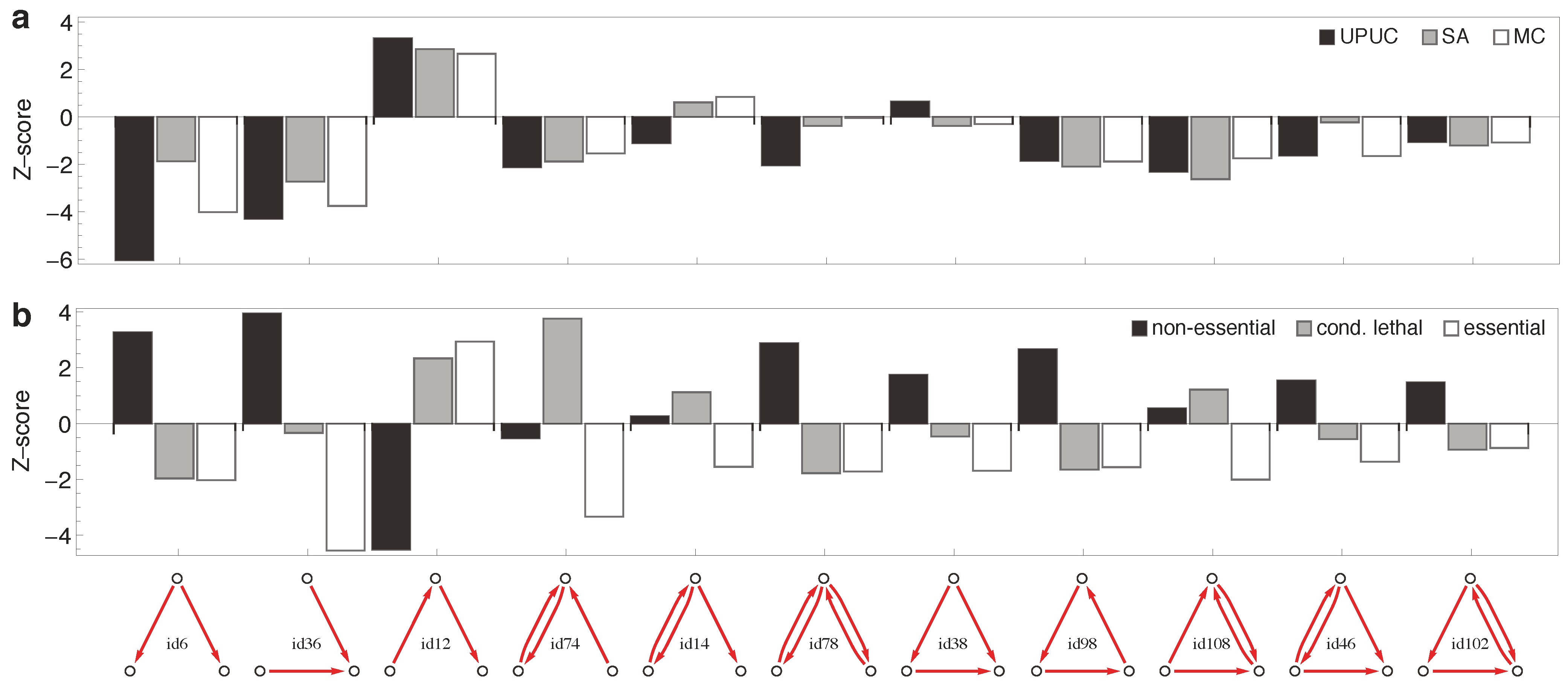
3. Methods
3.1. Metabolic Model and Network Representations
3.2. Flux-Balance Analysis
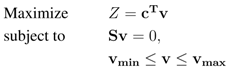
3.3. Combinatorial Minimal Media and Reaction Essentiality
3.4. Blocked Reactions
3.5. Metabolic Core
3.6. Synthetic Accessibility Reactions
3.7. UPUC Reactions
3.8. Enumeration of Three-Node Subgraphs
4. Conclusions
Acknowledgments
References
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’ networks. Nature 1998, 393, 440–442. [Google Scholar]
- Strogatz, S. Exploring complex networks. Nature 2001, 410, 268–276. [Google Scholar] [CrossRef]
- Handorf, T.; Ebenhöh, O.; Heinrich, R. Expanding metabolic networks: Scopes of compounds, robustness, and evolution. J. Mol. Evol. 2005, 61, 498–512. [Google Scholar] [CrossRef]
- Riehl, W.J.; Krapivsky, P.L.; Redner, S.; Segrè, D. Signatures of arithmetic simplicity in metabolic network architecture. PLoS Comput. Biol. 2010, 6, e1000725. [Google Scholar] [CrossRef]
- Noor, E.; Eden, E.; Milo, R.; Alon, U. Central carbon metabolism as a minimal biochemical walk between precursors for biomass and energy. Mol. Cell 2010, 39, 809–820. [Google Scholar] [CrossRef]
- Maslov, S.; Krishna, S.; Pang, T.; Sneppen, K. Toolbox model of evolution of prokaryotic metabolic networks and their regulation. Proc. Natl. Acad. Sci. USA 2009, 106, 9743–9748. [Google Scholar]
- Zhu, Q.; Qin, T.; Jiang, Y.Y.; Ji, C.; Kong, D.X.; Ma, B.G.; Zhang, H.Y. Chemical basis of metabolic network organization. PLoS Comput. Biol. 2011, 7, e1002214. [Google Scholar] [CrossRef]
- Albert, R.; DasGupta, B.; Hegde, R.; Sivanathan, G.S.; Gitter, A.; Güursoy, G.; Paul, P.; Sontag, E. Computationally efficient measure of topological redundancy of biological and social networks. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2011, 84, 036117. [Google Scholar] [CrossRef]
- Marr, C.; Müller-Linow, M.; Hütt, M.T. Regularizing capacity of metabolic networks. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2007, 75, 041917. [Google Scholar] [CrossRef]
- Borenstein, E.; Kupiec, M.; Feldman, M.W.; Ruppin, E. Large-scale reconstruction and phylogenetic analysis of metabolic environments. Proc. Natl. Acad. Sci. USA 2008, 105, 14482–14487. [Google Scholar] [CrossRef]
- Varma, A.; Palsson, B.Ø. Stoichiometric flux balance models quantitatively predict growth and metabolic by-product secretion in wild-type Escherichia coli W3110. Appl. Environ. Microbiol. 1994, 60, 3724–3731. [Google Scholar]
- Edwards, J.S.; Palsson, B.Ø. The Escherichia coli MG1655 in silico metabolic genotype: Its definition, characteristics, and capabilities. Proc. Natl. Acad. Sci. USA 2000, 97, 5528–5533. [Google Scholar]
- Price, N.D.; Reed, J.L.; Palsson, B.Ø. Genome-scale models of microbial cells: Evaluating the consequences of constraints. Nat. Rev. Microbiol. 2004, 2, 886–897. [Google Scholar] [CrossRef]
- Segrè, D.; Vitkup, D.; Church, G. Analysis of optimality in natural and perturbed metabolic networks. Proc. Natl. Acad. Sci. USA 2002, 99, 15112–15117. [Google Scholar] [CrossRef]
- Shlomi, T.; Berkman, O.; Ruppin, E. Regulatory on/off minimization of metabolic flux changes after genetic perturbations. Proc. Natl. Acad. Sci. USA 2005, 102, 7695–7700. [Google Scholar] [CrossRef]
- Albert, R.; Jeong, H.; Barabási, A.L. Error and attack tolerance of complex networks. Nature 2000, 406, 378–382. [Google Scholar] [CrossRef]
- Wagner, A.; Fell, D.A. The small world inside large metabolic networks. Proc. Biol. Sci. 2001, 268, 1803–1810. [Google Scholar] [CrossRef]
- Mahadevan, R.; Palsson, B.Ø. Properties of metabolic networks: Structure versus function. Biophys. J. 2005, 88, 7–9. [Google Scholar]
- Samal, A.; Singh, S.; Giri, V.; Krishna, S.; Raghuram, N.; Jain, S. Low degree metabolites explain essential reactions and enhance modularity in biological networks. BMC Bioinformatics 2006, 7. [Google Scholar] [CrossRef]
- Wunderlich, Z.; Mirny, L.A. Using the topology of metabolic networks to predict viability of mutant strains. Biophys. J. 2006, 91, 2304–2311. [Google Scholar] [CrossRef]
- Almaas, E.; Oltvai, Z.N.; Barabási, A.L. The activity reaction core and plasticity of metabolic networks. PLoS Comput. Biol. 2005, 1, e68. [Google Scholar] [CrossRef] [Green Version]
- Gerdes, S.Y.; Scholle, M.D.; Campbell, J.W.; Balázsi, G.; Ravasz, E.; Daugherty, M.D.; Somera, A.L.; Kyrpides, N.C.; Anderson, I.; Gelfand, M.S.; et al. Experimental determination and system level analysis of essential genes in Escherichia coli MG1655. J. Bacteriol. 2003, 185, 5673–5684. [Google Scholar] [CrossRef]
- Baba, T.; Ara, T.; Hasegawa, M.; Takai, Y.; Okumura, Y.; Baba, M.; Datsenko, K.A.; Tomita, M.; Wanner, B.L.; Mori, H. Construction of Escherichia coli K-12 in-frame, single-gene knockout mutants: The Keio collection. Mol. Syst. Biol. 2006, 2. [Google Scholar] [CrossRef]
- Papp, B.; Pál, C.; Hurst, L. Metabolic network analysis of the causes and evolution of enzyme dispensability in yeast. Nature 2004, 429, 661–664. [Google Scholar] [CrossRef]
- Harrison, R.; Papp, B.; Pál, C.; Oliver, S.; Delneri, D. Plasticity of genetic interactions in metabolic networks of yeast. Proc. Natl. Acad. Sci. USA 2007, 104, 2307–2312. [Google Scholar]
- Alon, U. Network motifs: Theory and experimental approaches. Nat. Rev. Genet. 2007, 8, 450–461. [Google Scholar] [CrossRef]
- Milo, R.; Shen-Orr, S.; Itzkovitz, S.; Kashtan, N.; Chklovskii, D.; Alon, U. Network motifs: Simple building blocks of complex networks. Science 2002, 298, 824–827. [Google Scholar] [CrossRef]
- Milo, R.; Itzkovitz, S.; Kashtan, N.; Levitt, R.; Shen-Orr, S.; Ayzenshtat, I.; Sheffer, M.; Alon, U. Superfamilies of evolved and designed networks. Science 2004, 303, 1538–1542. [Google Scholar] [CrossRef]
- Shen-Orr, S.; Milo, R.; Mangan, S.; Alon, U. Network motifs in the transcriptional regulation network of Escherichia coli. Nat. Genet. 2002, 31, 64–68. [Google Scholar] [CrossRef]
- Kremling, A.; Bettenbrock, K.; Gilles, E.D. A feed-forward loop guarantees robust behavior in Escherichia coli carbohydrate uptake. Bioinformatics 2008, 24, 704–710. [Google Scholar] [CrossRef]
- Orth, J.D.; Fleming, R.M.T.; Palsson, B.Ø. Reconstruction and Use of Microbial Metabolic Networks: The Core Escherichia coli Metabolic Model as an Educational Guide. In EcoSal–Escherichia coli and Salmonella: Cellular and Molecular Biology; Böck, A., Curtiss III, R., Kaper, J.B., Karp, P.D., Neidhardt, F.C., Nyström, T., Slauch, J.M., Squires, C.L., Ussery, D., Eds.; ASM Press: Washington, DC, USA, 2009; pp. 56–99, chapter 10.2.1. [Google Scholar]
- Burgard, A.; Nikolaev, E.; Schilling, C.H.; Maranas, C. Flux coupling analysis of genome-scale metabolic network reconstructions. Genome Res. 2004, 14, 301–312. [Google Scholar] [CrossRef]
- Reed, J.L.; Vo, T.D.; Schilling, C.H.; Palsson, B.O. An expanded genome-scale model of Escherichia coli K-12 (iJR904 GSM/GPR). Genome Biol. 2003, 4, R54. [Google Scholar] [CrossRef]
- Wolfram Demonstrations Project. Available online: http://demonstrations.wolfram.com/VennDiagrams/ (accessed on 17 September 2012).
- Sonnenschein, N.; Geertz, M.; Muskhelishvili, G.; Hütt, M.T. Analog regulation of metabolic demand. BMC Syst. Biol. 2011, 5. [Google Scholar] [CrossRef]
- Sonnenschein, N.; Golib Dzib, J.F.; Lesne, A.; Eilebrecht, S.; Boulkroun, S.; Zennaro, M.C.; Benecke, A.; Hütt, M.T. A network perspective on metabolic inconsistency. BMC Syst. Biol. 2012, 6. [Google Scholar] [CrossRef] [Green Version]
- Feist, A.M.; Henry, C.S.; Reed, J.L.; Krummenacker, M.; Joyce, A.R.; Karp, P.D.; Broadbelt, L.J.; Hatzimanikatis, V.; Palsson, B.Ø. A genome-scale metabolic reconstruction for Escherichia coli K-12 MG1655 that accounts for 1260 ORFs and thermodynamic information. Mol. Syst. Biol. 2007, 3. [Google Scholar] [CrossRef]
- Takemoto, K. Current understanding of the formation and adaptation of metabolic systems based on network theory. Metabolites 2012, 2, 429–457. [Google Scholar]
- Lewis, N.E.; Schramm, G.; Bordbar, A.; Schellenberger, J.; Andersen, M.P.; Cheng, J.K.; Patel, N.; Yee, A.; Lewis, R.A.; Eils, R.; et al. Large-scale in silico modeling of metabolic interactions between cell types in the human brain. Nat. Biotechnol. 2010, 28, 1279–1285. [Google Scholar] [CrossRef]
- Romero, P.R.; Karp, P. Nutrient-Related Analysis of Pathway/genome Databases. Pac. Symp. Biocomput. 2001, 6, 471–482. [Google Scholar]
Supplementary Files
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Sonnenschein, N.; Marr, C.; Hütt, M.-T. A Topological Characterization of Medium-Dependent Essential Metabolic Reactions. Metabolites 2012, 2, 632-647. https://doi.org/10.3390/metabo2030632
Sonnenschein N, Marr C, Hütt M-T. A Topological Characterization of Medium-Dependent Essential Metabolic Reactions. Metabolites. 2012; 2(3):632-647. https://doi.org/10.3390/metabo2030632
Chicago/Turabian StyleSonnenschein, Nikolaus, Carsten Marr, and Marc-Thorsten Hütt. 2012. "A Topological Characterization of Medium-Dependent Essential Metabolic Reactions" Metabolites 2, no. 3: 632-647. https://doi.org/10.3390/metabo2030632