Development of Metabolic Indicators of Burn Injury: Very Low Density Lipoprotein (VLDL) and Acetoacetate Are Highly Correlated to Severity of Burn Injury in Rats
Abstract
:1. Introduction
2. Experimental Methods
3. Numerical Methods
3.1. Theoretical Aspects
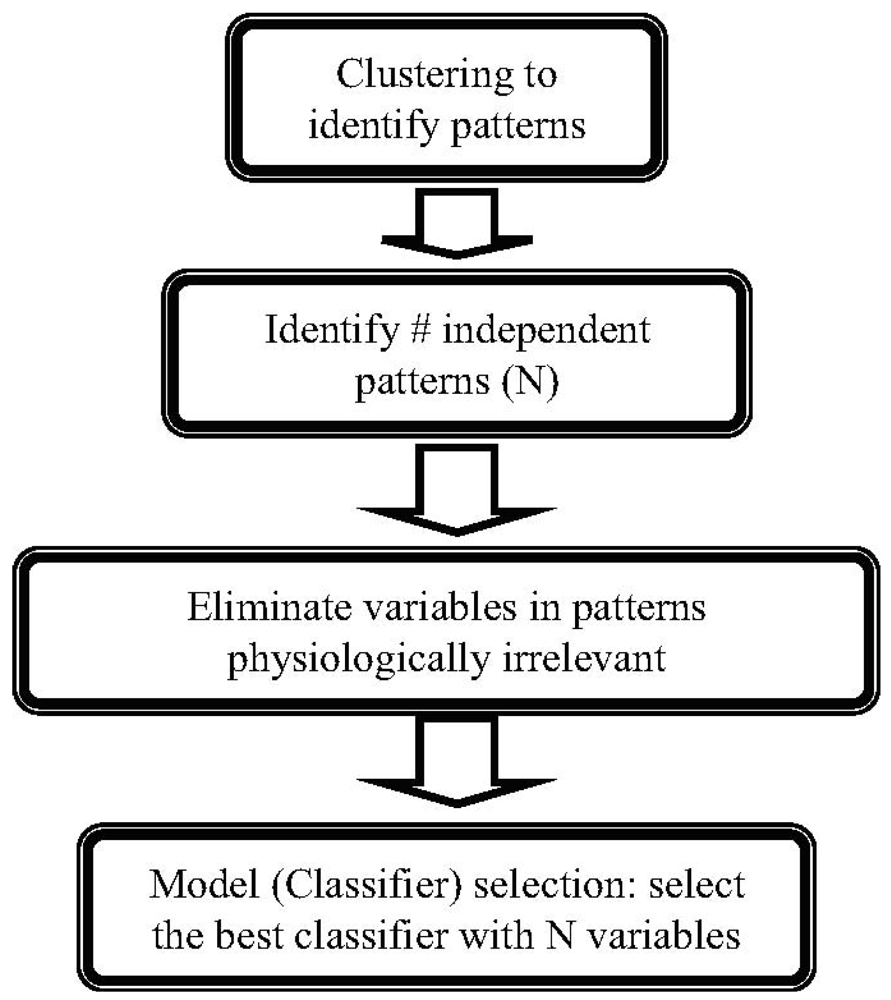
3.2. Methods
4. Results
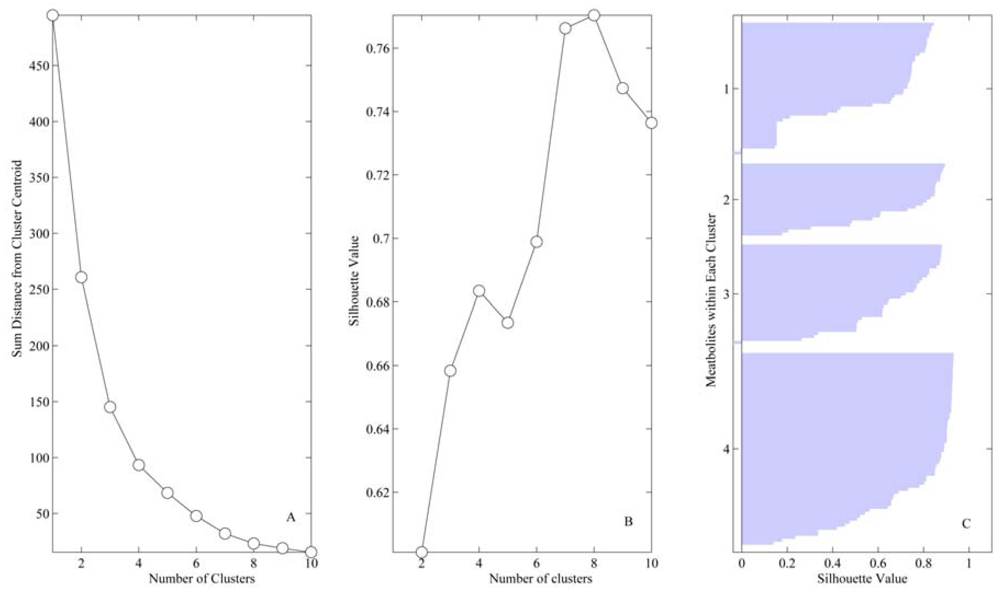
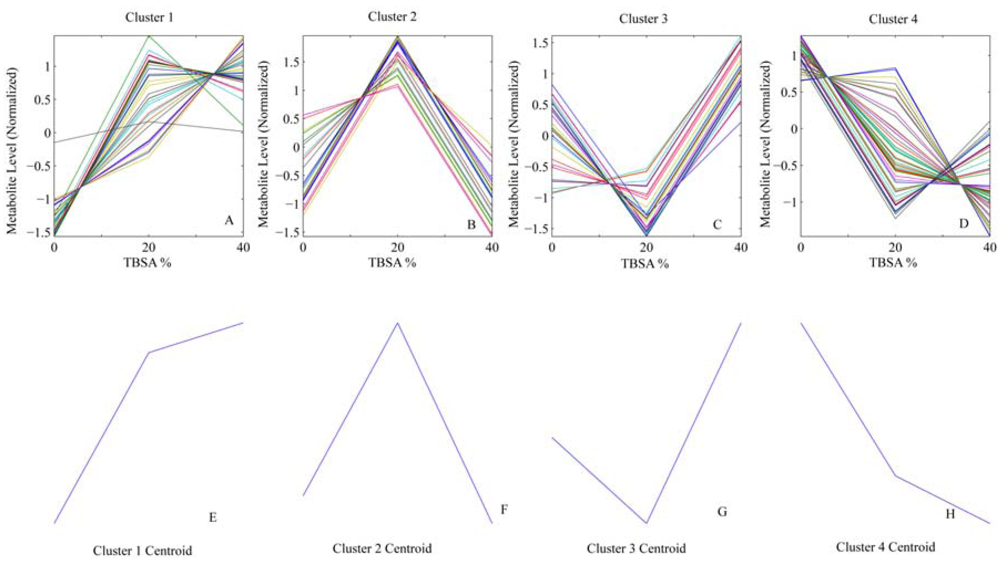
| Variable | Vessel | Cluster | Sham (median ± IQR) | 20%(median ± IQR) | 40%(median ± IQR) |
|---|---|---|---|---|---|
| Arginine | HA | 1 | 110.51 ± 10.239 | 182.13 ± 83.525 | 181.24 ± 14.245 |
| Creatinine (Cre) | HA | 1 | 0.2 ± 0 | 0.2 ± 0.05 | 0.2 ± 0 |
| Cysteine | HA | 1 | 15.76 ± 6.57 | 21.36 ± 0.92 | 25.55 ± 1.524 |
| Fraction of Carboxyhemoglobin (FCOHb) | HA | 1 | 7.9 ± 0.35 | 8.3 ± 1.5 | 8.5 ± 0.8 |
| Fraction of Methlyated hemoglobin (Fmeth) | HA | 1 | 0 ± 0 | 0 ± 0 | 0 ± 0 |
| Low Density Lipoprotein (LDL) | HA | 1 | 18 ± 14 | 22 ± 6 | 38 ± 8.75 |
| Ornithine | HA | 1 | 98.84 ± 22.359 | 117.73 ± 2.414 | 139.78 ± 12.129 |
| Total Bilirubin (TBIL) | HA | 1 | 0.3 ± 0.075 | 0.3 ± 0 | 0.3 ± 0.1 |
| Total cholesterol/HDL ratio (TC/H) | HA | 1 | 2.1 ± 0.1 | 2.2 ± 0.3 | 2.2 ± 0.05 |
| Arginine | PV | 1 | 113.3 ± 104.288 | 227.17 ± 42.862 | 223.04 ± 5.409 |
| Aspartate Amino Transferase (AST) | PV | 1 | 74 ± 16.5 | 83 ± 32.5 | 88 ± 27.5 |
| AST/ALT | PV | 1 | 1.73 ± 0.599 | 1.91 ± 0.82 | 2.1 ± 0.893 |
| Cholesterol | PV | 1 | 56 ± 24.5 | 74.5 ± 21.75 | 79 ± 10 |
| Creatinine (Cre) | PV | 1 | 0.2 ± 0 | 0.2 ± 0.05 | 0.2 ± 0 |
| Cysteine | PV | 1 | 14.89 ± 2.658 | 16.46 ± 1.543 | 16.55 ± 1.155 |
| Fraction of Carboxyhemoglobin (FCOHb) | PV | 1 | 7.2 ± 0.8 | 8.1 ± 1 | 7.7 ± 0.75 |
| Flow Rate | PV | 1 | 9 ± 9.226 | 20.5 ± 10.2 | 22 ± 6.5 |
| Fraction of Methlyated hemoglobin (Fmeth) | PV | 1 | 0 ± 0 | 0 ± 0.05 | 0 ± 0.1 |
| Isoleucine | PV | 1 | 91.03 ± 34.218 | 100.74 ± 12.663 | 99.65 ± 3.513 |
| Low Density Lipoprotein (LDL) | PV | 1 | 17 ± 6 | 30 ± 6 | 42.5 ± 9.5 |
| Leucine | PV | 1 | 243.09 ± 67.215 | 308.18 ± 25.007 | 336.71 ± 23.168 |
| Lysine | PV | 1 | 215.96 ± 92.604 | 234.02 ± 21.353 | 269.19 ± 20.227 |
| Phenylalanine | PV | 1 | 58.35 ± 9.465 | 65.69 ± 4.891 | 66.63 ± 7.422 |
| Total Bilirubin (TBIL) | PV | 1 | 0.3 ± 0.05 | 0.3 ± 0.05 | 0.3 ± 0.05 |
| Total cholesterol/HDL ratio (TC/H) | PV | 1 | 1.9 ± 0.1 | 2 ± 0.1 | 2.3 ± 0.05 |
| Total CO2 | PV | 1 | 20 ± 4.5 | 23 ± 0 | 23 ± 3.5 |
| Threonine | PV | 1 | 175.33 ± 61.707 | 219.96 ± 60.936 | 228.44 ± 50.882 |
| Tyrosine | PV | 1 | 62.95 ± 8.409 | 73.73 ± 6.036 | 78.49 ± 8.038 |
| Valine | PV | 1 | 176.6 ± 62.552 | 206.26 ± 19.143 | 206.03 ± 4.825 |
| Arginine | SHVC | 1 | 62.27 ± 2.077 | 211.01 ± 23.971 | 206.12 ± 37.934 |
| AST/ALT | SHVC | 1 | 2.03 ± 0.786 | 2.41 ± 1.036 | 2.36 ± 0.913 |
| Blood Urea Nitrogen (BUN) | SHVC | 1 | 13 ± 2 | 15.5 ± 1.5 | 17.5 ± 2.5 |
| Cholesterol | SHVC | 1 | 49 ± 10 | 55 ± 22 | 74 ± 7 |
| Creatinine (Cre) | SHVC | 1 | 0.2 ± 0 | 0.2 ± 0.05 | 0.2 ± 0 |
| Cysteine | SHVC | 1 | 12.07 ± 0.595 | 16.68 ± 2.042 | 18.37 ± 2.285 |
| Flow Rate | SHVC | 1 | 9.5 ± 9.255 | 20.9 ± 10.2 | 22.2 ± 6.7 |
| Fraction of Methlyated hemoglobin (Fmeth) | SHVC | 1 | 0.25 ± 0.25 | 0.3 ± 0.15 | 0.3 ± 0.3 |
| Isoleucine | SHVC | 1 | 79.1 ± 12.184 | 103.88 ± 12.065 | 103.42 ± 8.164 |
| Potassium (K) | SHVC | 1 | 3.2 ± 0.95 | 4.2 ± 0.95 | 4 ± 1.15 |
| Low Density Lipoprotein (LDL) | SHVC | 1 | 17 ± 10.25 | 23 ± 6 | 36 ± 0 |
| Ornithine | SHVC | 1 | 77.44 ± 19.421 | 89.36 ± 35.165 | 123.36 ± 14.992 |
| Total Bilirubin (TBIL) | SHVC | 1 | 0.3 ± 0.05 | 0.3 ± 0 | 0.3 ± 0.05 |
| Total cholesterol/HDL ratio (TC/H) | SHVC | 1 | 2.05 ± 0.2 | 2.1 ± 0.1 | 2.2 ± 0 |
| Valine | SHVC | 1 | 121.63 ± 54.408 | 204.83 ± 24.603 | 206.6 ± 21.909 |
| AST/ALT | HA | 2 | 2 ± 0.752 | 2.48 ± 1.04 | 2.07 ± 0.733 |
| Chloride (Cl) | HA | 2 | 109 ± 10.5 | 114 ± 19 | 109 ± 10.5 |
| Fraction of Oxyhemoglobin (FO2Hb) | HA | 2 | 91.2 ± 4.85 | 91.5 ± 2.15 | 84.8 ± 8.35 |
| Sodium (Na) | HA | 2 | 143 ± 6 | 153 ± 16.5 | 142 ± 9 |
| Partial pressure of CO2 (pCO2) | HA | 2 | 43.95 ± 4.9 | 51.3 ± 12.65 | 46.8 ± 1.4 |
| pH | HA | 2 | 7.27 ± 0.059 | 7.3 ± 0.034 | 7.27 ± 0.042 |
| Partial Oxygen pressure (PO2) | HA | 2 | 106.2 ± 19.85 | 117.3 ± 18.5 | 100.35 ± 35.525 |
| Tyrosine | HA | 2 | 79.81 ± 17.969 | 88.17 ± 6.785 | 78.64 ± 8.325 |
| Acetoacetate | PV | 2 | 115.35 ± 115.91 | 134.15 ± 91.278 | 50.81 ± 115.089 |
| Alanine | PV | 2 | 391.58 ± 10.724 | 452.9 ± 113.48 | 395.22 ± 95.64 |
| Alanine Amino Transferase (ALT) | PV | 2 | 42 ± 11 | 46 ± 4.5 | 42 ± 4.5 |
| β-hydroxybutyrate | PV | 2 | 81.41 ± 87.551 | 103.82 ± 64.453 | 88.47 ± 49.107 |
| Blood Urea Nitrogen (BUN) | PV | 2 | 12 ± 5.5 | 16 ± 2.5 | 14 ± 3.5 |
| Fraction of Oxyhemoglobin (FO2Hb) | PV | 2 | 73.6 ± 12.4 | 82.7 ± 18.75 | 73.7 ± 15.2 |
| Glucose | PV | 2 | 143 ± 126.5 | 183 ± 55.5 | 147 ± 48.5 |
| Potassium (K) | PV | 2 | 3.7 ± 1.25 | 4.1 ± 0.7 | 3.7 ± 0.6 |
| Partial pressure of CO2 (pCO2) | PV | 2 | 55.6 ± 3.05 | 60.55 ± 5.5 | 57.5 ± 2.3 |
| pH | PV | 2 | 7.28 ± 0.01 | 7.3 ± 0.077 | 7.26 ± 0.028 |
| Acetoacetate | SHVC | 2 | 126.21 ± 27.78 | 126.21 ± 13.89 | 30.96 ± 95.246 |
| Aspartate Amino Transferase (AST) | SHVC | 2 | 84 ± 16 | 85 ± 13 | 80 ± 31 |
| Fraction of Oxyhemoglobin (FO2Hb) | SHVC | 2 | 23.3 ± 5.55 | 28.7 ± 17.65 | 14.1 ± 14 |
| Leucine | SHVC | 2 | 218.34 ± 52.758 | 261.92 ± 91.466 | 210.42 ± 147.222 |
| pH | SHVC | 2 | 7.29 ± 0.02 | 7.32 ± 0.055 | 7.25 ± 0.021 |
| Partial Oxygen pressure (PO2) | SHVC | 2 | 27.2 ± 0.725 | 41.9 ± 15.6 | 15.1 ± 11.4 |
| Alkaline phosphatase (ALP) | HA | 3 | 192 ± 96.5 | 113 ± 21 | 194 ± 74 |
| Aspartate Amino Transferase (ALT) | HA | 3 | 49.5 ± 14.25 | 36 ± 7.5 | 39 ± 11.5 |
| β-hydroxybutyrate | HA | 3 | 183.61 ± 194.894 | 65.45 ± 39.132 | 165.2 ± 104.353 |
| Blood Urea Nitrogen (BUN) | HA | 3 | 12.5 ± 7 | 13 ± 1.5 | 17 ± 4.5 |
| Calcium (Ca) | HA | 3 | 8.5 ± 1.25 | 7 ± 1 | 8.8 ± 0.85 |
| Cholesterol | HA | 3 | 56.5 ± 14.75 | 58 ± 13 | 73 ± 21 |
| Fraction of Deoxyhemoglobin in Total Hemoglobin (FHHb) | HA | 3 | 0.3 ± 4.45 | 0.2 ± 0.4 | 0.3 ± 7.15 |
| Glutamine | HA | 3 | 406.45 ± 97.249 | 344.31 ± 47.021 | 414.34 ± 24.774 |
| High Density Lipoprotein (HDL) | HA | 3 | 33 ± 5 | 27 ± 18 | 36 ± 6.75 |
| Histidine | HA | 3 | 65.3 ± 0.404 | 61.03 ± 9.453 | 67.39 ± 8.07 |
| Lactate | HA | 3 | 0.84 ± 0.944 | 0.58 ± 0.942 | 3.47 ± 1.49 |
| Lysine | HA | 3 | 220.96 ± 66.163 | 181.93 ± 25.467 | 224.74 ± 13.38 |
| Phenylalanine | HA | 3 | 65.09 ± 7.564 | 63.2 ± 3.598 | 67.17 ± 1.202 |
| Total CO2 | HA | 3 | 21 ± 1.5 | 19 ± 1.5 | 25 ± 3 |
| Total Protein (TP) | HA | 3 | 5.3 ± 0.5 | 3.7 ± 0.7 | 4.7 ± 0.3 |
| Alkaline phosphatase (ALP) | PV | 3 | 174 ± 69 | 151 ± 33.5 | 184 ± 78 |
| Chloride (Cl) | PV | 3 | 110 ± 14.5 | 109 ± 13 | 112 ± 7 |
| Fraction of Deoxyhemoglobin in Total Hemoglobin (FHHb) | PV | 3 | 19.2 ± 13.25 | 9.2 ± 19.7 | 18.6 ± 15.85 |
| High Density Lipoprotein (HDL) | PV | 3 | 36 ± 12 | 33 ± 4.5 | 35.5 ± 2.5 |
| Histidine | PV | 3 | 140.94 ± 16.226 | 120.93 ± 9.821 | 147.78 ± 19.839 |
| Lactate | PV | 3 | 1.07 ± 0.095 | 0.68 ± 0.632 | 4.38 ± 1.986 |
| Sodium (Na) | PV | 3 | 146 ± 6.5 | 146 ± 12.5 | 149 ± 2.5 |
| Ornithine | PV | 3 | 119.81 ± 4.751 | 107.16 ± 6.154 | 120.82 ± 17.96 |
| Proline | PV | 3 | 161.22 ± 18.151 | 162.06 ± 8.013 | 171.2 ± 35.127 |
| Fraction of Deoxyhemoglobin in Total Hemoglobin (FHHb) | SHVC | 3 | 71.1 ± 6 | 59 ± 15.8 | 80 ± 13.45 |
| High Density Lipoprotein (HDL) | SHVC | 3 | 26.5 ± 6 | 24 ± 5 | 33 ± 0 |
| Histidine | SHVC | 3 | 53.01 ± 9.45 | 52.2 ± 18.937 | 61.6 ± 6.314 |
| Lactate | SHVC | 3 | 1 ± 0.34 | 0.74 ± 0.141 | 3.81 ± 2.135 |
| Lysine | SHVC | 3 | 205.05 ± 79.978 | 197.38 ± 80.877 | 210.04 ± 29.84 |
| Sodium (Na) | SHVC | 3 | 148 ± 7 | 148 ± 12.5 | 149 ± 7.5 |
| Partial pressure of CO2 (pCO2) | SHVC | 3 | 55.2 ± 6.9 | 51.3 ± 3.75 | 67.4 ± 7 |
| Total CO2 | SHVC | 3 | 22 ± 4 | 22 ± 2 | 25 ± 0.75 |
| Tyrosine | SHVC | 3 | 61.88 ± 6.68 | 61.29 ± 9.773 | 68.37 ± 7.3 |
| Acetoacetate | HA | 4 | 116.29 ± 22.819 | 110.34 ± 47.623 | 70.65 ± 31.749 |
| Alanine | HA | 4 | 348.27 ± 41.954 | 297.32 ± 22.715 | 281.4 ± 33.083 |
| Albumin | HA | 4 | 1.95 ± 0.175 | 1.2 ± 0.3 | 1.3 ± 0.25 |
| Alanine Amino Transferase (ALT) | HA | 4 | 49.5 ± 14.25 | 36 ± 7.5 | 39 ± 11.5 |
| Ammonia | HA | 4 | 49.7 ± 4.527 | 37.3 ± 4.081 | 23.1 ± 4.616 |
| Asparagine | HA | 4 | 41.98 ± 5.488 | 34.51 ± 3.945 | 32.73 ± 6.58 |
| Aspartate | HA | 4 | 11.83 ± 1.549 | 9.25 ± 5.852 | 10.16 ± 2.637 |
| Hemoglobin (%) | HA | 4 | 12.4 ± 1.35 | 12 ± 2.4 | 10.4 ± 1.05 |
| Flow Rate | HA | 4 | 0.65 ± 0.146 | 0.5 ± 0.069 | 0.5 ± 0.426 |
| Glucose | HA | 4 | 169 ± 87 | 134 ± 46 | 146.5 ± 16 |
| Glutamate | HA | 4 | 76.85 ± 6.662 | 54.15 ± 19.137 | 46.84 ± 17.453 |
| Glycine | HA | 4 | 216.75 ± 16.195 | 184.88 ± 25.974 | 163.76 ± 19.223 |
| Hematocrit | HA | 4 | 36 ± 3.5 | 35 ± 7 | 31 ± 3 |
| Isoleucine | HA | 4 | 113.82 ± 47.423 | 112.05 ± 19.396 | 108.01 ± 32.529 |
| Potassium (K) | HA | 4 | 4.25 ± 2.15 | 4.2 ± 1.45 | 3.9 ± 0.75 |
| Leucine | HA | 4 | 369.7 ± 174.817 | 275.1 ± 32.956 | 285.2 ± 87.999 |
| Methionine | HA | 4 | 52.33 ± 11.417 | 40.59 ± 8.321 | 38.75 ± 9.047 |
| Proline | HA | 4 | 164.52 ± 9.956 | 147.7 ± 27.492 | 147.69 ± 7.333 |
| Serine | HA | 4 | 223.83 ± 54.196 | 159.53 ± 12.872 | 169.06 ± 26.87 |
| Triglycerides (TG) | HA | 4 | 62 ± 35.75 | 29 ± 7 | 26 ± 6 |
| Threonine | HA | 4 | 256.03 ± 36.785 | 229.07 ± 41.332 | 202.04 ± 15.094 |
| Valine | HA | 4 | 234.98 ± 107.828 | 184.35 ± 36.559 | 178.74 ± 33.851 |
| Very low density lipoprotein (VLDL) | HA | 4 | 13 ± 0.5 | 6 ± 1 | 5 ± 0.5 |
| Albumin | PV | 4 | 2 ± 0.275 | 1.3 ± 0.35 | 1.3 ± 0.2 |
| Ammonia | PV | 4 | 108.65 ± 61.525 | 43.74 ± 33.121 | 72.67 ± 10.709 |
| Asparagine | PV | 4 | 51.08 ± 6.886 | 32.09 ± 3.895 | 31.74 ± 0.837 |
| Aspartate | PV | 4 | 19.18 ± 11.097 | 12.7 ± 1.594 | 12.06 ± 2.288 |
| Calcium (Ca) | PV | 4 | 8.7 ± 2.25 | 8.3 ± 0.55 | 7.9 ± 1.65 |
| Hemoglobin (%) | PV | 4 | 14.6 ± 0.95 | 13 ± 1.75 | 12.8 ± 0.5 |
| Glutamate | PV | 4 | 63.16 ± 13.278 | 42.22 ± 11.148 | 48.44 ± 15.319 |
| Glutamine | PV | 4 | 279.12 ± 59.911 | 253.05 ± 70.109 | 250.29 ± 33.243 |
| Glycine | PV | 4 | 273.49 ± 48.285 | 222.25 ± 33.939 | 204.59 ± 46.681 |
| Hematocrit | PV | 4 | 43 ± 3.5 | 40 ± 5 | 38 ± 2.5 |
| Methionine | PV | 4 | 44.77 ± 4.889 | 44.17 ± 4.749 | 43.82 ± 3.209 |
| Partial Oxygen pressure (PO2) | PV | 4 | 69.9 ± 11.75 | 54.2 ± 8.1 | 62.9 ± 15.65 |
| Serine | PV | 4 | 202.59 ± 14.805 | 148.88 ± 30.334 | 156.79 ± 14.701 |
| Triglycerides (TG) | PV | 4 | 52 ± 43 | 25.5 ± 11.75 | 23 ± 2 |
| Total Protein (TP) | PV | 4 | 5 ± 1.25 | 4.7 ± 0.9 | 4.8 ± 0.85 |
| Very low density lipoprotein (VLDL) | PV | 4 | 13 ± 5 | 6 ± 1 | 5 ± 0.5 |
| Alanine | SHVC | 4 | 246.38 ± 53.891 | 156.72 ± 42.529 | 152.26 ± 14.02 |
| Albumin | SHVC | 4 | 1.9 ± 0.25 | 1.3 ± 0.25 | 1.2 ± 0.25 |
| Alkaline phosphatase (ALP) | SHVC | 4 | 166 ± 67.5 | 129 ± 21 | 147 ± 82 |
| Alanine Amino Transferase (ALT) | SHVC | 4 | 40 ± 15.5 | 38 ± 14 | 37 ± 5.5 |
| Ammonia | SHVC | 4 | 40.44 ± 2.622 | 21.86 ± 10.951 | 15.01 ± 9.875 |
| Asparagine | SHVC | 4 | 27.87 ± 1.556 | 20.1 ± 3.165 | 18.34 ± 0.097 |
| Aspartate | SHVC | 4 | 13.57 ± 1.938 | 10.37 ± 4.932 | 8.47 ± 0.817 |
| β-hydroxybutyrate | SHVC | 4 | 275.69 ± 457.311 | 257.28 ± 244.001 | 223.51 ± 174.944 |
| Calcium (Ca) | SHVC | 4 | 8.6 ± 2.5 | 7.9 ± 0.3 | 8 ± 1.5 |
| Chloride (Cl) | SHVC | 4 | 111 ± 14.5 | 110.5 ± 4.75 | 109 ± 11 |
| Hemoglobin (%) | SHVC | 4 | 12.75 ± 0.875 | 10.7 ± 1.75 | 11.6 ± 0.65 |
| Fraction of Carboxyhemoglobin (FCOHb) | SHVC | 4 | 290 ± 73.75 | 130 ± 24 | 176 ± 50 |
| Glucose | SHVC | 4 | 263 ± 73 | 186 ± 72.5 | 152 ± 36.25 |
| Glutamate | SHVC | 4 | 76.77 ± 43.277 | 49.62 ± 15.79 | 44.7 ± 19.093 |
| Glutamine | SHVC | 4 | 299.7 ± 56.737 | 254.82 ± 97.786 | 228.06 ± 93.284 |
| Glycine | SHVC | 4 | 192.45 ± 57.864 | 148.04 ± 8.773 | 117.74 ± 58.252 |
| Hematocrit | SHVC | 4 | 37.5 ± 2.5 | 31 ± 5 | 34 ± 1.5 |
| Methionine | SHVC | 4 | 38.47 ± 1.541 | 32.45 ± 2.444 | 34.55 ± 1.049 |
| Phenylalanine | SHVC | 4 | 54.68 ± 3.359 | 52.83 ± 15.86 | 49.57 ± 14.92 |
| Proline | SHVC | 4 | 137.82 ± 37.486 | 115.64 ± 6.032 | 113.16 ± 16.448 |
| Serine | SHVC | 4 | 166.82 ± 20.803 | 105.99 ± 12.727 | 92.92 ± 42.759 |
| Triglycerides (TG) | SHVC | 4 | 25 ± 28.5 | 20 ± 3 | 20 ± 0 |
| Threonine | SHVC | 4 | 198.18 ± 20.372 | 186.17 ± 59.461 | 157.26 ± 6.575 |
| Total Protein (TP) | SHVC | 4 | 4.9 ± 1.05 | 4.3 ± 0.45 | 4 ± 0.85 |
| Very low density lipoprotein (VLDL) | SHVC | 4 | 9.5 ± 4.5 | 5 ± 0 | 5 ± 0 |
| Cluster | # variables in vessel/flux | ||||
|---|---|---|---|---|---|
| Hepatic Artery | Portal Vein | Vena Cava | Liver Flux | Total | |
| 1 | 9 | 20 | 15 | 9 | 45 |
| 2 | 8 | 10 | 6 | 8 | 26 |
| 3 | 15 | 9 | 9 | 15 | 36 |
| 4 | 23 | 16 | 25 | 23 | 68 |
| Total | 55 | 55 | 55 | 5 | |
4.1. Model Selection and Index of Burn Injury Severity
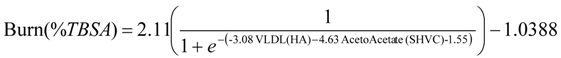
| Average Relative Accuracy | Variable 1 | Variable 2 | |
|---|---|---|---|
| RBF | 46.06 ± 4.59 | Ammonia (HA) | Ornithine (SHVC) |
| DT | 70.54 ± 7.83 | Asparagine (SHVC) | ALB (HA) |
| M5P-DT | 72.36 ± 1.03 | ALB (HA) | Ammonia (HA) |
| LR | 73.28 ± 0.55 | VLDL (HA) | Acetoacetate (SHVC) |
| SMOR | 75.92 ± 2.20 | VLDL (HA) | Acetoacetate (SHVC) |
| M5-R | 87.82 ± 1.31 | VLDL (HA) | Asparagine (SHVC) |
| NN | 87.89 ± 2.79 | VLDL (HA) | Acetoacetate (SHVC) |
| Method | Measure | 2 Variables | 3 Variables | 4 Variables | 5 Variables |
|---|---|---|---|---|---|
| NN | Average Relative Accuracy | 87.89 ± 2.789 | 89.46 ± 1.379 | 90.69 ± 1.508 | 89.18 ± 1.552 |
| Selected Variables | VLDL (HA), Acetoacetate (SHVC) | VLDL (HA), Acetoacetate (SHVC), pO2 (SHVC) | VLDL (SHVC), Acetoacetate (SHVC), pO2 (SHVC), CO2 (HA) | VLDL (SHVC), Acetoacetate (SHVC), pO2 (SHVC), Asparagine (SHVC), CO2 (HA) | |
| M5-R | Average Relative Accuracy | 87.82 ± 1.312 | 88.71 ± 0.983 | 87.66 ± 1.398 | 87.11 ± 1.038 |
| Selected Variables | VLDL (HA), Asparagine (SHVC) | Albumin (HA), Asparagine (SHVC), BUN (PV) | VLDL (HA), Acetoacetate (SHVC), Albumin (HA), pCO2(SHVC) | VLDL (HA), Acetoacetate (SHVC), Albumin (HA), pCO2(SHVC) Asparagine (SHVC) |
| Instance | Burn % (actual) | Predictions | |||
|---|---|---|---|---|---|
| 2 Variable Model (%burn) | 3 Variable Model (%burn) | 4 Variable Model (%burn) | 5 Variable Model (%burn) | ||
| 1 | 0 | 0.132 | 0.324 | 1.35 | 1.271 |
| 2 | 0 | −0.281 | −0.373 | −0.423 | −0.320 |
| 3 | 0 | 3.003 | 0.109 | 0.05 | −0.195 |
| 4 | 0 | −0.614 | 0.415 | −0.632 | −0.52 0a |
| 5 | 0 | 0.309 | −0.713 | −0.011 | −0.013 |
| 6 | 0 | −0.416 | −0.213 | −0.451 | −0.635 |
| 7 | 0 | −0.281 | 0.079 | −0.301 | −0.229 |
| 8 | 20 | 19.048 | 19.876 | 20.654 | 20.528 |
| 9 | 20 | 19.048 | 20.171 | 18.383 | 18.014 |
| 10 | 20 | 19.048 | 19.585 | 19.72 | 19.590 |
| 11 | 20 | 19.048 | 19.585 | 19.72 | 19.59 0 |
| 12 | 20 | 25.415 | 19.686 | 19.993 | 19.715 |
| 13 | 20 | 19.048 | 19.510 | 18.22 | 17.947 |
| 14 | 20 | 20.255 | 20.757 | 20.651 | 17.947 |
| 15 | 40 | 40.709 | 39.911 | 39.795 | 39.246 |
| 16 | 40 | 40.957 | 40.268 | 40.919 | 40.870 |
| 17 | 40 | 40.709 | 40.091 | 40.045 | 39.633 |
| 18 | 40 | 41.238 | 39.938 | 39.866 | 39.709 |
| 19 | 40 | 41.221 | 38.822 | 39.612 | 39.620 |
| 20 | 40 | 39.865 | 39.757 | 38.984 | 38.333 |
| 21 | 40 | 36.667 | 39.739 | 39.708 | 39.546 |
| Relative Absolute Error | 8.49% | 2.54% | 4.10% | 5.04% | |
5. Discussion and Conclusions
Acknowledgements
References
- Herndon, D.N.; Tompkins, R.G. Support of the metabolic response to burn injury. Lancet 2004, 363, 1895–1902. [Google Scholar] [CrossRef]
- Bosaeus, I. Nutritional support in multimodal therapy for cancer cachexia. Support. Care Cancer 2008, 16, 447–451. [Google Scholar] [CrossRef]
- Hart, D.W.; Wolf, S.E.; Herndon, D.N.; Chinkes, D.L.; Lal, S.O.; Obeng, M.K.; Beauford, R.B.; Mlcak, R.P. Energy expenditure and caloric balance after burn. Increased feeding leads to fat rather than lean mass accretion. Ann. Surg. 2002, 235, 152–161. [Google Scholar] [CrossRef]
- Patterson, B.W.; Nguyen, T.; Pierre, E.; Herndon, D.N.; Wolfe, R.R. Urea and protein metabolism in burned children: Effect of dietary protein intake. Metabolism 1997, 46, 573–578. [Google Scholar] [CrossRef]
- Windle, E.M. Glutamine supplementation in critical illness: Evidence, recommendations, and implications for clinical practice in burn care. J. Burn Care Res. 2006, 27, 764–772. [Google Scholar] [CrossRef]
- Yu, Y.M.; Young, V.R.; Tompkins, R.G.; Burke, J.F. Relationships among arginine, citrulline, ornithine, and leucine kinetics in adult burn patients. Am. J. Clin. Nutr. 1995, 62, 960–968. [Google Scholar]
- Jeschke, M.G.; Herndon, D.N.; Ebener, C.; Barrow, R.E.; Jauch, K.-W. Nutritional intervention high in vitamins, protein, amino acids, and omega-3 fatty acids improves protein metabolism during the hypermetabolic state after thermal injury. Arch. Surg. 2001, 136, 1301–1306. [Google Scholar] [CrossRef]
- Cree, M.G.; Newcomer, B.R.; Herndon, D.N.; Qian, T.; Sun, D.Y.; Morio, B.; Zwetsloot, J.J.; Dohm, G.L.; Fram, R.Y.; Aarsland, A.; et al. PPAR-alpha agonism improves whole body and muscle mitochondrial fat oxidation, but does not alter intracellular fat concentrations in burn trauma children. Fed. Am. Soc. Exp. Biol. 2007, A839. [Google Scholar]
- Cree, M.G.; Wolfe, R.R. Postburn trauma insulin resistance and fat metabolism. Am. J. Physiol. Endocrinol. Metab. 2008, 294, E1–E9. [Google Scholar]
- Gore, D.C.; Herndon, D.N.; Wolfe, R.R. Comparison of peripheral metabolic effects of insulin and metformin following severe burn injury. J. Trauma 2005, 59, 316–322. [Google Scholar] [CrossRef]
- Pierre, E.J.; Barrow, R.E.; Hawkins, H.K.; Nguyen, T.T.; Sakurai, Y.; Desai, M.; Wolfe, R.R.; Herndon, D.N. Effects of insulin on wound healing. J. Trauma 1998, 44, 342–345. [Google Scholar] [CrossRef]
- Van den Berghe, G.; Wouters, P.; Weekers, F.; Verwaest, C.; Bruyninckx, F.; Schetz, M.; Vlasselaers, D.; Ferdinande, P.; Lauwers, P.; Bouillon, R. Intensive insulin therapy in critically ill patients. N. Engl. J. Med. 2001, 345, 1359–1367. [Google Scholar] [CrossRef]
- Wanek, S.; Wolf, S.E. Metabolic response to injury and role of anabolic hormones. Curr. Opin. Clin. Nutr. Metab. Care 2007, 10, 272–277. [Google Scholar] [CrossRef]
- Herndon, D.N.; Hart, D.W.; Wolf, S.E.; Chinkes, D.L.; Wolfe, R.R. Reversal of catabolism by beta-blockade after severe burns. N. Engl. J. Med. 2001, 345, 1223–1229. [Google Scholar] [CrossRef]
- De-Souza, D.A.; Greene, L.J. Pharmacological nutrition after burn injury. J. Nutr. 1998, 128, 797–803. [Google Scholar]
- Cioffi, W.G. What's new in burns and metabolism. J. Am. Coll. Surg. 2001, 192, 241–254. [Google Scholar] [CrossRef]
- Steuer, R. Review: On the analysis and interpretation of correlations in metabolomic data. Brief. Bioinform. 2006, 7, 151–158. [Google Scholar] [CrossRef]
- Yarmush, D.M.; MacDonald, A.D.; Foy, B.D.; Berthiaume, F.; Tompkins, R.G.; Yarmush, M.L. Cutaneous burn injury alters relative tricarboxylic acid cycle fluxes in rat liver. J. Burn Care Rehabil. 1999, 20, 292–302. [Google Scholar] [CrossRef]
- Yamaguchi, Y.; Yu, Y.M.; Zupke, C.; Yarmush, D.M.; Berthiaume, F.; Tompkins, R.G.; Yarmush, M.L. Effect of burn injury on glucose and nitrogen metabolism in the liver: Preliminary studies in a perfused liver system. Surgery 1997, 121, 295–303. [Google Scholar] [CrossRef]
- Chen, C.L.; Fei, Z.; Carter, E.A.; Lu, X.M.; Hu, R.H.; Young, V.R.; Tompkins, R.G.; Yu, Y.M. Metabolic fate of extrahepatic arginine in liver after burn injury. Metabolism 2003, 52, 1232–1239. [Google Scholar] [CrossRef]
- Izamis, M.L.; Sharma, N.S.; Uygun, B.; Bieganski, R.; Saeidi, N.; Nahmias, Y.; Uygun, K.; Yarmush, M.L.; Berthiaume, F. In situ metabolic flux analysis to quantify the liver metabolic response to experimental burn injury. Biotechnol. Bioeng. 2011, 108, 839–852. [Google Scholar] [CrossRef]
- Kaddurah-Daouk, R.; Kristal, B.S.; Weinshilboum, R.M. Metabolomics: A global biochemical approach to drug response and disease. Annu. Rev. Pharmacol. Toxicol. 2008, 48, 653–683. [Google Scholar] [CrossRef]
- Beger, R.; Holland, R.; Sun, J.; Schnackenberg, L.; Moore, P.; Dent, C.; Devarajan, P.; Portilla, D. Metabonomics of acute kidney injury in children after cardiac surgery. Pediatr. Nephrol. 2008, 23, 977–984. [Google Scholar] [CrossRef]
- Keun, H.C.; Athersuch, T.J. Application of metabonomics in drug development. Pharmacogenomics 2007, 8, 731–741. [Google Scholar] [CrossRef]
- Clayton, A.T.; Lindon, J.C.; Cloarec, O.; Antti, H.; Charuel, C.; Hanton, G.; Provost, J.-P.; Le Net, J.-L.c.; Baker, D.; Walley, R.J.; et al. Pharmaco-metabonomic phenotyping and personalized drug treatment. Nature 2006, 440, 1073–1077. [Google Scholar] [CrossRef]
- Erb, G.; Elbayed, K.; Piotto, M.; Raya, J.; Neuville, A.; Mohr, M.; Maitrot, D.; Kehrli, P.; Namer, I.J. Toward improved grading of malignancy in oligodendrogliomas using metabolomics. Magn. Reson. Med. 2008, 59, 959–965. [Google Scholar] [CrossRef]
- Banta, S.; Vemula, M.; Yokoyama, T.; Jayaraman, A.; Berthiaume, F.; Yarmush, M.L. Contribution of gene expression to metabolic fluxes in hypermetabolic livers induced through burn injury and cecal ligation and puncture in rats. Biotechnol. Bioeng. 2007, 97, 118–137. [Google Scholar] [CrossRef]
- Banta, S.; Yokoyama, T.; Berthiaume, F.; Yarmush, M.L. Quantitative effects of thermal injury and insulin on the metabolism of the skeletal muscle using the perfused rat hindquarter preparation. Biotechnol. Bioeng. 2004, 88, 613–629. [Google Scholar] [CrossRef]
- Uygun, K.; Matthew, H.W.T.; Huang, Y.L. DFBA-LQR: An optimal control approach to flux balance analysis. Ind. Eng. Chem. Res. 2006, 45, 8554–8564. [Google Scholar] [CrossRef]
- Uygun, K.; Matthew, H.W.T.; Huang, Y. Investigation of metabolic objectives in cultured hepatocytes. Biotechnol. Bioeng. 2007, 97, 622–637. [Google Scholar] [CrossRef]
- Barber, R.C.; Maass, D.L.; White, J.; Horton, J.W. Increasing percent burn is correlated with increasing inflammation in an adult rodent model. Shock 2008, 30, 388–393. [Google Scholar] [CrossRef]
- Barrow, R.E.; Meyer, N.A.; Jeschke, M.G. Effect of varying burn sizes and ambient temperature on the hypermetabolic rate in thermally injured rats. J. Surg. Res. 2001, 99, 253–257. [Google Scholar] [CrossRef]
- Kaufman, L.; Rousseeuw, P. Finding Groups in Data: An Introduction to Cluster Analysis; Wiley: New York, NY, USA, 1990. [Google Scholar]
- Yang, E.; Maguire, T.; Yarmush, M.L.; Berthiaume, F.; Androulakis, I.P. Bioinformatics analysis of the early inflammatory response in a rat thermal injury model. BMC Bioinform. 2007, 8, 10. [Google Scholar] [CrossRef]
- Picard, R.R.; Cook, R.D. Cross-validation of regression-models. J. Am. Stat. Assoc. 1984, 79, 575–583. [Google Scholar]
- Witten, I.H.; Frank, E. Data Mining: Practical Machine Learning Tools and Techniques, 2nd ed; Morgan Kaufmann: San Francisco, CA, USA, 2005. [Google Scholar]
- Tukey, J.W. Exploratory Data Analysis; Addison-Wesley: Reading, MA, USA, 1977. [Google Scholar]
- Laun, R.A.; Rapsch, B.; Abel, W.; Schroder, O.; Roher, H.D.; Ekkernkamp, A.; Schulte, K.M. The determination of ketone bodies: Preanalytical, analytical and physiological considerations. Clin. Exp. Med. 2001, 1, 201–209. [Google Scholar] [CrossRef]
- Oda, S.; Hirasawa, H.; Sugai, T.; Shiga, H.; Matsuda, K.; Ueno, H. Cellular injury score for multiple organ failure severity scoring system. J. Trauma 1998, 45, 304–310, discussion 310–311.. [Google Scholar] [CrossRef]
- Martini, W.Z.; Irtun, O.; Chinkes, D.L.; Rasmussen, B.; Traber, D.L.; Wolfe, R.R. Alteration of hepatic fatty acid metabolism after burn injury in pigs. JPEN J. Parenter. Enteral Nutr. 2001, 25, 310–316. [Google Scholar]
- Yu, Y.-M.; Young, V.R.; Castillo, L.; Chapman, T.E.; Tompkins, R.G.; Ryan, C.M.; Burke, J.F. Plasma arginine and leucine kinetics and urea production rates in burn patients. Metabolism 1995, 44, 659–666. [Google Scholar] [CrossRef]
- Yu, Y.M.; Ryan, C.M.; Castillo, L.; Lu, X.M.; Beaumier, L.; Tompkins, R.G.; Young, V.R. Arginine and ornithine kinetics in severely burned patients: increased rate of arginine disposal. Am. J. Physiol. Endocrinol. Metab. 2001, 280, E509–E517. [Google Scholar]
- Nakatani, T.; Spolter, L.; Kobayashi, K. Arterial ketone body ratio as a parameter of hepatic mitochondrial redox state during and after hemorrhagic shock. World J. Surg. 1995, 19, 592–596. [Google Scholar] [CrossRef]
- Ozawa, K.; Mori, K.; Morimoto, T. Evaluation of hepatic function. Curr. Opin. Gen. Surg. 1994, 17–23. [Google Scholar]
- Dong, Y.L.; Sheng, C.Y.; Herndon, D.N.; Waymack, J.P. Metabolic abnormalities of mitochondrial redox potential in postburn multiple system organ failure. Burns 1992, 18, 283–286. [Google Scholar] [CrossRef]
- Gore, D.C.; Rinehart, A.; Asimakis, G. Temporal changes in cellular energy following burn injury. Burns 2005, 31, 998–1002. [Google Scholar] [CrossRef]
- Banta, S.; Yokoyama, T.; Berthiaume, F.; Yarmush, M.L. Effects of dehydroepiandrosterone administration on rat hepatic metabolism following thermal injury. J. Surg. Res. 2005, 127, 93–105. [Google Scholar] [CrossRef]
- Izamis, M.; Uygun, K.; Uygun, B.; Yarmush, M.; Berthiaume, F. Effects of burn injury on markers of hypermetabolism in rats. J. Burn Care Res. 2009, 30, 993–1001. [Google Scholar] [CrossRef]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Izamis, M.-L.; Uygun, K.; Sharma, N.S.; Uygun, B.; Yarmush, M.L.; Berthiaume, F. Development of Metabolic Indicators of Burn Injury: Very Low Density Lipoprotein (VLDL) and Acetoacetate Are Highly Correlated to Severity of Burn Injury in Rats. Metabolites 2012, 2, 458-478. https://doi.org/10.3390/metabo2030458
Izamis M-L, Uygun K, Sharma NS, Uygun B, Yarmush ML, Berthiaume F. Development of Metabolic Indicators of Burn Injury: Very Low Density Lipoprotein (VLDL) and Acetoacetate Are Highly Correlated to Severity of Burn Injury in Rats. Metabolites. 2012; 2(3):458-478. https://doi.org/10.3390/metabo2030458
Chicago/Turabian StyleIzamis, Maria-Louisa, Korkut Uygun, Nripen S. Sharma, Basak Uygun, Martin L. Yarmush, and Francois Berthiaume. 2012. "Development of Metabolic Indicators of Burn Injury: Very Low Density Lipoprotein (VLDL) and Acetoacetate Are Highly Correlated to Severity of Burn Injury in Rats" Metabolites 2, no. 3: 458-478. https://doi.org/10.3390/metabo2030458
APA StyleIzamis, M.-L., Uygun, K., Sharma, N. S., Uygun, B., Yarmush, M. L., & Berthiaume, F. (2012). Development of Metabolic Indicators of Burn Injury: Very Low Density Lipoprotein (VLDL) and Acetoacetate Are Highly Correlated to Severity of Burn Injury in Rats. Metabolites, 2(3), 458-478. https://doi.org/10.3390/metabo2030458




