1. Introduction
Optimal Power Flow (OPF) plays a significant role in power systems operation and control. The OPF mainly aims to optimize a certain objective function, such as minimizing the generation fuel cost and at the same time, satisfying the load balance constraints and bound constraints [
1,
2]. Under normal conditions, all devices in power systems should operate within their pre-determined range. Such constraints include the maximum and minimum active and reactive power of the generation units, voltage levels, loadability of power transmission lines, and transformers tap settings. Minimizing the operating costs and increasing the reliability of power systems are two main objectives from the power companies and utilities’ point of view. Basically, the power flow problem focuses on the economic aspect of operating the power systems due to the fact that a slight change in power flow may significantly increase the operating costs of power systems. To do so, an objective function is optimized considering various equality and inequality constraints. Solving the OPF problem precisely leads to proper control, planning, and protection of power systems. The OPF problem can be divided into two major problems: (1) the optimal active power flow problem, and (2) the optimal reactive power flow problem. Numerous papers have investigated the OPF problem using conventional optimization methods, such as the Newton Raphson (NR) method, and evolutionary optimization techniques, such as particle swarm optimization (PSO) and artificial bee colony (ABC) optimization algorithms.
Increasing the load demand over the last few decades has created different problems in power systems in terms of power transmission congestion and constraints. Those limitations are mainly due to maintaining the stability and maintaining the voltage range of the power system at its permissible level [
3,
4]. Distributed Generations (DGs) are one of the best solutions to prevent congestion in the transmission lines [
5]. DGs have several advantages, such as reducing energy costs, improving power quality and reliability, and preventing environmental pollutions. Among different DGs, wind power is one of the most popular power generations. However, wind behavior is often unpredictable, as it is a stochastic phenomenon, thereby, needing proper uncertainty modeling. To cope with this challenge, many research studies in the literature have investigated different methods to model the random behavior of the wind power generation, as depicted in
Table 1.
Another way to enhance the capacity of the transmission systems is by employing Flexible AC Transmission System (FACTS) devices [
10]. FACTS devices play a crucial role in improving the flexibility of power transmission and guaranteeing the stability of power systems. FACTS devices are used for improving power flow regardless of the costs of generating power. Two primary goals of using FACTS devices are (1) increasing capacity of transmission systems by controlling some characteristics, such as series/shunt impedances and phase angle; (2) transmitting power through the desired paths.
Table 2 shows a summary of the previous research studies related to the FACTS devices. Therefore, the conventional OPF problem, integrated with FACTS devices can open new opportunities for controlling the active and reactive power flow.
To date, numerous papers on the OPF problem with various optimization techniques have been published. However, previous studies have not dealt with the OPF incorporating FACTS devices and stochastic wind power generation at the same time. In this regard, this paper proposes an OPF solution of power system considering FACTS devices and stochastic wind power generation using the krill herd algorithm (KHA). The wind power uncertainty is modeled in the optimization problem using the Weibull probability density function. Minimization of fuel cost, active power losses across the transmission lines, emission, and combined economic and environmental costs (CEEC) are the objective functions.
To the best of the authors’ knowledge, solving the OPF problem considering the minimization of fuel cost, active power losses across transmission lines, emission, and CEEC, incorporating FACTS devices and dealing with the stochastic behavior of wind power generation has not been investigated before. Compared with the other techniques, the proposed method has better performance and achieves more accurate results.
The followings are the major contributions of this research study:
Modeling and including the stochastic nature of wind power generation in the problem formulation.
Unlike the other research studies, in this paper, the OPF problem incorporating FACTS devices and stochastic wind power generation at the same time is solved.
The KHA is used to minimize the fuel cost, active power losses across the transmission lines, emission, and CEEC, as the objective functions.
This paper is divided into four sections. In
Section 2, the problem formulation is given. The results are presented in
Section 3. Finally, the conclusions are presented.
2. Problem Formulation
In this part, the OPF problem formulation in the presence of FACTS devices, including thyristor controlled phase shifter (TCPS) as well as thyristor-controlled series compensator (TCSC), and stochastic wind power generation is presented. The frequency distribution is one of the most essential tools for planning and operating in power systems, and its general structure is divided into two parts of the objective function and constraints.
2.1. General Formulation
The general formulation for the constrained optimization problem in this paper is as follows:
subject to:
where
is the objective function that should be minimized,
is the set of equality constraints, and
is the set of inequality constraints. It should be noted that for
number of components in power systems,
is the vector of dependent variables that contains the active power of the slack generator, voltage of the loads
, reactive power generation by the generation units
, and the lines loadability
. Also,
is the vector of independent variables that contains active power generation by the generation unit except for the slack bus
, voltage of the generators
, transformers tap settings
, and the injected reactive power by the FACTS devices
. It should be noted that
,
,
,
, and
show the maximum number of generation buses, load buses, transmission lines, transformer tap settings, and FACTS devices, respectively.
The constraints of the OPF problem include active and reactive power of the generation units, transformer tap settings, and the loading of the power transmission lines.
2.2. FACTS Devices Modeling
2.2.1. TCSC Modeling
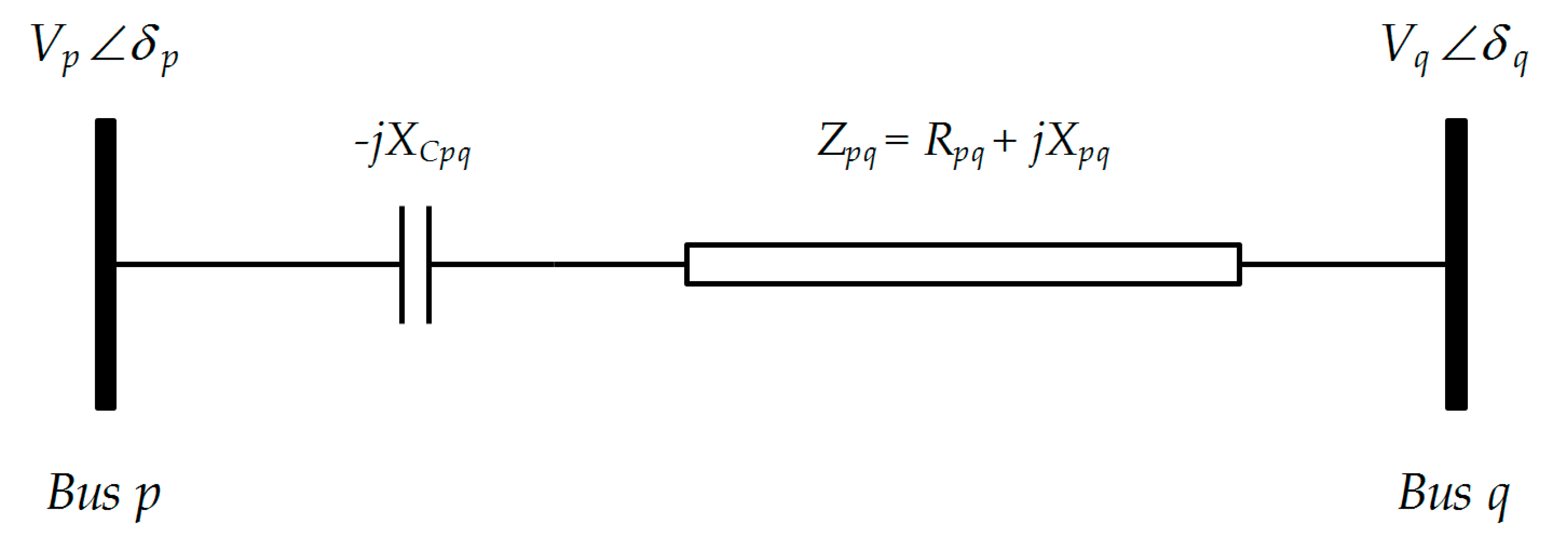
Figure 1 shows the static of a TCSC connected between bus
and
[
20,
21].
The power flow equations from bus
to bus
, including TCSC, are as follows [
21]:
where
where
and
are the active and reactive power flow from bus
to bus
with TCPS, respectively,
and
are the conductance and susceptance of transmission line between bus
and bus
, respectively,
and
are the voltage angles at the
bus and
bus, respectively,
and
denote the resistance and reactance of the transmission line between bus
and bus
, respectively, and lastly,
represents the reactance of the TCSC located in the transmission line between bus
and bus
.
Similarity, the power flow equations from bus
to bus
, including TCSC, are as follows:
where
and
are the active and reactive power flow from bus
to bus
with TCPS, respectively.
2.2.2. TCPS Modeling
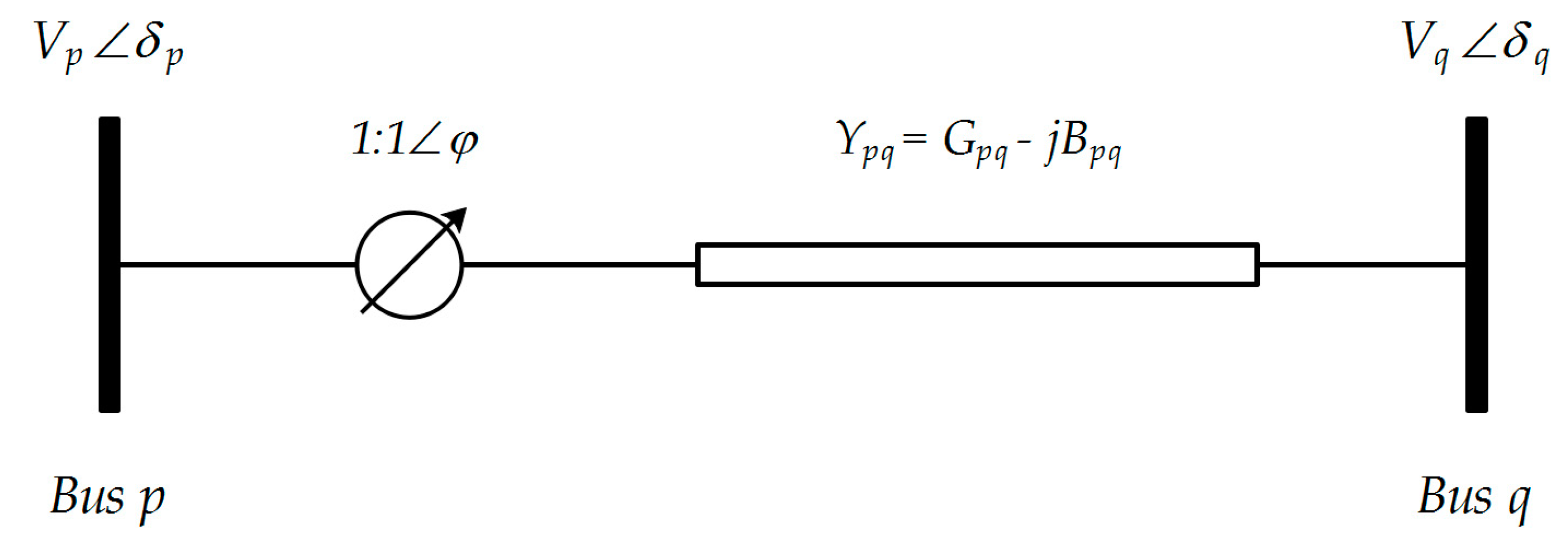
Figure 2 demonstrates the static of a TCPS connected between bus
and
, having a complex taping ratio of
and series admittance of
[
20].
The power flow equations from bus
to bus
, including the TCPS, are as follows:
where
and
are the active and reactive power flow from bus
to bus
with TCPS, respectively. In addition,
shows the phase shift angle of TCPS.
Likewise, the power flow equations from bus
to bus
, including the TCPS, are as follows:
where
and
are the active and reactive power flow from bus
to bus
with TCPS, respectively.
2.3. Wind Power Generation Modeling
The technology of wind turbines to generate electricity from wind can be divided into two major groups: (1) constant speed wind turbine, and (2) variable speed wind turbine. Fixed speed wind turbines are easy to install, more durable, and more affordable, while variable speed wind turbines should be installed according to the strategic and geographical conditions.
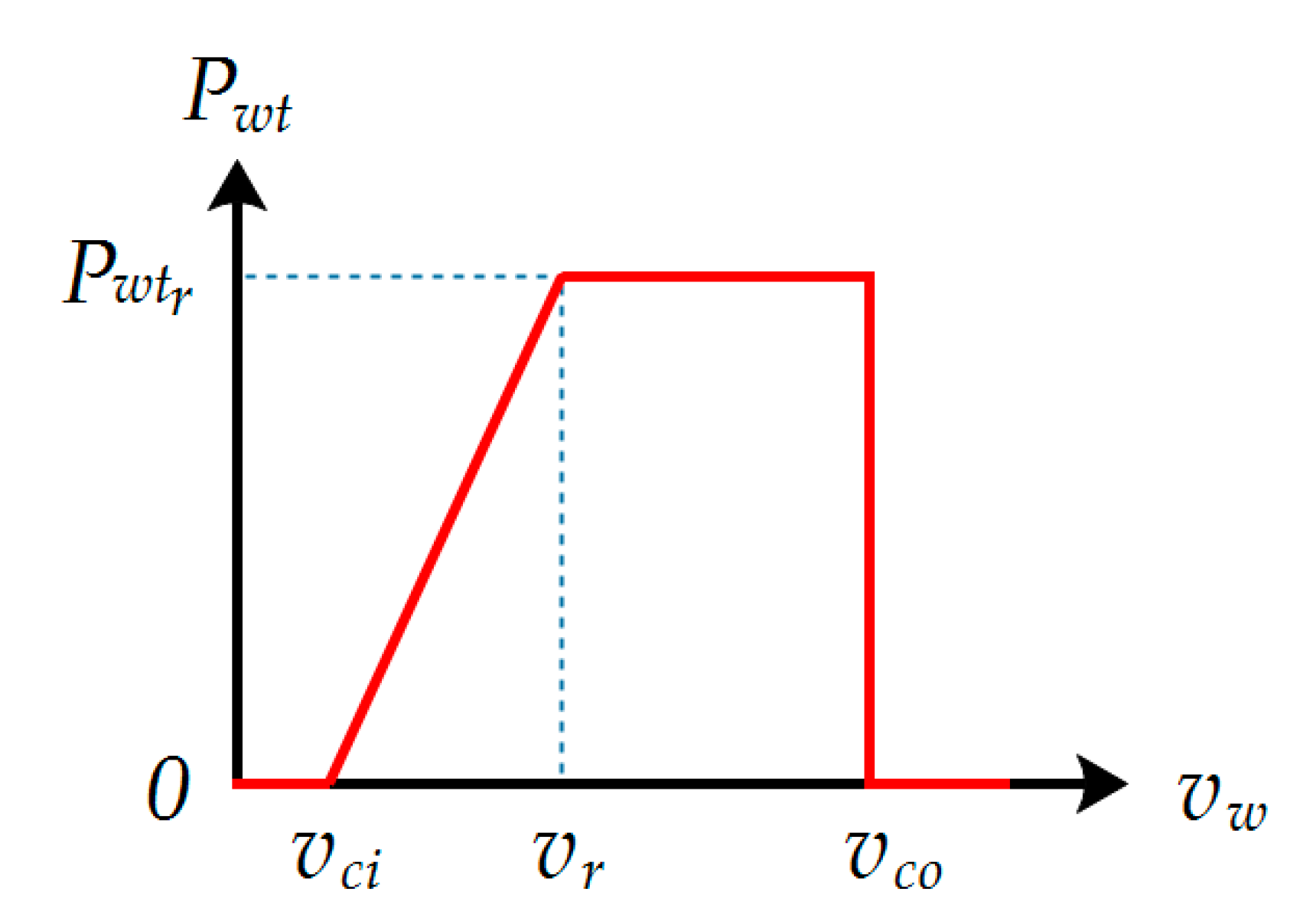
Figure 3 shows the output power curve of a typical wind turbine. In
Figure 3,
and
are the cut-in wind speed and cut-out wind speed, respectively,
is the rated wind speed, and
is the wind speed flowing into the wind turbine.
Since the wind speed is variable, the Weibull distribution is often considered as the probability density function that can be used to approximately model the behavior of the wind with a reasonable error. The Weibull distribution function to calculate the probability of the wind speed is as follows [
22,
23]:
where
shows the wind speed, and
(shape factor) and
(scale factor) are the wind speed parameters that vary depending on the region in which the wind blows.
It should be noted that to evaluate the power output of wind power, the problem has a general wind scenario, which initially generates a random number of wind speeds. Then, based on the Weibull distribution function considering the shape factor and scale factor, the probability of occurrence of those wind speeds is determined. Next, a certain number of wind speeds that most probably occur is selected. Finally, the average power of the wind farm is calculated.
2.4. Objective Functions
In this section, four different objective functions are presented.
2.4.1. Minimization of Fuel Cost
Fuel cost minimization with a quadratic function is considered as the first objective function, as follows [
24]:
where
is the total fuel cost of the generation units in (
$/h),
,
, and
are the fuel cost coefficients of the
generation unit,
shows the total number of generation units, and
denotes the generated active power by the
generation unit.
Considering the valve-point effect, Equation (15) can be rewritten as follows:
where
and
are the fuel cost coefficients to model the valve-point effect, and
denotes the minimum active power generated by the
generation unit.
2.4.2. Minimization of Active Power Losses across the Transmission Lines
This objective function can be formulated as follows:
where
is the total active power losses across the transmission lines in (MW),
is the conductance of the
transmission line connected between bus
and bus
,
is the total number of transmission lines,
and
are the voltage magnitudes of bus
and bus
, respectively, and
and
are the voltage angles of bus
and bus
, respectively.
2.4.3. Minimization of Emission
The third objective function is to minimize the total emission, which is formulated as follows:
where
is the total emission due to the generation of the
generation unit in (ton/h), and
,
,
,
, and
are the emission coefficients of the
generation unit.
2.4.4. Minimization of the Combined Economic and Environmental Costs
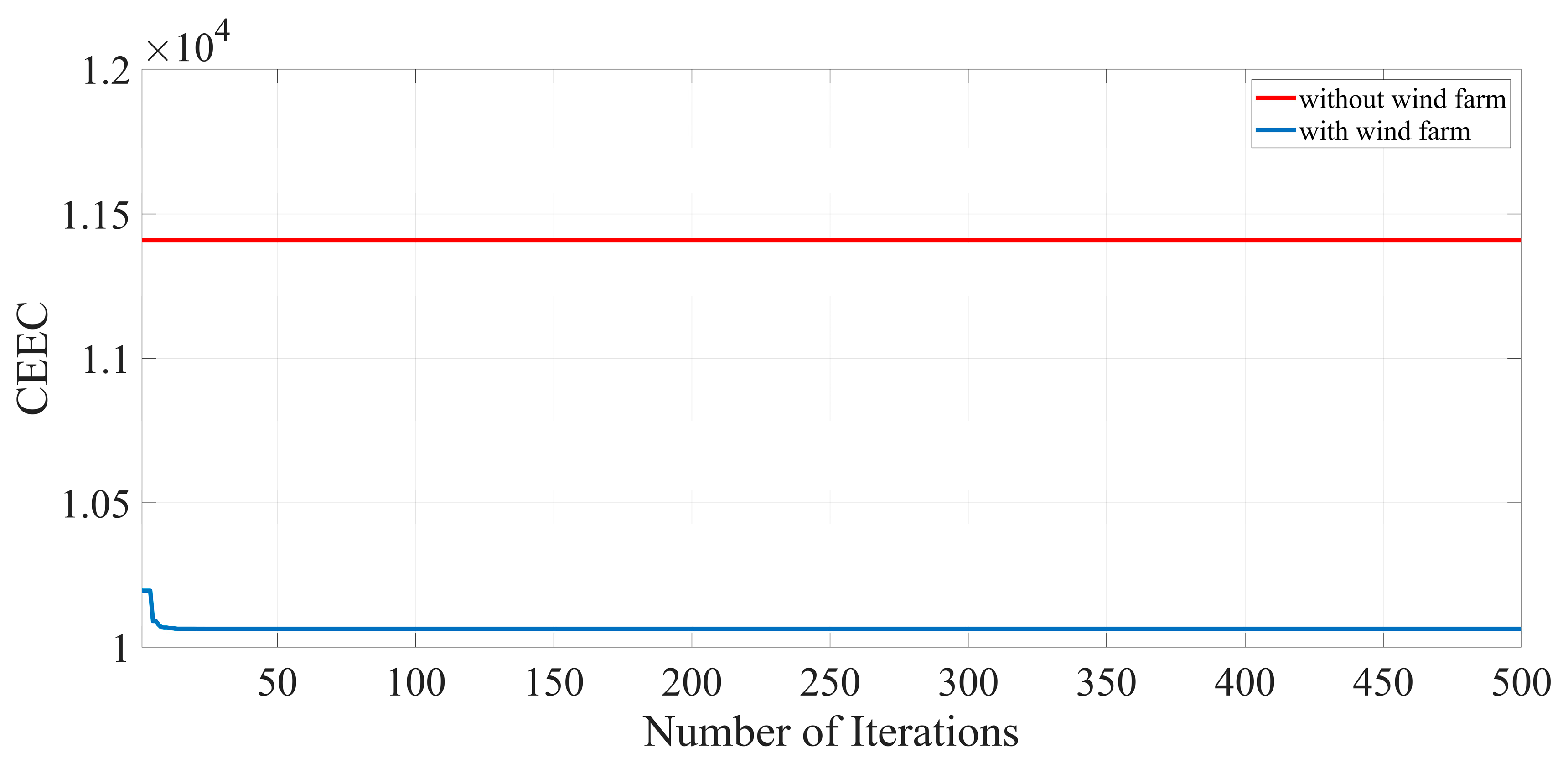
The last objective function is to minimize the CEEC according to Equations (15) and (17):
where
denotes the combined economic and environmental costs, and
is the penalty factor, and can be obtained as follows:
The pollution charge coefficient for each unit is defined as the amount of fuel cost divided by the amount of pollution at its maximum output active power ().
2.5. Constraints
In this section, different constraints are defined [
24].
2.5.1. Load Flow Constraints
where
and
are the generated active and reactive power at bus
, respectively,
and
are the consumed active and reactive power at bus
, respectively,
and
are the injected active and reactive power by the TCPSs at bus
, respectively,
indicates the generated active power by the wind turbine,
and
are the magnitude and phase of the admittance of the transmission line between bus
and bus
,
shows the total number of buses, and
denotes the total number of TCPSs.
2.5.2. Active and Reactive Power of the Generation Units
where for
(
is the total number of generators),
and
are the minimum and maximum limits of the active power of the
generator, respectively, and
and
are the minimum and maximum limits of the reactive power of the
generator, respectively.
2.5.3. Voltage at Each Bus
where for
(
is the total number of loads),
and
are the minimum and maximum level of the voltage at the
load center, respectively.
2.5.4. Transformer Tap Settings
where for
(
is the total number of transformers),
and
are the minimum and maximum tap settings limits of the
transformer, respectively.
2.5.5. Transmission Lines Loading
where for
(
is the total number of transmission lines),
and
are the apparent power flow and maximum apparent power flow of the
transmission line, respectively.
2.5.6. TCSC Reactance Constraints
where for
(
is the total number of TCSCs),
and
are the minimum and maximum reactance of the
TCSC, respectively.
2.5.7. TCPS Phase Shift
where for
(
is the total number of TCPSs),
and
are the minimum and maximum phase shift angle of the
TCPS, respectively.
2.6. Solution Method
The KHA is based on the herding behavior of krill swarms in response to the specific biological and environmental processes [
25]. In this paper, the KHA is used to solve the OPF problem incorporating stochastic wind power generation and FACTS devices considering uncertainty. The followings are the steps to implement the KHA.
Step 2:
Check the data structure
Step 4:
Fitness evaluation and check for constraints
Step 5:
Motion calculation
Induced motion
Foraging motion
Physical diffusion
Step 6:
Implementation of the genetic operator
Step 7:
Check the results based on updating the krill individual position in the search space
Step 8:
If the best results are achieved then
Go to Step 9
Otherwise
Go to Step 4
4. Conclusions
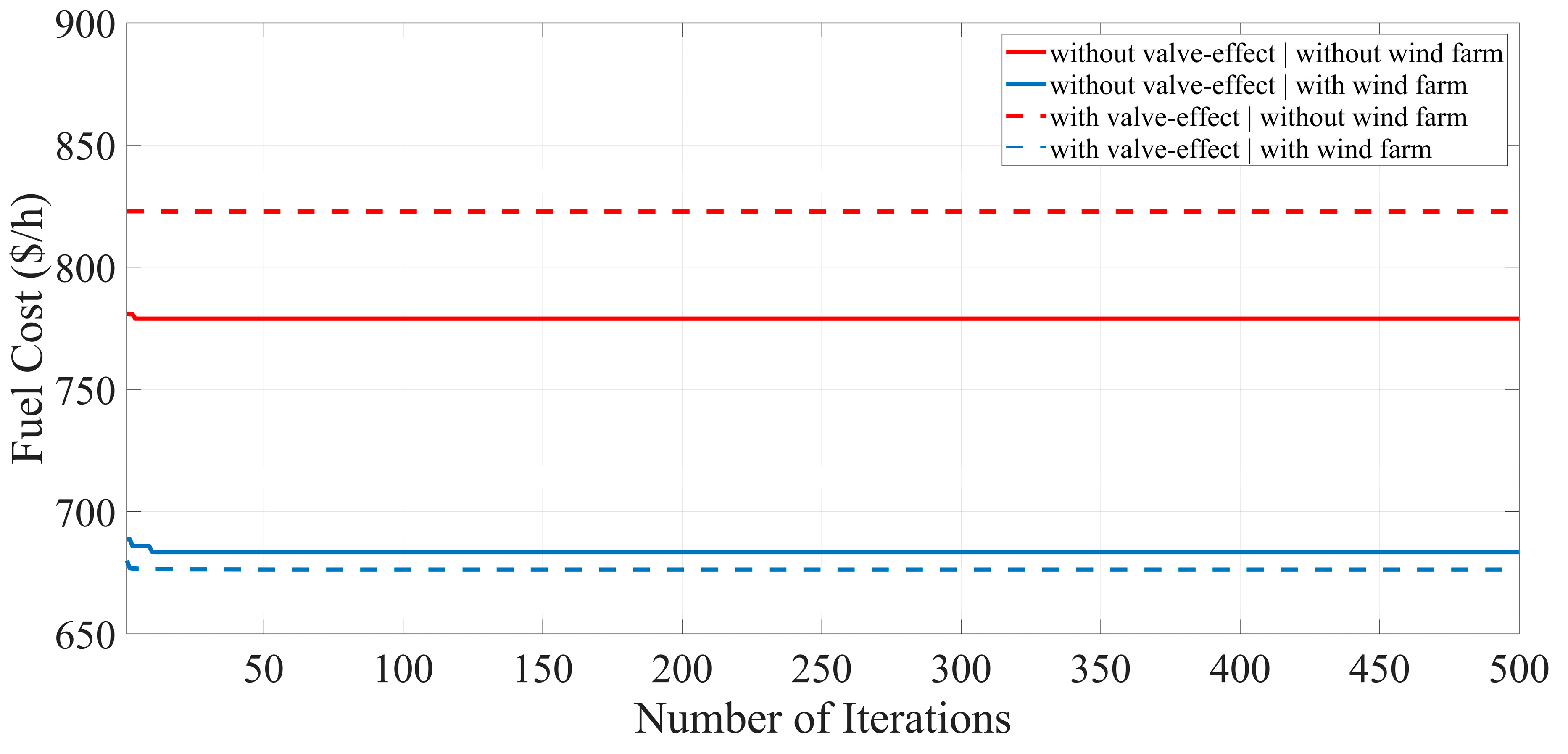
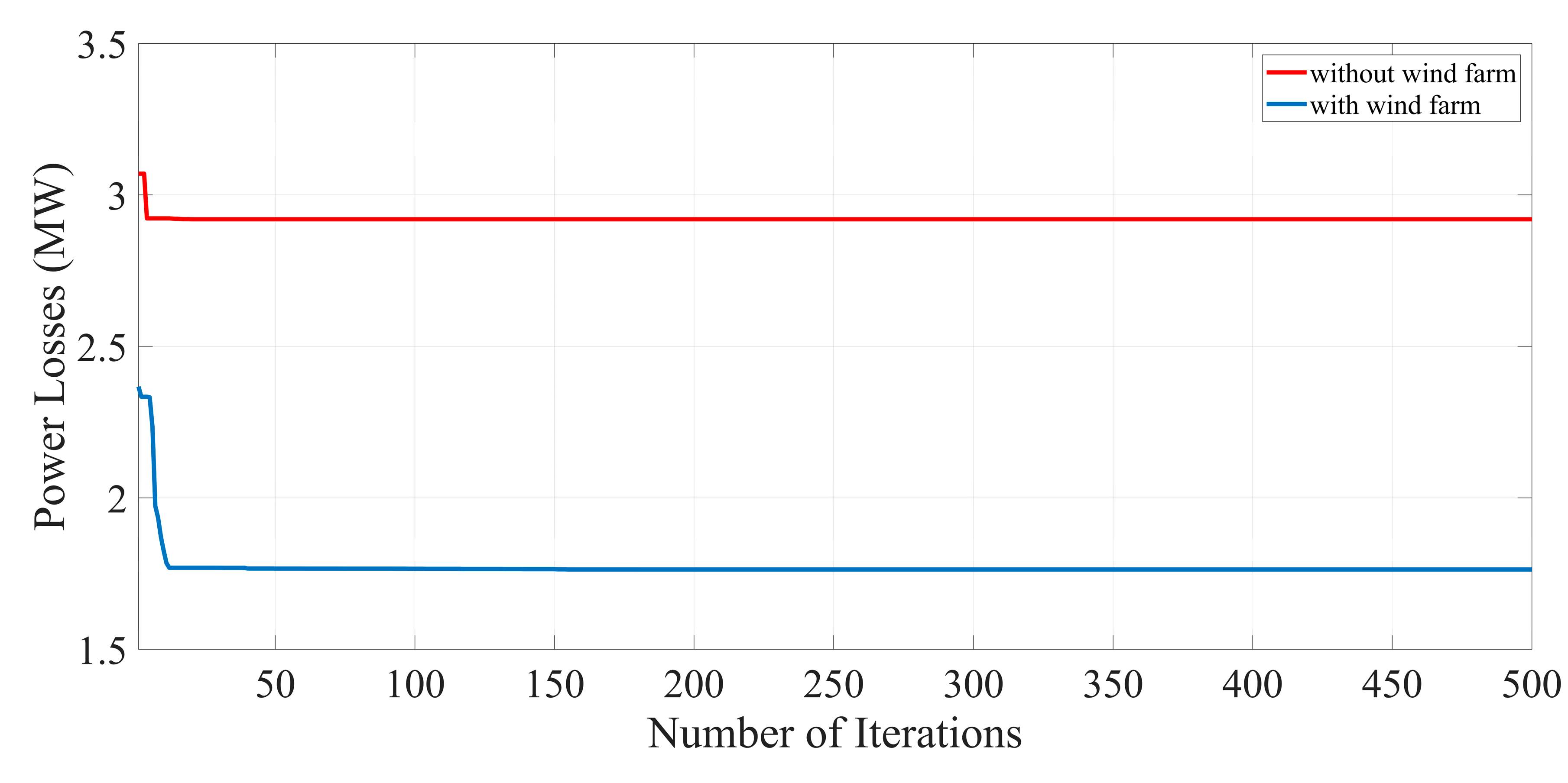
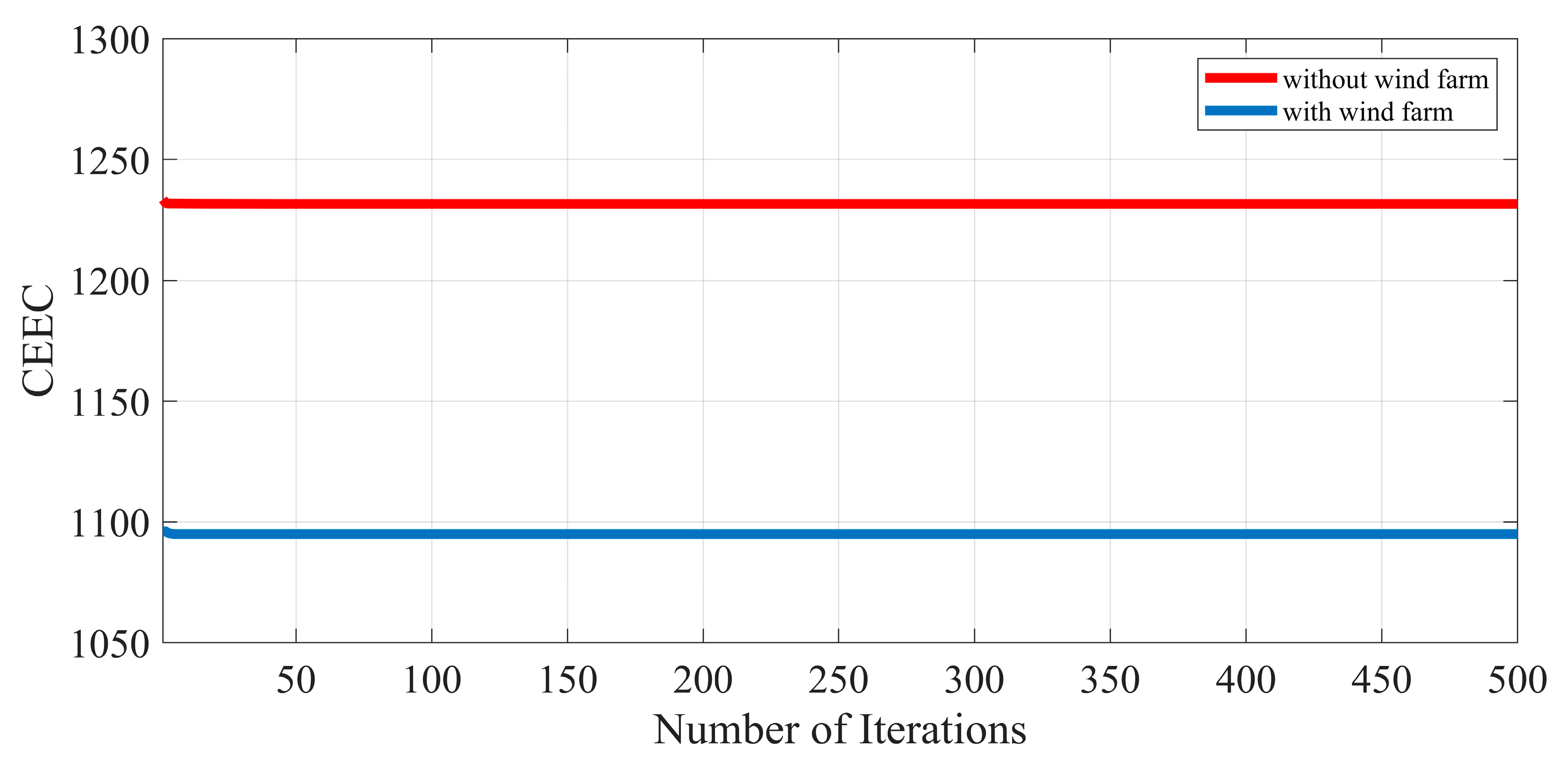
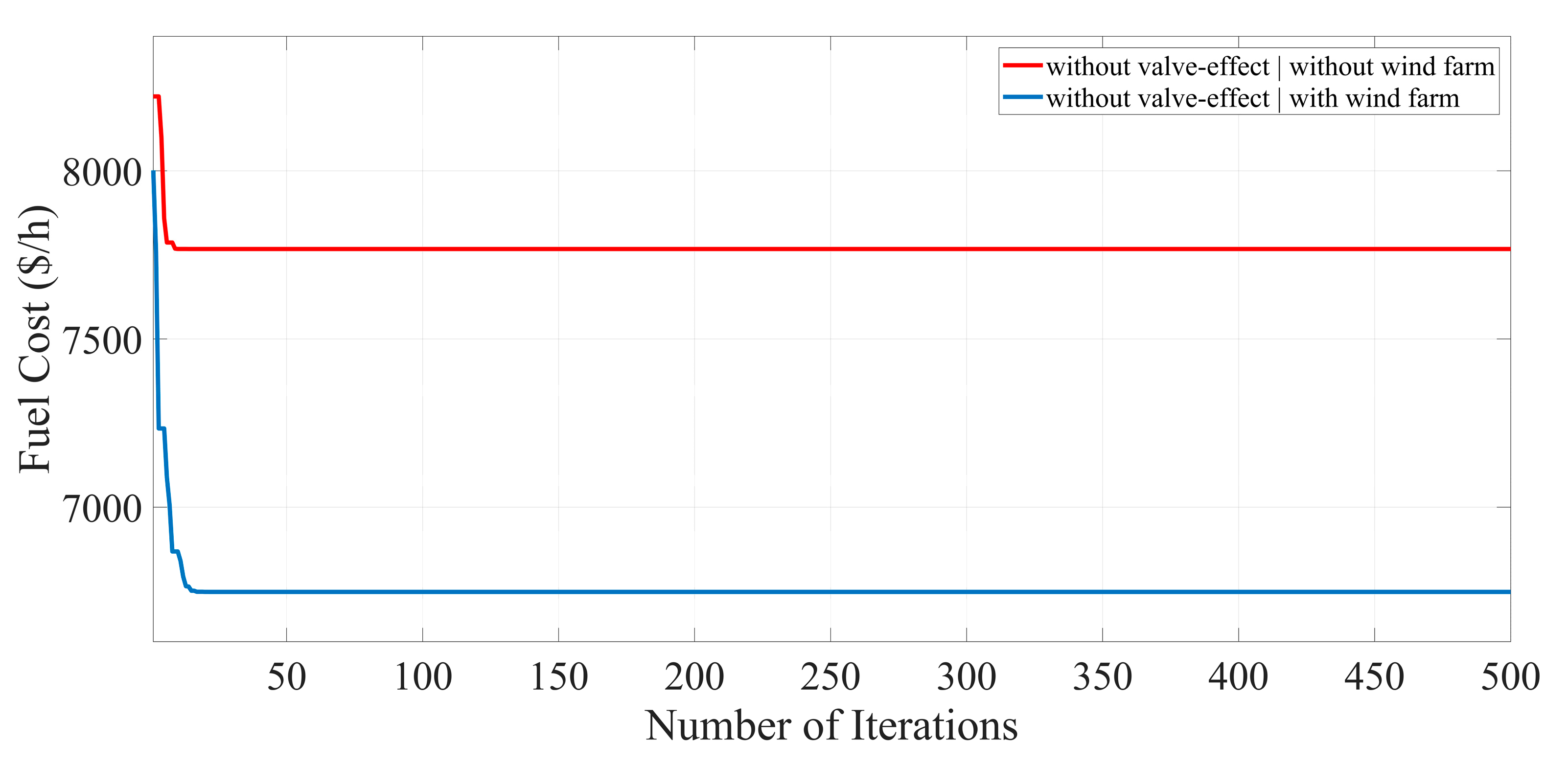
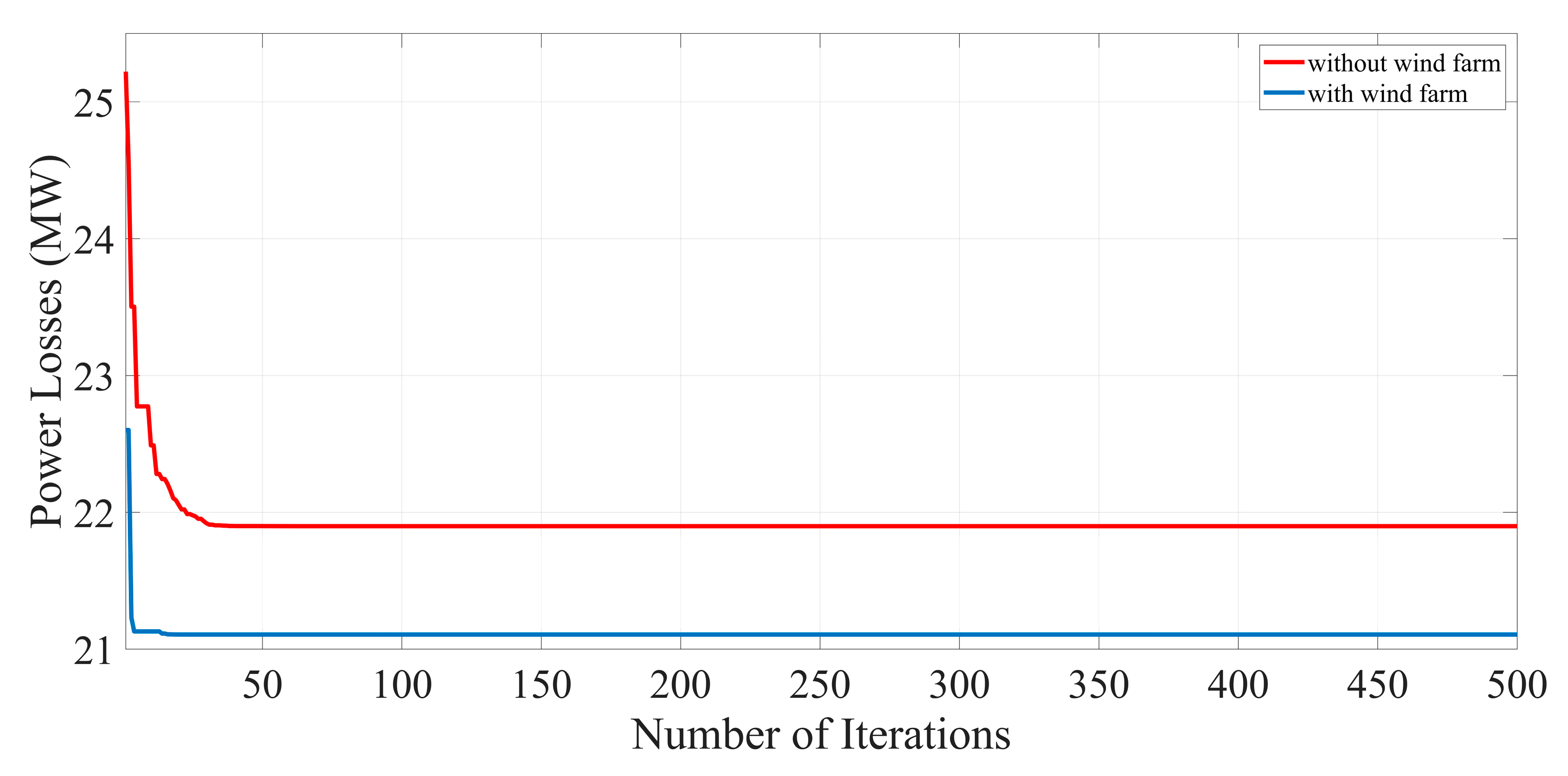
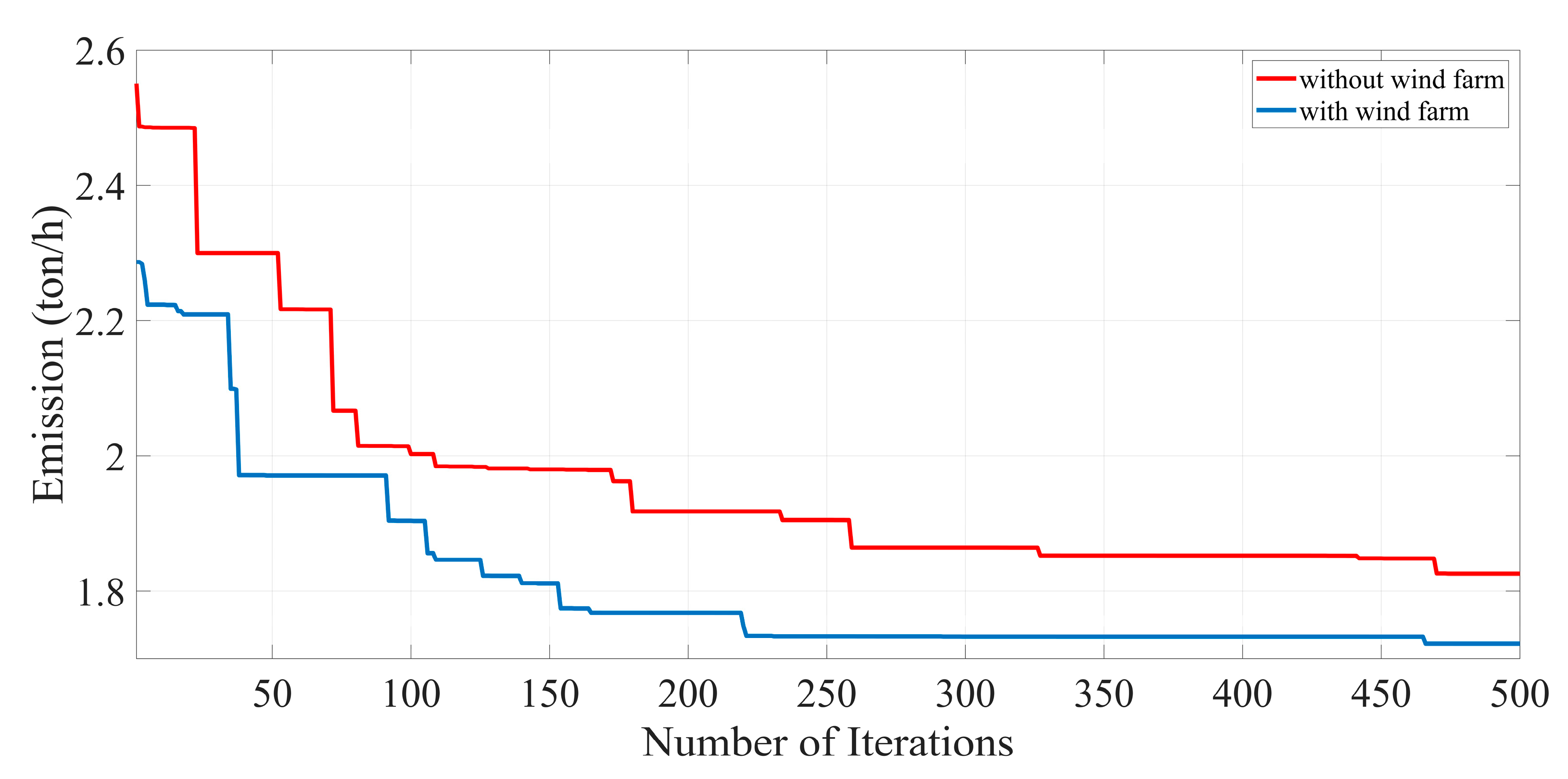
A new meta-heuristic algorithm is proposed in this paper to cope with the Optimal Power Flow (OPF) problem of power systems incorporated with wind farm and FACTS devices. Four different objective functions, including minimization of fuel cost, minimization of power losses across the transmission line, emission reduction, and combined economic and environmental cost minimization are formulated separately in this paper. To show the effectiveness of the proposed approach, the IEEE 30-bus test system and the IEEE 57-bus test system with the installation of thyristor controlled phase shifter (TCPS) and thyristor-controlled series compensator (TCSC) and a wind farm are simulated. Based on numerical results, it is observed that the krill herd algorithm (KHA) has great capability to achieve an optimal solution in the target functions with less computation time. The proposed method indicates an improved convergence performance to optimal solutions than other heuristic techniques and can be applied to cope with complex optimization problems in modern power systems. It can efficiently deal with the uncertainties in wind power generation. In addition, it is shown that the presence of the wind farm in power systems minimizes the d the generation capacity of the other generating unit, which reduces the dependency on conventional power plants, thus, reducing power losses across the transmission lines and reducing emission as well as the combined economic and environmental costs (CEEC).