Biosensor Using a One-Port Interdigital Capacitor: A Resonance-Based Investigation of the Permittivity Sensitivity for Microfluidic Broadband Bioelectronics Applications
Abstract
:1. Introduction
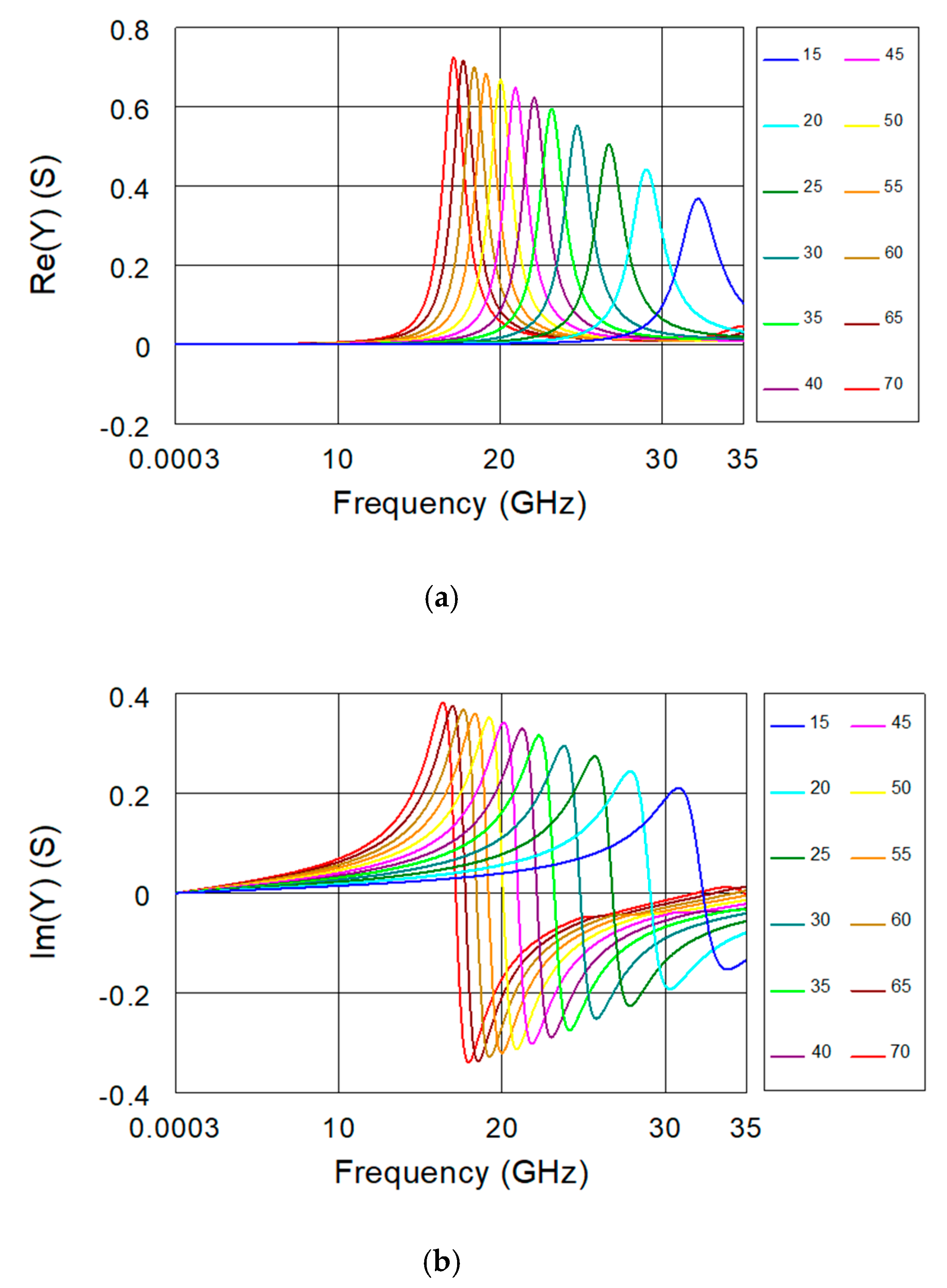
2. Biosensor Description and FEM Simulations
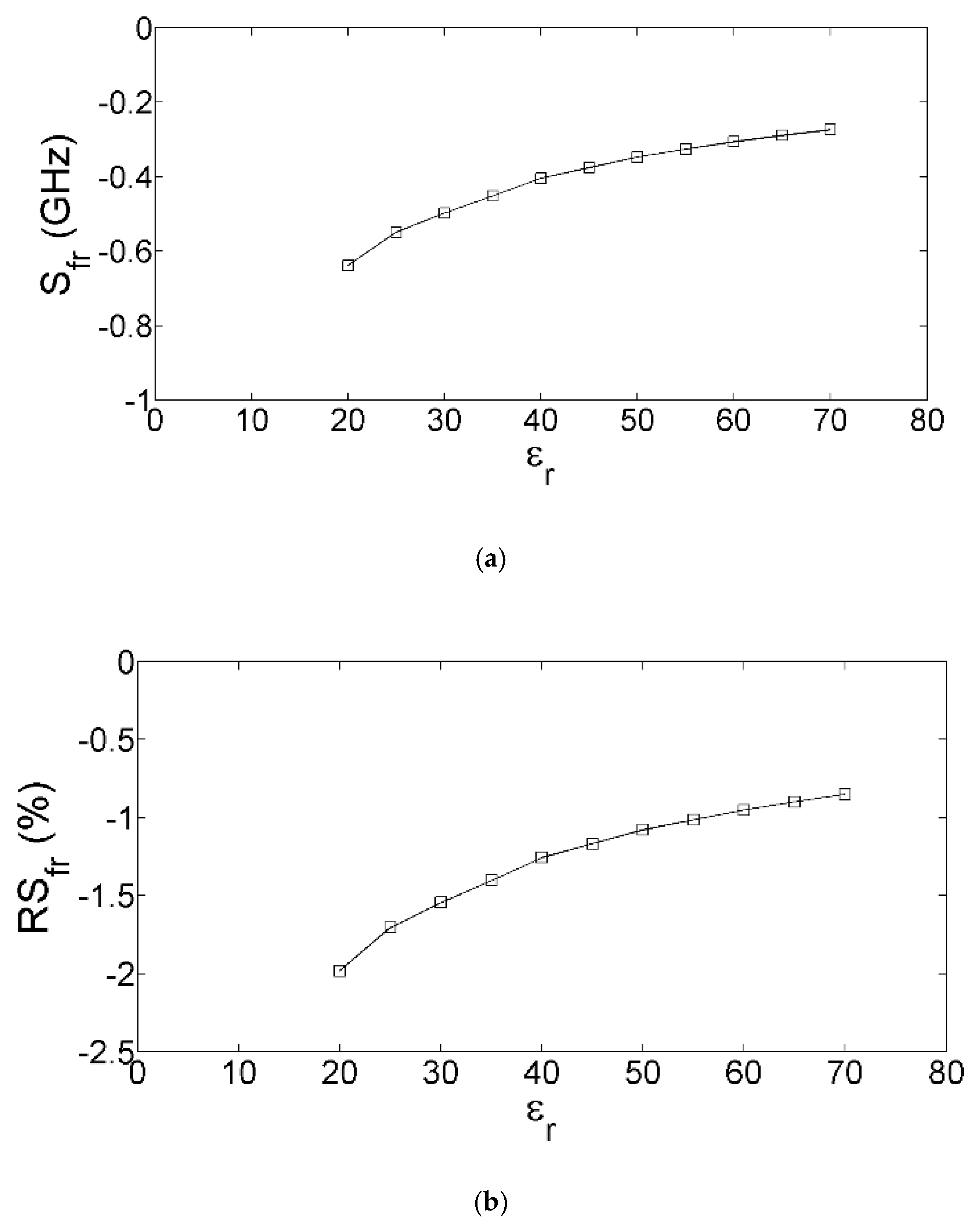
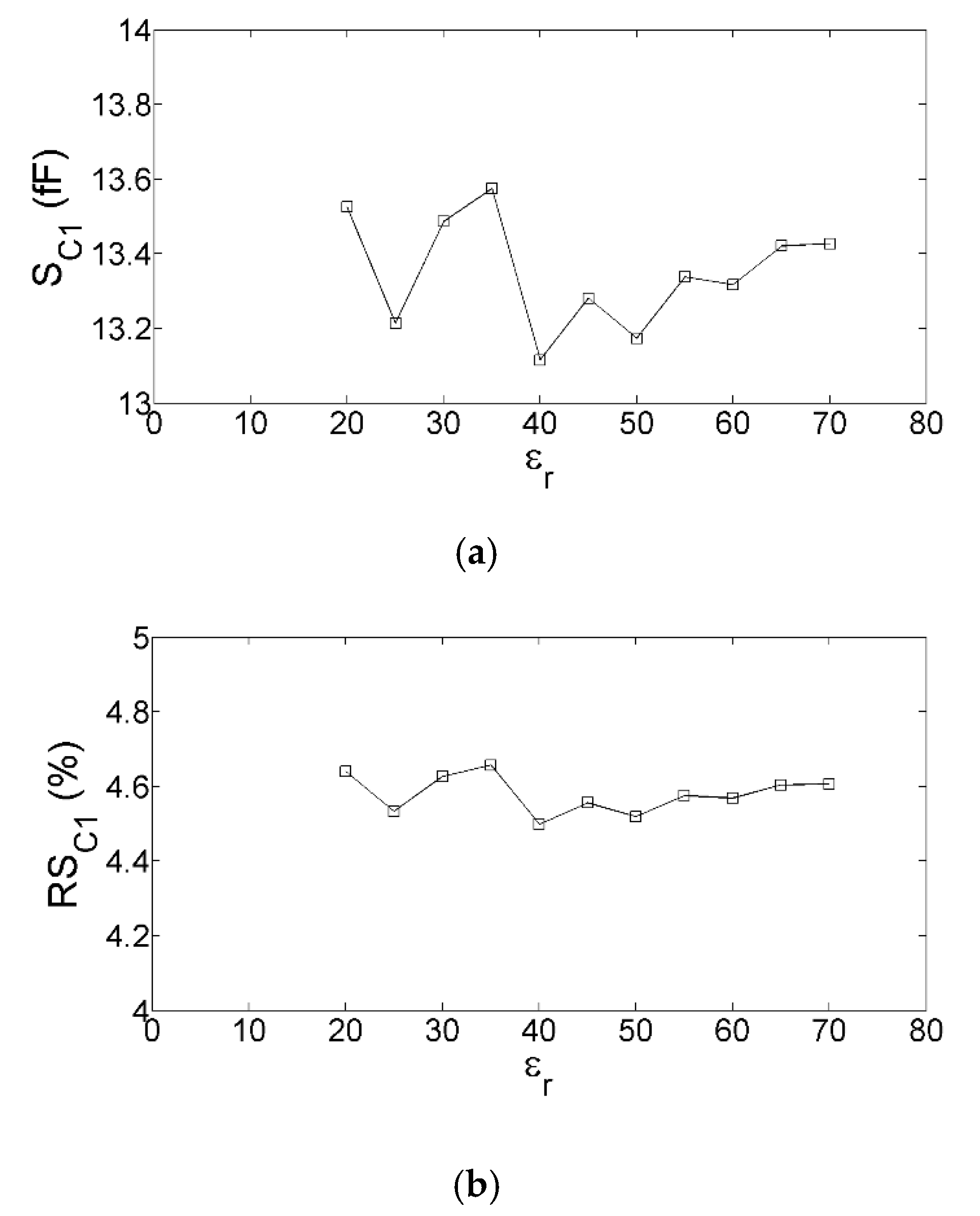
3. Equivalent-Circuit-Based Modeling and Sensitivity-Based Analysis
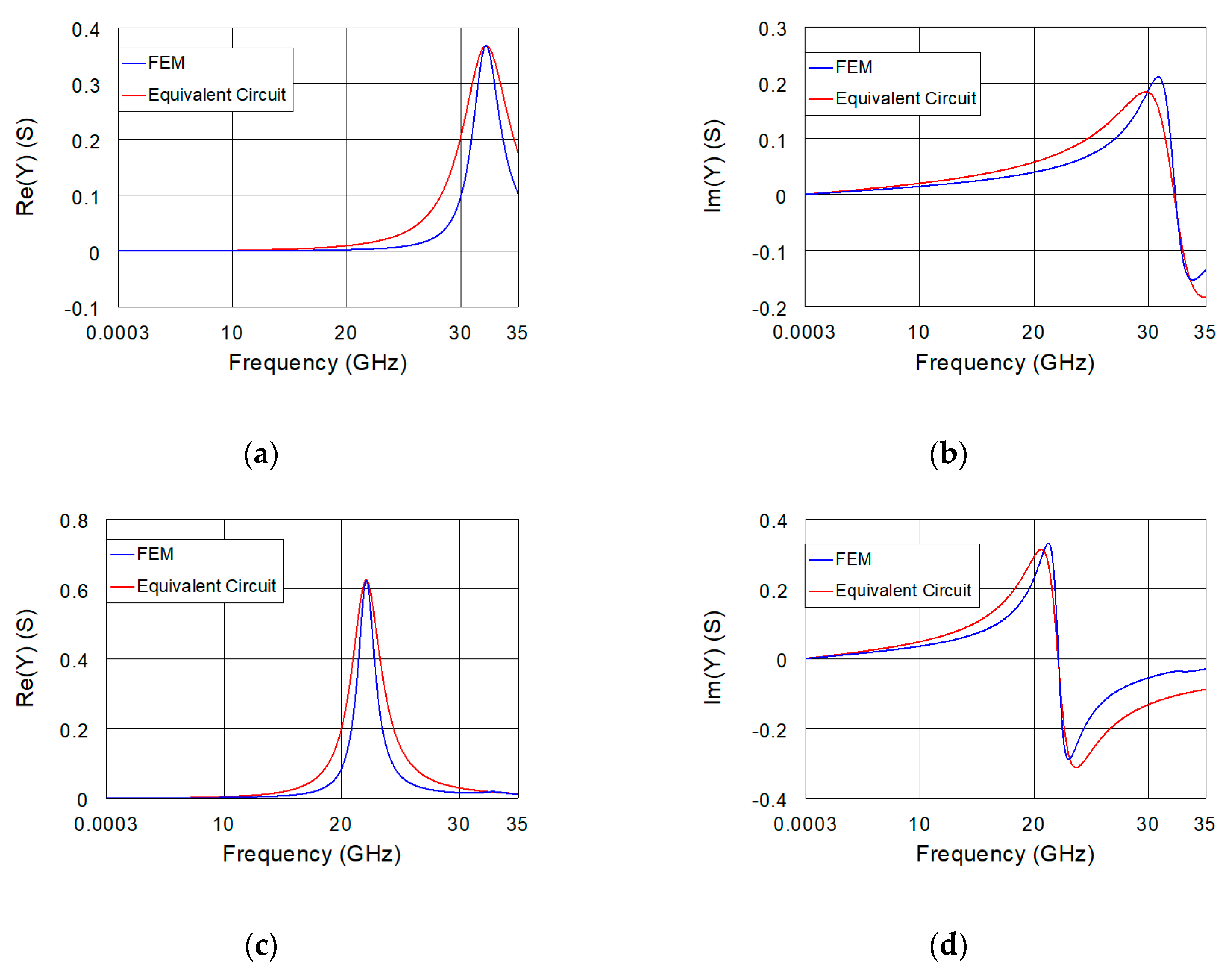
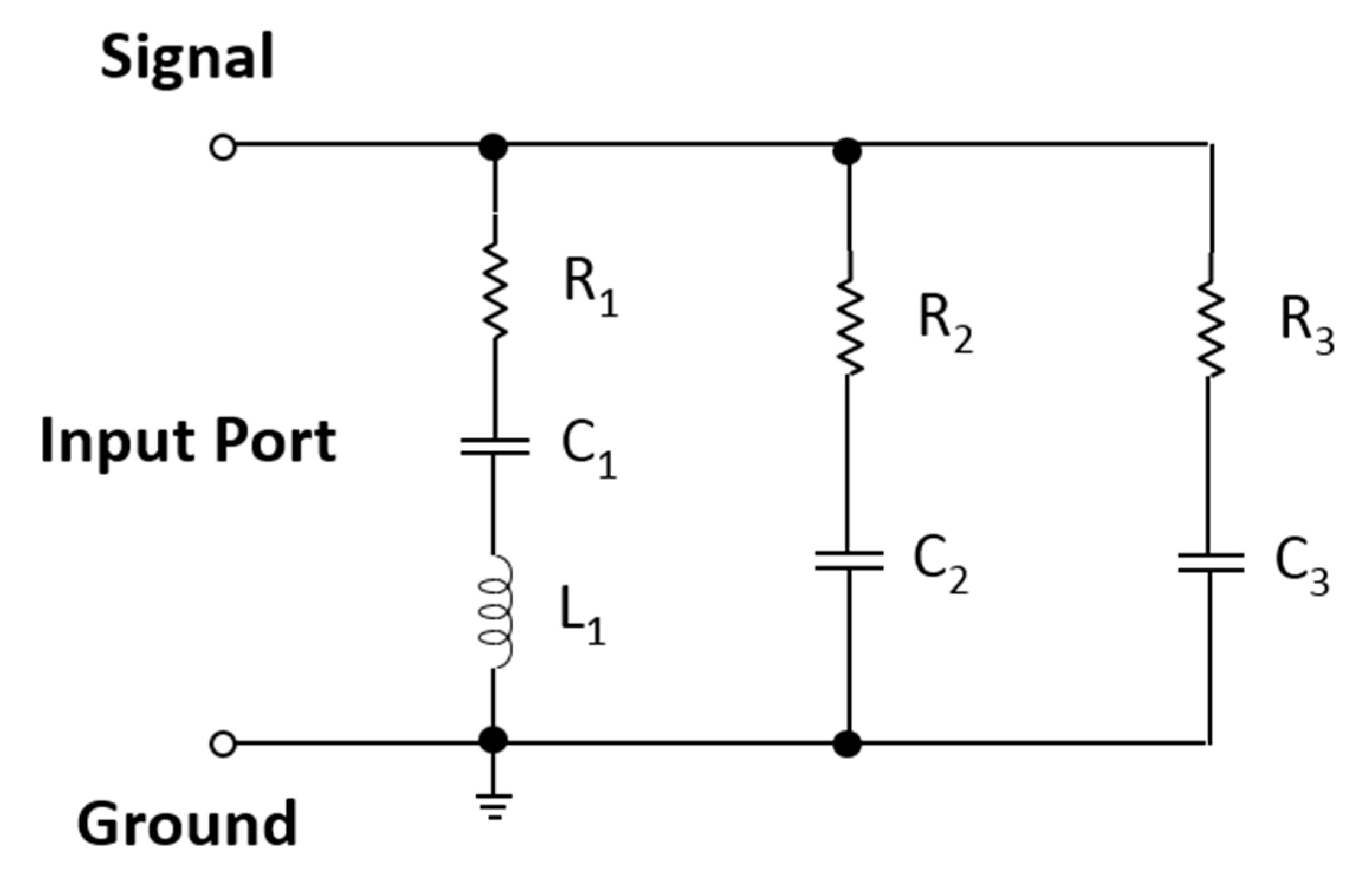
4. Modified Version of the Equivalent Circuit
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Piccolino, M. Luigi Galvani and animal electricity: Two centuries after the foundation of electrophysiology. Trends Neurosci. 1997, 20, 443–448. [Google Scholar] [CrossRef]
- Li, C.; Peng, Z.; Huang, T.-Y.; Fan, T.; Wang, F.-K.; Horng, T.-S.; Muñoz-Ferreras, J.-M.; Gómez-García, R.; Ran, L.; Lin, J. A review on recent progress of portable short-range noncontact microwave radar systems. IEEE Trans. Microw. Theory Tech. 2017, 65, 1692–1706. [Google Scholar] [CrossRef]
- Mercuri, M.; Soh, P.J.; Pandey, G.; Karsmakers, P.; Vandenbosch, G.A.E.; Leroux, P.; Schreurs, D.M.M.-P. Analysis of an indoor biomedical radar-based system for health monitoring. IEEE Trans. Microw. Theory Tech. 2013, 61, 2061–2068. [Google Scholar] [CrossRef] [Green Version]
- Garripoli, C.; Mercuri, M.; Karsmakers, P.; Soh, P.J.; Crupi, G.; Vandenbosch, G.A.E.; Pace, C.; Leroux, P.; Schreurs, D.M.M.-P. Embedded DSP-based telehealth radar system for remote in-door fall detection. IEEE J. Biomed. Health Inf. 2015, 19, 92–101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Álvarez López, Y.; García Fernández, M.; Grau, R.; Las-Heras, F. A synthetic aperture radar (SAR)-based technique for microwave imaging and material characterization. Electronics 2018, 7, 373. [Google Scholar] [CrossRef] [Green Version]
- Mercuri, M.; Lorato, I.R.; Liu, Y.H.; Wieringa, F.; Van Hoof, C.; Torfs, T. Vital-sign monitoring and spatial tracking of multiple people using a contactless radar-based sensor. Nat. Electron. 2019, 2, 252–262. [Google Scholar] [CrossRef]
- Whitesides, G.M. The origins and the future of microfluidics. Nature 2006, 442, 368–373. [Google Scholar] [CrossRef]
- Chretiennot, T.; Dubuc, D.; Grenier, K. A microwave and microfluidic planar resonator for efficient and accurate complex permittivity characterization of aqueous solutions. IEEE Trans. Microw. Theory Tech. 2013, 61, 972–978. [Google Scholar] [CrossRef] [Green Version]
- Abduljabar, A.A.; Clark, N.; Lees, J.; Porch, A. Dual mode microwave microfluidic sensor for temperature variant liquid characterization. IEEE Trans. Microw. Theory Tech. 2017, 65, 2572–2582. [Google Scholar] [CrossRef] [Green Version]
- Bao, X.; Liu, S.; Ocket, I.; Bao, J.; Schreurs, D.M.M.-P.; Zhang, S.; Cheng, C.; Feng, K.; Nauwelaers, B. A general line-line method for dielectric material characterization using conductors with the same cross-sectional geometry. IEEE Microw. Wirel. Compon. Lett. 2018, 28, 356–358. [Google Scholar] [CrossRef]
- Mohd Bahar, A.A.; Zakaria, Z.; Md Arshad, M.K.; Alahnomi, R.A.; Abu-Khadrah, A.I.; Sam, W.Y. Microfluidic biochemical sensor based on circular SIW-DMS approach for dielectric characterization application. Int. J. RF Microw. Comput.-Aided Eng. 2019, 29, e21801. [Google Scholar] [CrossRef]
- Markovic, T.; Bao, J.; Maenhout, G.; Ocket, I.; Nauwelaers, B. An interdigital capacitor for microwave heating at 25 GHz and wideband dielectric sensing of nL volumes in continuous microfluidics. Sensors 2019, 19, 715. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, L.W.; Kandwal, A.; Cheng, Q.; Shi, H.; Tobore, I.; Nie, Z. Non-invasive blood glucose monitoring using a curved Goubau line. Electronics 2019, 8, 662. [Google Scholar] [CrossRef] [Green Version]
- Yeo, J.; Lee, J.-I. High-sensitivity microwave sensor based on an interdigital-capacitor-shaped defected ground structure for permittivity characterization. Sensors 2019, 19, 498. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kremer, F. Dielectric spectroscopy–Yesterday, today and tomorrow. J. Non-Cryst. Solids 2002, 305, 1–9. [Google Scholar] [CrossRef]
- Gabriel, C.; Gabriel, S.; Corthout, E. The dielectric properties of biological tissues: I. Literature survey. Phys. Med. Biol. 1996, 41, 22–31. [Google Scholar] [CrossRef] [Green Version]
- Facer, G.R.; Notterman, D.A.; Sohn, L.L. Dielectric spectroscopy for bioanalysis: From 40 Hz to 26.5 GHz in a microfabricated wave guide. Appl. Phys. Lett. 2001, 78, 996–998. [Google Scholar] [CrossRef]
- Yokoyama, K.; Kamei, T.; Minami, H.; Suzuki, M. Hydration study of globular proteins by microwave dielectric spectroscopy. J. Phys. Chem. B 2001, 105, 12622–12627. [Google Scholar] [CrossRef]
- Asami, K. Characterization of biological cells by dielectric spectroscopy. J. Non-Cryst. Solids 2002, 305, 268–277. [Google Scholar] [CrossRef]
- Nikolova, N.K. Microwave imaging for breast cancer. IEEE Microw. Mag. 2011, 12, 78–94. [Google Scholar] [CrossRef]
- Bellizzi, G.G.; Crocco, L.; Battaglia, G.M.; Isernia, T. Multi-frequency constrained SAR focusing for patient specific hyperthermia treatment. IEEE J. Electromagn. RfMicrow. Med. Biol. 2017, 1, 74–80. [Google Scholar] [CrossRef]
- Artis, F.; Chen, T.; Chretiennot, T.; Fournie, J.-J.; Poupot, M.; Dubuc, D.; Grenier, K. Microwaving biological cells: Intracellular analysis with microwave dielectric spectroscopy. Ieee Microw. Mag. 2015, 16, 87–96. [Google Scholar] [CrossRef]
- Daw, R.; Finkelstein, J. Lab on a chip. Nature 2006, 442, 367. [Google Scholar] [CrossRef] [Green Version]
- Abgrall, P.; Gue, A. Lab-on-chip technologies: Making a microfluidic network and coupling it into a complete microsystem-A review. J. Micromech. Microeng. 2007, 17, R15–R49. [Google Scholar] [CrossRef]
- Grenier, K.; Dubuc, D.; Poleni, P.-E.; Kumemura, M.; Toshiyoshi, H.; Fujii, T.; Fujita, H. Integrated broadband microwave and microfluidic sensor dedicated to bioengineering. IEEE Trans. Microw. Theory Tech. 2009, 57, 3246–3253. [Google Scholar] [CrossRef]
- Grenier, K.; Dubuc, D.; Chen, T.; Artis, F.; Chretiennot, T.; Poupot, M.; Fournie, J.J. Recent advances in microwave-based dielectric spectroscopy at the cellular level for cancer investigations. IEEE Trans. Microw. Theory Tech. 2013, 61, 2023–2030. [Google Scholar] [CrossRef] [Green Version]
- Meyne née Haase, N.; Fuge, G.; Trieu, H.K.; Zeng, A.-P.; Jacob, A.F. Miniaturized transmission-line sensor for broadband dielectric characterization of biological liquids and cell suspensions. IEEE Trans. Microw. Theory Tech. 2015, 63, 3026–3033. [Google Scholar] [CrossRef]
- Bao, X.; Ocket, I.; Bao, J.; Doijen, J.; Zheng, J.; Kil, D.; Liu, Z.; Puers, B.; Schreurs, D.M.M.-P.; Nauwelaers, B. Broadband dielectric spectroscopy of cell cultures. IEEE Trans. Microw. Theory Tech. 2018, 66, 5750–5759. [Google Scholar] [CrossRef]
- Bao, X.; Liu, S.; Ocket, I.; Liu, Z.; Schreurs, D.M.M.-P.; Nauwelaers, B. A modeling procedure of the broadband dielectric spectroscopy for ionic liquids. IEEE Trans. Nanobiosci. 2018, 17, 387–393. [Google Scholar] [CrossRef]
- Bao, X.; Ocket, I.; Bao, J.; Liu, Z.; Puers, B.; Schreurs, D.M.M.-P.; Nauwelaers, B. Modeling of coplanar interdigital capacitor for microwave microfluidic application. IEEE Trans. Microw. Theory Tech. 2019, 67, 2674–2683. [Google Scholar] [CrossRef]
- Kilpijärvi, J.; Halonen, N.; Juuti, J.; Hannu, J. Microfluidic microwave sensor for detecting saline in biological range. Sensors 2019, 19, 819. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mehrotra, P.; Chatterjee, B.; Sen, S. EM-Wave Biosensors: A review of RF, microwave, mm-wave and optical sensing. Sensors 2019, 19, 1013. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Starzyk, F. Parametrisation of interdigit comb capacitor for dielectric impedance spectroscopy. Arch. Mater. Sci. Eng. 2008, 34, 31–34. [Google Scholar]
- Chen, T.; Dubuc, D.; Poupot, P.; Fournié, J.-J.; Grenier, K. Accurate nanoliter liquid characterization up to 40 GHz for biomedical applications: Toward non-invasive living cells monitoring. IEEE Trans. Microw. Theory Tech. 2012, 60, 4171–4177. [Google Scholar] [CrossRef]
- Su, W.; Cook, B.S.; Tentzeris, M.M. Additively manufactured microfluidics-based ‘peel-and-replace’ RF sensors for wearable applications. IEEE Trans. Microw. Theory Tech. 2016, 64, 1928–1936. [Google Scholar] [CrossRef]
- Ruvio, G.; Vaselli, M.; Lopresto, V.; Pinto, R.; Farina, L.; Cavagnaro, M. Comparison of different methods for dielectric properties measurements in liquid sample media. Int. J. RF Microw. Comput.-Aided Eng. 2018, 28, e21215. [Google Scholar] [CrossRef]
- Bao, X.; Ocket, I.; Crupi, G.; Schreurs, D.M.M.-P.; Bao, J.; Kil, D.; Puers, B.; Nauwelaers, B. A planar one-port microwave microfluidic sensor for microliter liquids characterization. IEEE J. Electromagn. RF Microw. Med. Biol. 2018, 2, 10–17. [Google Scholar] [CrossRef]
- Vélez, P.; Muñoz-Enano, J.; Gil, M.; Mata-Contreras, J.; Martín, F. Differential microfluidic sensors based on dumbbell-shaped defect ground structures in microstrip technology: Analysis, optimization, and applications. Sensors 2019, 19, 3189. [Google Scholar] [CrossRef] [Green Version]
- Crupi, G.; Bao, X.; Barmuta, P.; Ocket, I.; Schreurs, D.M.M.-P.; Nauwelaers, B. Microfluidic biosensor for bioengineering: High-frequency equivalent-circuit modeling of interdigital capacitor. In Proceedings of the IEEE International Conference on Telecommunications in Modern Satellite, Cable and Broadcasting Service (TELSIKS), Nis, Serbia, 23–35 October 2019; pp. 315–318. [Google Scholar]
- Stojanović, G.; Paroški, M.; Samardžić, N.; Radovanović, M.; Krstić, D. Microfluidics-based four fundamental electronic circuit elements resistor, inductor, capacitor and memristor. Electronics 2019, 8, 960. [Google Scholar] [CrossRef] [Green Version]
- Booth, J.C.; Orloff, N.D.; Mateu, J.; Janezic, M.; Rinehart, M.; Beall, J.A. Quantitative permittivity measurements of nanoliter liquid volumes in microfluidic channels to 40 GHz. IEEE Trans. Instrum. Meas. 2010, 59, 3279–3288. [Google Scholar] [CrossRef]
- Alley, G. Interdigital capacitors and their application to lumped-element microwave-integrated circuits. IEEE Trans. Microw. Theory Tech. 1970, 18, 1028–1033. [Google Scholar] [CrossRef]
- Van Gerwen, P.; Laureyn, W.; Laureys, W.; Huyberechts, G.; De Beeck, M.O.; Baert, K.; Suls, J.; Sansen, W.; Jacobs, P.; Hermans, L.; et al. Nanoscaled interdigitated electrode arrays for biochemical sensors. Sens. Actuators B Chem. 1998, 49, 73–80. [Google Scholar] [CrossRef]
- Laureyn, W.; Van Gerwen, P.; Suls, J.; Jacobs, P.; Maes, G. Characterization of nanoscaled interdigitated palladium electrodes of various dimensions in KCl solutions. Electroanalysis 2001, 13, 204–211. [Google Scholar] [CrossRef]
- Zhang, L.Y.; Landoulsi, A.; Bounaix, C.; du Punch, M.; Lacroix, A.; Dalmay, C.; Bessaudou, A.; Lautret, C.; Battu, S.; Lalloue, F.; et al. Label-free colorectal cancer cell line bio-sensing using RF resonator. In Proceedings of the IEEE International Conference on Solid-State Sensors, Actuators and Microsystems, Barcelona, Spain, 16–20 June 2013; pp. 1194–1197. [Google Scholar]
- Bao, X.; Ocket, I.; Bao, J.; Kil, D.; Brancato, L.; Nauwelaers, B. Broadband dielectric spectroscopy measurements of liquids combining interdigital capacitor and coplanar waveguide. In Proceedings of the European Microwave Conference (EuMC), Nuremberg, Germany, 10–12 October 2017; pp. 946–949. [Google Scholar]
- Booth, J.C.; Mateu, J.; Janezic, M.; Baker-Jarvis, J.; Beall, J.A. Broadband permittivity measurements of liquid and biological samples using microfluidic channels. In Proceedings of the IEEE MTT-S International Microwave Symposium Digest, San Francisco, CA, USA, 11–16 June 2006; pp. 1750–1753. [Google Scholar]
- Ou, J.; Glawdel, T.; Ren, C.L.; Pawliszyn, J. Fabrication of a hybrid PDMS/SU-8/quartz microfluidic chip for enhancing UV absorption whole-channel imaging detection sensitivity and application for isoelectric focusing of proteins. Lab Chip 2009, 9, 1926–1932. [Google Scholar] [CrossRef]
- Nihad, D.; Jehad, A.; Amjad, O. CAD modeling of coplanar waveguide interdigital capacitor. Int. J. RF Microw. Comput.-Aided Eng. 2005, 15, 551–558. [Google Scholar]
- Rohdin, H.; Lee, G.S. Interfacial gate resistance in schottky-barrier-gate field-effect transistors. IEEE Trans. Electron Dev. 1998, 45, 2407–2416. [Google Scholar] [CrossRef] [Green Version]
- Crupi, G.; Raffo, A.; Vadalà, V.; Avolio, G.; Schreurs, D.M.M.-P.; Vannini, G.; Caddemi, A. Technology-independent analysis of the double current-gain peak in millimeter-wave FETs. IEEE Microw. Wirel. Comp. Lett. 2018, 28, 326–328. [Google Scholar] [CrossRef]
- Crupi, G.; Raffo, A.; Vadalà, V.; Vannini, G.; Caddemi, A. A new study on the temperature and bias dependence of the kink effects in S22 and h21 for the GaN HEMT technology. Electronics 2018, 7, 353. [Google Scholar] [CrossRef] [Green Version]









| Reference | Channel-Electrode-Substrate Materials | Number of Ports | Volume | Analysis Method | Frequency Range | MUT |
|---|---|---|---|---|---|---|
| [34] | PDMS- Ti/Au- Quartz | 2 | 0.9 nL | FEM, EC parameters, and measurements | 40 MHz–40 GHz | Alcohol-based aqueous solutions and fetal bovine serum in water |
| [47] | PDMS- Au- Quartz | 2 | <1 μL | FEM, EC parameters, and measurements | 100 Hz–40 GHz | De-ionized water and methanol |
| [12] | PDMS- Au- Quartz | 1 | 1.2 nL | FEM and measurements | 7.8 GHz–8.4 GHz & @25 GHz | Water-isopropanol mixture |
| [46] | SU-8- Au- Quartz | 2 | 0.1 μL | FEM, EC parameters, and measurements | 10 MHz–50 GHz | De-ionized water and saline solutions |
| [28] | SU-8- Au- Quartz | 1 | 0.09 μL | FEM, EC parameters, and measurements | 300 kHz–50GHz | Yeast cell culture and mammalian cell culture |
| [Here] | SU-8- Au- Quartz | 1 | 0.054 μL | FEM and EC parameters | 0.3 MHz–35 GHz | Lossless MUTs with different εr |
| εr | fr (GHz) | Re(Y) @ fr (S) | C1 (fF) | R1 (Ω) |
|---|---|---|---|---|
| 15 | 32.20 | 0.368 | 291.5 | 2.72 |
| 20 | 29.01 | 0.442 | 359.1 | 2.26 |
| 25 | 26.71 | 0.505 | 423.6 | 1.98 |
| 30 | 24.74 | 0.551 | 493.8 | 1.81 |
| 35 | 23.17 | 0.595 | 563.0 | 1.68 |
| 40 | 22.09 | 0.623 | 619.4 | 1.61 |
| 45 | 20.93 | 0.648 | 689.9 | 1.54 |
| 50 | 20.04 | 0.668 | 752.6 | 1.50 |
| 55 | 19.14 | 0.684 | 825.0 | 1.46 |
| 60 | 18.42 | 0.700 | 890.8 | 1.43 |
| 65 | 17.72 | 0.717 | 962.5 | 1.39 |
| 70 | 17.13 | 0.725 | 1030.0 | 1.38 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Crupi, G.; Bao, X.; Babarinde, O.J.; Schreurs, D.M.M.-P.; Nauwelaers, B. Biosensor Using a One-Port Interdigital Capacitor: A Resonance-Based Investigation of the Permittivity Sensitivity for Microfluidic Broadband Bioelectronics Applications. Electronics 2020, 9, 340. https://doi.org/10.3390/electronics9020340
Crupi G, Bao X, Babarinde OJ, Schreurs DMM-P, Nauwelaers B. Biosensor Using a One-Port Interdigital Capacitor: A Resonance-Based Investigation of the Permittivity Sensitivity for Microfluidic Broadband Bioelectronics Applications. Electronics. 2020; 9(2):340. https://doi.org/10.3390/electronics9020340
Chicago/Turabian StyleCrupi, Giovanni, Xiue Bao, Oluwatosin John Babarinde, Dominique M. M.-P. Schreurs, and Bart Nauwelaers. 2020. "Biosensor Using a One-Port Interdigital Capacitor: A Resonance-Based Investigation of the Permittivity Sensitivity for Microfluidic Broadband Bioelectronics Applications" Electronics 9, no. 2: 340. https://doi.org/10.3390/electronics9020340








